The Dynamic Compressive Properties and Energy Dissipation Law of Sandstone Subjected to Freeze–Thaw Damage
Abstract
:1. Introduction
2. Material Preparation and Testing Method
2.1. Sandstone Specimens
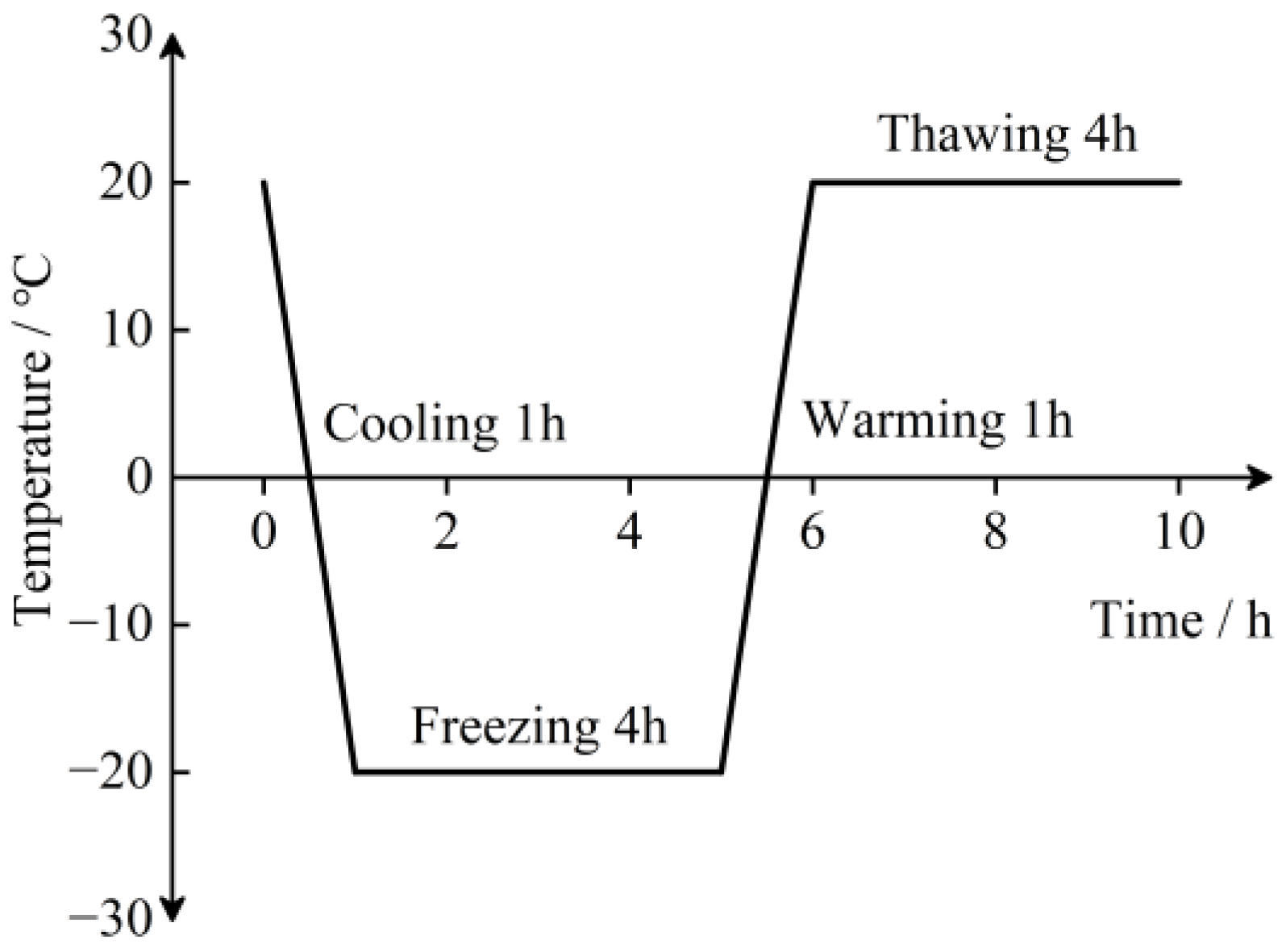
2.2. Testing Schemes of Freeze–Thaw Cycling
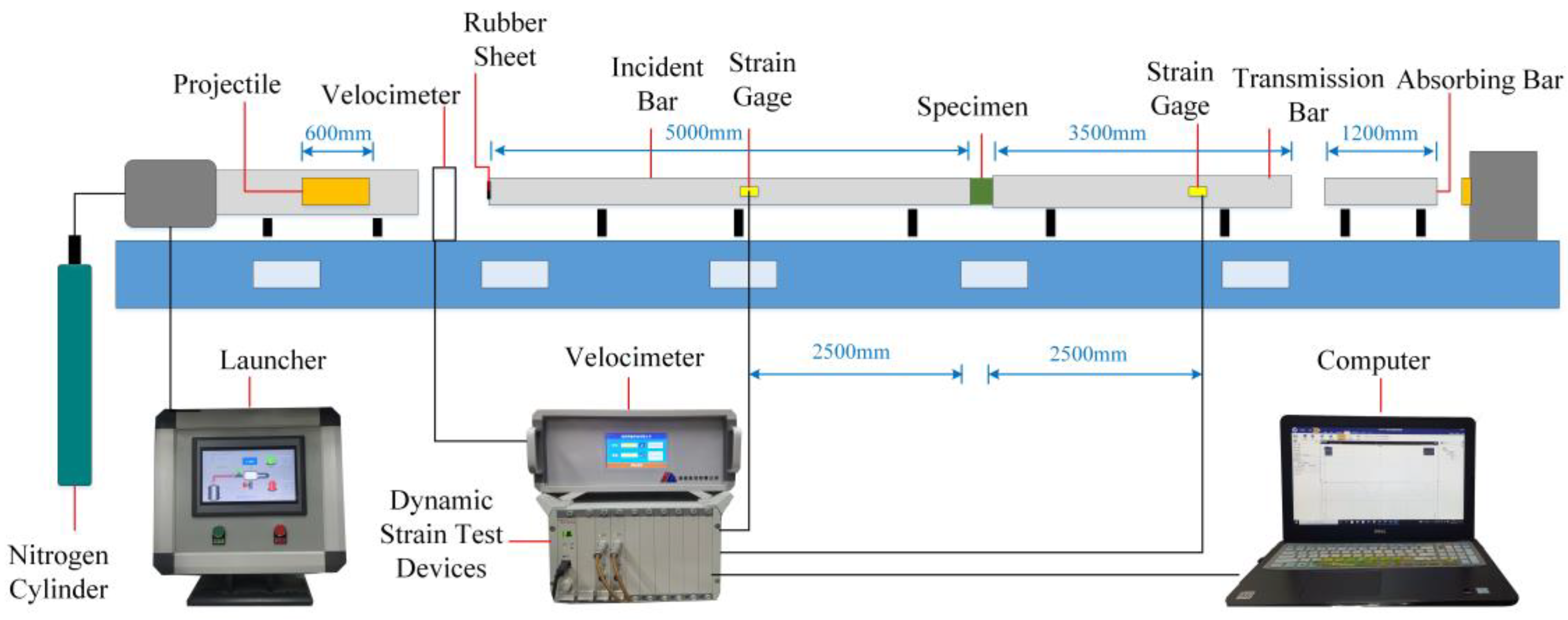
2.3. Static Loading and Impact Loading Testing Schemes
3. Results
3.1. Strength and Fracturing Characteristics of Freeze–Thawed Sandstone
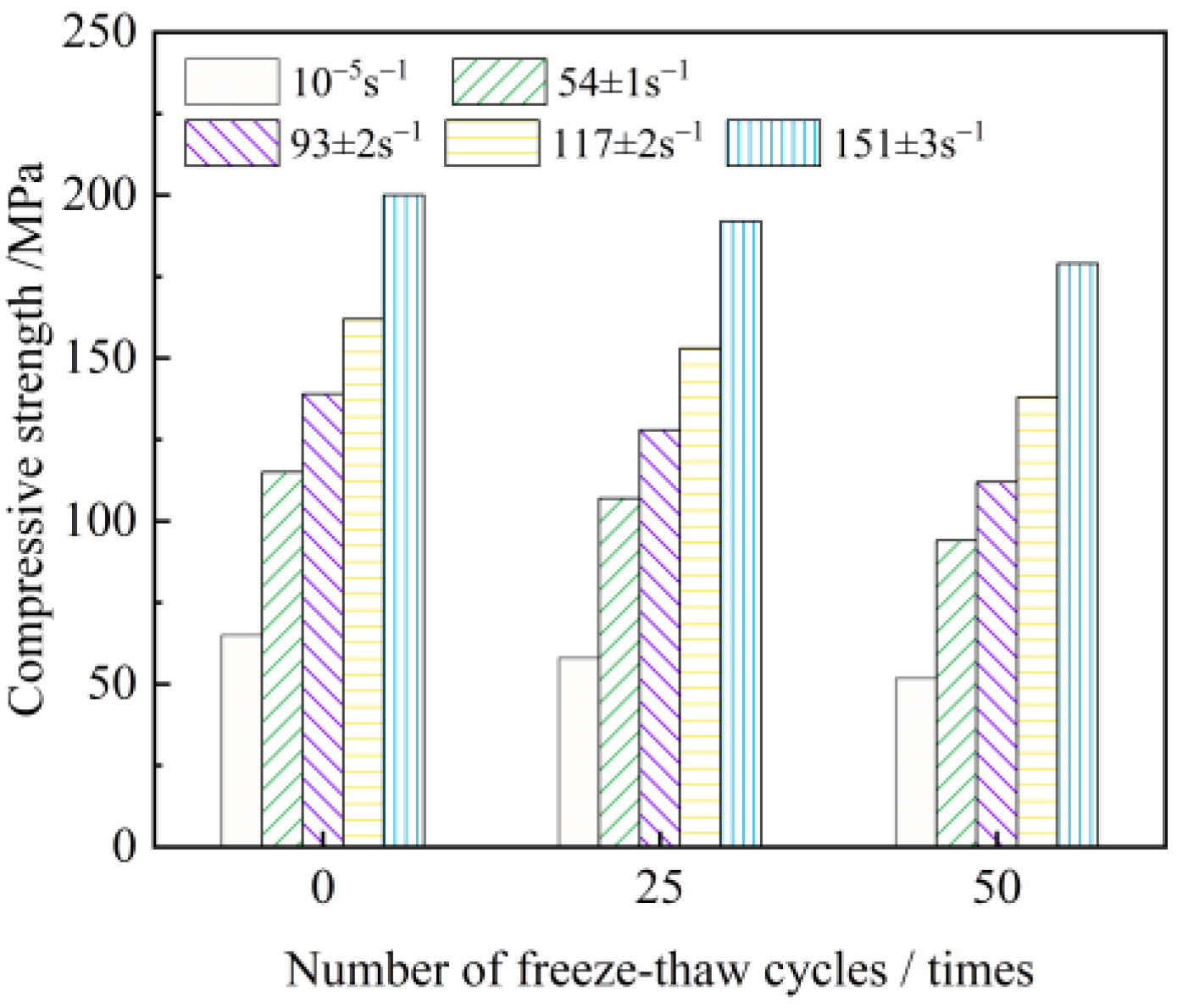
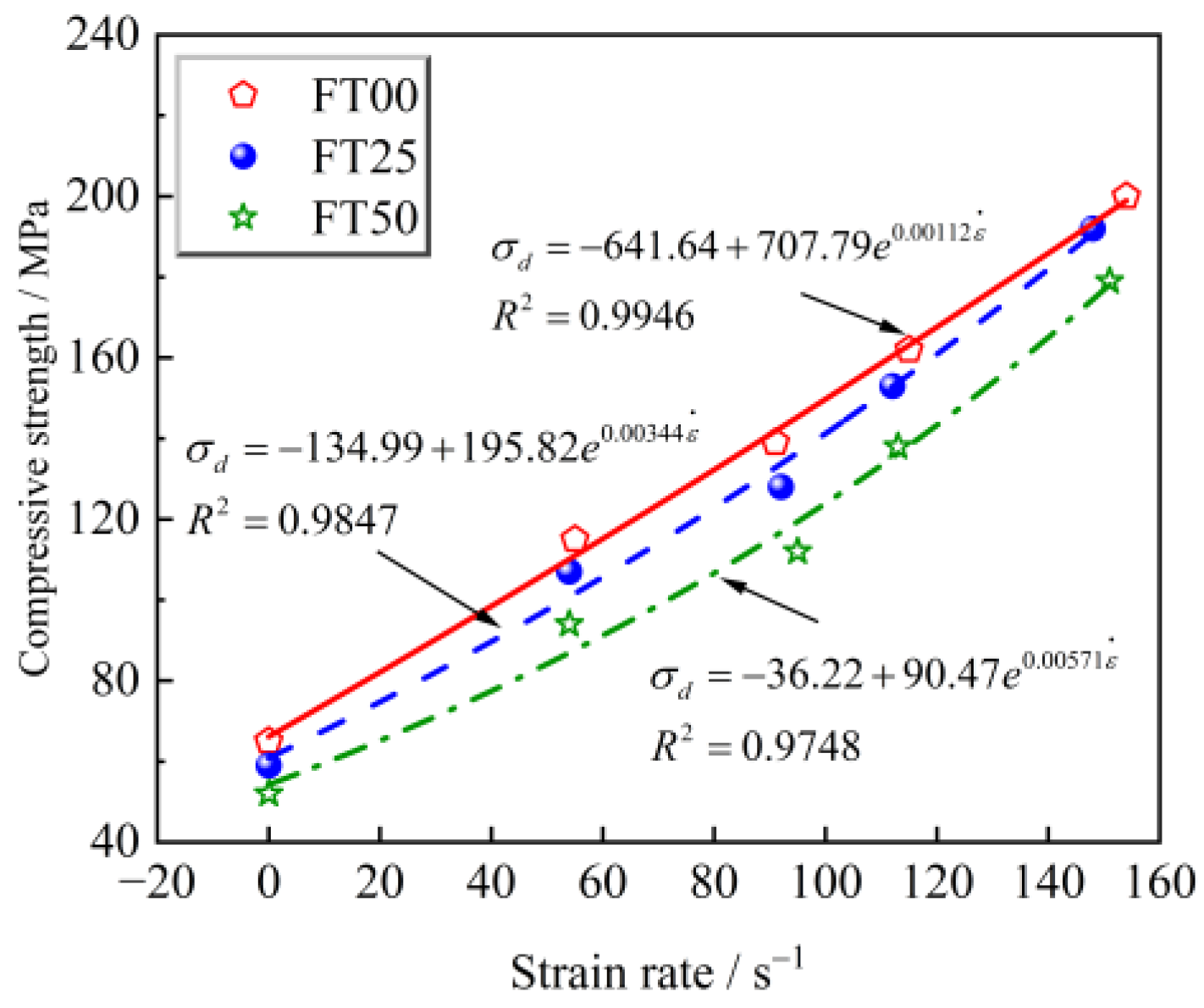
3.1.1. Strength Characteristics of Freeze–Thawed Sandstone
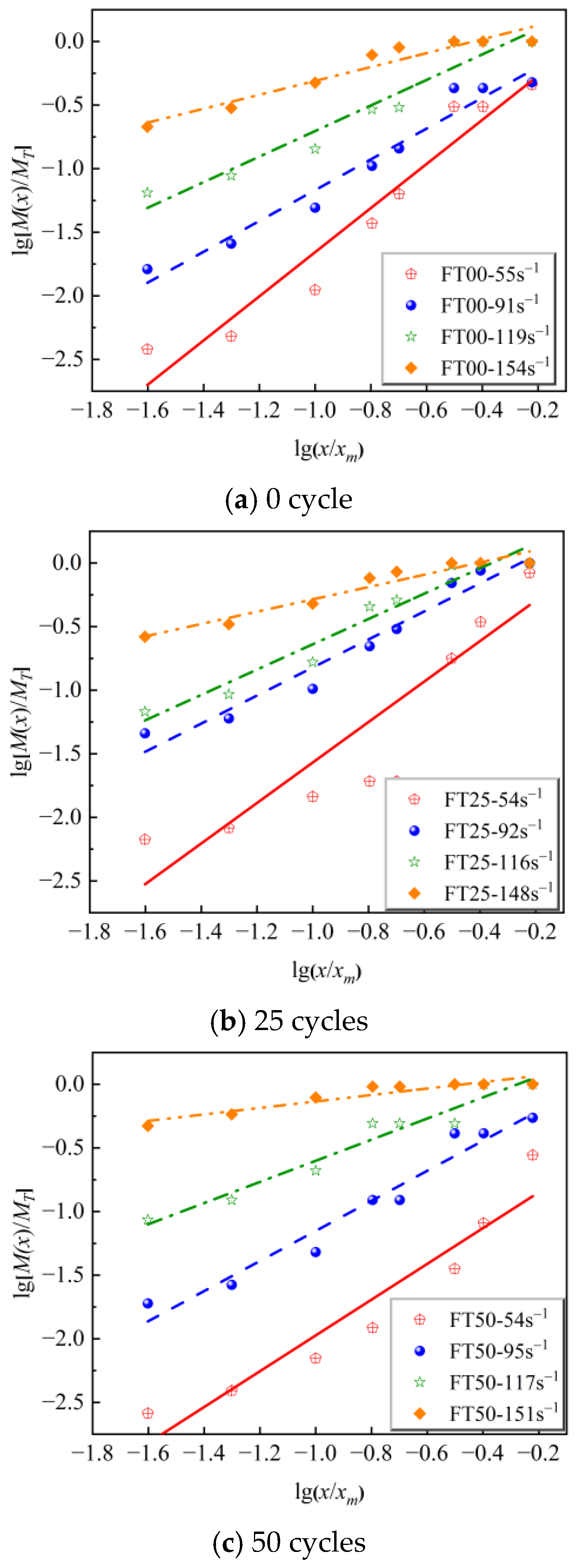
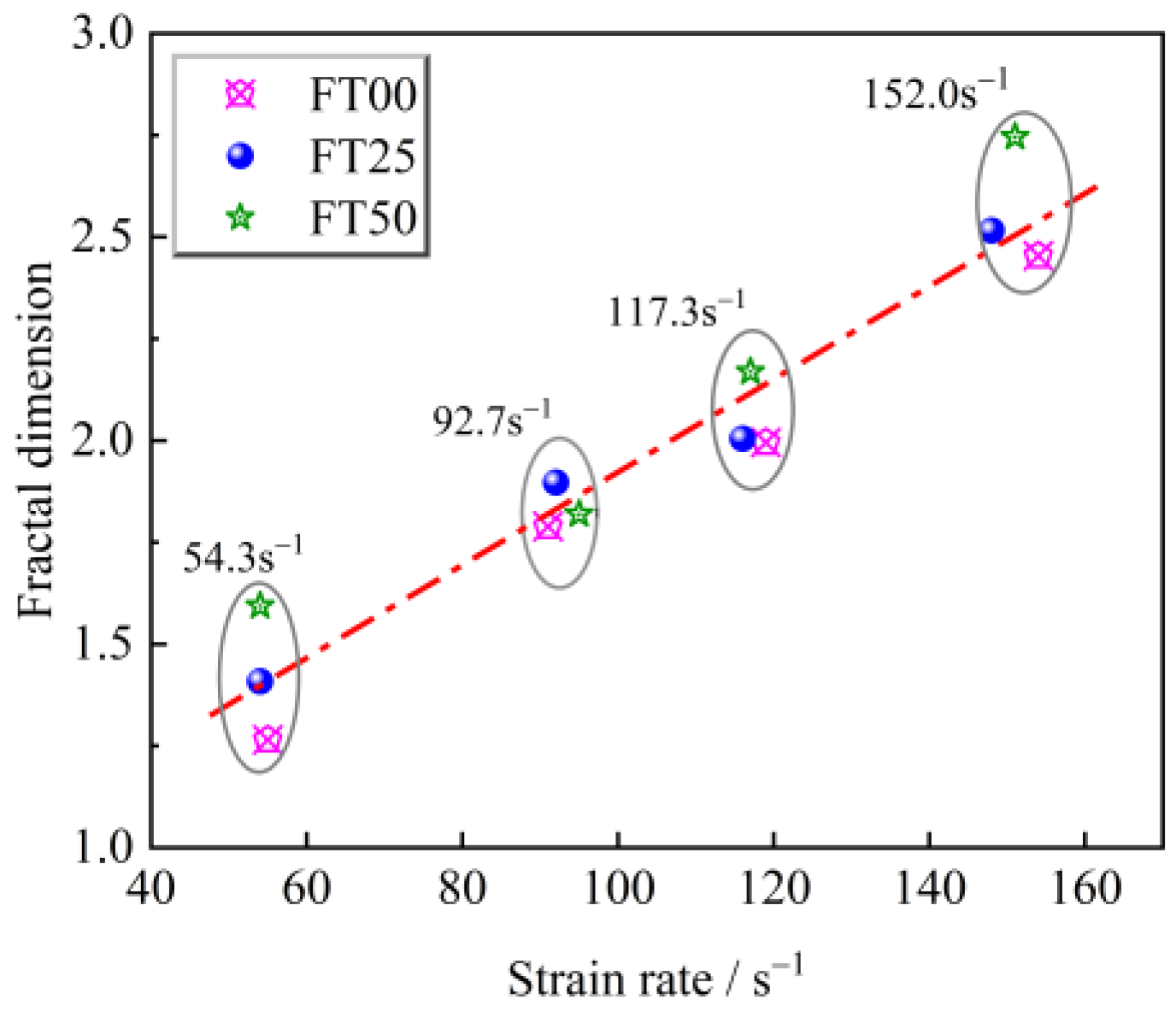
3.1.2. The Fractal Dimension Characteristics of Fractured Freeze–Thawed Sandstone under Impact Loading
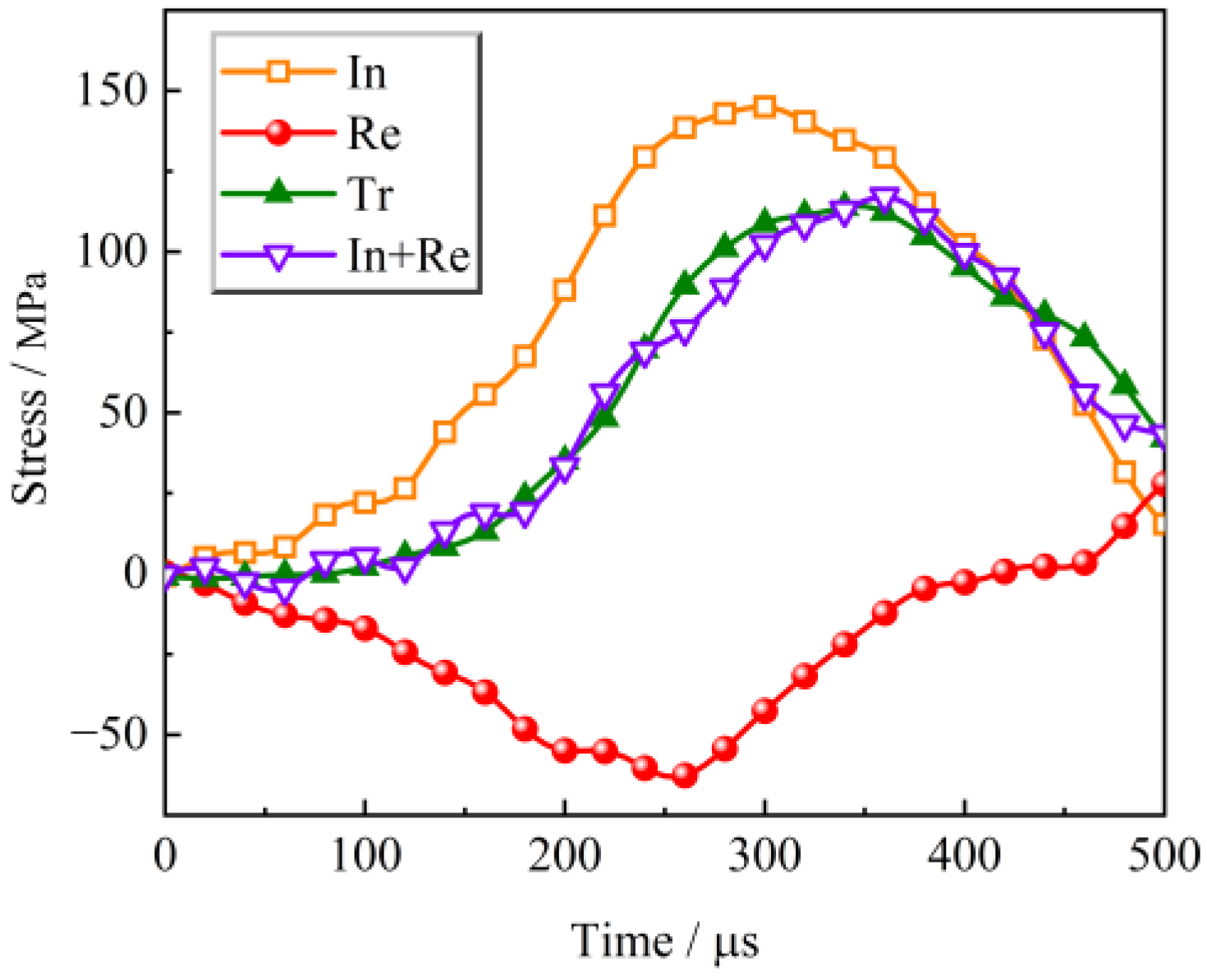
3.2. Law of Energy Dissipation of Freeze–Thawed Sandstone under Impact Loading
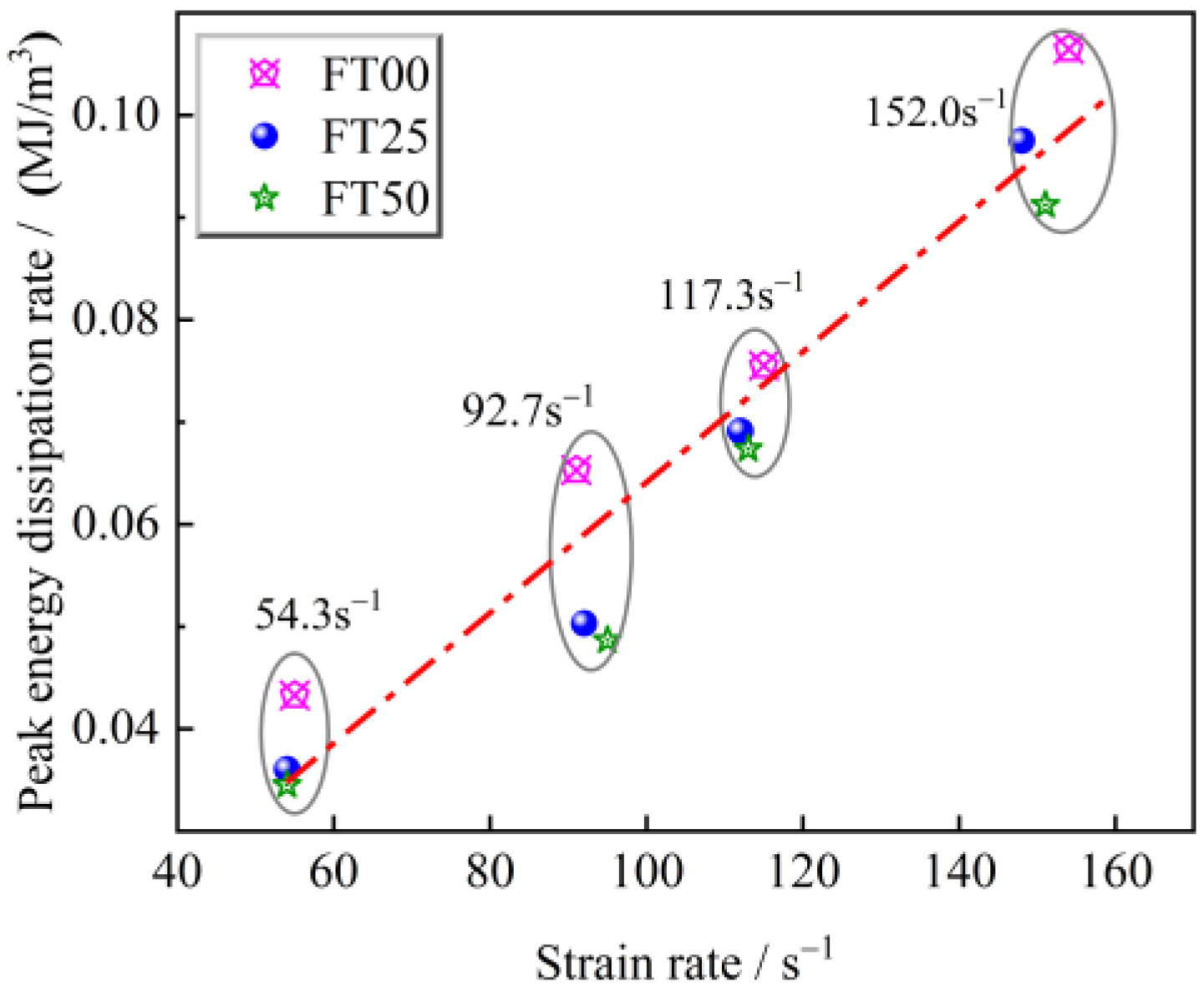
3.2.1. Change Law of Energy Dissipation Rate of Freeze–Thawed Sandstone under Different Strain Rates
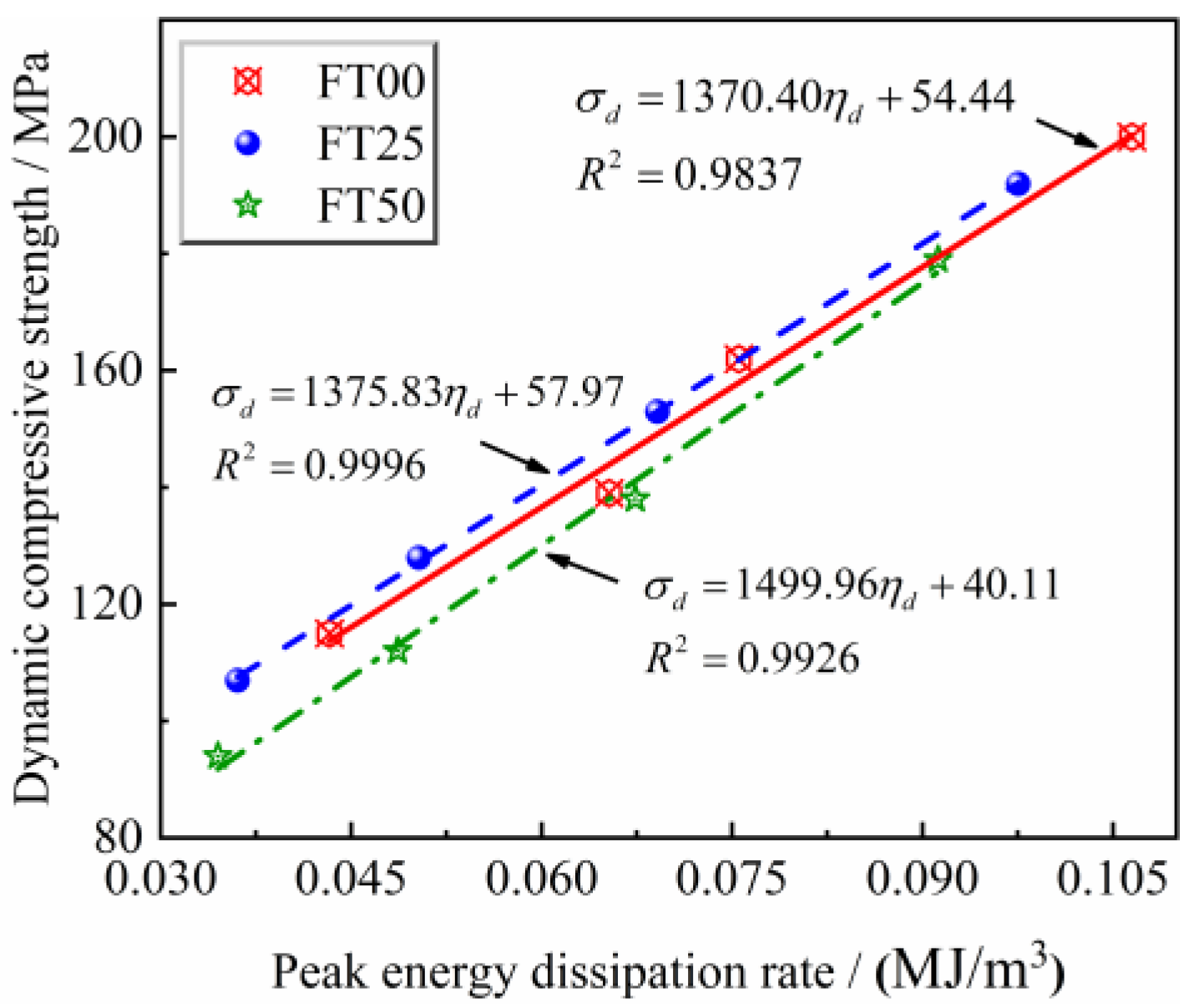
3.2.2. Relationship between Peak Strength and Peak Energy Dissipation Rate for Freeze–Thawed Sandstone
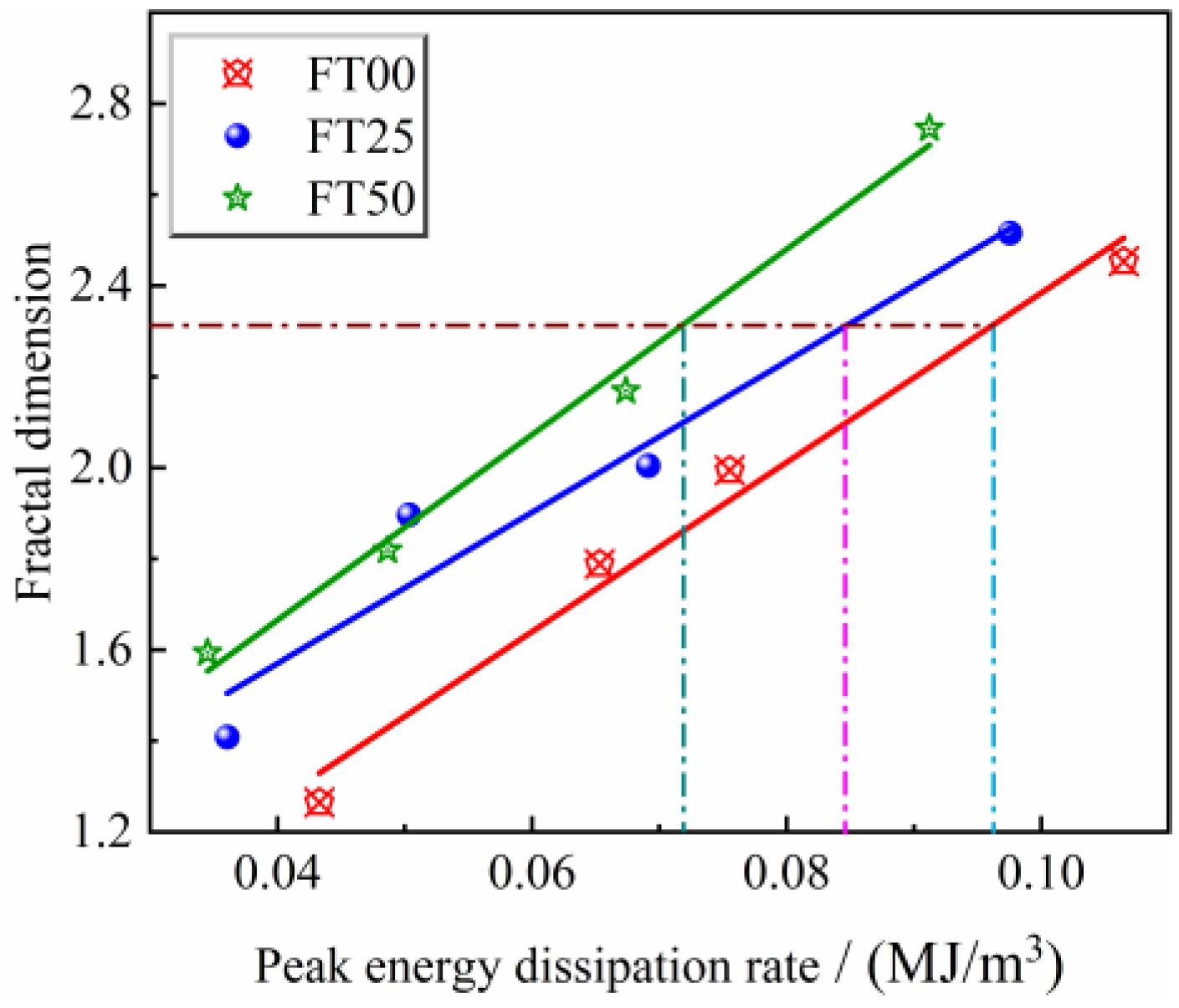
3.2.3. Relationship between Peak Energy Dissipation Rate and Fractal Dimension for Freeze–Thawed Sandstone
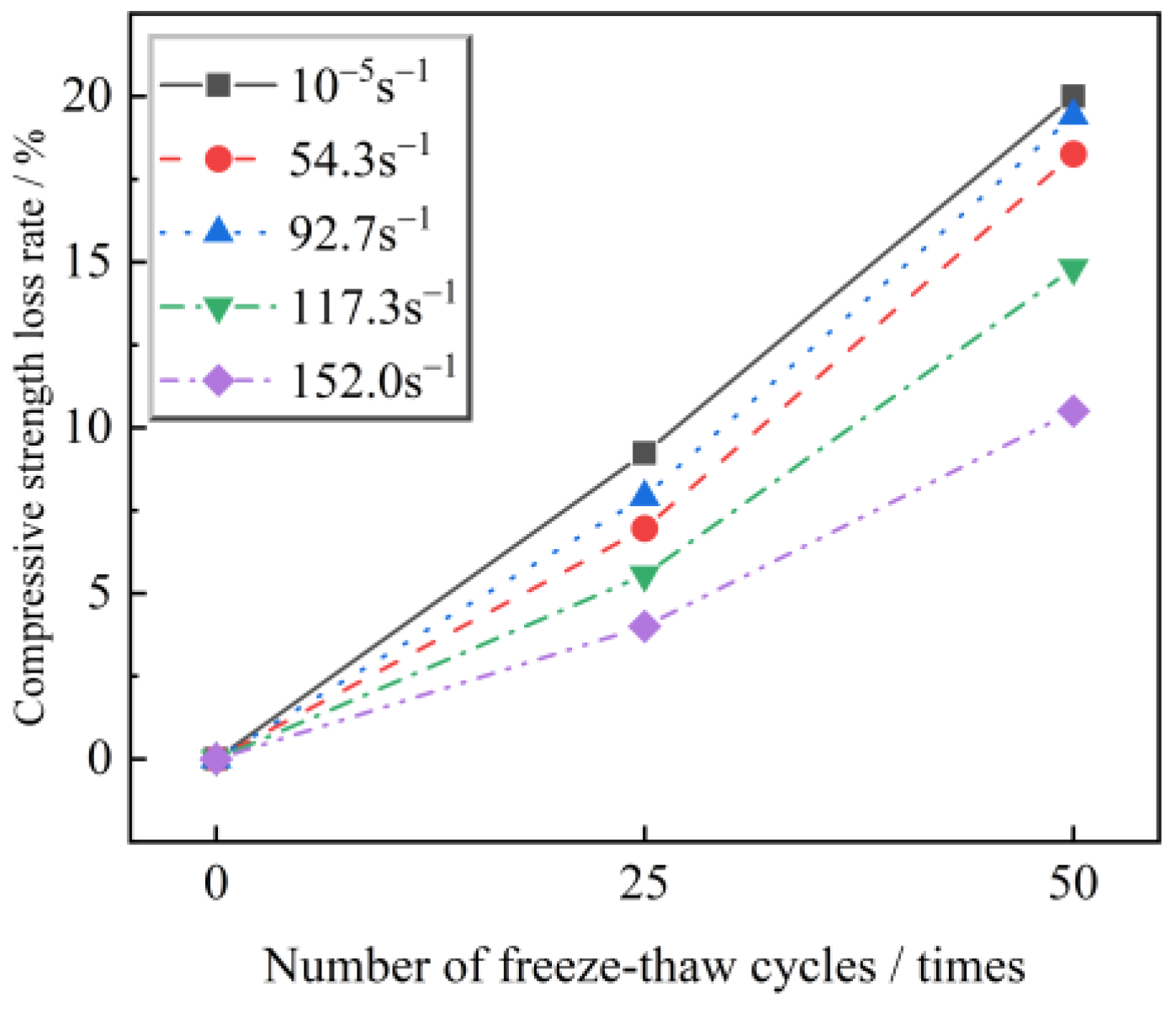
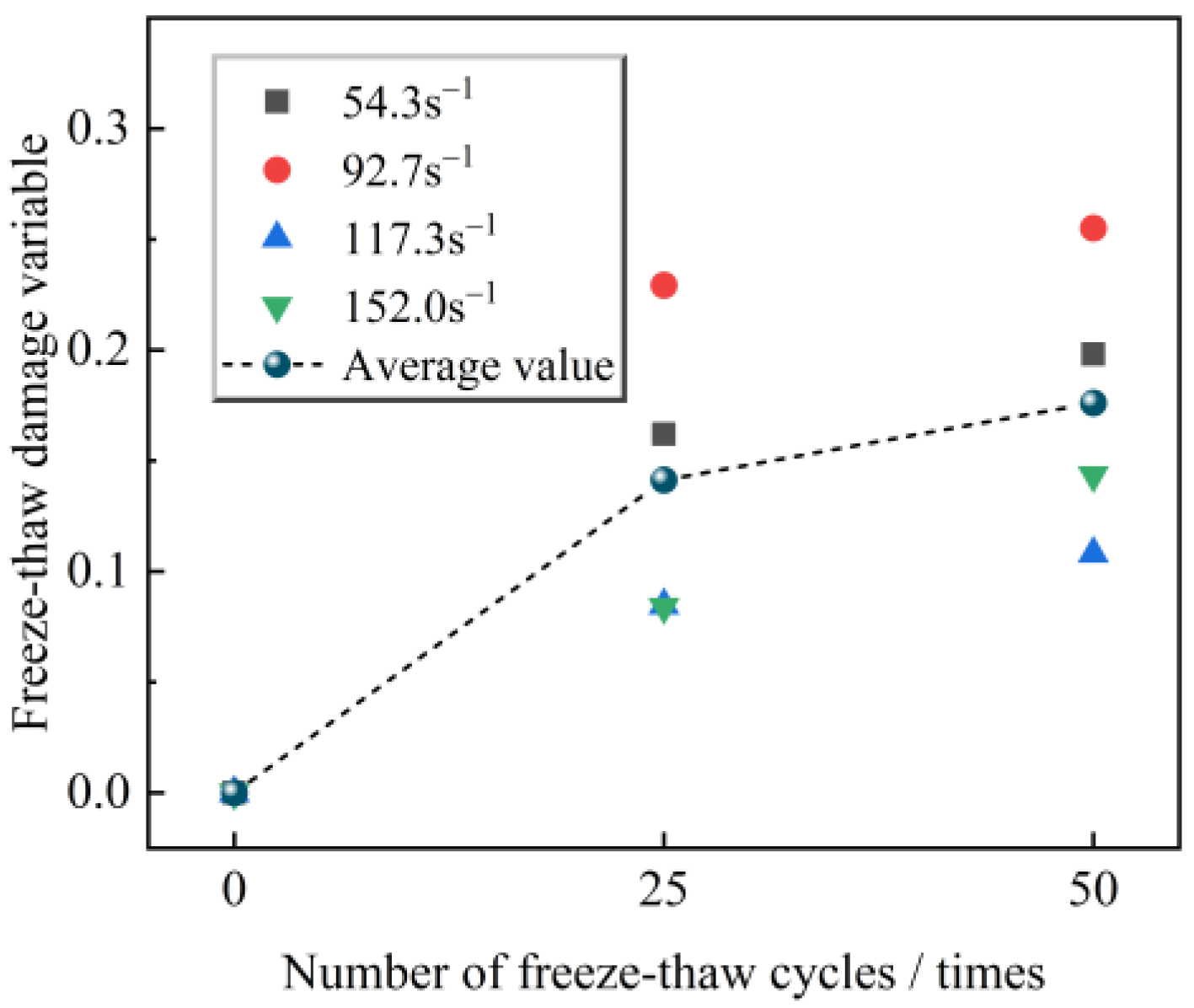
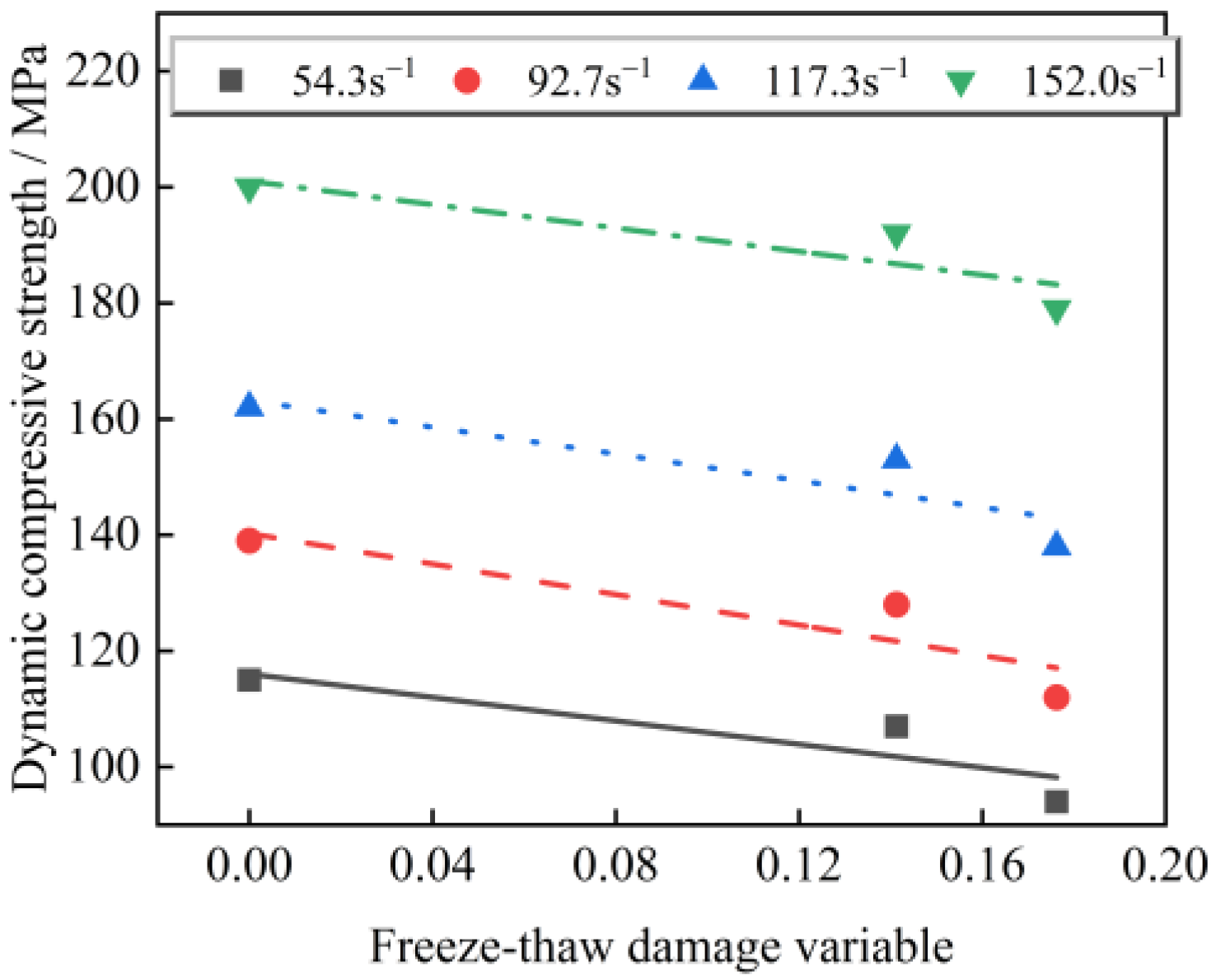
3.2.4. Analysis of Freeze–Thaw Damage to Sandstone Based on Peak Energy Dissipation Rate
4. Conclusions
- (1)
- The peak strength of sandstone subjected to different numbers of freeze–thaw cycles increases exponentially with growing strain rate, indicating a distinct strain rate effect.
- (2)
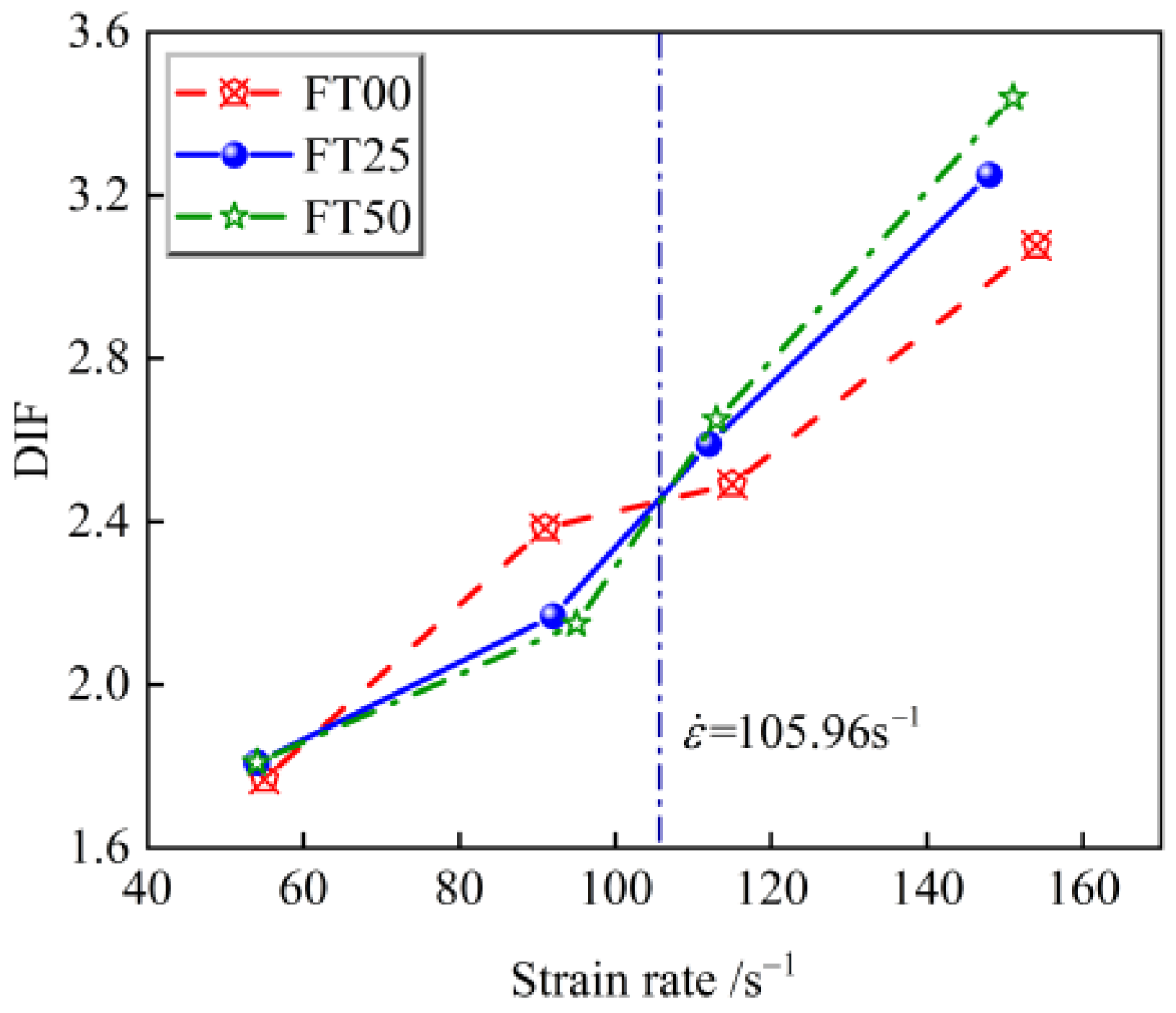
- The DIF of the freeze–thawed sandstone increases with the increase in strain rate. There is a strain rate threshold: when strain rate is smaller than 105.96 s−1, the increasing rate of the DIF slows down with the increase in the number of freeze–thaw cycles; when strain rate is higher than 105.96 s−1, the increasing rate of the DIF grows with the increase in the number of freeze–thaw cycles.
- (3)
- In the case of the same strain rate, the fractal dimension of fractured sandstone increases with the increase in the number of freeze–thaw cycles; in the case of the same number of freeze–thaw cycles, the fractal dimension of fractured sandstone gradually increases with increasing strain rate.
- (4)
- The freeze–thaw damage variable established based on peak energy dissipation rate can be used to elucidate the damage degree of sandstone under freeze–thaw cycling, and the peak dynamic compressive strength of freeze–thawed sandstone at different strain rates is reduced with the increase in the freeze–thaw damage variable.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, G.M.; Liu, Q.S. Analysis of mechanism of rock failure due to freeze-thaw cycling and mechanical testing study on frozen-thawed rocks. Chin. J. Rock Mech. Eng. 2005, 24, 3076–3082. (In Chinese) [Google Scholar]
- Hori, M.; Morihiro, H. Micromechanical analysis on deterioration due to freezing and thawing in porous brittle materials. Int. J. Eng. Sci. 1998, 36, 511–522. [Google Scholar] [CrossRef]
- Yang, G.; Shen, Y.; Jia, H.; Wei, R.; Zhang, H.; Liu, H. Research progress and tendency in characteristics of multi-scale damage mechanics of rock under freezing-thawing. Chin. J. Rock Mech. Eng. 2018, 37, 545–563. (In Chinese) [Google Scholar] [CrossRef]
- Jia, H.-L.; Zhao, S.-Q.; Ding, S.; Wang, T.; Dong, Y.-H.; Tan, X.-J. Study on the evolution and influencing factors of frost heaving force of water bearing cracks during freezing-thawing process. Chin. J. Rock Mech. Eng. 2022, 41, 1832–1845. (In Chinese) [Google Scholar] [CrossRef]
- Huang, S.; Yu, S.; Ye, Y.; Ye, Z.; Cheng, A. Pore structure change and physico-mechanical properties deterioration of sandstone suffering freeze-thaw actions. Constr. Build. Mater. 2022, 330, 127200. [Google Scholar] [CrossRef]
- Lan, Y.; Gao, H.; Zhao, Y. Pore Structure Characteristics and Strength Variation of Red Sandstone under Freeze–Thaw Cycles. Materials 2022, 15, 3856. [Google Scholar] [CrossRef]
- Huang, S.; Yu, S. Effect of water saturation on the strength of sandstones: Experimental investigation and statistical analysis. Bull. Eng. Geol. Environ. 2022, 81, 323. [Google Scholar] [CrossRef]
- Wang, P.; Xu, J.-Y.; Fang, X.-Y.; Wang, P.-X.; Liu, S.-H.; Wang, H.-Y. Water softening and freeze-thaw cycling induced decay of red-sandstone. Rock Soil Mech. 2018, 39, 2065–2072. (In Chinese) [Google Scholar] [CrossRef]
- Tan, X.; Chen, W.; Yang, J.; Cao, J. Laboratory investigations on the mechanical properties degradation of granite under freeze-thaw cycles. Cold Reg. Sci. Technol. 2011, 68, 130–138. [Google Scholar] [CrossRef]
- Shi, L.; Liu, Y.; Meng, X.; Zhang, H. Study on mechanical properties and damage characteristics of red sandstone under freeze-thaw and load. Adv. Civ. Eng. 2021, 2021, 8867489. [Google Scholar] [CrossRef]
- Zhou, Y.X.; Xia, K.; Li, X.B.; Li, H.B.; Ma, G.W.; Zhao, J.; Zhou, Z.; Dai, F. Suggested methods for determining the dynamic strength parameters and mode-I fracture toughness of rock materials. Int. J. Rock Mech. Min. Sci. 2012, 49, 105–112. [Google Scholar] [CrossRef]
- Wang, K.; Feng, G.; Bai, J.; Guo, J.; Yang, X.; Cui, B.; Shi, X.; Song, C. Experimental study on dynamic mechanical characteristics and fracture behaviors of coal under water–gas-temperature coupling conditions. Theor. Appl. Fract. Mech. 2022, 122, 103609. [Google Scholar] [CrossRef]
- Zhou, K.-P.; Li, B.; Li, J.; Deng, H.-W.; BIN, F. Microscopic damage and dynamic mechanical properties of rock under freeze-thaw environment. Trans. Nonferrous Met. Soc. China 2015, 25, 1254–1261. [Google Scholar] [CrossRef]
- Zhao, R.; Zhai, Y.; Meng, F.; Li, Y.; Li, Y. Research on interactions among parameters affecting dynamic mechanical properties of sandstone after freeze-thaw cycles. Eng. Geol. 2021, 293, 106332. [Google Scholar] [CrossRef]
- Takarli, M.; Prince, W.; Siddique, R. Damage in granite under heating/cooling cycles and water freeze–thaw condition. Int. J. Rock Mech. Min. Sci. 2008, 45, 1164–1175. [Google Scholar] [CrossRef]
- Chen, T.; Yeung, M.; Mori, N. Effect of water saturation on deterioration of welded tuff due to freeze-thaw action. Cold Reg. Sci. Technol. 2004, 38, 127–136. [Google Scholar] [CrossRef]
- Weng, L.; Wu, Z.; Taheri, A.; Liu, Q.; Lu, H. Deterioration of dynamic mechanical properties of granite due to freeze-thaw weathering: Considering the effects of moisture conditions. Cold Reg. Sci. Technol. 2020, 176, 103092. [Google Scholar] [CrossRef]
- Chen, C.; Zheng, Y.; Sun, C. Experimental study on dynamic tensile properties and energy evolution of sandstone after freeze-thaw cycles. Chin. J. Rock Mech. Eng. 2021, 40, 2445–2453. (In Chinese) [Google Scholar] [CrossRef]
- Liu, X.-H.; Xue, Y.; Zheng, Y.; Gui, X. Research on energy release in coal rock fragmentation process under impact load. Chin. J. Rock Mech. Eng. 2021, 40, 3201–3211. (In Chinese) [Google Scholar] [CrossRef]
- Weng, L.; Wu, Z.; Liu, Q.; Wang, Z. Energy dissipation and dynamic fragmentation of dry and water-saturated siltstones under sub-zero temperatures. Eng. Fract. Mech. 2019, 220, 106659. [Google Scholar] [CrossRef]
- Han, Z.; Li, D.; Zhou, T.; Zhu, Q.; Ranjith, P. Experimental study of stress wave propagation and energy characteristics across rock specimens containing cemented mortar joint with various thicknesses. Int. J. Rock Mech. Min. Sci. 2020, 131, 104352. [Google Scholar] [CrossRef]
- Feng, J.; Wang, E.; Shen, R.; Chen, L.; Li, X.; Xu, Z. Investigation on energy dissipation and its mechanism of coal under dynamic loads. Geomech. Eng. 2016, 11, 657–670. [Google Scholar] [CrossRef]
- Wang, P.; Xu, J.; Fang, X.; Wang, P. Energy dissipation and damage evolution analyses for the dynamic compression failure process of red-sandstone after freeze-thaw cycles. Eng. Geol. 2017, 221, 104–113. [Google Scholar] [CrossRef]
- Gao, F.; Cao, S.; Zhou, K.; Lin, Y.; Zhu, L. Damage characteristics and energy-dissipation mechanism of frozen-thawed sandstone subjected to loading. Cold Reg. Sci. Technol. 2020, 169, 102920. [Google Scholar] [CrossRef]
- Ping, Q.; Luo, X.; Ma, Q.-Y.; Yuan, P. Broken energy dissipation characteristics of sandstone specimens under impact loads. Chin. J. Rock Mech. Eng. 2015, 34, 4197–4203. (In Chinese) [Google Scholar] [CrossRef]
- Hong, L.; Zhou, Z.L.; Yin, T.B.; Liao, G.Y.; Ye, Z.Y. Energy consumption in rock fragmentation at intermediate strain rate. J. Cent. South Univ. Technol. 2009, 16, 677–682. [Google Scholar] [CrossRef]
- Liu, S.; Xu, J.; Liu, S.; Wang, P. Fractal study on the dynamic fracture of red sandstone after F-T cycles. Environ. Earth Sci. 2022, 81, 152. [Google Scholar] [CrossRef]
- Wang, K.; Feng, G.; Bai, J.; Guo, J.; Shi, X.; Cui, B.; Song, C. Dynamic behaviour and failure mechanism of coal subjected to coupled water-static-dynamic loads. Soil Dyn. Earthq. Eng. 2022, 153, 107084. [Google Scholar] [CrossRef]
- Feng, J.; Wang, E.; Chen, X.; Ding, H. Energy dissipation rate: An indicator of coal deformation and failure under static and dynamic compressive loads. Int. J. Min. Sci. Technol. 2018, 28, 397–406. [Google Scholar] [CrossRef]
- Jia, H.; Ding, S.; Zi, F.; Dong, Y.; Shen, Y. Evolution in sandstone pore structures with freeze-thaw cycling and interpretation of damage mechanisms in saturated porous rocks. Catena 2020, 195, 104915. [Google Scholar] [CrossRef]
- Liping, W.; Ning, L.; Jilin, Q.; Yanzhe, T.; Shuanhai, X. A study on the physical index change and triaxial compression test of intact hard rock subjected to freeze-thaw cycles. Cold Reg. Sci. Technol. 2019, 160, 39–47. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, H.; Wang, R.-H.; Wang, F.; He, Z.-W. Investigation of progressive damage and deterioration of sandstone under freezing-thawing cycle. Rock Soil Mech. 2021, 42, 1381–1394. (In Chinese) [Google Scholar] [CrossRef]
- Mousavi, S.Z.S.; Tavakoli, H.; Moarefvand, P.; Rezaei, M. Micro-structural, petro-graphical and mechanical studies of schist rocks under the freezing-thawing cycles. Cold Reg. Sci. Technol. 2020, 174, 103039. [Google Scholar] [CrossRef]
- Gao, F.; Xiong, X.; Zhou, K.-P.; Li, J.-L.; Shi, W.-C. Strength deterioration model of saturated sandstone under freeze-thaw cycles. Rock Soil Mech. 2019, 40, 926–932. (In Chinese) [Google Scholar] [CrossRef]
- GB/T 50266—2013; Standard for Tests Method of Engineering Rock Masses. China Planning Press: Beijing, China, 2013. (In Chinese)
- Shen, Y.J.; Yang, G.S.; Rong, T.L.; Liu, H.; Lv, W.Y. Proposed scheme for freeze-thaw cycle tests on rock. Chin. J. Geotech. Eng. 2016, 38, 1775–1782. (In Chinese) [Google Scholar] [CrossRef]
- Wang, P.; Xu, J.; Liu, S.; Wang, H. Dynamic mechanical properties and deterioration of red-sandstone subjected to repeated thermal shocks. Eng. Geol. 2016, 212, 44–52. [Google Scholar] [CrossRef]
- Xie, H.-P. Fractal geometry and its application to rock and soil materials. Chin. J. Geotech. Eng. 1992, 14, 14–24. (In Chinese) [Google Scholar]
- Xu, J.-Y.; Liu, S. Research on fractal characteristics of marble fragments subjected to impact loading. Rock Soil Mech. 2012, 33, 3225–3229. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, Z.; Kou, S.; Jiang, L.; Lindqvist, P.-A. Effects of loading rate on rock fracture: Fracture characteristics and energy partitioning. Int. J. Rock Mech. Min. Sci. 2000, 37, 745–762. [Google Scholar] [CrossRef]




| Dry Density (g/cm3) | P-Wave Velocity (m/s) | Porosity (%) | Uniaxial Compressive Strength (MPa) | Young’s Modulus (GPa) |
|---|---|---|---|---|
| 2.37 | 2900 ± 50 | 9.74 | 65.54 | 9.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, P.; Mao, S.; Qian, Y.; Wang, Q.; Lu, J. The Dynamic Compressive Properties and Energy Dissipation Law of Sandstone Subjected to Freeze–Thaw Damage. Water 2022, 14, 3632. https://doi.org/10.3390/w14223632
Jia P, Mao S, Qian Y, Wang Q, Lu J. The Dynamic Compressive Properties and Energy Dissipation Law of Sandstone Subjected to Freeze–Thaw Damage. Water. 2022; 14(22):3632. https://doi.org/10.3390/w14223632
Chicago/Turabian StyleJia, Peng, Songze Mao, Yijin Qian, Qiwei Wang, and Jialiang Lu. 2022. "The Dynamic Compressive Properties and Energy Dissipation Law of Sandstone Subjected to Freeze–Thaw Damage" Water 14, no. 22: 3632. https://doi.org/10.3390/w14223632
APA StyleJia, P., Mao, S., Qian, Y., Wang, Q., & Lu, J. (2022). The Dynamic Compressive Properties and Energy Dissipation Law of Sandstone Subjected to Freeze–Thaw Damage. Water, 14(22), 3632. https://doi.org/10.3390/w14223632








