Determination of Pore and Surface Diffusivities from Single Decay Curve in CSBR Based on Parallel Diffusion Model
Abstract
:1. Introduction
2. Parallel Diffusion Model in Dimensionless Form
3. Results and Discussion
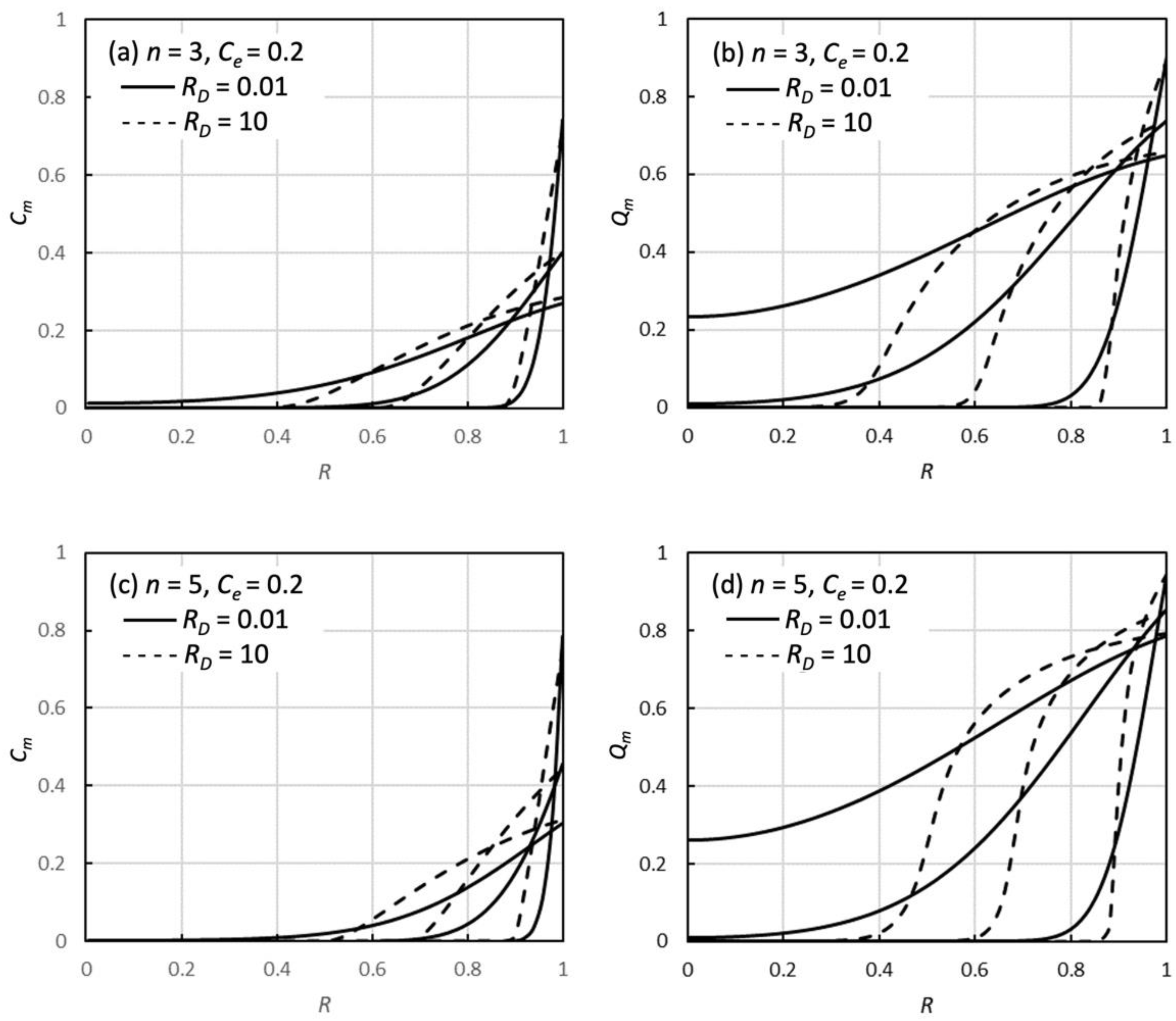
3.1. RD Dependence of Adsorption Profiles and Decay Curves
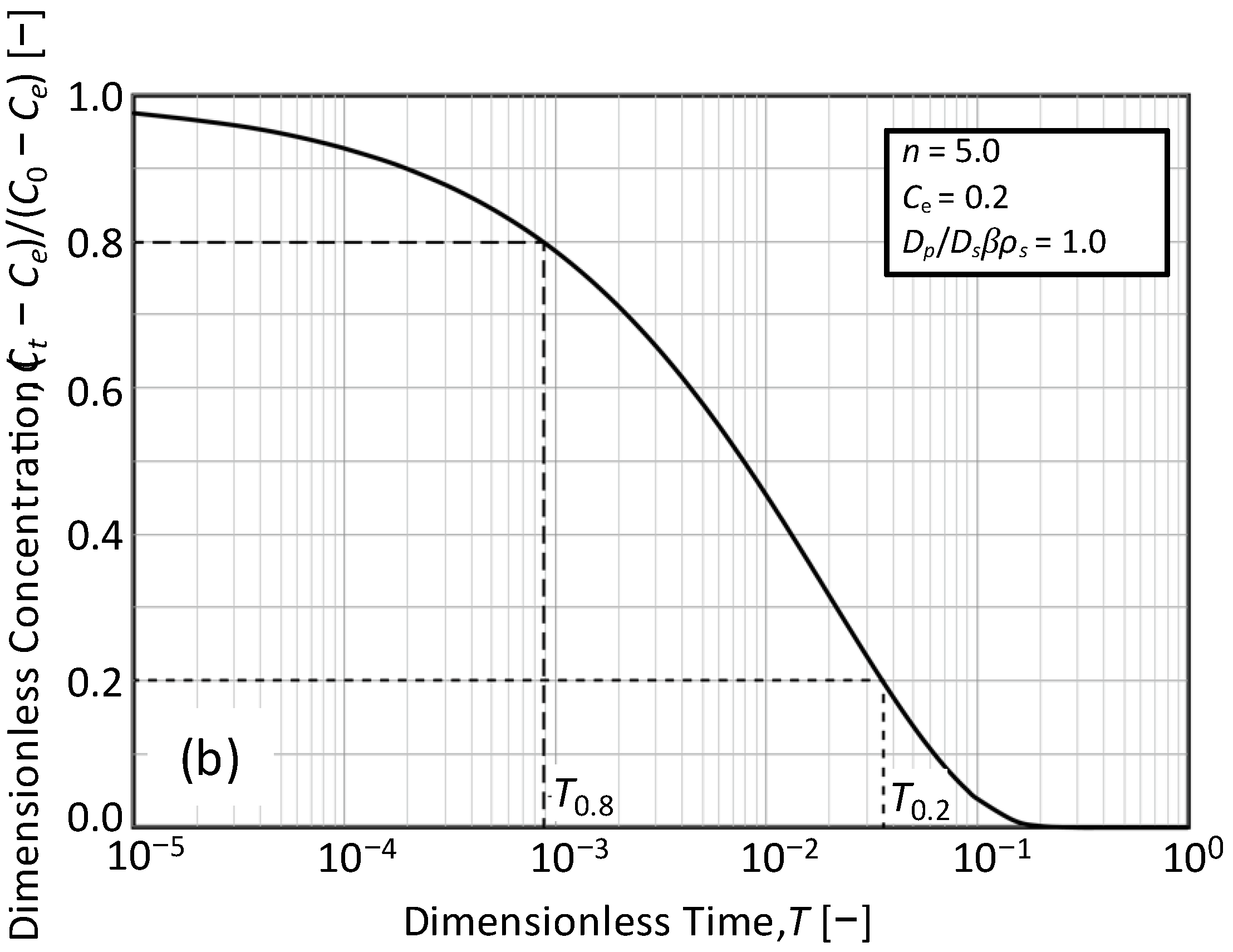
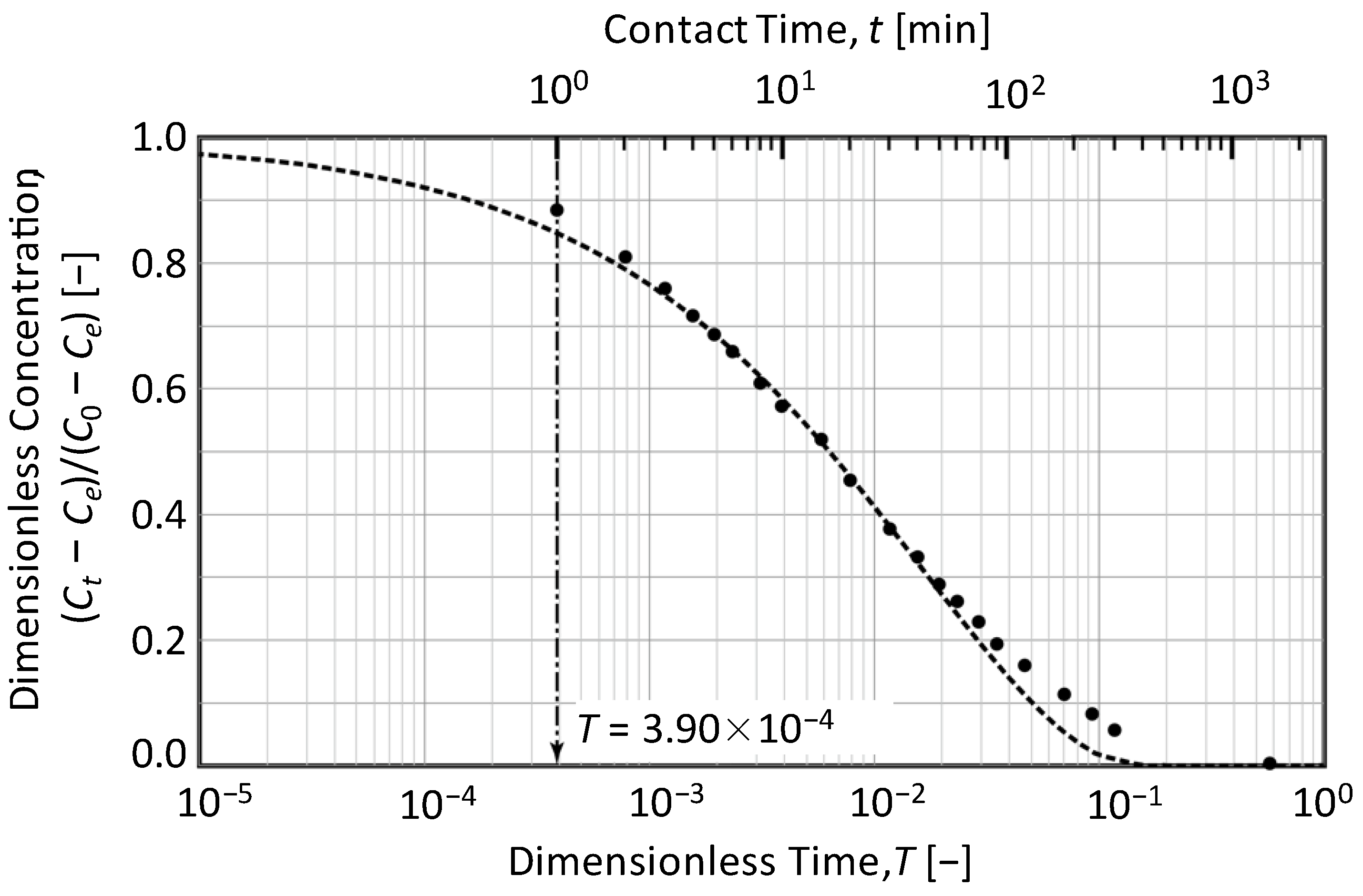
3.2. Determination of the Time Ratio T0.2/T0.8 from Concentration Decay Curves
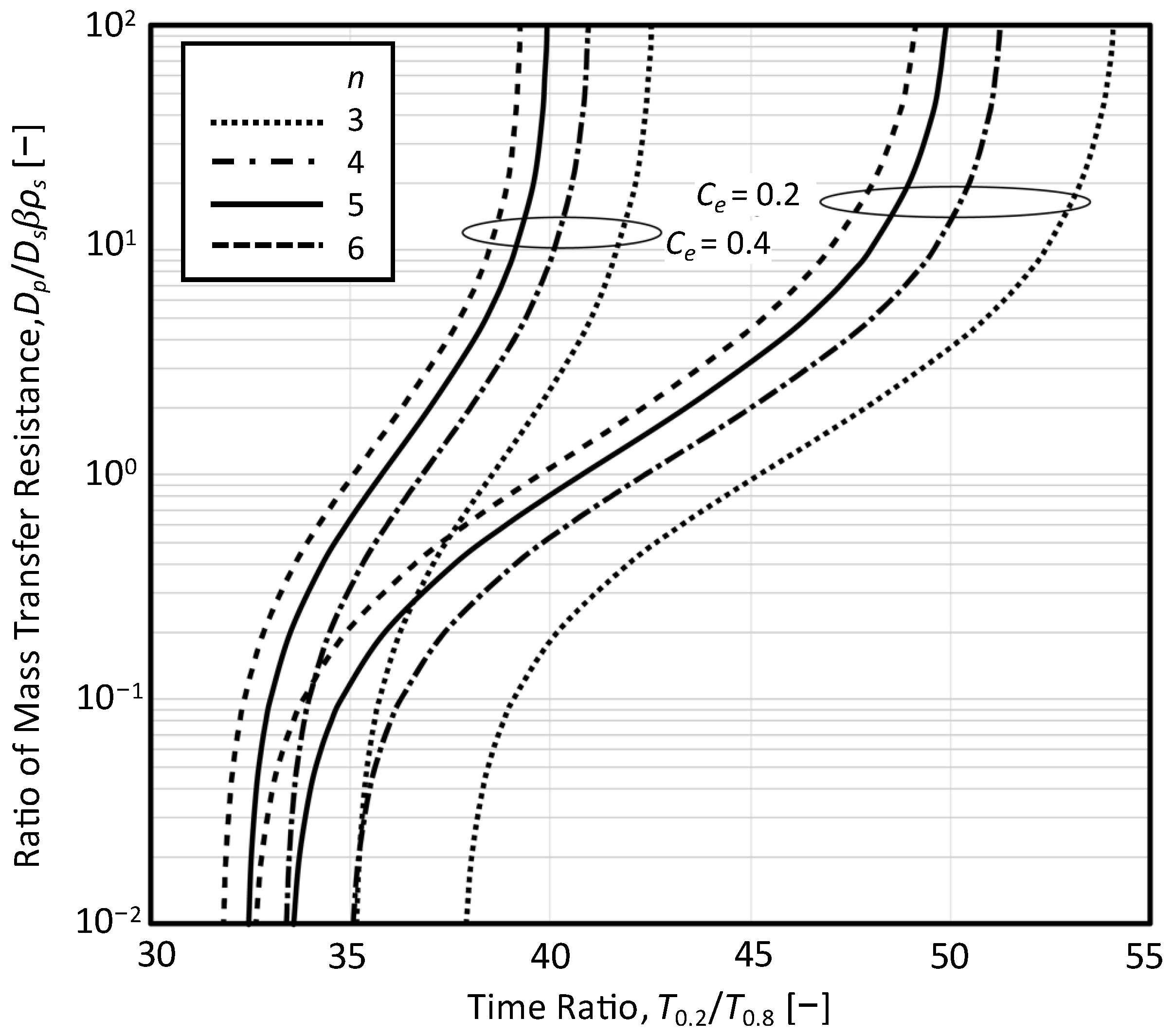
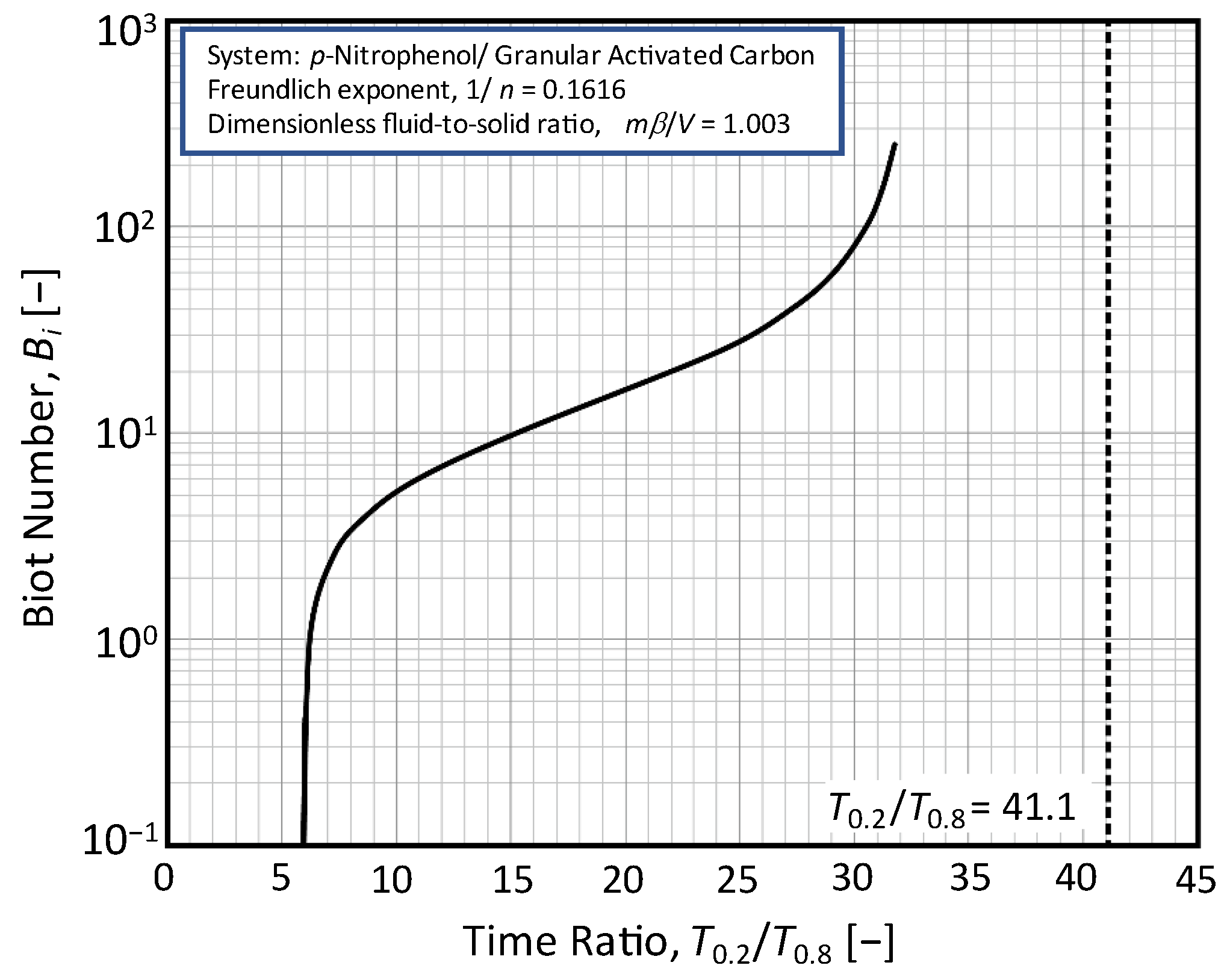
3.3. Relationship between T0.2/T0.8 and RD
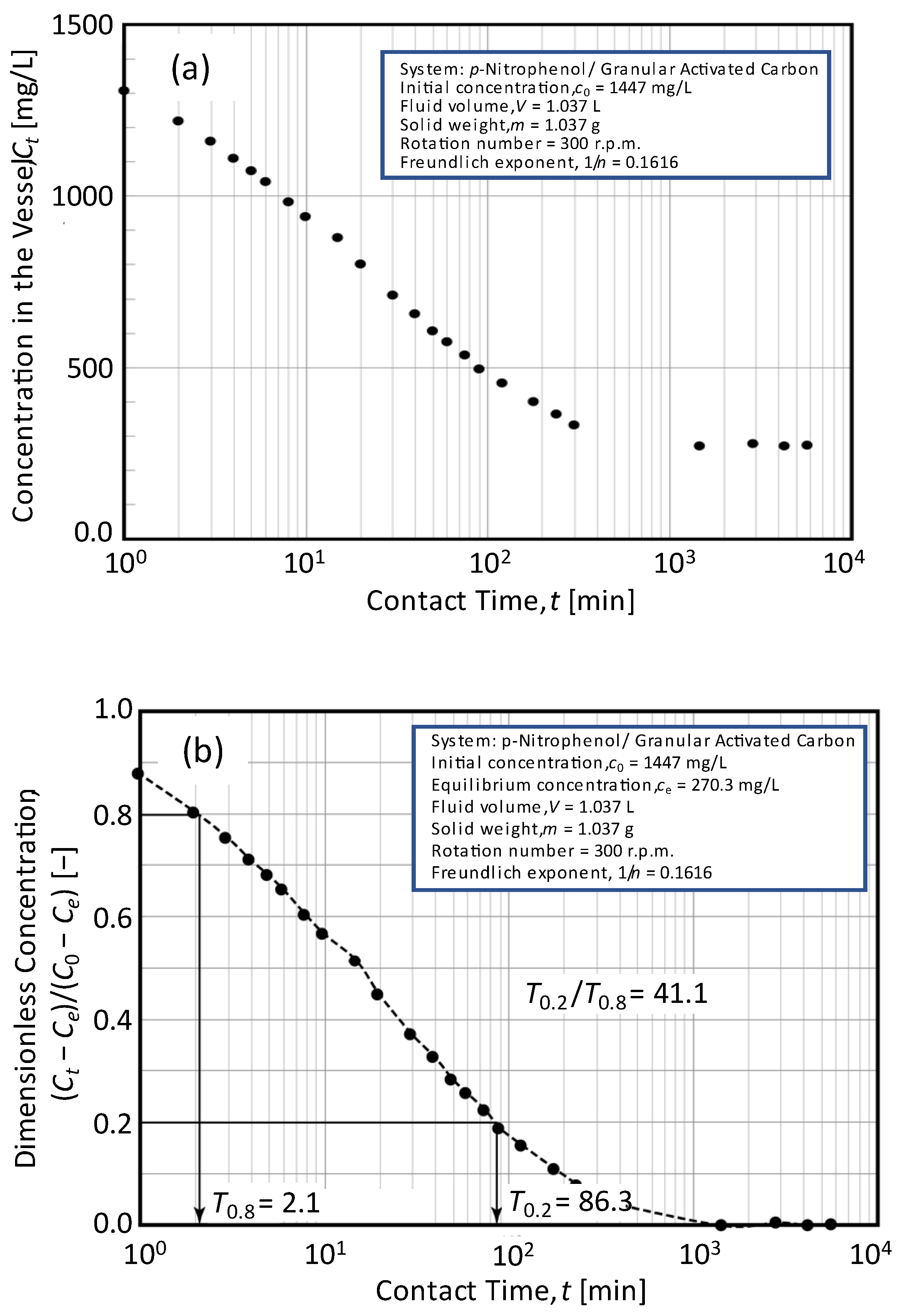
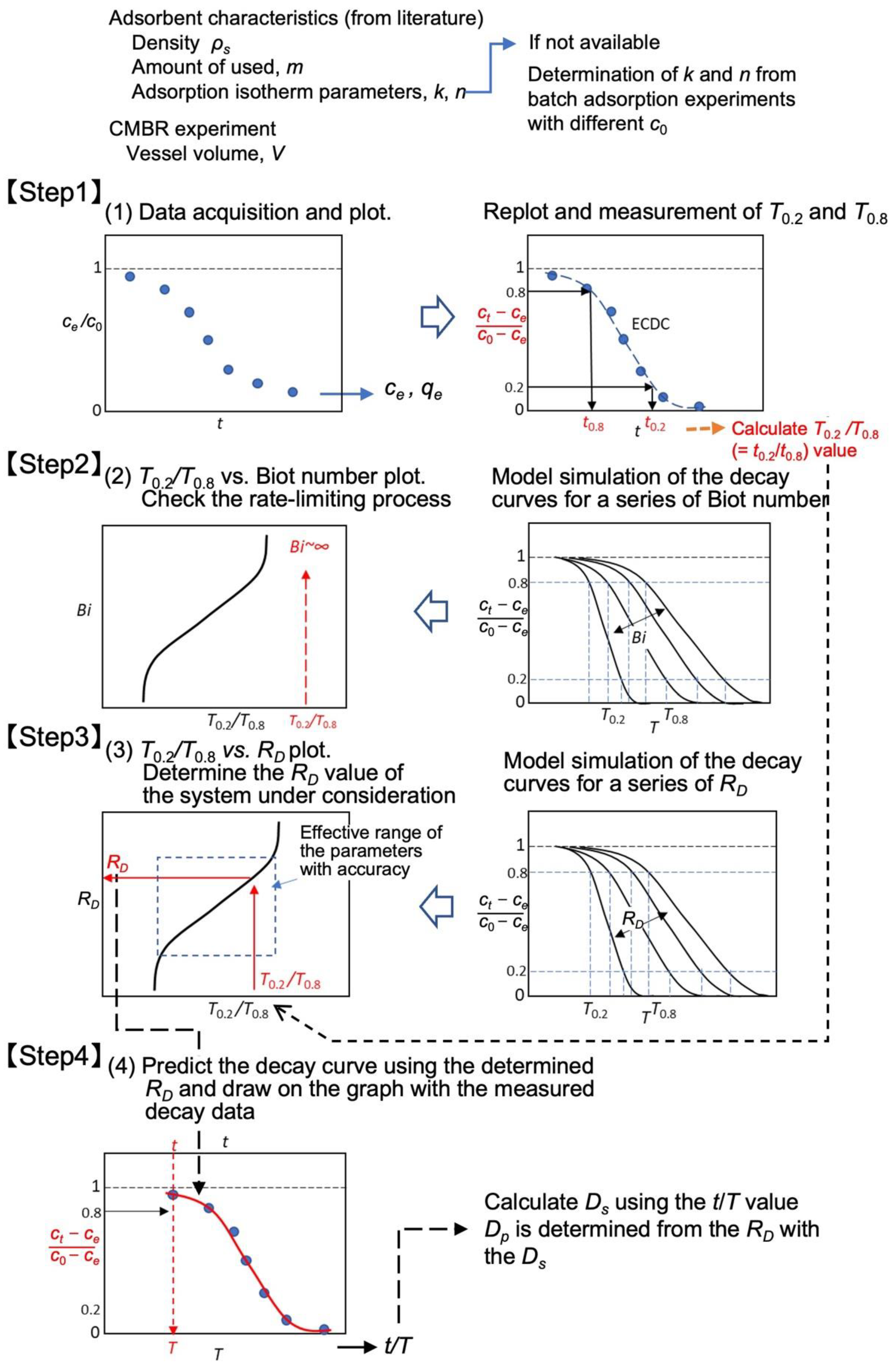
3.4. Determination Procedure with Experimental Data
3.5. Summary of the Determination Procedure
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| ap: | Surface area based on solid particle | [cm2/cm3] |
| Bi: | Biot number = kfrp/(Dsβρs) | [-] |
| ce: | Equilibrium concentration at time = infinity | [mg/L] |
| cs: | Fluid concentration at r = rp | [mg/L] |
| ct: | Concentration within the vessel at time t | [mg/L] |
| c0: | Concentration within the vessel at time = 0 | [mg/L] |
| Cm: | Dimensionless concentration | [-] |
| Dp: | Pore diffusivity | [cm2/s] |
| Ds: | Surface diffusivity | [cm2/s] |
| kf: | Fluid film mass transfer coefficient | [cm/s] |
| m: | Weight of adsorbent | [g] |
| 1/n: | Freundlich exponent | [-] |
| qe: | Amount adsorbed in equilibrium with ce | [mg/g] |
| qt: | Average amount adsorbed within the adsorbent at time t | [mg/g] |
| q0: | Amount adsorbed at equilibrium with fluid concentration c0 | [mg/g] |
| Qm: | Dimensionless amount of adsorption | [-] |
| r: | Internal radial length (length from the solid center) | [cm] |
| rp: | Particle radius | [cm] |
| RD: | Ratio of diffusion resistance = Dp/(Dsβρs) | [-] |
| t: | Time | [min] |
| V: | Volume of the vessel | [L] |
| β: | q0/c0 | [L/g] |
| ε: | Porosity | [-] |
References
- Takeuchi, Y. Chemical Engineers Handbook, 5th ed.; Maruzen: Tokyo, Japan, 1988; pp. 595–598. [Google Scholar]
- Bhatnagar, A.; Jain, A.K. A comparative adsorption study with different industrial wastes as adsorbents for the removal of cationic dyes from water. J. Colloid Interf. Sci. 2005, 281, 49–55. [Google Scholar] [CrossRef]
- Ip, A.W.; Barford, J.P.; McKay, G. A comparative study on the kinetics and mechanisms of removal of reactive black 5 by adsorption onto activated carbons and bone char. Chem. Eng. J. 2010, 157, 434–442. [Google Scholar] [CrossRef]
- Derylo-Marczewska, A.; Blachnio, M.; Marczewski, A.W.; Seczkowska, M.; Tarasiuk, B. Phenoxyacid pesticide adsorption on activated carbon—Equilibrium and kinetics. Chemosphere 2019, 214, 349–360. [Google Scholar] [CrossRef]
- Bosacka, A.; Zienkiewicz-Strzałka, M.; Wasilewska, M.; Deryło-Marczewska, A.; Podkościelna, B. Physicochemical and adsorption characteristics of divinylbenzene-co-triethoxyvinylsilane microspheres as materials for the removal of organic compounds. Molecules 2021, 26, 2396. [Google Scholar] [CrossRef]
- Wasilewska, M.; Marczewski, A.W.; Deryło-Marczewska, A.; Sternik, D. Nitrophenols removal from aqueous solutions by activated carbon—Temperature effect of adsorption kinetics and equilibrium. J. Environ. Chem. Eng. 2021, 9, 105459. [Google Scholar] [CrossRef]
- Wasilewska, M.; Deryło-Marczewska, A. Adsorption of non-steroidal anti-inflammatory drugs on alginate-carbon composites— equilibrium and kinetics. Materials 2022, 15, 6049. [Google Scholar] [CrossRef]
- Furuya, E.G.; Chang, H.T.; Miura, Y.; Yokomura, H.; Tajima, S.; Yamashita, S.; Noll, K.E. Intraparticle mass transport mechanism in activated carbon adsorption of phenols. J. Environ. Eng. 1996, 122, 909–916. [Google Scholar] [CrossRef]
- Kannan, P.; Pal, P.; Banat, F. Design of adsorption column for reclamation of methyldiethanolamine using homogeneous surface diffusion model. Oil Gas Sci. Technol. Rev. IFP Energ. Nouv. 2020, 75, 1–12. [Google Scholar] [CrossRef]
- Eder, S.; Müller, K.; Azzari, P.; Arcifa, A.; Peydayesh, M.; Nyström, L. Mass transfer mechanism and equilibrium modelling of hydroxytyrosol Adsorption on Olive Pit–Derived Activated Carbon. Chem. Eng. J. 2021, 404, 126519. [Google Scholar] [CrossRef]
- Kavand, M.; Fakoor, E.; Mahzoon, S.; Soleimani, M. An improved film–pore–surface diffusion model in the fixed-bed column adsorption for heavy metal ions: Single and multi-component systems. Process Saf. Environ. Prot. 2018, 113, 330–342. [Google Scholar] [CrossRef]
- Ocampo-Pérez, R.; Leyva-Ramos, R.; Padilla-Ortega, E. Equilibrium and kinetic adsorption of organic compounds onto organo bentonite: Application of a surface diffusion model. Adsorpt. Sci. Technol. 2011, 29, 1007–1024. [Google Scholar] [CrossRef]
- Medveď, I.; Černý, R. Surface diffusion in porous media: A critical review. Micropor. Mesopor. Mater. 2011, 142, 405–422. [Google Scholar] [CrossRef]
- Ma, Z.; Whitley, R.D.; Wang, N.-H.L. Pore and surface diffusion in multicomponent adsorption and liquid chromatography systems. AIChE J. 1996, 42, 1244–1262. [Google Scholar] [CrossRef]
- Rosen, J.B. Kinetics of a fixed bed system for solid diffusion into spherical particles. J. Chem. Phys. 1952, 20, 387–394. [Google Scholar] [CrossRef]
- Kavand, M.; Asasian, N.; Soleimani, M.; Kaghazchi, T.; Bardestani, R. Film-pore-[concentration-dependent] surface diffusion model for heavy metal ions adsorption: Single and multi-component systems. Process Saf. Environ. Prot. 2017, 107, 486–497. [Google Scholar] [CrossRef]
- Ma, A.; Abushaikha, A.; Allen, S.J.; McKay, G. Ion exchange homogeneous surface diffusion modelling by binary site resin for the removal of nickel ions from wastewater in fixed beds. Chem. Eng. J. 2019, 358, 1–10. [Google Scholar] [CrossRef]
- Souza, P.R.; Dotto, G.L.; Salau, N.P.G. Detailed numerical solution of pore volume and surface diffusion model in adsorption systems. Chem. Eng. Res. Des. 2017, 122, 298–307. [Google Scholar] [CrossRef]
- Souza, P.R.; Dotto, G.L.; Salau, N.P.G. Statistical evaluation of pore volume and surface diffusion model in adsorption systems. J. Environ. Chem. Eng. 2017, 5, 5293–5297. [Google Scholar] [CrossRef]
- Valderrama, C.; Gamisans, X.; de las Heras, X.; Farrán, A.; Cortina, J.L. Sorption kinetics of polycyclic aromatic hydrocarbons removal using granular activated carbon: Intraparticle diffusion coefficients. J. Hazard. Mater. 2008, 157, 386–396. [Google Scholar] [CrossRef]
- Saripall, K.P.; Serne, R.J.; Meyer, P.D.; McGrail, B.P. Prediction of diffusion coefficients in porous media using tortuosity factors based on interfacial areas. Ground Water. 2002, 40, 346–352. [Google Scholar] [CrossRef]
- Liu, B.J.; Yang, Y.W.; Ren, Q.L. Parallel pore and surface diffusion of levulinic acid in basic polymeric adsorbents. J. Chromatogr. A 2006, 1132, 190–200. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Zeng, L.; Mao, J.; Ren, Q. Simulation of levulinic acid adsorption in packed beds using parallel pore/surface diffusion model. Chem. Eng. Technol. 2010, 33, 1146–1152. [Google Scholar] [CrossRef]
- Yao, C.; Chen, T. A new simplified method for estimating film mass transfer and surface diffusion coefficients from batch adsorption kinetic data. Chem. Eng. J. 2015, 265, 93–99. [Google Scholar] [CrossRef]
- Chung, P.-L.; Bugayong, J.G.; Chin, C.Y.; Wang, N.H. A parallel pore and surface diffusion model for predicting the adsorption and elution profiles of lispro insulin and two impurities in gradient-elution reversed phase chromatography. J. Chromatogr. A 2010, 1217, 8103–8120. [Google Scholar] [CrossRef] [PubMed]
- Brzić, D.V.; Petkovska, M.T. Nonlinear frequency response analysis as a tool for identification of adsorption kinetics: Case study—Pore-surface diffusion control. Hindawi. Math. Probl. Eng. 2019, 2019, 7932967. [Google Scholar] [CrossRef] [Green Version]
- Petkovska, M.; Do, D.D. Nonlinear frequency response of adsorption systems. Chem. Eng. Sci. 1998, 53, 3081–3097. [Google Scholar] [CrossRef]
- Costa, E.; Calleja, G.; Marijuan, L. Adsorption of Phenol and p-Nitrophenol on Activated Carbon: Determination of Effective Diffusion Coefficients. Ads. Sci. Tech. 1987, 4, 59–77. [Google Scholar] [CrossRef]
- Shao, Y.; Chen, H. Adsorption kinetics of p-nitrophenol (PNP) on coal-based activated carbon: Experimental and simulation. Desalin. Water Treat. 2016, 57, 14496–14505. [Google Scholar] [CrossRef]
- Fujiki, J.; Sonetaka, N.; Ko, K.-P.; Furuya, E. Experimental determination of intraparticle diffusivity and fluid film mass transfer coefficient using batch contactors. Chem. Eng. J. 2010, 160, 683–690. [Google Scholar] [CrossRef]
- Wilke, C.R.; Chang, P. Correlation of diffusion coefficients in dilute solutions. AIChE J. 1955, 1, 264–270. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seida, Y.; Sonetaka, N.; Noll, K.E.; Furuya, E. Determination of Pore and Surface Diffusivities from Single Decay Curve in CSBR Based on Parallel Diffusion Model. Water 2022, 14, 3629. https://doi.org/10.3390/w14223629
Seida Y, Sonetaka N, Noll KE, Furuya E. Determination of Pore and Surface Diffusivities from Single Decay Curve in CSBR Based on Parallel Diffusion Model. Water. 2022; 14(22):3629. https://doi.org/10.3390/w14223629
Chicago/Turabian StyleSeida, Yoshimi, Noriyoshi Sonetaka, Kenneth E. Noll, and Eiji Furuya. 2022. "Determination of Pore and Surface Diffusivities from Single Decay Curve in CSBR Based on Parallel Diffusion Model" Water 14, no. 22: 3629. https://doi.org/10.3390/w14223629
APA StyleSeida, Y., Sonetaka, N., Noll, K. E., & Furuya, E. (2022). Determination of Pore and Surface Diffusivities from Single Decay Curve in CSBR Based on Parallel Diffusion Model. Water, 14(22), 3629. https://doi.org/10.3390/w14223629








