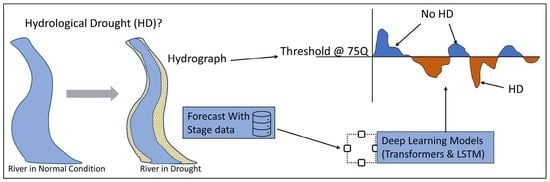
Hydrological Drought Forecasting Using a Deep Transformer Model
Abstract
:1. Introduction
| Forecasting | |||
|---|---|---|---|
| Authors | Models | Indices | Lead Time |
| [5] | ANN and SVM | WBC | Annual (18 years) |
| [7] | ANN, RBMs, and DBN | SSI | Monthly (6, 12, 24) |
| [9] | ANFIS, ANN, DLNN, SVM, FRBS, and DT | SRI | Monthly (3) |
| [11] | ANN combined with different optimization algorithms | SHDI | Monthly (1, 3, 6) |
| [12] | ELM | SHDI | Monthly (1, 3) |
| [20] | ANN | SPEI | Monthly (1–6) |
| [25] | ARIMA | SRI | Monthly (1–6) |
| [26] | ANN and SVR | SPEI | Monthly (8 years) |
| [27] | Meta-Gaussian | SRI | Monthly (1–2) |
| Hindcasting | |||
| Authors | Models | Indices | Timescales |
| [6] | ANN, ANFIS, SVM, and DT | SRI | Monthly (2, 6, 9, 12) |
| [28] | LSTM | SRM | Monthly (12) |
| [29] | SVR, GEP, and MT | SSI | Monthly (1–6) |
| [30] | MC | SHI | Monthly, weekly |
| [31] | BNM | SRI | Weekly (1, 4, 8, 12, 16, 20) |
| [32] | BNM | SRI | Monthly (1–2) |
| [33] | DT, NB, RF, and SVM | — | Monthly (10) |
| [34] | ANFIS and GMDH | SDI | Monthly (1, 3, 6, 9, 12) |
| [35] | CANFIS, MLPNN and MLR | SDI | Monthly (1, 3, 6, 9, 12, 24) |
| [36] | RF and GBM | SSI, SDI | Monthly (12) |
2. Materials and Methods
2.1. Case Study
2.2. Data and Methods
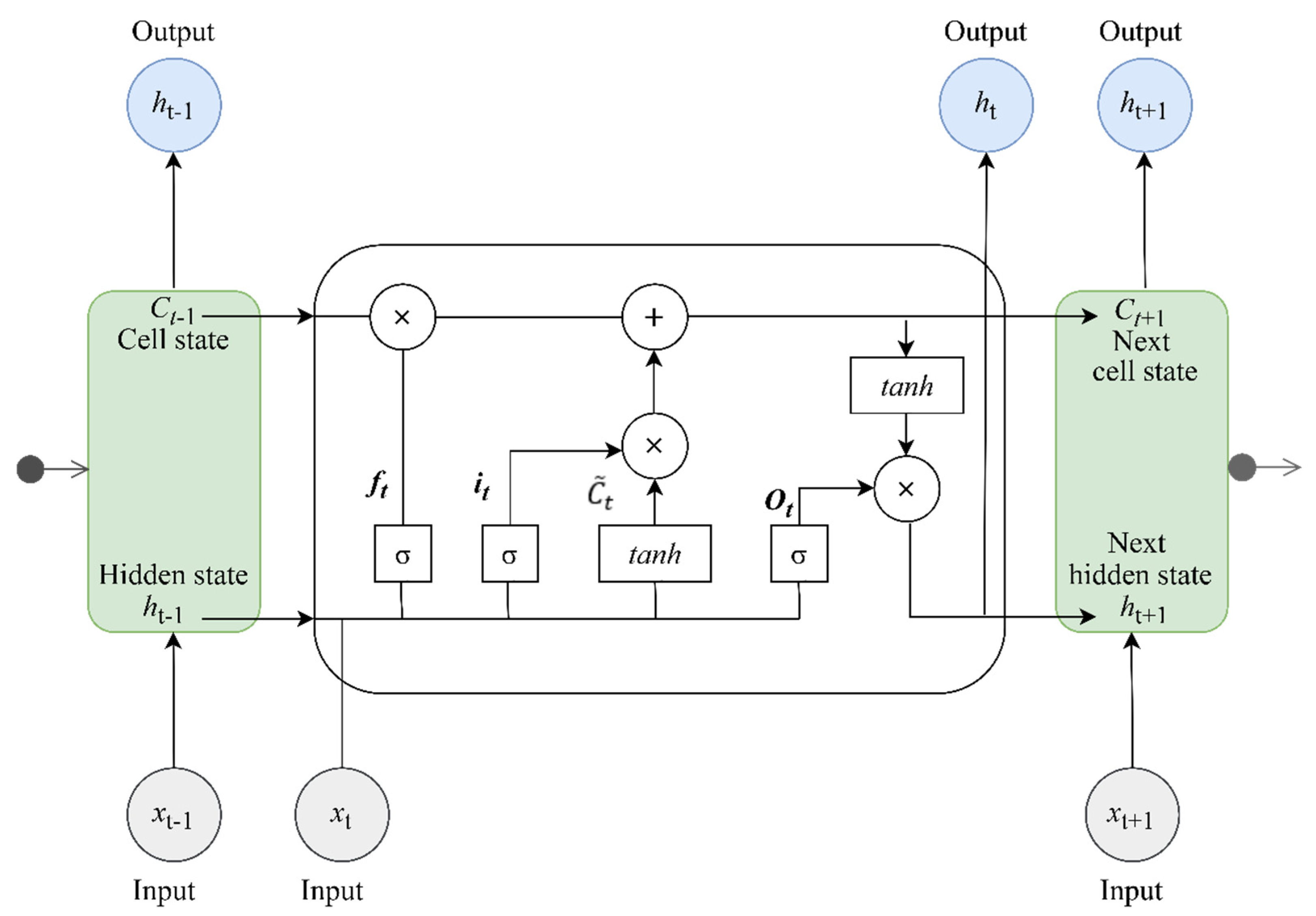
2.2.1. LSTM
2.2.2. Transformers
- i.
- Training
- ii.
- Optimizer
- iii.
- Regularization
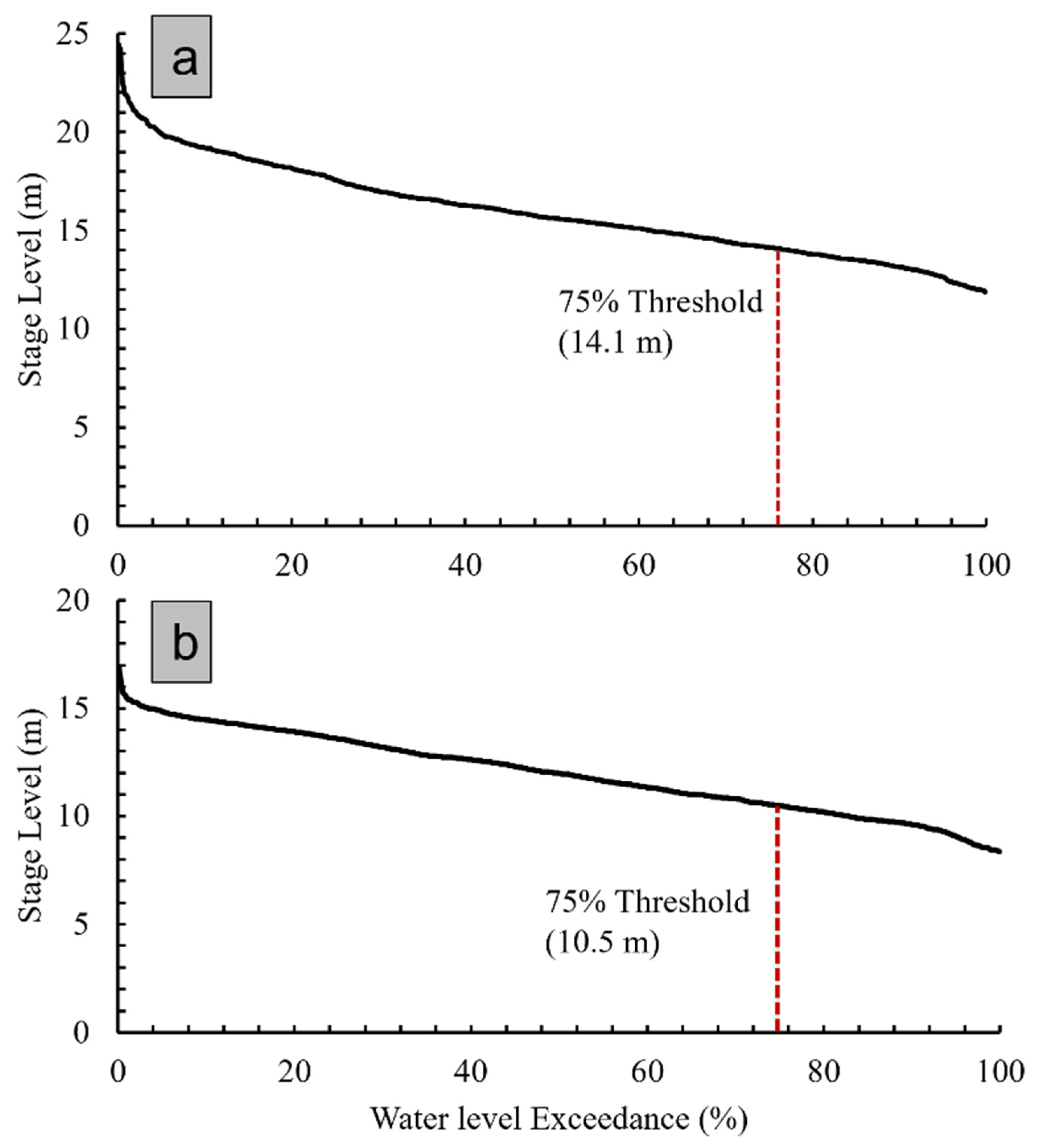
2.2.3. Flood Frequency Analysis
2.2.4. Model Evaluation
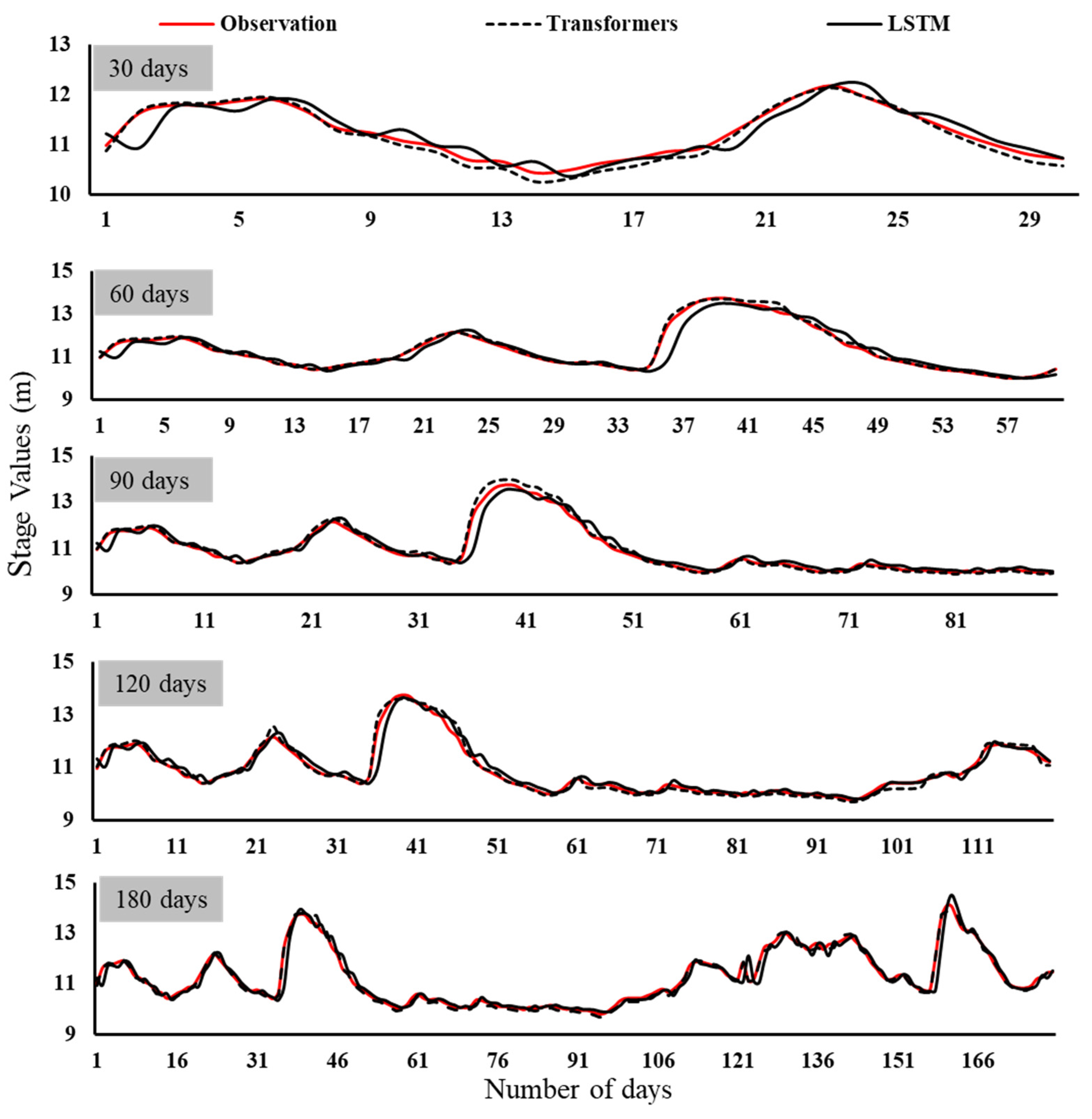
3. Results
4. Discussion
5. Conclusions
- i.
- Evaluation metrics reveal that, on average, the transformer models performed better than the LSTM models across all timestamps for predicting hydrological drought.
- ii.
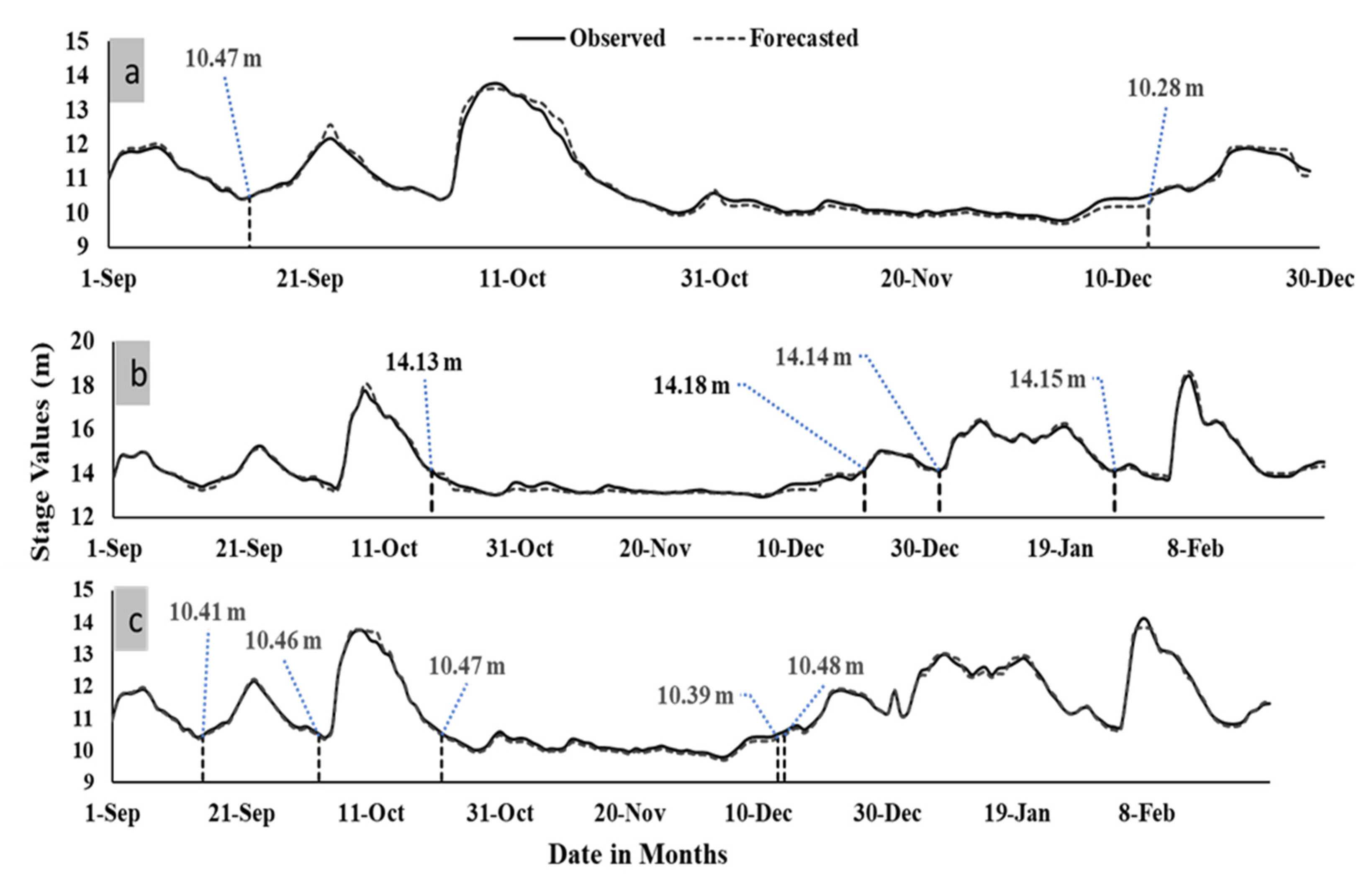
- The transformer models overestimated peak stage levels compared to the LSTM models, which accurately forecasted high-stage values.
- iii.
- The drought series generated from the flow–duration curves (FDCs) were forecasted accurately for the transformer models, except for a few instances in Chattahoochee and Blountstown.
- iv.
- Water-level data are an important metric for assessing hydrological drought in hydrological systems with increased human pressures.
- v.
- Although the DL model performed well in this river, model performance would be expected to vary with the characteristics of the river and its basin, including the drainage basin area, flashiness, climate, geology, vegetation, tidal influence, anthropogenic activities, and an array of other factors.
- vi.
- It is unknown how well the model would perform if there was an unusual event, such as a tropical cyclone passing over the study area during what is typically the dry season.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mind’je, R.; Li, L.; Amanambu, A.C.; Nahayo, L.; Nsengiyumva, J.B.; Gasirabo, A.; Mindje, M. Flood Susceptibility Modeling and Hazard Perception in Rwanda. Int. J. Disaster Risk Reduct. 2019, 38, 101211. [Google Scholar] [CrossRef]
- Tu, X.; Wu, H.; Singh, V.P.; Chen, X.; Lin, K.; Xie, Y. Multivariate Design of Socioeconomic Drought and Impact of Water Reservoirs. J. Hydrol. 2018, 566, 192–204. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A Review of Drought Concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Van Loon, A.F. Hydrological Drought Explained. WIREs Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Almikaeel, W.; Čubanová, L.; Šoltész, A. Hydrological Drought Forecasting Using Machine Learning—Gidra River Case Study. Water 2022, 14, 387. [Google Scholar] [CrossRef]
- Achite, M.; Jehanzaib, M.; Elshaboury, N.; Kim, T.-W. Evaluation of Machine Learning Techniques for Hydrological Drought Modeling: A Case Study of the Wadi Ouahrane Basin in Algeria. Water 2022, 14, 431. [Google Scholar] [CrossRef]
- Agana, N.A.; Homaifar, A. A Deep Learning Based Approach for Long-Term Drought Prediction. In Proceedings of the SoutheastCon 2017, Charlotte, NC, USA, 30 March–2 April 2017; pp. 1–8. [Google Scholar]
- Dikshit, A.; Pradhan, B. Explainable AI in Drought Forecasting. Mach. Learn. Appl. 2021, 6, 100192. [Google Scholar] [CrossRef]
- Jehanzaib, M.; Shah, S.A.; Yoo, J.; Kim, T.-W. Investigating the Impacts of Climate Change and Human Activities on Hydrological Drought Using Non-Stationary Approaches. J. Hydrol. 2020, 588, 125052. [Google Scholar] [CrossRef]
- Maity, R.; Khan, M.I.; Sarkar, S.; Dutta, R.; Maity, S.S.; Pal, M.; Chanda, K. Potential of Deep Learning in Drought Assessment by Extracting Information from Hydrometeorological Precursors. J. Water Clim. Chang. 2021, 12, 2774–2796. [Google Scholar] [CrossRef]
- Nabipour, N.; Dehghani, M.; Mosavi, A.; Shamshirband, S. Short-Term Hydrological Drought Forecasting Based on Different Nature-Inspired Optimization Algorithms Hybridized With Artificial Neural Networks. IEEE Access 2020, 8, 15210–15222. [Google Scholar] [CrossRef]
- Wang, G.C.; Zhang, Q.; Band, S.S.; Dehghani, M.; Chau, K.W.; Tho, Q.T.; Zhu, S.; Samadianfard, S.; Mosavi, A. Monthly and Seasonal Hydrological Drought Forecasting Using Multiple Extreme Learning Machine Models. Eng. Appl. Comput. Fluid Mech. 2022, 16, 1364–1381. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Nalbantis, I.; Tsakiris, G. Assessment of Hydrological Drought Revisited. Water Resour. Manag. 2009, 23, 881–897. [Google Scholar] [CrossRef]
- Garen, D.C. Revised Surface-Water Supply Index for Western United States. J. Water Resour. Plan. Manag. 1993, 119, 437–454. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
- Shukla, S.; Wood, A.W. Use of a Standardized Runoff Index for Characterizing Hydrologic Drought. Geophys. Res. Lett. 2008, 35, L02405. [Google Scholar] [CrossRef] [Green Version]
- Alley, W.M. The Palmer Drought Severity Index: Limitations and Assumptions. J. Appl. Meteorol. Climatol. 1984, 23, 1100–1109. [Google Scholar] [CrossRef]
- Narasimhan, B.; Srinivasan, R. Development and Evaluation of Soil Moisture Deficit Index (SMDI) and Evapotranspiration Deficit Index (ETDI) for Agricultural Drought Monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Dehghani, M.; Saghafian, B.; Zargar, M. Probabilistic Hydrological Drought Index Forecasting Based on Meteorological Drought Index Using Archimedean Copulas. Hydrol. Res. 2019, 50, 1230–1250. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Xu, Z.; Duan, Q. Conceptual Hydrological Models. In Handbook of Hydrometeorological Ensemble Forecasting; Duan, Q., Pappenberger, F., Thielen, J., Wood, A., Cloke, H.L., Schaake, J.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 1–23. ISBN 978-3-642-40457-3. [Google Scholar]
- Shirmohammadi, B.; Moradi, H.; Moosavi, V.; Semiromi, M.T.; Zeinali, A. Forecasting of Meteorological Drought Using Wavelet-ANFIS Hybrid Model for Different Time Steps (Case Study: Southeastern Part of East Azerbaijan Province, Iran). Nat. Hazards 2013, 69, 389–402. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J. Drought Forecasting Using New Machine Learning Methods. J. Water Land Dev. 2013, 18, 3–12. [Google Scholar] [CrossRef]
- Mokhtarzad, M.; Eskandari, F.; Jamshidi Vanjani, N.; Arabasadi, A. Drought Forecasting by ANN, ANFIS, and SVM and Comparison of the Models. Environ. Earth Sci. 2017, 76, 729. [Google Scholar] [CrossRef]
- Bazrafshan, O.; Salajegheh, A.; Bazrafshan, J.; Mahdavi, M.; Fatehi Maraj, A. Hydrological Drought Forecasting Using ARIMA Models (Case Study: Karkheh Basin). ECOPERSIA 2015, 3, 1099–1117. [Google Scholar]
- Dikshit, A.; Pradhan, B.; Alamri, A.M. Temporal Hydrological Drought Index Forecasting for New South Wales, Australia Using Machine Learning Approaches. Atmosphere 2020, 11, 585. [Google Scholar] [CrossRef]
- Hao, Z.; Hao, F.; Singh, V.P.; Sun, A.Y.; Xia, Y. Probabilistic Prediction of Hydrologic Drought Using a Conditional Probability Approach Based on the Meta-Gaussian Model. J. Hydrol. 2016, 542, 772–780. [Google Scholar] [CrossRef]
- Li, Y.; Wang, B.; Gong, Y. Drought Assessment Based on Data Fusion and Deep Learning. Comput. Intell. Neurosci. 2022, 2022, 4429286. [Google Scholar] [CrossRef]
- Shamshirband, S.; Hashemi, S.; Salimi, H.; Samadianfard, S.; Asadi, E.; Shadkani, S.; Kargar, K.; Mosavi, A.; Nabipour, N.; Chau, K.-W. Predicting Standardized Streamflow Index for Hydrological Drought Using Machine Learning Models. Eng. Appl. Comput. Fluid Mech. 2020, 14, 339–350. [Google Scholar] [CrossRef]
- Sharma, T.C.; Panu, U.S. Prediction of Hydrological Drought Durations Based on Markov Chains: Case of the Canadian Prairies. Hydrol. Sci. J. 2012, 57, 705–722. [Google Scholar] [CrossRef] [Green Version]
- Sattar, M.N.; Lee, J.-Y.; Shin, J.-Y.; Kim, T.-W. Probabilistic Characteristics of Drought Propagation from Meteorological to Hydrological Drought in South Korea. Water Resour. Manag. 2019, 33, 2439–2452. [Google Scholar] [CrossRef]
- Bae, D.-H.; Son, K.-H.; So, J.-M. Utilization of the Bayesian Method to Improve Hydrological Drought Prediction Accuracy. Water Resour. Manag. 2017, 31, 3527–3541. [Google Scholar] [CrossRef]
- Jehanzaib, M.; Shah, S.A.; Son, H.J.; Jang, S.-H.; Kim, T.-W. Predicting Hydrological Drought Alert Levels Using Supervised Machine-Learning Classifiers. KSCE J. Civ. Eng. 2022, 26, 3019–3030. [Google Scholar] [CrossRef]
- Aghelpour, P.; Bahrami-Pichaghchi, H.; Varshavian, V. Hydrological Drought Forecasting Using Multi-Scalar Streamflow Drought Index, Stochastic Models and Machine Learning Approaches, in Northern Iran. Stoch. Environ. Res. Risk Assess. 2021, 35, 1615–1635. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Singh, R.P. Application of Heuristic Approaches for Prediction of Hydrological Drought Using Multi-Scalar Streamflow Drought Index. Water Resour. Manag. 2019, 33, 3985–4006. [Google Scholar] [CrossRef]
- Rose, M.A.J.; Chithra, N.R. Tree-Based Ensemble Model Prediction for Hydrological Drought in a Tropical River Basin of India. Int. J. Environ. Sci. Technol. 2022, 1–18. [Google Scholar] [CrossRef]
- Anshuka, A.; Chandra, R.; Buzacott, A.J.V.; Sanderson, D.; van Ogtrop, F.F. Spatio Temporal Hydrological Extreme Forecasting Framework Using LSTM Deep Learning Model. Stoch. Environ. Res. Risk Assess. 2022, 36, 3467–3485. [Google Scholar] [CrossRef]
- Adikari, K.E.; Shrestha, S.; Ratnayake, D.T.; Budhathoki, A.; Mohanasundaram, S.; Dailey, M.N. Evaluation of Artificial Intelligence Models for Flood and Drought Forecasting in Arid and Tropical Regions. Environ. Model. Softw. 2021, 144, 105136. [Google Scholar] [CrossRef]
- Salleh, M.N.M.; Talpur, N.; Hussain, K. Adaptive Neuro-Fuzzy Inference System: Overview, Strengths, Limitations, and Solutions. In Proceedings of the International Conference on Data Mining and Big Data, Fukuoka, Japan, 27 July–1 August 2017; Tan, Y., Takagi, H., Shi, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 527–535. [Google Scholar]
- Yaseen, Z.M.; Sulaiman, S.O.; Deo, R.C.; Chau, K.-W. An Enhanced Extreme Learning Machine Model for River Flow Forecasting: State-of-the-Art, Practical Applications in Water Resource Engineering Area and Future Research Direction. J. Hydrol. 2019, 569, 387–408. [Google Scholar] [CrossRef]
- Wen, Q.; Zhou, T.; Zhang, C.; Chen, W.; Ma, Z.; Yan, J.; Sun, L. Transformers in Time Series: A Survey. arXiv 2022, arXiv:2202.07125. [Google Scholar]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting. Adv. Neural Inf. Process. Syst. 2022, 34, 22419–22430. [Google Scholar]
- Minixhofer, C.; Swan, M.; McMeekin, C.; Andreadis, P. DroughtED: A Dataset and Methodology for Drought Forecasting Spanning Multiple Climate Zones. In Proceedings of the Tackling Climate Change with Machine Learning: Workshop at ICML, Gainesville, FL, USA, 23–24 July 2021; p. 9. [Google Scholar]
- Light, H.M.; Vincent, K.R.; Darst, M.R.; Price, F.D. Water-Level Decline in the Apalachicola River, Florida, from 1954 to 2004, and Effects on Floodplain Habitats; Scientific Investigations Report; U.S. Geological Survey: Tallahassee, FL, USA, 2006; Volume 2006–5173, p. 61. [Google Scholar]
- Smith, M.C.; Anthony Stallins, J.; Maxwell, J.T.; Van Dyke, C. Hydrological Shifts and Tree Growth Responses to River Modification along the Apalachicola River, Florida. Phys. Geogr. 2013, 34, 491–511. [Google Scholar] [CrossRef]
- Mossa, J.; Chen, Y.-H.; Kondolf, G.M.; Walls, S.P. Channel and Vegetation Recovery from Dredging of a Large River in the Gulf Coastal Plain, USA. Earth Surf. Process. Landf. 2020, 45, 1926–1944. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Mossa, J.; Singh, K.K. Floodplain Response to Varied Flows in a Large Coastal Plain River. Geomorphology 2020, 354, 107035. [Google Scholar] [CrossRef]
- Mishra, A.K.; Desai, V.R. Drought Forecasting Using Feed-Forward Recursive Neural Network. Ecol. Model. 2006, 198, 127–138. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2021. [Google Scholar]
- Zou, F.; Shen, L.; Jie, Z.; Zhang, W.; Liu, W. A Sufficient Condition for Convergences of Adam and RMSProp. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2019, Long Beach, CA, USA, 15–16 June 2019; pp. 11127–11135. [Google Scholar]
- Yevjevich, V. An Objective Approach to Definitions and Investigations of Continental Hydrologic Droughts. J. Hydrol. 1969, 7, 353. [Google Scholar] [CrossRef]
- Tallaksen, L.M.; Hisdal, H.; Lanen, H.A.J.V. Space–Time Modelling of Catchment Scale Drought Characteristics. J. Hydrol. 2009, 375, 363–372. [Google Scholar] [CrossRef]
- Elshaboury, N.; Marzouk, M. Comparing Machine Learning Models For Predicting Water Pipelines Condition. In Proceedings of the 2020 2nd Novel Intelligent and Leading Emerging Sciences Conference (NILES), Giza, Egypt, 24–26 October 2020; pp. 134–139. [Google Scholar]
- Mossa, J.; Chen, Y.-H. Geomorphic Response to Historic and Ongoing Human Impacts in a Large Lowland River. Earth Surf. Process. Landf. 2022, 47, 1550–1569. [Google Scholar] [CrossRef]
- Mossa, J.; Chen, Y.-H. Geomorphic Insights from Eroding Dredge Spoil Mounds Impacting Channel Morphology. Geomorphology 2021, 376, 107571. [Google Scholar] [CrossRef]
- Ward, A.; Trimble, S.; Buckrard, S.; Lyon, S. Environmental Hydrology, 3rd ed.; Taylor and Francis Group: Abingdon, UK, 2016; ISBN 978-1-4665-8941-4. [Google Scholar]
- Rivera, J.A.; Araneo, D.C.; Penalba, O.C. Threshold Level Approach for Streamflow Drought Analysis in the Central Andes of Argentina: A Climatological Assessment. Hydrol. Sci. J. 2017, 62, 1949–1964. [Google Scholar] [CrossRef]
- Tallaksen, L.M.; Hisdal, H.E.G.E. Regional Analysis of Extreme Streamflow Drought Duration and Deficit Volume. IAHS Publ. 1997, 246, 141–150. [Google Scholar]
- Van Loon, A.F.; Van Lanen, H.A.J. A Process-Based Typology of Hydrological Drought. Hydrol. Earth Syst. Sci. 2012, 16, 1915–1946. [Google Scholar] [CrossRef] [Green Version]
- Pinter, N.; Ickes, B.S.; Wlosinski, J.H.; van der Ploeg, R.R. Trends in Flood Stages: Contrasting Results from the Mississippi and Rhine River Systems. J. Hydrol. 2006, 331, 554–566. [Google Scholar] [CrossRef]
- Graf, W.L. Downstream Hydrologic and Geomorphic Effects of Large Dams on American Rivers. Geomorphology 2006, 79, 336–360. [Google Scholar] [CrossRef]
- Hovenga, P.A.; Wang, D.; Medeiros, S.C.; Hagen, S.C.; Alizad, K. The Response of Runoff and Sediment Loading in the Apalachicola River, Florida to Climate and Land Use Land Cover Change. Earths Future 2016, 4, 124–142. [Google Scholar] [CrossRef] [Green Version]
- Elder, J.F.; Flagg, S.D.; Mattraw, H.C., Jr. Hydrology and Ecology of the Apalachicola River, Florida: A Summary of the River Quality Assessment; U.S. Government Publishing Office: Washington, DC, USA, 1988.
- Joshi, S. Long Term Hydrological Changes in the Apalachicola River, Florida. Int. J. Environ. Sci. Nat. Resour. 2019, 19, 152–159. [Google Scholar] [CrossRef]
- Piqué, G.; Batalla, R.J.; Sabater, S. Hydrological Characterization of Dammed Rivers in the NW Mediterranean Region. Hydrol. Process. 2016, 30, 1691–1707. [Google Scholar] [CrossRef]



| Performance Indicators | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| DL Model | Timescale (Days) | Chattahoochee | Blountstown | ||||||
| R2 | MSE | R2 | |||||||
| Transformers | 30 | 0.02 | 0.12 | 0.14 | 0.90 | 0.02 | 0.12 | 0.15 | 0.91 |
| 60 | 0.12 | 0.26 | 0.35 | 0.89 | 0.04 | 0.15 | 0.18 | 0.92 | |
| 90 | 0.12 | 0.20 | 0.35 | 0.94 | 0.08 | 0.26 | 0.33 | 0.92 | |
| 120 | 0.04 | 0.12 | 0.21 | 0.92 | 0.05 | 0.17 | 0.22 | 0.93 | |
| 180 | 0.23 | 0.37 | 0.48 | 0.96 | 0.09 | 0.25 | 0.29 | 0.97 | |
| Average | 0.106 | 0.214 | 0.306 | 0.922 | 0.056 | 0.190 | 0.234 | 0.930 | |
| LSTM | 30 | 0.07 | 0.20 | 0.26 | 0.77 | 0.04 | 0.17 | 0.21 | 0.85 |
| 60 | 0.14 | 0.28 | 0.38 | 0.85 | 0.11 | 0.21 | 0.32 | 0.87 | |
| 90 | 0.16 | 0.33 | 0.40 | 0.92 | 0.06 | 0.16 | 0.26 | 0.89 | |
| 120 | 0.08 | 0.15 | 0.28 | 0.90 | 0.05 | 0.23 | 0.23 | 0.89 | |
| 180 | 0.14 | 0.18 | 0.37 | 0.87 | 0.07 | 0.15 | 0.26 | 0.94 | |
| Average | 0.118 | 0.228 | 0.338 | 0.862 | 0.066 | 0.184 | 0.256 | 0.888 | |
| Chattahoochee | Blountstown | |||||
|---|---|---|---|---|---|---|
| Count (Drought Days) | Count (Drought Days) | |||||
| Model | Observed | Predicted | % Accuracy | Observed | Predicted | % Accuracy |
| TR-30 | 16 | 16 | 100 | 7 | 8 | 85.7 |
| TR-60 | 32 | 32 | 100 | 22 | 22 | 100 |
| TR-90 | 60 | 60 | 100 | 52 | 46 | 88.5 |
| TR-120 | 82 | 82 | 100 | 52 | 54 | 96.2 |
| TR-180 | 94 | 98 | 95.7 | 52 | 57 | 90.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amanambu, A.C.; Mossa, J.; Chen, Y.-H. Hydrological Drought Forecasting Using a Deep Transformer Model. Water 2022, 14, 3611. https://doi.org/10.3390/w14223611
Amanambu AC, Mossa J, Chen Y-H. Hydrological Drought Forecasting Using a Deep Transformer Model. Water. 2022; 14(22):3611. https://doi.org/10.3390/w14223611
Chicago/Turabian StyleAmanambu, Amobichukwu C., Joann Mossa, and Yin-Hsuen Chen. 2022. "Hydrological Drought Forecasting Using a Deep Transformer Model" Water 14, no. 22: 3611. https://doi.org/10.3390/w14223611
APA StyleAmanambu, A. C., Mossa, J., & Chen, Y.-H. (2022). Hydrological Drought Forecasting Using a Deep Transformer Model. Water, 14(22), 3611. https://doi.org/10.3390/w14223611