Hydrologic Performance of Low Impact Developments in a Cold Climate
Abstract
:1. Introduction
2. Study Area
3. Methods
3.1. Calculation in SWMM
3.2. Precipitation
3.3. Model Settings
3.4. Evaluation Indices
4. Results and Discussion
4.1. The LID Effect in the Study Area
4.2. Comparison of the Infiltration Methods
4.2.1. Design Storms
4.2.2. Measured Rain Events
4.3. Seasonal Variations of LID Performance
4.3.1. Seasonal Water Budgets Driven by the Measured Rain Events
4.3.2. Seasonal Runoff-Reduction Effects
5. Conclusions
- (1)
- In case of the design storms with the return periods of 1, 3, 10, 20, 50, and 100 years, the runoff coefficients of the LID scenario, according to the current design standards, were much smaller than those of the baseline, indicating that the LID facilities could effectively control the runoff generation. However, with the increase in rainfall, the storage capacity of the LID facilities became gradually used up and the runoff reduction rate gradually decreased.
- (2)
- The Horton and Green–Ampt methods were found to result in different estimations of the LID capacity for managing the surface runoff, especially during the real events. The outflows of the Horton method at the outlet were 17.4% higher than Green–Ampt for the 100-year design storm. It was also found through the measured precipitation time series of the dry, average, and wet years, the annual runoff coefficients with regards to the Horton method were at least 1.3 times higher than those modeled by the Green–Ampt method. This is because compared to the Green–Ampt method, the Horton method tended to generate lower infiltration, leading to a higher and faster outflow from the LID. In case of a simulation task driven by a heavy design storm, the Horton method resulted in a lower runoff reduction rate, which may be a more conservative estimate of the worst-case scenario for designing the drainage system, especially when the input and validation datasets are inadequate. This suggests that the choice of the infiltration method is critical when designing the LIDs by means of simulations.
- (3)
- Unlike summer, snowfall in winter did not melt immediately to form runoff or infiltration, so the effect of managing the winter runoff by the LID was not directly related to the snowfall intensity, but more to the temperature. The formation of the seasonal snow covers reduced the permeability of LID, undermining the LID capacity for runoff reduction in the winter. However, LID still exhibited an overall decent regulation of winter runoff compared with the baseline, possibly owing to the presence of frequent freezing-thawing cycles.
Author Contributions
Funding
Conflicts of Interest
References
- Yu, H.; Zhao, Y.; Fu, Y.; Li, L. Spatiotemporal Variance Assessment of Urban Rainstorm Waterlogging Affected by Impervious Surface Expansion: A Case Study of Guangzhou, China. Sustainability 2018, 10, 3761. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Mei, C.; Liu, J.; Shao, W. A new strategy for integrated urban water management in China: Sponge city. Sci. China Technol. Sci. 2018, 61, 317–329. [Google Scholar] [CrossRef]
- Yin, J.; Ye, M.; Yin, Z.; Xu, S. A review of advances in urban flood risk analysis over China. Stoch. Environ. Res. Risk Assess. 2015, 29, 1063–1070. [Google Scholar] [CrossRef]
- Dai, L.; van Rijswick, H.F.; Driessen, P.P.; Keessen, A.M. Governance of the Sponge City Programme in China with Wuhan as a case study. Int. J. Water Resour. Dev. 2018, 34, 578–596. [Google Scholar] [CrossRef]
- Liu, H.; Jia, Y.; Niu, C. “Sponge city” concept helps solve China’s urban water problems. Environ. Earth Sci. 2017, 76, 473. [Google Scholar] [CrossRef]
- Zaqout, T.; Andradóttir, H.Ó.; Arnalds, Ó. Infiltration capacity in urban areas undergoing frequent snow and freeze–thaw cycles: Implications on sustainable urban drainage systems. J. Hydrol. 2022, 607, 127495. [Google Scholar] [CrossRef]
- Sterpi, D. Effect of freeze–thaw cycles on the hydraulic conductivity of a compacted clayey silt and influence of the compaction energy. Soils Found. 2015, 55, 1326–1332. [Google Scholar] [CrossRef] [Green Version]
- Fouli, Y.; Cade-Menun, B.J.; Cutforth, H.W. Freeze–thaw cycles and soil water content effects on infiltration rate of three Saskatchewan soils. Can. J. Soil Sci. 2013, 93, 485–496. [Google Scholar] [CrossRef]
- Davis, A.P.; Stagge, J.H.; Jamil, E.; Kim, H. Hydraulic performance of grass swales for managing highway runoff. Water Res. 2012, 46, 6775–6786. [Google Scholar] [CrossRef]
- Van Der Kamp, G.; Hayashi, M.; Gallen, D. Comparing the hydrology of grassed and cultivated catchments in the semi-arid Canadian prairies. Hydrol. Process. 2003, 17, 559–575. [Google Scholar] [CrossRef]
- Moghadas, S.; Leonhardt, G.; Marsalek, J.; Viklander, M. Modeling Urban Runoff from Rain-on-Snow Events with the U.S. EPA SWMM Model for Current and Future Climate Scenarios. J. Cold Reg. Eng. 2018, 32, 04017021. [Google Scholar] [CrossRef]
- Valeo, C.; Ho, C.L.I. Modelling urban snowmelt runoff. J. Hydrol. 2004, 299, 237–251. [Google Scholar] [CrossRef]
- Heineman, M.; Bui, F.; Beasley, K. Calibration of urban snow process and water quality model for Logan Airport. In Proceedings of the World Environmental and Water Resources Congress 2010: Challenges of Change, Providence, RI, USA, 16–20 May 2010. [Google Scholar]
- Borris, M.; Österlund, H.; Marsalek, J.; Viklander, M. Snow pollution management in urban areas: An idea whose time has come? Urban Water J. 2021, 18, 840–849. [Google Scholar] [CrossRef]
- Zhicheng, G.; Yuansheng, D. Modeling the hydrological process of drainages in cold regions. J. Glaciol. Geocryol. 2003, 25 (Suppl. S2), 266–272. [Google Scholar]
- Chengshu, W.; Xiaonan, Y.; Wenyi, S.; Xingmin, M.U.; Peng, G.A.O.; Guangju, Z.H.A.O.; Xiaoyan, S.O.N.G. Soil Water Storage Capacity and Rainwater Infiltration in Hilly-Gully Loess Region under Severe Rainstorm. Acta Pedol. Sin. 2020, 57, 296–306. [Google Scholar]
- Yu, J.; Yang, C.; Liu, C.; Song, X.; Hu, S.; Li, F.; Tang, C. Slope runoff study in situ using rainfall simulator in mountainous area of North China. J. Geogr. Sci. 2009, 19, 461–470. [Google Scholar] [CrossRef]
- Mu, W.; Yu, F.; Li, C.; Xie, Y.; Tian, J.; Liu, J.; Zhao, N. Effects of rainfall intensity and slope gradient on runoff and soil moisture content on different growing stages of spring maize. Water 2015, 7, 2990–3008. [Google Scholar] [CrossRef] [Green Version]
- Baiti, H.B.; Bouziane, A.; Ouazar, D.; Hasnaoui, M.D. Storm Water Management Model Sensitivity to infiltration methods and soils impermeability: The Case of Tangier Experimental Basin, Morocco. J. Mater. Environ. Sci. 2017, 8, 3636–3647. [Google Scholar]
- Parnas, F.E.Å.; Abdalla, E.M.H.; Muthanna, T.M. Evaluating three commonly used infiltration methods for permeable surfaces in urban areas using the SWMM and STORM. Hydrol. Res. 2021, 52, 160–175. [Google Scholar] [CrossRef]
- Hashemi, M.; Mahjouri, N.J.W.R.M. Global Sensitivity Analysis-based Design of Low Impact Development Practices for Urban Runoff Management Under Uncertainty. Water Resour. Manag. 2022, 36, 2953–2972. [Google Scholar] [CrossRef]
- Knighton, J.; Lennon, E.; Bastidas, L.; White, E. Stormwater detention system parameter sensitivity and uncertainty analysis using SWMM. J. Hydrol. Eng. 2016, 21, 05016014. [Google Scholar] [CrossRef]
- Chahinian, N.; Moussa, R.; Andrieux, P.; Voltz, M. Comparison of infiltration models to simulate flood events at the field scale. J. Hydrol. 2005, 306, 191–214. [Google Scholar] [CrossRef]
- Van De Genachte, G.; Mallants, D.; Ramos, J.; Deckers, J.A.; Feyen, J. Estimating infiltration parameters from basic soil properties. Hydrol. Process. 1996, 10, 687–701. [Google Scholar] [CrossRef]
- Van Den Putte, A.; Govers, G.; Leys, A.; Langhans, C.; Clymans, W.; Diels, J. Estimating the parameters of the Green—Ampt infiltration equation from rainfall simulation data: Why simpler is better. J. Hydrol. 2013, 476, 332–344. [Google Scholar] [CrossRef]
- Xie, J.; Wu, C.; Li, H.; Chen, G. Study on storm-water management of grassed swales and permeable pavement based on SWMM. Water 2017, 9, 840. [Google Scholar] [CrossRef] [Green Version]
- Luan, Q.; Fu, X.; Song, C.; Wang, H.; Liu, J.; Wang, Y. Runoff Effect Evaluation of LID through SWMM in Typical Mountainous, Low-Lying Urban Areas: A Case Study in China. Water 2017, 9, 439. [Google Scholar] [CrossRef] [Green Version]
- Rossman, L.A. Storm Water Management Model User’s Manual, Version 5.0.; U.S. Environmental Protection Agency: Washington, DC, USA, 2010.
- Rossman, L.A.; Huber, W.C. Storm Water Management Model Reference Manual Volume I—Hydrology (Revised); U.S. EPA Office of Research and Development: Washington, DC, USA, 2016; Volume 104.
- Huber, W.C.; Dickinson, R.E. Storm-Water Management Model, Version 4. Part A: User’s Manual; U.S. Department of Energy Office of Scientific and Technical Information: Oak Ridge, TN, USA, 1988.
- Liu, Z.; Zhang, L.; Yang, Z.; Li, J.; Zhang, B. Derivation of a new generation of stormwater intensity formula for Changchun. China Water Wastewater 2014, 30, 147–150. [Google Scholar]
- Liu, S.; Yang, S.; Lian, Y.; Zheng, D.; Wen, M.; Tu, G.; Shen, B.; Gao, Z.; Wang, D. Time–frequency characteristics of regional climate over northeast China and their relationships with atmospheric circulation patterns. J. Clim. 2010, 23, 4956–4972. [Google Scholar] [CrossRef]
- Li, H.; Ding, L.; Ren, M.; Li, C.; Wang, H. Sponge city construction in China: A survey of the challenges and opportunities. Water 2017, 9, 594. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Wang, F.; Yu, Y.; Huang, Z.; Li, M.; Guan, Y. Comprehensive performance evaluation of LID practices for the sponge city construction: A case study in Guangxi, China. J. Environ. Manag. 2019, 231, 10–20. [Google Scholar] [CrossRef]
- Lynn, T.J.; Nachabe, M.H.; Ergas, S.J. SWMM5 unsaturated drainage models for stormwater biofiltration with an internal water storage zone. J. Sustain. Water Built Environ. 2018, 4, 04017018. [Google Scholar] [CrossRef]
- Beven, K.; Robert, E. Horton’s perceptual model of infiltration processes. Hydrol. Process. 2004, 18, 3447–3460. [Google Scholar] [CrossRef]
- Chen, L.; Xiang, L.; Young, M.H.; Yin, J.; Yu, Z.; van Genuchten, M.T. Optimal parameters for the Green-Ampt infiltration model under rainfall conditions. J. Hydrol. Hydromech. 2015, 63, 93–101. [Google Scholar] [CrossRef] [Green Version]
- He, H.; Dyck, M.F.; Si, B.C.; Zhang, T.; Lv, J.; Wang, J. Soil freezing–thawing characteristics and snowmelt infiltration in Cryalfs of Alberta, Canada. Geoderma Reg. 2015, 5, 198–208. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, M.; Horton, R.; Liu, F.; Peth, S.; Horn, R. Influence of winter grazing on water and heat flow in seasonally frozen soil of Inner Mongolia. Vadose Zone J. 2013, 12, 1–11. [Google Scholar] [CrossRef]
- Jin-Feng, H.; Shuo, L.; Jun, D.; Hao, Q. Simulation of rainfall and snowmelt runoff reduction in a northern city based on combination of green ecological strategies. Chin. J. Appl. Ecol. 2018, 29, 643–650. [Google Scholar]
- Rasmussen, R.; Liu, C.; Ikeda, K.; Gochis, D.; Yates, D.; Chen, F.; Tewari, M.; Barlage, M.; Dudhia, J.; Yu, W.; et al. High-resolution coupled climate runoff simulations of seasonal snowfall over Colorado: A process study of current and warmer climate. J. Clim. 2011, 24, 3015–3048. [Google Scholar] [CrossRef] [Green Version]
- Feng, Y.; Burian, S.; Pomeroy, C. Potential of green infrastructure to restore predevelopment water budget of a semi-arid urban catchment. J. Hydrol. 2016, 542, 744–755. [Google Scholar] [CrossRef]













| Parameter Name | Value | |
|---|---|---|
| Manning n-value Manning n-value | Permeable area | 0.05~0.24 |
| Impermeable area | 0.011~0.024 | |
| Depression Storage | Permeable area | 1.3 mm |
| Depression Storage | Impermeable area | 5 mm |
| Horton model | Maximum infiltration rate | 62 mm/h |
| Horton model | Minimum infiltration rate | 2.5 mm/h |
| Green–Ampt Model | Suction head | 290.068 mm |
| Green–Ampt Model | Conductivity | 2.5 mm/h |
| Green–Ampt Model | Initial loss | 0.108% |
| Conduit Manning n-value | 0.011~0.015 | |
| Layer | Parameter | Permeable Concrete Pavers | Permeable Plastic Pavers | Permeable Percolation Plates | Permeable Brick Pavers | Permeable Parking |
|---|---|---|---|---|---|---|
| Surface | Berm Height (mm) | 0 | 0 | 50 | 0 | 20 |
| Vegetation Volume Fraction | 0 | 0 | 0 | 0 | 0.15 | |
| Surface’s roughness | 0.11 * | 0.11 * | 0.11 * | 0.11 * | 0.11 * | |
| Surface Slope (%) | 1 * | 1 * | 1 * | 1 * | 1 * | |
| Pavement | Thickness (mm) | 100 | 120 | 182 | 190 | 180 |
| Void radio | 0.15 * | 0.15 * | 0.15 * | 0.15 * | 0.15 * | |
| Permeability (mm/h) | 100 * | 100 * | 100 * | 100 * | 100 * | |
| Storage | Thickness | 300 | 300 | 300 | 200 | 300 |
| Void radio | 0.75 * | 0.75 * | 0.75 * | 0.75 * | 0.75 * | |
| Seepage rate (mm/h) | 300 | 300 | 300 | 300 | 300 |
| Layer | Parameter | Bio-Retention Cell | Vegetative Swale |
|---|---|---|---|
| Surface | Berm Height (mm) | 100 | 200 |
| Vegetation Volume Fraction | 0.15 * | 0.10 | |
| Surface’s roughness | 0.24 | 0.24 | |
| Surface Slope (%) | 8.56 * | 2.50 | |
| Soil | Thickness (mm) | 400 | - |
| Porosity | 0.44 | - | |
| Field Capacity | 0.06 | - | |
| Wilting Point | 0.02 | - | |
| Conductivity (mm/h) | 210 | - | |
| Conductivity Slope (%) | 5 | - | |
| Suction Head | 49 | - | |
| Storage | Thickness | 100 | - |
| Void radio | 0.75 * | - | |
| Seepage rate (mm/h) | 300 | - |
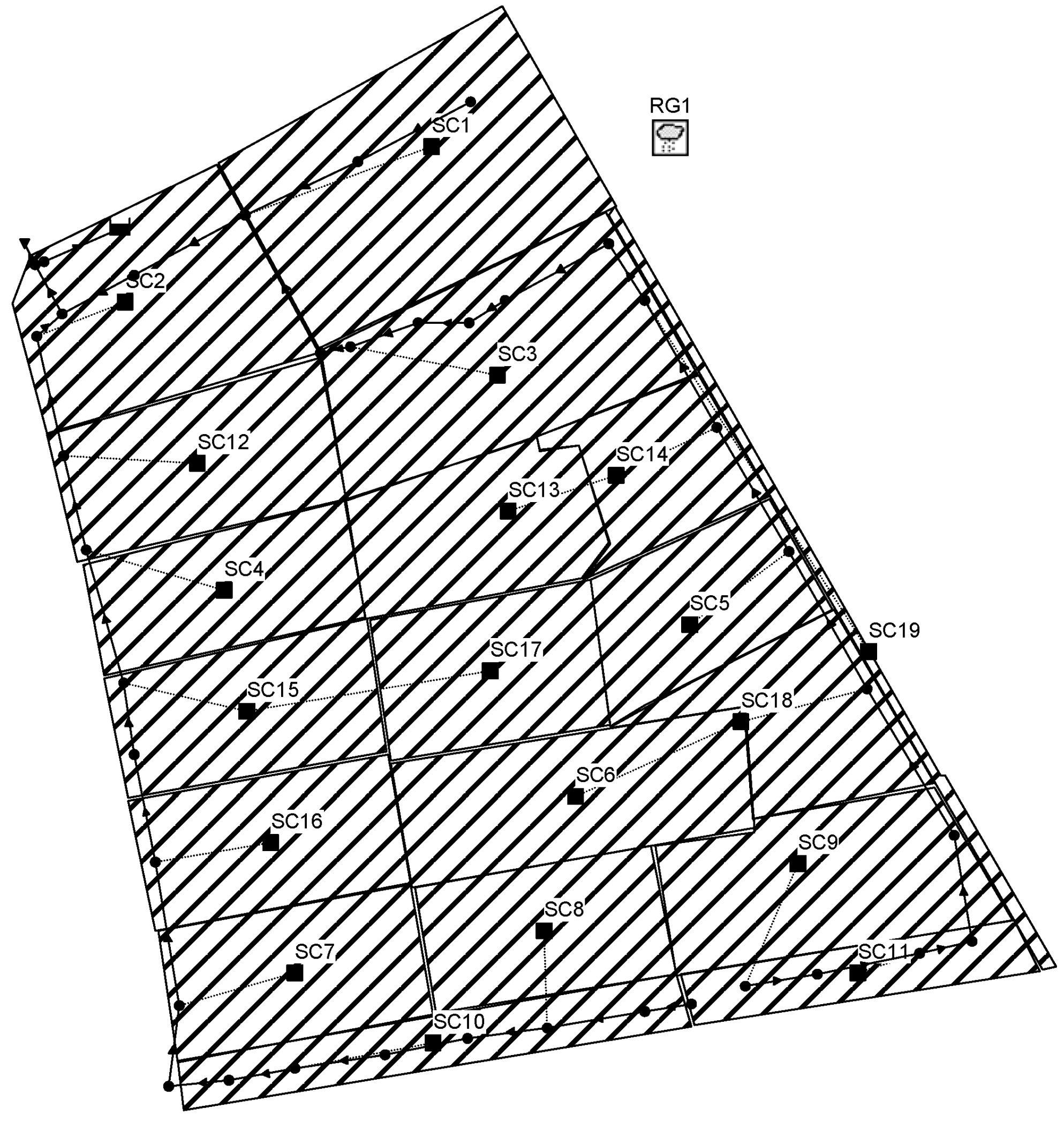
| Sub-Catchment | Areas (m2) | LID-Area (m2) | LID Area Ratio | % Impervious | ||
|---|---|---|---|---|---|---|
| Permeable Pavement | Bio-Retention Cell | Vegetative Swale | ||||
| SC1 | 4121 | 1825 | 372 | / | 0.53 | 45 |
| SC2 | 2675 | 866 | 830 | / | 0.63 | 37 |
| SC3 | 3289 | 315 | 1028 | / | 0.41 | 59 |
| SC4 | 1854 | 549 | 88 | / | 0.34 | 52 |
| SC5 | 1699 | 221 | 360 | / | 0.34 | 61 |
| SC6 | 2371 | 1172 | / | / | 0.49 | 33 |
| SC7 | 1988 | 426 | 467 | / | 0.45 | 45 |
| SC8 | 1992 | 409 | 279 | / | 0.35 | 53 |
| SC9 | 2710 | 309 | 573 | / | 0.33 | 55 |
| SC10 | 1557 | 1530 | / | / | 0.98 | 5 |
| SC11 | 1128 | 1010 | / | / | 0.90 | 10 |
| SC12 | 2240 | 767 | 648 | / | 0.63 | 29 |
| SC13 | 1893 | 1123 | 240 | / | 0.72 | 3 |
| SC14 | 1381 | 177 | 967 | / | 0.83 | 33 |
| SC15 | 1923 | 272 | 621 | / | 0.46 | 47 |
| SC16 | 2038 | 1056 | 368 | / | 0.70 | 41 |
| SC17 | 1938 | 409 | 505 | / | 0.47 | 46 |
| SC18 | 1663 | 342 | 913 | / | 0.75 | 28 |
| SC19 | 568 | 212 | / | 211.83 | 0.75 | 5 |
| Parameter Name | Value | References | ||
|---|---|---|---|---|
| Plowable | Impermeable | Permeable | ||
| Max. Melt Coefficient (mm/h/°C) | 0.000 | 0.020 | 0.020 | [12] |
| Min. Melt Coefficient (mm/h/°C) | 0.001 | 0.100 | 0.150 | [12] |
| Base Temperature (°C) | 0 | 0 | 0 | - |
| Fraction Free Water Capacity | 0.100 | 0.100 | 0.100 | [13] |
| Antecedent Temperature Index (ATI) | 0.5 | User Manual | ||
| Negative Melt Ratio | 0.6 | User Manual | ||
| Design Storms | Runoff Coefficient | Runoff Reduction Rates | |
|---|---|---|---|
| Baseline | LID | ||
| 1 year | 0.86 | 0.15 | 82.32% |
| 3 years | 0.90 | 0.20 | 77.31% |
| 10 years | 0.92 | 0.24 | 74.08% |
| 20 years | 0.93 | 0.25 | 72.71% |
| 50 years | 0.94 | 0.27 | 71.21% |
| 100 years | 0.95 | 0.28 | 70.19% |
| Recurrence (Years) | Rainfall | Baseline | LID Scenario | Flow Reduction Rates | |||
|---|---|---|---|---|---|---|---|
| Peak Flow (mm/h) | Arrival Time (h:mm) | Peak Flow Rate (m3/s) | Arrival Time (h:mm) | Peak Flow Rate (m3/s) | Arrival Time (h:mm) | ||
| 1 | 169.51 | 0:24 | 0.58 | 0:31 | 0 | 0:00 | 100.0% |
| 3 | 234.22 | 0:24 | 0.83 | 0:31 | 0.03 | 1:41 | 96.4% |
| 10 | 305.12 | 0:24 | 1.11 | 0:29 | 0.07 | 1:06 | 93.7% |
| 20 | 345.95 | 0:24 | 1.18 | 0:28 | 0.1 | 0:59 | 91.5% |
| 50 | 399.91 | 0:24 | 1.22 | 0:28 | 0.13 | 0:55 | 89.5% |
| 100 | 440.74 | 0:24 | 1.24 | 0:28 | 0.15 | 0:51 | 87.9% |
| Year | Rainfall (mm) | Infiltration Methods | Runoff Depth (mm) | Runoff Coefficients | ||
|---|---|---|---|---|---|---|
| Baseline | LID Scenario | Baseline | LID Scenario | |||
| Dry Year (2014) | 446 | Horton | 202.2 | 77.5 | 0.453 | 0.174 |
| Green–Ampt | 202.0 | 47.3 | 0.453 | 0.106 | ||
| Average Year (2018) | 607.3 | Horton | 337.0 | 111 | 0.555 | 0.183 |
| Green–Ampt | 336.5 | 77.2 | 0.554 | 0.127 | ||
| Wet Year (2016) | 890.8 | Horton | 549.2 | 160.8 | 0.617 | 0.181 |
| Green–Ampt | 547.2 | 121.9 | 0.614 | 0.137 | ||
| Water Balance | Baseline | LID Scenario |
|---|---|---|
| Initial LID water storage (mm) | \ | 1.91 |
| Total precipitation (mm) | 65.70 | 65.70 |
| Evaporation (mm) | 6.60 | 12.53 |
| Infiltration (mm) | 10.11 | 42.46 |
| Surface runoff (mm) | 49.03 | 11.04 |
| Final water storage (mm) | 0.00 | 1.91 |
| Year | Precipitation depths (mm) | ||
|---|---|---|---|
| Summer | Winter | Total | |
| 2014 | 394.1 | 52.3 | 446.4 |
| 2018 | 559.5 | 47.8 | 607.3 |
| 2016 | 837.4 | 53.4 | 890.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, S.; Feng, Y.; Xue, L.; Ma, Z.; Tian, L.; Sun, H. Hydrologic Performance of Low Impact Developments in a Cold Climate. Water 2022, 14, 3610. https://doi.org/10.3390/w14223610
Xiao S, Feng Y, Xue L, Ma Z, Tian L, Sun H. Hydrologic Performance of Low Impact Developments in a Cold Climate. Water. 2022; 14(22):3610. https://doi.org/10.3390/w14223610
Chicago/Turabian StyleXiao, Shunlin, Youcan Feng, Lijun Xue, Zhenjie Ma, Lin Tian, and Hongliang Sun. 2022. "Hydrologic Performance of Low Impact Developments in a Cold Climate" Water 14, no. 22: 3610. https://doi.org/10.3390/w14223610





