Repurposing of a Closed Surface Coal Mine with Respect to Pit Lake Development
Abstract
:1. Introduction
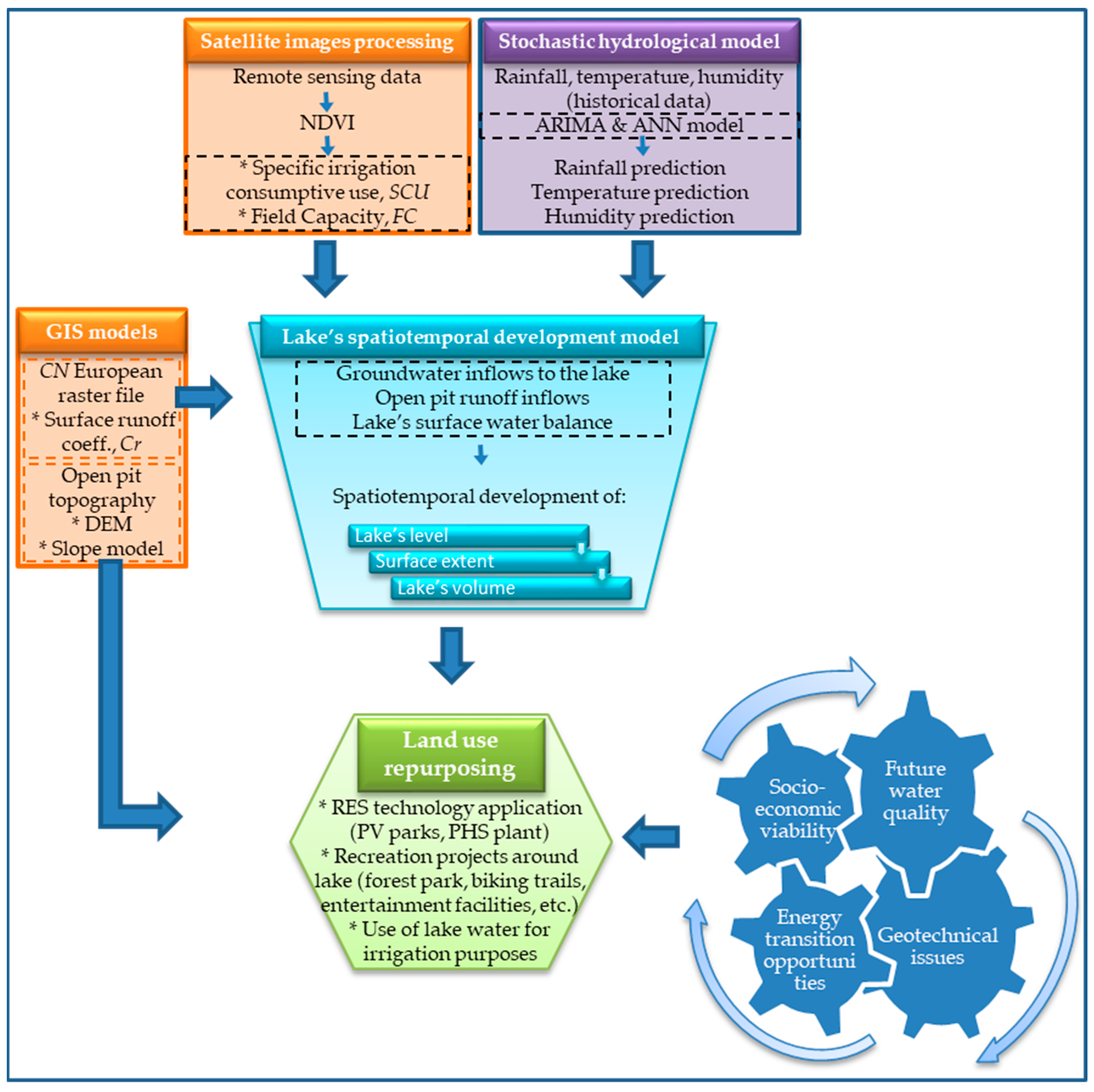
2. Materials and Methods
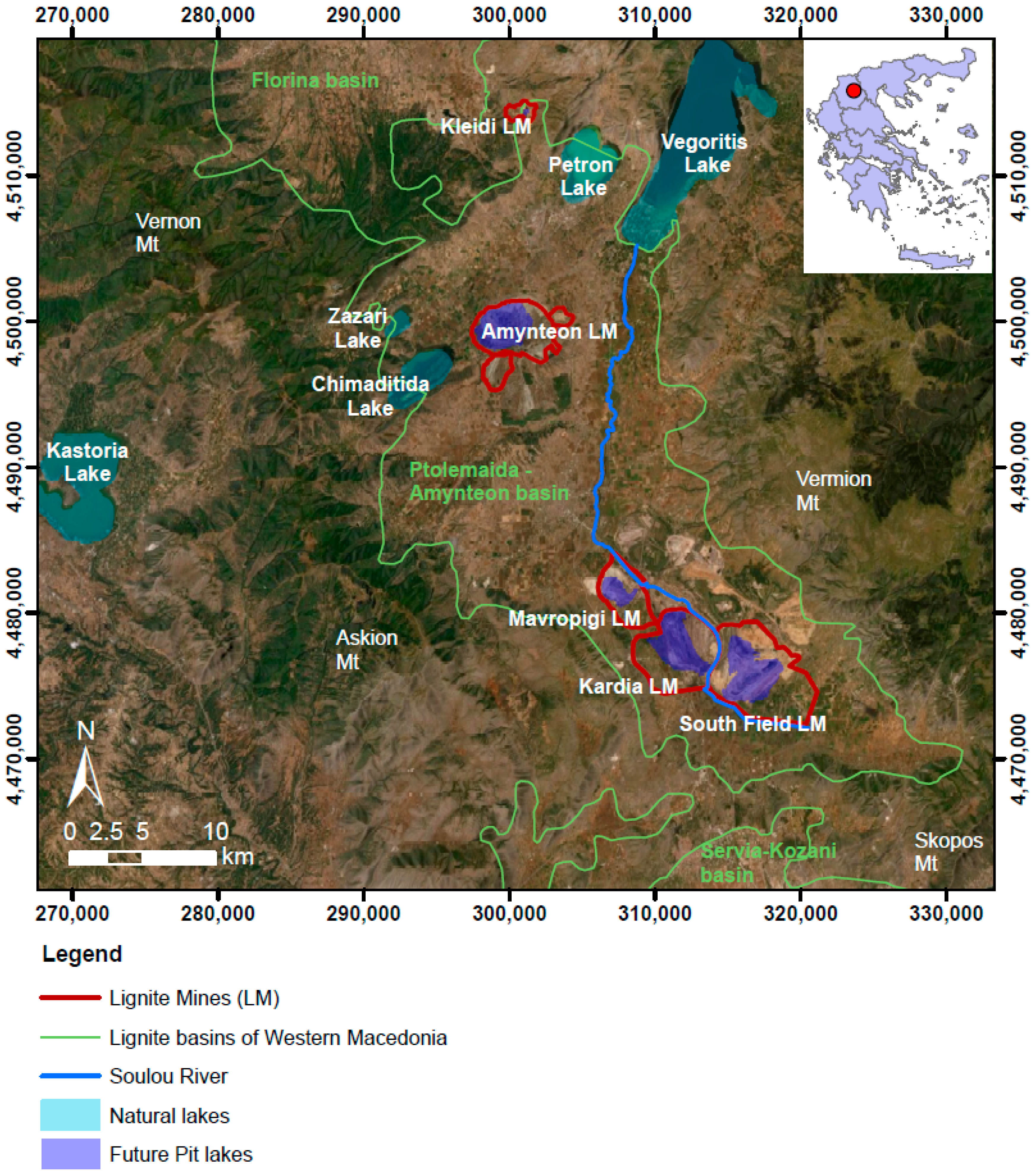
2.1. Research Area—Morphology of the Basin
2.2. Hydrological and Hydrogeological Setting
2.3. Conceptual Model for the Pit Lake Long-Term Water Balance
2.3.1. Groundwater Inflows
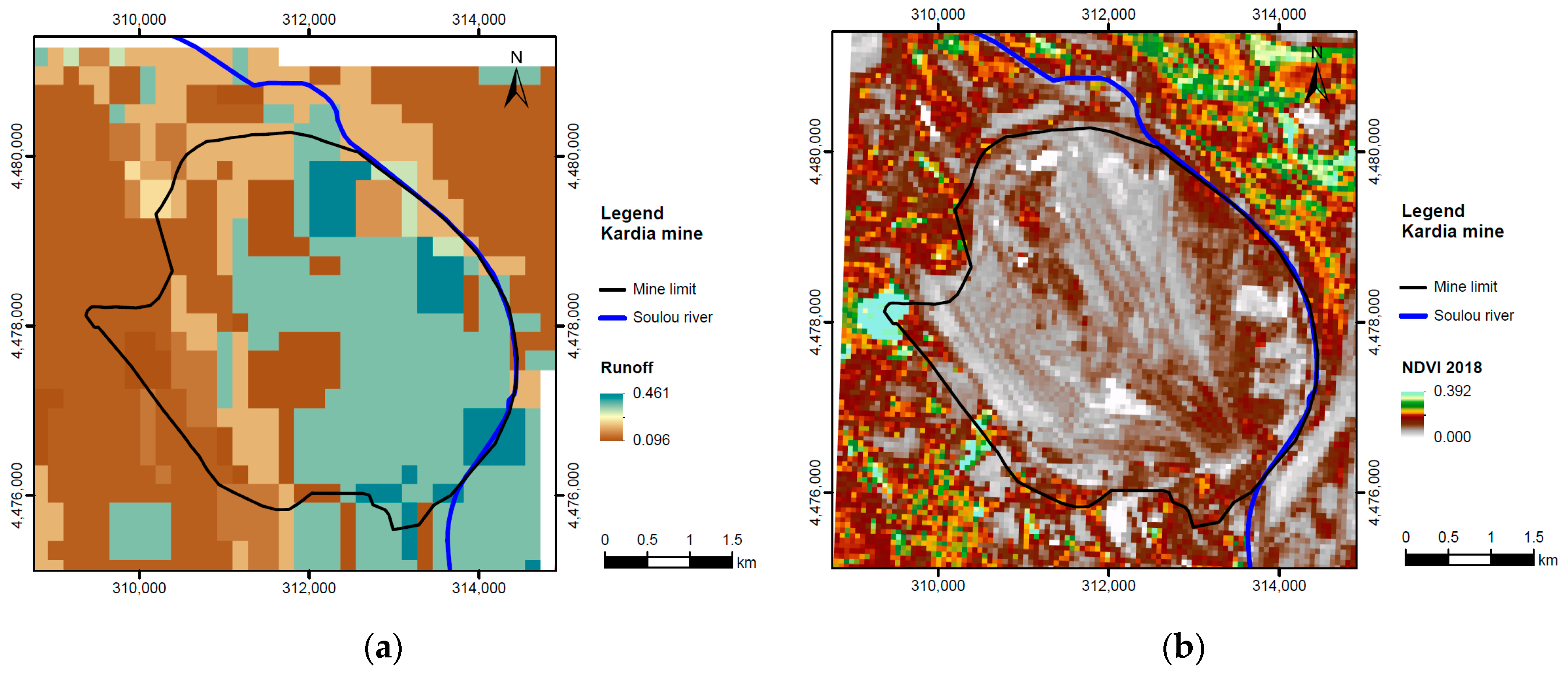
2.3.2. Surface Runoff
2.3.3. Water Losses from the Lake’s Surface
2.3.4. Spatiotemporal Development of the Pit Lake
2.4. Energy Transition Strategies in the Post-Mining Era
2.5. Economic Value
2.6. Geotechnical Issues to Be Considered in the Post-Mining Design
3. Results and Discussion
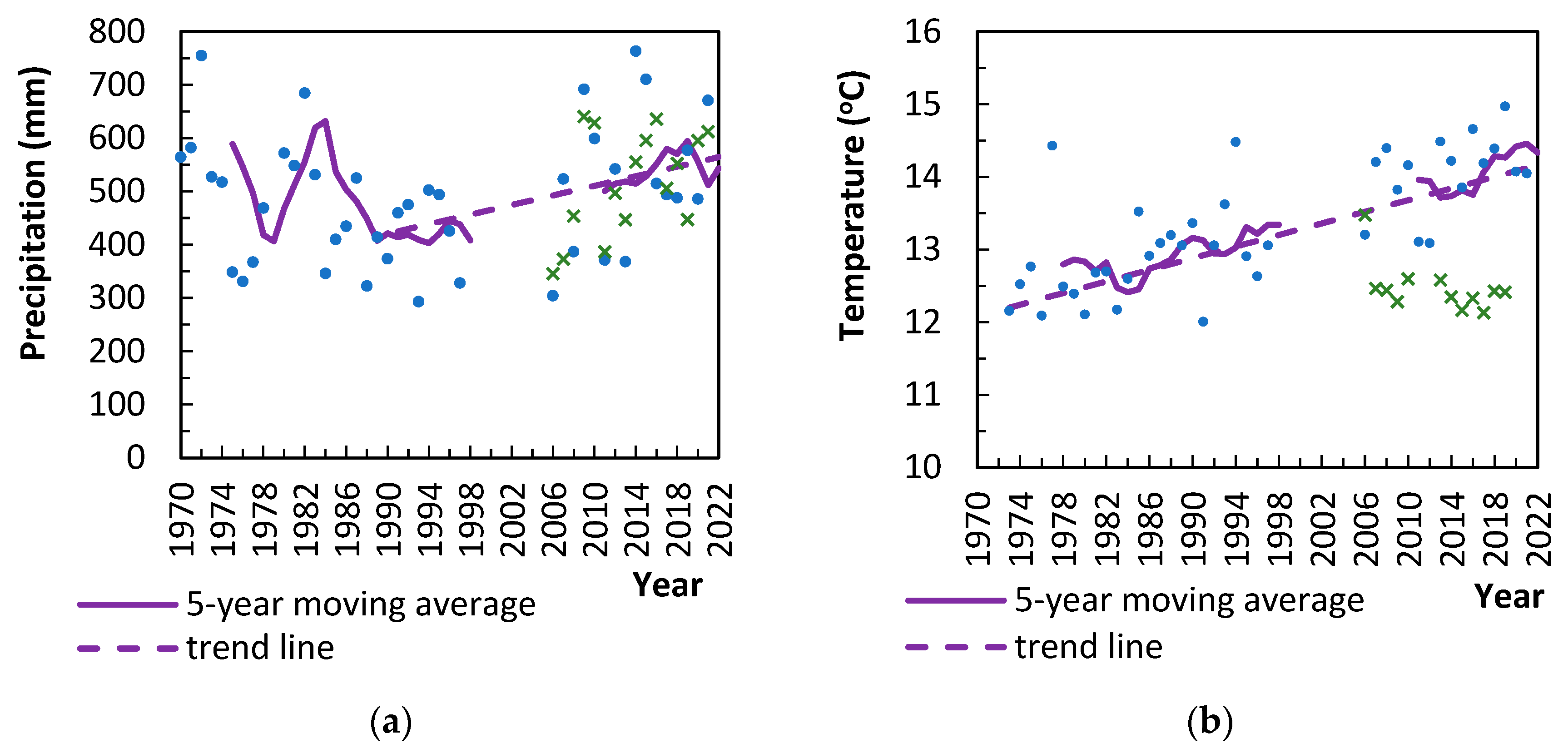
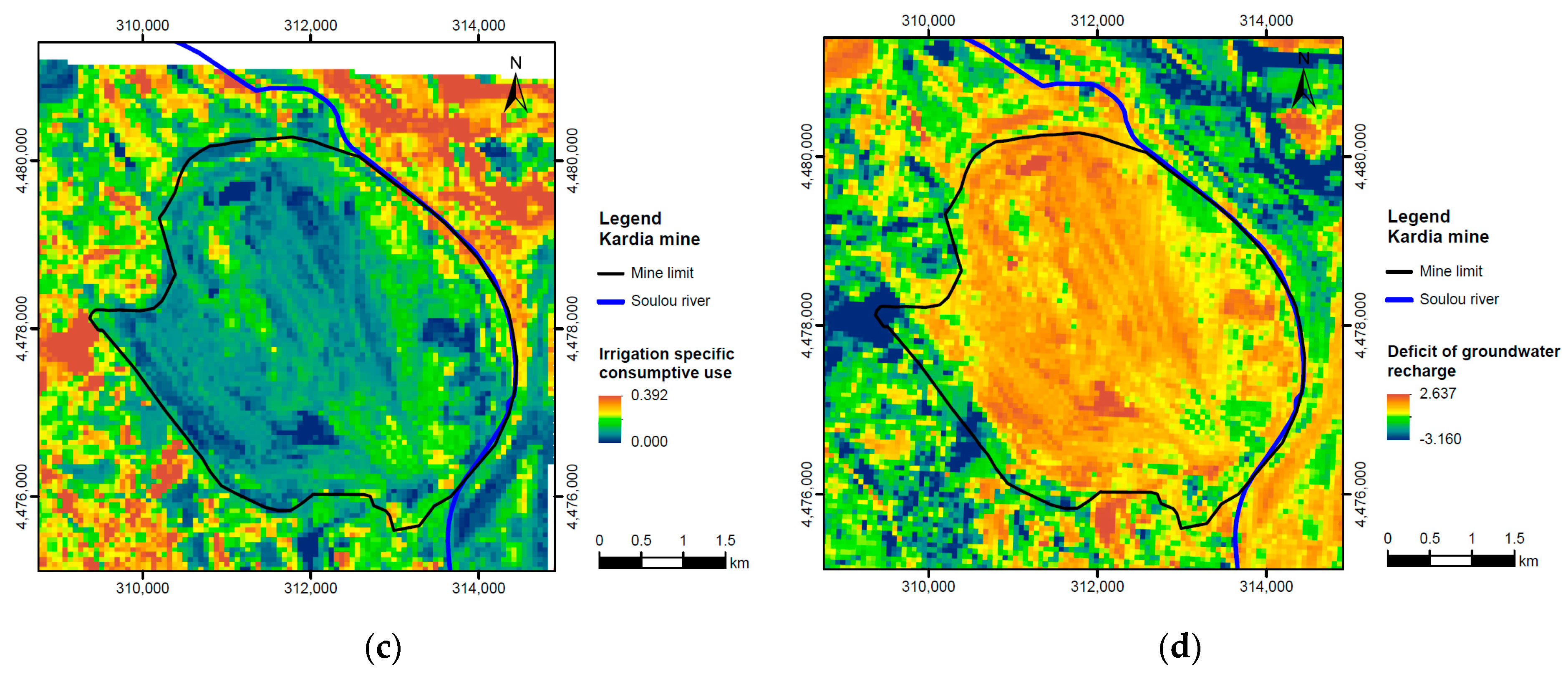
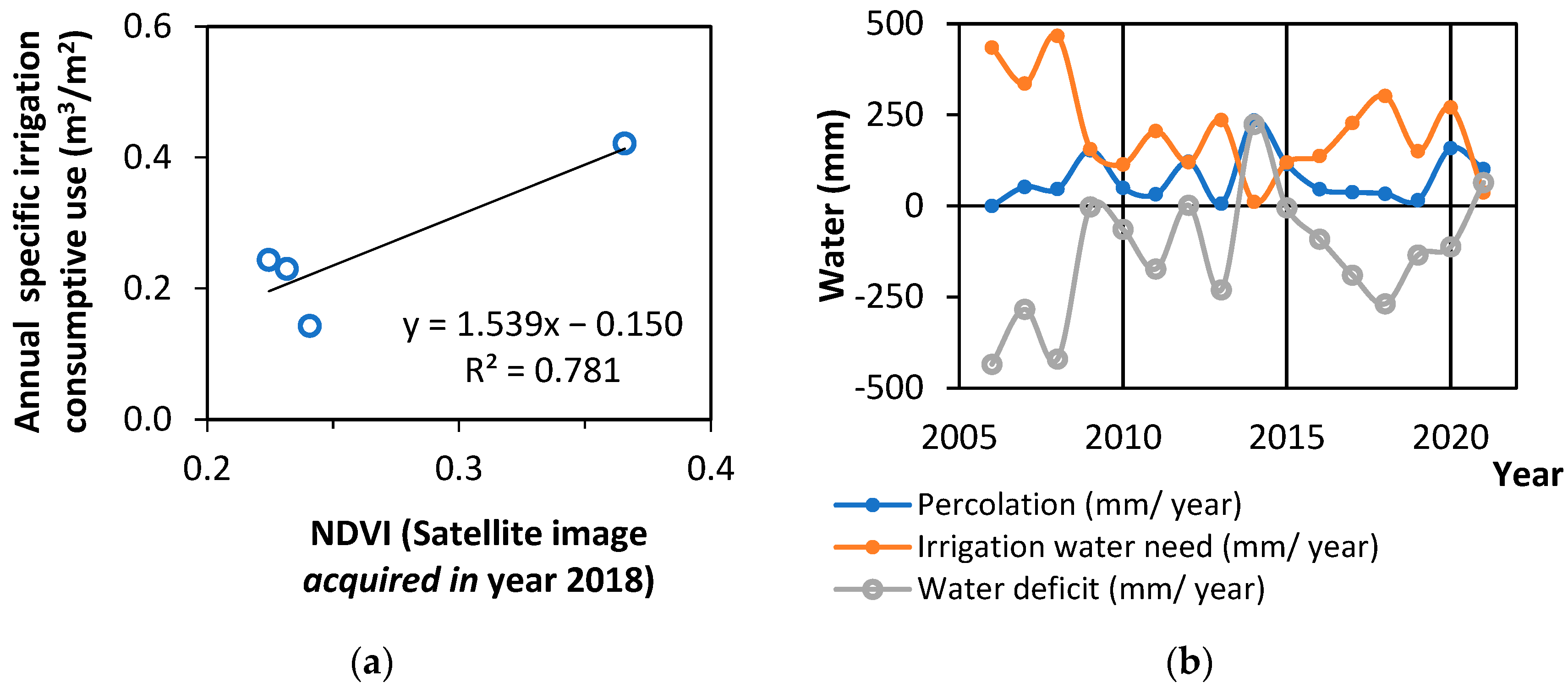
3.1. Water Flux Trends and Forecast of Lake’s Spatiotemporal Development
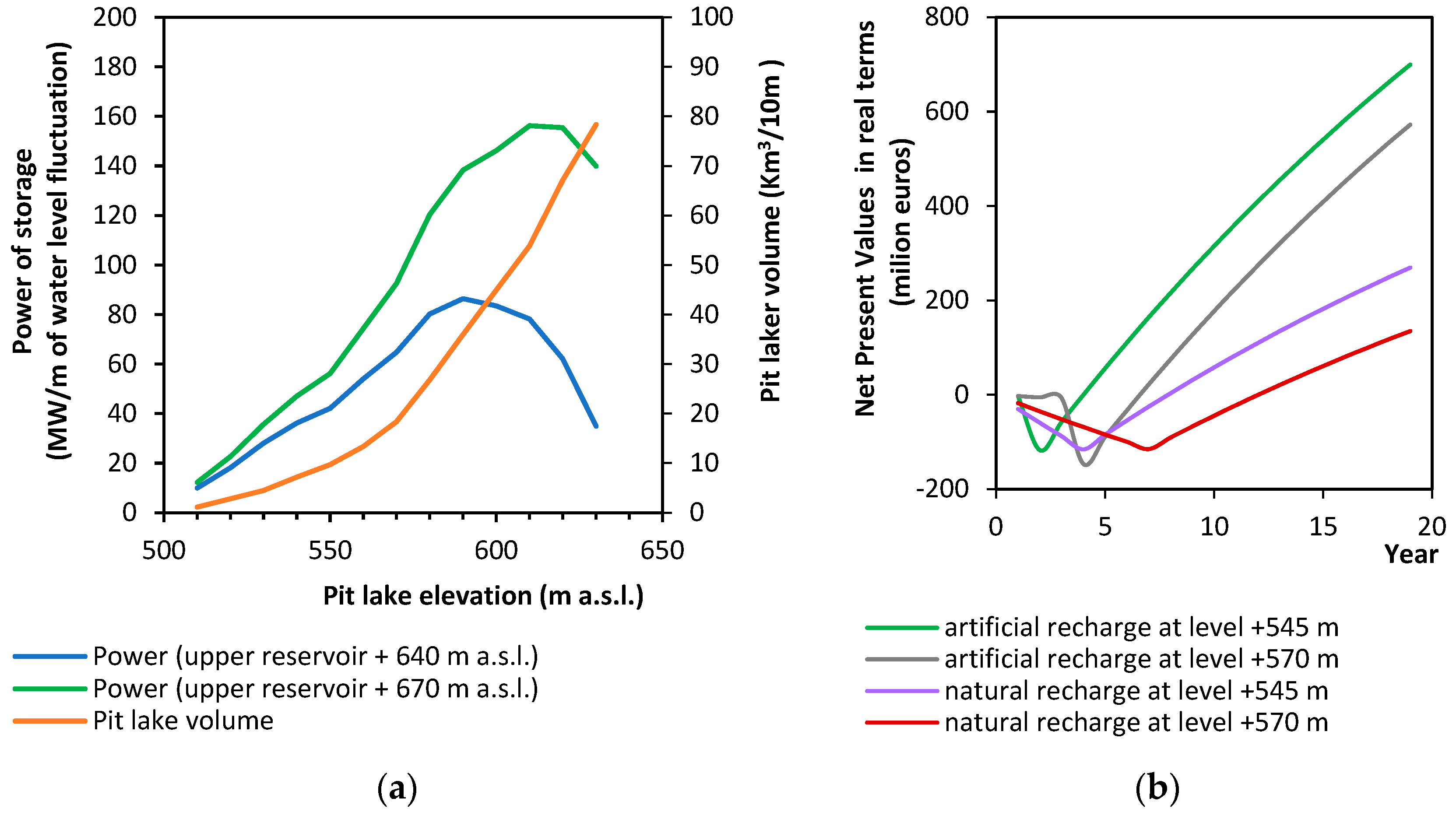
3.2. Evaluation of Potential Land Use Repurposing Scenarios
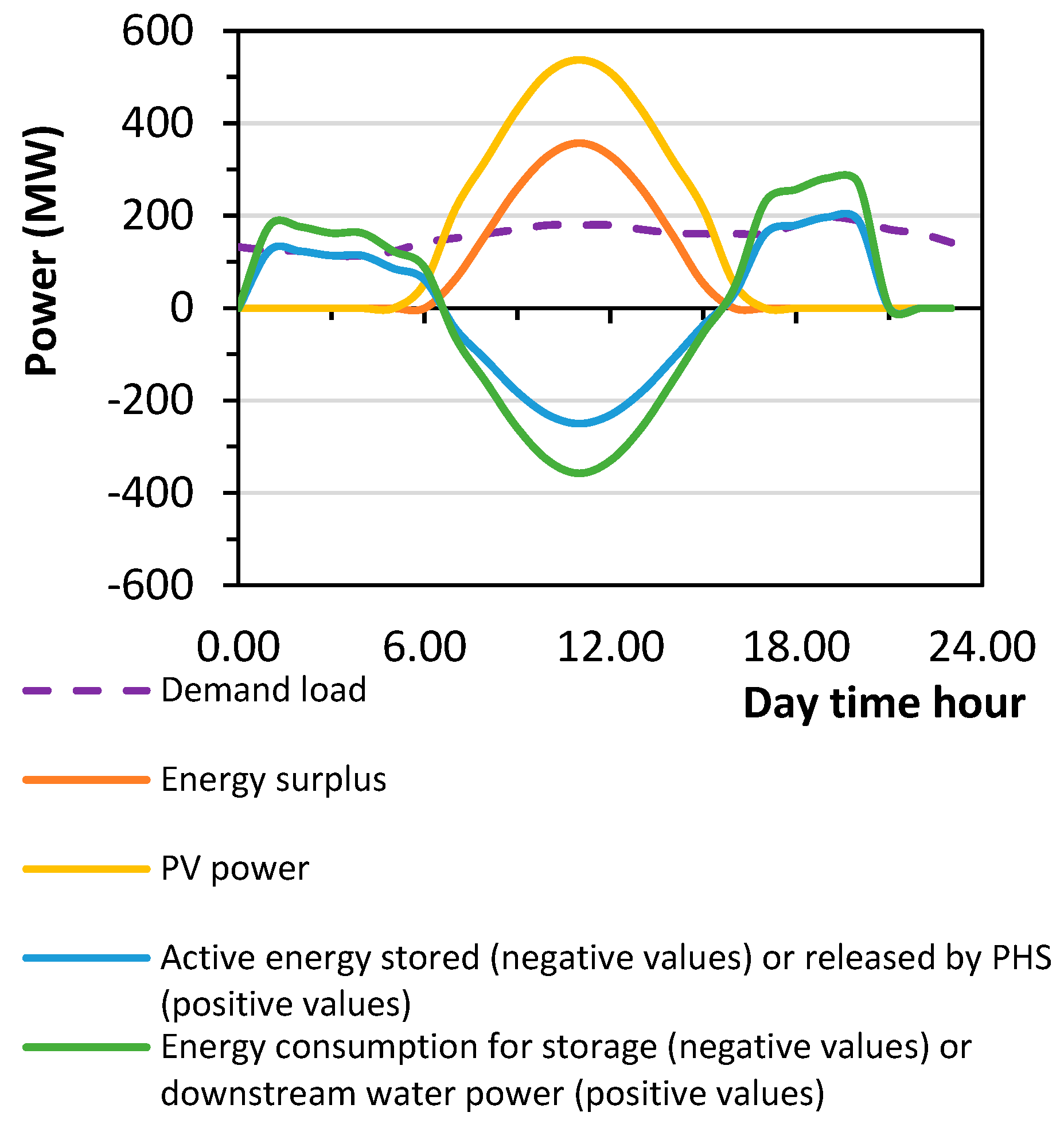
3.3. PHS Plant Efficiency Potential
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- European Commission. A Clean Planet for All a European Strategic Long-Term Vision for a Prosperous, Modern, Competitive and Climate Neutral Economy; Document EUR-Lex-52018DC0773. COM(2018) 773 Final; Publications Office of the European Union: Brussels, Belgium, 2018. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:52018DC0773 (accessed on 11 January 2021).
- European Commission. The European Green Deal; Document EUR-Lex-52019DC0640. COM(2019) 640 Final; Publications Office of the European Union: Brussels, Belgium, 2019. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:52019DC0640&from=EN (accessed on 11 January 2021).
- Sokratidou, A.; Gkouvatsou, E.; Roumpos, C.; Perdiou, A.; Tsagkarakis, G.; Kaimaki, S. Innovative Approaches to Coal Surface Mine Sites Rehabilitation: A Case Study of Megalopolis Lignite Fields. In Proceedings of the 14th International Symposium of Continuous Surface Mining, Thesaloniki, Greece, 24 September 2018; Sideri, D., Paraskevis, N., Eds.; pp. 437–452. [Google Scholar]
- Pachauri, R.K.; Mayer, L.; Intergovernmental Panel on Climate Change (Eds.) Climate Change 2014: Synthesis Report; IPCC: Geneva, Switzerland, 2015; ISBN 978-92-9169-143-2. Available online: https://climate-adapt.eea.europa.eu/countries-regions/countries/greece (accessed on 11 January 2021).
- Bistline, J.E.T.; Blanford, G.J. Value of Technology in the U.S. Electric Power Sector: Impacts of Full Portfolios and Technological Change on the Costs of Meeting Decarbonization Goals. Energy Econ. 2020, 86, 104694. [Google Scholar] [CrossRef]
- Pavloudakis, F.; Roumpos, C.; Karlopoulos, E.; Koukouzas, N. Sustainable Rehabilitation of Surface Coal Mining Areas: The Case of Greek Lignite Mines. Energies 2020, 13, 3995. [Google Scholar] [CrossRef]
- Bódis, K.; Kougias, I.; Taylor, N.; Jäger-Waldau, A. Solar Photovoltaic Electricity Generation: A Lifeline for the European Coal Regions in Transition. Sustainability 2019, 11, 3703. [Google Scholar] [CrossRef] [Green Version]
- Nikolić, Z.; Nikolić, D. Practical Example of Solar and Hydro Energy Hybrid System—The Need for a Reversible Power Plant. In Proceedings of the International Conference on Renewable Electrical Power Sources, Belgrade, Serbia, 2 October 2018; Volume 6, pp. 165–171. [Google Scholar]
- Keenan, J.; Holcombe, S. Mining as a Temporary Land Use: A Global Stocktake of Post-Mining Transitions and Repurposing. Extr. Ind. Soc. 2021, 8, 100924. [Google Scholar] [CrossRef]
- Wessel, M.; Madlener, R.; Hilgers, C. Economic Feasibility of Semi-Underground Pumped Storage Hydropower Plants in Open-Pit Mines. Energies 2020, 13, 4178. [Google Scholar] [CrossRef]
- McCullough, C.; Schultze, M.; Vandenberg, J. Realizing Beneficial End Uses from Abandoned Pit Lakes. Miner 2020, 10, 133. [Google Scholar] [CrossRef] [Green Version]
- Holcombe, S.; Keenan, J. Mining as a Temporary Land Use Scoping Project: Transitions and Repurposing; The Social Aspects of Mine Closure Research Consortium; Centre for Social Responsibility in Mining, Sustainable Minerals Institute: Brisbane, Australia, 2020; Available online: https://www.mineclosure.net/elibrary/mining-as-a-temporary-land-use-industry-led-transitions-and-repurposing (accessed on 13 January 2021).
- Gammons, C.H.; Harris, L.N.; Castro, J.M.; Cott, P.A.; Hanna, B.W. Creating Lakes from Open Pit Mines: Processes and Considerations, Emphasis on Northern Environments. Can. Tech. Rep. Fish. Aquat. Sci. 2826 2009, 106. [Google Scholar]
- Schultze, M. The Filling and Remediation of Pit Lakes in Former Open Cast Lignite Mines. Ph.D. Dissertation, Tech Univ Braunschweig Fac Archit Constr Eng Environ Sci, Braunschweig, Germany, 2012. [Google Scholar]
- McCullough, C.D. Rehabilitation of Lake Kepwari: A Previously Acidic Mine Lake in Western Australia. In Proceedings of the IMWA—Mine Water Management for Future Generations; Stanley, P., Wolkersdorfer, C., Wolkersdorfer, K., Eds.; Cardiff University: Cardiff, Wales, UK, 2021; pp. 346–351. Available online: https://www.imwa.info/imwaconferencesandcongresses/proceedings/325-proceedings-2021.html (accessed on 20 January 2022).
- Lund, M.; van Etten, E.; Polifka, J.; Vasquez, M.Q.; Ramessur, R.; Yangzom, D.; Blanchette, M.L. The Importance of Catchments to Mine-Pit Lakes: Implications for Closure. Mine Water Environ. 2020, 39, 572–588. [Google Scholar] [CrossRef]
- Lund, M.A.; Blanchette, M. Can Saline Pit Lakes Offer Biodiversity Values at Closure? In Proceedings of the IMWA—Mine Water Management for Future Generations; Stanley, P., Wolkersdorfer, C., Wolkersdorfer, K., Eds.; Cardiff University: Cardiff, Wales, UK, 2021; pp. 300–306. Available online: https://www.imwa.info/imwaconferencesandcongresses/proceedings/325-proceedings-2021.html (accessed on 20 January 2022).
- Blanchette, M.L.; Lund, M.A. Pit Lakes Are a Global Legacy of Mining: An Integrated Approach to Achieving Sustainable Ecosystems and Value for Communities. Curr. Opin. Environ. Sustain. 2016, 23, 28–34. [Google Scholar] [CrossRef]
- Snashall, D.; Cox, K. Woodlawn Advanced Energy Recovery Centre Scoping Report; Australia. Available online: https://majorprojects.planningportal.nsw.gov.au (accessed on 11 May 2021).
- Pytel, S.; Sitek, S.; Chmielewska, M.; Zuzańska-Żyśko, E.; Runge, A.; Markiewicz-Patkowska, J. Transformation Directions of Brownfields: The Case of the Górnośląsko-Zagłębiowska Metropolis. Sustainability 2021, 13, 2075. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L.; Peng, J. Technical Feasibility Study on a Standalone Hybrid Solar-Wind System with Pumped Hydro Storage for a Remote Island in Hong Kong. Renew. Energy 2014, 69, 7–15. [Google Scholar] [CrossRef]
- Matos, C.R.; Carneiro, J.F.; Silva, P.P. Overview of Large-Scale Underground Energy Storage Technologies for Integration of Renewable Energies and Criteria for Reservoir Identification. J. Energy Storage 2019, 21, 241–258. [Google Scholar] [CrossRef]
- Kavvadas, M.J.; Marinos, P.G. Prediction of Groundwater Table Lowering for Lignite Open-Cast Mining in a Karstic Terrain in Western Macedonia, Greece. Q. J. Eng. Geol. Hydrogeol. 1994, 27, S41–S55. [Google Scholar] [CrossRef] [Green Version]
- Louloudis, G. Hydrogeological conditions of South Lignite Bearing Field of Ptolemais region. Confrontation of groundwater problems during the exploitation. Ph.D. Dissertation, Natl Tech University Athen Sch Min Metall Eng, Athens, Greece, 1991. (In Greek). [Google Scholar]
- Dimitrakopoulos, D.; Grigorakou, E. Aquatic Balance of Vegoritis Lake, West Macedonia, Greece, Ralated to Mining Activity. In Proceedings of the Mine Water 2004—International Mine Water Association Symposium 1; Jarvis, A.P., Dudgeon, B.A., Younger, P.L., Eds.; University of Newcastle: Newcastle upon Tyne, UK, 2004; pp. 201–207. Available online: https://www.imwa.info/imwaconferencesandcongresses/proceedings/189-proceedings-2004.html (accessed on 20 January 2022).
- Koukouzas, N.; Ward, C.R.; Li, Z. Mineralogy of Lignites and Associated Strata in the Mavropigi Field of the Ptolemais Basin, Northern Greece. Int. J. Coal Geol. 2010, 81, 182–190. [Google Scholar] [CrossRef]
- Kavvadas, M.; Roumpos, C.; Schilizzi, P. Stability of Deep Excavation Slopes in Continuous Surface Lignite Mining Systems. Geotech. Geol. Eng. 2020, 38, 791–812. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and Future Köppen-Geiger Climate Classification Maps at 1-Km Resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thornthwaite, C.W.; Mather, J.R. The Water Balance; Drexel Institute of Technology, Laboratory of Climatology, N.J. Publications in Climatology, 1955; Volume VIII, p. 104. Available online: https://www.jstor.org/stable/210739?origin=crossref (accessed on 20 January 2022).
- Kinzelbach, W. Groundwater Modelling: An Introduction with Sample Programs in BASIC; Developments in water science; Elsevier: Amsterdam, The Netherlands; Oxford, UK; New York, NY, USA; Tokyo, Japan, 1986; ISBN 978-0-444-42582-9. [Google Scholar]
- Calvo, J.C. An Evaluation of Thornthwaite’s Water Balance Technique in Predicting Stream Runoff in Costa Rica. Hydrol. Sci. J. 1986, 31, 51–60. [Google Scholar] [CrossRef] [Green Version]
- Blau, R.V.; Hoehn, P.; Hufschmied, P.; Werner, A. Ermittlung Der Grundwasserneubildung Aus Niederschlägen. Gas Wasser Abwasser Schweiz. Ver. Des Gas- Und Wasserfaches 1983, 63, 45–54. [Google Scholar]
- Louloudis, G.; Louloudis, E.; Roumpos, C.; Mertiri, E.; Kasfikis, G.; Chatzopoulos, K. Forecasting Development of Mine Pit Lake Water Surface Levels Based on Time Series Analysis and Neural Networks. Mine Water Environ. 2021, 41, 458–474. [Google Scholar] [CrossRef]
- Manning, J.C. Applied Principles of Hydrology, 3rd ed.; Prentice Hall: Hoboken, NJ, USA, 1997. [Google Scholar]
- Dupuit, J. Theoretical and Practical Studies on the Movement of Water in Open Channels and through Permeable Soils; Dunod: Paris, Frence, 1863. (In French) [Google Scholar]
- Krassakis, P.; Pyrgaki, K.; Gemeni, V.; Roumpos, C.; Louloudis, G.; Koukouzas, N. GIS-Based Subsurface Analysis and 3D Geological Modeling as a Tool for Combined Conventional Mining and In-Situ Coal Conversion: The Case of Kardia Lignite Mine, Western Greece. Mining 2022, 2, 297–314. [Google Scholar] [CrossRef]
- Zhan, G.; Lin Shelp, M. Modified Blaney-Criddle Method—An Empirical Approach to Estimate Potential Evaporation Using Air Temperature; The University of Western Australia: Perth, Australia, 2009; pp. 461–471. [Google Scholar]
- Tasumi, M.; Allen, R.G.; Trezza, R. Calibrating Satellite-Based Vegetation Indices to Estimate Evapotranspiration and Crop Coefficients. In Proceedings of the USCID Water Management Conference; Wichelns, D., Anderson, S.S., Eds.; U.S. Committee on Irrigation and Drainage: Denver, CO, USA, 2006; pp. 103–112. [Google Scholar]
- Memmos, N. Soil Survey Report of the Drained Giannitsa Lake; Ministry of Agriculture, Sector of Land Reclamation Service (YEB, Acronym in Greek): Thessaloniki, Greece, 1973; unpublished. (In Greek)
- Louloudis, G.; Stathopoulos, N. Irrigation Water Consumptive Use Changes in South Ptolemais Lignite Bearing Hydrogeological Basin (Greece) Using NDVI Remotely Sensed Data. In Proceedings of the 15th Internat ional Congress of the Geological Society of Greece; Kranis, H., Ed.; Bulletin of the Geological Society of Greece; Harokopio University of Athens: Athens, Greece, 2019; Volume 7, pp. 611–612. Available online: https://ejournals.epublishing.ekt.gr/index.php/geosociety/issue/view/1265 (accessed on 20 January 2022).
- Panagos, P.; Van Liedekerke, M.; Jones, A.; Montanarella, L. European Soil Data Centre: Response to European Policy Support and Public Data Requirements. Land Use Policy 2012, 29, 329–338. [Google Scholar] [CrossRef]
- McCuen, R.H.; Bondelid, T.R. Relation Between Curve Number and Runoff Coefficient. J. Irrig. Drain. Div. 1981, 107, 395–400. [Google Scholar] [CrossRef]
- Kim, N.; Shin, M.-J. Estimation of Peak Flow in Ungauged Catchments Using the Relationship between Runoff Coefficient and Curve Number. Water 2018, 10, 1669. [Google Scholar] [CrossRef] [Green Version]
- Giandotti, M. Previsione delle piene e delle magre dei corsi d’acqua. In Memorie e Studi Idrografici; Ministero dei LL.PP., Servizio Idrografico Italiano: Rome, Italy, 1934; Volume 8, pp. 107–117. [Google Scholar]
- Penman, H.L. Natural Evaporation from Open Water, Bare Soil and Grass. Proc. R. Soc. Lond. A 1948, 193, 120–145. [Google Scholar] [CrossRef] [Green Version]
- Sellers, W.D. Physical Climatology; The University of Chicago Press: Chicago, IL, USA, 1965. [Google Scholar]
- Tetens, O. About some meteorological terms. J. Geophys. 1930, 6, 297–309. (In German) [Google Scholar]
- Eagleman, J.R. Pan Evaporation, Potential and Actual Evapotranspiration. J. Appl. Meteorol. Climatol. 1967, 6, 482–488. [Google Scholar] [CrossRef]
- Monteith, J.; Unsworth, M. Principles of Environmental Physics: Plants, Animals, and the Atmosphere; Academic Press: Warszawa, Poland, 2013; Volume 4, ISBN 978-0-12-386910-4. [Google Scholar]
- Gass, S.I. Linear Programming. In Encyclopedia of Statistical Sciences; Kotz, S., Read, C.B., Balakrishnan, N., Vidakovic, B., Johnson, N.L., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; p. ess1466.pub2. ISBN 978-0-471-66719-3. [Google Scholar]
- Boretti, A.; Castelletto, S.; Al-Kouz, W.; Nayfeh, J. Capacity Factors of Solar Photovoltaic Energy Facilities in California, Annual Mean and Variability. E3S Web Conf. 2020, 181, 02004. [Google Scholar] [CrossRef]
- Tyralis, H.; Karakatsanis, G.; Tzouka, K.; Mamassis, N. Data and Code for the Exploratory Data Analysis of the Electrical Energy Demand in the Time Domain in Greece. Data Brief 2017, 13, 700–702. [Google Scholar] [CrossRef]
- Koudouris, G.; Dimitriadis, P.; Iliopoulou, T.; Mamassis, N.; Koutsoyiannis, D. Investigation on the Stochastic Nature of the Solar Radiation Process. Energy Procedia 2017, 125, 398–404. [Google Scholar] [CrossRef]
- Faour, K. Farm Budget Handbook, Southern NSW-Irrigated Winter Crops 2001; NSW Agriculture, 2001; Available online: https://lib.k-state.edu/gracroplands/cite.php?CiteID=3758 (accessed on 20 January 2022).
- Gemitzi, A.; Lakshmi, V. Estimating Groundwater Abstractions at the Aquifer Scale Using GRACE Observations. Geosciences 2018, 8, 419. [Google Scholar] [CrossRef] [Green Version]
- Pujades, E.; Orban, P.; Bodeux, S.; Archambeau, P.; Erpicum, S.; Dassargues, A. Underground Pumped Storage Hydropower Plants Using Open Pit Mines: How Do Groundwater Exchanges Influence the Efficiency? Appl. Energy 2017, 190, 135–146. [Google Scholar] [CrossRef]
- Kavvadas, M.; Roumpos, C.; Servou, A.; Paraskevis, N. Geotechnical Issues in Decommissioning Surface Lignite Mines—The Case of Amyntaion Mine in Greece. Mining 2022, 2, 278–296. [Google Scholar] [CrossRef]
- Jiskani, I.M.; Cai, Q.; Zhou, W.; Ali Shah, S.A. Green and Climate-Smart Mining: A Framework to Analyze Open-Pit Mines for Cleaner Mineral Production. Resour. Policy 2021, 71, 102007. [Google Scholar] [CrossRef]
- Richards, L.A.; Allison, L.E.; Brown, J.W.; Hayward, H.E.; Richards, L.A.; Bernstein, L.; Fireman, M.; Pearson, G.A.; Wilcox, L.V.; Bower, C.A.; et al. Diagnosis and Improvement of Saline and Alkali Soils; Agricultural Handbook No. 60; Salinity Laboratory, Soil and Water Conservation Research Branch, Agricultural Research Service, US Department of Agriculture: Washington, DC, USA, 1954; pp. 69–82.
- Wilcox, L.V. Classification and Use of Irrigation Waters; Salinity Laboratory, US Department of Agriculture: Washington, DC, USA, 1955; Circular No. 969; pp. 1–19.
- Wilcox, L.V. The Quality of Water for Irrigation Use; Salinity Laboratory, US Department of Agriculture: Washington, DC, USA, 1948; Technical Bulletin No. 962; pp. 1–40. [CrossRef]








| Hydrological Cycle in Sarigiol Basin (2006–2021) | mm/yr | 106 m3/yr | Precipitation (%) |
|---|---|---|---|
| Mean annual precipitation | 584 | 123 | 100 |
| Mean annual real evaporation | 425 | 90 | 73 |
| Mean annual percolation | 86 | 18 | 15 |
| Mean annual runoff | 72 | 15 | 12 |
| Lake Water Depth (Hw)/Height of the Slope (H) | FS/FSo* |
|---|---|
| 0 | 1.0 |
| 0.1 | <1.0 |
| 0.2 | 1.0 |
| 0.4 | 1.075 |
| 0.6 | 1.25 |
| 0.8 | 1.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Louloudis, G.; Roumpos, C.; Louloudis, E.; Mertiri, E.; Kasfikis, G. Repurposing of a Closed Surface Coal Mine with Respect to Pit Lake Development. Water 2022, 14, 3558. https://doi.org/10.3390/w14213558
Louloudis G, Roumpos C, Louloudis E, Mertiri E, Kasfikis G. Repurposing of a Closed Surface Coal Mine with Respect to Pit Lake Development. Water. 2022; 14(21):3558. https://doi.org/10.3390/w14213558
Chicago/Turabian StyleLouloudis, Georgios, Christos Roumpos, Emmanouil Louloudis, Eleni Mertiri, and Georgios Kasfikis. 2022. "Repurposing of a Closed Surface Coal Mine with Respect to Pit Lake Development" Water 14, no. 21: 3558. https://doi.org/10.3390/w14213558








