Comparison of Different Artificial Intelligence Techniques to Predict Floods in Jhelum River, Pakistan
Abstract
:1. Introduction
2. Materials and Methods
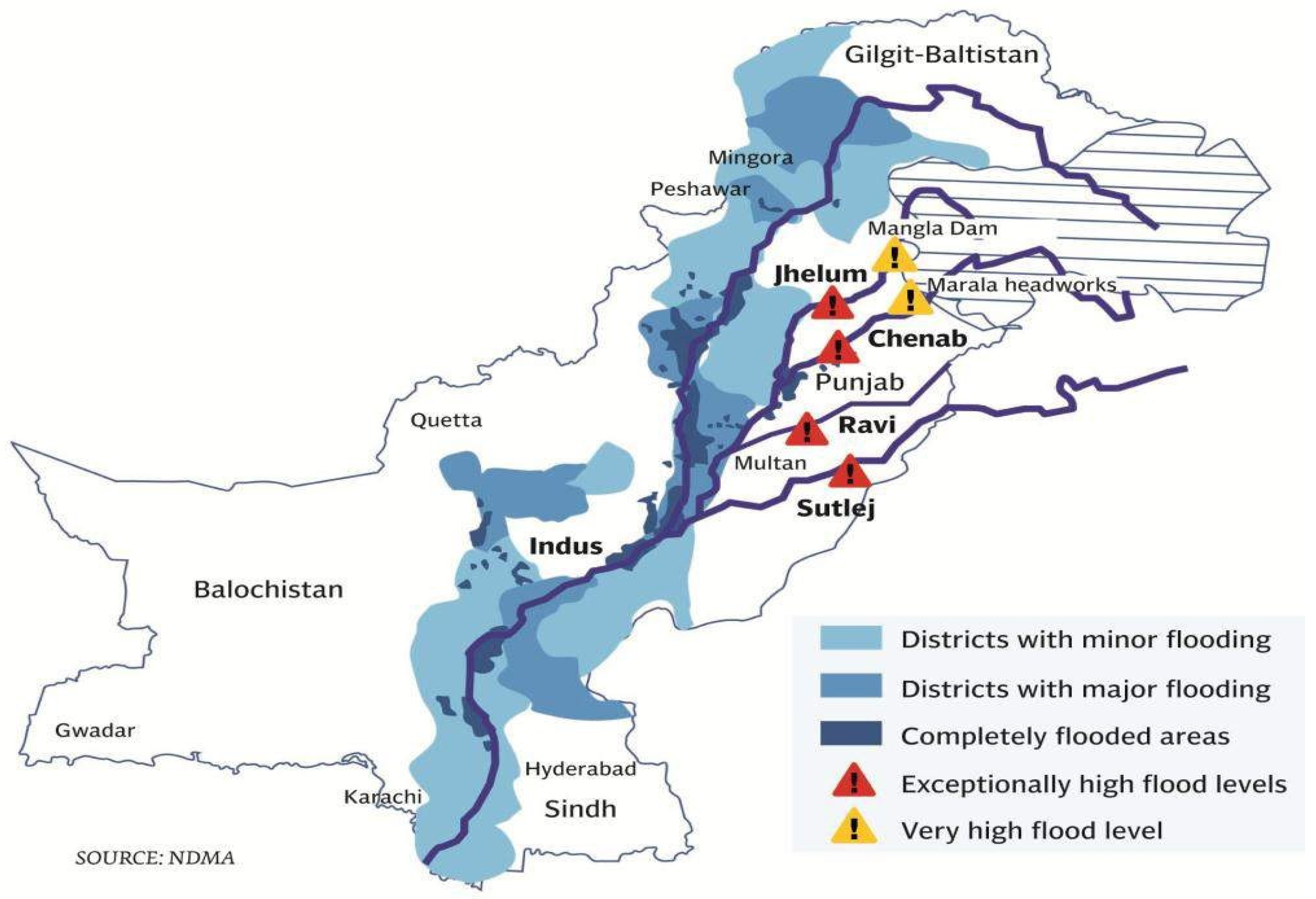
2.1. Study Area and Dataset
2.2. Datasets
2.3. Data Normalization
2.4. Input Combination Selection Using Gamma Test and Advanced Model Identification Techniques
2.5. Model Development
2.5.1. Local Linear Regression (LLR)
2.5.2. Dynamic Local Linear Regression (DLLR)
2.5.3. Artificial Neural Networks (ANNs)
3. Results
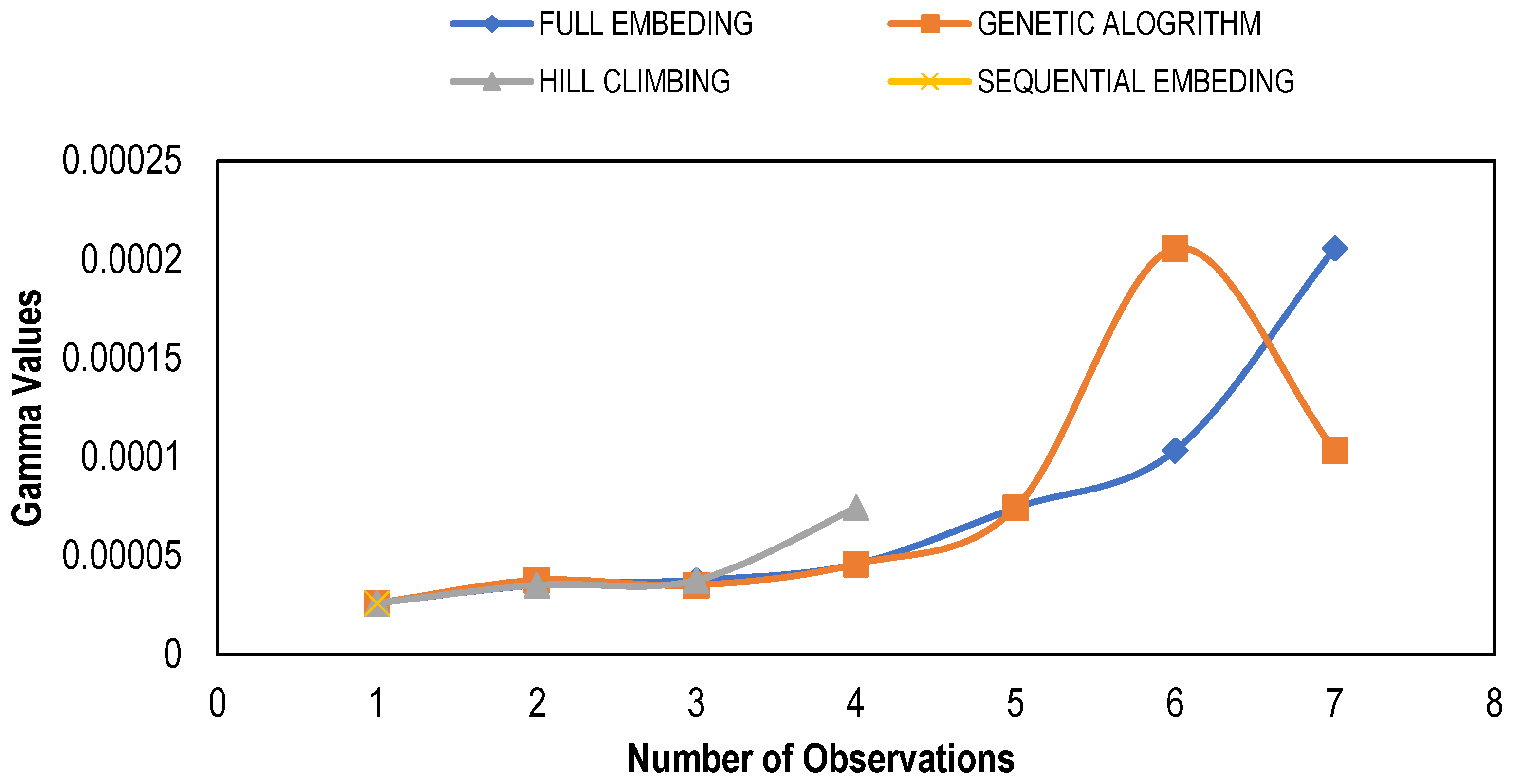
3.1. Gamma Test Results
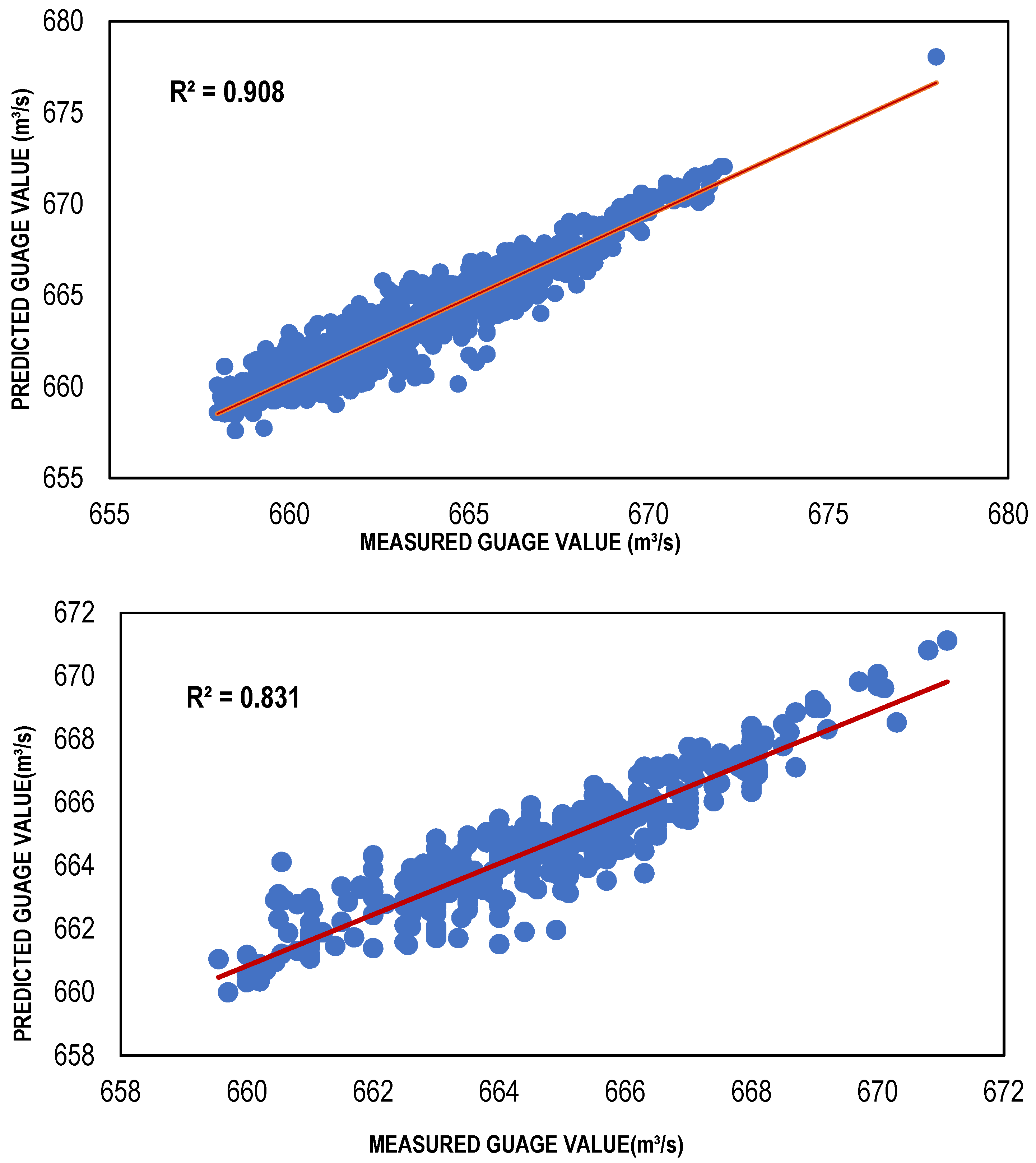
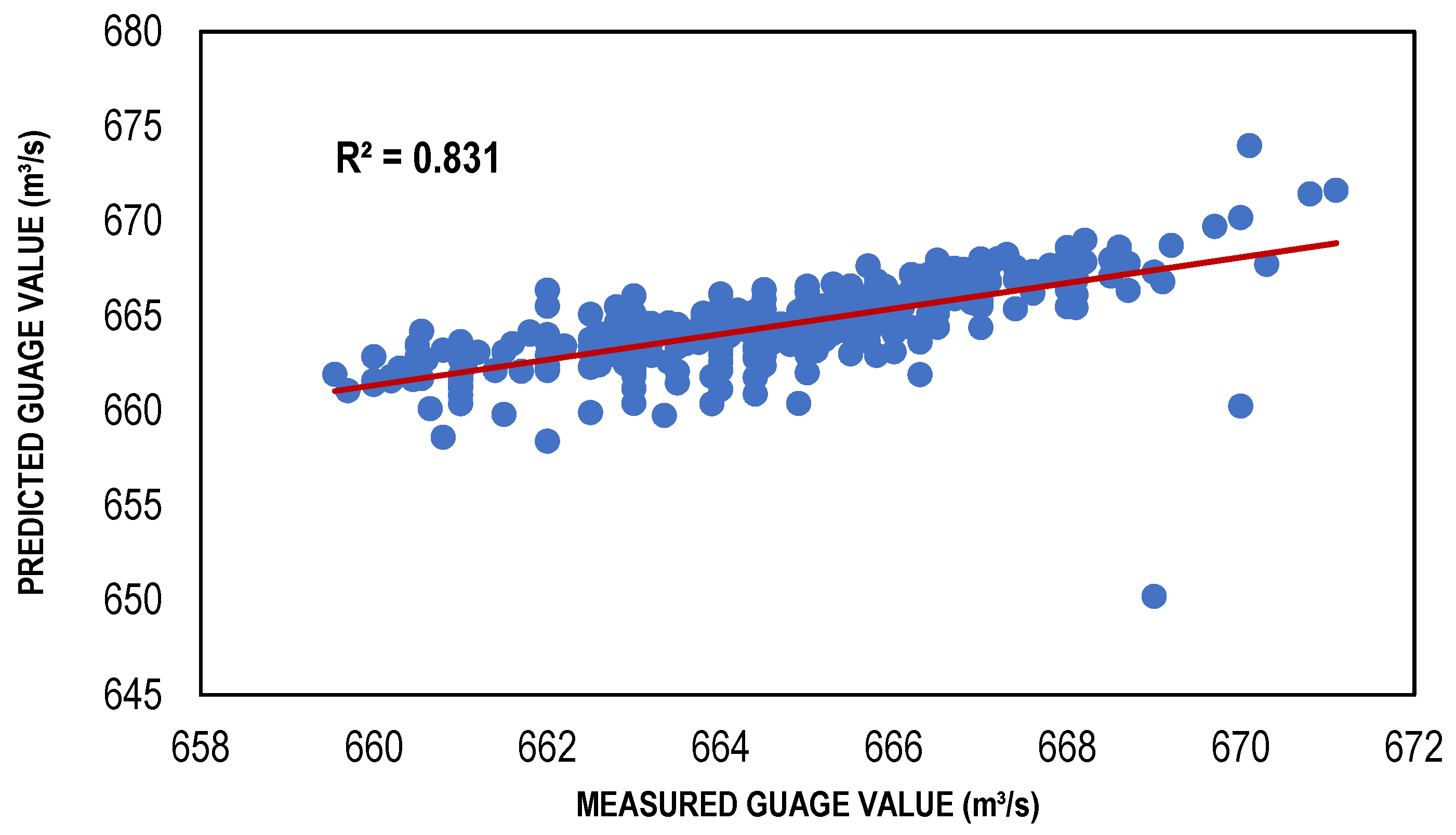
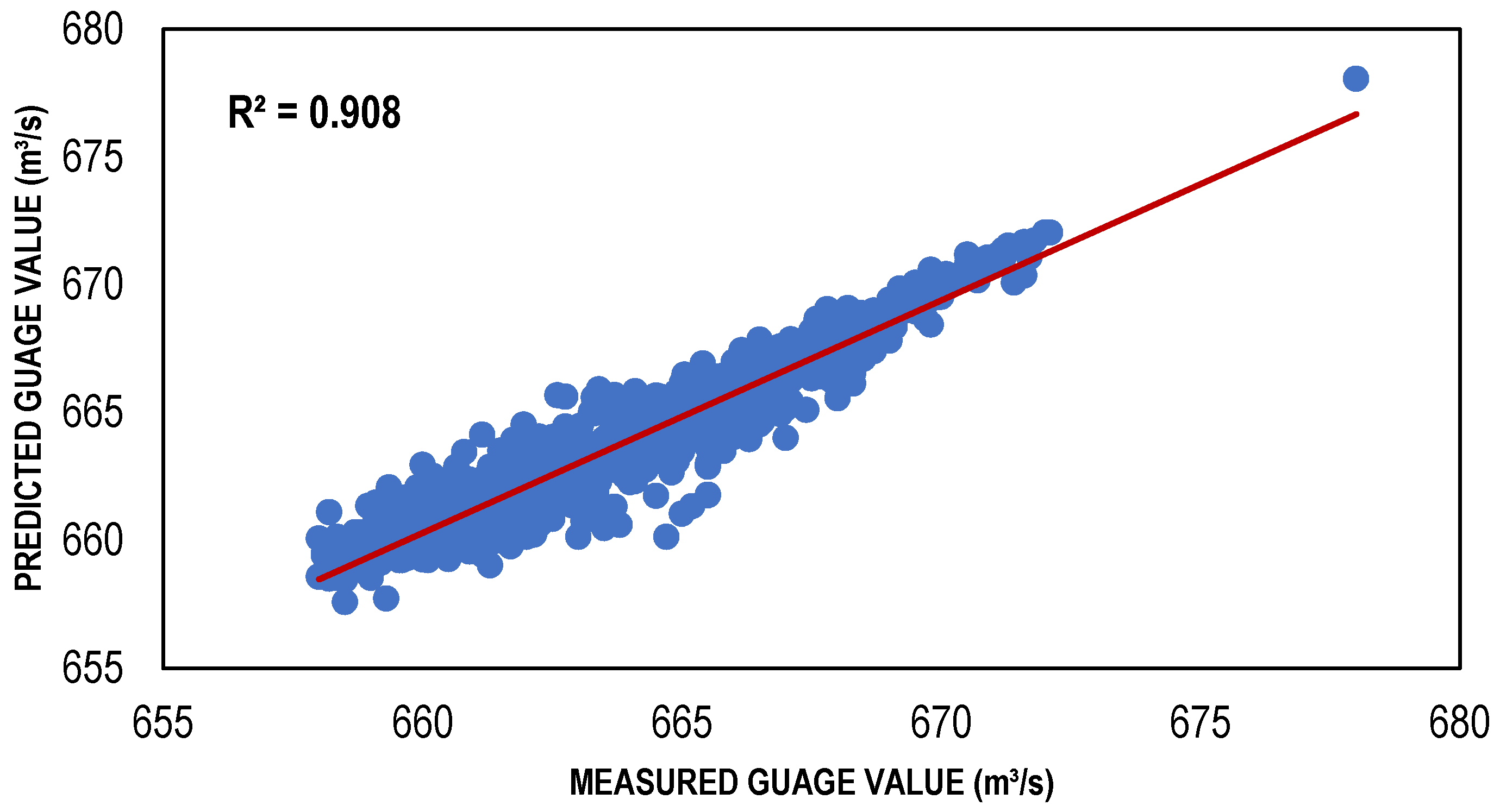
3.2. LLR and DLLR Results
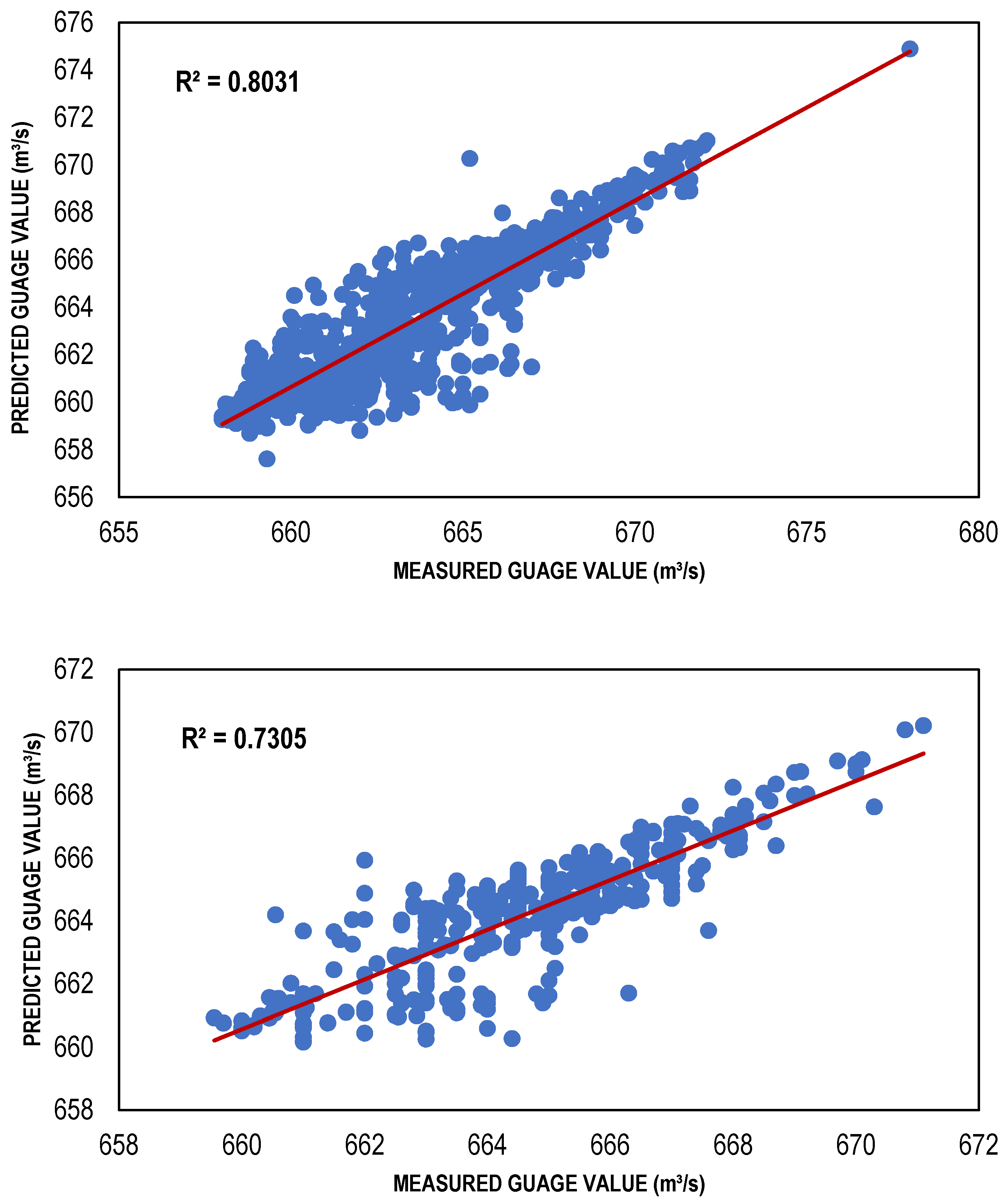
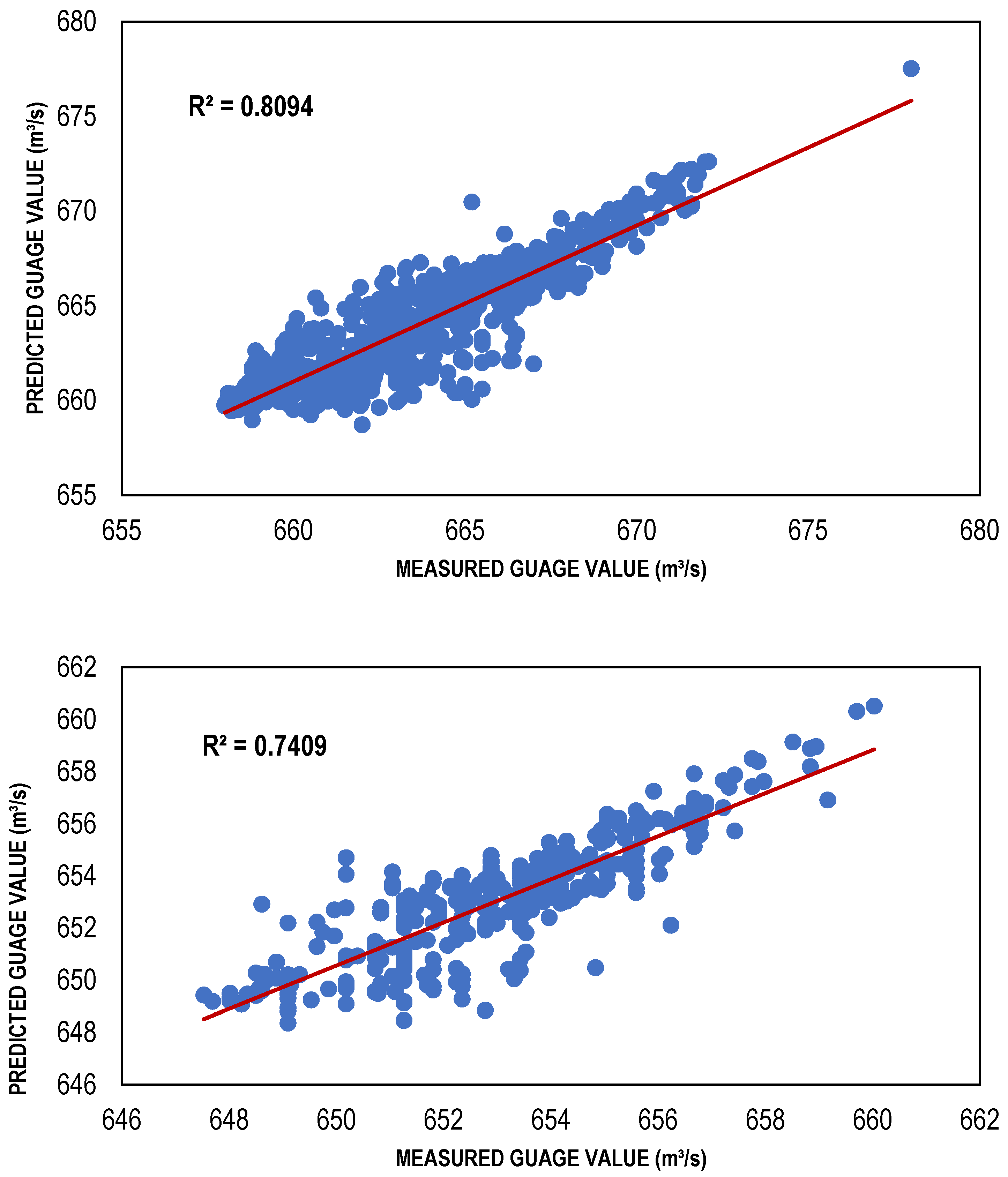
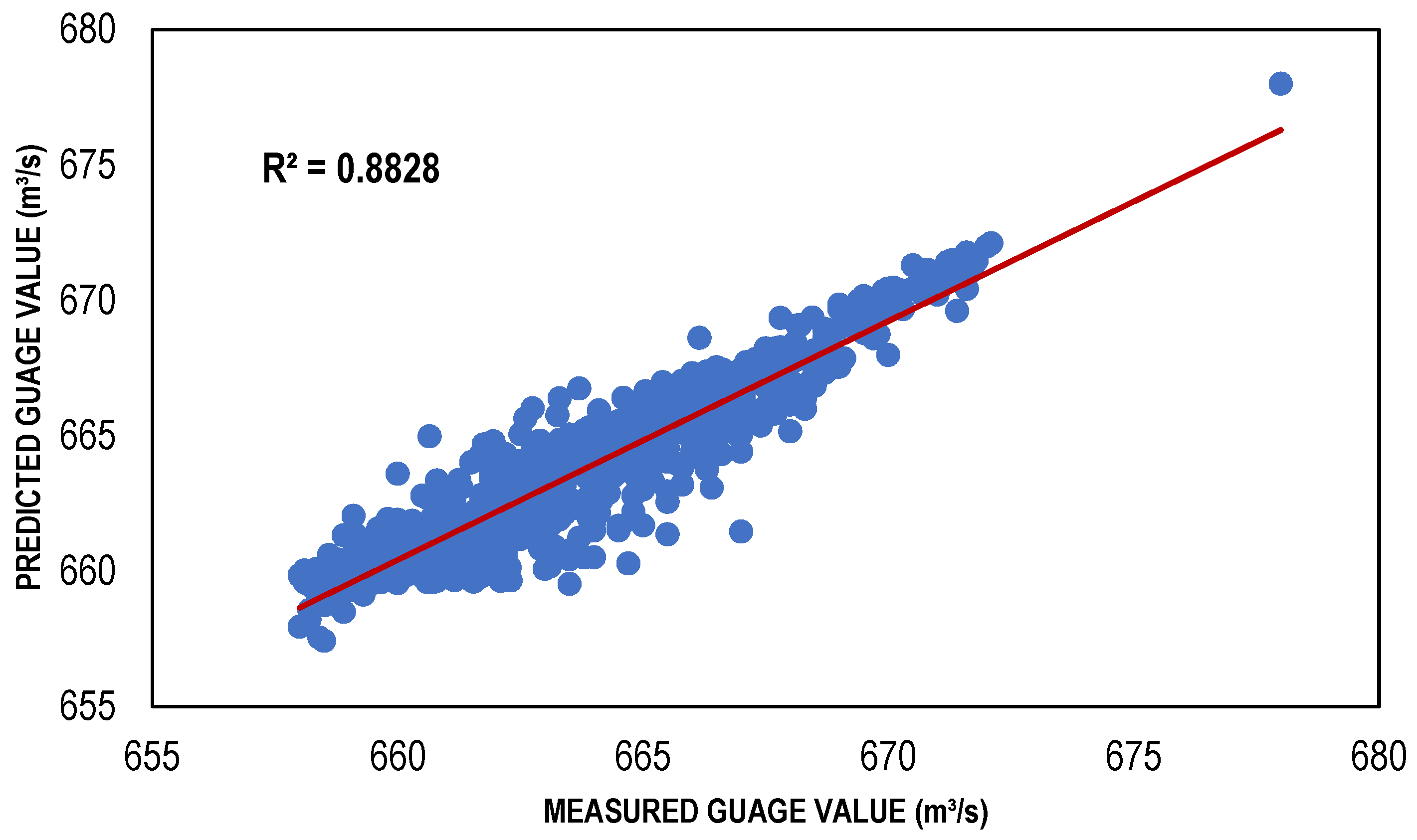
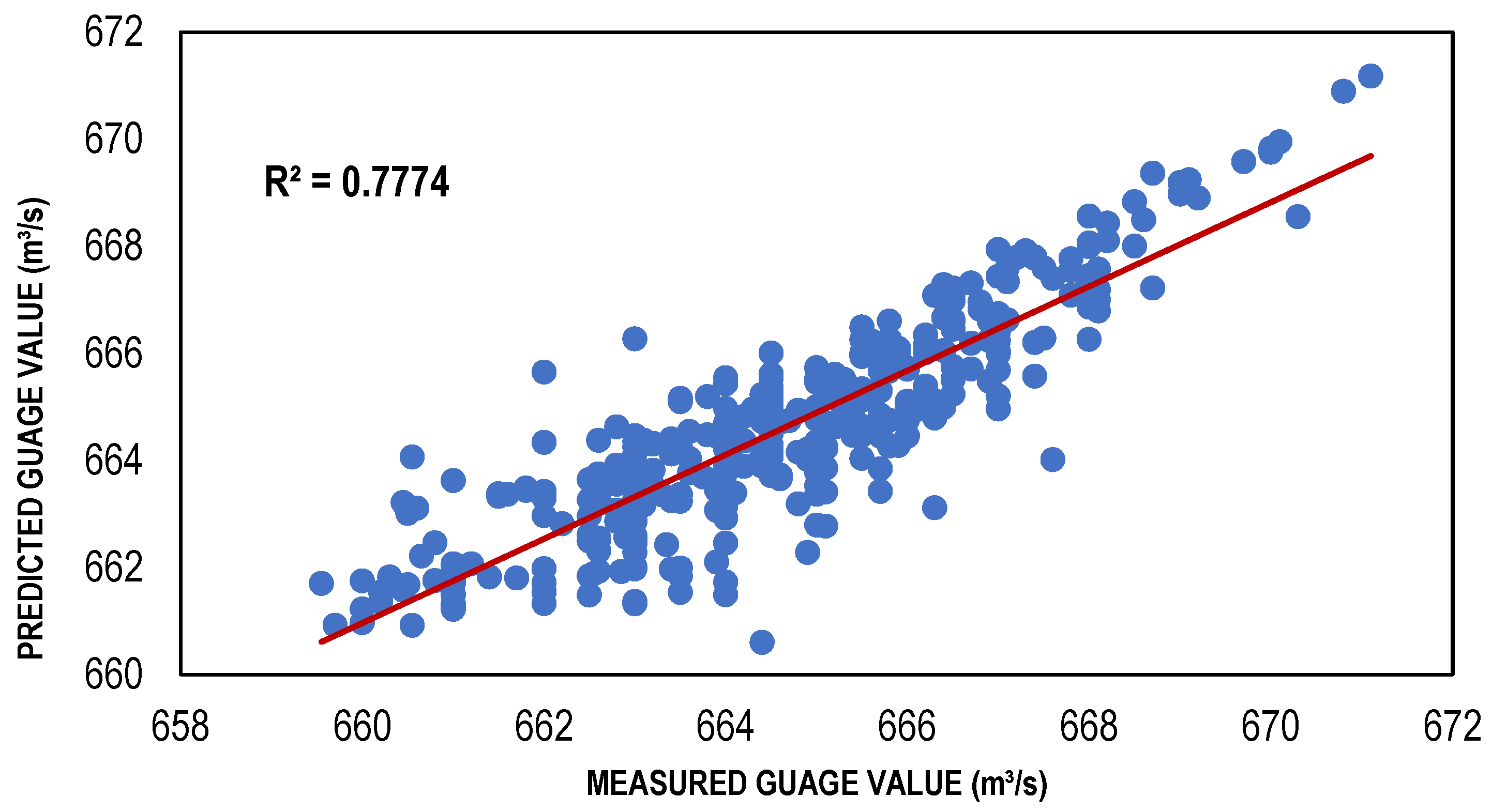
3.3. ANN Results
| Model | Training | |||
|---|---|---|---|---|
| Mask | R sq. | Bias | RMSE | |
| LLR model | 001 | 0.908 | 0.009205 | 1.018017 |
| DLLR model | 001 | 0.908 | −0.01095 | 1.008635 |
| TLBP-based ANN model | 111 | 0.8031 | −0.09179 | 1.493783 |
| CG-based ANN model | 111 | 0.8094 | 0.401287 | 1.520267 |
| BFGS-based ANN model | 111 | 0.8828 | 0.012462 | 1.149249 |
| Model | Testing | |||
| Mask | R sq. | Bias | RMSE | |
| LLR model | 001 | 0.831 | −0.05344 | 0.919695 |
| DLLR model | 001 | 0.831 | −0.16991 | 1.766721 |
| TLBP-based ANN model | 111 | 0.7305 | −0.4131 | 1.238525 |
| CG-based ANN model | 111 | 0.7409 | 0.036029 | 1.251868 |
| BFGS-based ANN model | 111 | 0.7774 | −0.03043 | 1.052597 |
4. Comparison and Discussion
5. Summary & Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sapitang, M.; Ridwan, W.M.; Kushiar, K.F.; Ahmed, A.N.; El-Shafie, A. Machine Learning Application in Reservoir Water Level Forecasting for Sustainable Hydropower Generation Strategy. Sustainability 2020, 12, 6121. [Google Scholar] [CrossRef]
- Berz, G. Flood Disasters: Lessons from the Past—Worries for the Future. Proc. Inst. Civ. Eng. —Water Marit. Eng. 2000, 142, 3–8. [Google Scholar] [CrossRef]
- Arduino, G.; Reggiani, P.; Todini, E. Recent Advances in Flood Forecasting and Flood Risk Assessment. Hydrol. Earth Syst. Sci. 2005, 9, 280–284. [Google Scholar] [CrossRef] [Green Version]
- Courtney, C. The Nature of Disaster in China: The 1931 Yangzi River Flood; Cambridge University Press: Cambridge, UK, 2018; ISBN 9781108278362. [Google Scholar]
- Loc, H.H.; Park, E.; Chitwatkulsiri, D.; Lim, J.; Yun, S.-H.; Maneechot, L.; Minh Phuong, D. Local Rainfall or River Overflow? Re-Evaluating the Cause of the Great 2011 Thailand Flood. J. Hydrol. 2020, 589, 125368. [Google Scholar] [CrossRef]
- Loc, H.H.; Emadzadeh, A.; Park, E.; Nontikansak, P.; Deo, R.C. The Great 2011 Thailand Flood Disaster Revisited: Could It Have Been Mitigated by Different Dam Operations Based on Better Weather Forecasts? Environ. Res. 2023, 216, 114493. [Google Scholar] [CrossRef] [PubMed]
- Kala, C.P. Deluge, Disaster and Development in Uttarakhand Himalayan Region of India: Challenges and Lessons for Disaster Management. Int. J. Disaster Risk Reduct. 2014, 8, 143–152. [Google Scholar] [CrossRef]
- Shah, S.M.H.; Mustaffa, Z.; Teo, F.Y.; Imam, M.A.H.; Yusof, K.W.; Al-Qadami, E.H.H. A Review of the Flood Hazard and Risk Management in the South Asian Region, Particularly Pakistan. Sci. Afr. 2020, 10, e00651. [Google Scholar] [CrossRef]
- Ghatak, M.; Ahmed; Mishra, O.P. Background Paper on Flood Risk Management in South Asia. In Proceedings of the SAARC Workshop on Flood Risk Management in South Asia, Islamabad, Pakistan, 9–10 October 2012. [Google Scholar]
- Ministry of Water Resources, Government of Pakistan. Federal Flood Commission Report; Ministry of Water Resources, Government of Pakistan: Islamabad, Pakistan, 2018. [Google Scholar]
- Sen, D. Flood Hazards in India and Management Strategies. In Natural and Anthropogenic Disasters; Springer: Dordrecht, The Netherlands, 2010; pp. 126–146. [Google Scholar]
- Altaf, F.; Meraj, G.; Romshoo, S.A. Morphometric Analysis to Infer Hydrological Behaviour of Lidder Watershed, Western Himalaya, India. Geogr. J. 2013, 2013, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Akhter, M.; Manzoor Ahmad, A. Climate Modeling of Jhelum River Basin-A Comparative Study. Environ. Pollut. Clim. Change 2017, 1, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Siddiqui, M.J.; Haider, S.; Gabriel, H.F.; Shahzad, A. Rainfall–Runoff, Flood Inundation and Sensitivity Analysis of the 2014 Pakistan Flood in the Jhelum and Chenab River Basin. Hydrol. Sci. J. 2018, 63, 1976–1997. [Google Scholar] [CrossRef]
- Parvaze, S.; Khan, J.N.; Kumar, R.; Allaie, S.P. Flood Forecasting in Jhelum River Basin Using Integrated Hydrological and Hydraulic Modeling Approach with a Real-Time Updating Procedure. Clim. Dyn. 2022, 59, 2231–2255. [Google Scholar] [CrossRef]
- Thirumalaiah, K.; Deo, M.C. Real-Time Flood Forecasting Using Neural Networks. Comput. -Aided Civ. Infrastruct. Eng. 1998, 13, 101–111. [Google Scholar] [CrossRef]
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Comparison of the ARMA, ARIMA, and the Autoregressive Artificial Neural Network Models in Forecasting the Monthly Inflow of Dez Dam Reservoir. J. Hydrol. 2013, 476, 433–441. [Google Scholar] [CrossRef]
- Adamowski, J.; Fung Chan, H.; Prasher, S.O.; Ozga-Zielinski, B.; Sliusarieva, A. Comparison of Multiple Linear and Nonlinear Regression, Autoregressive Integrated Moving Average, Artificial Neural Network, and Wavelet Artificial Neural Network Methods for Urban Water Demand Forecasting in Montreal, Canada. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Wu, C.L.; Chau, K.W.; Li, Y.S. Predicting Monthly Streamflow Using Data-Driven Models Coupled with Data-Preprocessing Techniques. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef] [Green Version]
- Park, E.; Ho, H.L.; Tran, D.D.; Yang, X.; Alcantara, E.; Merino, E.; Son, V.H. Dramatic Decrease of Flood Frequency in the Mekong Delta Due to River-Bed Mining and Dyke Construction. Sci. Total Environ. 2020, 723, 138066. [Google Scholar] [CrossRef]
- Qiu, J.; Cao, B.; Park, E.; Yang, X.; Zhang, W.; Tarolli, P. Flood Monitoring in Rural Areas of the Pearl River Basin (China) Using Sentinel-1 SAR. Remote Sens. 2021, 13, 1384. [Google Scholar] [CrossRef]
- Chitwatkulsiri, D.; Miyamoto, H.; Irvine, K.N.; Pilailar, S.; Loc, H.H. Development and Application of a Real-Time Flood Forecasting System (RTFlood System) in a Tropical Urban Area: A Case Study of Ramkhamhaeng Polder, Bangkok, Thailand. Water 2022, 14, 1641. [Google Scholar] [CrossRef]
- Latrubesse, E.M.; Park, E.; Sieh, K.; Dang, T.; Lin, Y.N.; Yun, S.-H. Dam Failure and a Catastrophic Flood in the Mekong Basin (Bolaven Plateau), Southern Laos, 2018. Geomorphology 2020, 362, 107221. [Google Scholar] [CrossRef]
- Cluckie, I.D.; Han, D. Fluvial Flood Forecasting. Water Environ. J. 2000, 14, 270–276. [Google Scholar] [CrossRef]
- Remesan, R.; Ahmadi, A.; Shamim, M.A.; Han, D. Effect of Data Time Interval on Real-Time Flood Forecasting. J. Hydroinformatics 2010, 12, 396–407. [Google Scholar] [CrossRef]
- Wang, W. Stochasticity, Nonlinearity and Forecasting of Streamflow Processes; IOS Press: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Tsai, W.-P.; Chang, F.-J.; Chang, L.-C.; Herricks, E.E. AI Techniques for Optimizing Multi-Objective Reservoir Operation upon Human and Riverine Ecosystem Demands. J. Hydrol. 2015, 530, 634–644. [Google Scholar] [CrossRef]
- Chang, F.-J.; Tsai, M.-J. A Nonlinear Spatio-Temporal Lumping of Radar Rainfall for Modeling Multi-Step-Ahead Inflow Forecasts by Data-Driven Techniques. J. Hydrol. 2016, 535, 256–269. [Google Scholar] [CrossRef]
- Nayak, P.C.; Sudheer, K.P.; Ramasastri, K.S. Fuzzy Computing Based Rainfall-Runoff Model for Real Time Flood Forecasting. Hydrol. Process. 2005, 19, 955–968. [Google Scholar] [CrossRef]
- Hassan, Z.; Shamsudin, S.; Harun, S.; Malek, M.A.; Hamidon, N. Suitability of ANN Applied as a Hydrological Model Coupled with Statistical Downscaling Model: A Case Study in the Northern Area of Peninsular Malaysia. Environ. Earth Sci. 2015, 74, 463–477. [Google Scholar] [CrossRef] [Green Version]
- Shamim, M.A.; Bray, M.; Remesan, R.; Han, D. A Hybrid Modelling Approach for Assessing Solar Radiation. Theor. Appl. Climatol. 2015, 122, 403–420. [Google Scholar] [CrossRef]
- Shamim, M.A.; Hassan, M.; Ahmad, S.; Zeeshan, M. A Comparison of Artificial Neural Networks (ANN) and Local Linear Regression (LLR) Techniques for Predicting Monthly Reservoir Levels. KSCE J. Civ. Eng. 2016, 20, 971–977. [Google Scholar] [CrossRef]
- Ahmed, F.; Hassan, M.; Hashmi, H.N. Developing Nonlinear Models for Sediment Load Estimation in an Irrigation Canal. Acta Geophys. 2018, 66, 1485–1494. [Google Scholar] [CrossRef]
- Lee, S.; Lee, K.-K.; Yoon, H. Using Artificial Neural Network Models for Groundwater Level Forecasting and Assessment of the Relative Impacts of Influencing Factors. Hydrogeol. J. 2019, 27, 567–579. [Google Scholar] [CrossRef]
- Wunsch, A.; Liesch, T.; Broda, S. Forecasting Groundwater Levels Using Nonlinear Autoregressive Networks with Exogenous Input (NARX). J. Hydrol. 2018, 567, 743–758. [Google Scholar] [CrossRef]
- Van, S.P.; Le, H.M.; Thanh, D.V.; Dang, T.D.; Loc, H.H.; Anh, D.T. Deep Learning Convolutional Neural Network in Rainfall–Runoff Modelling. J. Hydroinformatics 2020, 22, 541–561. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, U.; Mumtaz, R.; Anwar, H.; Shah, A.A.; Irfan, R.; García-Nieto, J. Efficient Water Quality Prediction Using Supervised Machine Learning. Water 2019, 11, 2210. [Google Scholar] [CrossRef] [Green Version]
- Loc, H.H.; Do, Q.H.; Cokro, A.A.; Irvine, K.N. Deep Neural Network Analyses of Water Quality Time Series Associated with Water Sensitive Urban Design (WSUD) Features. J. Appl. Water Eng. Res. 2020, 8, 313–332. [Google Scholar] [CrossRef]
- Pradhan, P.; Kriewald, S.; Costa, L.; Rybski, D.; Benton, T.G.; Fischer, G.; Kropp, J.P. Urban Food Systems: How Regionalization Can Contribute to Climate Change Mitigation. Environ. Sci. Technol. 2020, 54, 10551–10560. [Google Scholar] [CrossRef] [PubMed]
- Pham, B.T.; Nguyen, M.D.; van Dao, D.; Prakash, I.; Ly, H.-B.; Le, T.-T.; Ho, L.S.; Nguyen, K.T.; Ngo, T.Q.; Hoang, V.; et al. Development of Artificial Intelligence Models for the Prediction of Compression Coefficient of Soil: An Application of Monte Carlo Sensitivity Analysis. Sci. Total Environ. 2019, 679, 172–184. [Google Scholar] [CrossRef]
- DAWSON, C.W.; WILBY, R. An Artificial Neural Network Approach to Rainfall-Runoff Modelling. Hydrol. Sci. J. 1998, 43, 47–66. [Google Scholar] [CrossRef]
- Sudheer, K.P.; Gosain, A.K.; Ramasastri, K.S. A Data-Driven Algorithm for Constructing Artificial Neural Network Rainfall-Runoff Models. Hydrol. Process. 2002, 16, 1325–1330. [Google Scholar] [CrossRef]
- Sudheer, K.P. Knowledge Extraction from Trained Neural Network River Flow Models. J. Hydrol. Eng. 2005, 10, 264–269. [Google Scholar] [CrossRef]
- CHANG, F.-J.; CHIANG, Y.-M.; CHANG, L.-C. Multi-Step-Ahead Neural Networks for Flood Forecasting. Hydrol. Sci. J. 2007, 52, 114–130. [Google Scholar] [CrossRef]
- Padmawar, P.M.; Shinde, A.S.; Sayyed, T.Z.; Shinde, S.K.; Moholkar, K. Disaster Prediction System Using Convolution Neural Network. In Proceedings of the 2019 IEEE International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 17–19 July 2019; pp. 808–812. [Google Scholar]
- Li, W.; Kiaghadi, A.; Dawson, C. Exploring the Best Sequence LSTM Modeling Architecture for Flood Prediction. Neural Comput. Appl. 2021, 33, 5571–5580. [Google Scholar] [CrossRef]
- Danandeh Mehr, A.; Kahya, E.; Yerdelen, C. Linear Genetic Programming Application for Successive-Station Monthly Streamflow Prediction. Comput. Geosci. 2014, 70, 63–72. [Google Scholar] [CrossRef]
- Kao, I.-F.; Zhou, Y.; Chang, L.-C.; Chang, F.-J. Exploring a Long Short-Term Memory Based Encoder-Decoder Framework for Multi-Step-Ahead Flood Forecasting. J. Hydrol. 2020, 583, 124631. [Google Scholar] [CrossRef]
- Hassan, M.; Hassan, I. Improving Artificial Neural Network Based Streamflow Forecasting Models through Data Preprocessing. KSCE J. Civ. Eng. 2021, 25, 3583–3595. [Google Scholar] [CrossRef]
- Kisi, O.; Cimen, M. A Wavelet-Support Vector Machine Conjunction Model for Monthly Streamflow Forecasting. J. Hydrol. 2011, 399, 132–140. [Google Scholar] [CrossRef]
- Chandrashekar, G.; Sahin, F. A Survey on Feature Selection Methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Chuzhanova, N.A.; Jones, A.J.; Margetts, S. Feature Selection for Genetic Sequence Classification. Bioinformatics 1998, 14, 139–143. [Google Scholar] [CrossRef] [Green Version]
- de Oliveira, M.C. Linear Systems Control Design Based on Linear Matrix Inequalities; University of Campinas: Campinas, SP, Brazil, 1999. (In Portuguese) [Google Scholar]
- Koncar, N. Optimization Methodologies for Direct Inverse Neurocontrol. Ph.D. Thesis, University of London, London, UK, 1997. [Google Scholar]
- Remesan, R.; Shamim, M.A.; Han, D.; Mathew, J. Runoff Prediction Using an Integrated Hybrid Modelling Scheme. J. Hydrol. 2009, 372, 48–60. [Google Scholar] [CrossRef]
- Piri, J.; Amin, S.; Moghaddamnia, A.; Keshavarz, A.; Han, D.; Remesan, R. Daily Pan Evaporation Modeling in a Hot and Dry Climate. J. Hydrol. Eng. 2009, 14, 803–811. [Google Scholar] [CrossRef]
- Shamim, M.A.; Remesan, R.; Bray, M.; Han, D. An Improved Technique for Global Solar Radiation Estimation Using Numerical Weather Prediction. J. Atmos. Sol. Terr. Phys. 2015, 129, 13–22. [Google Scholar] [CrossRef]
- Hassan, M.; Zaffar, H.; Mehmood, I.; Khitab, A. Development of Streamflow Prediction Models for a Weir Using ANN and Step-Wise Regression. Model. Earth Syst. Environ. 2018, 4, 1021–1028. [Google Scholar] [CrossRef]
- Stefánsson, A.; Končar, N.; Jones, A.J. A Note on the Gamma Test. Neural Comput. Appl. 1997, 5, 131–133. [Google Scholar] [CrossRef]
- Reyhani, N.; Hao, J.; Ji, Y.; Lendasse, A. Mutual Information and Gamma Test for Input Selection; ESANN: Bruges, Belgium, 2005. [Google Scholar]
- Afan, H.A.; Allawi, M.F.; El-Shafie, A.; Yaseen, Z.M.; Ahmed, A.N.; Malek, M.A.; Koting, S.B.; Salih, S.Q.; Mohtar, W.H.M.W.; Lai, S.H.; et al. Input Attributes Optimization Using the Feasibility of Genetic Nature Inspired Algorithm: Application of River Flow Forecasting. Sci. Rep. 2020, 10, 4684. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jones, A.J. The WinGamma-User Guide; Department of Computer Science, University of Wales: Cardiff, UK, 2001. [Google Scholar]
- Remesan, R.; Shamim, M.A.; Han, D. Nonlinear Modelling of Daily Solar Radiation Using the Gamma Test. In Proceedings of the BHS 10th National Hydrology Symposium, Exeter, UK, 15–17 September 2008. [Google Scholar]
- Fletcher, R. Practical Methods of Optimization, 2nd ed.; John Wiley and Sons: Chichester, UK, 1987. [Google Scholar]
- Brownlee, J. Deep Learning Performance; Machine Learning Mastery: San Francisco, CA, USA, 2018. [Google Scholar]
- Jones, A.; Tsui, A.; Oliveira, A. Neural Models of Arbitrary Chaotic Systems: Construction and the Role of Time Delayed Feedback in Control and Synchronization. Complexity 2002, 9. Available online: https://www.semanticscholar.org/paper/Neural-models-of-arbitrary-chaotic-systems%3A-and-the-Jones-Tsui/2644d9c74565e26ddb089b630c371ab56c130919 (accessed on 23 July 2022).
- Laimighofer, J.; Melcher, M.; Laaha, G. Parsimonious Statistical Learning Models for Low-Flow Estimation. Hydrol. Earth Syst. Sci. 2022, 26, 129–148. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Yildirim, A.; Gabbouj, M. Evolutionary Artificial Neural Networks by Multi-Dimensional Particle Swarm Optimization. Neural Netw. 2009, 22, 1448–1462. [Google Scholar] [CrossRef] [Green Version]
- Lone, S.A.; Jeelani, G.; Padhya, V.; Deshpande, R.D. Identifying and Estimating the Sources of River Flow in the Cold Arid Desert Environment of Upper Indus River Basin (UIRB), Western Himalayas. Sci. Total Environ. 2022, 832, 154964. [Google Scholar] [CrossRef]
- Garee, K.; Chen, X.; Bao, A.; Wang, Y.; Meng, F. Hydrological Modeling of the Upper Indus Basin: A Case Study from a High-Altitude Glacierized Catchment Hunza. Water 2017, 9, 17. [Google Scholar] [CrossRef] [Green Version]
- Umer, M.; Gabriel, H.F.; Haider, S.; Nusrat, A.; Shahid, M.; Umer, M. Application of Precipitation Products for Flood Modeling of Transboundary River Basin: A Case Study of Jhelum Basin. Theor. Appl. Climatol. 2021, 143, 989–1004. [Google Scholar] [CrossRef]
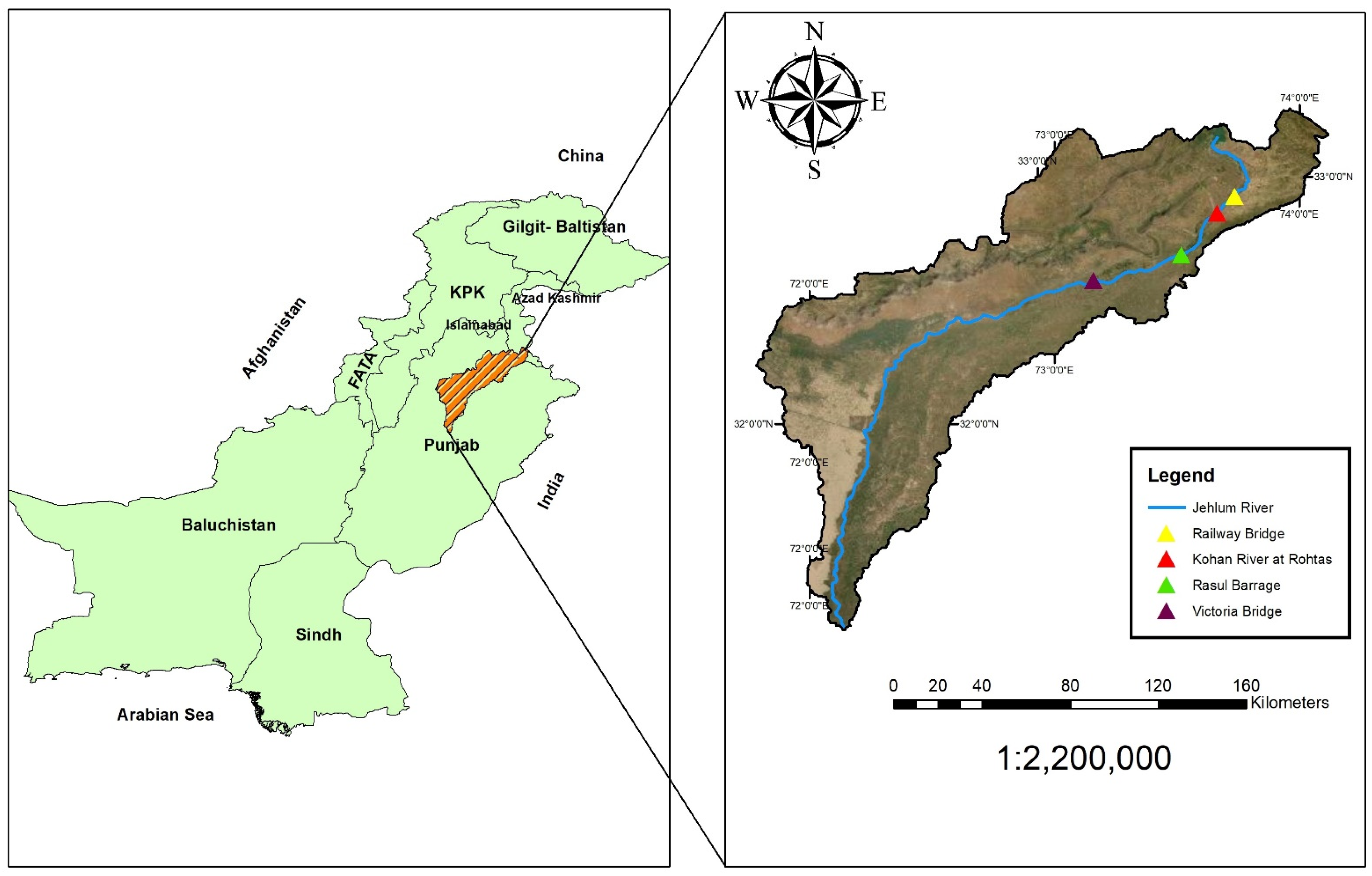
| Stations | Parameters | Inputs | Outputs | Data Length | Location |
|---|---|---|---|---|---|
| Jhelum at Railway Bridge | Discharge (Q) | Qin | - - - - - - Qo | 1991–2017 | 32°55′–73°44′ |
| Kohan River at Rohtas | Qin | 32°51′–73°39′ | |||
| Rasul Barrage | Qin | 32°40′–73°31′ | |||
| Jhelum at Victoria Bridge | 32°34′–73°9′ |
| Test No | Mask | LLR | DLLR | TLBP | |||
|---|---|---|---|---|---|---|---|
| Nearest Neighbors (NN) | Nearest Neighbors (NN) | Nodes (Layer 1) | Nodes (Layer 2) | Target MSE | Achieved MSE | ||
| 1 | 001 | 10 | 10 | 5 | 5 | 0.000025 | 5.3 × 10−5 |
| 2 | 111 | 10 | 10 | 6 | 6 | 0.00024 | 0.00011 |
| 3 | 111 | 10 | 10 | 10 | 10 | 0.00037 | 0.00022 |
| Test No | Mask | BFGS | |||||
| Nodes (Layer 1) | Nodes (Layer 2) | Target MSE | Achieved MSE | ||||
| 1 | 001 | 8 | 8 | 0.0008 | 0.00015 | ||
| 2 | 111 | 6 | 6 | 0.0007 | 0.00088 | ||
| 3 | 111 | 5 | 5 | 0.0002 | 0.0002 | ||
| Test No | Mask | CGNN | |||||
| Nodes (Layer 1) | Nodes (Layer 2) | Target MSE | Achieved MSE | ||||
| 1 | 001 | 5 | 5 | 0.004 | 0.00039 | ||
| 2 | 111 | 7 | 7 | 0.002 | 0.00019 | ||
| 3 | 111 | 9 | 9 | 0.01 | 0.00024 | ||
| Trial No. | Modeling Technique | Mask | Gamma Value | Gradient | V Ratio |
|---|---|---|---|---|---|
| 1 | Full Embedding | 001 | 0.00021 | 0.01 | 1.01 |
| 2 | Genetic Algorithm | 001 | 3.8 × 10−5 | 0.14 | 0.18 |
| 3 | Hill Climbing | 111 | 3.5 × 10−5 | 0.01 | 0.17 |
| 4 | Sequential Embedding | 111 | 2.6 × 10−5 | 0.01 | 0.13 |
| 5 | Increasing Embedding | 111 | 2.6 × 10−5 | 0.01 | 0.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, F.; Loc, H.H.; Park, E.; Hassan, M.; Joyklad, P. Comparison of Different Artificial Intelligence Techniques to Predict Floods in Jhelum River, Pakistan. Water 2022, 14, 3533. https://doi.org/10.3390/w14213533
Ahmed F, Loc HH, Park E, Hassan M, Joyklad P. Comparison of Different Artificial Intelligence Techniques to Predict Floods in Jhelum River, Pakistan. Water. 2022; 14(21):3533. https://doi.org/10.3390/w14213533
Chicago/Turabian StyleAhmed, Fahad, Ho Huu Loc, Edward Park, Muhammad Hassan, and Panuwat Joyklad. 2022. "Comparison of Different Artificial Intelligence Techniques to Predict Floods in Jhelum River, Pakistan" Water 14, no. 21: 3533. https://doi.org/10.3390/w14213533






