Application of Empirical Approaches for Fast Landslide Hazard Management: The Case Study of Theilly (Italy)
Abstract
:1. Introduction
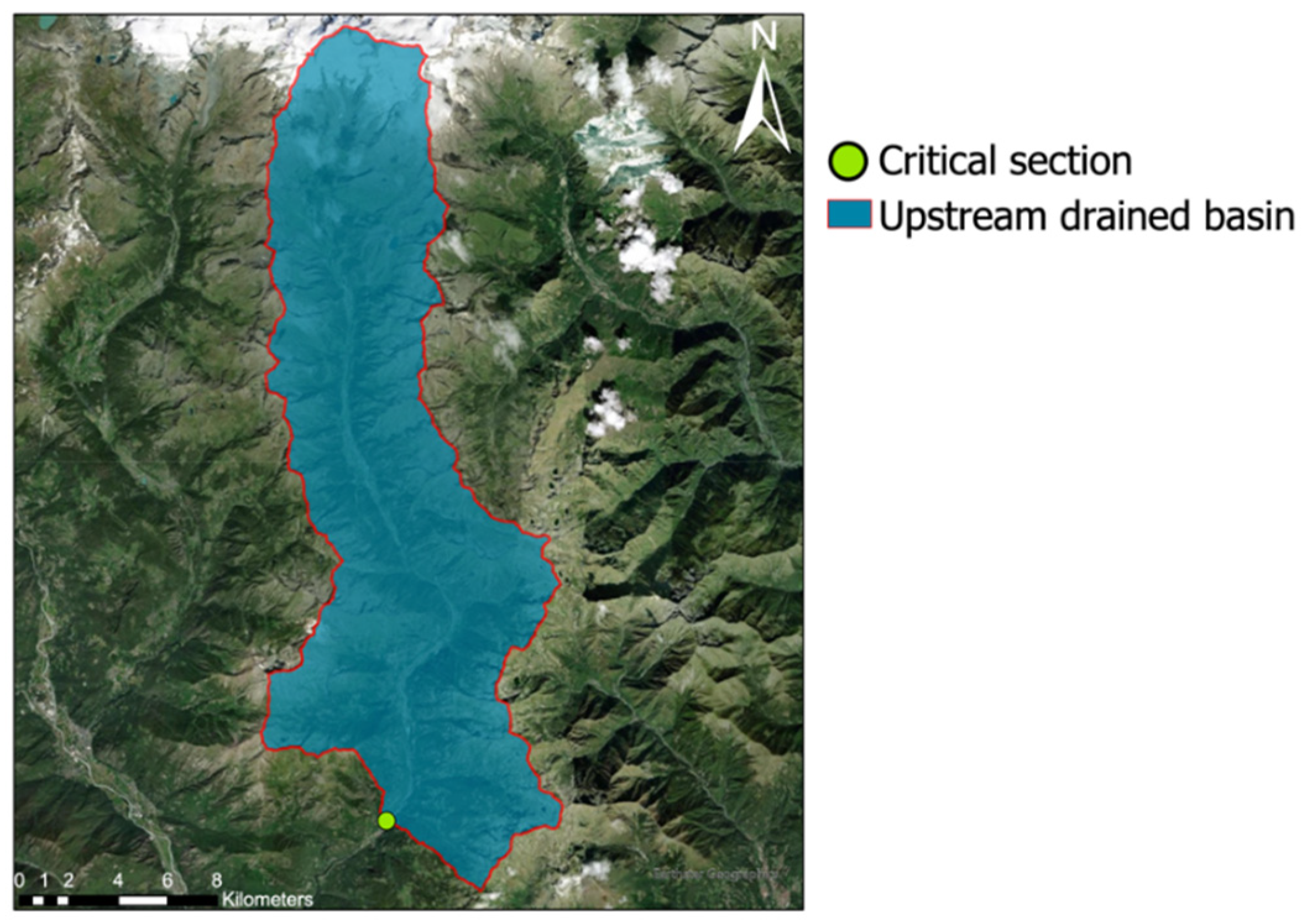
Test Site Description
2. Materials and Methods
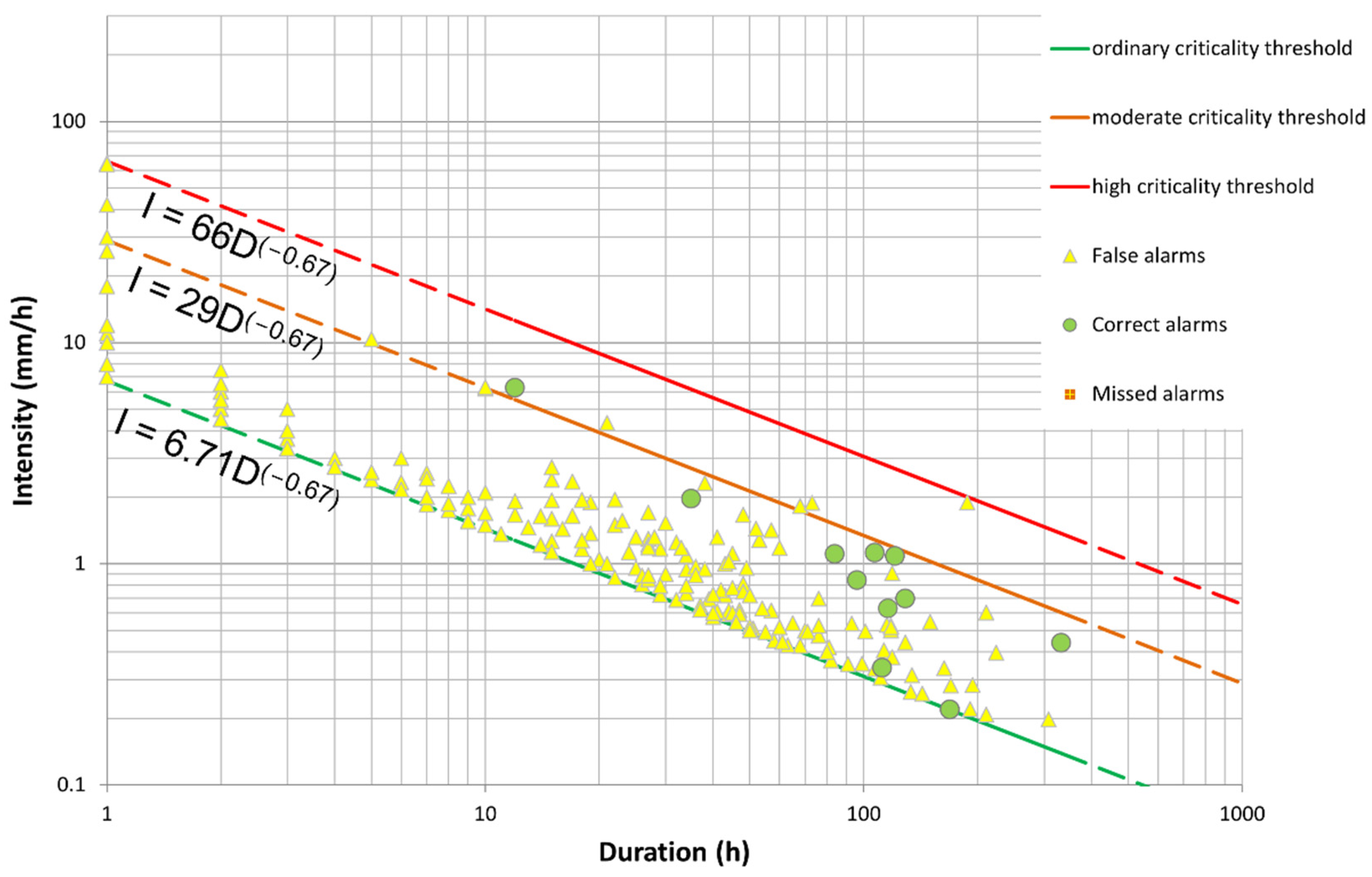
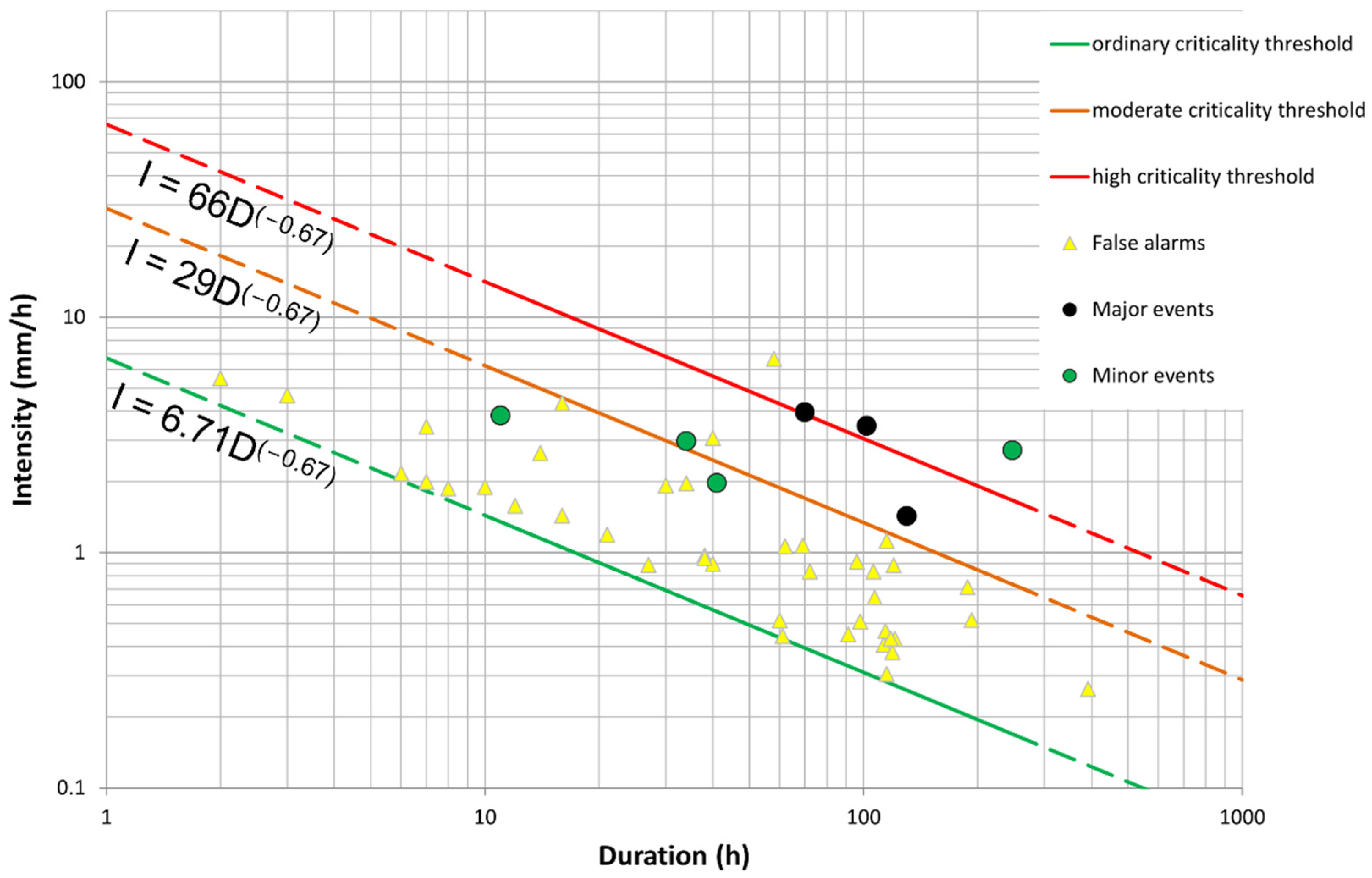
2.1. Rainfall Threshold Analysis
2.2. Landslide Dam Analysis
- MOI < 3.00 non-formation domain
- 3.00 < MOI < 4.60 uncertainty domain
- MOI > 4.60 formation domain
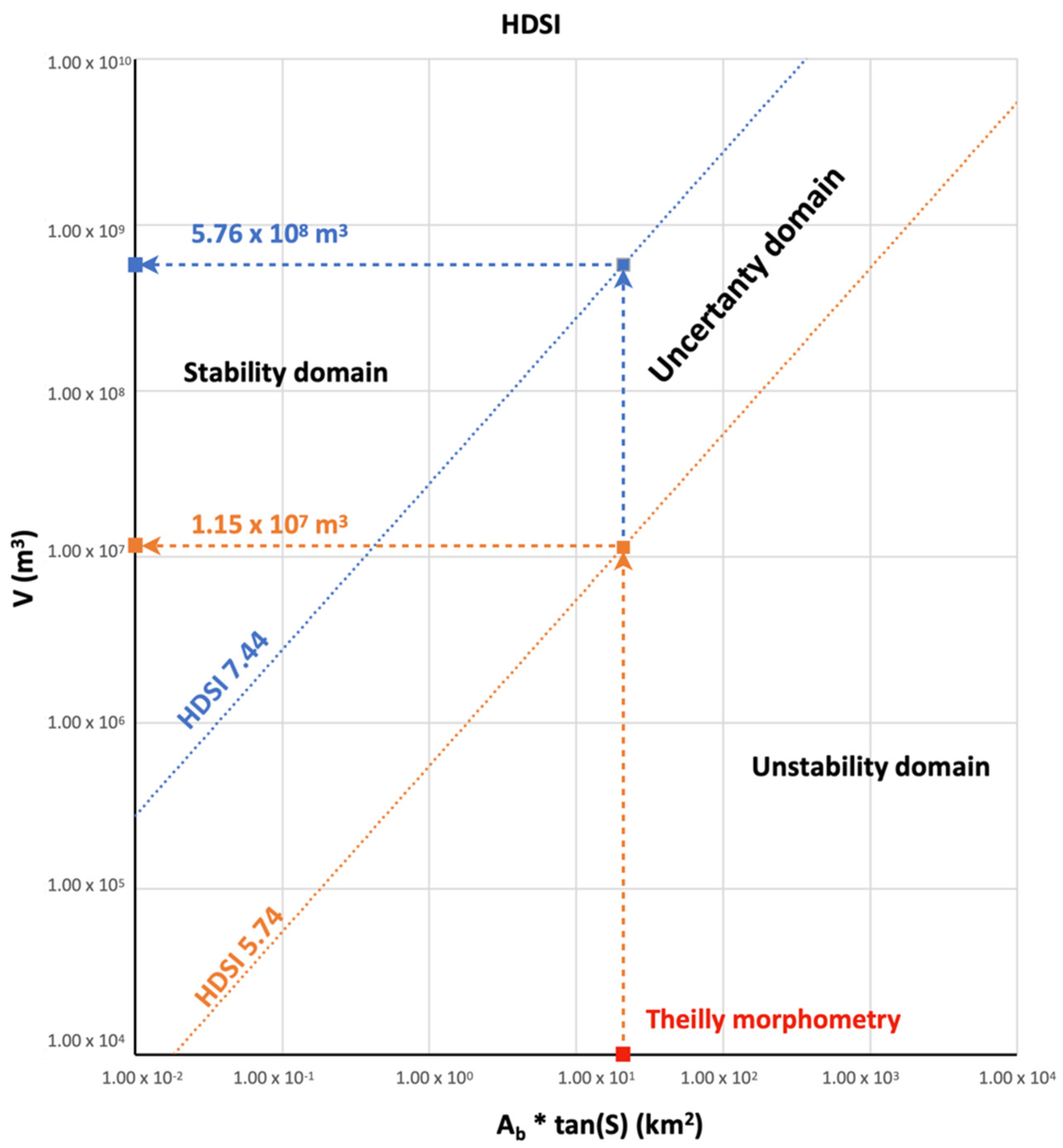
- HDSI > 7.44 stability domain
- 7.44 < HDSI < 5.74 uncertainty domain
- HDSI < 5.74 instability domain
3. Results
3.1. Rainfall Threshold Analysis
3.2. Landslide Dam Analysis
3.2.1. MOI Index Analysis
3.2.2. HDSI Index Analysis
- Stability critical volume (for HDSI = 7.44): Vlst = 5.76 ∗ 108 m3
- Instability critical volume (for HDSI = 5.74): Vlinst = 1.15 ∗ 107 m3
4. Discussion
- If the thresholds are not overcome, no relevant event is expected.
- If the lower threshold (ordinary criticality) is overcome, the minimum rainfall conditions for landslide triggering are reached: it is possible that mass movements or erosional processes are reactivated along the slope. However, their occurrence is not certain, and the occurrence of false alarms is also likely, as demonstrated by the empirical calibration procedure. No counteraction is expected except for intensifying the monitoring duty.
- If the moderate criticality threshold is overcome, the reactivation of mass movements or severe erosional processes should be expected. Local authorities should be contacted to receive a first-hand description of the evolution of the hazard scenario.
- When the high criticality threshold is overcome, the reactivation of larger mass movements or severe erosive processes should be expected. In addition to the aforementioned actions, an inspection to the site is recommended during or shortly after the event, and extraordinary maintenance should be performed on the remedial works and on the surroundings of the slope (e.g., cleaning of the drainages and outlets, removal of debris, and so on).
- for volumes less than 13,400 m3, a river dam would not form;
- from 13,400 m3 to 236,000 m3, the river dam formation is uncertain, and in the case of formation, the dam would be unstable;
- from 236,000 m3 to 11.5 × 106 m3, an unstable river dam would form;
- from 11.5 × 106 m3 to 576 × 106 m3, a dam would form with uncertain evolution;
- over 576 × 106 m3, a dam would form and would be stable even in the long term.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schuster, R.L. Socioeconomic and environmental impacts of landslide. In Landslides Investigation and Mitigation, 1st ed.; Turner, A.K., Schuster, R.L., Eds.; Transportation Research Board: Washington, DC, USA; Citeseer: Princeton, NJ, USA, 1996; Volume 247, pp. 12–35. [Google Scholar]
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef] [Green Version]
- Haque, U.; da Silva, P.F.; Devoli, G.; Pilz, J.; Zhao, B.; Khaloua, A.; Wilopo, W.; Andersen, P.; Lu, P.; Lee, J.; et al. The human cost of global warming: Deadly landslides and their triggers (1995–2014). Sci. Total Environ. 2019, 682, 673–684. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.; Dufresne, A.; Subramanian, S.S.; Strom, A.; Hermanns, R.; Stefanelli, C.T.; Hewitt, K.; Yunus, A.P.; Dunning, S.; Capra, L.; et al. The formation and impact of landslide dams—State of the art. Earth-Sci. Rev. 2020, 203, 103116. [Google Scholar] [CrossRef]
- Korup, O. Recent research on landslide dams—A literature review with special attention to New Zealand. Prog. Phys. Geogr. Earth Environ. 2002, 26, 206–235. [Google Scholar] [CrossRef]
- Fan, X.; Scaringi, G.; Korup, O.; West, A.J.; Van Westen, C.J.; Tanyas, H.; Hovius, N.; Hales, T.C.; Jibson, R.W.; Allstadt, K.E.; et al. Earthquake-Induced Chains of Geologic Hazards: Patterns, Mechanisms, and Impacts. Rev. Geophys. 2019, 57, 421–503. [Google Scholar] [CrossRef] [Green Version]
- Dai, F.; Lee, C.; Deng, J.; Tham, L. The 1786 earthquake-triggered landslide dam and subsequent dam-break flood on the Dadu River, southwestern China. Geomorphology 2005, 65, 205–221. [Google Scholar] [CrossRef]
- Chae, B.-G.; Park, H.-J.; Catani, F.; Simoni, A.; Berti, M. Landslide prediction, monitoring and early warning: A concise review of state-of-the-art. Geosci. J. 2017, 21, 1033–1070. [Google Scholar] [CrossRef]
- Segoni, S.; Piciullo, L.; Gariano, S.L. A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
- Aleotti, P.; Chowdhury, R. Landslide hazard assessment: Summary review and new perspectives. Bull. Eng. Geol. Environ. 1999, 58, 21–44. [Google Scholar] [CrossRef]
- Catani, F.; Segoni, S. Prediction and Forecasting of Mass-Movements. In Treatise on Geomorphology; Elsevier: Amsterdam, The Netherlands, 2022; pp. 531–545. [Google Scholar] [CrossRef]
- Piciullo, L.; Calvello, M.; Cepeda, J.M. Territorial early warning systems for rainfall-induced landslides. Earth Sci. Rev. 2018, 179, 228–247. [Google Scholar] [CrossRef]
- Guzzetti, F.; Gariano, S.L.; Peruccacci, S.; Brunetti, M.T.; Marchesini, I.; Rossi, M.; Melillo, M. Geographical landslide early warning systems. Earth-Sci. Rev. 2020, 200, 102973. [Google Scholar] [CrossRef]
- Caine, N. The Rainfall Intensity—Duration Control of Shallow Landslides and Debris Flows. Geogr. Ann. Ser. A Phys. Geogr. 1980, 62, 23–27. [Google Scholar] [CrossRef]
- Tiranti, D.; Rabuffetti, D. Estimation of rainfall thresholds triggering shallow landslides for an operational warning system implementation. Landslides 2010, 7, 471–481. [Google Scholar] [CrossRef]
- Devoli, G.; Tiranti, D.; Cremonini, R.; Sund, M.; Boje, S. Comparison of landslide forecasting services in Piedmont (Italy) and Norway, illustrated by events in late spring 2013. Nat. Hazards Earth Syst. Sci. 2018, 18, 1351–1372. [Google Scholar] [CrossRef] [Green Version]
- Kong, V.W.W.; Kwan, J.S.H.; Pun, W.K. Hong Kong’s landslip warning system—40 years of progress. Landslides 2020, 17, 1453–1463. [Google Scholar] [CrossRef]
- Gariano, S.L.; Brunetti, M.T.; Iovine, G.; Melillo, M.; Peruccacci, S.; Terranova, O.; Vennari, C.; Guzzetti, F. Calibration and validation of rainfall thresholds for shallow landslide forecasting in Sicily, southern Italy. Geomorphology 2015, 228, 653–665. [Google Scholar] [CrossRef]
- Fan, X.; Dufresne, A.; Whiteley, J.; Yunus, A.P.; Subramanian, S.S.; Okeke, C.A.; Pánek, T.; Hermanns, R.L.; Ming, P.; Strom, A.; et al. Recent technological and methodological advances for the investigation of landslide dams. Earth-Sci. Rev. 2021, 218, 103646. [Google Scholar] [CrossRef]
- Zheng, H.; Shi, Z.; Shen, D.; Peng, M.; Hanley, K.J.; Ma, C.; Zhang, L. Recent Advances in Stability and Failure Mechanisms of Landslide Dams. Front. Earth Sci. 2021, 9, 659935. [Google Scholar] [CrossRef]
- Braun, A.; Cuomo, S.; Petrosino, S.; Wang, X.; Zhang, L. Numerical SPH analysis of debris flow run-out and related river damming scenarios for a local case study in SW China. Landslides 2018, 15, 535–550. [Google Scholar] [CrossRef]
- Swanson, F.J.; Oyagi, N.; Tominaga, M. Landslide dams in Japan. In Landslide Dams: Processes, Risk, and Mitigation; ASCE: Reston, VA, USA, 1986; pp. 131–145. [Google Scholar]
- Ermini, L.; Casagli, N. Prediction of the behaviour of landslide dams using a geomorphological dimensionless index. Earth Surf. Process. Landf. 2003, 28, 31–47. [Google Scholar] [CrossRef]
- Liao, H.-M.; Yang, X.-G.; Xu, F.-G.; Xu, H.; Zhou, J.-W. A fuzzy comprehensive method for the risk assessment of a landslide-dammed lake. Environ. Earth Sci. 2018, 77, 750. [Google Scholar] [CrossRef]
- Korup, O. Geomorphometric characteristics of New Zealand landslide dams. Eng. Geol. 2004, 73, 13–35. [Google Scholar] [CrossRef]
- Stefanelli, C.T.; Segoni, S.; Casagli, N.; Catani, F. Geomorphic indexing of landslide dams evolution. Eng. Geol. 2016, 208, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Corominas, J.; Moya, J. Reconstructing recent landslide activity in relation to rainfall in the Llobregat River basin, Eastern Pyrenees, Spain. Geomorphology 1999, 30, 79–93. [Google Scholar] [CrossRef]
- Giannecchini, R.; Galanti, Y.; D’Amato Avanzi, G. Critical rainfall thresholds for triggering shallow landslides in the Serchio River Valley (Tuscany, Italy). Nat. Hazards Earth Syst. Sci. 2012, 12, 829–842. [Google Scholar] [CrossRef]
- Rosi, A.; Canavesi, V.; Segoni, S.; Nery, T.D.; Catani, F.; Casagli, N. Landslides in the Mountain Region of Rio de Janeiro: A Proposal for the Semi-Automated Definition of Multiple Rainfall Thresholds. Geosciences 2019, 9, 203. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Won, J.-S.; Jeon, S.; Park, I.; Lee, M.J. Spatial Landslide Hazard Prediction Using Rainfall Probability and a Logistic Regression Model. Math. Geol. 2015, 47, 565–589. [Google Scholar] [CrossRef]
- Ma, C.; Hu, K.-H.; Zou, Q.; Tian, M. Characteristics of clustering debris flows in Wenchuan earthquake zone. J. Mt. Sci. 2013, 10, 953–961. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity–duration control of shallow landslides and debris flows: An update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
- Zêzere, J.L.; Vaz, T.; Pereira, S.; Oliveira, S.C.; Marques, R.; Garcia, R.A.C. Rainfall thresholds for landslide activity in Portugal: A state of the art. Environ. Earth Sci. 2015, 73, 2917–2936. [Google Scholar] [CrossRef]
- Tiranti, D.; Nicolò, G.; Gaeta, A.R. Shallow landslides predisposing and triggering factors in developing a regional early warning system. Landslides 2019, 16, 235–251. [Google Scholar] [CrossRef]
- Sengupta, A.; Gupta, S.; Anbarasu, K. Rainfall thresholds for the initiation of landslide at Lanta Khola in north Sikkim, India. Nat. Hazards 2010, 52, 31–42. [Google Scholar] [CrossRef]
- Chen, H.; Wang, J. Regression analyses for the minimum intensity-duration conditions of continuous rainfall for mudflows triggering in Yan’an, northern Shaanxi (China). Bull. Eng. Geol. Environ. 2014, 73, 917–928. [Google Scholar] [CrossRef]
- Franceschini, R.; Rosi, A.; Catani, F.; Casagli, N. Exploring a landslide inventory created by automated web data mining: The case of Italy. Landslides 2022, 19, 841–853. [Google Scholar] [CrossRef]
- Battistini, A.; Rosi, A.; Segoni, S.; Lagomarsino, D.; Catani, F.; Casagli, N. Validation of landslide hazard models using a semantic engine on online news. Appl. Geogr. 2017, 82, 59–65. [Google Scholar] [CrossRef]
- Abraham, M.T.; Satyam, N.; Rosi, A.; Pradhan, B.; Segoni, S. The Selection of Rain Gauges and Rainfall Parameters in Estimating Intensity-Duration Thresholds for Landslide Occurrence: Case Study from Wayanad (India). Water 2020, 12, 1000. [Google Scholar] [CrossRef] [Green Version]
- Gariano, S.L.; Melillo, M.; Peruccacci, S.; Brunetti, M.T. How much does the rainfall temporal resolution affect rainfall thresholds for landslide triggering? Nat. Hazards 2020, 100, 655–670. [Google Scholar] [CrossRef] [Green Version]
- Rossi, M.; Luciani, S.; Valigi, D.; Kirschbaum, D.; Brunetti, M.; Peruccacci, S.; Guzzetti, F. Statistical approaches for the definition of landslide rainfall thresholds and their uncertainty using rain gauge and satellite data. Geomorphology 2017, 285, 16–27. [Google Scholar] [CrossRef]
- Segoni, S.; Rossi, G.; Rosi, A.; Catani, F. Landslides triggered by rainfall: A semi-automated procedure to define consistent intensity–duration thresholds. Comput. Geosci. 2014, 63, 123–131. [Google Scholar] [CrossRef]



| Day of Landslide Occurrence |
|---|
| 3 September 2012 |
| 3 September 2012 |
| 17 May 2013 |
| 25 June 2016 |
| 23 November 2016 |
| 25 March 2017 |
| 4 September 2017 |
| 12 January 2018 |
| 29 May 2018 |
| 11 June 2018 |
| 1 November 2018 |
| 22 November 2019 |
| End Day of the Event | Intensity (mm/h) | Duration (h) | Amount of Rain (mm) |
|---|---|---|---|
| 5 September 2012 | 0.22 | 169 | 37 |
| 5 September 2012 | 0.22 | 169 | 37 |
| 19 May 2013 | 1.12 | 107 | 120 |
| 25 June 2016 | 6.25 | 12 | 75 |
| 25 November 2016 | 0.84 | 96 | 81 |
| 26 March 2017 | 1.11 | 84 | 93 |
| 5 September 2017 | 0.34 | 112 | 38 |
| 13 January 2018 | 0.44 | 333 | 146 |
| 31 May 2018 | 0.63 | 116 | 73 |
| 12 June 2018 | 1.97 | 35 | 69 |
| 1 November 2018 | 1.08 | 121 | 131 |
| 27 November 2019 | 0.70 | 129 | 90 |
| Theilly Landslide Events | |
|---|---|
| 25 November 2016 | major and first activation |
| 11 October 2018 | minor event |
| 7 November 2018 | minor event |
| 4 and 7 April/2019 | two minor events |
| 24 November 2019 | major event |
| 3 October 2020 | major event |
| End Day of the Event | Intensity (mm/h) | Duration (h) | Amount of Rain (mm) |
|---|---|---|---|
| 25 November 2016 | 3.46 | 102 | 353 |
| 27 November 2019 | 1.43 | 130 | 186 |
| 4 October 2020 | 3.96 | 70 | 277 |
| End Day of the Event | Intensity (mm/h) | Duration (h) | Amount of Rain (mm) |
|---|---|---|---|
| 11 October 2018 | 2.97 | 34 | 101 |
| 7 November 2018 | 2.72 | 247 | 671 |
| 4 April 2019 | 1.98 | 41 | 81 |
| 7 April 2019 | 3.82 | 11 | 42 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Segoni, S.; Barbadori, F.; Gatto, A.; Casagli, N. Application of Empirical Approaches for Fast Landslide Hazard Management: The Case Study of Theilly (Italy). Water 2022, 14, 3485. https://doi.org/10.3390/w14213485
Segoni S, Barbadori F, Gatto A, Casagli N. Application of Empirical Approaches for Fast Landslide Hazard Management: The Case Study of Theilly (Italy). Water. 2022; 14(21):3485. https://doi.org/10.3390/w14213485
Chicago/Turabian StyleSegoni, Samuele, Francesco Barbadori, Alessio Gatto, and Nicola Casagli. 2022. "Application of Empirical Approaches for Fast Landslide Hazard Management: The Case Study of Theilly (Italy)" Water 14, no. 21: 3485. https://doi.org/10.3390/w14213485
APA StyleSegoni, S., Barbadori, F., Gatto, A., & Casagli, N. (2022). Application of Empirical Approaches for Fast Landslide Hazard Management: The Case Study of Theilly (Italy). Water, 14(21), 3485. https://doi.org/10.3390/w14213485








