Soil Moisture Data Assimilation in MISDc for Improved Hydrological Simulation in Upper Huai River Basin, China
Abstract
:1. Introduction
- Which layer of CLDAS SM data is most suitable for DA experiments in the MISDc model? (Section 2.6);
- To what extent does the assimilation of CLDAS SM products improve the runoff simulation capability of the model? What is the effect of SM bias correction (i.e., using CLDAS-BPNN SSM data) on the results? (Section 3.3);
- What are the implications of using the EnKF method for high and low-flow simulations in the hydrological model? (Section 3.4);
- What is the effect of different ensemble numbers on the results of the EnKF method for the hydrological model runoff simulations? (Section 3.2).
2. Materials and Methods
2.1. Study Area
2.2. Observed Discharge Data
2.3. China Land Data Assimilation System Product
2.3.1. Forcing Data
2.3.2. Soil Moisture Data
2.4. Hydrological Model
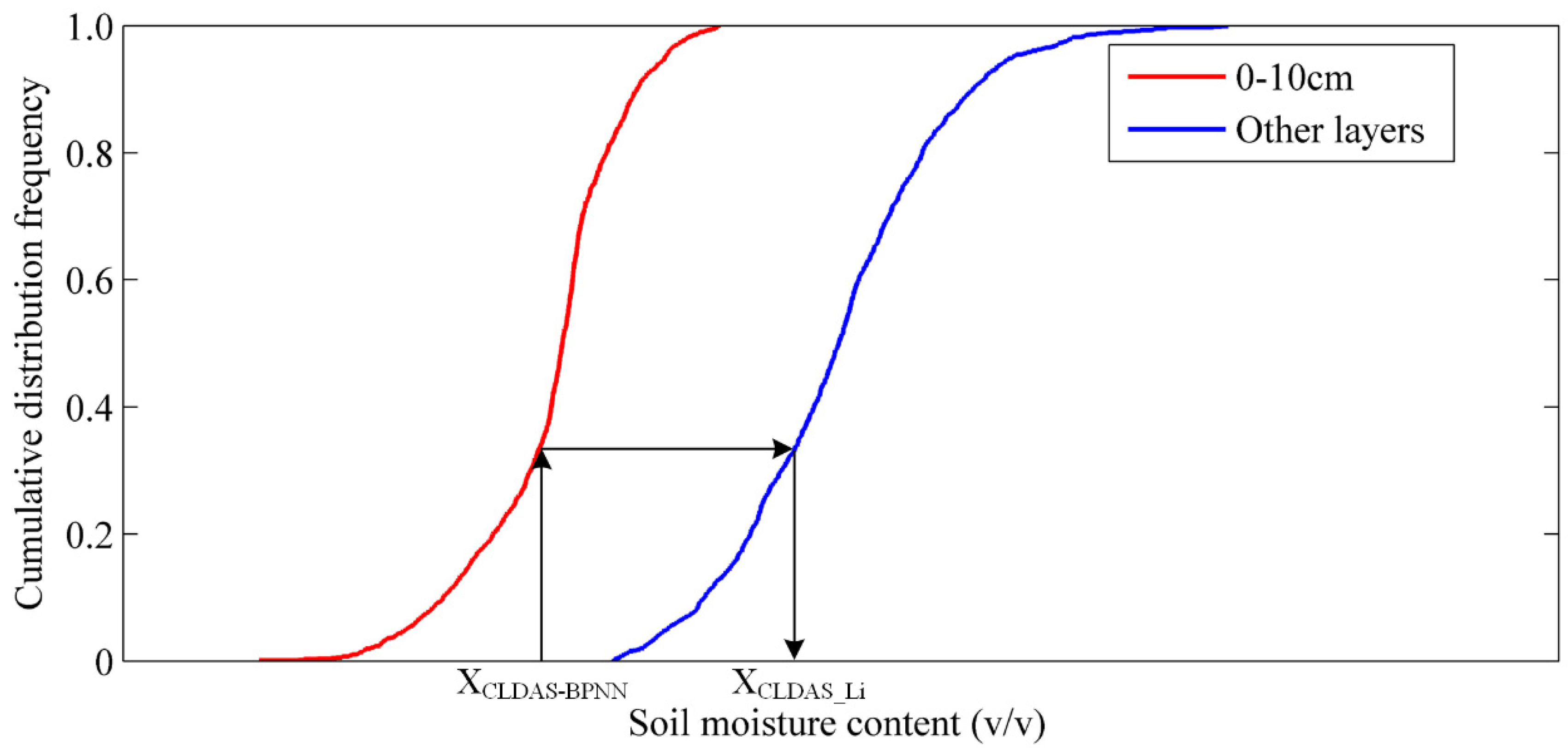
2.5. Cumulative Distribution Function
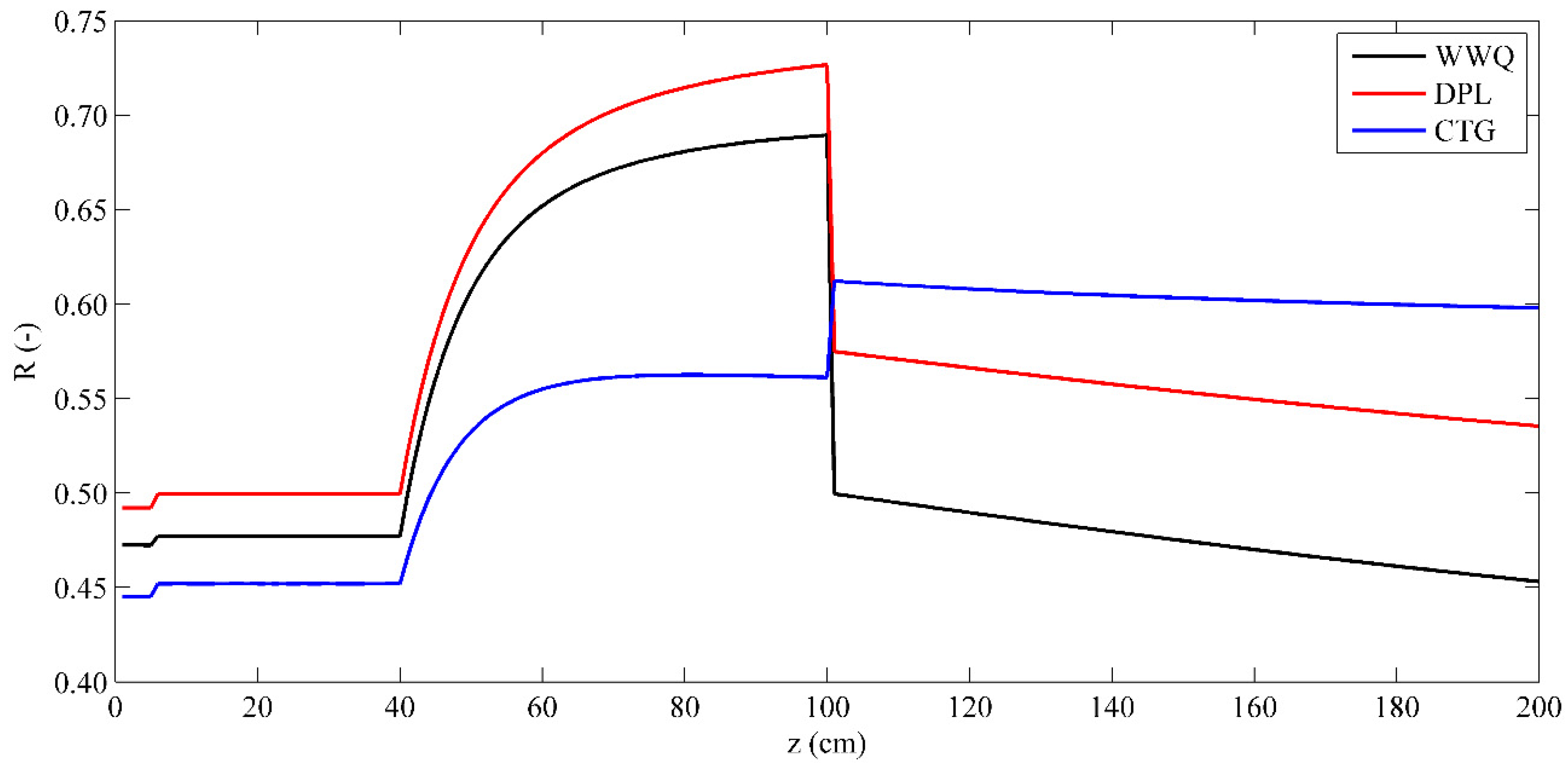
2.6. Determination of the Thickness of the Model Soil Layer
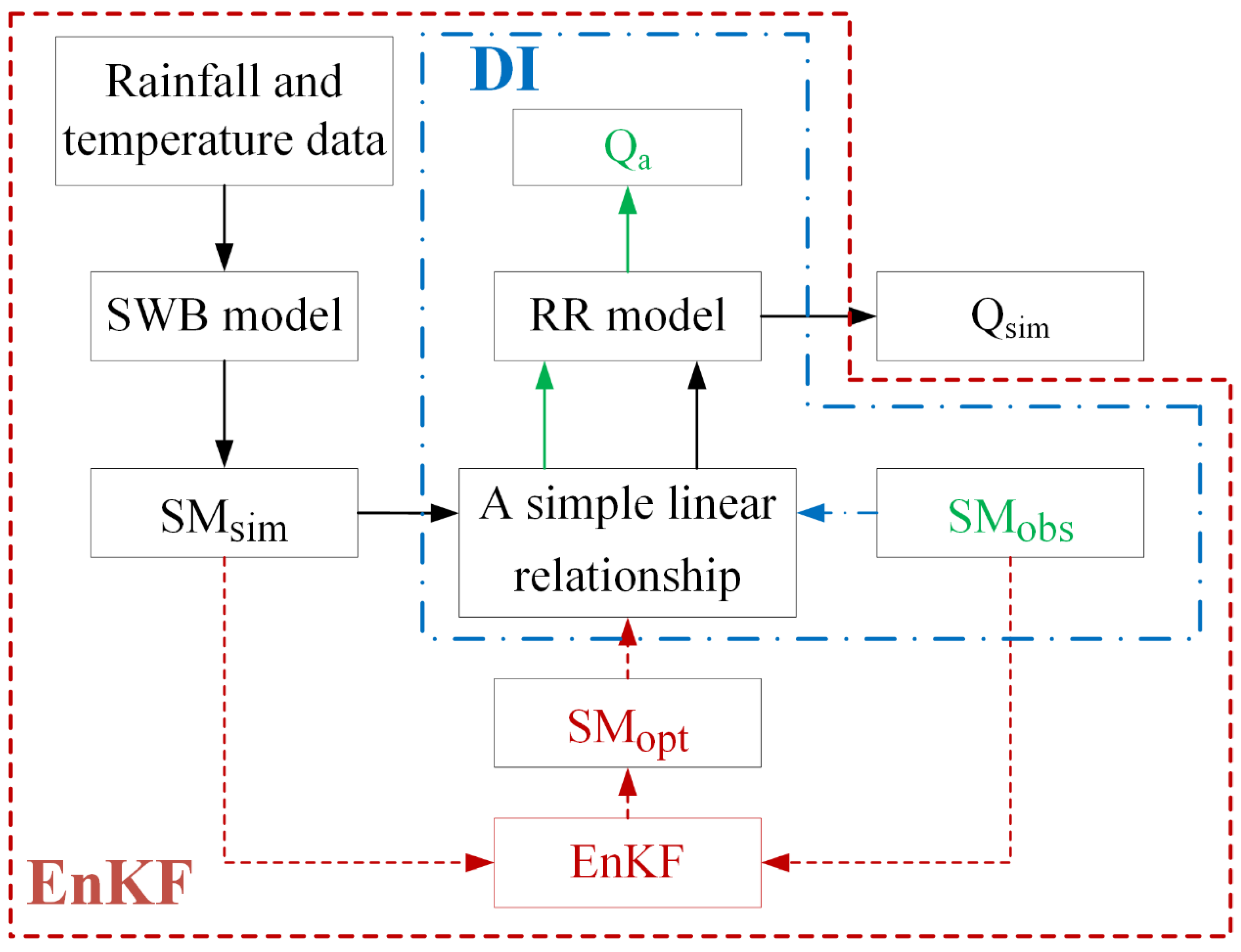
2.7. Ensemble Kalman Filter
2.8. Performance Indexes
3. Results
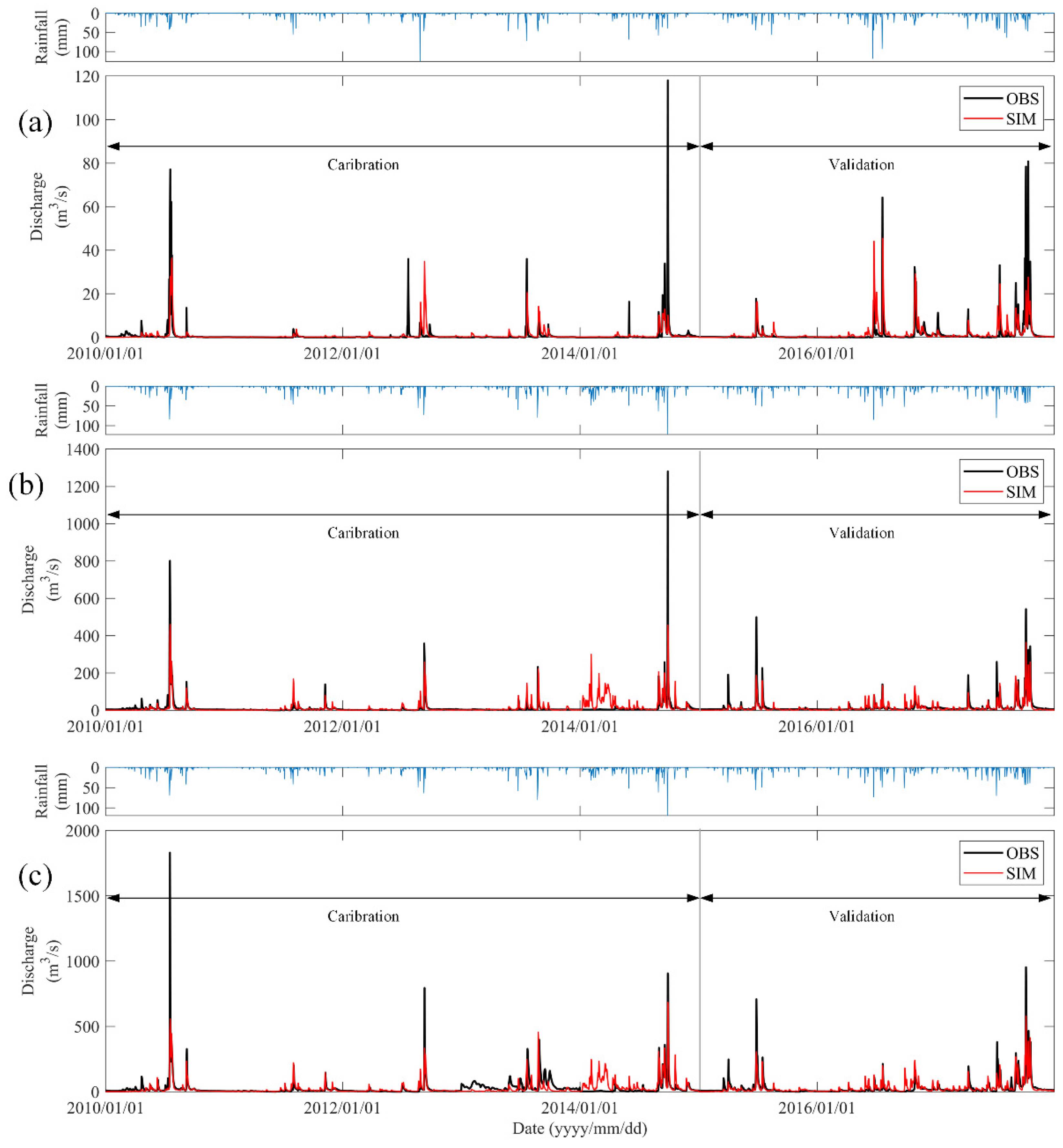
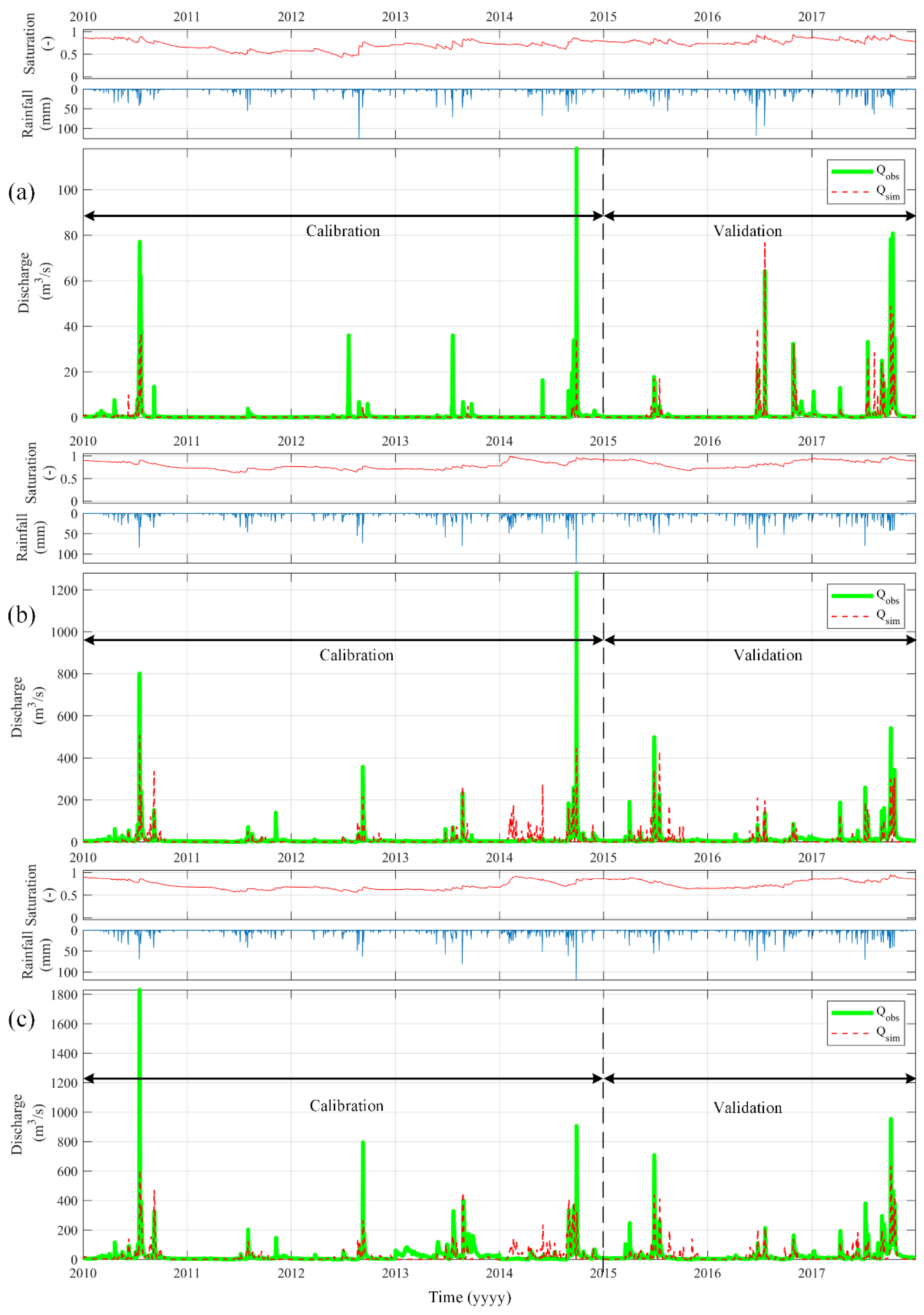
3.1. Model Calibration and Validation
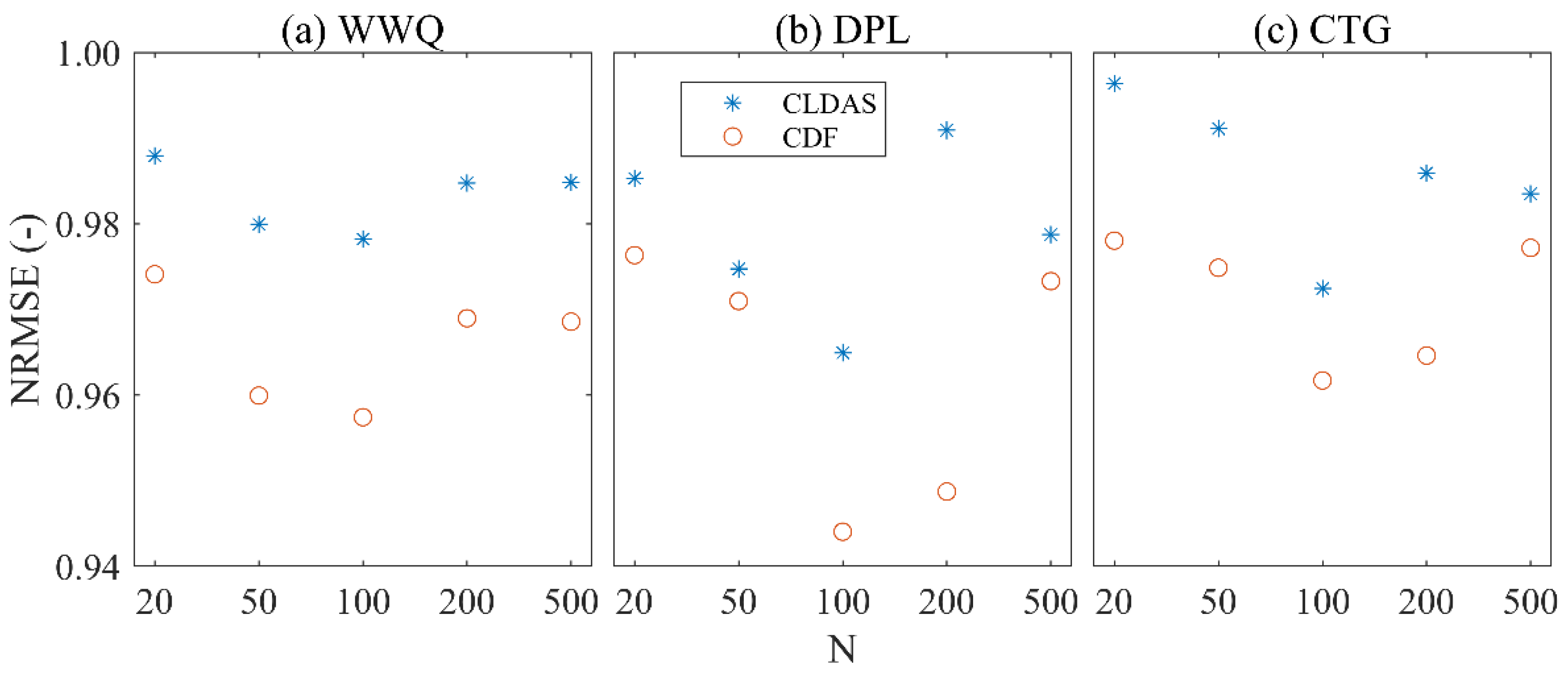
3.2. The Influence of Different Numbers of Ensemble Members on the Results of the EnKF Method
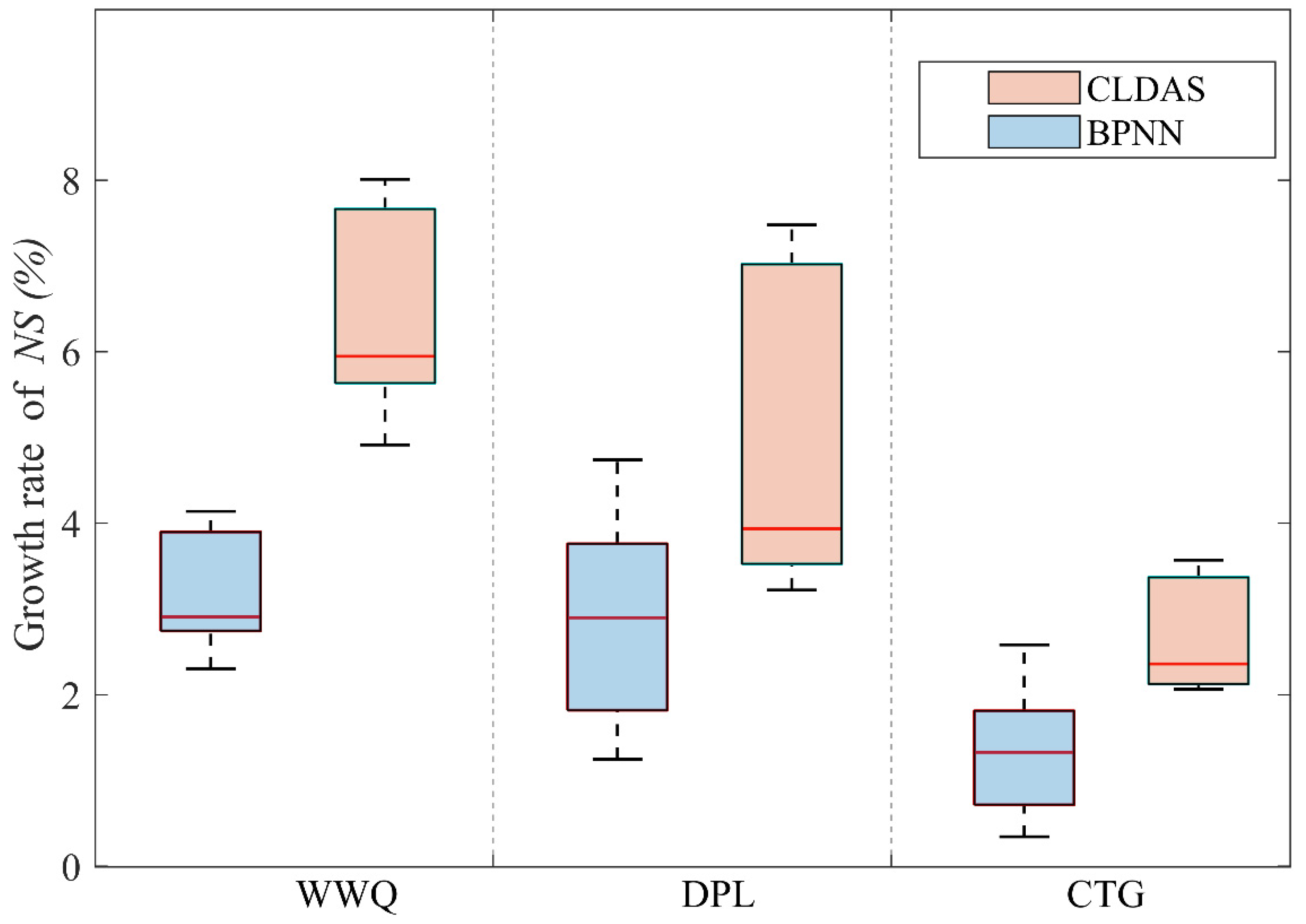
3.3. Data Assimilation Experiments
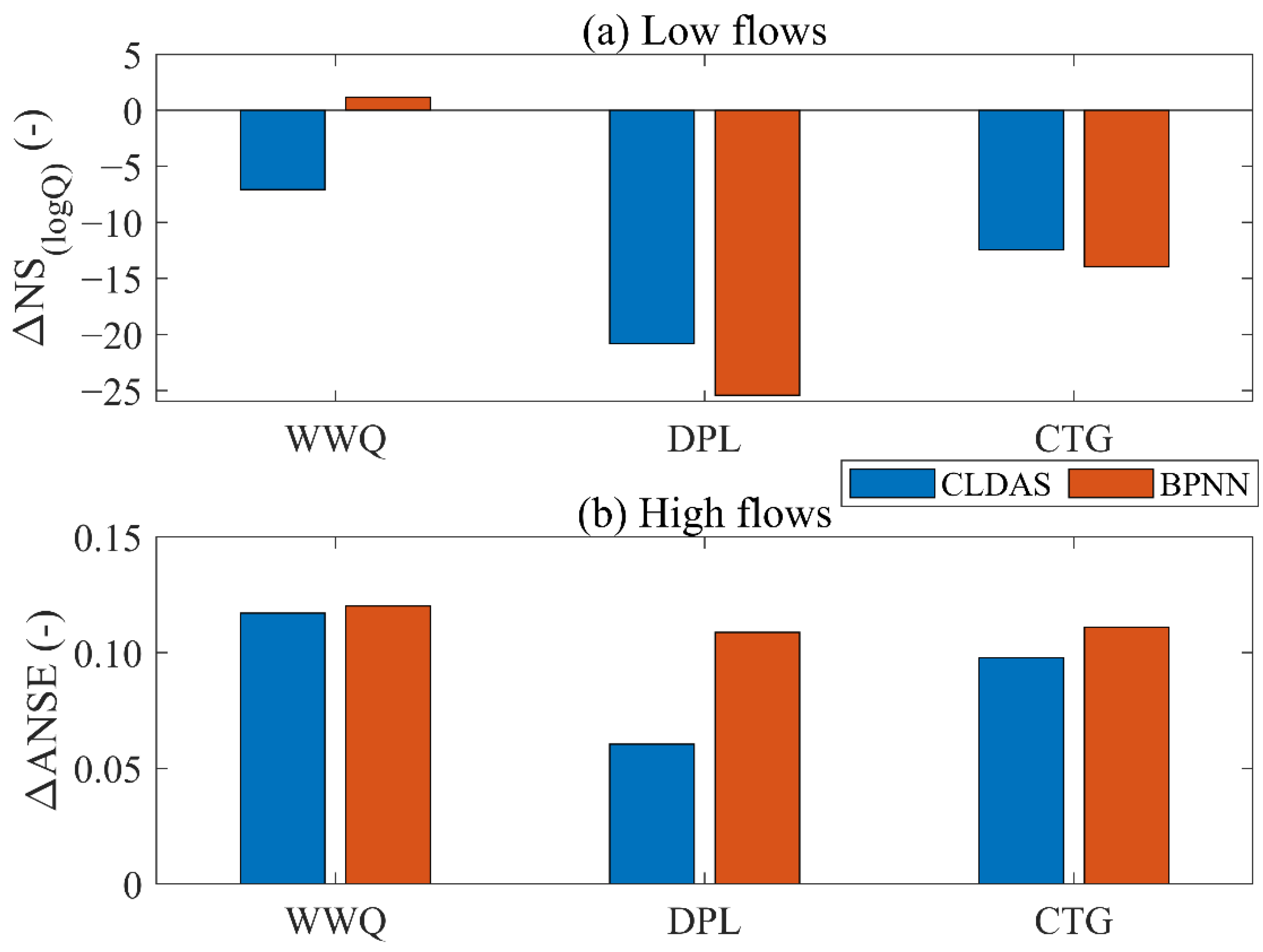
3.4. The Impact of the EnKF Method on High and Low Flows
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Catchments | Calibration (1 January 2010–31 December 2013) | Validation (1 January 2014–31 December 2016) | ||||
|---|---|---|---|---|---|---|
| WWQ | 0.287 | 0.321 | 0.536 | 0.357 | 0.442 | 0.613 |
| DPL | 0.464 | 0.586 | 0.687 | 0.727 | 0.760 | 0.865 |
| CTG | 0.471 | 0.566 | 0.689 | 0.610 | 0.741 | 0.781 |
| Abbreviation | Full Name | Abbreviation | Full Name | Abbreviation | Full Name |
|---|---|---|---|---|---|
| CDF | Cumulative distribution function | DI | Direct insertion | MISDc | Modello Idrologico Semi-Distribuito in continuo |
| CLDAS | China land data assimilation system | DPL | Dapoling | ||
| CTG | Changtaiguan | EnKF | Ensemble Kalman filter | SM | Soil moisture |
| DA | Data assimilation | KF | Kalman filter | WWQ | Wangwuqiao |
References
- Boithias, L.; Sauvage, S.; Lenica, A.; Roux, H.; Abbaspour, K.; Larnier, K.; Dartus, D.; Sánchez-Pérez, J. Simulating Flash Floods at Hourly Time-Step Using the SWAT Model. Water 2017, 9, 929. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Qu, S.; Shi, P.; Chen, X.; Xue, F.; Gou, J.; Zhang, W. Development and Integration of Sub-Daily Flood Modelling Capability within the SWAT Model and a Comparison with XAJ Model. Water 2018, 10, 1263. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Bárdossy, A.; Zhang, K. Sensitivity of hydrological models to temporal and spatial resolutions of rainfall data. Hydrol. Earth Syst. Sci. 2019, 23, 2647–2663. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Gupta, H.V. Uncertainty in hydrologic modeling: Toward an integrated data assimilation framework. Water Resour. Res. 2007, 43, W07401. [Google Scholar] [CrossRef]
- Meixner, T. Spatial Patterns in Catchment Hydrology: Observations and Modelling. Vadose Zone J. 2002, 1, 202. [Google Scholar]
- Zehe, E.; Becker, R.; Bárdossy, A.; Plate, E. Uncertainty of simulated catchment runoff response in the presence of threshold processes: Role of initial soil moisture and precipitation. J. Hydrol. 2005, 315, 183–202. [Google Scholar] [CrossRef]
- Bárdossy, A.; Das, T. Influence of rainfall observation network on model calibration and application. Hydrol. Earth Syst. Sci. Discuss. 2006, 3, 3691–3726. [Google Scholar] [CrossRef] [Green Version]
- Tramblay, Y.; Bouvier, C.; Ayral, P.-A.; Marchandise, A. Impact of rainfall spatial distribution on rainfall-runoff modelling efficiency and initial soil moisture conditions estimation. Nat. Hazards Earth Syst. Sci. 2011, 11, 157–170. [Google Scholar] [CrossRef] [Green Version]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. Earth Surf. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Montzka, C.; Pauwels, V.R.N.; Franssen, H.-J.H.; Han, X.; Vereecken, H. Multivariate and multiscale data assimilation in terrestrial systems: A review. Sensers 2012, 12, 16291–16333. [Google Scholar] [CrossRef] [Green Version]
- Cenci, L.; Laiolo, P.; Gabellani, S.; Campo, L.; Silvestro, F.; Delogu, F.; Boni, G.; Rudari, R. Assimilation of H-SAF Soil Moisture Products for Flash Flood Early Warning Systems. Case Study: Mediterranean Catchments. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5634–5646. [Google Scholar] [CrossRef]
- Es, A.; Mil, A.; Rhr, B. Assimilation of SMAP and ASCAT soil moisture retrievals into the JULES land surface model using the Local Ensemble Transform Kalman Filter—ScienceDirect. Remote Sens. Environ. 2021, 253, 112222. [Google Scholar]
- Lu, H.; Crow, W.T.; Zhu, Y.; Yu, Z.; Sun, J. The Impact of Assumed Error Variances on Surface Soil Moisture and Snow Depth Hydrologic Data Assimilation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 8, 5116–5129. [Google Scholar] [CrossRef]
- Meng, S.; Xie, X.; Liang, S. Assimilation of soil moisture and streamflow observations to improve flood forecasting with considering runoff routing lags—ScienceDirect. J. Hydrol. 2017, 550, 568–579. [Google Scholar] [CrossRef]
- Reichle, R.H.; Walker, J.P.; Koster, R.D.; Houser, P.R. Extended versus Ensemble Kalman Filtering for Land Data Assimilation. J. Hydrometeorol. 2002, 3, 728–740. [Google Scholar] [CrossRef]
- Trudel, M.; Leconte, R.; Paniconi, C. Analysis of the hydrological response of a distributed physically-based model using post-assimilation (EnKF) diagnostics of streamflow and in situ soil moisture observations. J. Hydrol. 2014, 514, 192–201. [Google Scholar] [CrossRef]
- Wang, W.; Kou, X. Methods for hydrological data assimilation and advances of assimilating remotely sensed data into rainfall-runoff models. J. Hohai Univ. (Nat. Sci.) 2009, 37, 556–562. [Google Scholar] [CrossRef]
- Vereecken, H.; Huisman, J.A.; Bogena, H.; Vanderborght, J.; Vrugt, J.A.; Hopmans, J. On the value of soil moisture measurements in vadose zone hydrology: A review. Water Resour. Res. 2008, 44, W00D06. [Google Scholar] [CrossRef] [Green Version]
- Mao, Y.; Crow, W.T.; Nijssen, B. Dual state/rainfall correction via soil moisture assimilation for improved streamflow simulation: Evaluation of a large-scale implementation with Soil Moisture Active Passive (SMAP) satellite data. Hydrol. Earth Syst. Sci. 2019, 24, 615–631. [Google Scholar]
- Brocca, L.; Melone, F.; Moramarco, T. On the estimation of antecedent wetness conditions in rainfall-runoff modelling. Hydrol. Process. 2010, 22, 629–642. [Google Scholar] [CrossRef]
- Chu, N.; Huang, C.L.; Xin, L.I.; Peijun, D.U. Simultaneous estimation of surface soil moisture and soil properties with a dual ensemble Kalman smoother. Sci. China Earth Sci. 2015, 58, 2327–2339. [Google Scholar] [CrossRef]
- De Santis, D.; Biondi, D.; Crow, W.T.; Camici, S.; Modanesi, S.; Brocca, L.; Massari, C. Assimilation of Satellite Soil Moisture Products for River Flow Prediction: An Extensive Experiment in Over 700 Catchments Throughout Europe. Water Resour. Res. 2021, 57, e2021WR029643. [Google Scholar] [CrossRef]
- Gavahi, K.; Abbaszadeh, P.; Moradkhani, H.; Zhan, X.; Hain, C. Multivariate Assimilation of Remotely Sensed Soil Moisture and Evapotranspiration for Drought Monitoring. J. Hydrometeorol. 2020, 21, 2293–2308. [Google Scholar] [CrossRef]
- Massari, C.; Brocca, L.; Ciabatta, L.; Moramarco, T.; Gabellani, S.; Albergel, C.; De Rosnay, P.; Puca, S.; Wagner, W. The Use of H-SAF Soil Moisture Products for Operational Hydrology: Flood Modelling over Italy. Hydrology 2015, 2, 2. [Google Scholar] [CrossRef] [Green Version]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Toward improved calibration of hydrologic models: Multiple and noncommensurable measures of information. Water Resour. Res. 1998, 34, 751–763. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Lü, H.; Crow, W.T.; Zhu, Y.; Wang, Q.; Su, J.; Zheng, J.; Gou, Q. Assessment of SMOS and SMAP soil moisture products against new estimates combining physical model, a statistical model, and in-situ observations: A case study over the Huai River Basin, China. J. Hydrol. 2021, 598, 126468. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T. Distributed rainfall-runoff modelling for flood frequency estimation and flood forecasting. Hydrol. Process. 2011, 25, 2801–2813. [Google Scholar] [CrossRef]
- Brocca, L.; Liersch, S.; Melone, F.; Moramarco, T.; Volk, M. Application of a model-based rainfall-runoff database as efficient tool for flood risk management. Hydrol. Earth Syst. Sci. 2013, 17, 3159–3169. [Google Scholar] [CrossRef] [Green Version]
- Masseroni, D.; Cislaghi, A.; Camici, S.; Massari, C.; Brocca, L. A reliable rainfall–runoff model for flood forecasting: Review and application to a semi-urbanized watershed at high flood risk in Italy. Water Policy 2017, 48, 726–740. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T.; Morbidelli, R. Antecedent Wetness Conditions Based on Ers Scatterometer Data. J. Hydrol. 2009, 364, 73–87. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T.; Singh, V.P. Assimilation of Observed Soil Moisture Data in Storm Rainfall-Runoff Modeling. J. Hydrol. Eng. 2009, 14, 153–165. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T.; Wagner, W.; Naeimi, V.; Bartalis, Z.; Hasenauer, S. Improving runoff prediction through the assimilation of the ASCAT soil moisture product. Hydrol. Earth Syst. Sci. 2010, 14, 1881–1893. [Google Scholar] [CrossRef] [Green Version]
- Massari, C.; Brocca, L.; Tarpanelli, A.; Moramarco, T. Data Assimilation of Satellite Soil Moisture into Rainfall-Runoff Modelling: A Complex Recipe? Remote Sens. 2015, 7, 11403–11433. [Google Scholar] [CrossRef]
- Shi, C.; Xie, Z.; Qian, H.; Liang, M.; Yang, X. China land soil moisture EnKF data assimilation based on satellite remote sensing data. Sci. China Earth Sci. 2011, 54, 1430–1440. [Google Scholar] [CrossRef]
- Calheiros, R.V.; Zawadzki, I.I. Reflectivity-Rain Rate Relationships for Radar Hydrology in Brazil. J. Clim. Appl. Meteorol. 1987, 26, 118–132. [Google Scholar] [CrossRef]
- Ning, Y.; Qian, M.; Wang, Y. Huai River Basin Water Conservancy Manual; Science Press: Beijing, China, 2003. [Google Scholar]
- Famiglietti, J.S.; Wood, E.F. Multiscale modeling of spatially variable water and energy balance processes. Water Resour. Res. 1994, 30, 3061–3078. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.G.; Jensen, M.E.; Wright, J.L.; Burman, R.D. Operational Estimates of Reference Evapotranspiration. Agron. J. 1989, 81, 650–662. [Google Scholar] [CrossRef]
- Corradini, C.; Melone, F.; Smith, R.E. A unified model for infiltration and redistribution during complex rainfall patterns. J. Hydrol. Amst. 1997, 192, 104–124. [Google Scholar] [CrossRef]
- Burgers, G.; Leeuwen, P.; Evensen, G. On the Analysis Scheme in the Ensemble Kalman Filter. OAI 1997. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles—ScienceDirect. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Hoffmann, L.; El Idrissi, A.; Pfister, L.; Hingray, B.; Guex, F.; Musy, A.; Humbert, J.; Drogue, G.; Leviandier, T. Development of regionalized hydrological models in an area with short hydrological observation series. River Res. Appl. 2010, 20, 243–254. [Google Scholar] [CrossRef]
- Alvarez-Garreton, C.; Ryu, D.; Western, A.W.; Su, C.-H.; Crow, W.T.; Robertson, D.E.; Leahy, C. Improving operational flood ensemble prediction by the assimilation of satellite soil moisture: Comparison between lumped and semi-distributed schemes. Hydrol. Earth Syst. Sci. 2015, 19, 1659–1676. [Google Scholar] [CrossRef] [Green Version]
- Nayak, A.K.; Biswal, B.; Sudheer, K.P. Role of hydrological model structure in the assimilation of soil moisture for streamflow prediction. J. Hydrol. 2021, 598, 126465. [Google Scholar] [CrossRef]
- Berardi, M.; Andrisani, A.; Lopez, L.; Vurro, M. A new data assimilation technique based on ensemble Kalman filter and Brownian bridges: An application to Richards’ equation. Comput. Phys. Commun. 2016, 208, 43–53. [Google Scholar] [CrossRef]
- Jamal, A.; Linker, R. Inflation method based on confidence intervals for data assimilation in soil hydrology using the ensemble Kalman filter. Vadose Zone J. 2020, 19, e20000. [Google Scholar] [CrossRef] [Green Version]
- Helgert, S.; Khodayar, S. Improvement of the soil-atmosphere interactions and subsequent heavy precipitation modelling by enhanced initialization using remotely sensed 1 km soil moisture information. Remote Sens. Environ. 2020, 246, 111812. [Google Scholar] [CrossRef]
- Tavakol, A.; Rahmani, V.; Quiring, S.M.; Kumar, S.V. Evaluation analysis of NASA SMAP L3 and L4 and SPoRT-LIS soil moisture data in the United States. Remote Sens. Environ. 2019, 229, 234–246. [Google Scholar] [CrossRef]
- Yang, H.; Xiong, L.; Liu, D.; Cheng, L.; Chen, J. High spatial resolution simulation of profile soil moisture by assimilating multi-source remote-sensed information into a distributed hydrological model. J. Hydrol. 2021, 597, 126311. [Google Scholar] [CrossRef]


| Model Component | Parameter | Description | Unit | Range |
|---|---|---|---|---|
| SWB | Maximum water storage of the soil layer | 100–1000 | ||
| Saturated hydraulic conductivity | 0.01–20 | |||
| Drainage exponent | - | 5.0–60 | ||
| Fraction of drainage versus interflow | - | 0–1.0 | ||
| Correction coefficient for the potential evapotranspiration | - | 0.4–2.0 | ||
| RR | Lag–area relationship parameter | - | 0.5–6.5 | |
| λ | Initial abstraction coefficient | - | 0.0001–0.2 | |
| Relationship between modelled SM and the of the SCS-CN method | - | 1.0–5.0 |
| Catchments | Calibration (1 January 2010–31 December 2014) | Validation (1 January 2015–31 December 2017) | ||||
|---|---|---|---|---|---|---|
| WWQ | 0.494 | 0.532 | 0.799 | 0.512 | 0.688 | 0.737 |
| DPL | 0.561 | 0.641 | 0.750 | 0.594 | 0.806 | 0.795 |
| CTG | 0.374 | 0.487 | 0.676 | 0.628 | 0.856 | 0.829 |
| Catchments | WWQ | DPL | CTG | ||||
|---|---|---|---|---|---|---|---|
| OL | 0.510 | 0.593 | 0.678 | ||||
| DI | CLDAS | 0.025 | 1.411 | −0.121 | 1.660 | 0.120 | 1.653 |
| BPNN | 0.007 | 1.423 | −0.124 | 1.662 | 0.109 | 1.664 | |
| EnKF | CLDAS | 0.531 | 0.978 | 0.621 | 0.965 | 0.696 | 0.972 |
| BPNN | 0.551 | 0.957 | 0.637 | 0.944 | 0.702 | 0.962 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Z.; Lü, H.; Ahmed, N.; Zhu, Y.; Gou, Q.; Wang, X.; Liu, E.; Xu, H.; Pan, Y.; Sun, M. Soil Moisture Data Assimilation in MISDc for Improved Hydrological Simulation in Upper Huai River Basin, China. Water 2022, 14, 3476. https://doi.org/10.3390/w14213476
Ding Z, Lü H, Ahmed N, Zhu Y, Gou Q, Wang X, Liu E, Xu H, Pan Y, Sun M. Soil Moisture Data Assimilation in MISDc for Improved Hydrological Simulation in Upper Huai River Basin, China. Water. 2022; 14(21):3476. https://doi.org/10.3390/w14213476
Chicago/Turabian StyleDing, Zhenzhou, Haishen Lü, Naveed Ahmed, Yonghua Zhu, Qiqi Gou, Xiaoyi Wang, En Liu, Haiting Xu, Ying Pan, and Mingyue Sun. 2022. "Soil Moisture Data Assimilation in MISDc for Improved Hydrological Simulation in Upper Huai River Basin, China" Water 14, no. 21: 3476. https://doi.org/10.3390/w14213476






