Radar Quantitative Precipitation Estimation Algorithm Based on Precipitation Classification and Dynamical Z-R Relationship
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data
3. Methodology
3.1. Optimization Process (OP)
3.2. Optimization Process of Dynamical Adjustment (ODA)
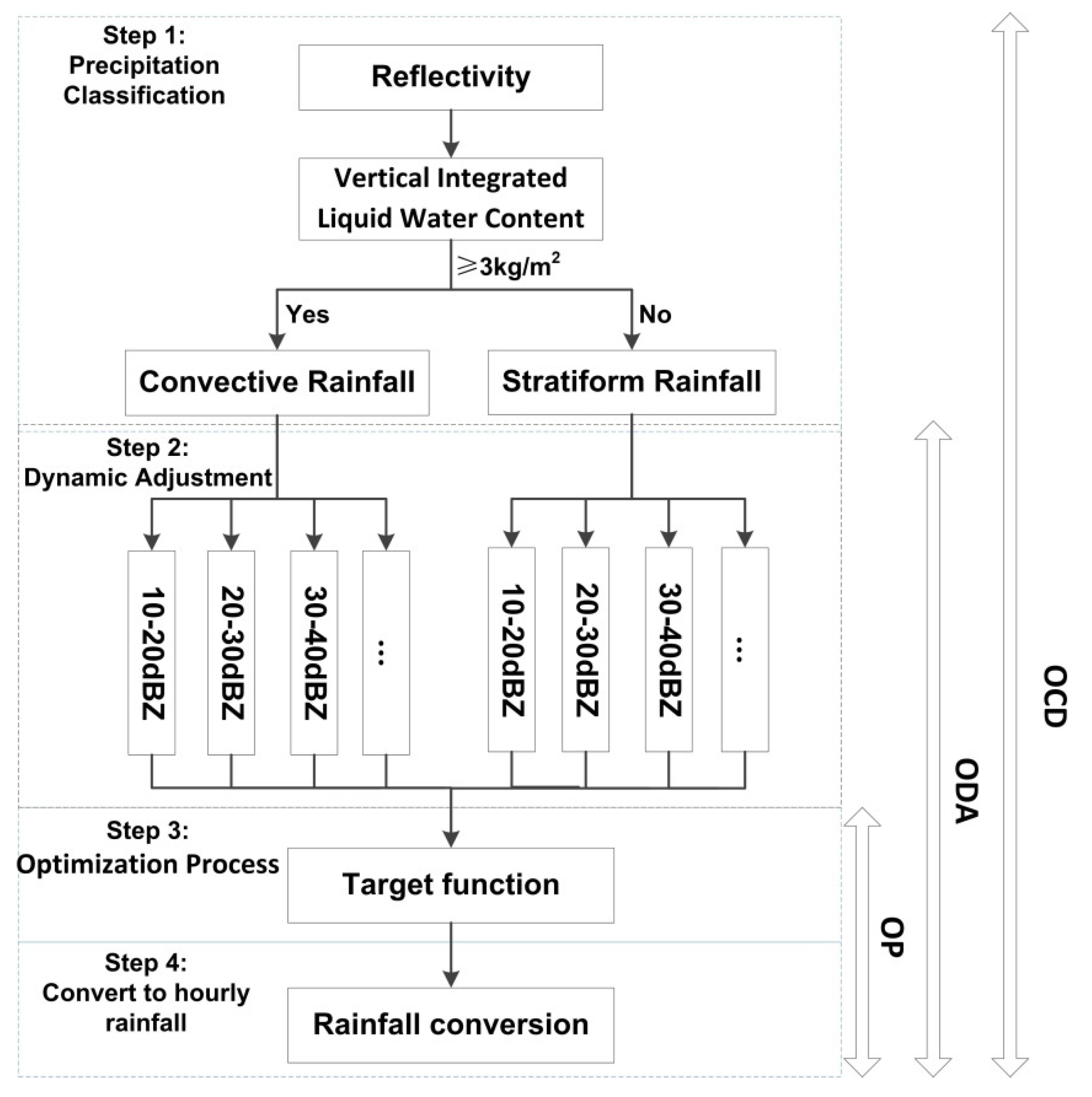
3.3. Optimization Process of Precipitation Classification and Dynamical Adjustments (OCD)
3.4. Evaluation Indicators
4. Results and Discussion
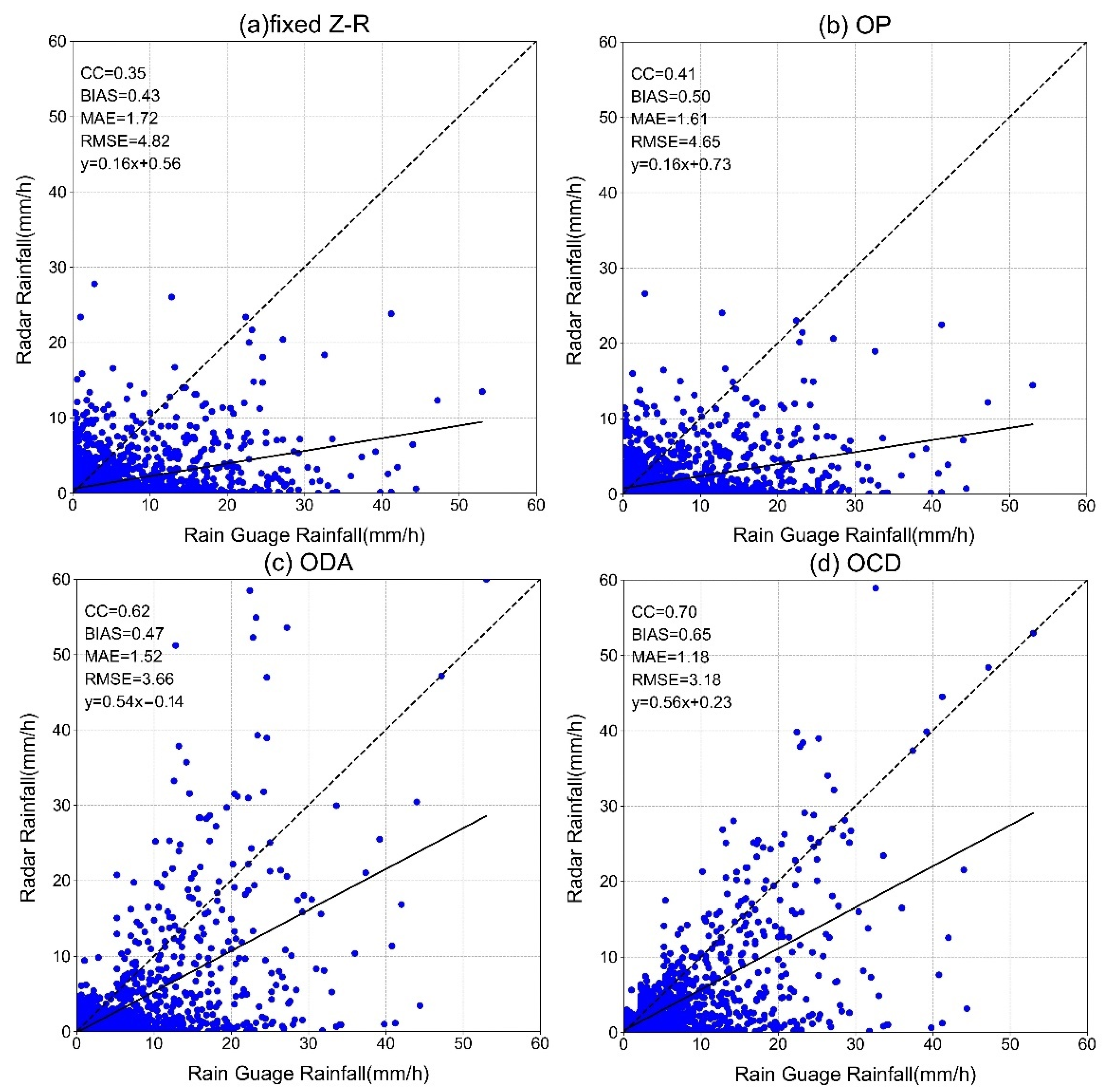
4.1. Scatter Distribution of Inversion Results by Algorithms
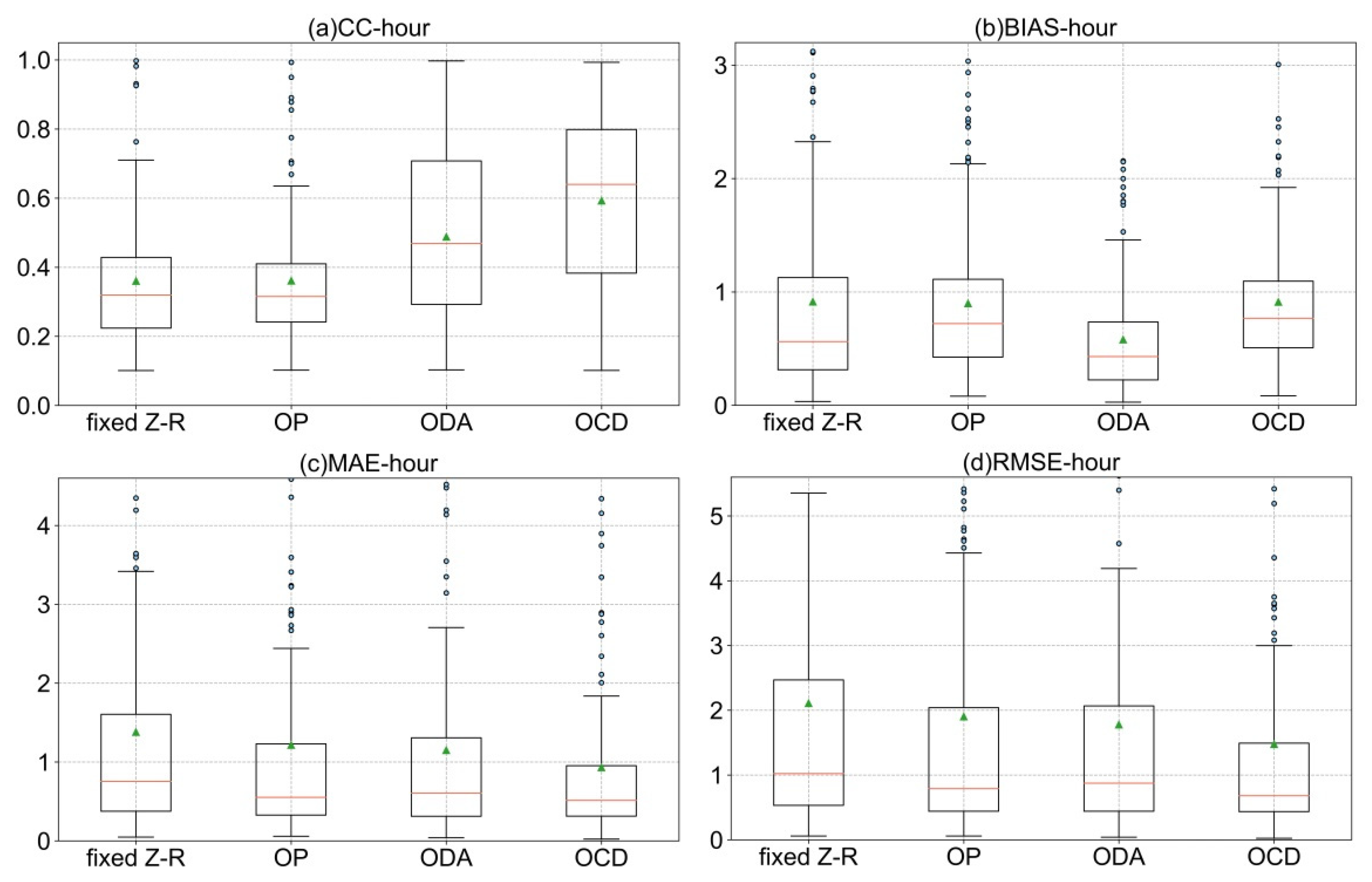
4.2. Evaluation Indicators Distribution of the Algorithms
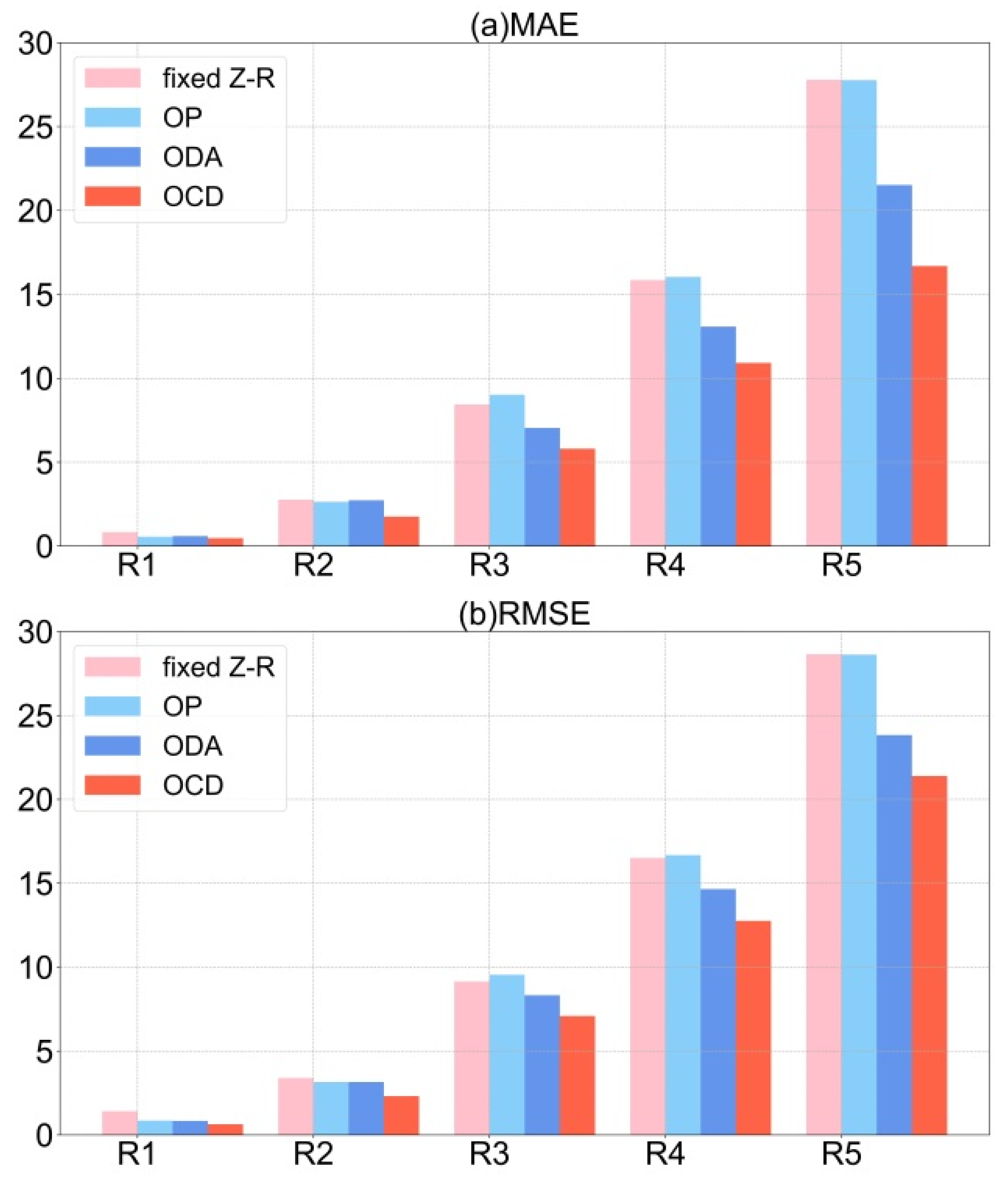
4.3. Performance of Algorithms under Different Rain Rates
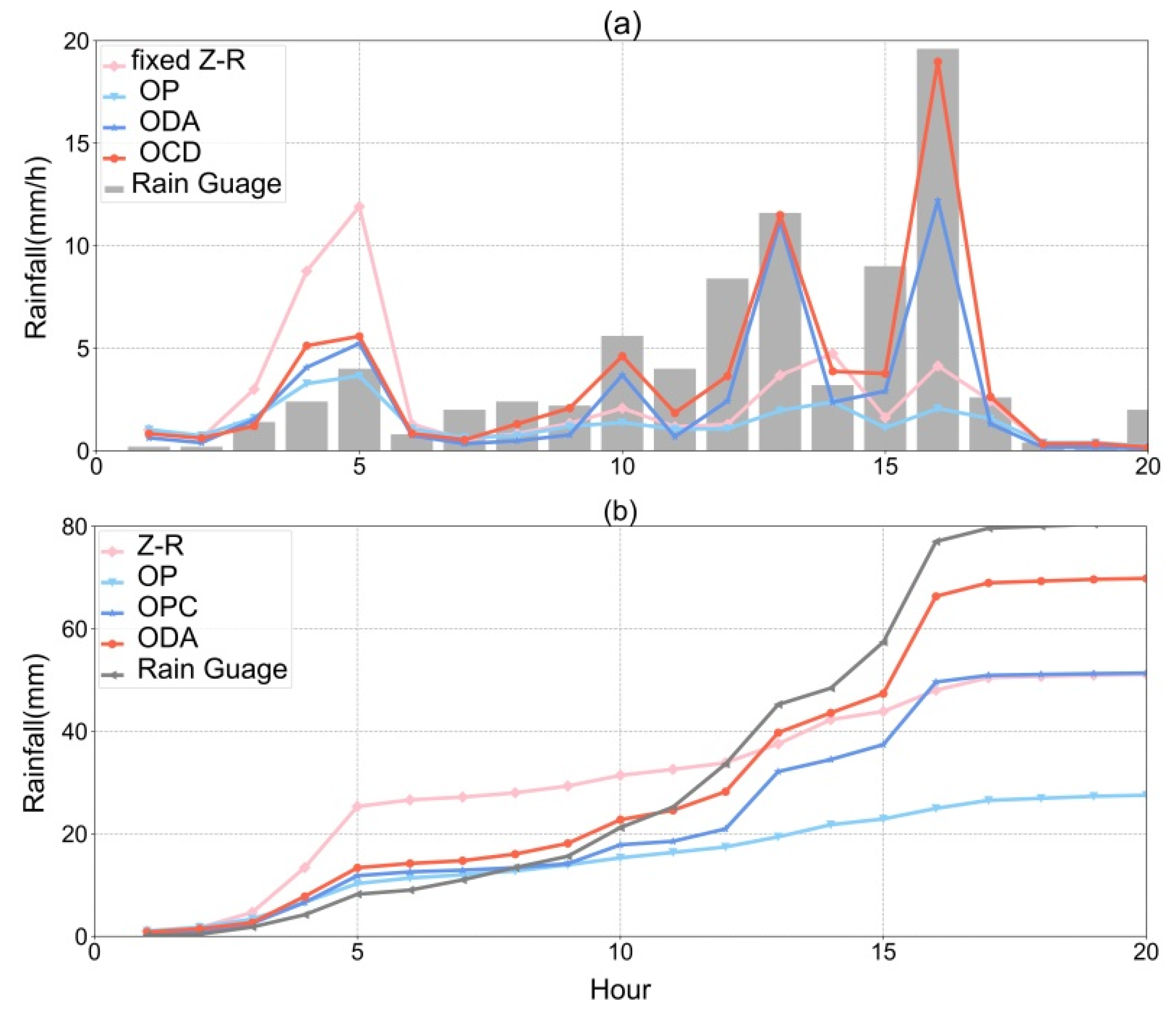
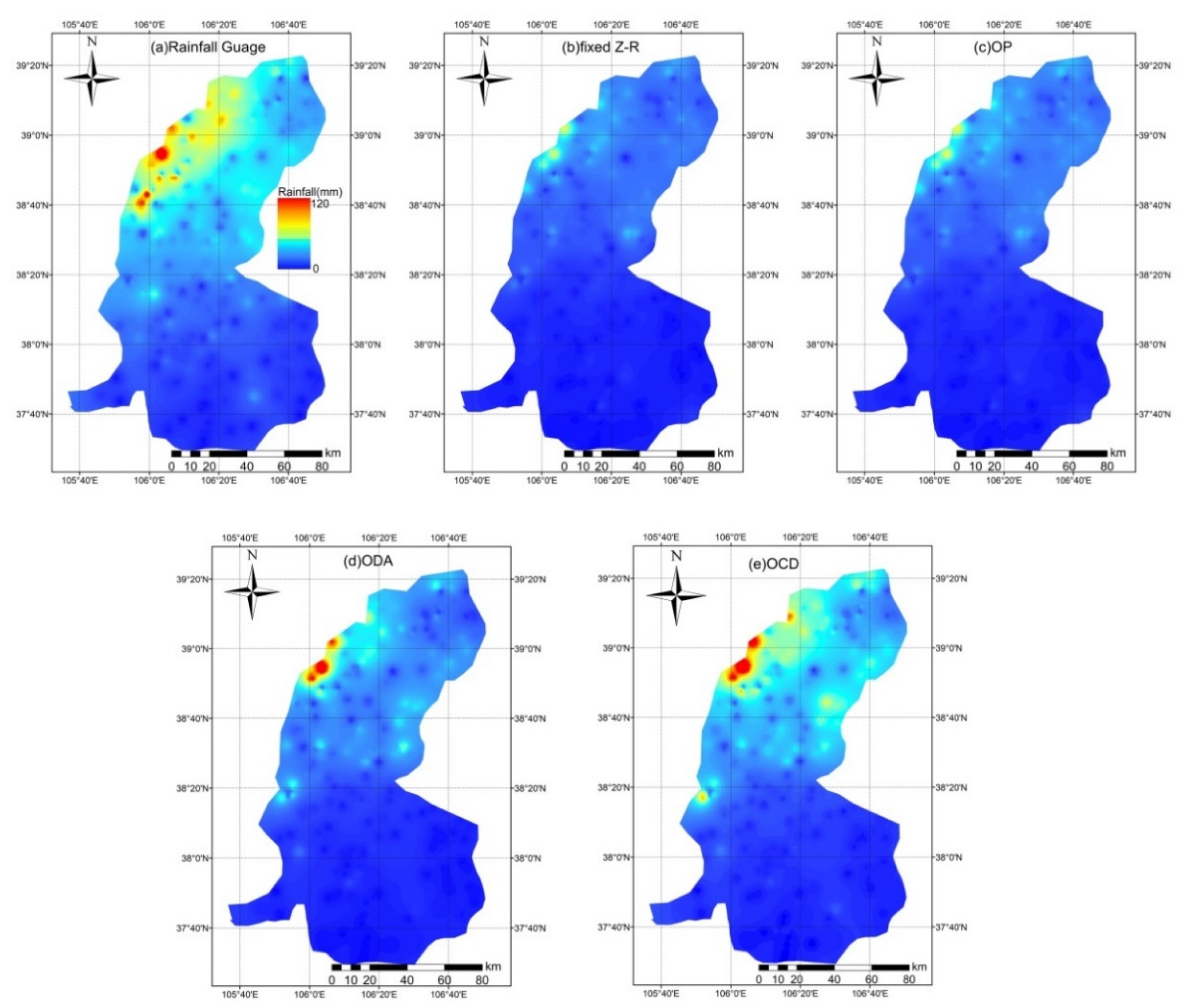
4.4. Case Analysis of Rainfall Event
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Andersen, C.T.; Foster, I.D.L.; Pratt, C.J. The role of urban surfaces (permeable pavements) in regulating drainage and evaporation: Development of a laboratory simulation experiment. Hydrol. Process. 2015, 13, 597–609. [Google Scholar] [CrossRef]
- Zhou, Y.; Smith, S.J.; Zhao, K.; Imhoff, M.; Thomson, A.; Bond-Lamberty, B.; Asrar, G.R.; Zhang, X.; He, C.; Elvidge, C.D. A global map of urban extent from nightlights. Environ. Res. Lett. 2015, 10, 054011. [Google Scholar] [CrossRef]
- Goudenhoofdt, E.; Delobbe, L. Evaluation of radar-gauge merging methods for quantitative precipitation estimates. Hydrol. Earth Syst. Sci. 2009, 13, 195–203. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Tian, F.; Smith, J.A.; Hu, H. Urban signatures in the spatial clustering of summer heavy rainfall events over the Beijing metropolitan region. J. Geophys. Res. Atmos. 2014, 119, 1203–1217. [Google Scholar] [CrossRef]
- Ochoa-Rodriguez, S.; Wang, L.P.; Willems, P.; Onof, C. A Review of Radar-Rain Gauge Data Merging Methods and Their Potential for Urban Hydrological Applications. Water Resour. Res. 2019, 55, 6356–6391. [Google Scholar] [CrossRef]
- Berne, A.; Krajewski, W.F. Radar for hydrology: Unfulfilled promise or unrecognized potential? Adv. Water Resour. 2013, 51, 357–366. [Google Scholar] [CrossRef]
- Auipong, N.; Trivej, P. Study of Z-R relationship among different topographies in Northern Thailand. J. Phys. Conf. Ser. 2018, 1144, 012098. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W. The Distribution of Raindrops With Size. J. Meteor. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Vieux, B.E.; Bedient, P.B. Estimation of Rainfall for Flood Prediction from WSR-88D Reflectivity: A Case Study, 17–18 October 1994. Weather Forecast. 1998, 13, 407–415. [Google Scholar] [CrossRef]
- Fulton, R.A.; Breidenbach, J.P.; Seo, D.J.; Miller, D.A.; O’Bannon, T. The WSR-88D Rainfall Algorithm. Weather Forecast. 1997, 13, 377–395. [Google Scholar] [CrossRef]
- Ciach, G.J.; Krajewski, W.F. Radar-Rain Gauge Comparisons under Observational Uncertainties. J. Appl. Meteorol. 1998, 38, 1519–1525. [Google Scholar] [CrossRef]
- Ulbrich, C.W.; Lee, L.G. Rainfall Measurement Error by WSR-88D Radars due to Variations in Z–R Law Parameters and the Radar Constant. J. Atmos. Ocean. Technol. 1999, 16, 1017–1024. [Google Scholar] [CrossRef]
- Kato, A.; Maki, M. Localized Heavy Rainfall Near Zoshigaya, Tokyo, Japan on 5 August 2008 Observed by X-band Polarimetric Radar—Preliminary Analysis—. Sola 2009, 5, 89–92. [Google Scholar] [CrossRef] [Green Version]
- Atlas, D.; Rosenfeld, D.; Wolff, D.B. Climatologically tuned reflectivity-rain rate relations and links to area-time integrals. J. Appl. Meteorol. 1990, 29, 1120–1135. [Google Scholar] [CrossRef]
- Xu, Z.F.; Xiong, J.; Ge, W.Z. Application of Genetic Algorit h min Optimizing the Z-R Parameter to Radar Rainfall Estimati on. Plateau Meteorol. 2006, 4, 710–715. [Google Scholar]
- Zhang, Y.; Yang, J.; Zhang, W.Q. Study on modification to optimization method of Z-I relationship. J. Meteorol. Environ. 2015, 31, 97–102. [Google Scholar]
- Chapon, B.; Delrieu, G.; Gosset, M.; Boudevillain, B. Variability of rain drop size distribution and its effect on the Z–R relationship: A case study for intense Mediterranean rainfall. Atmos. Res. 2008, 87, 52–65. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Zrnić, D.S.; Goldhirsh, J.; Rowland, J. Comparison of Simulated Rain rates from Disdrometer Data Employing Polarimetric Radar Algorithms. J. Atmos. Ocean. Technol. 1989, 6, 476–486. [Google Scholar] [CrossRef]
- Uijlenhoet, R.; Steiner, M.; Smith, J.A. Variability of Raindrop Size Distributions in a Squall Line and Implications for Radar Rainfall Estimation. J. Hydrometeorol. 2003, 4, 43–61. [Google Scholar] [CrossRef]
- Ulbrich, C.W.; Atlas, D. On the Separation of Tropical Convective and Stratiform Rains. J. Appl. Meteorol. 2002, 41, 188–195. [Google Scholar] [CrossRef]
- Steiner, M.; Houze, R.A., Jr.; Yuter, S.E. Climatological characterization of three-dimensional storm structure from operational radar and rain gauge data. J. Appl. Meteorol. Climatol. 1995, 34, 1978–2007. [Google Scholar] [CrossRef]
- Chumchean, S.; Sharma, A.; Seed, A. An Integrated Approach to Error Correction for Real-Time Radar-Rainfall Estimation. J. Atmos. Ocean. Technol. 2006, 23, 67–79. [Google Scholar] [CrossRef]
- Zhang, J.; Langston, C.; Howard, K. Brightband Identification Based on Vertical Profiles of Reflectivity from the WSR-88D. J. Atmos. Ocean. Technol. 2008, 25, 1859–1872. [Google Scholar] [CrossRef]
- Howard, K.; Zhang, J. Multi-sensor QPE in the National Mosaic and QPE (NMQ) System. AGU Spring Meet. Abstr. 2007, 2007, H52A-04. [Google Scholar]
- Alfieri, L.; Claps, P.; Laio, F. Time-dependent Z-R relationships for estimating rainfall fields from radar measurements. Nat. Hazards Earth Syst. Sci. 2010, 10, 149–158. [Google Scholar] [CrossRef] [Green Version]
- Crosson, W.L.; Duchon, C.E.; Raghavan, R.; Goodman, S.J. Assessment of rainfall estimates using a standard ZR relationship and the probability matching method applied to composite radar data in central Florida. J. Appl. Meteorol. Climatol. 1996, 35, 1203–1219. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, Y.; Cai, J.; Hu, S. An approach for radar quantitative precipitation estimate based on categorical ZI relations. J. Trop. Meteorol. 2011, 27, 601–608. [Google Scholar]
- Gou, Y.B.; Liu, L.; Wang, D.; Zhong, L.; Chen, C. Evaluation and Analysis of the Z-R Storm-Grouping Relationships Fitting Scheme based on Storm Identification. Torrential Rain Disasters 2015, 34, 1–8. [Google Scholar]
- Duan, Y.; Wang, G.; Zhi, S.; Ling, T.; Fu, W.B. Area Rainfall Estimation Based on Cloud Grouping Z-R Relationship Along Zhejiang Jiangxi Railway Lines. J. Arid Meteorol. 2019, 37, 972–978. [Google Scholar]
- Wu, W.; Zou, H.; Shan, J.; Wu, S. A Dynamical Z-R Relationship for Precipitation Estimation Based on Radar Echo-Top Height Classification. Adv. Meteorol. 2018, 2018, 8202031. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Wei, H.; Liu, Y.; Ma, W.; Gu, Y.; Peng, Y.; Li, C. Runoff prediction for Ningxia Qingshui River Basin under scenarios of climate and land use changes. Acta Ecol. Sin. 2017, 37, 1252–1260. [Google Scholar]
- Yuan, X.Q.; Ni, G.H.; Pan, A.J. NEXRAD Z-R Power Relationship in Beijing Based on Optimization Algorithm. J. China Hydrol. 2010, 30, 1–6. [Google Scholar]
- Houghton, H.G. On precipitation mechanisms and their artificial modification. J. Appl. Meteorol. Climatol. 1968, 7, 851–859. [Google Scholar] [CrossRef]
- Qi, Y.; Zhang, J.; Zhang, P. A real-time automated convective and stratiform precipitation segregation algorithm in native radar coordinates. Q. J. R. Meteorol. Soc. 2013, 139, 2233–2240. [Google Scholar] [CrossRef]


| Event | Date | Start Time | Duration (hours) | Max Rain Rates (mm/h) | Average Rain Rates (mm/h) | Type | Note |
|---|---|---|---|---|---|---|---|
| 1 | 12 April 2018 | 5:00 | 14 | 13.4 | 1.25 | Stratiform | train |
| 2 | 19 April 2018 | 10:00 | 15 | 28.4 | 1.87 | Stratocumulus | train |
| 3 | 18 May 2018 | 17:00 | 8 | 8 | 1.21 | Stratiform | test |
| 4 | 30 June 2018 | 19:00 | 24 | 37.6 | 2.37 | Convective | train |
| 5 | 22 July 2018 | 11:00 | 29 | 53 | 4.83 | Convective | test |
| 6 | 15 August 2018 | 9:00 | 41 | 25.2 | 1.23 | Stratocumulus | train |
| 7 | 26 April 2019 | 11:00 | 7 | 27.6 | 2.04 | Stratocumulus | test |
| 8 | 18 June 2019 | 23:00 | 39 | 3.4 | 0.49 | Stratiform | test |
| 9 | 11 September 2019 | 23:00 | 22 | 5.6 | 1.58 | Stratiform | test |
| 10 | 18 September 2019 | 12:00 | 10 | 3 | 0.57 | Stratiform | train |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, W.; Bao, S.; Yang, K.; Wei, J.; Zhu, X.; Qiao, Z.; Wang, Y.; Li, Q. Radar Quantitative Precipitation Estimation Algorithm Based on Precipitation Classification and Dynamical Z-R Relationship. Water 2022, 14, 3436. https://doi.org/10.3390/w14213436
Peng W, Bao S, Yang K, Wei J, Zhu X, Qiao Z, Wang Y, Li Q. Radar Quantitative Precipitation Estimation Algorithm Based on Precipitation Classification and Dynamical Z-R Relationship. Water. 2022; 14(21):3436. https://doi.org/10.3390/w14213436
Chicago/Turabian StylePeng, Wang, Shuping Bao, Kan Yang, Jiahua Wei, Xudong Zhu, Zhen Qiao, Yongcan Wang, and Qiong Li. 2022. "Radar Quantitative Precipitation Estimation Algorithm Based on Precipitation Classification and Dynamical Z-R Relationship" Water 14, no. 21: 3436. https://doi.org/10.3390/w14213436







