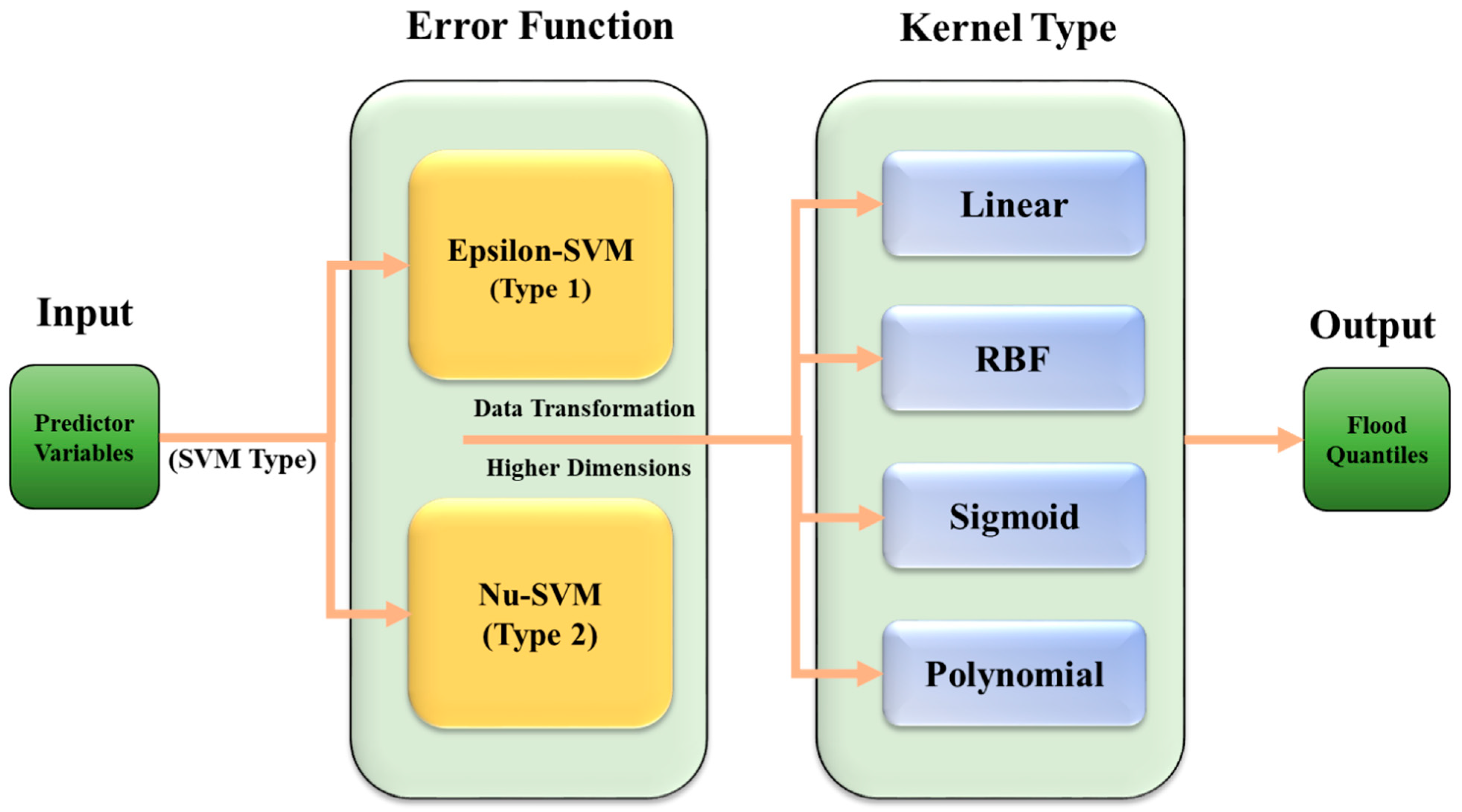
1. Introduction
Floods are one of the most destructive natural hazards, resulting in billions of dollars’ of annual damage across the globe [
1,
2]. Floods cause damage to infrastructures [
3,
4], transportation systems [
5,
6], properties, heritage sites, environments and death to humans [
7,
8]. Due to global warming, floods are becoming more frequent and destructive [
9,
10]. Although intense rainfall and snow melt are the main causes of flooding, environmental degradation [
11], land-use change [
12] and other anthropogenic factors increase the severity of flooding [
13,
14]. Many countries are in danger of floods at different scales, with an estimated 1.3 billion people to be directly impacted by floods by 2050 [
15].
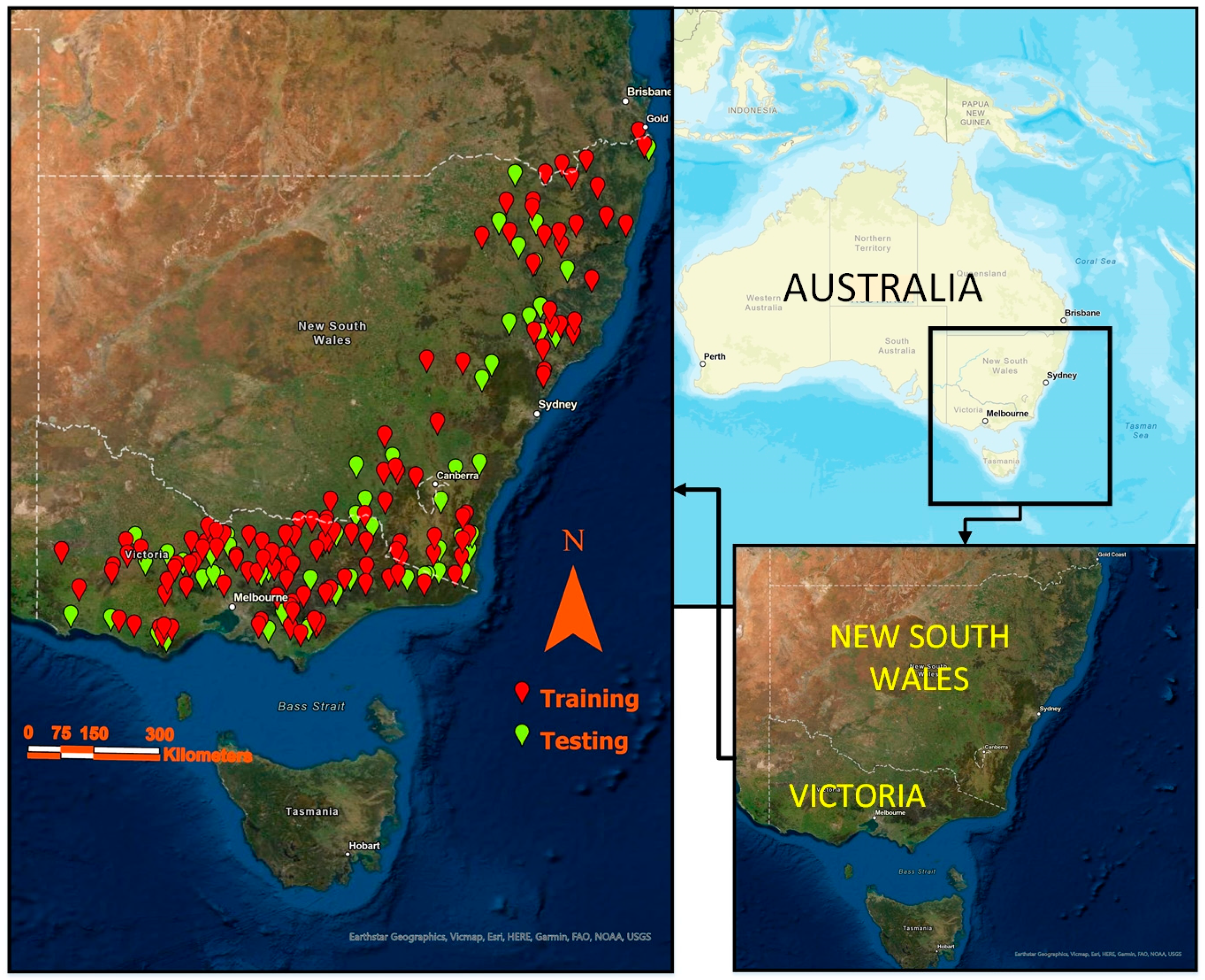
Australia has faced many devastating floods in the past, which resulted in thousands of casualties, mental and physical losses. Additionally, millions of dollars have been spent on the maintenance and rehabilitation of flood-affected infrastructures and communities across Australia [
16]. Subtropical climates, low-lying cities and heavy rainfall put the eastern part of Australia at serious flood risk [
17,
18].
To reduce flood damage, a risk-based approach is generally adopted in the design of hydraulic structures and for numerous flood management tasks. Here, a design flood/flood quantile is defined as a flood discharge with a certain return period (such as 100-year flood). Both the flood frequency analysis (FFA) and regional flood frequency (RFFA) are widely used for this purpose for gauged and ungauged catchments, respectively [
19]. Most of the previously developed RFFA models are linear in nature, such as the index flood method of Hosking and Wallis (1997) [
19,
20]. More recently, artificial intelligence (AI)-based RFFA models are becoming popular, which are nonlinear methods and do not depend on a fixed model structure such as the multiple linear regression (MLR) models.
In the past two decades, AI-based RFFA methods have been used in several countries [
21,
22]. The artificial neural network (ANN) and ANN ensembles were some of the methods [
23] used in RFFA, and the results of these models were generally more accurate than the conventional linear models [
21,
24]. For example, Jingi and Hall [
23] compared the results of ANN with several linear methods and reported that the ANN-based method outperformed the linear methods. Since 2004, AI-based methods have gained popularity among hydrologists such as support vector machine (SVM) and ANN methods [
25,
26]. Different combinations of ANN and SVM have been proposed for countries such as Iran, Canada and Australia [
27,
28]. Dawson et al. [
29] and Shu and Ouarda [
30] adopted the ANN method to estimate the design floods and reported that ANN performed better than the traditional methods. Dawson et al. [
29] also noted that the application of AI-based methods is easier than many other methods, since they rely on the recorded flow and catchment data rather than the physics of flood generation processes. Shu and Ouarda [
30] also noted that the combination of different data-driven methods could increase the accuracy of flood estimation models.
Shu and Ouarda [
31] applied the ANN and adaptive neuro fuzzy inference system (ANFIS) in estimating the streamflow at ungauged sites. They compared a single ANN, ANN ensemble and a MLR method to estimate regional low flows at ungauged sites. They reported that the AI-based methods were more accurate than the traditional ones. They also noted that the ANN ensemble outperformed the single ANN [
32]. Aziz et al. [
33] used data from Australia to compare the performance of the ANN method with the quantile regression technique. Various ensembles of ANN methods were proposed by scientists. For example, Alobaidi et al. [
34] and Durocher et al. [
35] used data from 151 hydrometric stations in Canada to compare different combinations of models. Alobaidi et al. [
34] compared the results of their study with an ANN method used by Shu and Ouarda [
30] and reported that ANN-ensembles such as the event adversarial neural network (EANN) and generalised EANN (G-EANN) enhanced the accuracy of the flood estimation. A combination of the ANN and generalised additive model (GAM) was proposed by Durocher et al. [
35]. The advantage of this method was that it was simpler than the ANN while giving a similar accuracy. They compared their results with other studies [
36,
37,
38,
39] and reported that their model had a better performance than several previous studies. The genetic algorithm-based artificial neural network (GAANN) and back propagation-based artificial neural network (BPANN) were evaluated by Aziz et al. [
40] using data from 452 catchments in Australia. They reported that both the combinations exhibited better results than the single ANN method. Aziz et al. [
22] noted that ANN, GAANN, gene expression programming (GEP) and coactive neuro fuzzy inference system (CANFIS) methods could provide quite accurate design flood estimates where the ANN outperformed the other models.
RFFA based on the ANN and support vector regression (SVR) methods were used by Gizaw and Gan [
25], who used data from 49 stations in Canada. They reported that the results of the SVR method were more consistent and had a better generalisation ability than the ANN. However, they mentioned that the ANN method performs better for a larger dataset. Over 15 years of data collected from 424 catchments in Canada and the United States were used by Ouali et al. [
41] to compare the performances of different combinations of the ANN-based methods. In addition, they compared their results with the findings of other studies such as Ouarda et al. [
42], Chebana et al. [
38] and Ouali et al. [
43] and reported that nonlinear methods generally outperformed the linear methods. The ANN, SVR, nonlinear regression (NLR) and ANFIS methods were used in another study by Sharifi Garmdareh et al. [
24], where they used gamma testing (GT) to improve the results of the SVR and ANFIS models by finding the best combination of input variables. They used data from 55 hydrometric stations in Iran and reported that GT+ANFIS followed by the GT+SVR were the best-performing models.
Using 21 years of data from 47 catchments in Iran, Ghaderi et al. [
44] compared the performances of the SVM, ANFIS and GEP models. They also used the M-test and GM-test to find the best test and training data ratio and the most critical input variables. They reported that the SVM method was the best-performing method in terms of the coefficient of determination (
R2) and root mean square error (RMSE). The ANN, SVR and NLR methods were compared by Vafakhah and Khosrobeigi Bozchaloei [
28] using a dataset from 33 stations in Iran. They reported that the SVR was the best-performing method for a regional analysis of flood duration curves. Using a dataset from 202 catchments in Australia, Haddad and Rahman [
45] compared the performances of 15 combinations of RFFA methods, including Bayesian generalised least squares (BGLSR), multidimensional scaling (MDS) and SVR. They reported that the MDS-based SVR method using a radial basis function (RBF) kernel was the best-performing model in terms of consistency, accuracy of the results and generalisation.
Five different types of ANN methods were used by Kordrostami et al. [
46] to estimate design floods in Australia, where they used a dataset from 88 gauging stations. They reported that using fewer predictor variables improved the performance of the ANN method, except when all the eight were used. The performances of some AI-based RFFA methods, including SVR, projection pursuit regression (PPR), boosted regression trees (BRT) and multivariate adaptive regression spline (MARS), were compared by Allahbakhshian-Farsani et al. [
26] using data from 54 hydrometric stations in Iran. They used statistical indices such as RMSE and relative root mean square error (RRMSE) to compare the methods and reported that the SVR model based on the RBF kernel outperformed the other methods.
Using a dataset of 37 years from three hydrometric stations, Linh et al. [
27] compared the performances of the ANN, MLR and WNN (variation methods of ANN) to estimate design floods. They used RMSE,
R2 and NASH to evaluate the performances of these methods. They reported that the WNN method had a better performance in terms of generalisation capability and accuracy. A dataset from 151 catchments in Canada was used by Desai and Ouarda [
47] to compare the performance of different combinations of the canonical correlation analysis (CCA) with ANN, random forest regression (RFR), MLR and ANN ensembles. They reported that a combination of CCA and RFR to be the best-performing method. In another study, Bozchaloei and Vafakhah [
48] used 20 years of data recorded from 33 hydrometric stations to estimate design floods, in which they compared the performances of the ANN, ANFIS and NLR methods and reported ANFIS to be the best-performing method. In another study, Kumar et al. [
49] used the fuzzy inference system (FIS), ANN and L-moment methods using a dataset of 15–29 years from 17 catchments in India. They reported FIS to be the best-performing method, followed by ANN in terms of accuracy and reliability.
AI-based RFFA models are generally more complex than the simplified RFFA techniques, such as the index flood method [
20] and quantile regression technique [
50]. Some of the simplified RFFA techniques use only a few predictor variables, such as the catchment area and mean annual rainfall, and are easier to apply in practice. However, AI-based techniques are becoming more popular as computing powers are increasing, and these often provide more accurate results [
51]. Based on the previous studies on AI-based RFFA methods, the SVM and ANN are found to be quite popular in other countries; however, their application to Australia is quite limited. Hence, the objective of this study is to develop and test the ANN and SVM-based RFFA methods on South-East Australian catchments. The results of this study will help to recommend more accurate RFFA models in Australia for design applications.
4. Results
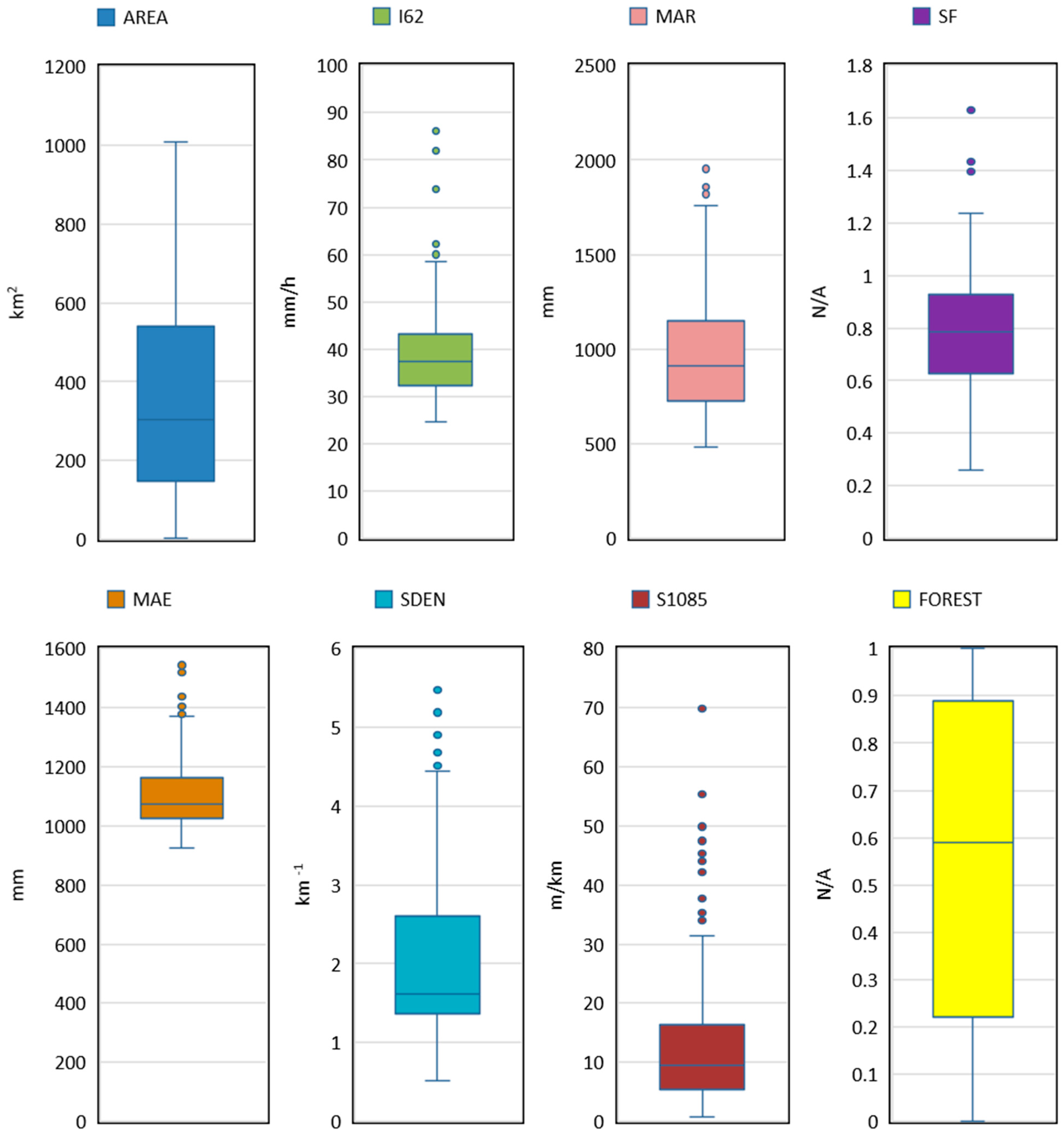
The final predictor variables were selected based on their
p-values (
p-value must not exceed 0.10). The final predictor variables used are (i) AREA,
I62, MAR and SDEN (for
Q2); (ii) AREA,
I62 and SDEN (for
Q5 and
Q10); (iii) AREA,
I62, SDEN and MAR (for
Q20 and
Q50); and (iv) AREA,
I62, MAE and MAR (for
Q100).
Table 2 shows the statistical metrices of the best ANN model for different flood quantiles. As shown in
Appendix A (
Table A1), the best methods were selected based on the most common evaluation statistics, such as MSE, RMSE, RRMSE, REr and Rbias.
Table A1 shows some of the best-performing ANN methods with different algorithms; from these, the best one is presented in
Table 2 and used for further investigation.
Table A2 shows the different parameters used in developing the SVM methods, and
Table A3 represents the best-performing SVM methods with different algorithms used in developing the SVM methods. The best-performing SVM methods are selected based on statistical indices and are represented in
Table 3 and are used for further investigation. From
Table 2, it can be seen that, for the ANN-based models,
Q10 has the smallest Rbias and RMSNE values, whereas
Q5 has the smallest REr value. From
Table 3, it is found that
Q2 has the smallest Rbias value, and
Q5 has the smallest RMSNE value.
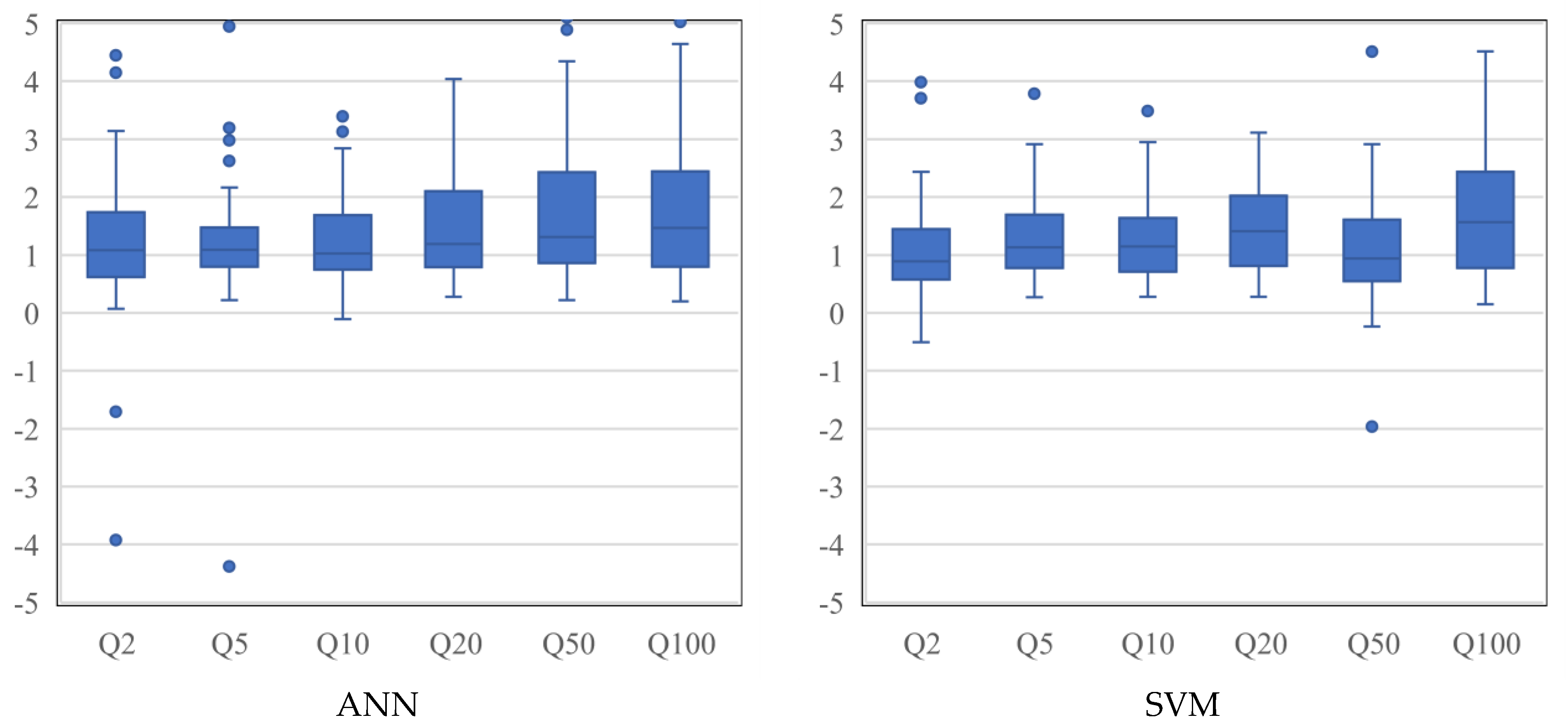
Figure 6 shows boxplot of
Qratio values for ANN and SVM models. As can be seen in this figure, the ANN model shows some overestimation for
Q20,
Q50 and
Q100, whereas, for the SVM model, there is an overestimation for
Q20 and
Q100. In terms of
Qratio, the ANN presents better results for
Q5 (with a smaller box width) as compared to SVM. As can be seen in
Figure 6, the results of
Q2 for SVM are better than the ANN. In terms of
Q10,
Q20 and
Q100, both the models perform very similarly; however, the median values for SVM seem to be further away from the 1:1 line. The
Qratio results for
Q50 show that the SVM method has a better performance than the ANN, with a smaller box width and median value located near the 1:1 line Overall, the
Q5 model for ANN is the best model (with the smallest box width), followed by
Q10 (ANN),
Q2 (SVM),
Q5 (SVM),
Q10 (SVM) and
Q50 (SVM). For
Q100, both the ANN and SVM and, for
Q50, the ANN shows remarkable overestimations.
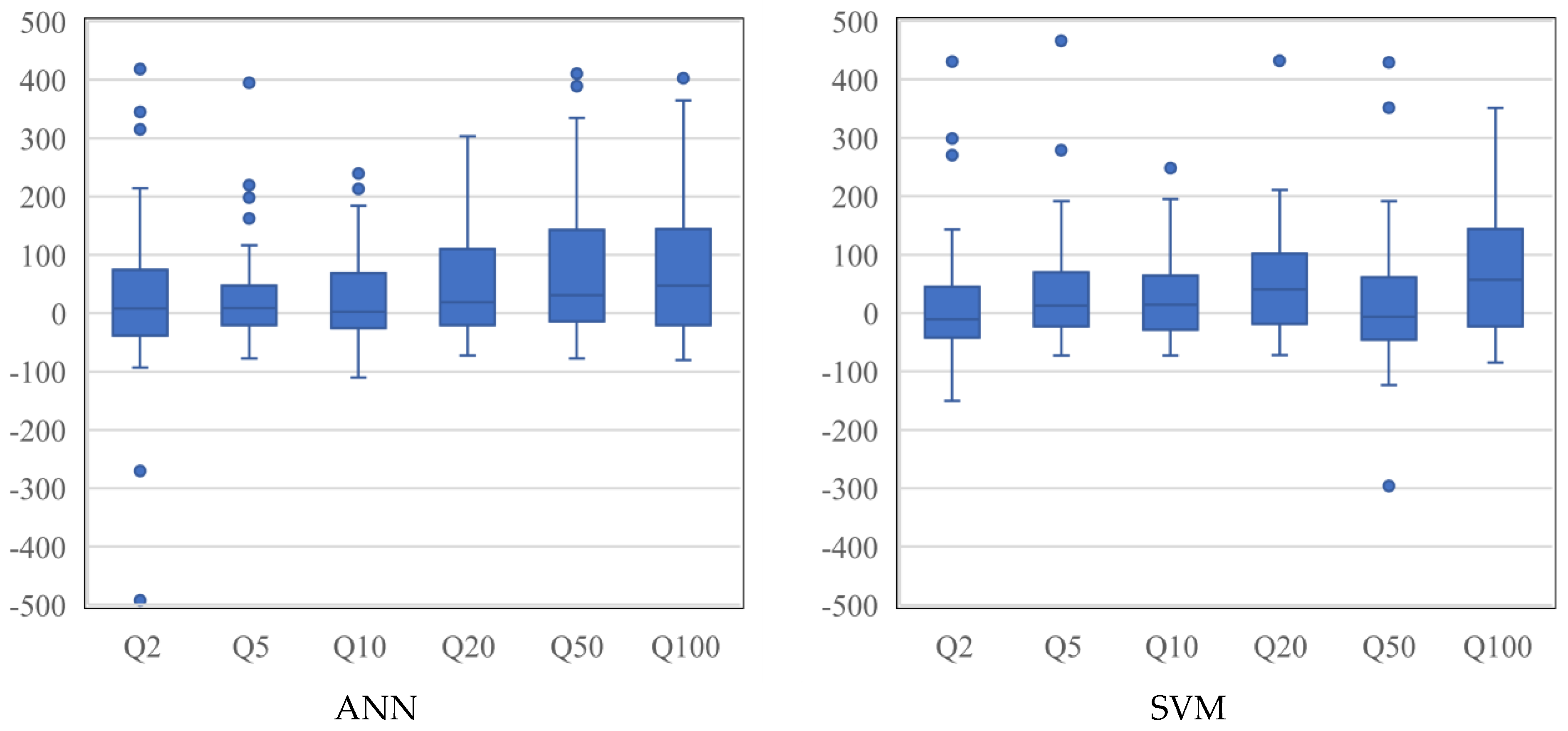
Figure 7 shows the boxplots of RE values for the ANN and SVM models. For
Q2, SVM has a better performance, since it produces a smaller box width with a median value closer to the 0:0 line. The ANN produces better results for
Q5 with a smaller box width. In terms of
Q10,
Q20 and
Q100, both the models perform similarly; however, SVM produces better results for
Q50. Overall, SVM shows better performance with smaller box widths. In terms of bias,
Q5 (ANN),
Q10 (ANN) and
Q50 (SVM) present the best performances, as the median values are located closer to the 0:0 line. The
Q100 model for both the ANN and SVM and
Q50 (ANN) and
Q20 (SVM) models produce notable overestimations. The best model is found for
Q5 (ANN), followed by
Q5 (SVM).
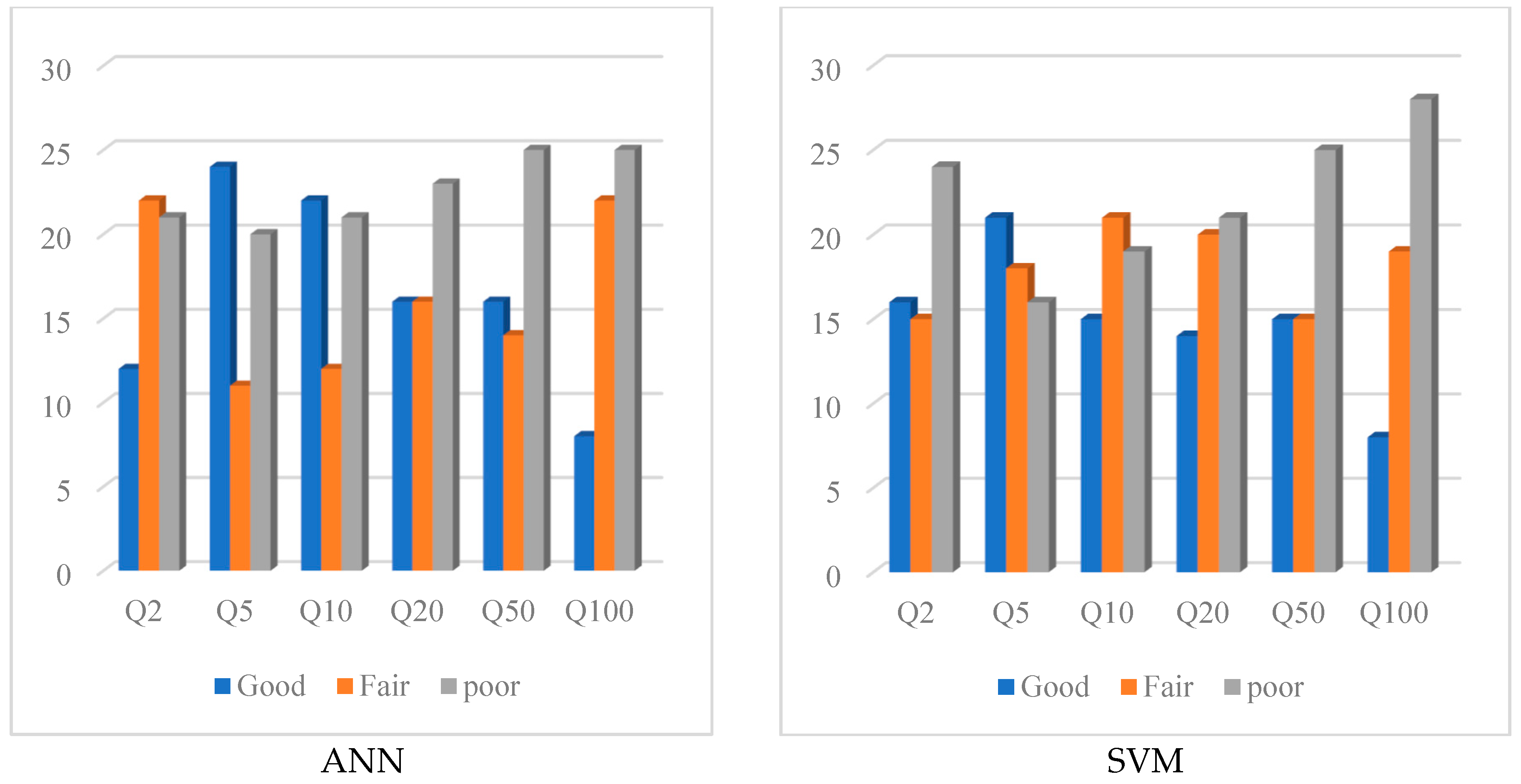
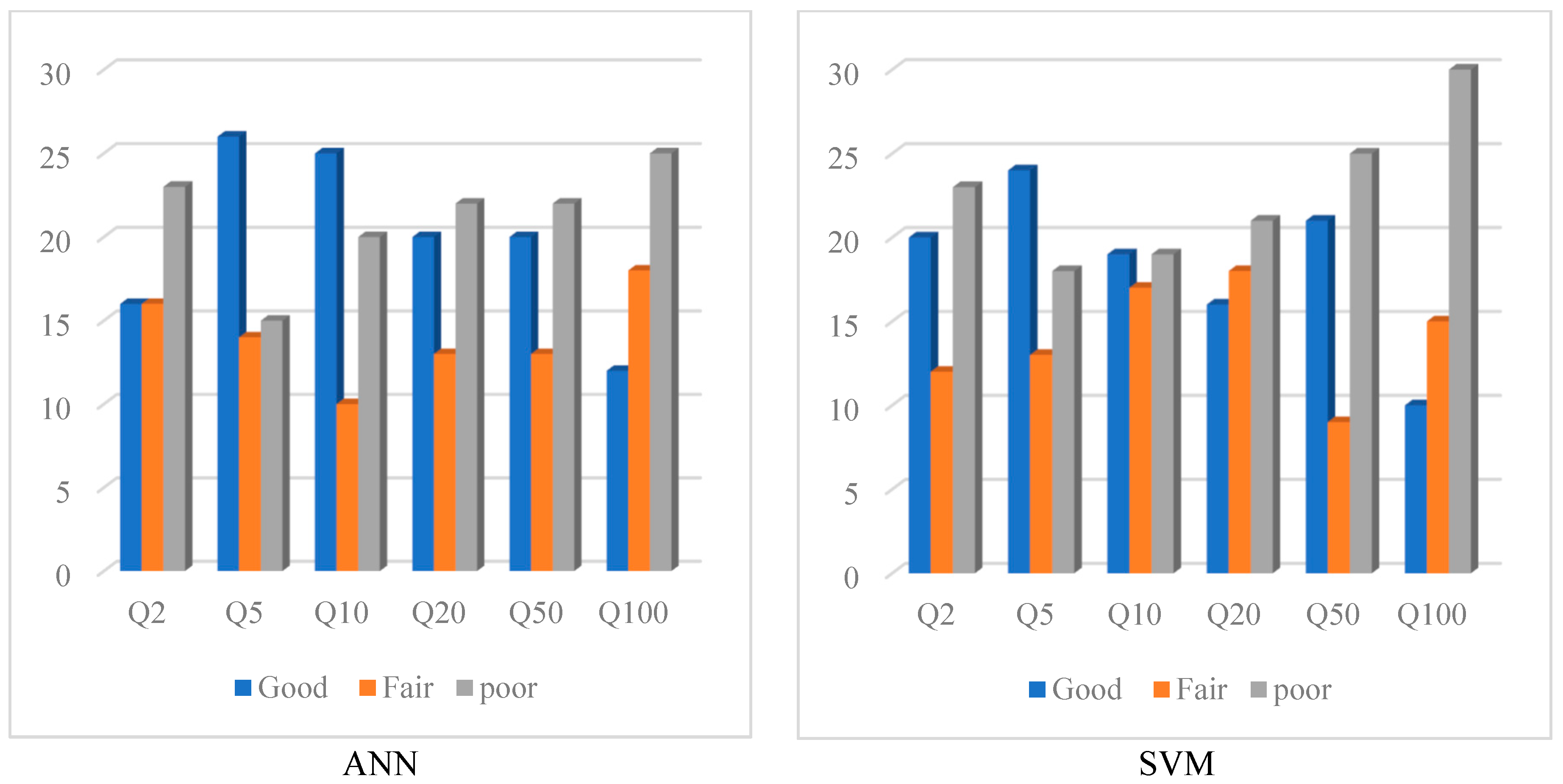
Figure 8 and
Figure 9 show the qualitative comparison of the performance of the ANN and SVM methods based on the classification of the result in three groups (Good, Fair and Poor). These identifiers are used for different ranges of REr and
Qratio values [
63]. As seen in
Figure 8, catchments with REr values falling in the range of 0–30% are rated as “Good”, catchments with REr values in the range of 31–60% are rated as “Fair” and “Poor” is assigned to the remaining catchments with REr values beyond 61%.
Figure 7 shows the qualitative comparison of the performance of the ANN and SVM models for different test catchments based on
Qratio. In this figure “Good” is assigned to the test catchments with the
Qratio values falling between 0.8 and 1.3, “Fair” is assigned to the test catchments with
Qratio values falling in the range of 0.6–0.79 and 1.31–2 and “Poor” is assigned to the remaining test catchments. The ANN method outperforms the SVM method in terms of REr values, because it has a Good-rated performance for more test catchments than SVM—in particular, for smaller return periods. Overall, both the SVM and ANN show a poor performance for
Q100.
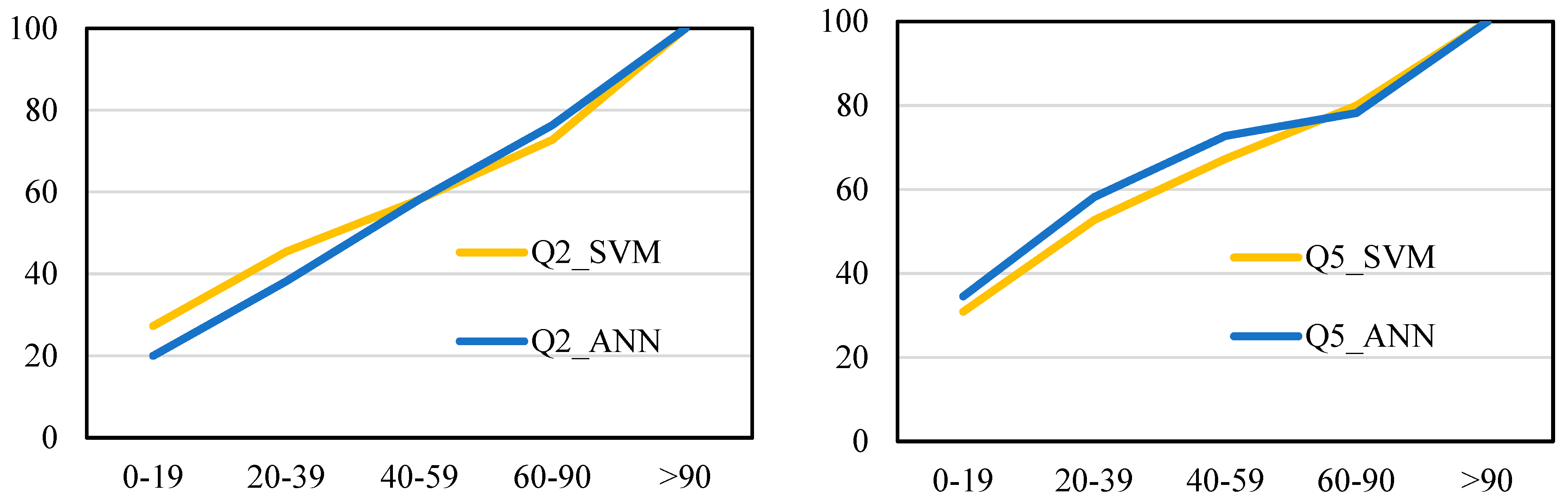
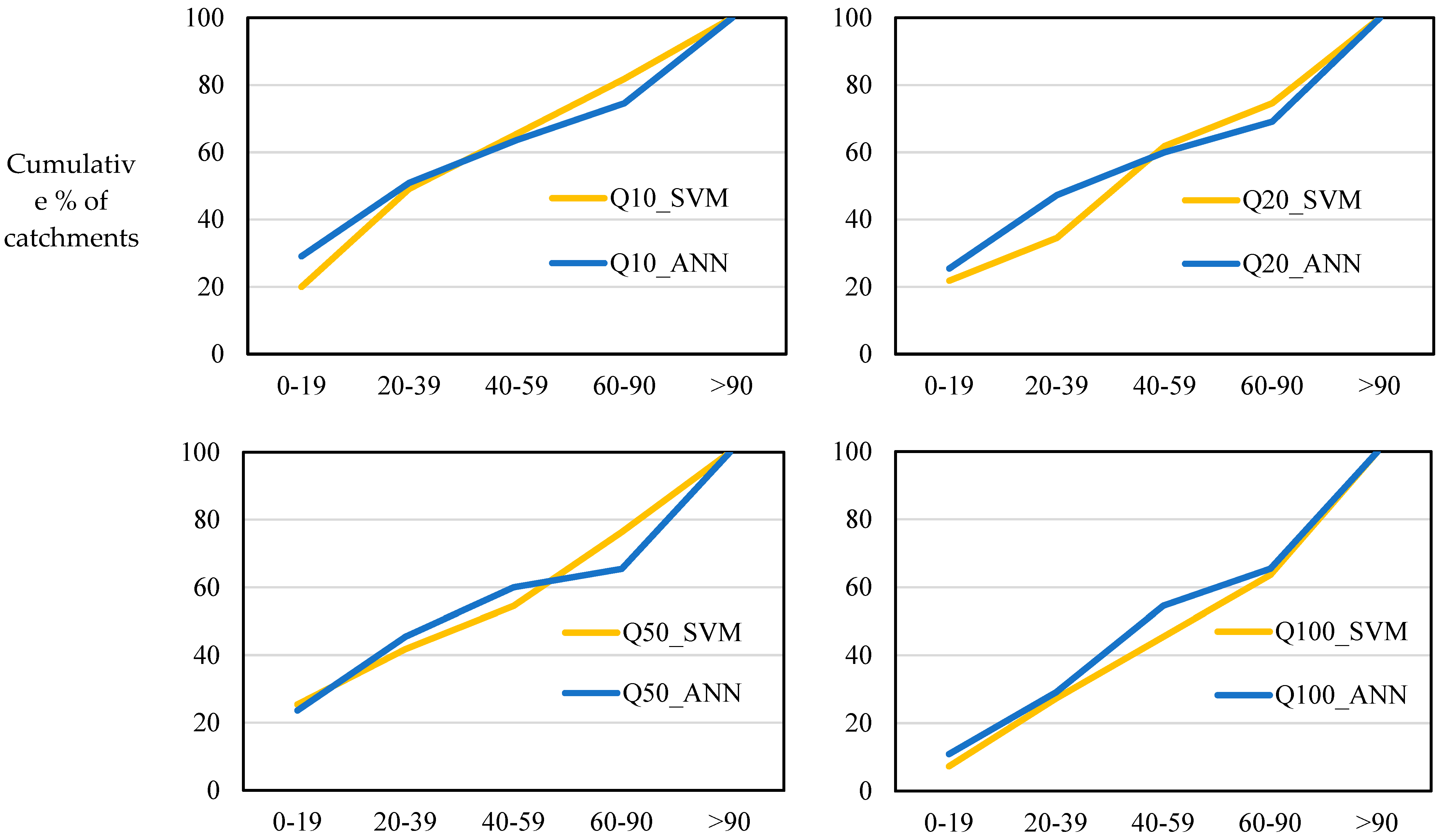
In terms of the cumulative percentage of stations based on Abs RE values, shown in
Figure 10, both models perform very similarly, with the ANN method performing slightly better than the SVM for all the return periods, where the curve for ANN is above the SVM, except for
Q2, showing that the ANN method performs better for a greater number of test catchments with lower ranges of Abs RE values.
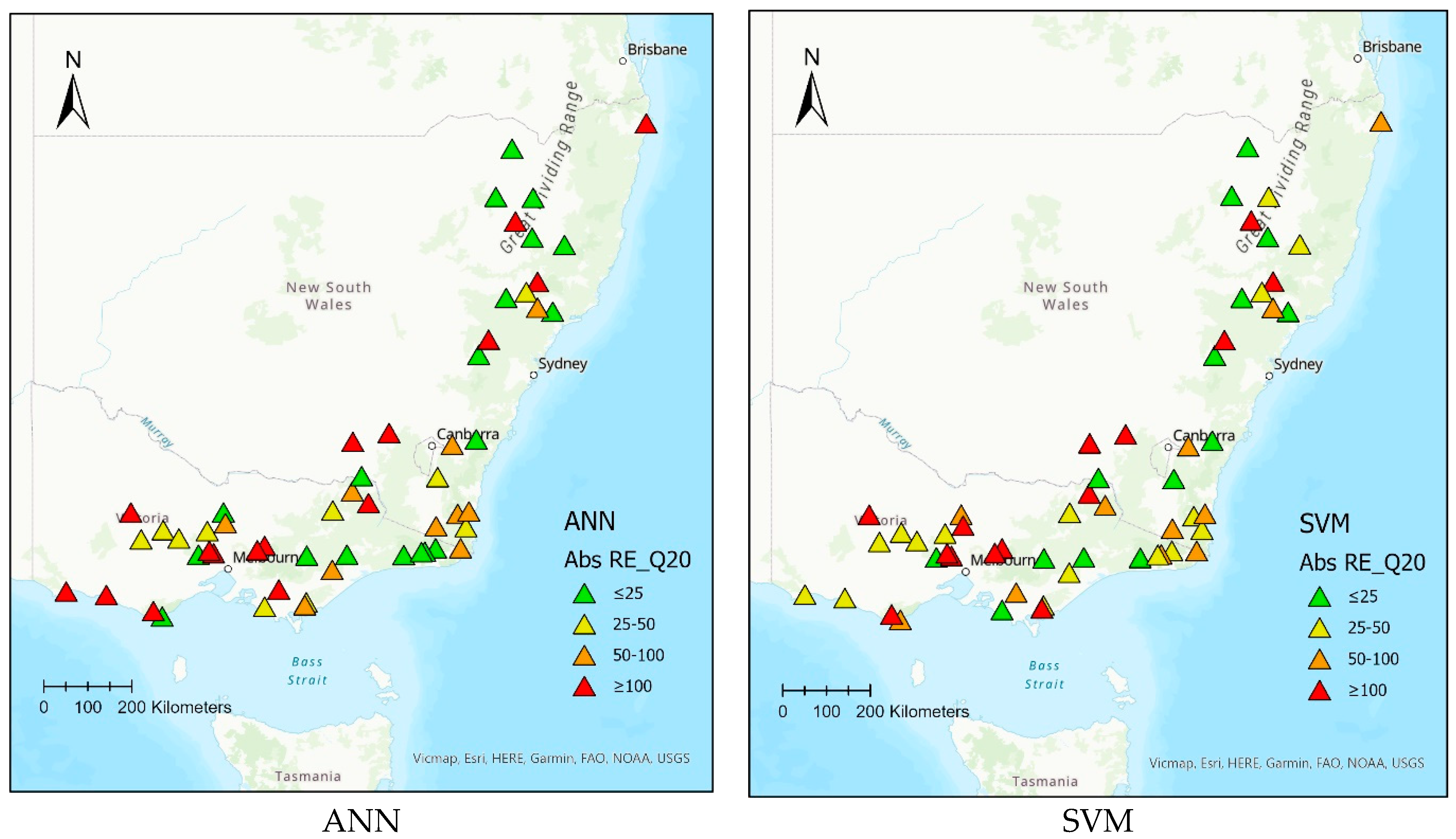
Figure 11 shows the performance of the ANN and SVM models based on Abs RE values for 55 test catchments over the geographical space for
Q20 as an example. The ANN model performs better than the SVM, having 19 catchments with Abs RE values less than 25%, while there are only 14 catchments for the SVM method. There is no spatial pattern of the Abs RE values of the 55 test catchments.
Table 4 shows a comparison between the REr values for the ANN, SVM and the Australian Rainfall and Runoff (ARR) recommended RFFA model. REr values for the ANN method range 33.27–54.38%, which are smaller than those for the SVM (37.13–64.29%) and the ARR RFFA model (57.25–64.06%). It should be noted that the RFFA model was based on 558 stations from eastern Australia. Additionally, the ARR RFFA model used leave-one-out validation (as opposed to the split-sample validation adopted in this study), which generally generates a higher model error, because it is a more rigorous validation method. It should also be noted that the streamflow data lengths of the selected stations are much higher in the present study than the ARR RFFE model. This has given more advantage to the present study as compared to ARR RFFE model.
It should be noted that ARR RFFE model used only four predictor variables, whereas the ANN and SVM-based RFFA models in the present study used eight predictor variables. The use of higher number of predictor variables played a role in reducing the REr values associated with the ANN and SVM-based RFFA models; however, these models have higher bias than the ARR RFFE model [
55]. Further investigation is needed to reduce the bias of these AI-based RFFA models.
The results of the present study are compared with similar ones. For example, Allahbakhshian-Farsani et al. [
26] compared the results of the SVM, MARS, BRT, PPR and NLR methods and reported a RMSE value of 50.70 for their best-performing method (SVM); this value is 50.15 for the ANN-
Q2 and 50.17 for the SVM-
Q2 models in the present study. Similarly, Ghaderi et al. [
44] reported a RMSE value of 239.94 for their best-performing method (SVM) when comparing it with the ANFIS and GEP methods. Vafakhah and Bozchaloei [
28] compared the results of the ANN, SVM and NLR methods and reported a RRMSE of 1.45 for their best-performing method (SVM); these values were 0.79 and 0.80 for our ANN-
Q5 and SVM-
Q5 models, respectively. Ouarda and Shu [
32] compared the results of the ANN method with MLR model and reported a RRMSE value of 36.17 and RMSE value of 27.33 for the ANN method as the best-performing method. Shu and Ouarda [
31] used the ANFIS, ANN, NLR and NLR methods and reported RMSE and RRMSE values of 316 and 57, respectively, for their best-performing method. Jingyi and Hall [
23] used cluster analysis and ANN methods and reported the best RMSE value of 47 for their best-performing method. The above discussion shows that the ANN and SVM models developed in the present study provided results similar to the relevant international studies.
5. Conclusions
In this study, the ANN-based RFFA models are compared with the SVM-based models. The performance of these two models varies with the return periods. Overall, based on the median relative error, the ANN outperforms the SVM. The best model is found to be for Q5 and Q10 with the ANN, giving the smallest median relative error (33–36%). This is notably smaller than the ARR-RFFE model (57%). It should be noted that the ARR-RFFE model adopted only four predictors, whereas the ANN and SVM-based models presented here adopted eight predictor variables, which played a role in reducing the prediction error.
For Q100, both the SVM and ARR-RFFE models provide similar relative errors (64%). In terms of bias, both the ANN and SVM models provide significant overestimations for Q100. This highlights that the estimation of floods with higher return periods is challenging. even with the artificial intelligence-based models.
A split-sample validation is adopted for comparing different models in the present study; in future studies, a Monte Carlo cross-validation should be adopted where the dataset can be randomly divided into numerous training and testing datasets. Furthermore, hybrid methods could be applied by combining different AI-based methods to reduce the prediction error and bias.
It should be noted that the relative accuracy of any RFFA technique depends on the quality and quantity of the streamflow and predictor variable data, which are used to develop and test the technique. For example, a short streamflow record length can introduce significant a sampling error in flood quantile estimates, which are used as a dependent variable in RFFA. Hence, the RFFA techniques examined in the present study should be repeated when a greater streamflow record length is available in the study area in the future. Furthermore, the impacts of climate change on RFFA need to be evaluated. The observed bias for the AI-based based RFFA models should be subjected to bias correction similar to the ARR RFFA technique, which, however, was not implemented here, as it needs further research.