Temporal Scour Variations at Permeable and Angled Spur Dikes under Steady and Unsteady Flows
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiments
2.2. Dimensional Analysis
3. Results
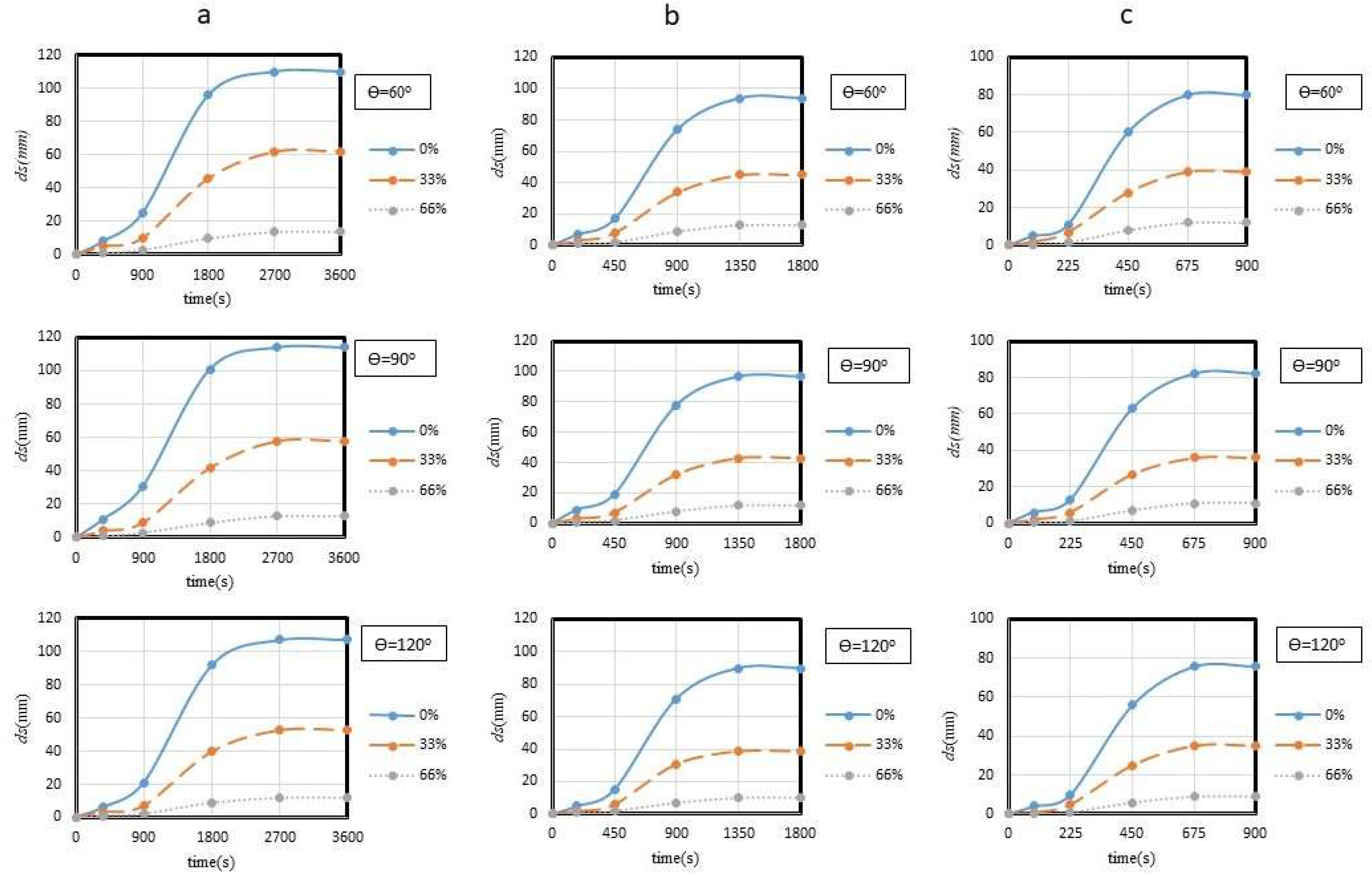
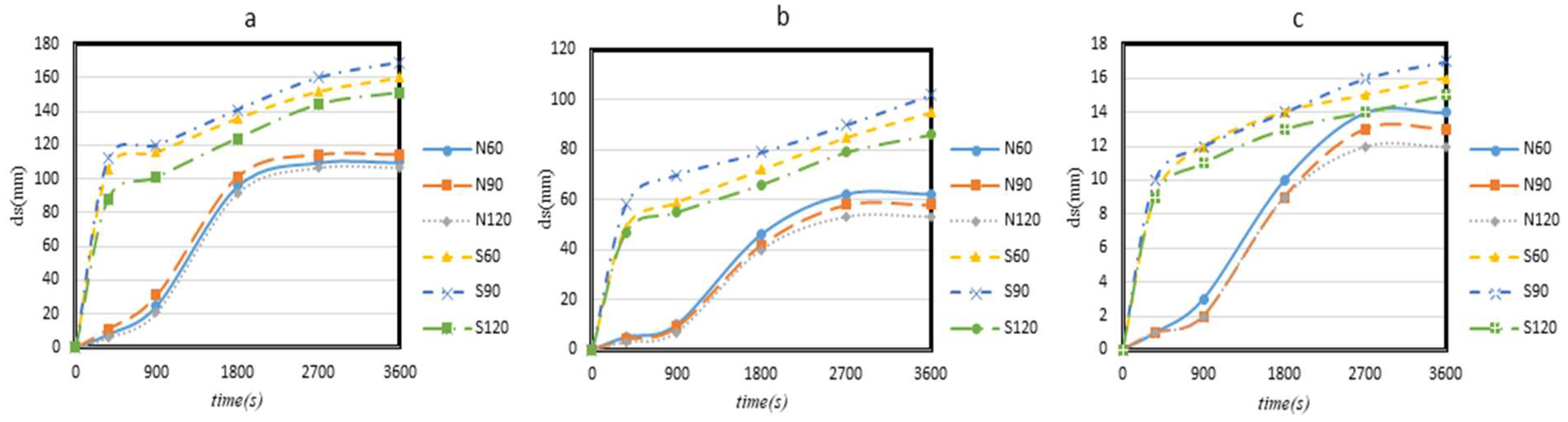
3.1. Impact of the Spur Dike Orientation Angle on the Temporal Scour Development
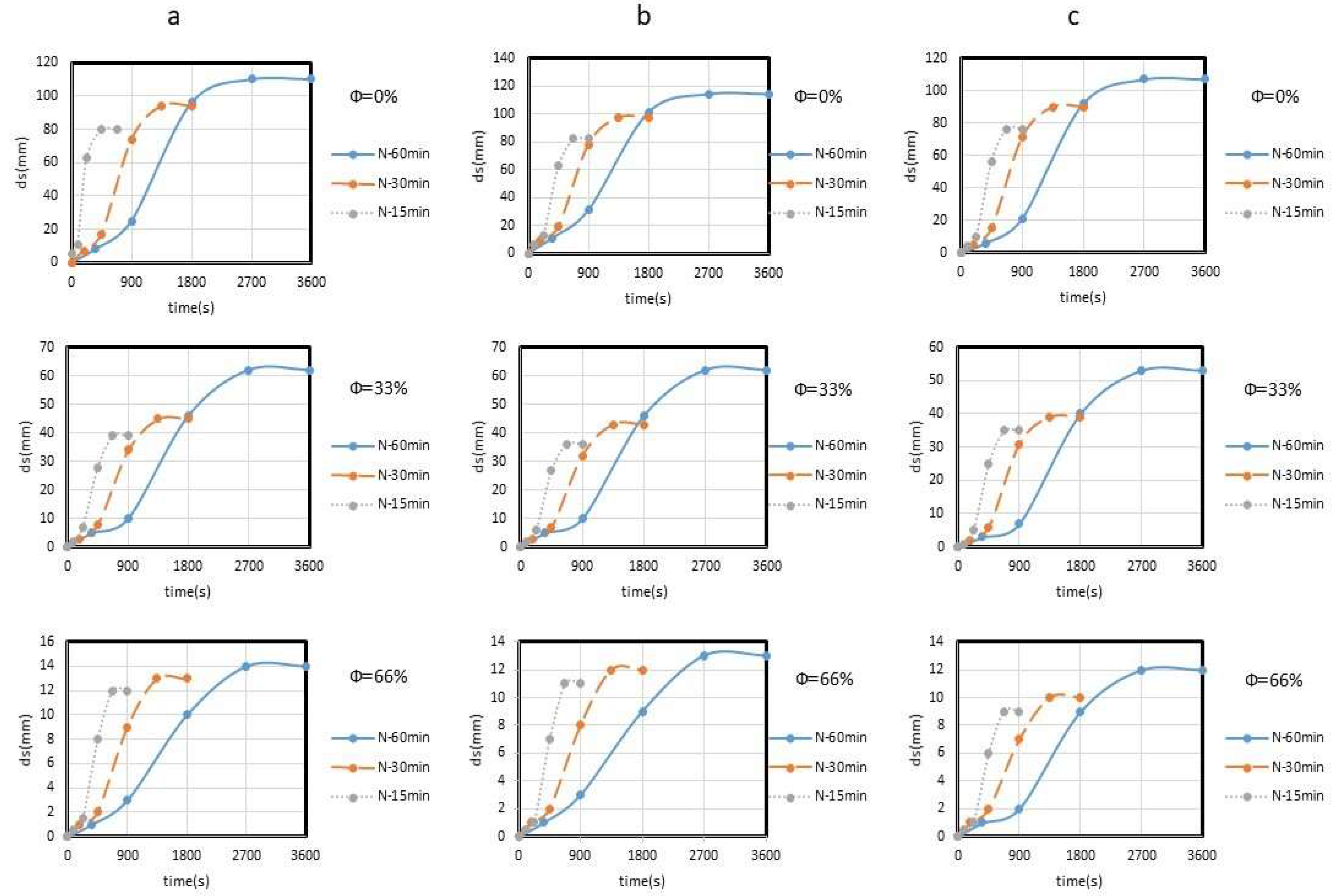
3.2. Impact of the Spur Dike Permeability on the Temporal Scour Development
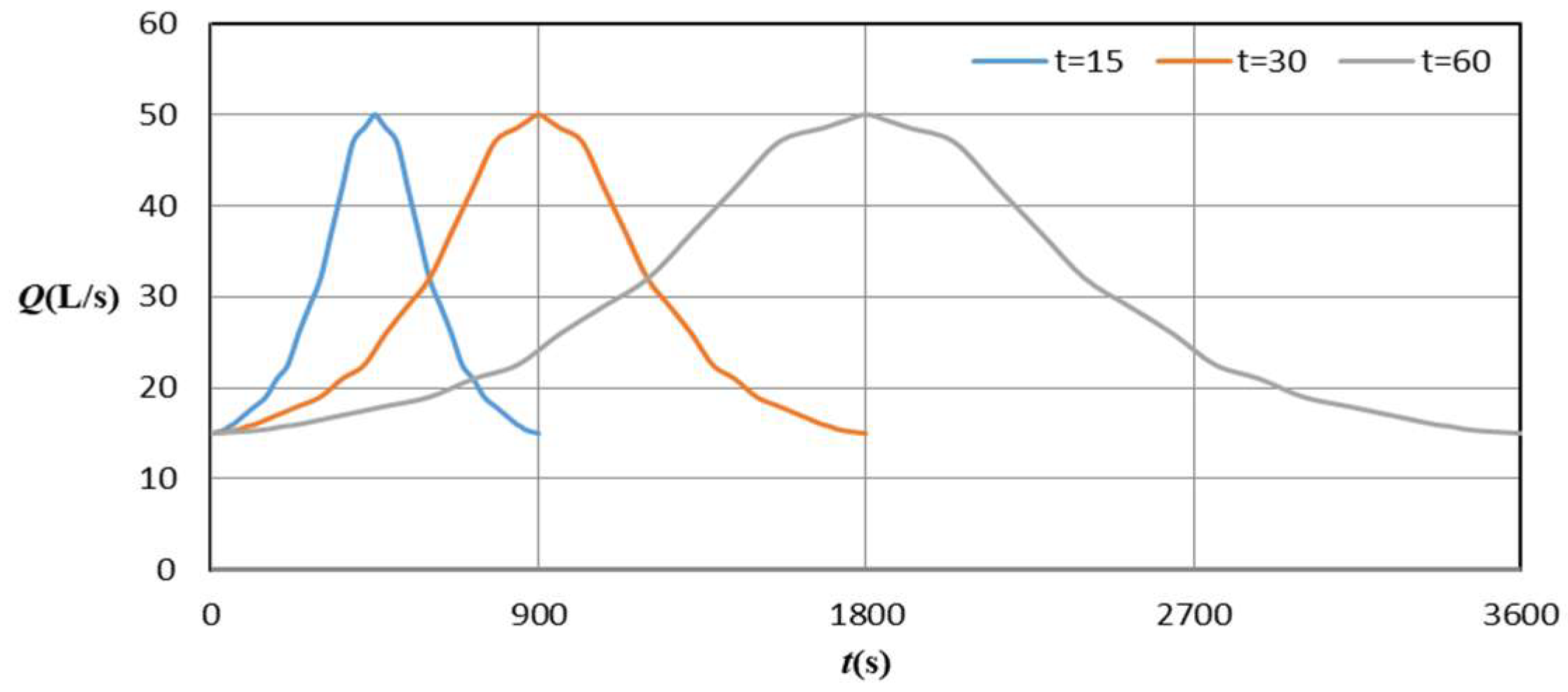
3.3. Impact of the Duration of the Hydrograph on the Temporal Scour Development
3.4. Comparison of the Scouring Conditions under Steady and Unsteady Flows
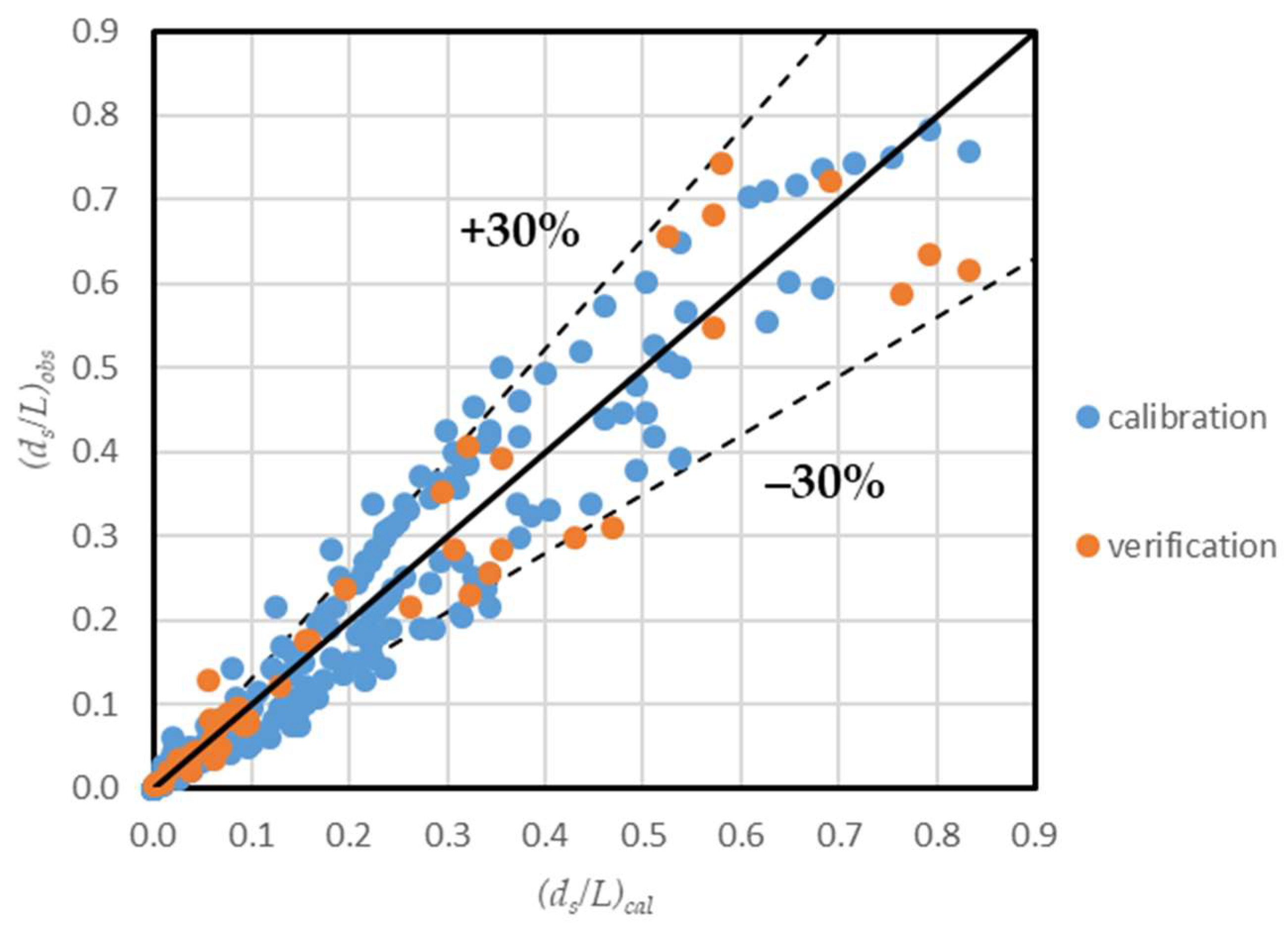
3.5. A New Empirical Model for Temporal Scour Development under Unsteady Flows
4. Discussion
5. Conclusions
- The orientation angle θ of the spur dike had not relevant effect on the scour depth especially in case of impermeable spur dikes. The impact of θ was increasingly evident although always restricted with increasing the degree of permeability;
- The spur dike permeability had a consistent effect on the scour depth around the spur dike with the scouring process reducing significantly as the degree of permeability increases. The differences in percentage between the maximum scour depth for impermeable spur dikes and the maximum scour depths for various degrees of spur dike permeability were found ranging from 44% (at φ = 33% and θ = 60°) up to 88% (at φ = 66% and θ = 120°);
- By quadrupling the hydrograph base-times, keeping constant the peak and base flood discharges, the maximum scour depths increased by about 29%, 42%, and 25% in case of impermeable spur dike, spur dike with 33% degree of permeability, and spur dike with 66% degree of permeability, respectively;
- The results from steady flow experiments were significantly different in comparison to those for unsteady flows, as expected. The maximum percentage differences in terms of maximum scour depths were observed for spur dikes with an orientation angle of 90° and this for various degrees of permeability;
- Finally, a new empirical formula was developed based on the experimental data collected in this study. The ranges of applications are those related to this experimental work.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pinter, N.; Jemberie, A.A.; Remo, J.W.F.; Heine, R.A.; Ickes, B.S. Cumulative impacts of river engineering, Mississippi and Lower Missouri rivers. River Res. Appl. 2010, 26, 546–571. [Google Scholar] [CrossRef]
- Cao, X.-M.; Gu, Z.-H. Three classification criteria and their comparison impact scale between double non-submerged spur dikes. J. Zhejiang Univ. 2015, 49, 200–207. [Google Scholar]
- Pandey, M.; Valyrakis, M.; Qi, M.; Sharma, A.; Lodhi, A.S. Experimental assessment and prediction of temporal scour depth around a spur dike. Int. J. Sediment Res. 2021, 36, 17–28. [Google Scholar] [CrossRef]
- Shampa; Hasegawa, Y.; Nakagawa, H.; Takebayashi, H.; Kawaike, K. Three-dimensional flow characteristics in slit-type permeable spur dike fields: Efficacy in riverbank protection. Water 2020, 12, 964. [Google Scholar] [CrossRef] [Green Version]
- Gu, Z.; Cao, X.; Gu, Q.; Lu, W.-Z. Exploring proper spacing threshold of non-submerged spur dikes with ipsilateral layout. Water 2020, 12, 172. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, M. Experiments on design and behavior of spur dikes. In Proceedings of the International Hydraulics Convention; University of Minnesota: Minneapolis, MN, USA, 1953; pp. 145–159. [Google Scholar]
- Chen, F.-Y.; Ikeda, S. Horizontal separation flows in shallow open channels with spur dikes. J. Hydrosci. Hydraul. Eng. 1997, 15, 15–30. [Google Scholar]
- Diplas, P.; Dancey, C.L.; Celik, A.O.; Valyrakis, M.; Greer, K.; Akar, T. The role of impulse on the initiation of particle movement under turbulent flow conditions. Science 2008, 322, 717–720. [Google Scholar] [CrossRef] [Green Version]
- Valyrakis, M.; Diplas, P.; Dancey, C.L.; Greer, K.; Celik, A.O. Role of instantaneous force magnitude and duration on particle entrainment. J. Geophys. Res. Earth 2010, 115, F02006. [Google Scholar] [CrossRef]
- Valyrakis, M.; Diplas, P.; Dancey, C.L. Entrainment of coarse particles in turbulent flows: An energy approach. J. Geophys. Res. Earth 2013, 118, 42–53. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Wang, H.; Zhang, X.; Wang, B.; Chen, J. The 3-D morphology evolution of spur dike scour under clear-water scour conditions. Water 2018, 10, 1583. [Google Scholar] [CrossRef] [Green Version]
- Valyrakis, M.; Michalis, P.; Zhang, H. A new system for bridge scour monitoring and prediction. In Proceedings of the 36th IAHR World Congress, The Hague, The Netherlands, 28 June–3 July 2015. [Google Scholar]
- Liu, D.; Valyrakis, M.; Williams, R. Flow hydrodynamics across open channel flows with riparian zones: Implications for riverbank stability. Water 2017, 9, 720. [Google Scholar] [CrossRef] [Green Version]
- Kothyari, U.C.; Ranga Raju, K.G. Scour around spur dikes and bridge abutments. J. Hydraul. Res. 2001, 39, 367–374. [Google Scholar] [CrossRef]
- Ezzeldin, M.M.; Saafan, T.A.; Rageh, O.S.; Nejm, L.M. Local scour around spur dikes. In Proceedings of the Eleventh International Water Technology Conference, IWTC11, Sharm El-Sheikh, Egypt, 15–18 March 2007; pp. 779–795. [Google Scholar]
- Cao, Y.; Liu, P.; Enhui, J. The design and application of permeable groynes. Appl. Mech. Mat. 2013, 353–356, 2502–2505. [Google Scholar] [CrossRef]
- Li, Z.; Michioku, K.; Maeno, S.; Ushita, T.; Fujii, A. Hydraulic characteristics of a group of permeable groins constructed in an open channel flow. J. Appl. Mech. 2005, 8, 773–782. [Google Scholar] [CrossRef]
- Fukuoka, S.; Watanabe, A.; Kawaguchi, H.; Yasutake, Y. A study of permeable groins in series installed in a straight channel. Proc. Hydraul. Eng. 2000, 44, 1047–1052. [Google Scholar] [CrossRef]
- Kang, J.; Yeo, H.; Kim, S.; Ji, U. Permeability effects of single groin on flow characteristics. J. Hydraul. Res. 2011, 49, 728–735. [Google Scholar] [CrossRef]
- Zhang, H.; Nakagawa, H. Scour Around Spur Dyke: Recent Advances and Future Researches; Annuals of Disaster Prevention Research Institute, No. 51B; Kyoto University: Kyoto, Japan, 2008; pp. 633–652. [Google Scholar]
- Pandey, M.; Ahmad, Z.; Sharma, P.K. Estimation of maximum scour depth near a spur dike. Can. J. Civil. Eng. 2016, 43, 270–278. [Google Scholar] [CrossRef] [Green Version]
- Teraguchi, H.; Nakagawa, H.; Kawaike, K.; Baba, Y.; Zhang, H. Morphological Change Induced by River Training Structures: Bandal-like and Groins; Annuals of Disaster Prevention Research Institute, No. 51B; Kyoto University: Kyoto, Japan, 2010. [Google Scholar]
- Link, O.; Castillo, C.; Pizarro, A.; Rojas, A.; Ettmer, B.; Escauriaza, C.; Manfreda, S. A model of bridge pier scour during flood waves. J. Hydraul. Res. 2017, 55, 310–323. [Google Scholar] [CrossRef]
- Raikar, R.V.; Hong, J.-H.; Deshmukh, A.R.; Guo, W.-D. Parametric study on abutment scour under unsteady flow. Water 2022, 14, 1820. [Google Scholar] [CrossRef]
- Melville, B.W.; Chiew, Y.-M. Time scale for local scour at bridge piers. J. Hydraul. Eng. ASCE 1999, 125, 59–65. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Temporal evolution of clear-water pier and abutment scour. J. Hydraul. Eng. ASCE 2002, 128, 811–820. [Google Scholar] [CrossRef]
- Graf, W.H.; Altinakar, M.S. Fluvial Hydraulics-Flow and Transport Processes in Channels of Simple Geometry; John Wiley & Sons Inc.: Chichester, UK, 1998; pp. 10–12. [Google Scholar]
- Özyaman, C.; Yerdelen, C.; Eris, E.; Daneshfaraz, R. Experimental investigation of scouring around a single spur under clear water conditions. Water Supply 2022, 22, 3484. [Google Scholar] [CrossRef]
- Dey, S.; Raikar, R.V. Scour in long contractions. J. Hydraul. Eng. ASCE 2005, 131, 1036–1049. [Google Scholar] [CrossRef]
- Niazkar, M.; Afzali, S.H. Developing a new accuracy-improved model for estimating scour depth around piers using a hybrid method. Iran J. Sci. Technol. Trans. Civ. Eng. 2019, 43, 179–189. [Google Scholar] [CrossRef]
- Lu, J.-Y.; Shi, Z.-Z.; Hong, J.-H.; Lee, J.-J.; Raikar, R.V. Temporal Variation of Scour Depth at Nonuniform Cylindrical Piers. J. Hydraul. Eng. ASCE 2011, 137, 45–56. [Google Scholar] [CrossRef] [Green Version]
- Chang, W.-Y.; Lai, J.-S.; Yen, C.-L. Evolution of scour depth at circular bridge piers. J. Hydraul. Eng. ASCE 2004, 130, 905–913. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Further results to time-dependent local scour at bridge elements. J. Hydraul. Eng. ASCE 2005, 131, 97–105. [Google Scholar] [CrossRef]
- Raikar, R.V.; Dey, S. Clear-water scour at bridge piers in fine and medium gravel beds. Can. J. Civil. Eng. 2005, 32, 775–781. [Google Scholar] [CrossRef]

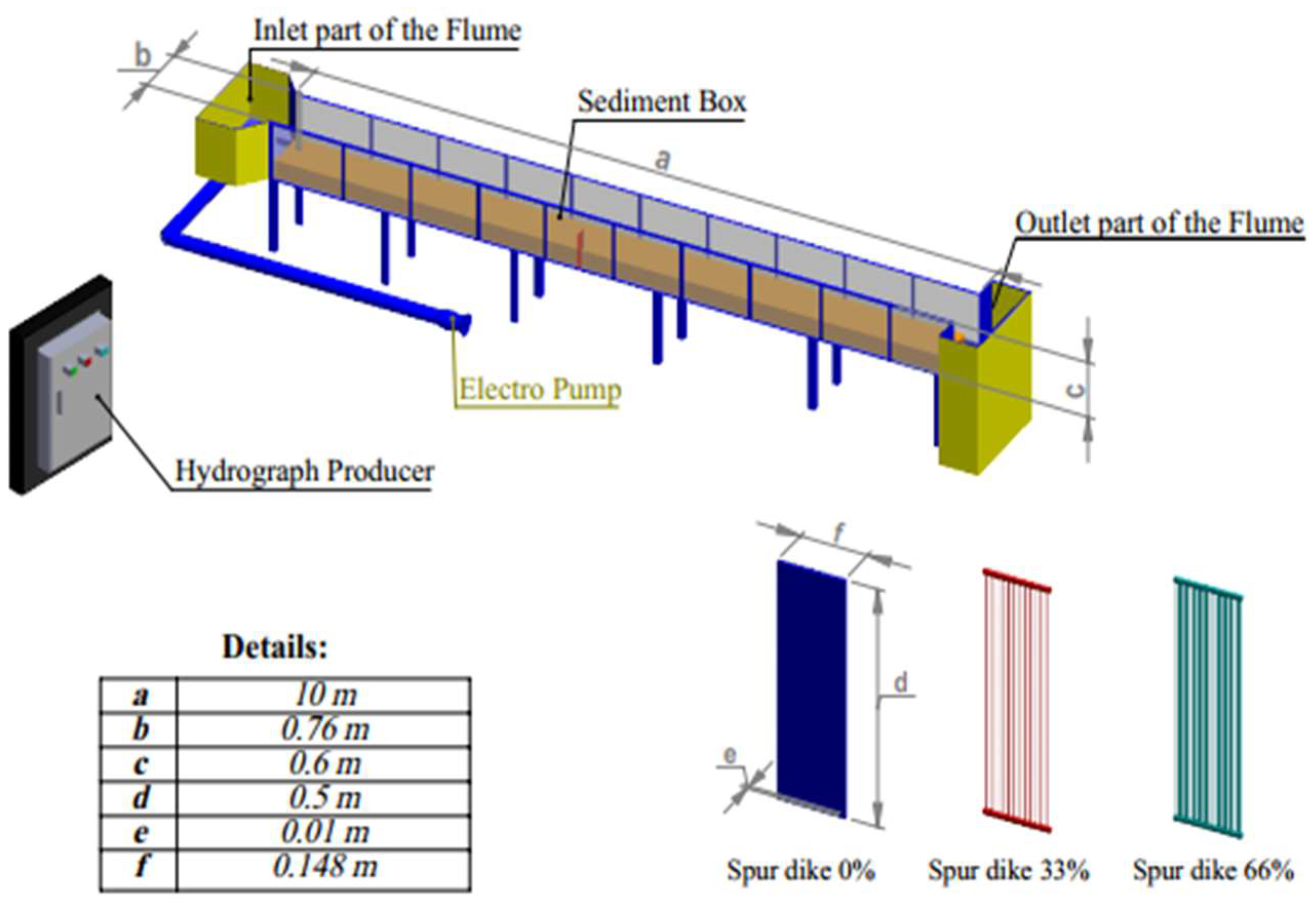

| h | F | Fd | V/VC | tb | θ | φ | |
|---|---|---|---|---|---|---|---|
| (m) | (-) | (-) | (-) | (min) | (°) | (%) | |
| Qb = 15 L/s | 0.137 | 0.12 | 1.30 | 0.48 | 15, 30, 60 | 60, 90, 120 | 0, 33, 66 |
| Qp = 50 L/s | 0.202 | 0.24 | 2.93 | 0.95 | 15, 30, 60 | 60, 90, 120 | 0, 33, 66 |
| φ (%) | tb (min) | θ = 60° | θ = 90° | θ = 120° |
|---|---|---|---|---|
| 0% | 60 | 13% | 11% | 14% |
| 30 | 21% | 20% | 21% | |
| 15 | 25% | 23% | 26% | |
| 33% | 60 | 26% | 28% | 25% |
| 30 | 24% | 26% | 21% | |
| 15 | 28% | 25% | 29% | |
| 66% | 60 | 29% | 31% | 25% |
| 30 | 33% | 30% | 31% | |
| 15 | 33% | 36% | 33% |
| tb [min] | φ [%] | θ = 60° | θ = 90° | θ = 120° |
|---|---|---|---|---|
| 60 | 33% | 44% | 49% | 51% |
| 66% | 87% | 89% | 89% | |
| 30 | 33% | 52% | 56% | 57% |
| 66% | 86% | 88% | 89% | |
| 15 | 33% | 51% | 56% | 54% |
| 66% | 85% | 87% | 88% |
| φ [%]-θ [°] | tb = 15 min | tb = 30 min |
|---|---|---|
| 0%-60° | 27% | 15% |
| 0%-90° | 23% | 7% |
| 0%-120° | 29% | 15% |
| 33%-60° | 37% | 32% |
| 33%-90° | 42% | 34% |
| 33%-120° | 34% | 28% |
| 66%-60° | 14% | 7% |
| 66%-90° | 15% | 8% |
| 66%-120° | 25% | 17% |
| φ (%) | θ = 60° | θ = 90° | θ = 120° |
|---|---|---|---|
| 0% | 31% | 33% | 29% |
| 33% | 35% | 43% | 38% |
| 66% | 13% | 24% | 20% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farshad, R.; Kashefipour, S.M.; Ghomeshi, M.; Oliveto, G. Temporal Scour Variations at Permeable and Angled Spur Dikes under Steady and Unsteady Flows. Water 2022, 14, 3310. https://doi.org/10.3390/w14203310
Farshad R, Kashefipour SM, Ghomeshi M, Oliveto G. Temporal Scour Variations at Permeable and Angled Spur Dikes under Steady and Unsteady Flows. Water. 2022; 14(20):3310. https://doi.org/10.3390/w14203310
Chicago/Turabian StyleFarshad, Reza, Seyed Mahmood Kashefipour, Mehdi Ghomeshi, and Giuseppe Oliveto. 2022. "Temporal Scour Variations at Permeable and Angled Spur Dikes under Steady and Unsteady Flows" Water 14, no. 20: 3310. https://doi.org/10.3390/w14203310
APA StyleFarshad, R., Kashefipour, S. M., Ghomeshi, M., & Oliveto, G. (2022). Temporal Scour Variations at Permeable and Angled Spur Dikes under Steady and Unsteady Flows. Water, 14(20), 3310. https://doi.org/10.3390/w14203310







