Simpler Is Better—Calibration of Pipe Roughness in Water Distribution Systems
Abstract
:1. Introduction
2. Methods
2.1. Calibration Process
2.2. Model Simplification
2.3. Optimization Problem Formulation
2.4. Decision Variable Formulations
2.5. Optimization Methods
2.6. Common Engineering Practice and Model Validation
3. Case Study System
3.1. System Overview
3.2. Existing Hydraulic Model
3.3. Data Collection and Processing
3.3.1. Data Monitoring
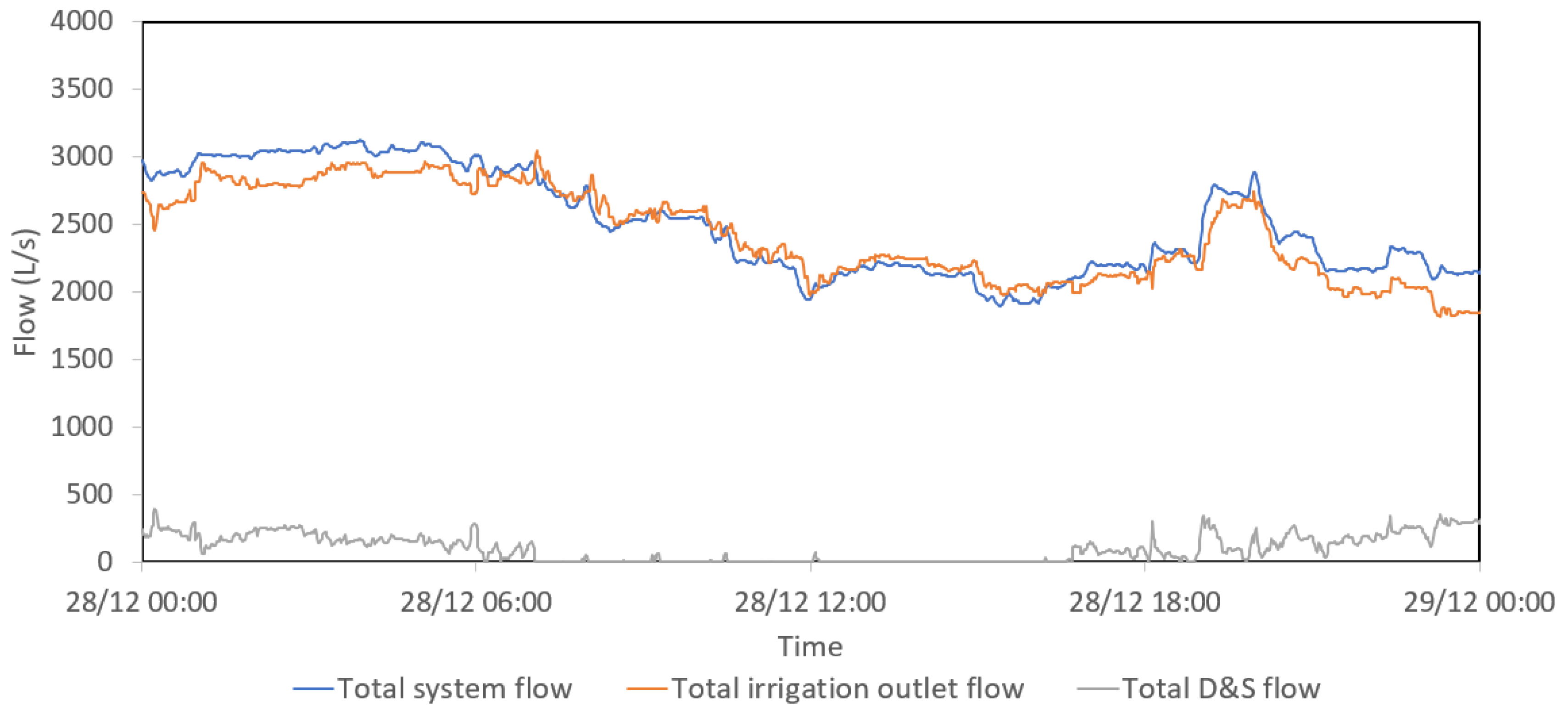
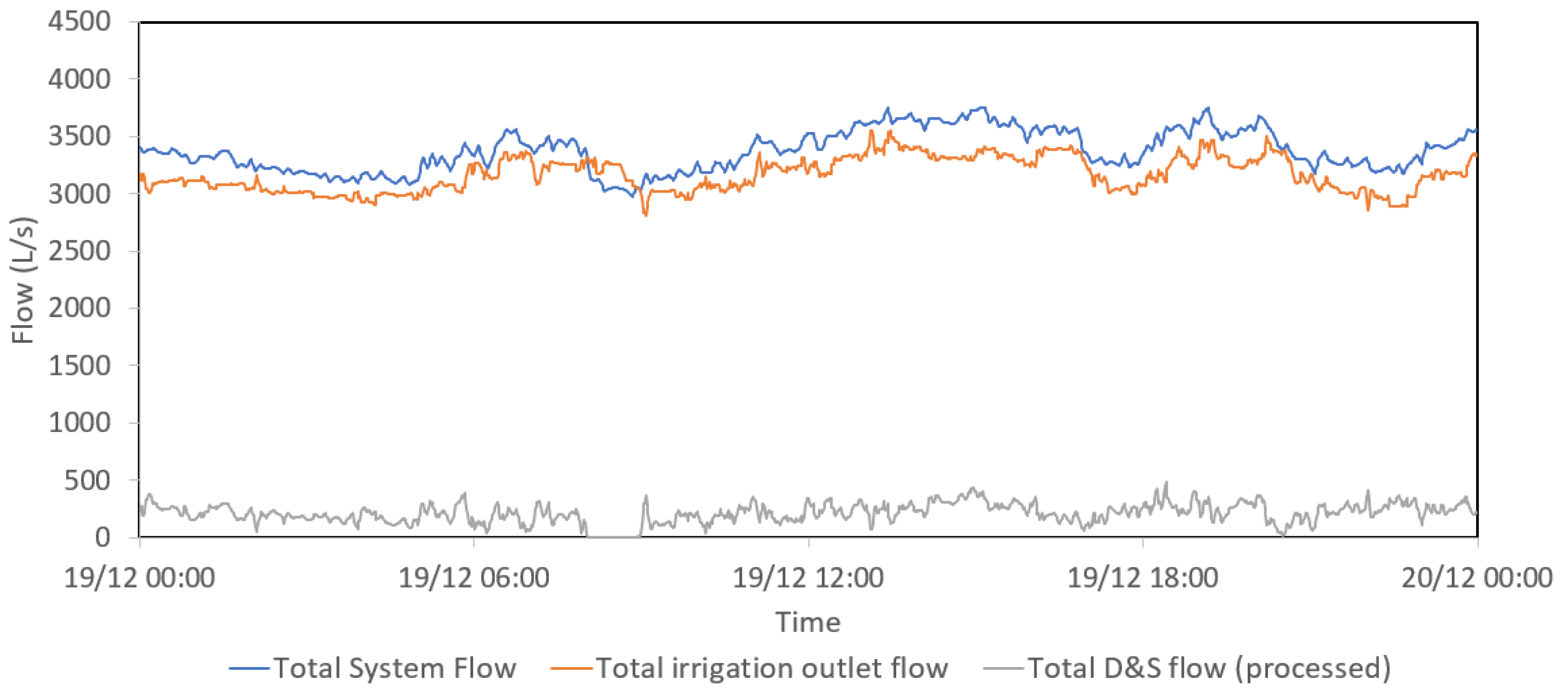
3.3.2. Selection of Calibration and Validation Period
3.3.3. Data Pre-Processing
3.4. Model Calibration
3.4.1. Calibration Process
3.4.2. Decision Variable Set Formulations
4. Results and Discussion
4.1. Model Calibration Results
4.1.1. Optimization Settings for Model Calibration
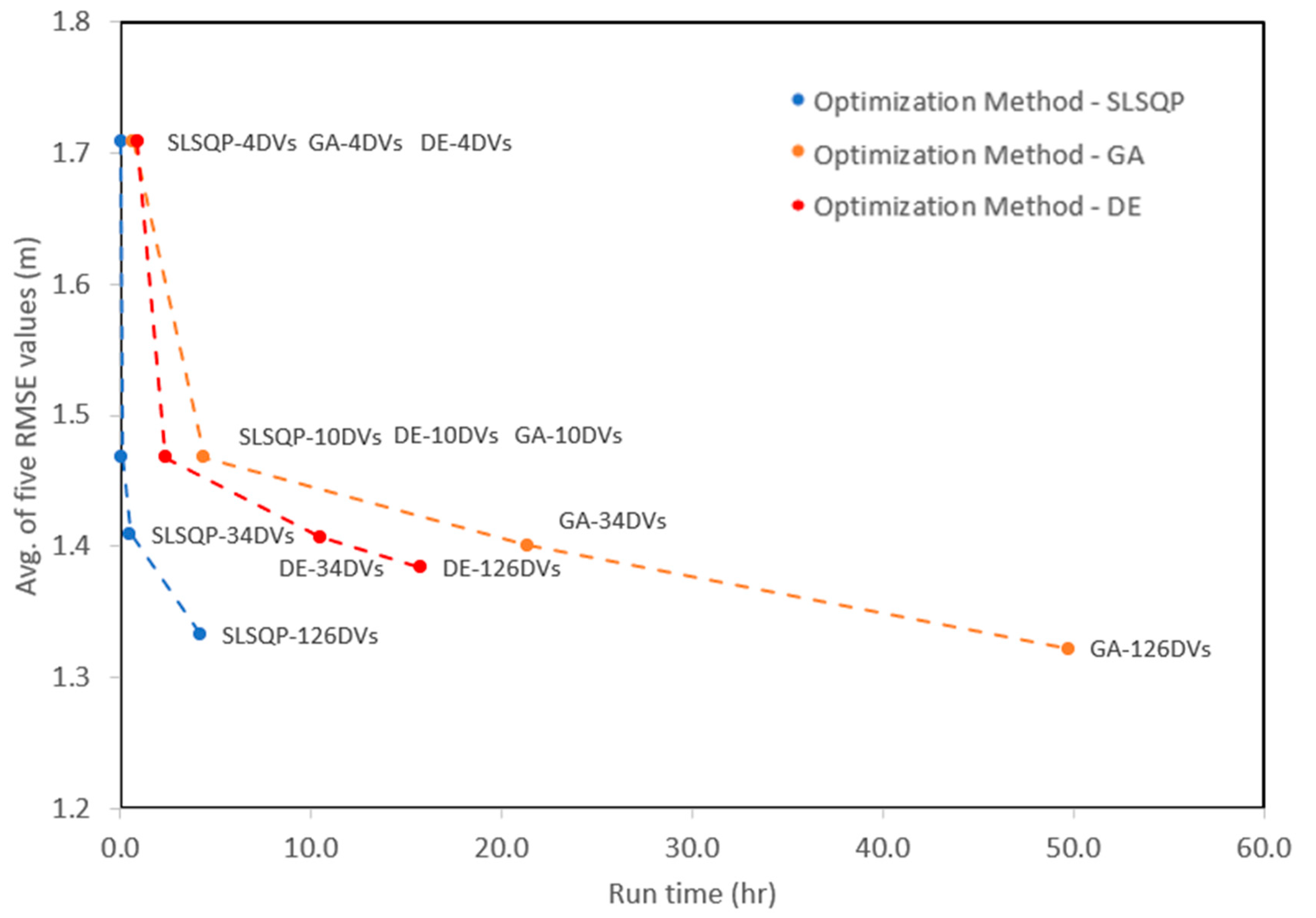
4.1.2. Model Calibration Results
4.2. Discussion of Model Calibration Results
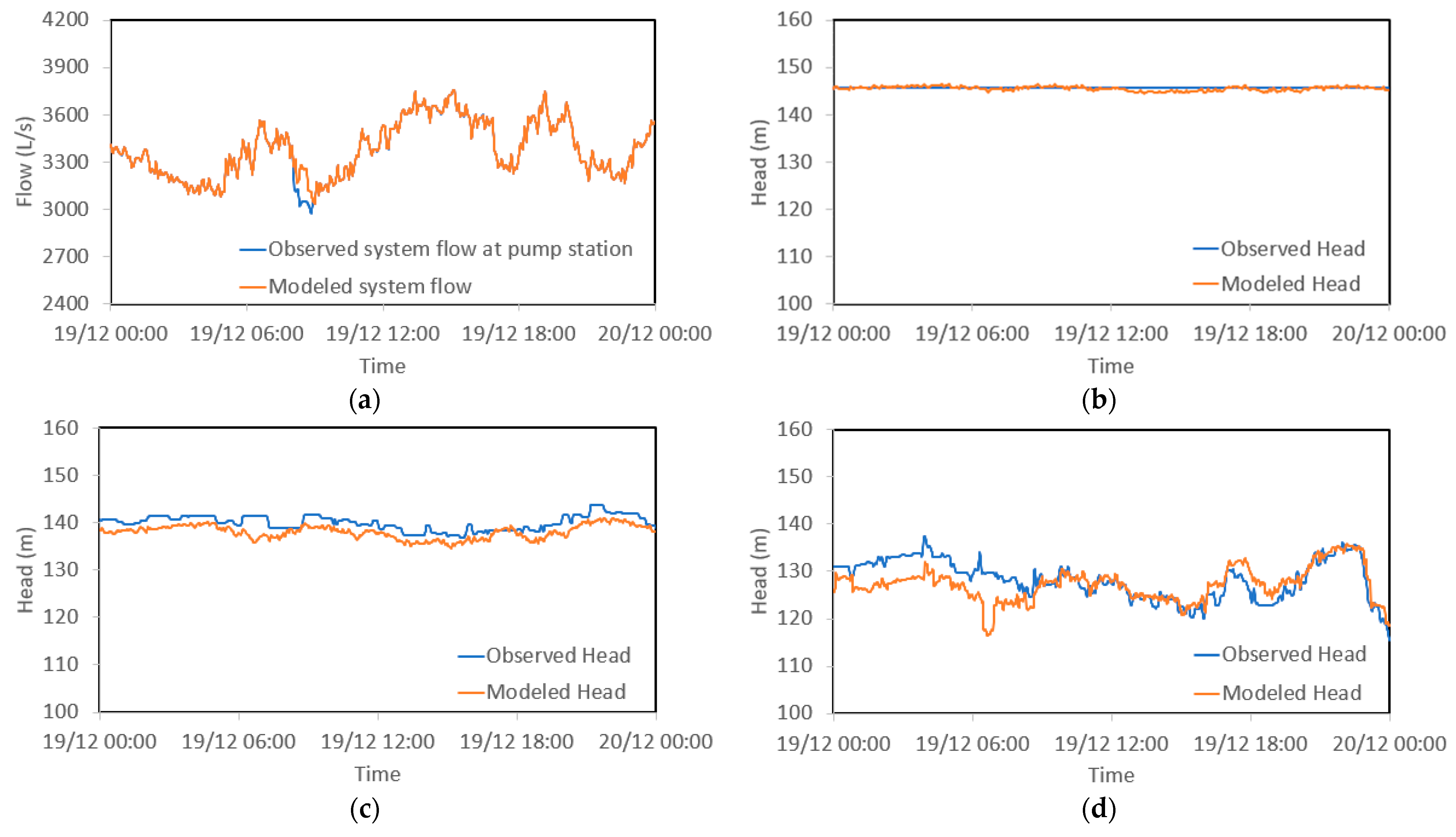
4.3. Evaluation of Formulation 2 (4 DVs) Using Validation Data
5. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mendez, M.; Araya, J.A.; Sanchez, L.D. Automated parameter optimization of a water distribution system. J. Hydroinform. 2013, 15, 71–85. [Google Scholar] [CrossRef]
- Zhang, Q.; Zheng, F.; Duan, H.-F.; Jia, Y.; Zhang, T.; Guo, X. Efficient numerical approach for simultaneous calibration of pipe roughness coefficients and nodal demands for water distribution systems. J. Water Resour. Plan. Manag. 2018, 144, 04018063. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Walski, T.M.; Mankowski, R.; Herrin, G.; Gurierri, R.; Tryby, M. Calibrating water distribution model via genetic algorithms. In Proceedings of the AWWA Information Management and Technology Conference, Kansas City, MO, USA, 14–17 April 2002. [Google Scholar]
- Savic, D.A.; Kapelan, Z.S.; Jonkergouw, P.M.R. Quo vadis water distribution model calibration? Urban Water J. 2009, 6, 3–22. [Google Scholar] [CrossRef]
- Walski, T.M.; DeFrank, N.; Voglino, T.; Wood, R.; Whitman, B.E. Determining the accuracy of automated calibration of pipe network models. In Proceedings of the Eighth Annual Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar]
- Ormsbee, L.E.; Wood, D.J. Explicit pipe network calibration. J. Water Resour. Plan. Manag. 1986, 112, 166–182. [Google Scholar] [CrossRef]
- Shamir, U.Y.; Howard, C.D.D. Water distribution systems analysis. J. Hydraul. Div. 1968, 94, 219–234. [Google Scholar] [CrossRef]
- Gao, T. Pipe roughness estimation in water distribution networks using head loss adjustment. J. Water Resour. Plan. Manag. 2017, 143, 04017007. [Google Scholar] [CrossRef]
- Walski, T.M. Technique for calibrating network models. J. Water Resour. Plan. Manag. 1983, 109, 360–372. [Google Scholar] [CrossRef]
- Walski, T.M. Case-study—Pipe network model calibration issues. J. Water Resour. Plan. Manag. 1986, 112, 238–249. [Google Scholar] [CrossRef]
- Hutton, C.J.; Kapelan, Z.; Vamvakeridou-Lyroudia, L.; Savic, D.A. Dealing with uncertainty in water distribution system models: A framework for real-time modeling and data assimilation. J. Water Resour. Plan. Manag. 2014, 140, 169–183. [Google Scholar] [CrossRef]
- Maier, H.R.; Ascough Ii, J.C.; Wattenbach, M.; Renschler, C.S.; Labiosa, W.B.; Ravalico, J.K. Chapter five uncertainty in environmental decision making: Issues, challenges and future directions. In Developments in Integrated Environmental Assessment; Jakeman, A.J., Voinov, A.A., Rizzoli, A.E., Chen, S.H., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; Volume 3, pp. 69–85. [Google Scholar]
- Walski, T.M.; Chase, D.V.; Savic, D.A. Water Distribution Modeling; Haestad Press: Waterbury, CT, USA, 2001. [Google Scholar]
- Walski, T.M.; Chase, D.V.; Savic, D.A.; Grayman, W.; Beckwith, S.; Koelle, E. Advanced Water Distribution Modeling and Management; Haestad Press: Waterbury, CT, USA, 2003. [Google Scholar]
- Ostfeld, A.; Salomons, E.; Ormsbee, L.; Uber, J.G.; Bros, C.M.; Kalungi, P.; Burd, R.; Zazula-Coetzee, B.; Belrain, T.; Kang, D. Battle of the water calibration networks. J. Water Resour. Plan. Manag. 2012, 138, 523–532. [Google Scholar] [CrossRef]
- Do, N.C.; Simpson, A.R.; Deuerlein, J.W.; Piller, O. Calibration of water demand multipliers in water distribution systems using genetic algorithms. J. Water Resour. Plan. Manag. 2016, 142, 04016044. [Google Scholar] [CrossRef]
- Kang, D.; Lansey, K. Demand and roughness estimation in water distribution systems. J. Water Resour. Plan. Manag. 2011, 137, 20–30. [Google Scholar] [CrossRef]
- Kapelan, Z. Calibration of Water Distribution System Hydraulic Models. Ph.D. Thesis, University of Exeter, Exeter, UK, 2002. [Google Scholar]
- Rahal, C.M.; Sterling, M.J.H.; Coulbeck, B. Parameter tuning for simulation-models of water distribution networks. Proc. Inst. Civ. Eng. 1980, 69 Pt 2, 751–762. [Google Scholar] [CrossRef]
- Bhave, P.R. Calibrating water distribution network models. J. Environ. Eng. 1988, 114, 120–136. [Google Scholar] [CrossRef]
- Lansey, K.E.; Basnet, C. Parameter-estimation for water distribution networks. J. Water Resour. Plan. Manag. 1991, 117, 126–144. [Google Scholar] [CrossRef]
- Boulos, P.F.; Ormsbee, L.E. Explicit network calibration for multiple loading conditions. Civ. Eng. Syst. 1991, 8, 153–160. [Google Scholar] [CrossRef]
- Boulos, P.F.; Wood, D.J. Explicit calculation of pipe-network parameters. J. Hydraul. Eng. 1990, 116, 1329–1344. [Google Scholar] [CrossRef]
- Ferreri, G.B.; Napoli, E.; Tumbiolo, A. Calibration of roughness in water distribution networks. In Proceedings of the 2nd International Conference on Water Pipeline System, Edinburgh, UK, 24–26 May 1994. [Google Scholar]
- Andersen, J.H.; Powell, R.S. Implicit state-estimation technique for water network monitoring. Urban Water 2000, 2, 123–130. [Google Scholar] [CrossRef]
- Hutton, C.J.; Kapelan, Z.; Vamvakeridou-Lyroudia, L.; Savic, D.A. Real-time demand estimation in water distrubtion systems under uncertainty. In Proceedings of the WDSA 2012: 14th Water Distribution Systems Analysis Conference, Adelaide, SA, Australia, 24–27 September 2012. [Google Scholar]
- Kang, D.; Lansey, K. Real-time demand estimation and confidence limit analysis for water distribution systems. J. Hydraul. Eng. 2009, 135, 825–837. [Google Scholar] [CrossRef]
- Ormsbee, L.E. Implicit network calibration. J. Water Resour. Plan. Manag. 1989, 115, 243–257. [Google Scholar] [CrossRef]
- Ormsbee, L.E.; Lingireddy, S. Calibrating hydraulic network models. J. Am. Water Work. Assoc. 1997, 89, 42–50. [Google Scholar] [CrossRef]
- Savic, D.A.; Walters, G.A. Genetic Algorithm Techniques for Calibrating Network Models; University of Exeter: Exeter, UK, 1995. [Google Scholar]
- Shang, F.; Uber, J.G.; van Bloemen Waanders, B.G.; Boccelli, D.; Janke, R. Real time water demand estimation in water distribution system. In Proceedings of the Water Distribution Systems Analysis Symposium, Kruger National Park, South Africa, 17–20 August 2008. [Google Scholar]
- Walski, T.; Wu, Z.; Hartell, W. Performance of automated calibration for water distribution systems. In Critical Transitions in Water and Environmental Resources Management; Amer Society of Civil Engineers: Reston, VA, USA, 2004; pp. 1–10. [Google Scholar]
- Maier, H.R.; Razavi, S.; Kapelan, Z.; Matott, L.S.; Kasprzyk, J.; Tolson, B.A. Introductory overview: Optimization using evolutionary algorithms and other metaheuristics. Environ. Model. Softw. 2019, 114, 195–213. [Google Scholar] [CrossRef]
- Bagloee, S.A.; Asadi, M.; Patriksson, M. Minimization of water pumps’ electricity usage: A hybrid approach of regression models with optimization. Expert Syst. Appl. 2018, 107, 222–242. [Google Scholar] [CrossRef]
- Coelho, B.; Andrade-Campos, A. Efficiency achievement in water supply systems—A review. Renew. Sustain. Energy Rev. 2014, 30, 59–84. [Google Scholar] [CrossRef]
- Abkenar, S.M.S.; Stanley, S.D.; Miller, C.J.; Chase, D.V.; McElmurry, S.P. Evaluation of genetic algorithms using discrete and continuous methods for pump optimization of water distribution systems. Sustain. Comput. Inform. Syst. 2015, 8, 18–23. [Google Scholar]
- Shamir, U. Optimal design and operation of water distribution systems. Water Resour. Res. 1974, 10, 27–36. [Google Scholar] [CrossRef]
- Datta, R.S.N.; Sridharan, K. Parameter-estimation in water-distribution systems by least-squares. J. Water Resour. Plan. Manag. 1994, 120, 405–422. [Google Scholar] [CrossRef]
- Reddy, P.V.N.; Sridharan, K.; Rao, P.V. Wls method for parameter estimation in water distribution networks. J. Water Resour. Plan. Manag. 1996, 122, 157–164. [Google Scholar] [CrossRef]
- Press, W.H.; William, H.; Teukolsky, S.A.; Vetterling, W.T.; Saul, A.; Flannery, B.P. Numerical Recipes 3rd Edition: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Creaco, E.; Pezzinga, G. Embedding linear programming in multi objective genetic algorithms for reducing the size of the search space with application to leakage minimization in water distribution networks. Environ. Model. Softw. 2015, 69, 308–318. [Google Scholar] [CrossRef]
- Maier, H.R.; Kapelan, Z.; Kasprzyk, J.; Kollat, J.; Matott, L.S.; Cunha, M.C.; Dandy, G.C.; Gibbs, M.S.; Keedwell, E.; Marchi, A.; et al. Evolutionary algorithms and other metaheuristics in water resources: Current status, research challenges and future directions. Environ. Model. Softw. 2014, 62, 271–299. [Google Scholar] [CrossRef] [Green Version]
- Coelho, B.; Andrade-Campos, A. Using different strategies for improving efficiency in water supply systems. In Proceedings of the 1st ECCOMAS Young Investigators Conference, Aveiro, Portugal, 24–27 April 2012. [Google Scholar]
- Zecchin, A.C.; Maier, H.R.; Simpson, A.R.; Leonard, M.; Nixon, J.B. Ant colony optimization applied to water distribution system design: Comparative study of five algorithms. J. Water Resour. Plan. Manag. 2007, 133, 87–92. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Letting, L.K.; Hamam, Y.; Abu-Mahfouz, A.M. Estimation of water demand in water distribution systems using particle swarm optimization. Water 2017, 9, 593. [Google Scholar] [CrossRef] [Green Version]
- Zanfei, A.; Menapace, A.; Santopietro, S.; Righetti, M. Calibration procedure for water distribution systems: Comparison among hydraulic models. Water 2020, 12, 1421. [Google Scholar] [CrossRef]
- Minaee, R.P.; Afsharnia, M.; Moghaddam, A.; Ebrahimi, A.A.; Askarishahi, M.; Mokhtari, M. Calibration of water quality model for distribution networks using genetic algorithm, particle swarm optimization, and hybrid methods. MethodsX 2019, 6, 540–548. [Google Scholar] [CrossRef]
- Roma, J.; Perez, R.; Sanz, G.; Grau, S. Model calibration and leakage assessment applied to a real water distribution network. Procedia Eng. 2015, 119, 603–612. [Google Scholar] [CrossRef] [Green Version]
- Walters, G.; Savic, D.; Morley, M.; De Schaetzen, W.; Atkinson, R. Calibration of water distribution network models using genetic algorithms. WIT Trans. Ecol. Environ. 1998, 26, 131–140. [Google Scholar]
- Gong, J.; Erkelens, M.; Lambert, M.F.; Forward, P. Experimental study of dynamic effects of iron bacteria–formed biofilms on pipeline head loss and roughness. J. Water Resour. Plan. Manag. 2019, 145, 04019038. [Google Scholar] [CrossRef]
- Lambert, M.F.; Brookes, J.; Kildea, M.; Grantham, T.; McFarlane, B. Understanding the impact of biofilm growth on pipe roughness. In Proceedings of the World Environmental and Water Resources Congress 2008, Honolulu, HI, USA, 12–16 May 2008. [Google Scholar]
- Lambert, M.F.; Edwards, R.W.J.; Howie, S.J.; De Gilio, B.B.; Quinn, S.P. The impact of biofilm development on pipe roughness and velocity profile. In Proceedings of the World Environmental and Water Resources Congress 2009, Kansas City, MO, USA, 17–21 May 2009. [Google Scholar]
- Kraft, D. A Software Package for Sequential Quadratic Programming; DFVLR Obersfaffeuhofen: Weßling, Germany, 1988. [Google Scholar]
- Golberg, D.E. Genetic algorithms in search, optimization, and machine learning. Addion Wesley 1989, 1989, 36. [Google Scholar]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Ahmad, M.F.; Isa, N.A.M.; Lim, W.H.; Ang, K.M. Differential evolution: A recent review based on state-of-the-art works. Alex. Eng. J. 2021, 61, 3831–3872. [Google Scholar] [CrossRef]
- Kachitvichyanukul, V. Comparison of three evolutionary algorithms: Ga, pso, and de. Ind. Eng. Manag. Syst. 2012, 11, 215–223. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Lampinen, J. A fuzzy adaptive differential evolution algorithm. Soft Comput. 2005, 9, 448–462. [Google Scholar] [CrossRef]
- Blank, J.; Deb, K. Pymoo: Multi-objective optimization in python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
- Open Water Analytics. Owa-Epanet 2.2.4; Open Water Analytics: Andover, MA, USA, 2020. Available online: https://community.wateranalytics.org/ (accessed on 4 July 2022).
- Rossman, L. The Epanet Programmer’s Toolkit; National Risk Management Research Laboratory, Office of Research and Development, U.S. Environmental Protection Agency: Cincinnati, OH, USA, 1999.
- Walski, T. Procedure for hydraulic model calibration. J. Am. Water Work. Assoc. 2017, 109, 55–61. [Google Scholar] [CrossRef]
- Lower Murray Water. Lower Murray Water Annual Report 2018–2019; Lower Murray Water: Mildura, VIC, Australia, 2019.
- Lower Murray Water. Lower Murray Water Corporate Plan 2019–2020; Lower Murray Water: Mildura, VIC, Australia, 2019.
- Google Maps. Victoria, Australia; Google Maps: Mountain View, CA, USA, 2022; Available online: https://www.google.com/maps/place/%E7%B6%AD%E5%A4%9A%E5%88%A9%E4%BA%9E%E7%9C%81/@-36.5052093,140.9779493,6z/data=!3m1!4b1!4m5!3m4!1s0x6ad4314b7e18954f:0x5a4efce2be829534!8m2!3d-36.9847807!4d143.3906074 (accessed on 4 July 2022).
- Walski, T.M. Model calibration data: The good, the bad, and the useless. J. Am. Water Work. Assoc. 2000, 92, 94–99. [Google Scholar] [CrossRef]
- Pietrucha-Urbanik, K.; Studzinski, A. Selected issues of costs and failure of pipes in an exemplary water supply system. Rocz. Ochr. Srodowiska 2016, 18, 616–627. [Google Scholar]
- Studziński, A.; Pietrucha-Urbanik, K. Failure risk analysis of water distributions systems using hydraulic models on real field data. Ekon. Sr. 2019, 68, 152–165. [Google Scholar]
- Blank, J.; Deb, K. Termination Criterion. Available online: https://pymoo.org/interface/termination.html (accessed on 4 July 2022).
- Picologlou, B.F.; Characklis, W.G.; Zelver, N. Biofilm growth and hydraulic performance. J. Hydraul. Div. 1980, 106, 733–746. [Google Scholar] [CrossRef]
- Centeno-Telleria, M.; Zulueta, E.; Fernandez-Gamiz, U.; Teso-Fz-Betoño, D.; Teso-Fz-Betoño, A. Differential evolution optimal parameters tuning with artificial neural network. Mathematics 2021, 9, 427. [Google Scholar] [CrossRef]
- Ronkkonen, J.; Kukkonen, S.; Price, K.V. Real-parameter optimization with differential evolution. In Proceedings of the IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005. [Google Scholar]
- Storn, R. On the usage of differential evolution for function optimization. In Proceedings of the North American Fuzzy Information Processing, Berkeley, CA, USA, 19 June 1996. [Google Scholar]
- Dawar, D.; Ludwig, S.A. Differential evolution with dither and annealed scale factor. In Proceedings of the 2014 IEEE Symposium on Differential Evolution (SDE), Orlando, FL, USA, 9–12 December 2014. [Google Scholar]
- Blank, J.; Deb, K. De: Differential Evolution. Available online: https://pymoo.org/algorithms/soo/de.html#DE:-Differential-Evolution (accessed on 4 July 2022).
- Standards Australia. AS 2200: 2006; Design Charts for Water Supply and Sewerage. Standards Australia: Sydney, NSW, Australia, 2006.
- Cowle, M.W.; Babatunde, A.O.; Rauen, W.B.; Bockelmann-Evans, B.N.; Barton, A.F. Biofilm development in water distribution and drainage systems: Dynamics and implications for hydraulic efficiency. Environ. Technol. Rev. 2014, 3, 31–47. [Google Scholar] [CrossRef]
- Characklis, W.G. Attached microbial growths-ii. Frictional resistance due to microbial slimes. Water Res. 1973, 7, 1249–1258. [Google Scholar] [CrossRef] [Green Version]
- Beven, K. Prophecy, reality and uncertainty in distributed hydrological modeling. Adv. Water Resour. 1993, 16, 41–51. [Google Scholar] [CrossRef]
- Beven, K. A manifesto for the equifinality thesis. J. Hydrol. 2006, 320, 18–36. [Google Scholar] [CrossRef]




| Decision Variable Set Formulation No. | Basis for Grouping Pipes |
|---|---|
| Formulation 1 | Every pipe in the pruned network as an individual decision variable |
| Formulation 2 | Pipe material |
| Formulation 3 | Pipe material + Pipe diameter |
| Formulation 4 | Pipe material + Pipe velocity under peak flows |
| Parameters | Formulation 1 126 DVs 1 | Formulation 2 4 DVs | Formulation 3 10 DVs | Formulation 4 34 DVs | |
|---|---|---|---|---|---|
| GA | 400 | 50 | 100 | 350 | |
| 0.7 | 0.7 | 0.7 | 0.7 | ||
| 0.01 | 0.01 | 0.01 | 0.03 | ||
| DE | 400 | 100 | 100 | 340 | |
| 0.9 | 0.9 | 0.9 | 0.9 | ||
| Initial | 0.8 | 0.8 | 0.8 | 0.8 |
| SLSQP | GA | DE | ||
|---|---|---|---|---|
| Avg. of 10 Runs | Avg. of 10 Runs | Avg. of 10 Runs | ||
| Formulation 1: 126 DVs | Ave RMSE (m) | 1.333 | 1.322 | 1.384 |
| Run Time (h) | 4.21 | 49.73 | 15.76 | |
| No. of generations | 318 | 1155 | 250 | |
| No. of evaluations | 39,980 | 462,000 | 100,000 | |
| Formulation 2: 4 DVs | Ave RMSE (m) | 1.709 | 1.709 | 1.709 |
| Run Time (h) | 0.02 | 0.68 | 0.88 | |
| No. of generations | 27 | 126 | 85 | |
| No. of evaluations | 147 | 6280 | 8500 | |
| Formulation 3: 10 DVs | Ave RMSE (m) | 1.468 | 1.468 | 1.468 |
| Run Time (h) | 0.08 | 4.38 | 2.38 | |
| No. of generations | 69 | 406 | 224 | |
| No. of evaluations | 770 | 40,550 | 22,400 | |
| Formulation 4: 34 DVs | Ave RMSE (m) | 1.409 | 1.4 | 1.407 |
| Run Time (h) | 0.51 | 21.33 | 10.47 | |
| No. of generations | 138 | 562 | 295 | |
| No. of evaluations | 4825 | 196,840 | 100,300 | |
| Decision Variable No. | DV1 | DV2 | DV3 | DV4 |
|---|---|---|---|---|
| Pipe Material | MSCL | DICL | GRP | mPVC |
| Run No. | Roughness Values | |||
| 1 | 10.62 | 0.44 | 2.91 | 0.01 |
| 2 | 10.65 | 0.44 | 2.91 | 0.01 |
| 3 | 10.59 | 0.44 | 2.91 | 0.01 |
| 4 | 10.60 | 0.44 | 2.91 | 0.01 |
| 5 | 10.63 | 0.44 | 2.91 | 0.01 |
| 6 | 10.63 | 0.44 | 2.91 | 0.01 |
| 7 | 10.62 | 0.44 | 2.91 | 0.01 |
| 8 | 10.63 | 0.44 | 2.91 | 0.01 |
| 9 | 10.60 | 0.44 | 2.91 | 0.01 |
| 10 | 10.60 | 0.44 | 2.90 | 0.01 |
| Avg. | 10.62 | 0.44 | 2.91 | 0.01 |
| Decision Variable No. | DV1 | DV2 | DV3 | DV4 | DV5 | DV6 | DV7 | DV8 | DV9 | DV10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Pipe Material | mPVC | mPVC | DICL | DICL | DICL | DICL | DICL | GRP | MSCL | GRP |
| Nominal Diameter (mm) | 300 | 375 | 375 | 450 | 500 | 600 | 750 | 1000 | 1200 | 1400 |
| Run No. | Roughness Values | |||||||||
| 1 | 0.01 | 20.00 | 0.01 | 0.01 | 12.54 | 4.47 | 0.01 | 1.98 | 11.02 | 1.56 |
| 2 | 0.01 | 20.00 | 0.01 | 0.01 | 17.08 | 4.43 | 0.01 | 1.41 | 11.31 | 1.56 |
| 3 | 0.01 | 20.00 | 0.01 | 0.01 | 18.84 | 4.46 | 0.01 | 1.28 | 10.96 | 1.56 |
| 4 | 0.01 | 20.00 | 0.01 | 0.01 | 13.71 | 4.48 | 0.01 | 1.82 | 10.87 | 1.57 |
| 5 | 0.01 | 20.00 | 0.01 | 0.01 | 17.03 | 4.46 | 0.01 | 1.44 | 10.87 | 1.58 |
| 6 | 0.01 | 20.00 | 0.01 | 0.01 | 14.59 | 4.48 | 0.01 | 1.71 | 10.94 | 1.57 |
| 7 | 0.01 | 20.00 | 0.01 | 0.01 | 12.81 | 4.49 | 0.01 | 1.93 | 11.01 | 1.57 |
| 8 | 0.01 | 20.00 | 0.01 | 0.01 | 15.03 | 4.46 | 0.01 | 1.65 | 11.07 | 1.56 |
| 9 | 0.01 | 20.00 | 0.01 | 0.01 | 14.44 | 4.47 | 0.01 | 1.74 | 10.93 | 1.56 |
| 10 | 0.01 | 20.00 | 0.01 | 0.01 | 13.20 | 4.46 | 0.01 | 1.89 | 11.04 | 1.55 |
| Avg. | 0.01 | 20.00 | 0.01 | 0.01 | 14.93 | 4.47 | 0.01 | 1.68 | 11.00 | 1.56 |
| Pressure Monitoring Sites | |||||||
|---|---|---|---|---|---|---|---|
| Pressure monitoring site | Average observed HGL (m) | Average modeled HGL (m) | Average observed pressure (m) | Average modeled pressure (m) | Average difference (m) | Percentage difference in pressures | RMSE (m) |
| RTU1 | 145.80 | 145.55 | 75.06 | 74.81 | 0.26 | 0.34% | 0.508 |
| RTU2 | 139.98 | 138.01 | 70.95 | 68.98 | 1.47 | 2.77% | 2.196 |
| RTU3 | 128.27 | 127.23 | 66.36 | 65.32 | 1.04 | 1.57% | 3.646 |
| RTU4 | 137.60 | 137.66 | 74.86 | 74.92 | −0.06 | −0.08% | 1.809 |
| RTU5 | 128.77 | 128.03 | 59.15 | 58.41 | 0.74 | 1.24% | 1.585 |
| Avg. | 1.949 | ||||||
| Flow monitoring site | |||||||
| Flow monitoring site | Average observed flow (L/s) | Average modeled flow (L/s) | Average difference (L/s) | Percentage difference | RMSE (L/s) | ||
| Sys_Flow | 3374 | 3379 | −5 | 0.16% | 31 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Q.; Wu, W.; Simpson, A.R.; Willis, A. Simpler Is Better—Calibration of Pipe Roughness in Water Distribution Systems. Water 2022, 14, 3276. https://doi.org/10.3390/w14203276
Zhao Q, Wu W, Simpson AR, Willis A. Simpler Is Better—Calibration of Pipe Roughness in Water Distribution Systems. Water. 2022; 14(20):3276. https://doi.org/10.3390/w14203276
Chicago/Turabian StyleZhao, Qi, Wenyan Wu, Angus R. Simpson, and Ailsa Willis. 2022. "Simpler Is Better—Calibration of Pipe Roughness in Water Distribution Systems" Water 14, no. 20: 3276. https://doi.org/10.3390/w14203276






