Dynamic Compression Characteristics and Failure Mechanism of Water-Saturated Granite
Abstract
:1. Introduction
2. Test Method and Technology
2.1. Dynamic Test Equipment
2.2. Preparation of Water-Saturated Rock Specimens
3. Test Results and Analysis
3.1. Mechanical Properties of Static Water-Saturated Granite
3.2. Impact Test Results and Analysis
4. Dynamic Failure Mechanism of Water-saturated Granite
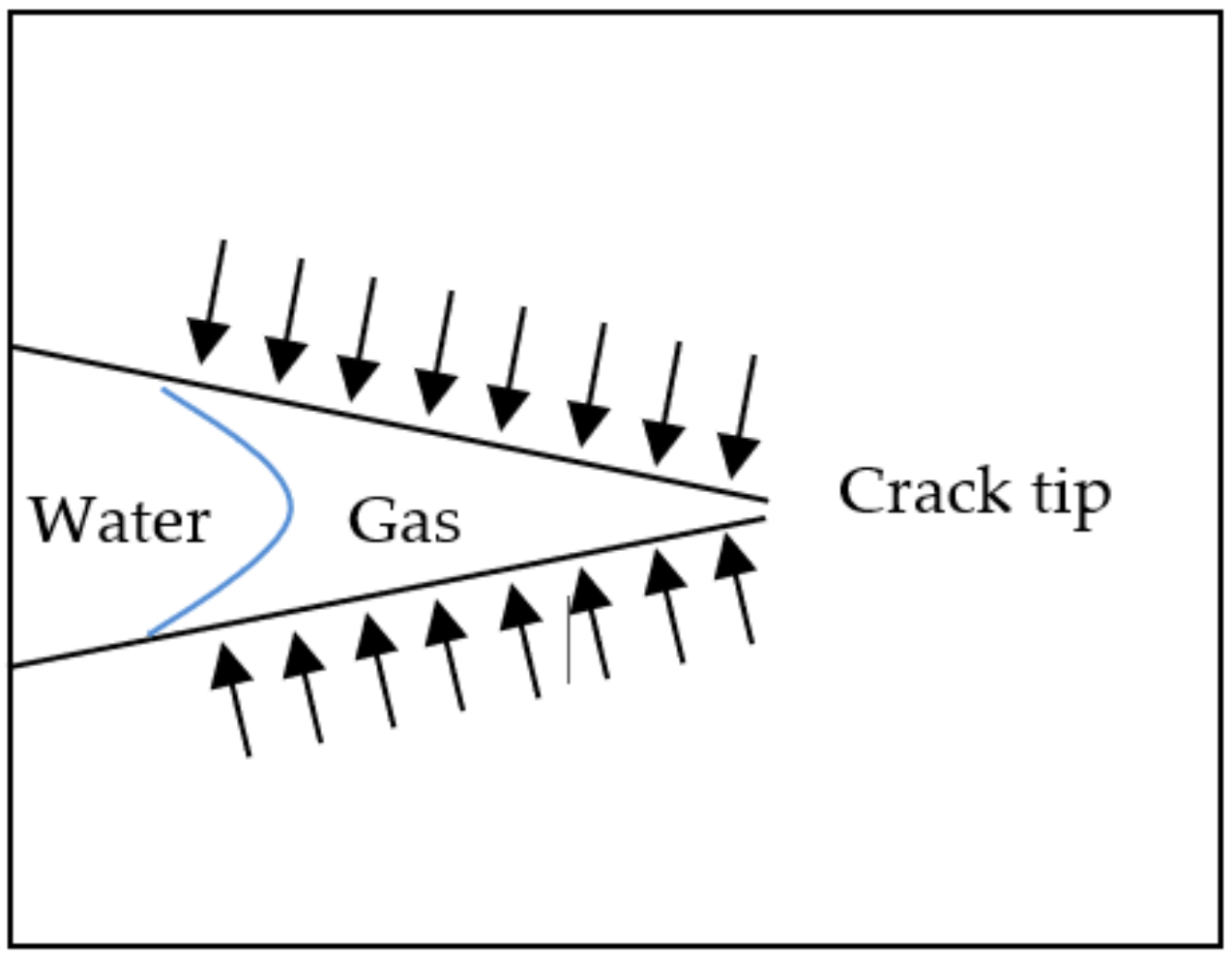
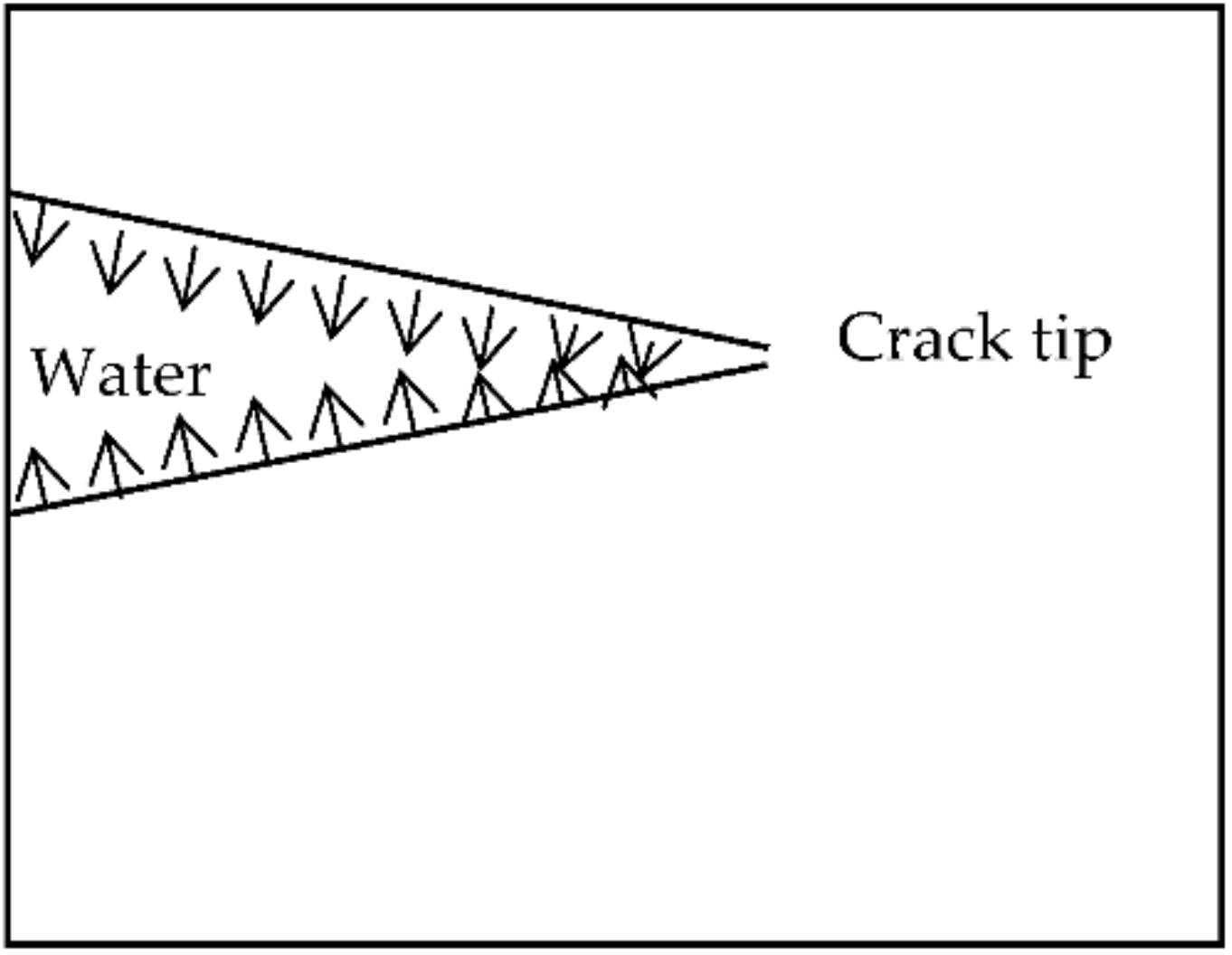
4.1. Meniscus Effect
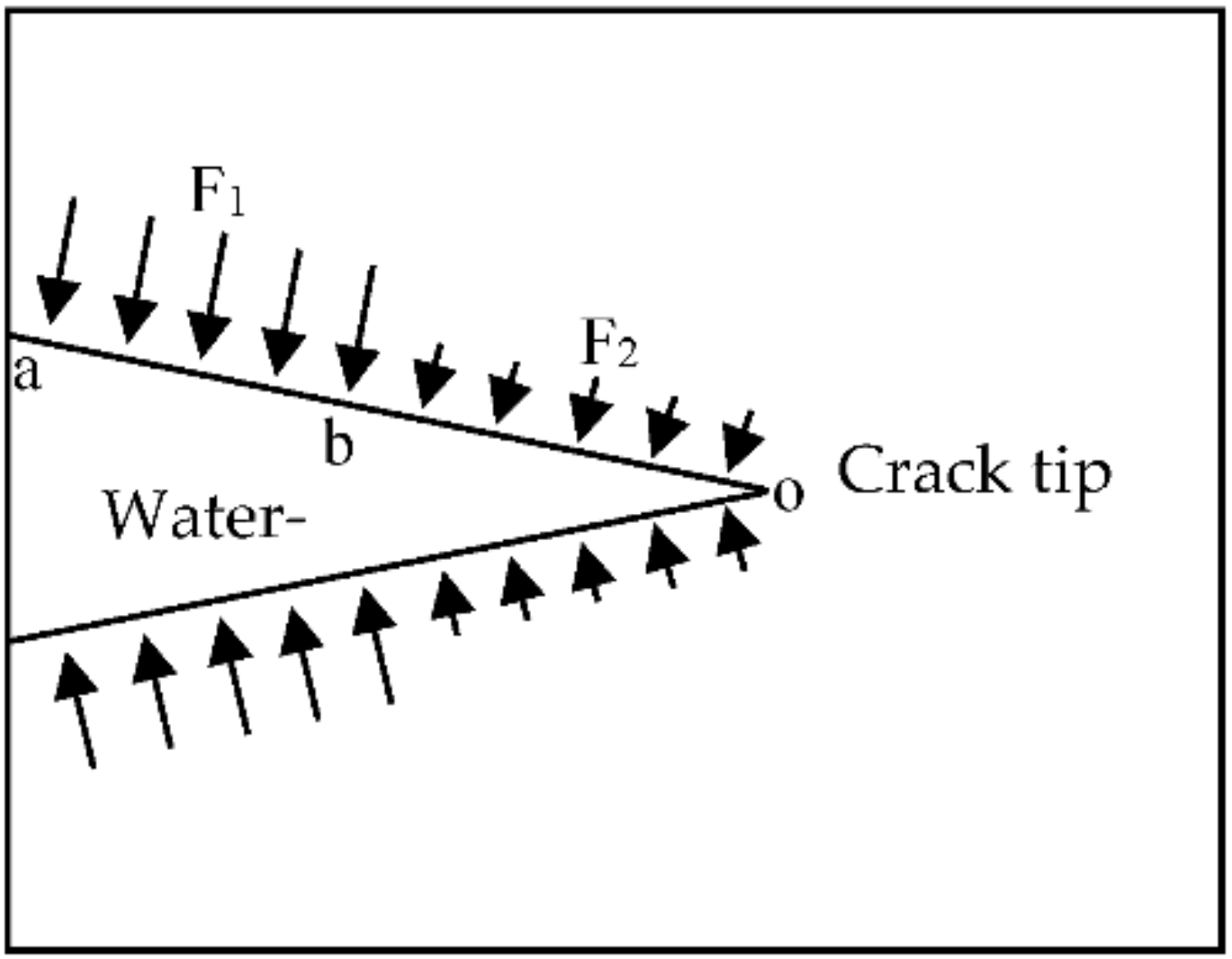
4.2. Bernoulli Effect
4.3. Stefan Effect
5. Conclusions
- (1)
- The dynamic compression strength of water-saturated granite under impact loading is higher than that of air-dried granite, which is contrary to the result that the compression strength of water-saturated rock is lower than that of air-dried rock under static loading.
- (2)
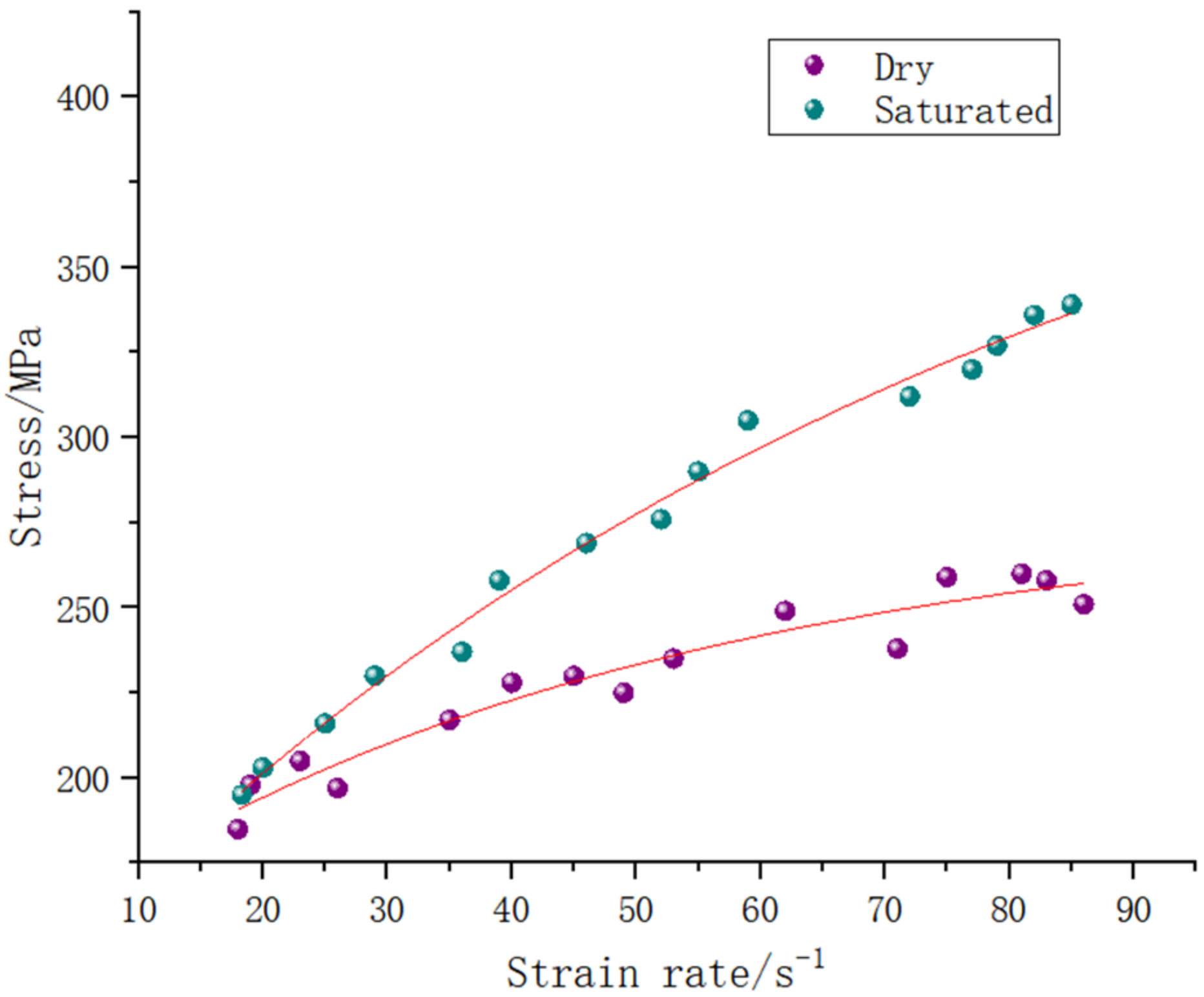
- Under the condition of medium strain rate, the dynamic strength of natural air-dried granite could be increased by nearly 0.5 times compared with its static state (when the strain rate is about 85 s−1), and the dynamic strength of water-saturated granite can be increased by nearly 1–2 times compared with its static state, which shows stronger strain rate sensitivity than natural air-dried granite.
- (3)
- The Bernoulli effect of fluid, the adhesion effect of free water and the Stefan effect of fluid in water-saturated granite have been revealed separately. These above effects are the essential reason affecting the dynamic strength of water-saturated granite from the perspective of water-bearing occurrence.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y. Rock Hydraulics and Engineering; China Water Power Press: Beijing, China, 2005. (In Chinese) [Google Scholar]
- Grant, A.G. Fluid effect on velocity and attenuation in sandstone. J. Acoust. Soc. Am. 1994, 96, 1158–1173. [Google Scholar]
- Laurent, L.; Christian, D.; Philippe, R. Comparison of the anisotropic behavior of undeformed sandstones under dry and saturated conditions. Tectonophysics 2003, 370, 193–212. [Google Scholar]
- Zhang, Q.B.; Zhao, J. A review of dynamic experimental techniques and mechanical behaviour of rock materials. Rock Mech. Rock Eng. 2014, 47, 1411–1478. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Du, Y.; Wan, X.; Xi, D. Responses of saturated rocks to mean stress and dynamic stress amplitude. Chin. J. Rock Mech. Eng. 2008, 27, 161–168. (In Chinese) [Google Scholar]
- Wang, H.; Li, Q. Micro-mechanism of static and dynamic strengths for saturated concrete. J. Hydraul. Eng. 2006, 37, 958–962. (In Chinese) [Google Scholar]
- Liu, G.; Zhou, F. Relation between pore liquid pressures and bulk elastic modulus of loaded saturated rock of low permeability. Chin. J. Rock Mech. Eng. 2004, 23, 1792–1796. (In Chinese) [Google Scholar]
- Erguler, Z.A.; Ulusay, R. Water-induced variations in mechanical properties of clay-bearing rocks. Int. J. Rock Mech. Min. Sci. 2009, 46, 355–370. [Google Scholar] [CrossRef]
- Li, X.; Gu, D. Rock Impact Dynamics; Central South University of Technology Press: Changsha, China, 1994. (In Chinese) [Google Scholar]
- Li, X.; Zhou, Z.; Lok, T.S.; Hong, L.; Yin, T. Innovative testing technique of rock subjected to coupled static and dynamic loads. Int. J. Rock Mech. Min. Sci. 2008, 45, 739–748. [Google Scholar] [CrossRef]
- Zuo, Y.J.; Li, X.B.; Zhou, Z.L.; Ma, C.D.; Zhang, Y.P.; Wang, W.H. Damage and failure rule of rock undergoing uniaxial compressive load and dynamic load. J. Cent. South Univ. Technol. 2005, 12, 742–748. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Yu, J.; Kou, S.Q.; Lindqvist, P.A. Effects of high temperatures on dynamic rock fracture. Int. J. Rock Mech. Min. Sci. 2001, 38, 211–225. [Google Scholar] [CrossRef]
- Ruhbin, A.M.; Ahrens, T.J. Dynamic tensile-failure-induced velocity deficits in rock. Geophys. Res. Lett. 1991, 18, 219–222. [Google Scholar] [CrossRef] [Green Version]
- Lou, W. Dynamic fracture behaviour of dry and waterlogged granite. Explos. Shock. Waves 1994, 14, 249–254. (In Chinese) [Google Scholar]
- Nikolaevskiy, V.N.; Kapustyanskiy, S.M.; Thiercelin, M.; Zhilenkov, A.G. Explosion dynamics in saturated rock sand solids. Transp. Porous Media 2006, 65, 485–504. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, L.; Ding, Y.; Jiang, J.; Sun, F.; Zhang, B.; Liu, Z. Experimental study of damage and fracture zone in cement specimen subjected to exploding wave. Explos. Shock. Waves 2008, 14, 249–254. (In Chinese) [Google Scholar]
- Deng, X.F.; Zhu, J.B.; Chen, S.G.; Zhao, Z.Y.; Zhou, Y.X.; Zhao, J. Numerical study on tunnel damage subject to blast-induced shock wave in jointed rock masses. Tunn. Undergr. Space Technol. 2014, 43, 88–100. [Google Scholar] [CrossRef]
- Li, D.; Wong, L.N.Y. The Brazilian disc test for rock Mechanics applications: Review and new insights. Rock Mech. Rock Eng. 2013, 46, 269–287. [Google Scholar] [CrossRef]
- Man, K.; Song, Z.; Liu, X. Dynamic tensile test of granite and its tensile sensitivity. Adv. Civ. Eng. 2020, 2020, 8837865. [Google Scholar] [CrossRef]
- Industry Standard Compilation Group of the People’s Republic of China. Code for Rock Test of Water Resources and Hydro Power Engineering (SL264-2001); China Water Resources and Hydro Power Press: Beijing, China, 2001. [Google Scholar]
- Li, Y.; Zhu, W.; Bai, S.; Yang, C. Uniaxial experimental study on rheological properties of granite under air-dried and saturated states. Chin. J. Rock Mech. Eng. 2003, 22, 1673–1677. [Google Scholar]
- Yilmaz, I. Influence of water content on the strength and deformability of gypsum. Int. J. Rock Mech. Min. Sci. 2010, 47, 342–347. [Google Scholar] [CrossRef]
- Vásárhelyi, B.; Ván, P. Influence of water content on the strength of rock. Eng. Geol. 2015, 84, 70–74. [Google Scholar] [CrossRef]
- Li, X.B.; Lok, T.S.; Zhao, J. Dynamic characteristics of granite subjected to intermediate loading rate. Rock Mech. Rock Eng. 2005, 38, 21–39. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Ming, C.J. Water saturation effects on the brazilian tensile strength of gypsum and assessment of cracking processes using high-speed video. Rock Mech. Rock Eng. 2014, 47, 1103–1115. [Google Scholar] [CrossRef]
- Hashiba, K.; Fukui, K. Effect of water on the deformation and failure of rock in uniaxial tension. Rock Mech. Rock Eng. 2015, 48, 1751–1761. [Google Scholar] [CrossRef]
- Zhou, Z.; Cai, X.; Cao, W.; Li, X.; Xiong, C. Influence of water content on mechanical properties of rock in both saturation and drying processes. Rock Mech. Rock Eng. 2016, 49, 3009–3025. [Google Scholar] [CrossRef]
- Li, X.B.; Zhou, Z.L.; Zhao, F.J. Rock properties under coupled static-dynamic loads. J. Rock Mech. Geotech. Eng. 2009, 1, 41–47. [Google Scholar] [CrossRef] [Green Version]
- Olsson, W.A. The compressive strength of tuff as a function of strain rate from 10−6 to 103/sec. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1991, 28, 115–118. [Google Scholar] [CrossRef]
- Wang, B.; Li, X.; Yin, T.; Ma, C.; Yin, Z.; Li, Z. Split hopkinson pressure bar(SHPB) experiments on dynamic strength of water-saturated sandstone. Chin. J. Rock Mech. Eng. 2010, 29, 1003–1009. [Google Scholar]
- Zhang, Q.B.; Zhao, J. Effect of loading rate on fracture toughness and failure micromechanisms in marble. Eng. Fract. Mech. 2013, 102, 288–309. [Google Scholar] [CrossRef]
- Rossi, P.; Van Mier JG, M.; Boulay, C.; Le Maou, F. The dynamic behavior of concrete: Influence of free water. Mater. Struct. 1992, 25, 509–514. [Google Scholar] [CrossRef]
- Zheng, D.; Li, Q.B. An explanation for rate effect of concrete strength based on fracture toughness including free water viscosity. Eng. Fract. Mech. 2004, 71, 2319–2327. [Google Scholar] [CrossRef]




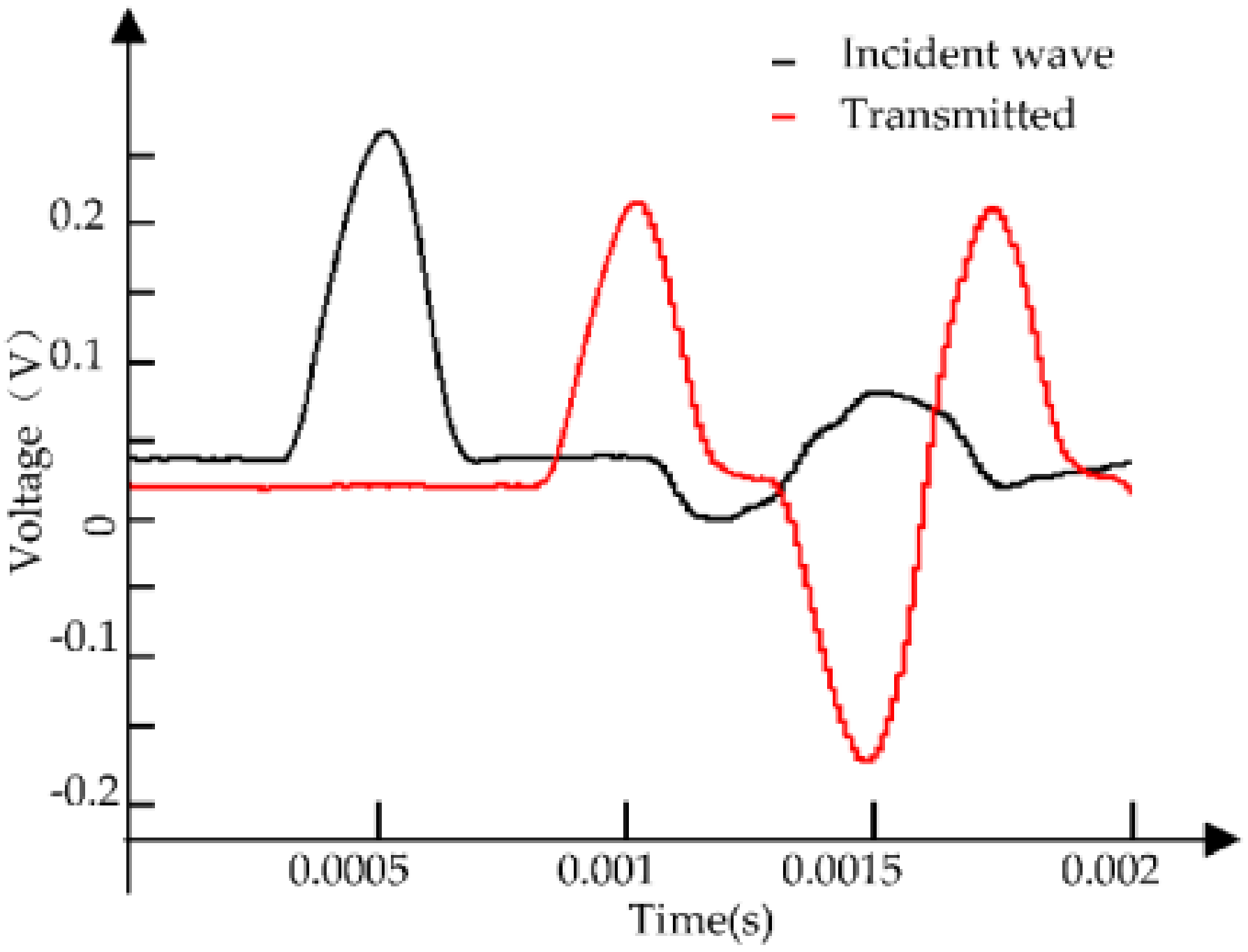

| Diameter of the Bar/mm | Length of the Input Bar/mm | Length of the Output Bar/mm | Elastic Modulus/GPa | Longitudinal Wave Velocity | Poisson Ratio | Pressure/MPa | Density/kg·m−3 |
|---|---|---|---|---|---|---|---|
| 75 | 2000 | 2000 | 250 | 5400 | 0.285 | 0~10 | 7810 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Man, K.; Liu, X.; Song, Z.; Liu, Z.; Liu, R.; Wu, L.; Cao, Z. Dynamic Compression Characteristics and Failure Mechanism of Water-Saturated Granite. Water 2022, 14, 216. https://doi.org/10.3390/w14020216
Man K, Liu X, Song Z, Liu Z, Liu R, Wu L, Cao Z. Dynamic Compression Characteristics and Failure Mechanism of Water-Saturated Granite. Water. 2022; 14(2):216. https://doi.org/10.3390/w14020216
Chicago/Turabian StyleMan, Ke, Xiaoli Liu, Zhifei Song, Zongxu Liu, Ruilin Liu, Liwen Wu, and Zixiang Cao. 2022. "Dynamic Compression Characteristics and Failure Mechanism of Water-Saturated Granite" Water 14, no. 2: 216. https://doi.org/10.3390/w14020216
APA StyleMan, K., Liu, X., Song, Z., Liu, Z., Liu, R., Wu, L., & Cao, Z. (2022). Dynamic Compression Characteristics and Failure Mechanism of Water-Saturated Granite. Water, 14(2), 216. https://doi.org/10.3390/w14020216







