Topography Impacts Hydrology in the Sub-Humid Ethiopian Highlands
Abstract
:1. Introduction
2. Materials and Methods
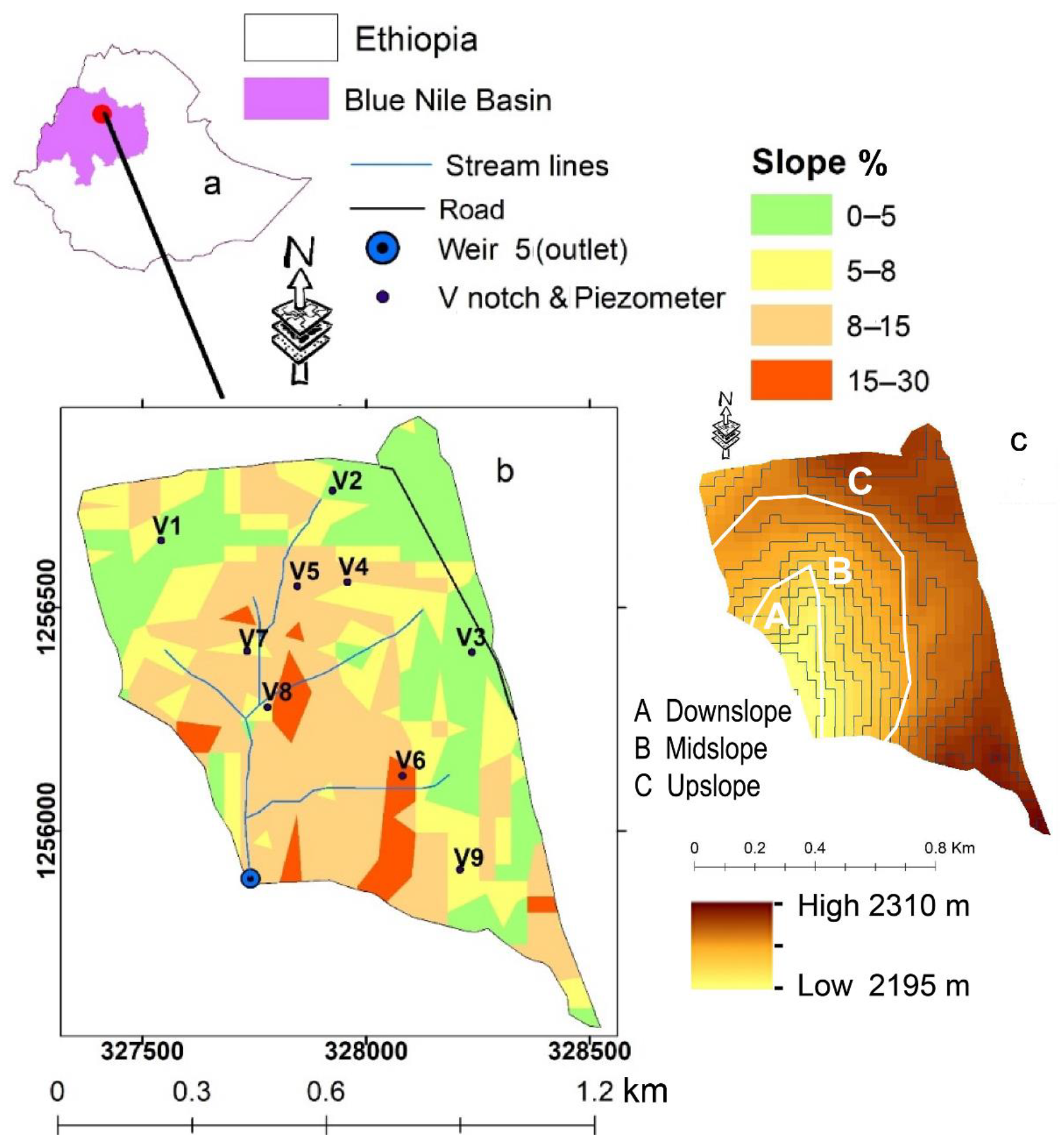
2.1. Description of the Study Area
2.1.1. Topographic Units
2.1.2. Geology
2.1.3. Eucalyptus Tree Expansion
2.1.4. Experimental Fields
2.2. Data and Methods
3. Results
3.1. Precipitation
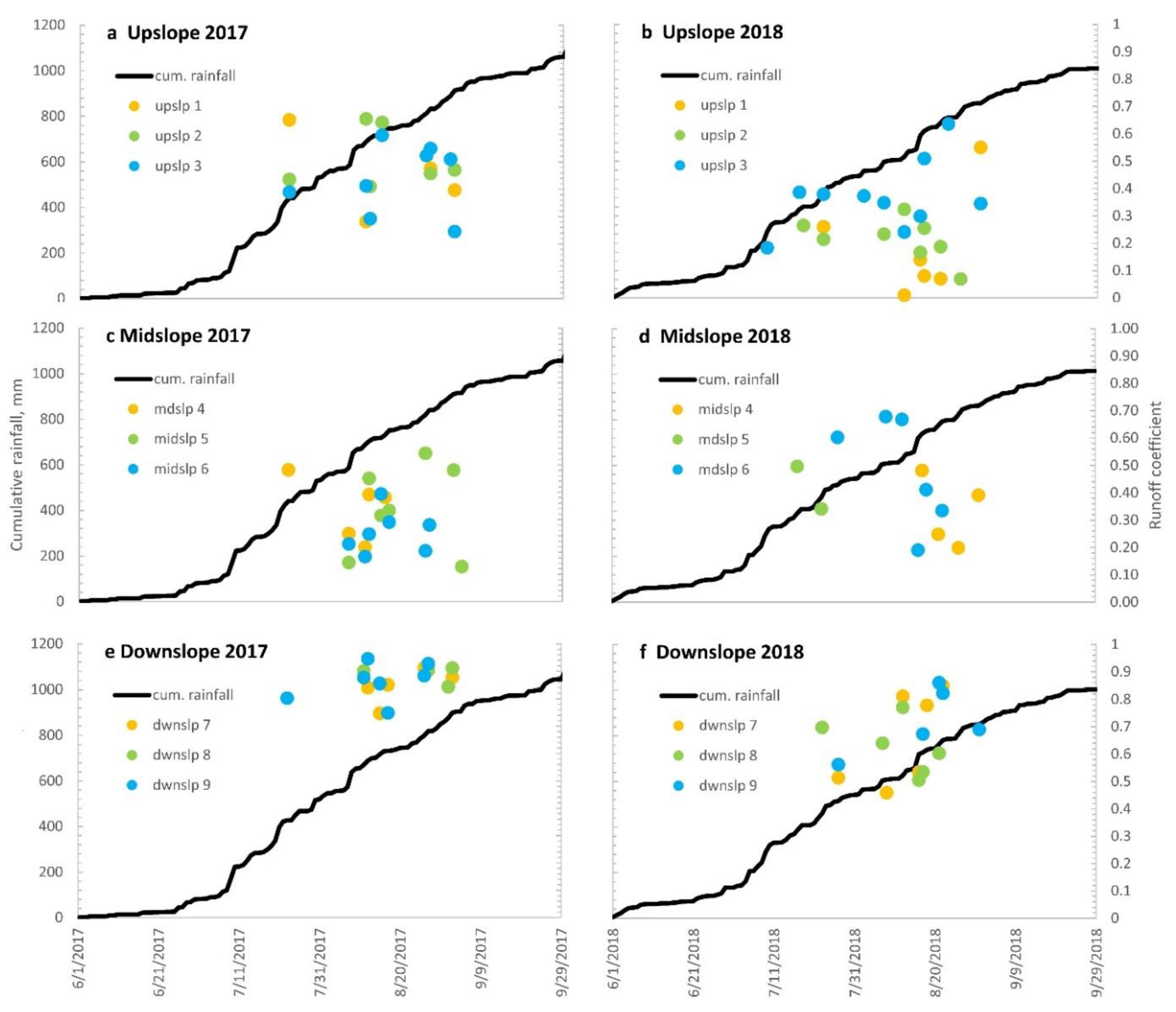
3.2. Surface Runoff
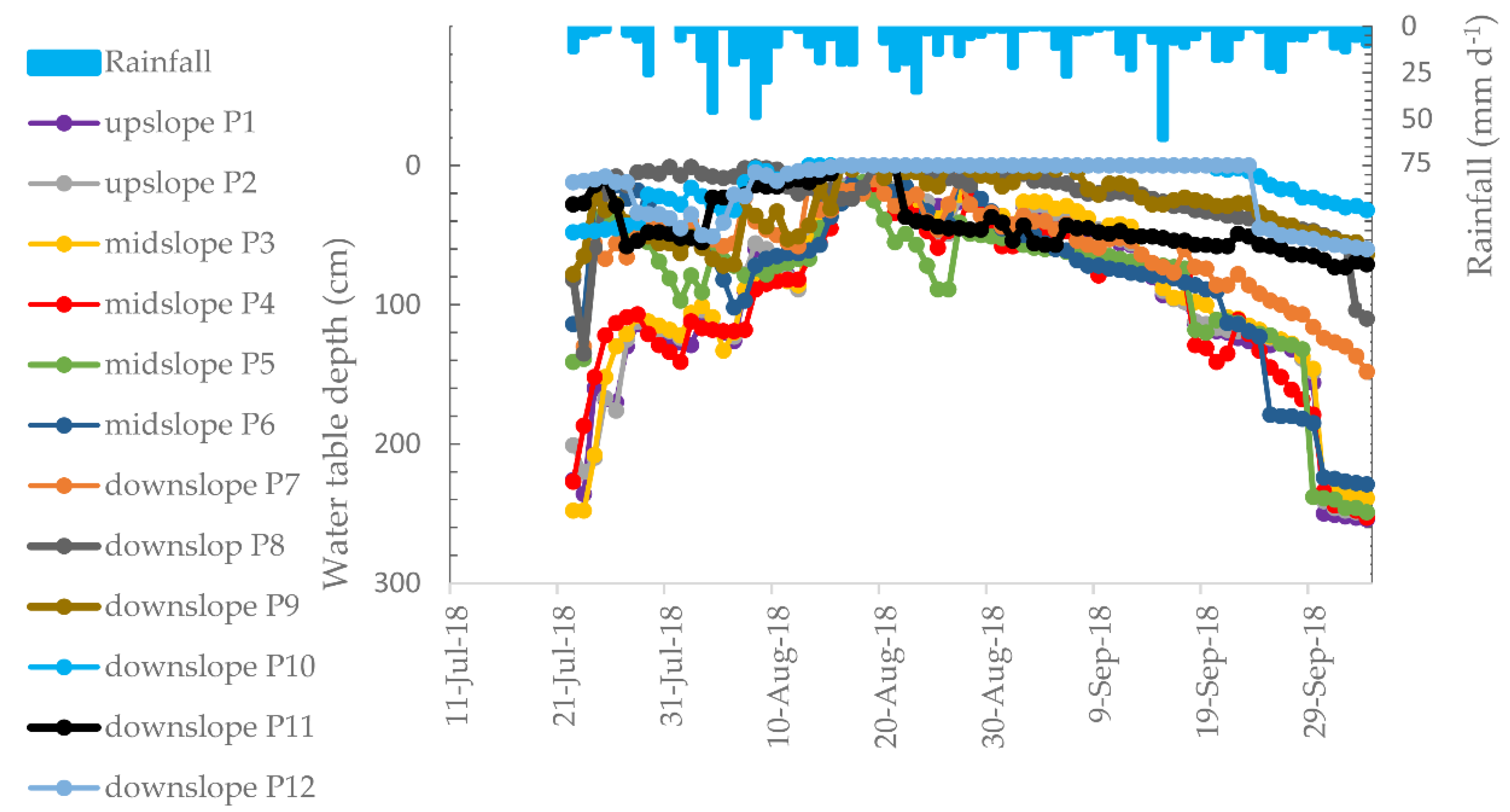
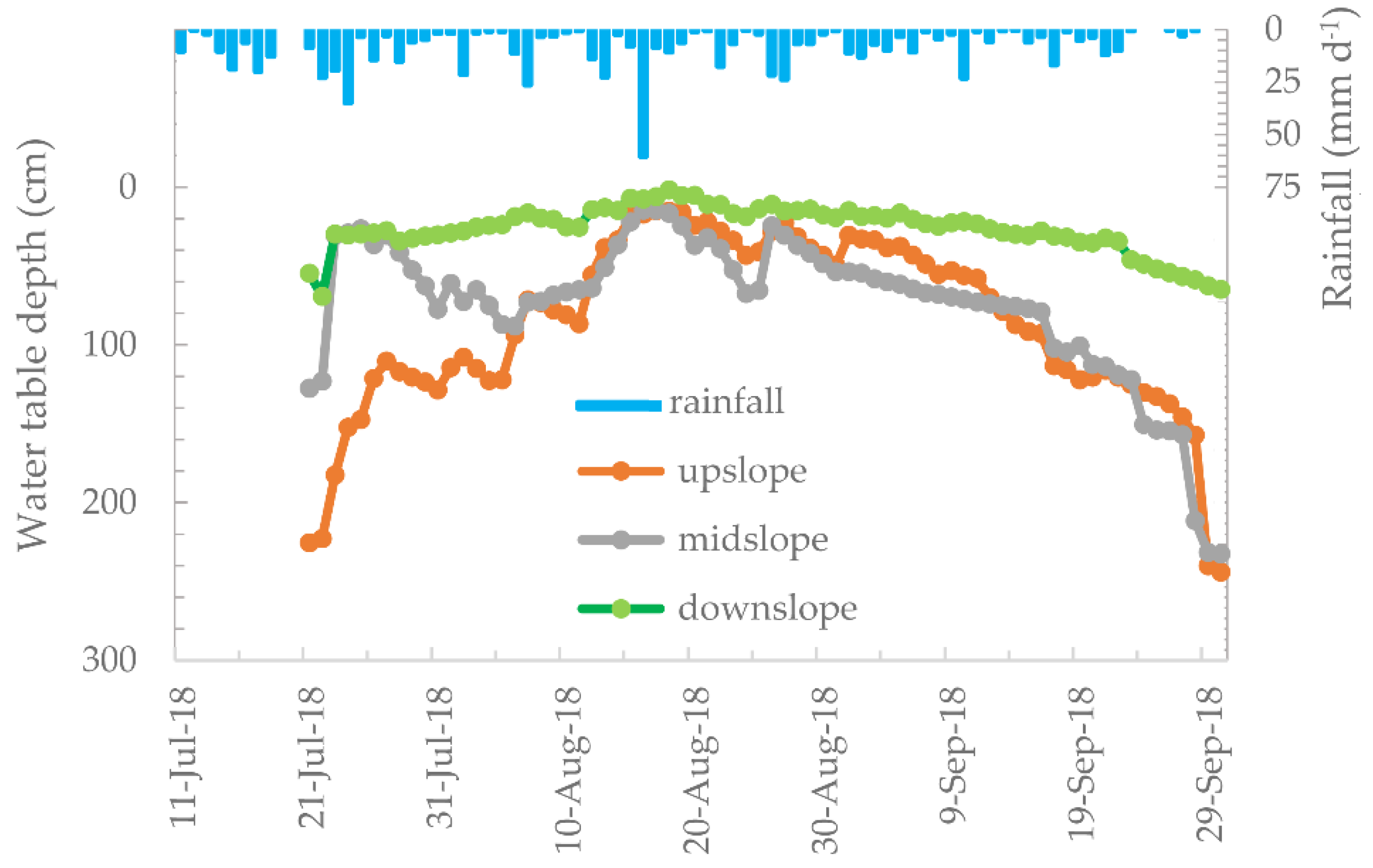
3.3. Groundwater Table Depth
3.4. Infiltration
4. Discussion
4.1. Relationship of Groundwater Table Depth, Slope Position and Distance from the Divide
4.2. Hydrological Correlation Analysis on Seasonal Averaged Data
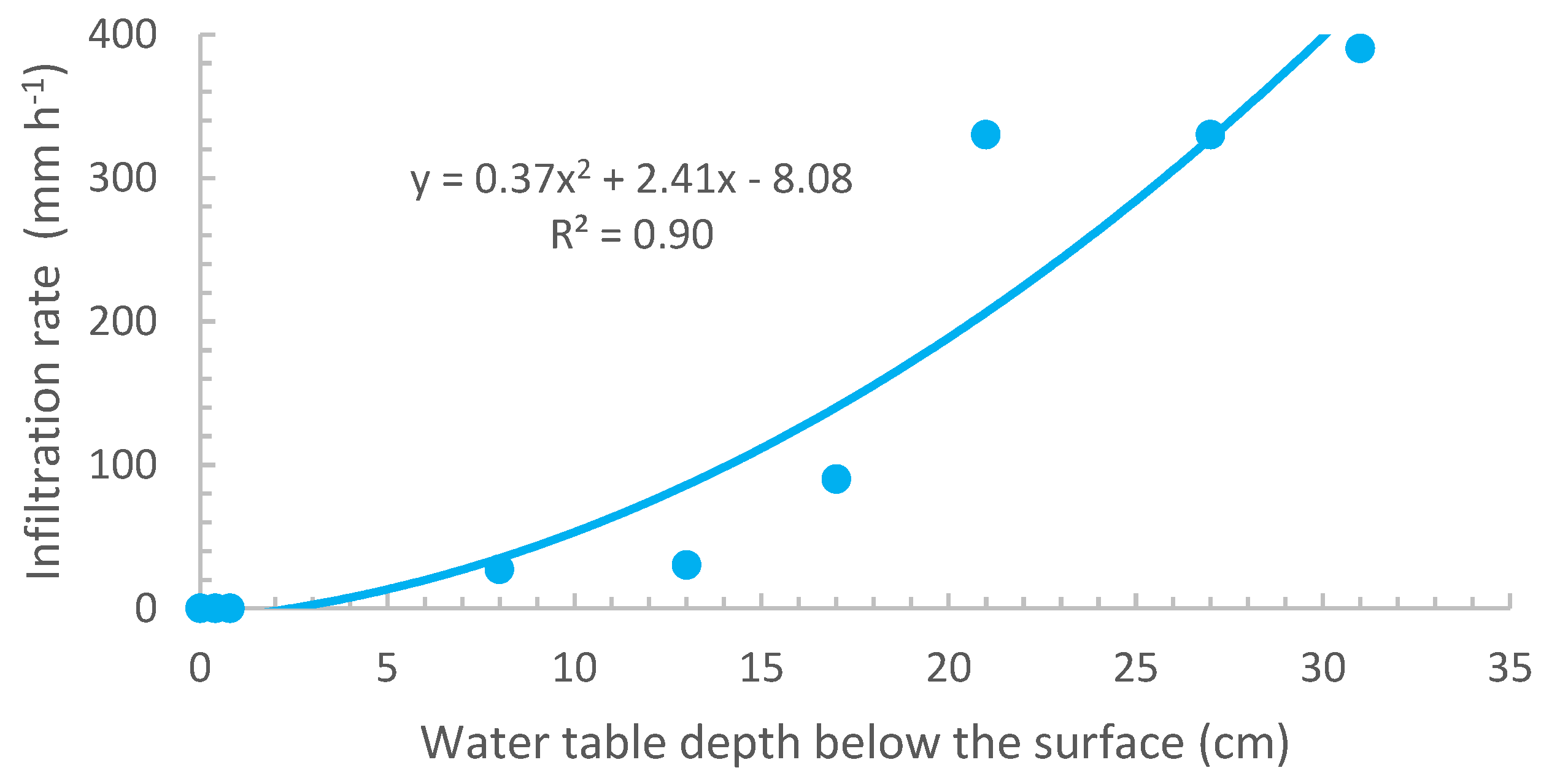
4.2.1. Infiltration Rate as a Function of Groundwater Table Depth
4.2.2. Interaction of Runoff with Rainfall Amount
4.3. Effect of Slope Position and Soil Type on Runoff and Infiltration Capacity
4.4. Interaction of Land Use and Slope Position with Runoff
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, B.M.; Collick, A.S.; Zeleke, G.; Adgo, E.; Easton, Z.M.; Steenhuis, T.S. Rainfall-discharge relationships for a monsoonal climate in the Ethiopian highlands. Hydrol. Process. 2008, 22, 1059–1067. [Google Scholar] [CrossRef]
- Tilahun, S.A.; Guzman, C.D.; Zegeye, A.D.; Ayana, E.K.; Collick, A.S.; Yitaferu, B.; Steenhuis, T.S. Spatial and Temporal Patterns of Soil Erosion in the Semi-humid Ethiopian Highlands: A Case Study of Debre Mawi Watershed. In Nile River Basin; Springer: Berlin/Heidelberg, Germany, 2014; pp. 149–163. [Google Scholar] [CrossRef]
- McDonnell, J.J. Hewlett, J.D.; Hibbert, A.R. Factors affecting the response of small watersheds to precipitation in humid areas. In Forest Hydrology; Sopper, W.E., Lull, H.W., Eds.; Pergamon Press: New York, NY, USA, 1967; pp. 275–290. Phys. Geogr. Earth Environ. 2009, 33, 288–293. [Google Scholar] [CrossRef]
- McMillan, H. Linking hydrologic signatures to hydrologic processes: A review. Hydrol. Process. 2019, 34, 1393–1409. [Google Scholar] [CrossRef]
- Bayabil, H.K.; Tebebu, T.Y.; Stoof, C.R.; Steenhuis, T.S. Spatial and temporal runoff processes in the degraded Ethiopian Highlands: The Anjeni Watershed. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 4387–4411. [Google Scholar] [CrossRef]
- Bayabil, H.K.; Tilahun, S.A.; Collick, A.S.; Yitaferu, B.; Steenhuis, T.S. Are runoff processes ecologically or topographically driven in the (sub) humid Ethiopian highlands? The case of the Maybar watershed. Ecohydrology 2010, 3, 457–466. [Google Scholar] [CrossRef] [Green Version]
- Akale, A.T.; Dagnew, D.C.; Belete, M.A.; Tilahun, S.A.; Mekuria, W.; Steenhuis, T.S. Impact of Soil Depth and Topography on the Effectiveness of Conservation Practices on Discharge and Soil Loss in the Ethiopian Highlands. Land 2017, 6, 78. [Google Scholar] [CrossRef] [Green Version]
- Guillén, L.A.; Fernández, R.; Gaertner, B.; Zégre, N.P. Climate and Landscape Controls on the Water Balance in Temperate Forest Ecosystems: Testing Large Scale Controls on Undisturbed Catchments in the Central Appalachian Mountains of the US. Water Resour. Res. 2021, 57, 2411–2502. [Google Scholar] [CrossRef]
- Camporese, M.; Paniconi, C.; Putti, M.; McDonnell, J.J. Fill and Spill Hillslope Runoff Representation with a Richards Equation-Based Model. Water Resour. Res. 2019, 55, 8445–8462. [Google Scholar] [CrossRef]
- Savenije, H.H.G. HESS Opinions Topography driven conceptual modelling (FLEX-Topo). Hydrol. Earth Syst. Sci. 2010, 14, 2681–2692. [Google Scholar] [CrossRef] [Green Version]
- Nyssen, J.; Clymans, W.; Descheemaeker, K.; Poesen, J.; Vandecasteele, I.; Vanmaercke, M.; Zenebe, A.; Van Camp, M.; Haile, M.; Haregeweyn, N.; et al. Impact of soil and water conservation measures on catchment hydrological response-a case in north Ethiopia. Hydrol. Process. 2010, 24, 1880–1895. [Google Scholar] [CrossRef] [Green Version]
- Assefa, T.T.; Jha, M.K.; Tilahun, S.A.; Yetbarek, E.; Adem, A.A.; Wale, A. Identification of Erosion Hotspot Area using GIS and MCE Technique for Koga Watershed in the Upper Blue Nile Basin, Ethiopia. Am. J. Environ. Sci. 2015, 11, 245–255. [Google Scholar] [CrossRef] [Green Version]
- Mhiret, D.A.; Dagnew, D.C.; Assefa, T.T.; Tilahun, S.A.; Zaitchik, B.F.; Steenhuis, T.S. Erosion hotspot identification in the sub-humid Ethiopian highlands. Ecohydrol. Hydrobiol. 2019, 19, 146–154. [Google Scholar] [CrossRef]
- Moges, M.A.; Schmitter, P.; Tilahun, S.A.; Langan, S.; Dagnew, D.C.; Akale, A.T.; Steenhuis, T.S. Suitability of Watershed Models to Predict Distributed Hydrologic Response in the Awramba Watershed in Lake Tana Basin. Land Degrad. Dev. 2017, 28, 1386–1397. [Google Scholar] [CrossRef]
- Akale, A.T.; Dagnew, D.C.; Moges, M.A.; Tilahun, S.A.; Steenhuis, T.S. The Effect of Landscape Interventions on Groundwater Flow and Surface Runoff in a Watershed in the Upper Reaches of the Blue Nile. Water 2019, 11, 2188. [Google Scholar] [CrossRef] [Green Version]
- Tilahun, S.A.; Guzman, C.D.; Zegeye, A.D.; Engda, T.A.; Collick, A.S.; Rimmer, A.; Steenhuis, T.S. An efficient semi-distributed hillslope erosion model for the subhumid Ethiopian Highlands. Hydrol. Earth Syst. Sci. 2013, 17, 1051–1063. [Google Scholar] [CrossRef] [Green Version]
- Alemie, T.C.; Tilahun, S.A.; Ochoa-Tocachi, B.F.; Schmitter, P.; Buytaert, W.; Parlange, J.; Steenhuis, T.S. Predicting Shallow Groundwater Tables for Sloping Highland Aquifers. Water Resour. Res. 2019, 55, 11088–11100. [Google Scholar] [CrossRef]
- Sultan, D.; Tsunekawa, A.; Haregeweyn, N.; Adgo, E.; Tsubo, M.; Meshesha, D.T.; Masunaga, T.; Aklog, D.; Fenta, A.A.; Ebabu, K. Efficiency of soil and water conservation practices in different agro-ecological environments in the Upper Blue Nile Basin of Ethiopia. J. Arid Land 2018, 10, 249–263. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Gascuel-Odoux, C.; Cros-Cayot, S. Hillslope topographic and hydrologic effects on overland flow and erosion. Catena 2002, 46, 177–188. [Google Scholar] [CrossRef]
- Cerdà, A.; Rodrigo-Comino, J. Is the hillslope position relevant for runoff and soil loss activation under high rainfall conditions in vineyards? Ecohydrol. Hydrobiol. 2020, 20, 59–72. [Google Scholar] [CrossRef]
- Tebebu, T.Y.; Abiy, A.Z.; Zegeye, A.D.; Dahlke, H.E.; Easton, Z.M.; Tilahun, S.A.; Collick, A.S.; Kidnau, S.; Moges, S.; Dadgari, F.; et al. Surface and subsurface flow effect on permanent gully formation and upland erosion near Lake Tana in the northern highlands of Ethiopia. Hydrol. Earth Syst. Sci. 2010, 14, 2207–2217. [Google Scholar] [CrossRef] [Green Version]
- Tilahun, S.A.; Guzman, C.D.; Zegeye, A.D.; Dagnew, D.C.; Collick, A.S.; Yitaferu, B.; Steenhuis, T.S. Distributed discharge and sediment concentration predictions in the sub-humid Ethiopian highlands: The Debre Mawi watershed. Hydrol. Process. 2015, 29, 1817–1828. [Google Scholar] [CrossRef]
- Dagnew, D.C.; Guzman, C.D.; Zegeye, A.D.; Tebebu, T.Y.; Getaneh, M.; Abate, S.; Zemale, F.A.; Ayana, E.K.; Tilahun, S.A.; Steenhuis, T.S. Impact of conservation practices on runoff and soil loss in the sub-humid Ethiopian Highlands: The Debre Mawi watershed. J. Hydrol. Hydromech. 2015, 63, 210–219. [Google Scholar] [CrossRef] [Green Version]
- Mhiret, D.A.; Dagnew, D.C.; Alemie, T.C.; Guzman, C.D.; Tilahun, S.A.; Zaitchik, B.F.; Steenhuis, T.S. Impact of Soil Conservation and Eucalyptus on Hydrology and Soil Loss in the Ethiopian Highlands. Water 2019, 11, 2299. [Google Scholar] [CrossRef] [Green Version]
- Mhiret, D.A.; Dagnew, D.C.; Guzman, C.D.; Alemie, T.C.; Zegeye, A.D.; Tebebu, T.Y.; Langendoen, E.J.; Zaitchik, B.F.; Tilahun, S.A.; Steenhuis, T.S. A nine-year study on the benefits and risks of soil and water conservation practices in the humid highlands of Ethiopia: The Debre Mawi watershed. J. Environ. Manag. 2020, 270, 110885. [Google Scholar] [CrossRef] [PubMed]
- Abiy, A.Z. Geological Controls in the Formations and Expansions of Gullies Over Hillslope Hydrological Processes in the Highlands of Ethiopia, Northern Blue Nile Region. Master’s Thesis, Graduate School of Cornell University, Ithaca, NY, USA, August 2009. [Google Scholar]
- Zegeye, A.D.; Steenhuis, T.S.; Blake, R.W.; Kidnau, S.; Collick, A.S.; Dadgari, F. Assessment of Upland Erosion Processes and Farmer Perception of Land Conservation in Debre Mewi Watershed, near Lake Tana, Ethiopia. Ecohydrol. Hydrobiol. 2011, 10, 297–306. [Google Scholar] [CrossRef]
- Zegeye, A.D.; Langendoen, E.J.; Guzman, C.D.; Dagnew, D.C.; Amare, S.D.; Tilahun, S.A.; Steenhuis, T.S. Gullies, a critical link in landscape soil loss: A case study in the subhumid highlands of Ethiopia. Land Degrad. Dev. 2018, 29, 1222–1232. [Google Scholar] [CrossRef]
- Tilahun, S.A.; Yilak, D.L.; Schmitter, P.; Langan, S.; Barron, J.; Parlange, J.Y.; Steenhuis, T.S. Establishing irrigation potential of a hillside aquifer in the African highlands. Hydrol. Process 2020, 34, 1741–1753. [Google Scholar] [CrossRef] [Green Version]
- Shen, J. Discharge Characteristics of Triangular-Notch Thin-Plate Weirs: Studies of Flow to Water Over Weirs and Dams; USGPO: Washington, DC, USA, 1981. [Google Scholar] [CrossRef]
- Greve, F.W. Flow of Water Through Circular, Parabolic, and Triangular Vertical Notch-Ueirs; Purdue University: West Lafayette, IN, USA, 1932. [Google Scholar]
- Lee, D.M.; Elrick, D.E.; Reynolds, W.D.; Clothier, B.E. A Comparison of three field methods for measuring saturated hydraulic conductivity. Can. J. Soil Sci. 1985, 65, 563–573. [Google Scholar] [CrossRef]
- Guzman, C.D.; Tilahun, S.A.; Dagnew, D.C.; Zimale, F.A.; Zegeye, A.D.; Boll, J.; Parlange, J.-Y.; Steenhuis, T.S. Spatio-temporal patterns of groundwater depths and soil nutrients in a small watershed in the Ethiopian highlands: Topographic and land-use controls. J. Hydrol. 2017, 555, 420–434. [Google Scholar] [CrossRef]
- Engda, T.A.; Bayabil, H.K.; Legesse, E.S.; Ayana, E.K.; Tilahun, S.A.; Collick, A.S.; Easton, Z.M.; Rimmer, A.; Awulachew, S.B.; Steenhuis, T.S. Watershed Hydrology of the (Semi) Humid Ethiopian Highlands. In Nile River Basin; Springer: Dordrecht, The Netherlands, 2011; pp. 145–162. [Google Scholar] [CrossRef]
- Walraevens, K.K.; Vandecasteele, I.; Martens, K.K.; Nyssen, J.; Moeyersons, J.J.; Gebreyohannes, T.T.; De Smedt, F.; Poesen, J.J.; Deckers, J.J.; Van Camp, M.M. Groundwater recharge and flow in a small mountain catchment in northern Ethiopia. Hydrol. Sci. J. 2009, 54, 739–753. [Google Scholar] [CrossRef]
- McGlynn, B.L.; McDonnell, J.J. Quantifying the relative contributions of riparian and hillslope zones to catchment runoff. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef] [Green Version]
- McGlynn, B.L.; McDonnell, J.J.; Seibert, J.; Kendall, C. Scale effects on headwater catchment runoff timing, flow sources, and groundwater-streamflow relations. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef] [Green Version]
- Jencso, K.G.; McGlynn, B.L.; Gooseff, M.; Wondzell, S.M.; Bencala, K.E.; Marshall, L. Hydrologic connectivity between landscapes and streams: Transferring reach- and plot-scale understanding to the catchment scale. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef] [Green Version]
- Han, S.; Xu, D.; Wang, S. Runoff formation from experimental plot, field, to small catchment scales in agricultural North Huaihe River Plain, China. Hydrol. Earth Syst. Sci. 2012, 16, 3115–3125. [Google Scholar] [CrossRef] [Green Version]
- Yenehun, A.; Nigate, F.; Belay, A.S.; Desta, M.T.; Van Camp, M.; Walraevens, K. Groundwater recharge and water table response to changing conditions for aquifers at different physiography: The case of a semi-humid river catchment, northwestern highlands of Ethiopia. Sci. Total Environ. 2020, 748, 142243. [Google Scholar] [CrossRef] [PubMed]
- Adem, A.A.; Addis, G.G.; Aynalem, D.W.; Tilahun, S.A.; Mekuria, W.; Azeze, M.; Steenhuis, T.S. Hydrogeology of Volcanic Highlands Affects Prioritization of Land Management Practices. Water 2020, 12, 2702. [Google Scholar] [CrossRef]
- Cerdà, A. Seasonal variability of infiltration rates under contrasting slope conditions in southeast Spain. Geoderma 1996, 69, 217–232. [Google Scholar] [CrossRef] [Green Version]


| Field ID (Piezometer) | Topographic Position | Area (m2) | Slope (%) | Soil Type | Crop Grown | Bund Length (m) |
|---|---|---|---|---|---|---|
| V1 (P1–2) | upslope 1 | 2200 | 6 | Nitisols | teff | 51 |
| V2 | upslope 2 | 600 | 4 | Nitisols | teff | 47 |
| V3 | upslope 3 | 900 | 5 | Nitisols | Finger millet | 51 |
| V4 (P3–4) | midslope 4 | 2400 | 10 | Nitic-Vertisols | teff | 56 |
| V5 (P5–6) | midslope 5 | 800 | 12 | Nitic-Vertisols | wheat | 18 |
| V6 | midslope 6 | 600 | 19 | Nitic-Vertisols | teff | 49 |
| V7 (P7–8) | downslope 7 | 400 | 5 | Vertisols | teff | 35 |
| V8 (P9–10) | downslope 8 | 500 | 6 | Vertisols | teff | 37 |
| V9 (P11–12) | downslope 9 | 600 | 6 | Vertisols | teff | 28 |
| Topographic Position | Runoff Coefficient | ||
|---|---|---|---|
| 2017 | 2018 | Average | |
| upslope V1 | 0.39 | 0.14 | 0.28 |
| upslope V2 | 0.51 | 0.15 | 0.25 |
| upslope V3 | 0.43 | 0.31 | 0.34 |
| upslope average | 0.44 | 0.21 | 0.29 |
| midslope V5 | 0.35 | 0.42 | 0.39 |
| midslope V6 | 0.2 | 0.31 | 0.25 |
| midslope average | 0.27 | 0.31 | 0.29 |
| downslope V7 | 0.86 | 0.62 | 0.71 |
| downslope V8 | 0.89 | 0.59 | 0.69 |
| downslope V9 | 0.89 | 0.78 | 0.85 |
| downslope average | 0.88 | 0.63 | 0.73 |
| Topographic Position | Infiltration Rate (mm h−1) | Water Table Depth from the Surface (cm) |
|---|---|---|
| upslope V1 | 330 | 31 |
| upslope V2 | 390 | 27 |
| upslope V3 | 330 | 21 |
| midslope V4 | 90 | 17 |
| midslope V5 | 30 | 13 |
| midslope V6 | 27 | 8 |
| downslope V7 | 0 | 0 |
| downslope V8 | 0 | 0 |
| downslope V9 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mhiret, D.A.; Dersseh, M.G.; Guzman, C.D.; Dagnew, D.C.; Abebe, W.B.; Zimale, F.A.; Zaitchik, B.F.; Tilahun, S.A.; Walraevens, K.; Steenhuis, T.S. Topography Impacts Hydrology in the Sub-Humid Ethiopian Highlands. Water 2022, 14, 196. https://doi.org/10.3390/w14020196
Mhiret DA, Dersseh MG, Guzman CD, Dagnew DC, Abebe WB, Zimale FA, Zaitchik BF, Tilahun SA, Walraevens K, Steenhuis TS. Topography Impacts Hydrology in the Sub-Humid Ethiopian Highlands. Water. 2022; 14(2):196. https://doi.org/10.3390/w14020196
Chicago/Turabian StyleMhiret, Demesew A., Minychl G. Dersseh, Christian D. Guzman, Dessalegn C. Dagnew, Wubneh B. Abebe, Fasikaw A. Zimale, Benjamin F. Zaitchik, Seifu A. Tilahun, Kristine Walraevens, and Tammo S. Steenhuis. 2022. "Topography Impacts Hydrology in the Sub-Humid Ethiopian Highlands" Water 14, no. 2: 196. https://doi.org/10.3390/w14020196
APA StyleMhiret, D. A., Dersseh, M. G., Guzman, C. D., Dagnew, D. C., Abebe, W. B., Zimale, F. A., Zaitchik, B. F., Tilahun, S. A., Walraevens, K., & Steenhuis, T. S. (2022). Topography Impacts Hydrology in the Sub-Humid Ethiopian Highlands. Water, 14(2), 196. https://doi.org/10.3390/w14020196









