Effects of Barrier Stiffness on Debris Flow Dynamic Impact—II: Numerical Simulation
Abstract
:1. Introduction
2. Flow–Structure Coupled SPH Model
2.1. Smooth Function
2.2. Governing Equations
2.3. Setup of the Numerical Model and Simulation Plan
3. Validation of the Flow–Structure Coupled SPH Model
4. Interpretation of the Computed Results
4.1. Effects of the Barrier Stiffness on the Earth Pressure Coefficient
4.2. Effects of the Frontal Velocity
5. Discussion
6. Conclusions
- (1)
- The presented flow–structure coupled SPH modeling solves the governing equations of the flow and structure and considers the flow–structure interaction. A comparison of the results of numerical and physical tests showed that the proposed numerical model can be used to simulate the problem of a large deformation flow effectively and predict the flow kinematics and impact force appropriately;
- (2)
- The deduced static earth pressure coefficients revealed that barriers with lower stiffness tend to deform downstream upon loading, shifting the pressure coefficient of the deposited sand toward the active pressure coefficient (Ka);
- (3)
- The peak impact force generally increases with the frontal velocity of the debris flow. Moreover, the stiffness of the deformable barrier affects the load attenuation when the debris flow has larger frontal velocity, in the situation that the impact force on the barrier is dominated by the dynamic component.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Moriguchi, S.; Borja, R.I.; Yashima, A.; Sawada, K. Estimating the impact force generated by granular flow on a rigid obstruction. Acta Geotech. 2009, 4, 57–71. [Google Scholar] [CrossRef]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Choi, S.-K.; Park, J.-Y.; Lee, D.-H.; Lee, S.-R.; Kim, Y.-T.; Kwon, T.-H. Assessment of barrier location effect on debris flow based on smoothed particle hydrodynamics (SPH) simulation on 3D terrains. Landslides 2021, 18, 217–234. [Google Scholar] [CrossRef]
- Marchetti, E.; Walter, F.; Barfucci, G.; Genco, R.; Wenner, M.; Ripepe, M.; McArdell, B.; Price, C. Infrasound Array Analysis of Debris Flow Activity and Implication for Early Warning. J. Geophys. Res.-Earth Surf. 2019, 124, 567–587. [Google Scholar] [CrossRef] [Green Version]
- Allstadt, K. Extracting source characteristics and dynamics of the August 2010 Mount Meager landslide from broadband seismograms. J. Geophys. Res.-Earth Surf. 2013, 118, 1472–1490. [Google Scholar] [CrossRef]
- Guerriero, L.; Revellino, P.; Diodato, N.; Grelle, G.; De Vito, A.; Guadagno, F.M. Morphological and Climatic Aspects of the Initiation of the San Mango Sul Calore Debris Avalanche in Southern Italy. In Engineering Geology for Society and Territory, Proceedings of the 12th International IAEG Congress, Torino, Italy, 15–19 September 2014; Springer: Cham, Switzerland, 2015; Volume 2. [Google Scholar]
- Iverson, R.M.; George, D.L.; Allstadt, K.; Reid, M.E.; Collins, B.D.; Vallance, J.W.; Schilling, S.P.; Godt, J.W.; Cannon, C.M.; Magirl, C.S.; et al. Landslide mobility and hazards: Implications of the 2014 Oso disaster. Earth Planet. Sci. Lett. 2015, 412, 197–208. [Google Scholar] [CrossRef] [Green Version]
- Petley, D. Global patterns of loss of life from landslides. Geology 2012, 40, 927–930. [Google Scholar] [CrossRef]
- Zhang, J.; Gurung, D.R.; Liu, R.; Murthy, M.S.R.; Su, F. Abe Barek landslide and landslide susceptibility assessment in Badakhshan Province, Afghanistan. Landslides 2015, 12, 597–609. [Google Scholar] [CrossRef]
- Wartman, J.; Montgomery, D.R.; Anderson, S.A.; Keaton, J.R.; Benoit, J.; dela Chapelle, J.; Gilbert, R. The 22 March 2014 Oso landslide, Washington, USA. Geomorphology 2016, 253, 275–288. [Google Scholar] [CrossRef]
- Wang, F.; Wu, Y.-H.; Yang, H.; Tanida, Y.; Kamei, A. Preliminary investigation of the 20 August 2014 debris flows triggered by a severe rainstorm in Hiroshima City, Japan. Geoenviron. Disasters 2015, 2, 1. [Google Scholar] [CrossRef] [Green Version]
- Tang, C.; van Asch, T.W.J.; Chang, M.; Chen, G.Q.; Zhao, X.H.; Huang, X.C. Catastrophic debris flows on 13 August 2010 in the Qingping area, southwestern China: The combined effects of a strong earthquake and subsequent rainstorms. Geomorphology 2012, 139, 559–576. [Google Scholar] [CrossRef]
- Xu, Q.; Li, W.; Dong, X.; Xiao, X.; Fan, X.; Pei, X. The Xinmocun landslide on 24 June 2017 in Maoxian, Sichuan: Characteristics and failure mechanism. Chin. J. Rock Mech. Eng. 2017, 36, 2612–2628. [Google Scholar]
- Huebl, J.; Fiebiger, G. Debris-flow mitigation measures. In Debris-Flow Hazards and Related Phenomena; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Albaba, A.; Lambert, S.; Faug, T. Dry granular avalanche impact force on a rigid wall: Analytic shock solution versus discrete element simulations. Phys. Rev. E 2018, 97, 052903. [Google Scholar] [CrossRef] [PubMed]
- Armanini, A.; Rossi, G.; Larcher, M. Dynamic impact of a water and sediments surge against a rigid wall. J. Hydraul. Res. 2020, 58, 314–325. [Google Scholar] [CrossRef] [Green Version]
- Bi, Y.-z.; He, S.-m.; Li, X.-p.; Wu, Y.; Xu, Q.; Ouyang, C.-j.; Su, L.-J.; Wang, H. Geo-engineered buffer capacity of two-layered absorbing system under the impact of rock avalanches based on Discrete Element Method. J. Mt. Sci. 2016, 13, 917–929. [Google Scholar] [CrossRef]
- Chen, H.-X.; Li, J.; Feng, S.-J.; Gao, H.-Y.; Zhang, D.-M. Simulation of interactions between debris flow and check dams on three-dimensional terrain. Eng. Geol. 2019, 251, 48–62. [Google Scholar] [CrossRef]
- Jiang, Y.J.; Fan, X.-Y.; Li, T.-H.; Xiao, S.-Y. Influence of particle-size segregation on the impact of dry granular flow. Powder Technol. 2018, 340, 39–51. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Choi, C.E.; Liu, L.H.D.; Wang, Y.; Song, D.; Yang, N. Influence of particle size on the mechanism of dry granular run-up on a rigid barrier. Geotech. Lett. 2017, 7, 79–89. [Google Scholar] [CrossRef]
- Remaitre, A.; van Asch, T.W.J.; Malet, J.P.; Maquaire, O. Influence of check dams on debris-flow run-out intensity. Nat. Hazards Earth Syst. Sci. 2008, 8, 1403–1416. [Google Scholar] [CrossRef]
- Shen, W.; Wang, D.; Qu, H.; Li, T. The effect of check dams on the dynamic and bed entrainment processes of debris flows. Landslides 2019, 16, 2201–2217. [Google Scholar] [CrossRef]
- Zhou, G.G.D.; Song, D.; Choi, C.E.; Pasuto, A.; Sun, Q.C.; Dai, D.F. Surge impact behavior of granular flows: Effects of water content. Landslides 2018, 15, 695–709. [Google Scholar] [CrossRef]
- Dai, Z.; Huang, Y.; Cheng, H.; Xu, Q. SPH model for fluid-structure interaction and its application to debris flow impact estimation. Landslides 2017, 14, 917–928. [Google Scholar] [CrossRef]
- Huang, Y.; Jin, Y.X.; Ji, J.J. Effects of barrier stiffness on debris flow dynamic impact—I: Laboratory flume test. Water 2021, 3, 26. [Google Scholar]
- Khan-Mozahedy, A.B.M.; Munoz-Perez, J.J.; Neves, M.G.; Sancho, F.; Cavique, R. Mechanics of the scouring and sinking of submerged structures in a mobile bed: A physical model study. Coast. Eng. 2016, 110, 50–63. [Google Scholar] [CrossRef]
- Chen, J.; Chen, X.; Zhao, W.; You, Y. Debris Flow Drainage Channel with Energy Dissipation Structures: Experimental Study and Engineering Application. J. Hydraul. Eng. 2018, 144, 06018012. [Google Scholar] [CrossRef]
- Ma, Z.Y.; Zhang, J.; Liao, H.J. Numerical simulation of viscous debris flow block engineering. Rock Soil Mech. 2007, 28, 389–392. [Google Scholar]
- Li, J.; Wang, X.; Ran, Y. Analysis on bearing performance of new-style steel-concrete combined dam under action of debris flow slurry. Chin. J. Geol. Hazard Control. 2016, 27, 85–94. [Google Scholar]
- Abdelrazek, A.M.; Kimura, I.; Shimizu, Y. Simulation of three-dimensional rapid free-surface granular flow past different types of obstructions using the SPH method. J. Glaciol. 2016, 62, 335–347. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Qiu, T. Numerical Simulations for Large Deformation of Granular Materials Using Smoothed Particle Hydrodynamics Method. Int. J. Geomech. 2012, 12, 127–135. [Google Scholar] [CrossRef]
- Bui, H.H.; Fukagawa, R.; Sako, K.; Ohno, S. Lagrangian meshfree particles method (SPH) for large deformation and failure flows of geomaterial using elastic-plastic soil constitutive model. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 1537–1570. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Choi, C.E.; Goodwin, G.R.; Cheung, W.W. Interaction between dry granular flow and deflectors. Landslides 2017, 14, 1375–1387. [Google Scholar] [CrossRef]
- He, X.; Liang, D.; Wu, W.; Cai, G.; Zhao, C.; Wang, S. Study of the interaction between dry granular flows and rigid barriers with an SPH model. Int. J. Numer. Anal. Methods Geomech. 2018, 42, 1217–1234. [Google Scholar] [CrossRef]
- Nohara, S.; Suenaga, H.; Nakamura, K. Large deformation simulations of geomaterials using moving particle semi-implicit method. J. Rock Mech. Geotech. Eng. 2018, 10, 1122–1132. [Google Scholar] [CrossRef]
- Wang, C.; Deng, A.; Taheri, A.; Ge, L. A Mesh-Free Approach for Multiscale Modeling in Continuum-Granular Systems. Int. J. Comput. Methods 2020, 17, 2050006. [Google Scholar] [CrossRef]
- Qin, X.; Hu, G.; Peng, G. Finite Point Method of Nonlinear Convection Diffusion Equation. Filomat 2020, 34, 1517–1533. [Google Scholar] [CrossRef]
- Li, S.; Peng, C.; Wu, W.; Wang, S.; Chen, X.; Chen, J.; Zhou, G.G.D.; Chitneedi, B.K. Role of baffle shape on debris flow impact in step-pool channel: An SPH study. Landslides 2020, 17, 2099–2111. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, W.; Xu, Q.; Xie, P.; Hao, L. Run-out analysis of flow-like landslides triggered by the Ms 8.0 2008 Wenchuan earthquake using smoothed particle hydrodynamics. Landslides 2012, 9, 275–283. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Kos, A.; Issa, N. Fluid motion generated by impact. J. Waterw. Port Coast. Ocean. Eng. 2003, 129, 250–259. [Google Scholar] [CrossRef]
- Pastor, M.; Yague, A.; Stickle, M.M.; Manzanal, D.; Mira, P. A two-phase SPH model for debris flow propagation. Int. J. Numer. Anal. Methods Geomech. 2018, 42, 418–448. [Google Scholar] [CrossRef]
- Wang, W.; Chen, G.; Han, Z.; Zhou, S.; Zhang, H.; Jing, P. 3D numerical simulation of debris-flow motion using SPH method incorporating non-Newtonian fluid behavior. Nat. Hazards 2016, 81, 1981–1998. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed Particle Hydrodynamics—Theory and Application to Non-spherical Stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Han, Z.; Su, B.; Li, Y.; Dou, J.; Wang, W.; Zhao, L. Modeling the progressive entrainment of bed sediment by viscous debris flows using the three-dimensional SC-HBP-SPH method. Water Res. 2020, 182, 116031. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.P.; He, S.M.; Fan, X.Y.; Tian, S.J.; Zhang, L.L.; Tian, W.G. The effect of particle size on the impact of rockfall debris on obstacles. J. Zhejiang Univ. Technol. 2016, 44, 222–225. [Google Scholar]
- Sheikh, B.; Qiu, T.; Ahmadipur, A. Comparison of SPH boundary approaches in simulating frictional soil-structure interaction. Acta Geotech. 2021, 16, 2389–2408. [Google Scholar] [CrossRef]
- Zhu, H.; Kim, Y.; De Kee, D. Non-Newtonian fluids with a yield stress. J. Non-Newton. Fluid Mech. 2005, 129, 177–181. [Google Scholar] [CrossRef]
- Monaghan, J.J. SPH without a tensile instability. J. Comput. Phys. 2000, 159, 290–311. [Google Scholar] [CrossRef]
- Bonet, J.; Lok, T.S.L. Variational and momentum preservation aspects of Smooth Particle Hydrodynamic formulations. Comput. Methods Appl. Mech. Eng. 1999, 180, 97–115. [Google Scholar] [CrossRef]
- Pastor, M.; Blanc, T.; Haddad, B.; Petrone, S.; Sanchez Morles, M.; Drempetic, V.; Issler, D.; Crosta, G.B.; Cascini, L.; Sorbino, G.; et al. Application of a SPH depth-integrated model to landslide run-out analysis. Landslides 2014, 11, 793–812. [Google Scholar] [CrossRef] [Green Version]
- McDougall, S.; Hungr, O. Dynamic modelling of entrainment in rapid landslides. Can. Geotech. J. 2005, 42, 1437–1448. [Google Scholar] [CrossRef]
- Dragoni, M.; Bonafede, M.; Boschi, E. Downslope flow models of a bingham liquid—Implications for lava flows. J. Volcanol. Geotherm. Res. 1986, 30, 305–325. [Google Scholar] [CrossRef]
- Kaitna, R.; Rickenmann, D.; Schatzmann, M. Experimental study on rheologic behaviour of debris flow material. Acta Geotech. 2007, 2, 71–85. [Google Scholar] [CrossRef]
- Dai, Z.; Huang, Y.; Cheng, H.; Xu, Q. 3D numerical modeling using smoothed particle hydrodynamics of flow-like landslide propagation triggered by the 2008 Wenchuan earthquake. Eng. Geol. 2014, 180, 21–33. [Google Scholar] [CrossRef]
- Bao, Y.; Huang, Y.; Liu, G.R.; Zeng, W. SPH Simulation of High-Volume Rapid Landslides Triggered by Earthquakes Based on a Unified Constitutive Model. Part II: Solid-Liquid-Like Phase Transition and Flow-Like Landslides. Int. J. Comput. Methods 2020, 17, 1850149. [Google Scholar] [CrossRef]
- Hübl, J.; Holzinger, G. Entwicklung von Grundlagen zur Dimensionierung Kronenoffener Bauwerke für die Geschiebebewirtschaftung in Wildbächen: Klassifikation von Wildbachsperren; WLS Report 50; Im Auftrag des BMLFUW VC 7a (Unveröffentlicht); Institut für Alpine Naturgefahren, Universität für Bodenkultur: Wien, Austria, 2003. [Google Scholar]
- Song, D.; Zhou, G.G.D.; Xu, M.; Choi, C.E.; Li, S.; Zheng, Y. Quantitative analysis of debris-flow flexible barrier capacity from momentum and energy perspectives. Eng. Geol. 2019, 251, 81–92. [Google Scholar] [CrossRef]
- Zhan, L.; Peng, C.; Zhang, B.; Wu, W. Three-dimensional modeling of granular flow impact on rigid and deformable structures. Comput. Geotech. 2019, 112, 257–271. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, B. Challenges and perspectives in designing engineering structures against debris-flow disaster. Eur. J. Environ. Civ. Eng. 2020, 8, 4126. [Google Scholar] [CrossRef]
- Sun, Q.; Jin, F.; Wang, G. The multiscale structure of dense granular matter. Mech. Eng. 2010, 32, 10–15. [Google Scholar]
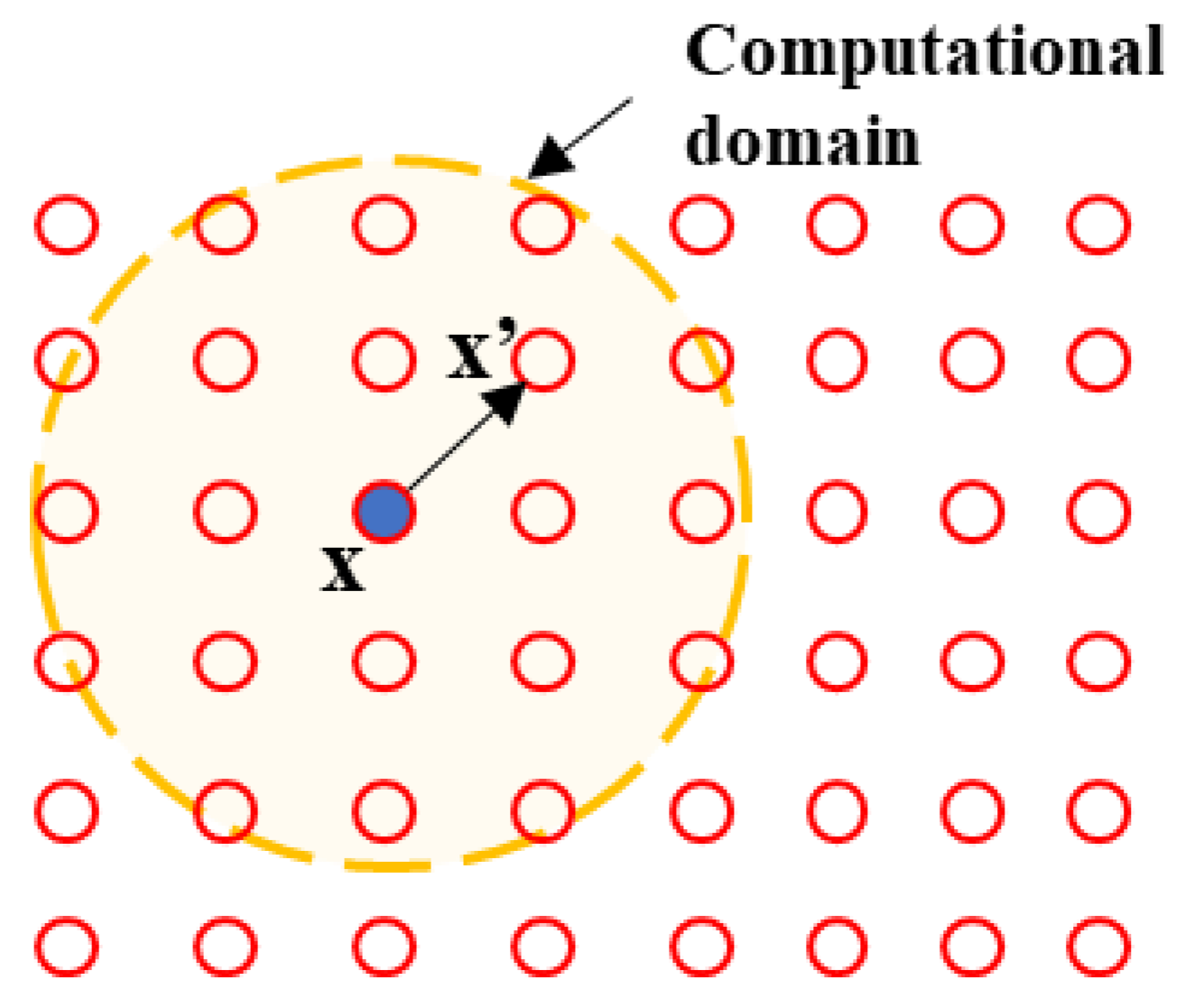
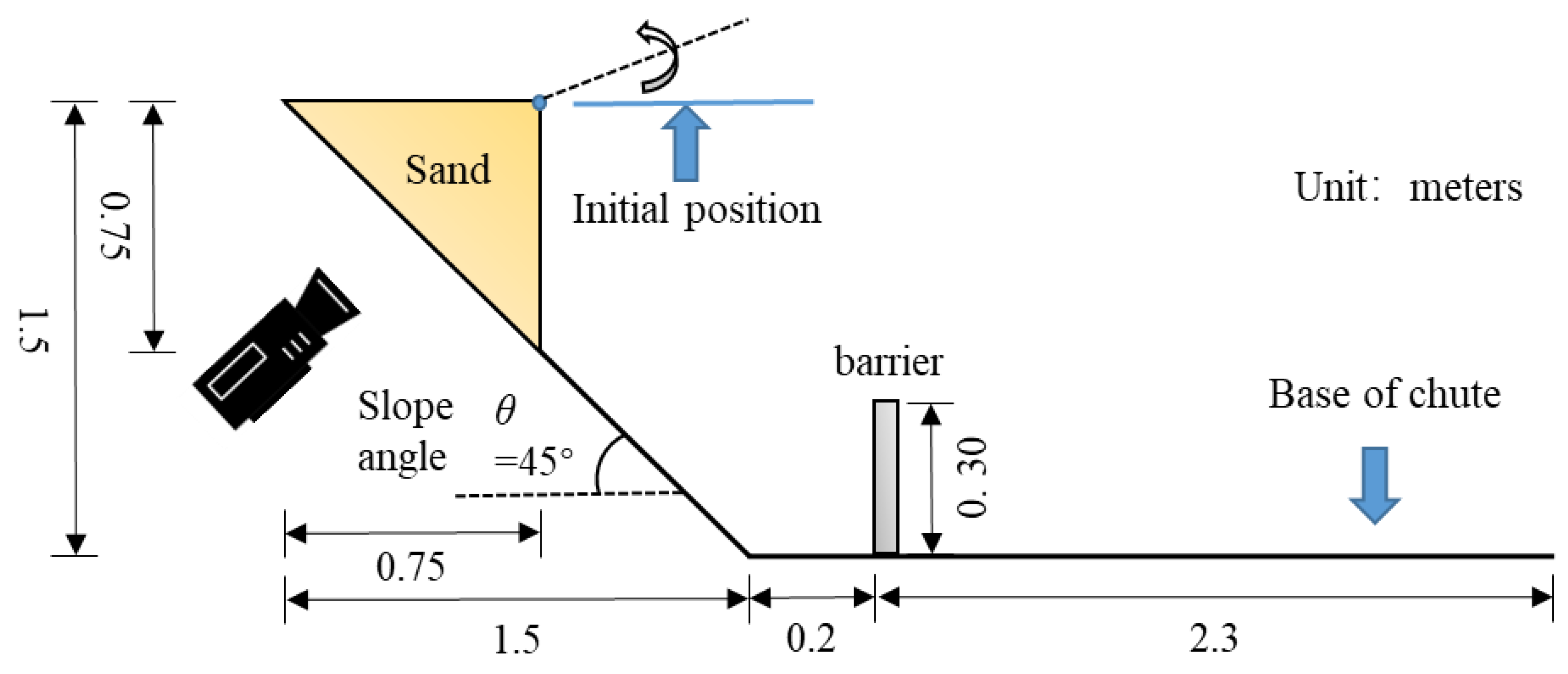

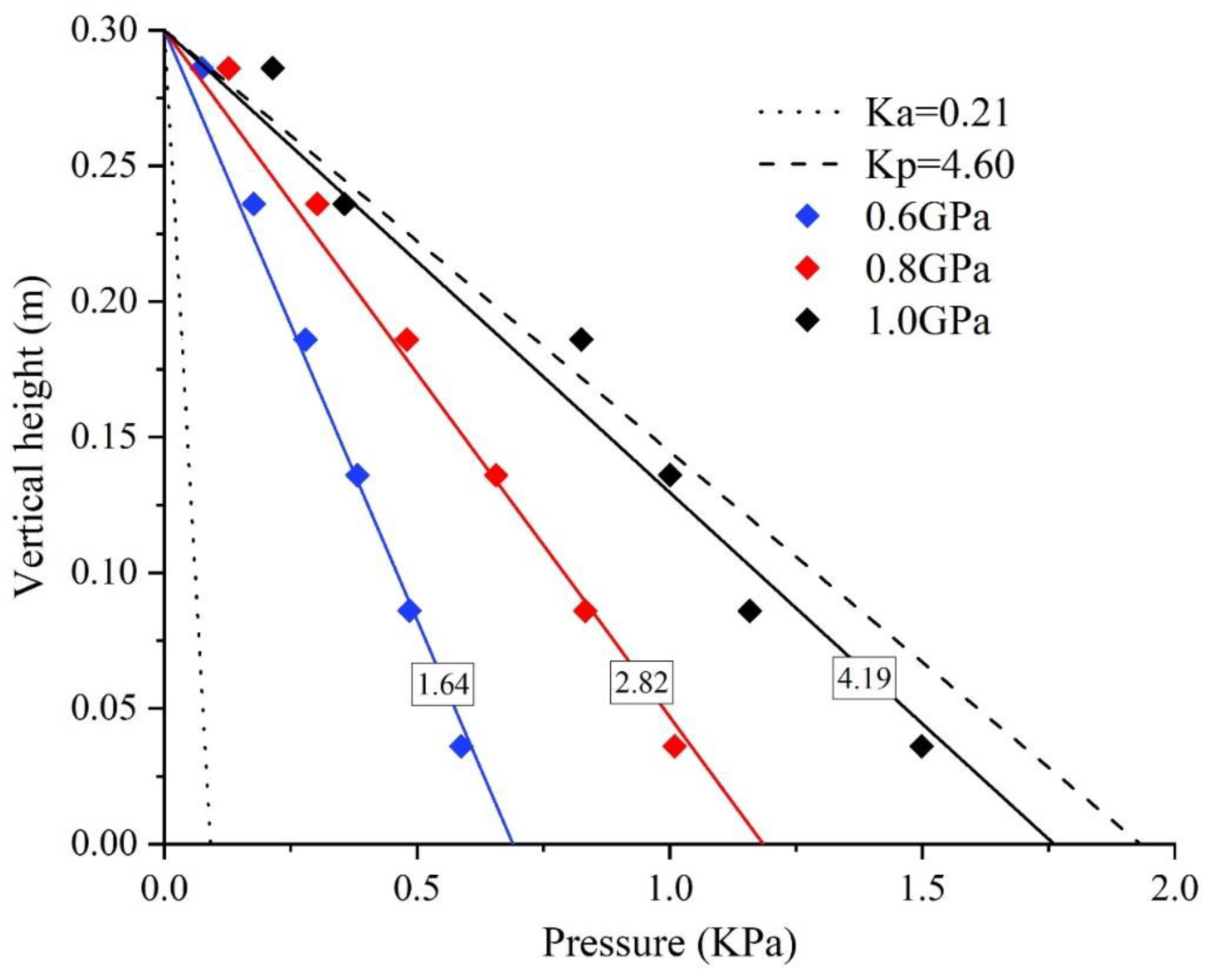
| Material Property | Parameters | |
|---|---|---|
| Bulk density | ρ (kg/m) | 1400 |
| Cohesion | c (kPa) | 0.0 |
| Internal friction angle | φ (°) | 34 |
| Equivalent viscosity | η (Pa·s) | 1.0 |
| Young’s modulus of sand | E (GPa) | 0.01 |
| Poisson’s ratio of sand | ν (\) | 0.25 |
| Poisson’s ratio of barrier | ν (\) | 0.30 |
| The initial distance | △r (m) | 0.01 |
| Unit time step | dt (s) | 2.0 × 10−6 |
| Test ID | Young’s Modulus/E | Initial Height of Sand |
|---|---|---|
| P_13/S_6 | 0.6 GPa | 1.3 m |
| P_14/S_6 | 1.4 m | |
| P_15/S_6 | 1.5 m | |
| P_16/S_6 | 1.6 m | |
| P_17/S_6 | 1.7 m | |
| P_13/S_8 | 0.8 GPa | 1.3 m |
| P_14/S_8 | 1.4 m | |
| P_15/S_8 | 1.5 m | |
| P_16/S_8 | 1.6 m | |
| P_17/S_8 | 1.7 m | |
| P_13/S_10 | 1.0 GPa | 1.3 m |
| P_14/S_10 | 1.4 m | |
| P_15/S_10 | 1.5 m | |
| P_16/S_10 | 1.6 m | |
| P_17/S_10 | 1.7 m |
| Test ID | The Peak Force | The Static Force |
|---|---|---|
| P_13/S_6 | 0.61 | 0.38 |
| P_13/S_8 | 0.71 | 0.46 |
| P_13/S_10 | 0.87 | 0.52 |
| P_14/S_6 | 0.67 | 0.36 |
| P_14/S_8 | 0.78 | 0.45 |
| P_14/S_10 | 0.95 | 0.53 |
| P_15/S_6 | 0.70 | 0.36 |
| P_15/S_8 | 0.82 | 0.47 |
| P_15/S_10 | 1 | 0.51 |
| P_16/S_6 | 0.84 | 0.38 |
| P_16/S_8 | 0.98 | 0.51 |
| P_16/S_10 | 1.18 | 0.54 |
| P_17/S_6 | 0.90 | 0.35 |
| P_17/S_8 | 1.04 | 0.40 |
| P_17/S_10 | 1.25 | 0.45 |
| Frontal Velocity Ratio ζ | Impact Force Ratio F/Fζ = 1.0 | Impact Force Ratio F/Fstatic | Impact Force Attenuation Percentage (%) |
|---|---|---|---|
| 0.76 | 0.87 | 1.67 | 25.85 |
| 0.88 | 0.95 | 1.78 | 27.82 |
| 1 | 1 | 1.94 | 29.56 |
| 1.06 | 1.18 | 2.17 | 33.78 |
| 1.15 | 1.25 | 2.77 | 35.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Jin, X.; Ji, J. Effects of Barrier Stiffness on Debris Flow Dynamic Impact—II: Numerical Simulation. Water 2022, 14, 182. https://doi.org/10.3390/w14020182
Huang Y, Jin X, Ji J. Effects of Barrier Stiffness on Debris Flow Dynamic Impact—II: Numerical Simulation. Water. 2022; 14(2):182. https://doi.org/10.3390/w14020182
Chicago/Turabian StyleHuang, Yu, Xiaoyan Jin, and Junji Ji. 2022. "Effects of Barrier Stiffness on Debris Flow Dynamic Impact—II: Numerical Simulation" Water 14, no. 2: 182. https://doi.org/10.3390/w14020182
APA StyleHuang, Y., Jin, X., & Ji, J. (2022). Effects of Barrier Stiffness on Debris Flow Dynamic Impact—II: Numerical Simulation. Water, 14(2), 182. https://doi.org/10.3390/w14020182







