Effects of Barrier Stiffness on Debris Flow Dynamic Impact—I: Laboratory Flume Test
Abstract
:1. Introduction
2. Laboratory Flume Test
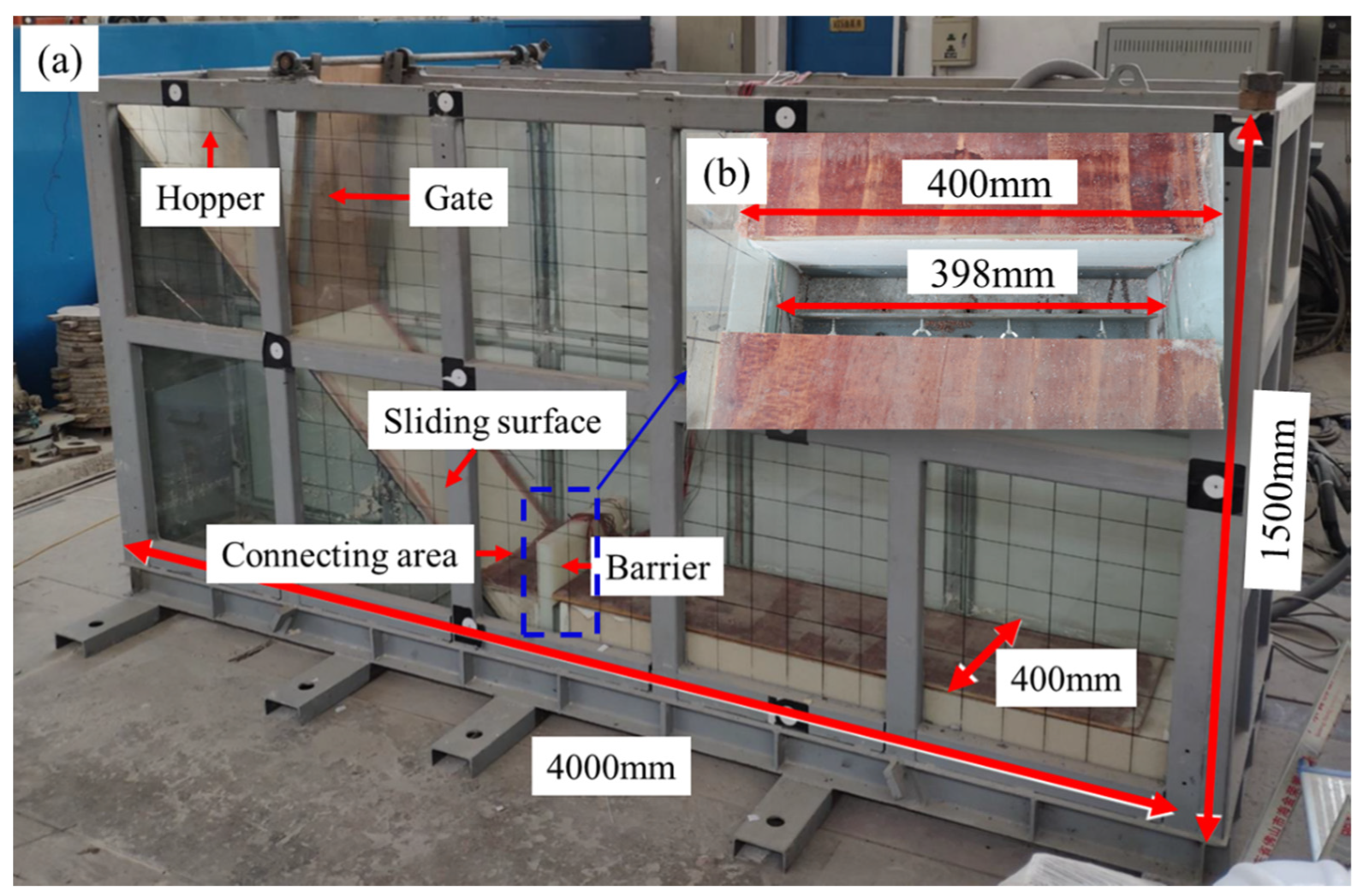
2.1. Flume Modelling
2.2. Parameters of Barrier Design
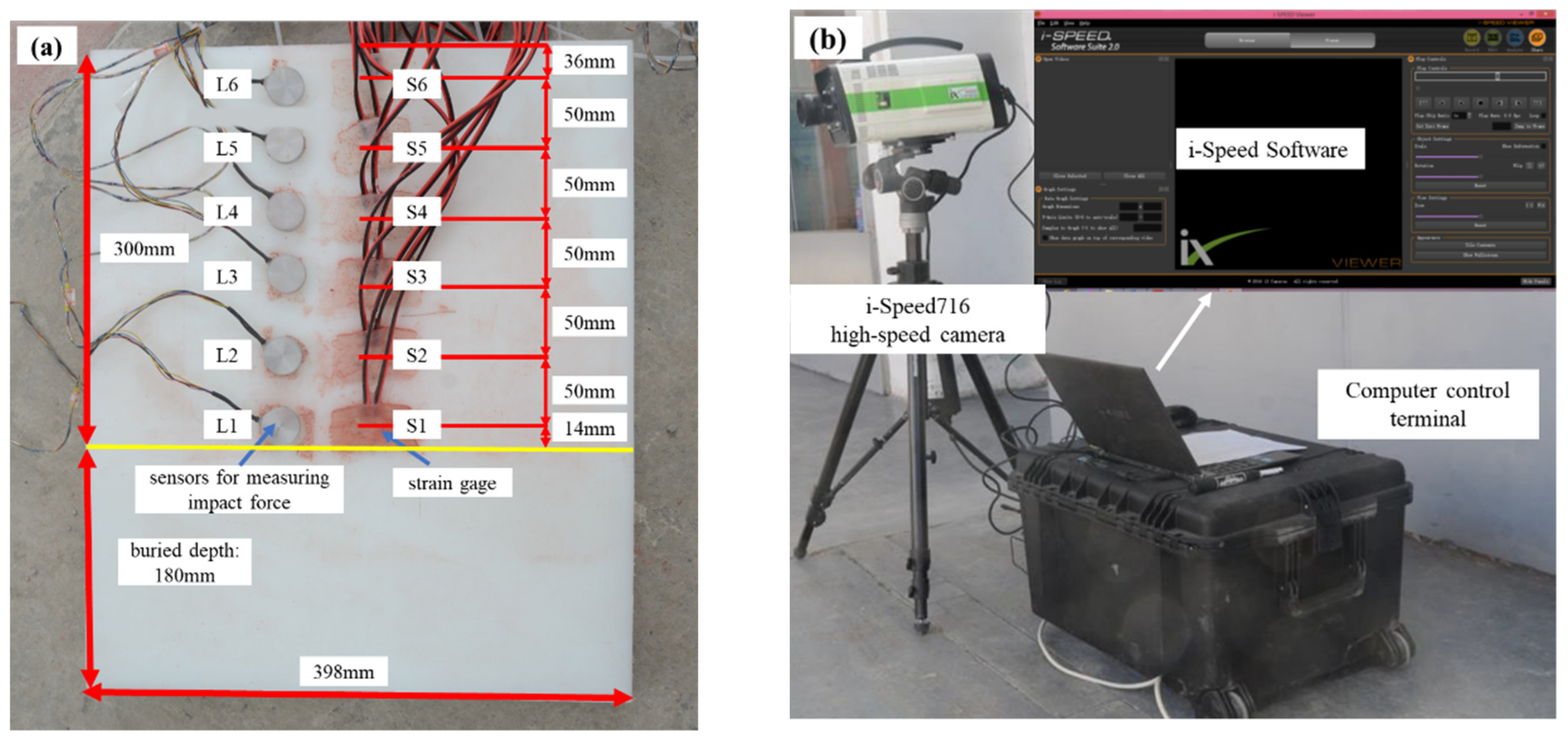
2.3. Instrumentation
- High resolution pixel sensor: 2048 × 1536
- 7540 fps @ 1080 p
- Ultra-high speed 16 GP/sec data bandwidth
- Maximum frame rate: 500,000 fps
- Frame synchronization: 24 Hz–500 kHz
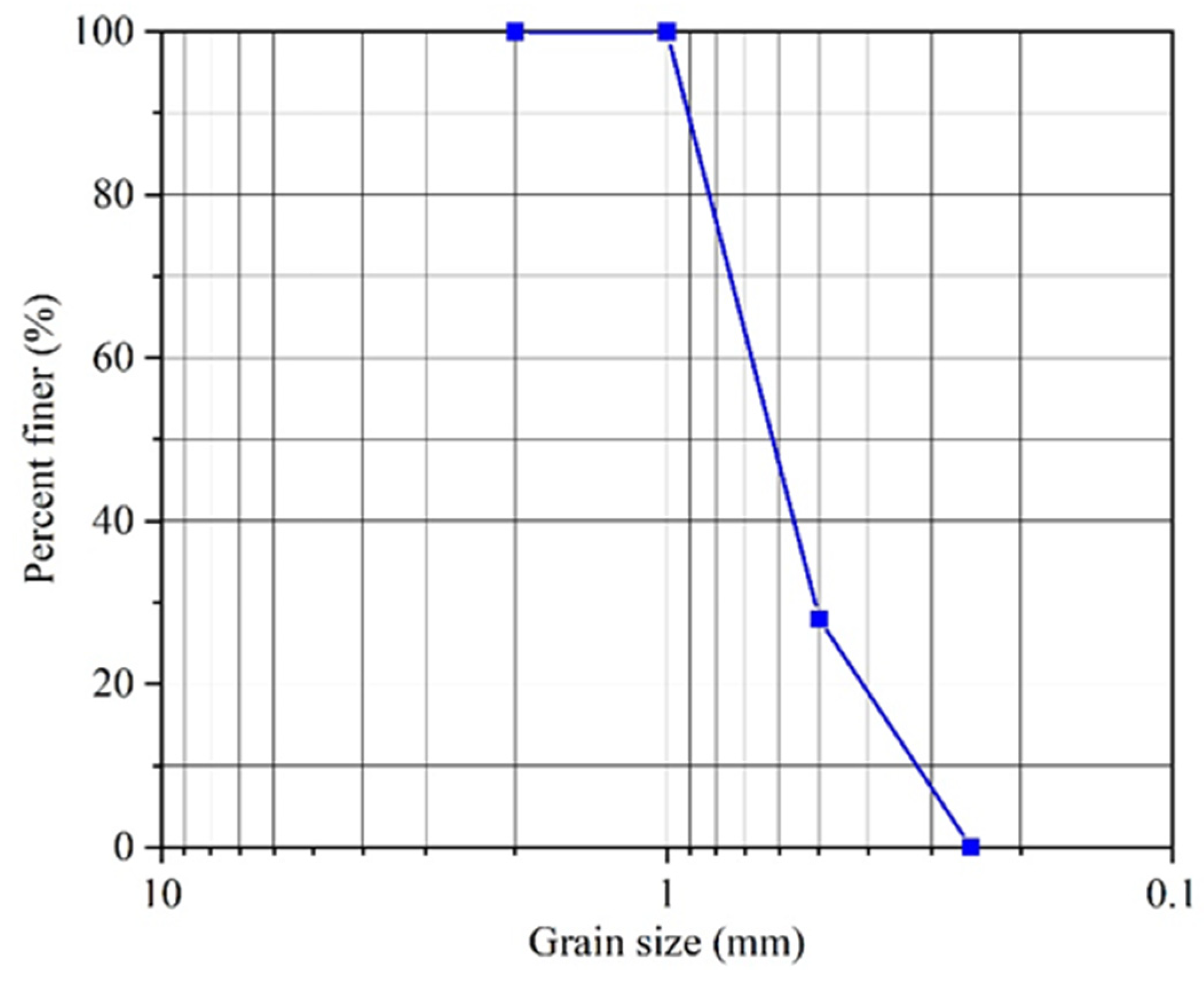
2.4. Test Materials and Scheme
3. Debris Flow Velocity Measurements and Impact Signal Processing
4. Interpretation of Test Results
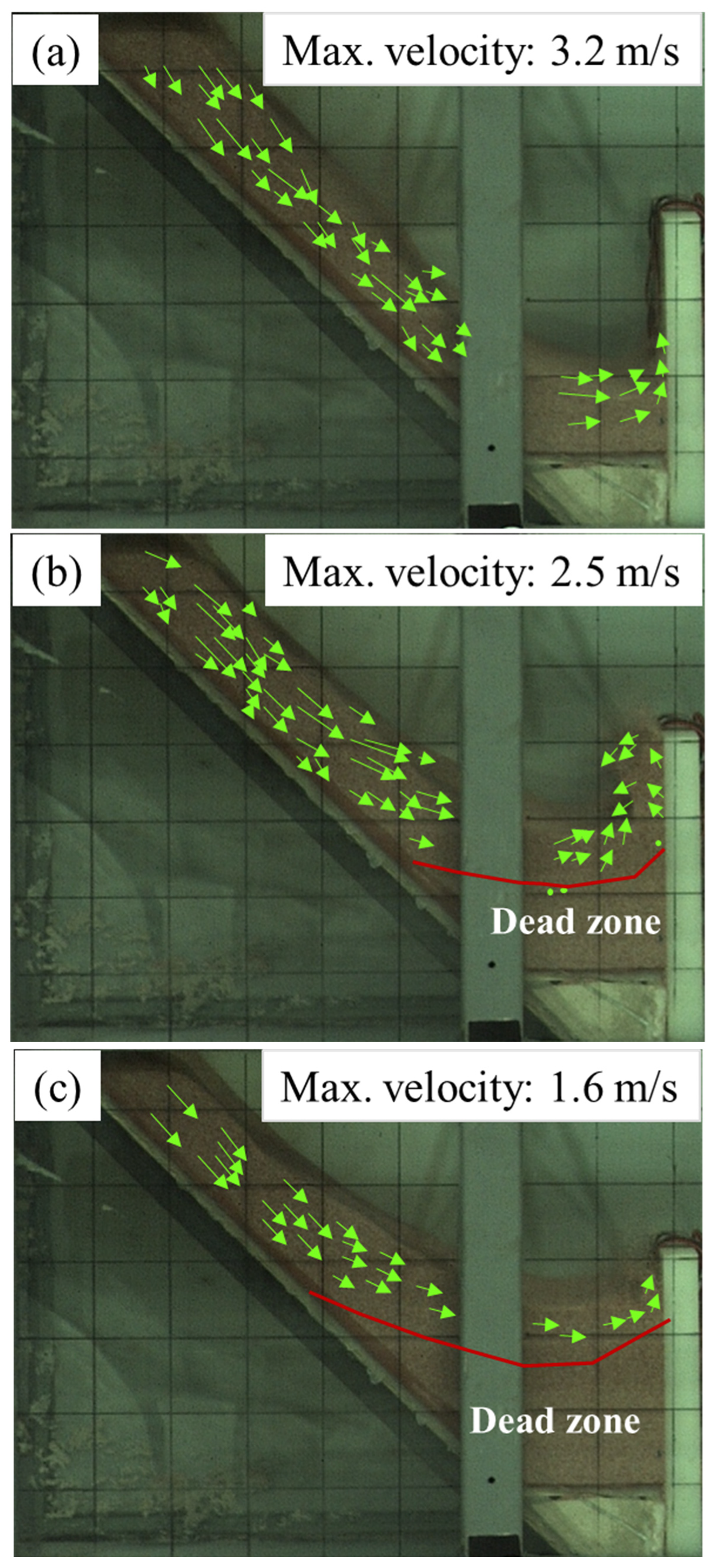
4.1. Observed Debris Flow Impact Kinematics
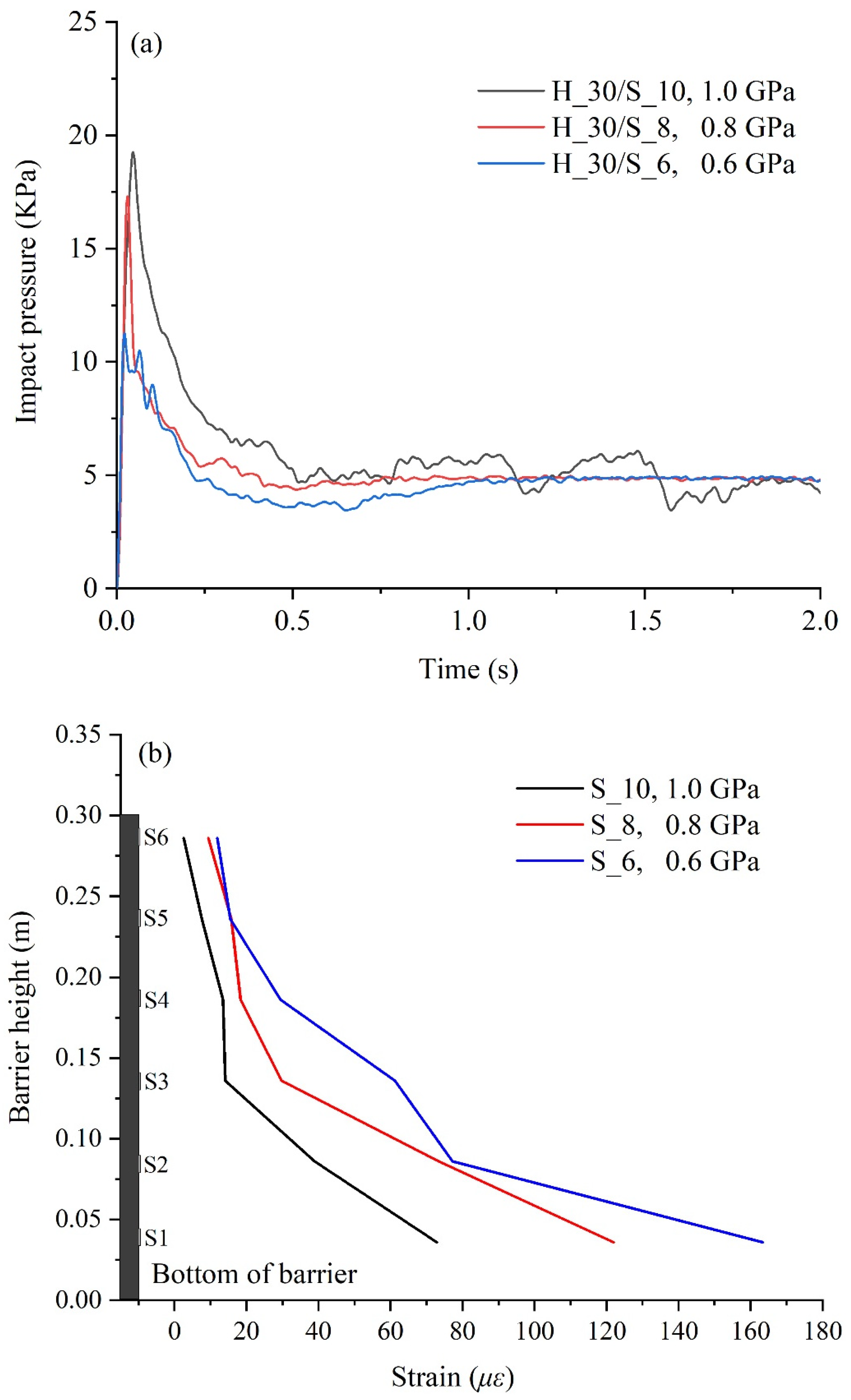
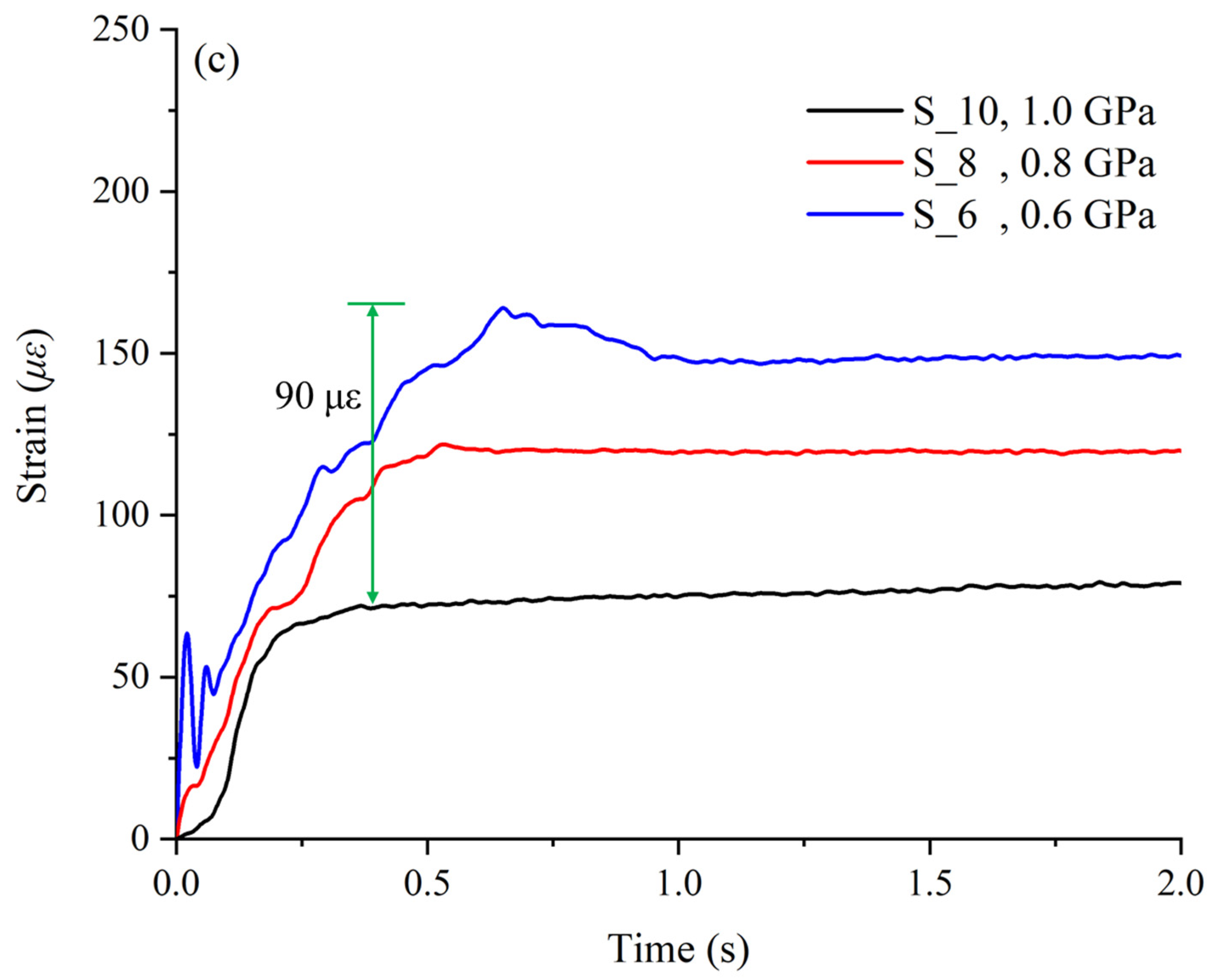
4.2. Effects of Barrier Stiffness on Peak Impact
5. Discussion
6. Conclusions
- (1)
- The flow kinematics of debris flow observed under three barrier stiffness values are essentially consistent with the impact–run-up–falling–pile-up process. The development of a dead zone provided a cushion that diminished the impact of the follow-up debris flow on the barrier.
- (2)
- The respective peak impact force evolved strongly with the barrier stiffness. The peak impact forces attenuated with the decrease of the barrier stiffness, which is attributed to the barrier deformation playing a buffer role in flow–structure interaction with lower stiffness.
- (3)
- Notably, even the slight deflections of the deformable barrier were sufficient for peak load attenuation by up to 30%. As the barrier stiffness decreased, the recoverable elastic strain became larger and the strain peak was more obvious when the debris flow made impact.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Moriguchi, S.; Borja, R.I.; Yashima, A.; Sawada, K. Estimating the impact force generated by granular flow on a rigid obstruction. Acta Geotech. 2009, 4, 57–71. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, B.; Zhu, C. Computational assessment of baffle performance against rapid granular flows. Landslides 2021, 18, 485–501. [Google Scholar] [CrossRef]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Dowling, C.A.; Santi, P.M. Debris flows and their toll on human life: A global analysis of debris-flow fatalities from 1950 to 2011. Nat. Hazards 2014, 71, 203–227. [Google Scholar] [CrossRef]
- Xu, Q.; Li, W.; Dong, X.; Xiao, X.; Fan, X.; Pei, X. The Xinmocun landslide on 24 June 2017 in Maoxian, Sichuan: Characteristics and failure mechanism. Chin. J. Rock Mech. Eng. 2017, 36, 2612–2628. [Google Scholar]
- Tang, C.; van Asch, T.W.J.; Chang, M.; Chen, G.Q.; Zhao, X.H.; Huang, X.C. Catastrophic debris flows on 13 August 2010 in the Qingping area, southwestern China: The combined effects of a strong earthquake and subsequent rainstorms. Geomorphology 2012, 139–140, 559–576. [Google Scholar] [CrossRef]
- Abdelrazek, A.M.; Kimura, I.; Shimizu, Y. Simulation of three-dimensional rapid free-surface granular flow past different types of obstructions using the SPH method. J. Glaciol. 2016, 62, 335–347. [Google Scholar] [CrossRef] [Green Version]
- Armanini, A.; Rossi, G.; Larcher, M. Dynamic impact of a water and sediments surge against a rigid wall. J. Hydraul. Res. 2020, 58, 314–325. [Google Scholar] [CrossRef] [Green Version]
- Bi, Y.-Z.; He, S.-M.; Li, X.-P.; Wu, Y.; Xu, Q.; Ouyang, C.-J.; Su, L.-J.; Wang, H. Geo-engineered buffer capacity of two-layered absorbing system under the impact of rock avalanches based on Discrete Element Method. J. Mt. Sci. 2016, 13, 917–929. [Google Scholar] [CrossRef]
- Chen, H.-X.; Li, J.; Feng, S.-J.; Gao, H.-Y.; Zhang, D.-M. Simulation of interactions between debris flow and check dams on three-dimensional terrain. Eng. Geol. 2019, 251, 48–62. [Google Scholar] [CrossRef]
- Jiang, Y.-J.; Fan, X.-Y.; Li, T.-H.; Xiao, S.-Y. Influence of particle-size segregation on the impact of dry granular flow. Powder Technol. 2018, 340, 39–51. [Google Scholar] [CrossRef]
- Naaim, M.; Faug, T.; Naaim, F.; Eckert, N. Return period calculation and passive structure design at the Taconnaz avalanche path, France. Ann. Glaciol. 2010, 51, 89–97. [Google Scholar] [CrossRef] [Green Version]
- Ng, C.W.W.; Choi, C.E.; Liu, L.H.D.; Wang, Y.; Song, D.; Yang, N. Influence of particle size on the mechanism of dry granular run-up on a rigid barrier. Géotech. Lett. 2017, 7, 79–89. [Google Scholar] [CrossRef]
- Remaitre, A.; van Asch, T.W.J.; Malet, J.P.; Maquaire, O. Influence of check dams on debris-flow run-out intensity. Nat. Hazards Earth Syst. Sci. 2008, 8, 1403–1416. [Google Scholar] [CrossRef]
- Shen, W.; Wang, D.; Qu, H.; Li, T. The effect of check dams on the dynamic and bed entrainment processes of debris flows. Landslides 2019, 16, 2201–2217. [Google Scholar] [CrossRef]
- Shen, W.; Zhao, T.; Zhao, J.; Dai, F.; Zhou, G.G.D. Quantifying the impact of dry debris flow against a rigid barrier by DEM analyses. Eng. Geol. 2018, 241, 86–96. [Google Scholar] [CrossRef]
- Song, D.; Ng, C.W.W.; Choi, C.E.; Zhou, G.G.D.; Kwan, J.S.H.; Koo, R.C.H. Influence of debris flow solid fraction on rigid barrier impact. Can. Geotech. J. 2017, 54, 1421–1434. [Google Scholar] [CrossRef] [Green Version]
- Teufelsbauer, H.; Wang, Y.; Chiou, M.-C.; Wu, W. Flow–obstacle interaction in rapid granular avalanches: DEM simulation and comparison with experiment. Granul. Matter 2009, 11, 209–220. [Google Scholar] [CrossRef]
- Teufelsbauer, H.; Wang, Y.; Pudasaini, S.P.; Borja, R.I.; Wu, W. DEM simulation of impact force exerted by granular flow on rigid structures. Acta Geotech. 2011, 6, 119–133. [Google Scholar] [CrossRef]
- Zhou, G.G.D.; Song, D.; Choi, C.E.; Pasuto, A.; Sun, Q.C.; Dai, D.F. Surge impact behavior of granular flows: Effects of water content. Landslides 2018, 15, 695–709. [Google Scholar] [CrossRef]
- Dai, Z.; Huang, Y.; Cheng, H.; Xu, Q. SPH model for fluid–structure interaction and its application to debris flow impact estimation. Landslides 2017, 14, 917–928. [Google Scholar] [CrossRef]
- Khan-Mozahedy, A.B.M.; Muñoz-Perez, J.J.; Neves, M.G.; Sancho, F.; Cavique, R. Mechanics of the scouring and sinking of submerged structures in a mobile bed: A physical model study. Coast. Eng. 2016, 110, 50–63. [Google Scholar] [CrossRef]
- Chen, J.; Chen, X.; Zhao, W.; You, Y. Debris Flow Drainage Channel with Energy Dissipation Structures: Experimental Study and Engineering Application. J. Hydraul. Eng. 2018, 144, 06018012. [Google Scholar] [CrossRef]
- Nohara, S.; Suenaga, H.; Nakamura, K. Large deformation simulations of geomaterials using moving particle semi-implicit method. J. Rock Mech. Geotech. Eng. 2018, 10, 1122–1132. [Google Scholar] [CrossRef]
- Wang, C.; Deng, A.; Taheri, A.; Ge, L. A Mesh-Free Approach for Multiscale Modeling in Continuum–Granular Systems. Int. J. Comput. Methods 2020, 17, 2050006. [Google Scholar] [CrossRef]
- Qin, X.; Hu, G.; Peng, G. Finite point method of nonlinear convection diffusion equation. Filomat 2020, 34, 1517–1533. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, W.; Xu, Q.; Xie, P.; Hao, L. Run-out analysis of flow-like landslides triggered by the Ms 8.0 2008 Wenchuan earthquake using smoothed particle hydrodynamics. Landslides 2012, 9, 275–283. [Google Scholar] [CrossRef]
- Li, S.; Peng, C.; Wu, W.; Wang, S.; Chen, X.; Chen, J.; Zhou, G.G.; Chitneedi, B.K. Role of baffle shape on debris flow impact in step-pool channel: An SPH study. Landslides 2020, 17, 2099–2111. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Kos, A.; Issa, N. Fluid Motion Generated by Impact. J. Waterw. Port Coast. Ocean Eng. 2003, 129, 250–259. [Google Scholar] [CrossRef]
- Pastor, M.; Yague, A.; Stickle, M.M.; Manzanal, D.; Mira, P. A two-phase SPH model for debris flow propagation. Int. J. Numer. Anal. Methods Géoméch. 2018, 42, 418–448. [Google Scholar] [CrossRef]
- Wang, W.; Chen, G.; Han, Z.; Zhou, S.; Zhang, H.; Jing, P. 3D numerical simulation of debris-flow motion using SPH method incorporating non-Newtonian fluid behavior. Nat. Hazards 2016, 81, 1981–1998. [Google Scholar] [CrossRef]
- Huang, Y.; Jin, X.Y.; Ji, J.J. Effects of barrier stiffness on debris flow dynamic impact–II: Numerical simulation. Water, in press.
- Scheidl, C.; Chiari, M.; Kaitna, R.; Müllegger, M.; Krawtschuk, A.; Zimmermann, T.; Proske, D. Analysing Debris-Flow Impact Models, Based on a Small Scale Modelling Approach. Surv. Geophys. 2013, 34, 121–140. [Google Scholar] [CrossRef] [Green Version]
- Laigle, D.; Lachamp, P.; Naaim, M. SPH-based numerical investigation of mudflow and other complex fluid flow interactions with structures. Comput. Geosci. 2007, 11, 297–306. [Google Scholar] [CrossRef]
- Cui, P.; Zeng, C.; Lei, Y. Experimental analysis on the impact force of viscous debris flow. Earth Surf. Process. Landf. 2015, 40, 1644–1655. [Google Scholar] [CrossRef] [Green Version]
- Bugnion, L.; McArdell, B.W.; Bartelt, P.; Wendeler, C. Measurements of hillslope debris flow impact pressure on obstacles. Landslides 2012, 9, 179–187. [Google Scholar] [CrossRef] [Green Version]
- Kwan, J.S.H.; Chan, S.L.; Cheuk, J.C.Y.; Koo, R.C.H. A case study on an open hillside landslide impacting on a flexible rockfall barrier at Jordan Valley, Hong Kong. Landslides 2014, 11, 1037–1050. [Google Scholar] [CrossRef]
- He, S.; Wu, Y.; Shen, J. Simplified calculation of impact force of massive stone in debris flow. J. Nat. Disasters 2009, 18, 51–56. [Google Scholar]
- Ashwood, W.; Hungr, O. Estimating total resisting force in flexible barrier impacted by a granular avalanche using physical and numerical modeling. Can. Geotech. J. 2016, 53, 1700–1717. [Google Scholar] [CrossRef]
- Rickenmann, D. Empirical Relationships for Debris Flows. Nat. Hazards 1999, 19, 47–77. [Google Scholar] [CrossRef]
- Adrian, R.J. Particle-imaging techniques for experimental fluid-mechanics. Annu. Rev. Fluid Mech. 1991, 23, 261–304. [Google Scholar] [CrossRef]
- White, D.J.; Take, W.A.; Bolton, M.D. Soil deformation measurement using particle image velocimetry (PIV) and photogrammetry. Geotechnique 2003, 53, 619–631. [Google Scholar] [CrossRef]
- Keane, R.D.; Adrian, R.J. Theory of cross-correlation analysis of PIV images. Appl. Sci. Res. 1992, 49, 191–215. [Google Scholar] [CrossRef]
- Utami, T.; Blackwelder, R.F.; Ueno, T. A cross-correlation technique for velocity field extraction from particulate visualization. Exp. Fluids 1991, 10, 213–223. [Google Scholar] [CrossRef]
- Abdolmaleki, M.; Tabaei, M.; Fathianpour, N.; Gorte, B.G.H. Selecting optimum base wavelet for extracting spectral alteration features associated with porphyry copper mineralization using hyperspectral images. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 134–144. [Google Scholar] [CrossRef]
- Song, D.; Zhou, G.G.D.; Xu, M.; Choi, C.E.; Li, S.; Zheng, Y. Quantitative analysis of debris-flow flexible barrier capacity from momentum and energy perspectives. Eng. Geol. 2019, 251, 81–92. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Wang, C.; Choi, C.E.; De Silva, W.A.R.K.; Poudyal, S. Effects of barrier deformability on load reduction and energy dissipation of granular flow impact. Comput. Geotech. 2020, 121, 103445. [Google Scholar] [CrossRef]
- Zhang, B.; Huang, Y. Unsteady overflow behavior of polydisperse granular flows against closed type barrier. Eng. Geol. 2021, 280, 105959. [Google Scholar] [CrossRef]
- Jiang, Y.-J.; Zhao, Y.; Towhata, I.; Liu, D.-X. Influence of particle characteristics on impact event of dry granular flow. Powder Technol. 2015, 270, 53–67. [Google Scholar] [CrossRef]
- Song, D.; Choi, C.E.; Zhou, G.G.D.; Kwan, J.S.H.; Sze, H.Y. Impulse load characteristics of bouldery debris flow impact. Géotech. Lett. 2018, 8, 111–117. [Google Scholar] [CrossRef]
- Choi, C.E.; Au-Yeung, S.C.H.; Ng, C.W.W.; Song, D. Flume investigation of landslide granular debris and water runup mechanisms. Géotech. Lett. 2015, 5, 28–32. [Google Scholar] [CrossRef]
- Song, D.; Choi, C.E.; Ng, C.W.W.; Zhou, G.G.D. Geophysical flows impacting a flexible barrier: Effects of solid-fluid interaction. Landslides 2018, 15, 99–110. [Google Scholar] [CrossRef]
- Zhou, G.G.D.; Cui, K.F.E.; Jing, L.; Zhao, T.; Song, D.; Huang, Y. Particle Size Segregation in Granular Mass Flows With Different Ambient Fluids. J. Geophys. Res. Solid Earth 2020, 125, e2020JB019536. [Google Scholar] [CrossRef]
| Barrier Materials | Barrier Height (H: mm) | Young’s Modulus (E: GPa) | Poisson’s Ratio (υ: \) | Test ID |
|---|---|---|---|---|
| Low-density polyethylene (LDPE) | 300 | 0.6 | 0.30 | S_6 |
| High-density polyethylene (HDPE) | 300 | 0.8 | 0.30 | S_8 |
| Polypropylene (PP) | 300 | 1.0 | 0.30 | S_10 |
| Material Property | Parameters | |
|---|---|---|
| Maximum grain size | d (mm) | 1.00 |
| Medium grain size | d (mm) | 0.50 |
| Minimum grain size | d (mm) | 0.25 |
| Coefficient of uniformity | 2.3 | |
| Maximum dry density | γmax (g/cm3) | 1.53 |
| Minimum dry density | γmin (g/cm3) | 1.32 |
| Bulk density | γ (g/cm3) | 1.40 |
| Cohesion | c (kPa) | 0.0 |
| Angle of internal friction | φ (°) | 34 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Jin, X.; Ji, J. Effects of Barrier Stiffness on Debris Flow Dynamic Impact—I: Laboratory Flume Test. Water 2022, 14, 177. https://doi.org/10.3390/w14020177
Huang Y, Jin X, Ji J. Effects of Barrier Stiffness on Debris Flow Dynamic Impact—I: Laboratory Flume Test. Water. 2022; 14(2):177. https://doi.org/10.3390/w14020177
Chicago/Turabian StyleHuang, Yu, Xiaoyan Jin, and Junji Ji. 2022. "Effects of Barrier Stiffness on Debris Flow Dynamic Impact—I: Laboratory Flume Test" Water 14, no. 2: 177. https://doi.org/10.3390/w14020177
APA StyleHuang, Y., Jin, X., & Ji, J. (2022). Effects of Barrier Stiffness on Debris Flow Dynamic Impact—I: Laboratory Flume Test. Water, 14(2), 177. https://doi.org/10.3390/w14020177