Pressure Sensor Placement in Water Supply Network Based on Graph Neural Network Clustering Method
Abstract
:1. Introduction
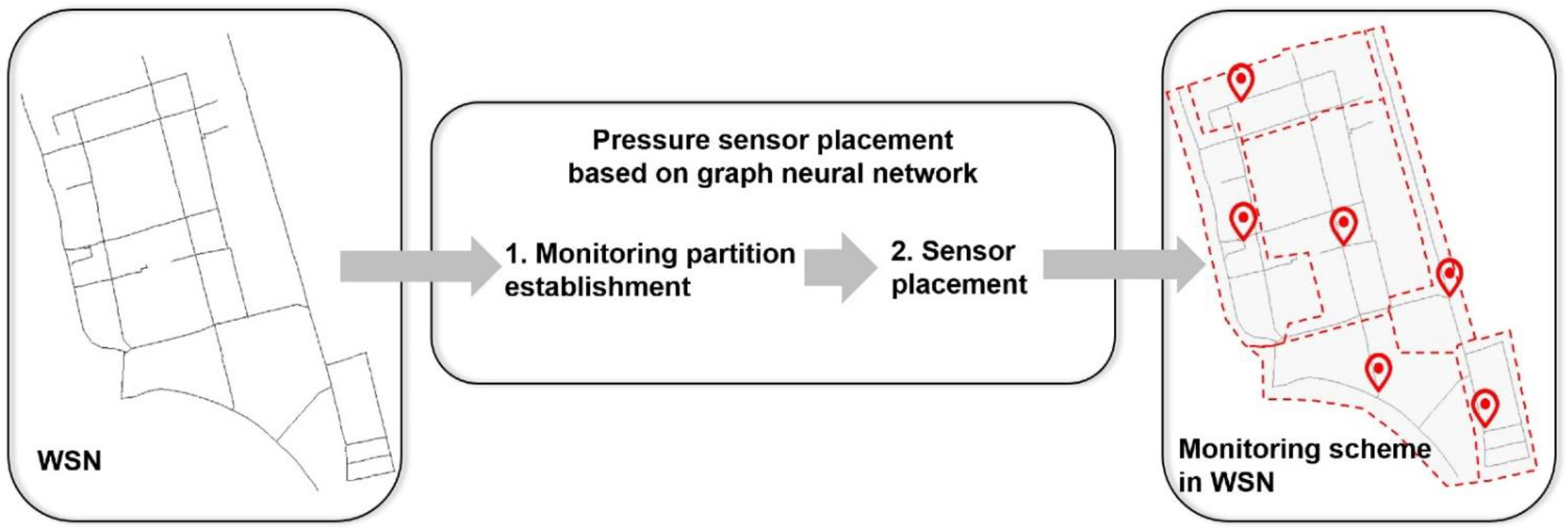
2. Methodology
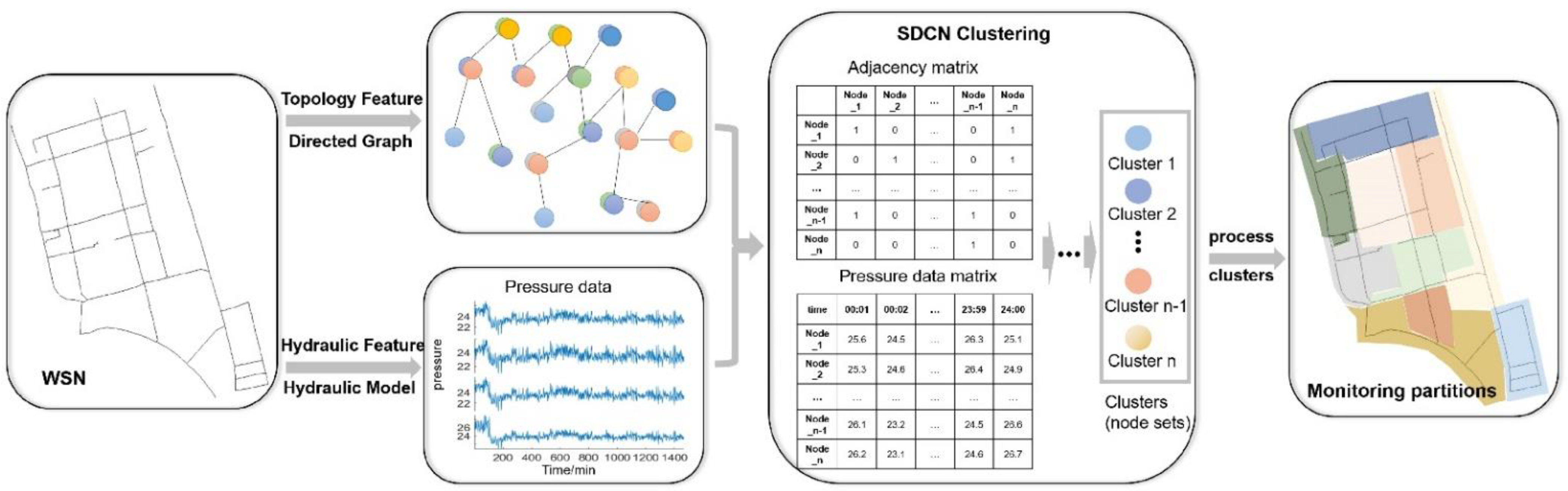
2.1. Monitoring Partition Establishment of WSNs
- (1)
- Hydraulic characteristics and topological characteristics
- (2)
- Node clustering with SDCN algorithm
- (3)
- Monitoring partitions
| Algorithm1 Monitoring partition establishment |
| Input: WDN’s graph G, SDCN’s clusters , ProNodes×n Output: optimized clusters 1: S = {} 2: for do 3: 4: S append 5: end 6: repeat 7: for do 8: for do 9: if {, node} is connected graph do 10: append node 11: break 12: end 13: end 14: end 15: until S is empty 16: return |
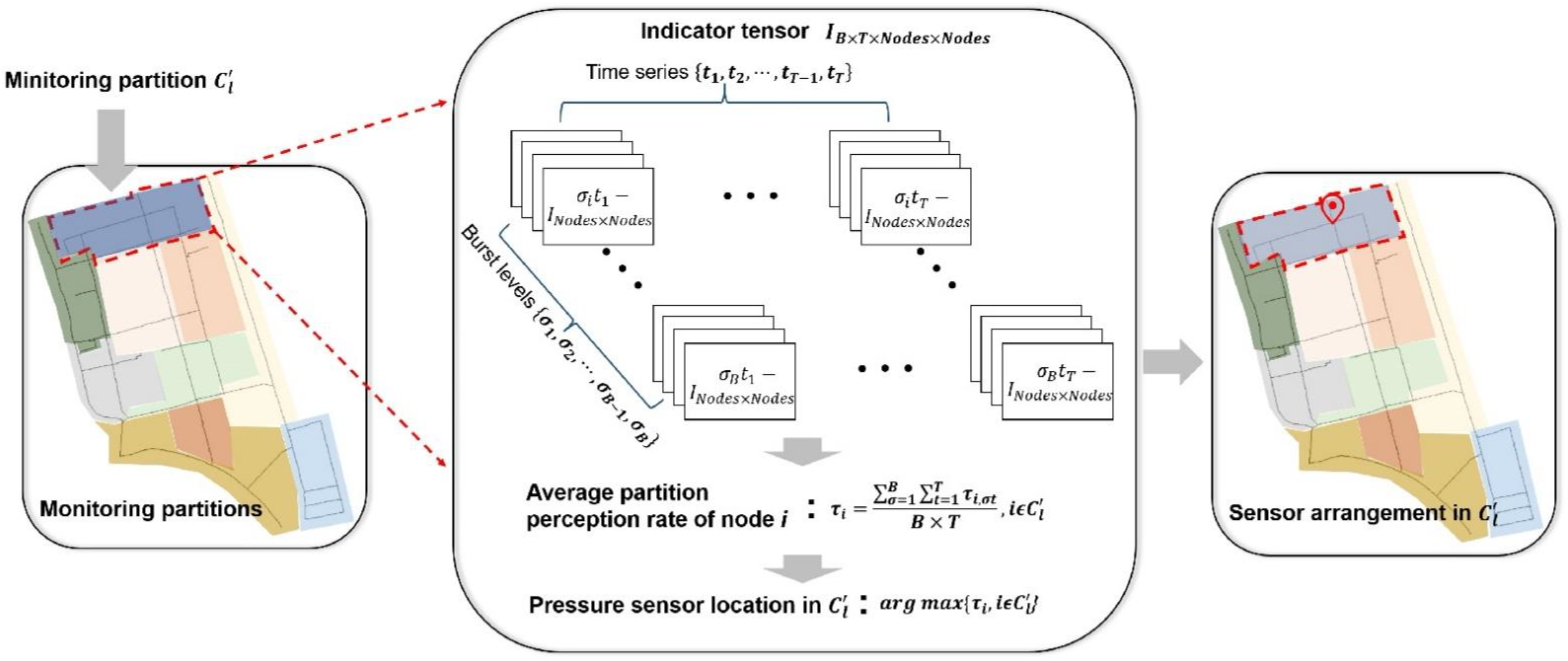
2.2. Pressure Sensor Arrangement
- (1)
- Pipe bursting simulation
- (2)
- Indicator tensor
- (a)
- Pressure threshold:
- (b)
- Perception node:
- (c)
- Indicator matrix:
- (d)
- Indicator tensor:
- (3)
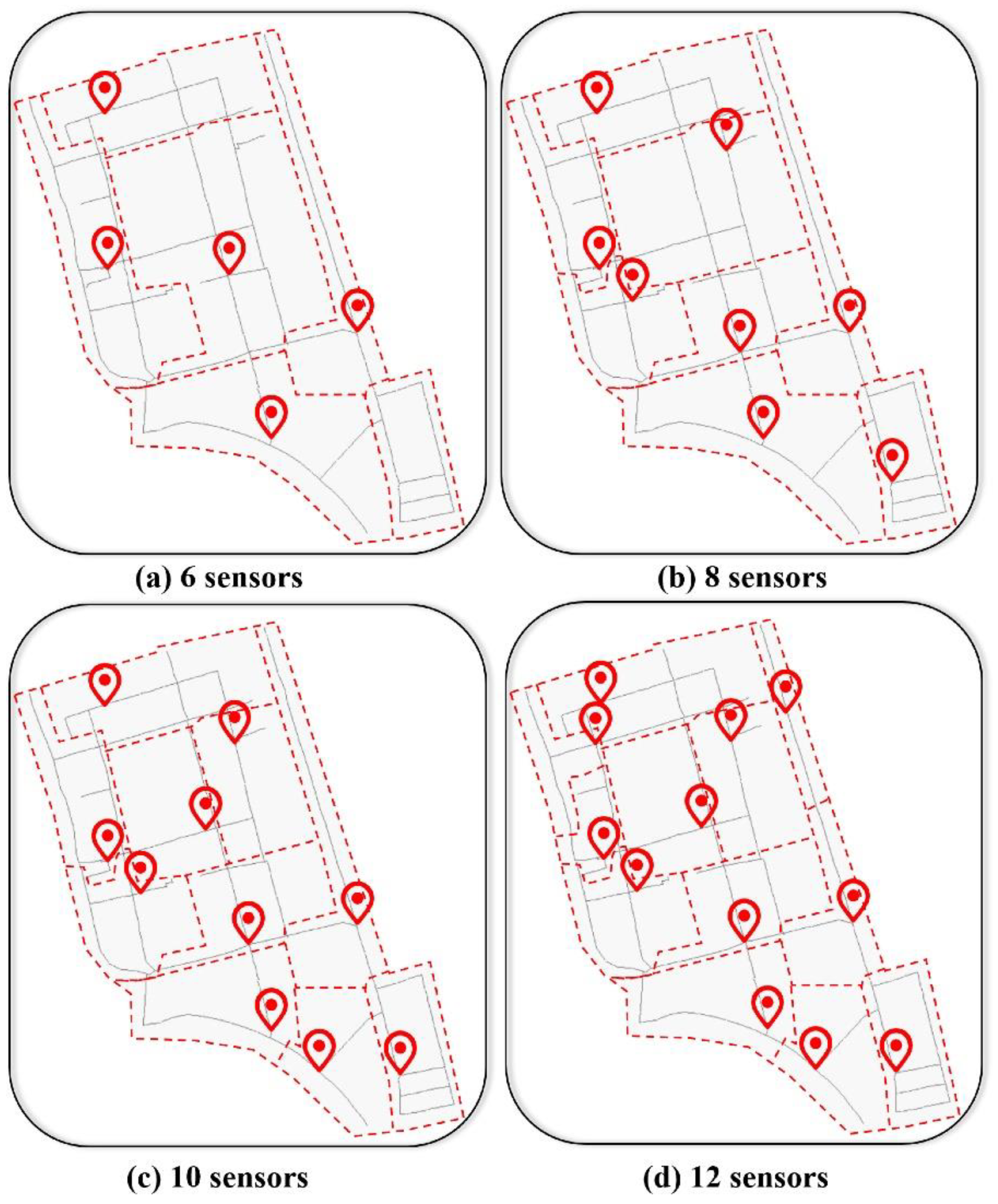
- Pressure sensor arrangement
3. Case Studies
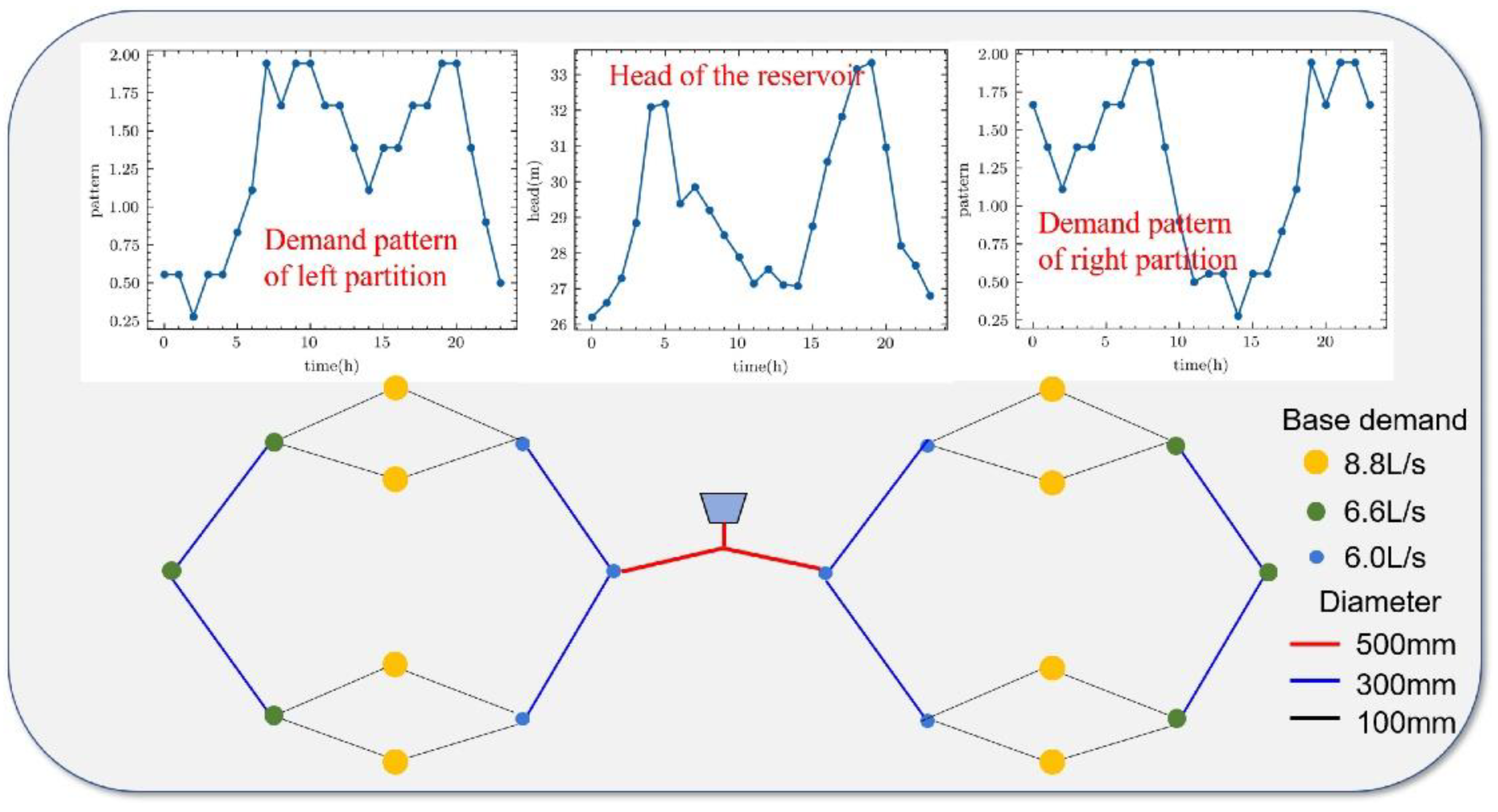
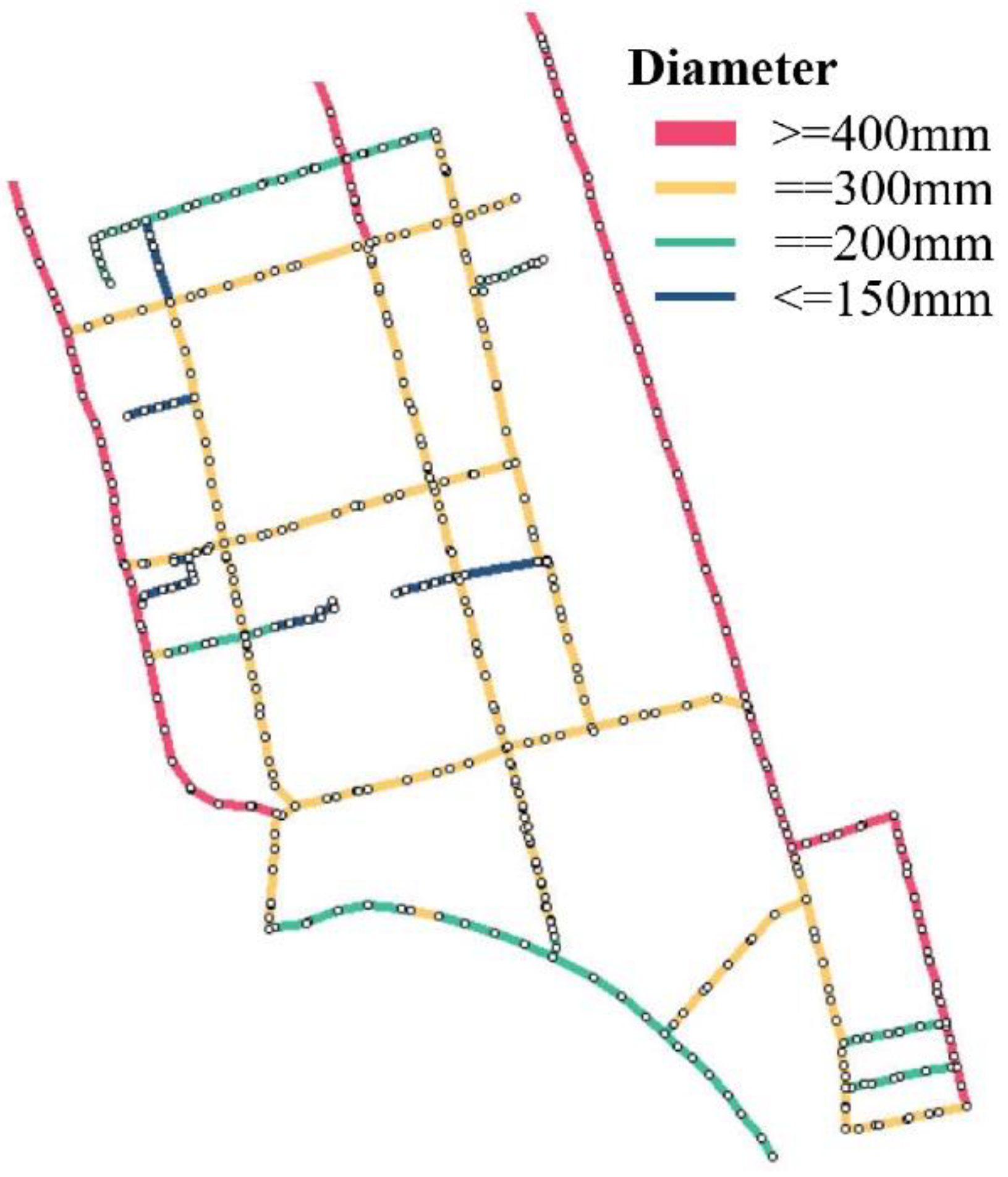
3.1. Case 1
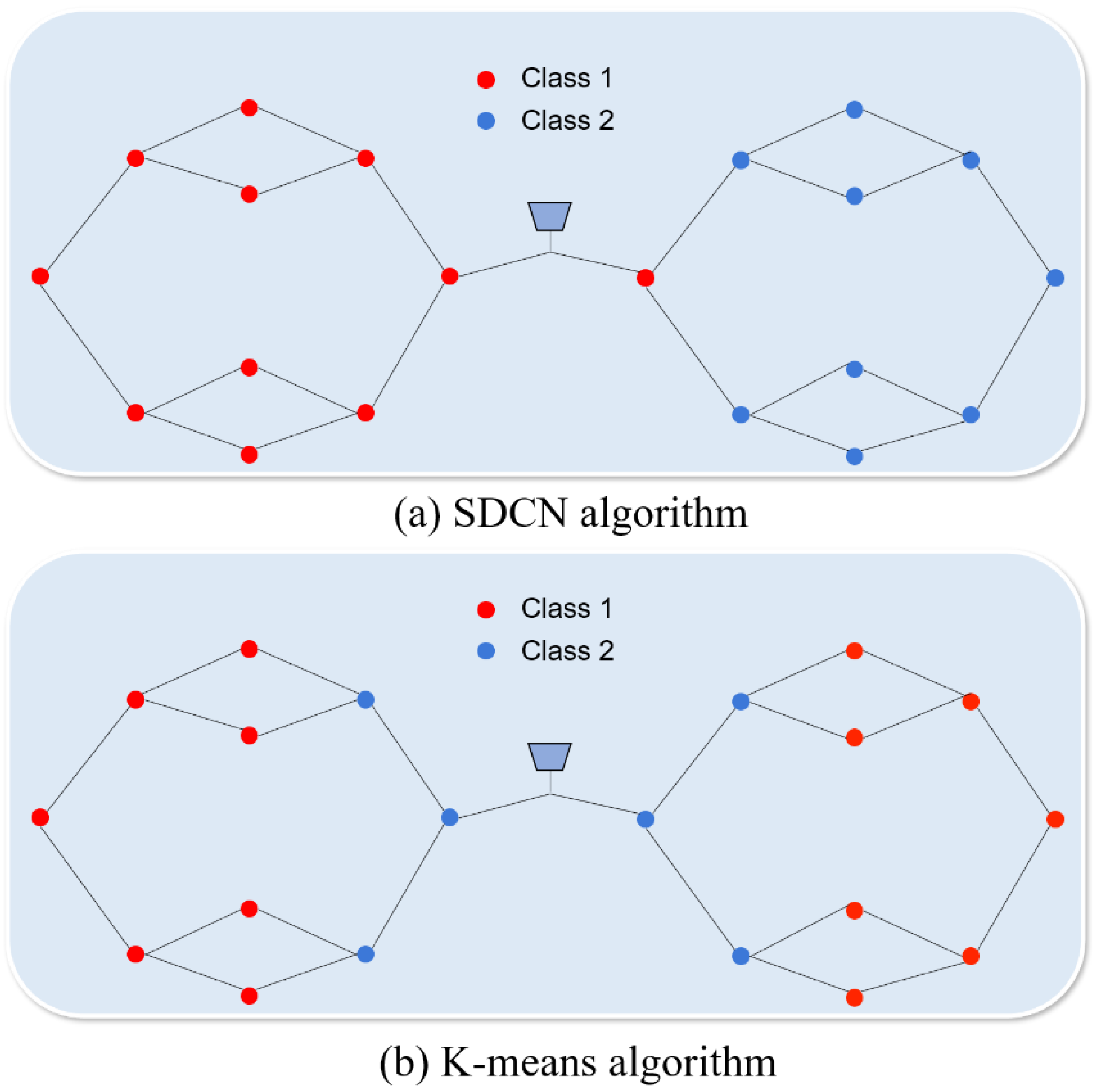
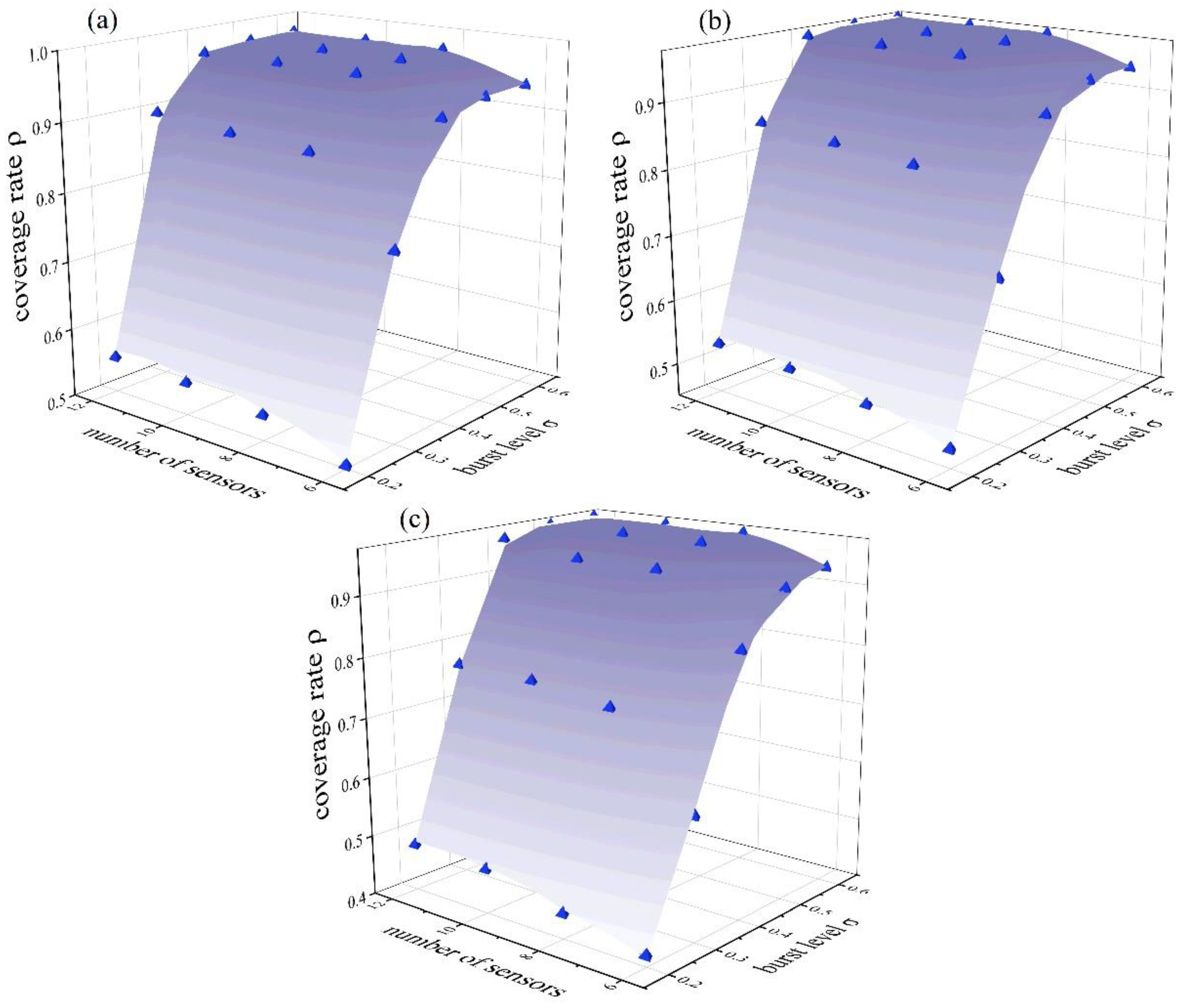
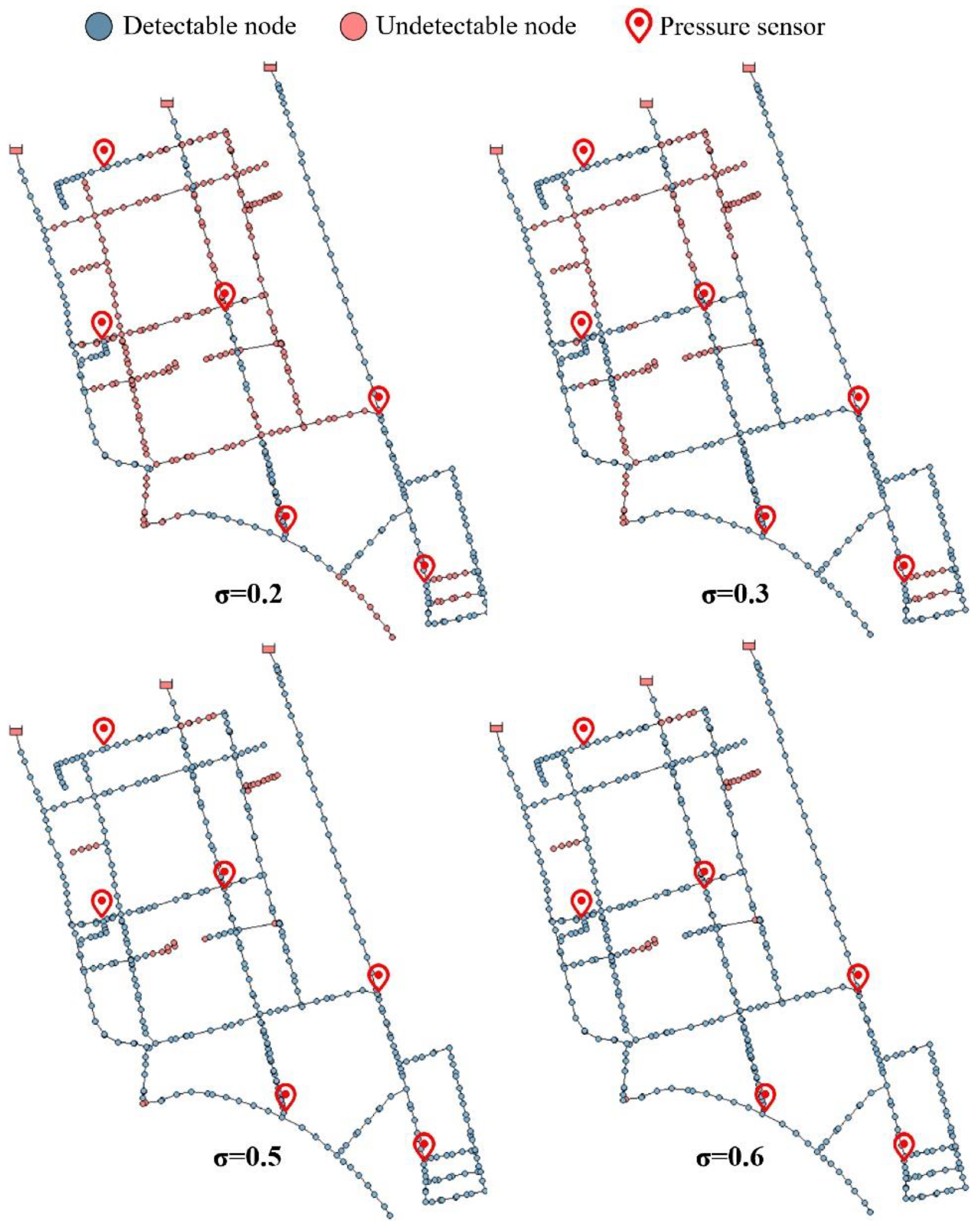
3.2. Case 2
- (1)
- Proposed method
- (2)
- K-means Clustering method
- (3)
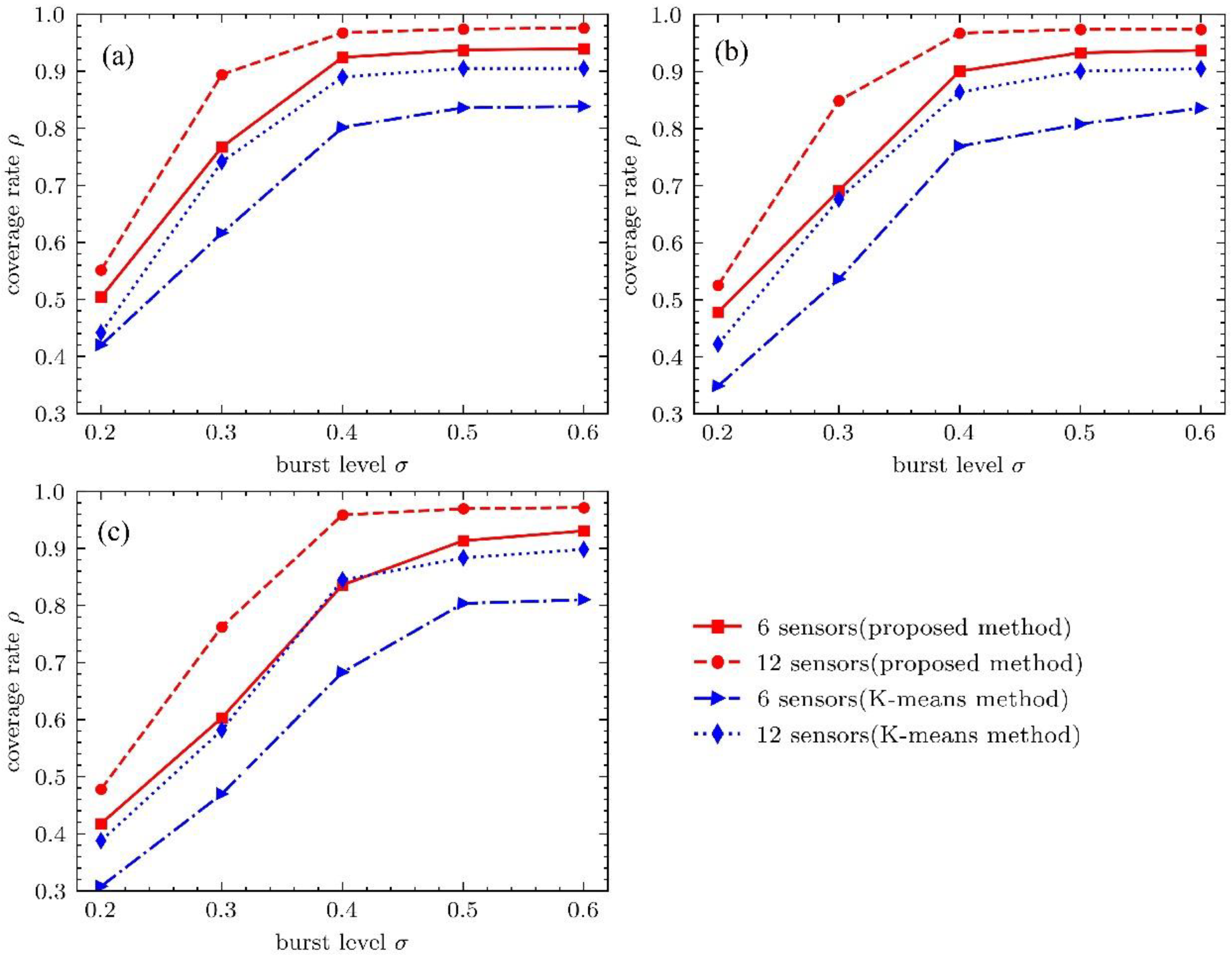
- Comparison and analysis of results
- (4)
- Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Azevedo, B.; Saurin, T.A. Losses in Water Distribution Systems: A Complexity Theory Perspective. Water Resour. Manag. 2018, 32, 1–18. [Google Scholar] [CrossRef]
- Frances-Chust, J.; Brentan, B.M.; Carpitella, S.; Izquierdo, J.; Montalvo, I. Optimal Placement of Pressure Sensors Using Fuzzy DEMATEL-Based Sensor Influence. Water 2020, 12, 493. [Google Scholar] [CrossRef] [Green Version]
- Meier, R.W.; Barkdoll, B.D. Sampling design for network model calibration using genetic algorithms. J. Water Resour. Plan. Manag. 2000, 126, 245–250. [Google Scholar] [CrossRef]
- Deschaetzen, W.; Walters, G.A.; Savic, D.A. Optimal sampling design for model calibration using shortest path, genetic and entropy algorithms. Urban Water 2000, 2, 141–152. [Google Scholar] [CrossRef]
- Kang, D.; Pasha, M.; Lansey, K. Approximate methods for uncertainty analysis of water distribution systems. Urban Water J. 2009, 6, 233–249. [Google Scholar] [CrossRef]
- Kang, D.; Lansey, K. Optimal Meter Placement for Water Distribution System State Estimation. J. Water Resour. Plan. Manag. 2010, 136, 337–347. [Google Scholar] [CrossRef]
- Zhou, X.; Tang, Z.; Xu, W.; Meng, F.; Chu, X.; Xin, K.; Fu, G. Deep learning identifies accurate burst locations in water distribution networks. Water Res. 2019, 166, 115058. [Google Scholar] [CrossRef]
- Cheng, W.; Chen, Y.; Xu, G. Optimizing Sensor Placement and Quantity for Pipe Burst Detection in a Water Distribution Network. J. Water Resour. Plan. Manag. 2020, 146, 04020088. [Google Scholar] [CrossRef]
- Sousa, J.; Ribeiro, L.; Muranho, J.; Marques, A.S. Locating Leaks in Water Distribution Networks with Simulated Annealing and Graph Theory. Procedia Eng. 2015, 119, 63–71. [Google Scholar] [CrossRef] [Green Version]
- Afsar, M.M.; Tayarani-N, M.-H. Clustering in sensor networks: A literature survey. J. Netw. Comput. Appl. 2014, 46, 198–226. [Google Scholar] [CrossRef]
- Jun, S.; Kwon, H.J. The Optimum Monitoring Location of Pressure in Water Distribution System. Water 2019, 11, 307. [Google Scholar] [CrossRef] [Green Version]
- Starczewska, D.; Collins, R.; Boxall, J. Transient Behavior in Complex Distribution Network: A Case Study. Procedia Eng. 2014, 70, 1582–1591. [Google Scholar] [CrossRef] [Green Version]
- Cheng, L.; Du, K.; Tu, J.P.; Dong, W.X. Optimal Placement of Pressure Sensors in Water Distribution System Based on Clustering Analysis of Pressure Sensitive Matrix. Procedia Eng. 2017, 186, 405–411. [Google Scholar] [CrossRef]
- Likas, A.; Vlassis, N.; Verbeek, J.J. The global k-means clustering algorithm. Pattern Recognit. 2003, 36, 451–461. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Liu, S.; Wu, X.; Liu, Y.; Guan, Y. Burst detection in district metering areas using a data driven clustering algorithm. Water Res. 2016, 100, 28–37. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Sun, H. Optimal Algorithm of Pressure Measurement Node Layout in Water Distribution Network. J. Beijing Inst. Civ. Eng. Archit. 2005, 21, 51–54. [Google Scholar]
- Dong, L.; Xue, H.; Zhang, W. Optimal layout method of water pressure monitoring points for water supply network based on fault diagnosis. J. Civ. Archit. Environ. Eng. 2018, 40, 53–61. [Google Scholar]
- Farley, B.; Mounce, S.; Boxall, J. Field testing of an optimal sensor placement methodology for event detection in an urban water distribution network. Urban Water J. 2010, 7, 345–356. [Google Scholar] [CrossRef]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How powerful are graph neural networks? arXiv 2018, arXiv:1810.00826. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bo, D.; Wang, X.; Shi, C.; Zhu, M.; Lu, E.; Cui, P. Structural deep clustering network. In Proceedings of the Web Conference, Taipei, Taiwan, 20–24 April 2020; pp. 1400–1410. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Atwood, J.; Towsley, D. Diffusion-convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 1993–2001. [Google Scholar]
- Wagner, J.M.; Shamir, U.; Marks, D.H. Water distribution reliability: Simulation methods. J. Water Resour. Plan. Manag. 1988, 114, 276–294. [Google Scholar] [CrossRef] [Green Version]
- Kittel, T.; Heitzig, J.; Webster, K.; Kurths, J. Timing of transients: Quantifying reaching times and transient behavior in complex systems. New J. Phys. 2017, 19, 83005. [Google Scholar] [CrossRef]
- He, P.; Tao, T.; Xin, K.; Li, S.; Yan, H. Modelling Water Distribution Systems with Deficient Pressure: An Improved Iterative Methodology. Water Resour. Manag. 2016, 30, 593–606. [Google Scholar] [CrossRef]
- Lambert, A. What do we know about pressure: Leakage relationships in distribution systems? In Proceedings of the IWA System Approach to Leakage Control and Water Distribution Systems Management, Brno, Czech Republic, 16–18 May 2001. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, S.; Cheng, J.; Wu, X.; Fang, X.; Wu, Q. Pressure Sensor Placement in Water Supply Network Based on Graph Neural Network Clustering Method. Water 2022, 14, 150. https://doi.org/10.3390/w14020150
Peng S, Cheng J, Wu X, Fang X, Wu Q. Pressure Sensor Placement in Water Supply Network Based on Graph Neural Network Clustering Method. Water. 2022; 14(2):150. https://doi.org/10.3390/w14020150
Chicago/Turabian StylePeng, Sen, Jing Cheng, Xingqi Wu, Xu Fang, and Qing Wu. 2022. "Pressure Sensor Placement in Water Supply Network Based on Graph Neural Network Clustering Method" Water 14, no. 2: 150. https://doi.org/10.3390/w14020150






