Abstract
Empirical formulas to estimate the radius of influence, such as the Sichardt formula, occasionally appear in studies assessing the environmental impact of groundwater extractions. As they are inconsistent with fundamental hydrogeological principles, the term “radius of influence myth” is used by analogy with the water budget myth. Alternative formulations based on the well-known de Glee and Theis equations are presented, and the contested formula that estimates the radius of influence by balancing pumping and infiltration rate is derived from an asymptotic solution of an analytical model developed by Ernst in 1971. The transient state solution of this model is developed applying the Laplace transform, and it is verified against the finite-difference solution. Examining drawdown and total storage change reveals the relations between the presented one-dimensional radial flow solutions. The assumptions underlying these solutions are discussed in detail to show their limitations and to refute misunderstandings about their applicability. The discussed analytical models and the formulas derived from it to estimate the radius of influence cannot be regarded as substitutes for advanced modeling, although they offer valuable insights on relevant parameter combinations.
1. Introduction
This paper stems from our concern about the use of empirical formulas to assess the impact of groundwater extractions. Zhai et al. [1] give an overview of different empirical relations that are in use. This study focuses on the formula of Sichardt as it is frequently applied by groundwater consultants in Flanders and the Netherlands to estimate the radius of influence in case of pumping or dewatering [2,3,4,5,6,7]. Since the formula and its variants are recommended in many textbooks on geotechnical engineering [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22] and applied in dewatering and groundwater studies published in peer-reviewed journals [23,24,25,26,27,28,29,30,31,32], we may conclude its use is worldwide, although some researchers advise against it [1,33,34,35].
The formula was published first by Kyrieleis and Sichardt in 1930 [36], but they mention Sichardt as the discoverer, unfortunately without citation. Some authors refer to [37], and although the problem concerning the radius of influence is addressed in Sichardt’s dissertation, the formula itself is not given. Cashman and Preene [21] state that the formula was based on earlier work by Weber, but they give no references. According to Narasimhan [38], Weber [39] made the first successful attempt to analyze non-steady flow towards a well. However, it is not clear if Sichardt was inspired by this work, as the Sichardt equation holds for steady state conditions [36]. In many cases, however, the Sichardt formula [36] is applied without citation, which may indicate it has become a standard tool in dewatering studies.
Since empirical formulas such as the Sichardt equation [36] are widely used, yet not in agreement with some of the fundamental principles of groundwater flow [1], we consider the term “radius of influence myth” well placed by analogy with the groundwater budget myth introduced by Bredehoeft et al. [40] and revisited by Bredehoeft [41]. The main objective of this paper is to debunk the myth and to present alternative formulas that are consistent with fundamental laws and principles applied in hydrogeology. In fact, the work of Bredehoeft et al. [40] and Bredehoeft [41] is highly relevant, as it addresses sustainable groundwater development and brings up the fundamental hydrological principles that were stated first by Theis in 1940 [42] and revisited recently by Konikow and Leake [43]. According to Theis [42], the essential factors controlling the response of an aquifer system to pumping are (1) the distance to, and character of the recharge, (2) the distance to the locality of natural discharge, and (3) the character of the cone of depression.
When the extraction starts, groundwater is taken from storage to create gradients towards the well [40], and the resulting decline of water levels is observed only locally around the well. When pumping continues, the cone of depression expands and deepens, as more groundwater is released from storage to support the extraction. When it reaches areas of natural recharge or discharge, the lowering of the water table in these areas induces additional recharge or reduces the discharge [42]. Examples of the first are an increase in vertical soil percolation or infiltration from streams, whereas a decrease in evapotranspiration or drainage are examples of the latter. The cone of depression ceases to expand when the amount of extracted water is balanced completely by the total change in recharge and discharge, which is called the capture [40,41,43,44,45]. Note that this concept of capture has a distinct meaning from the capture zone of a well [46,47]. The capture zone is defined as the three-dimensional volumetric portion of a groundwater-flow field that discharges water to a well [47], and it may not be confused with the cone of depression [48].
When the pumping rate is balanced completely by the capture, a further decline of water levels is not needed anymore; hence, the aquifer system is brought into a new state of dynamic equilibrium. The time to full capture may range from seconds to centuries [45,49] and depends on the hydraulic properties of the aquifer system, the interacting sources and sinks, and the positioning of the extraction within the system [40]. It is also possible, however, that the capture may never be large enough to balance the pumping. In this case, the aquifer continues to be depleted, until the well goes dry [45], which may also occur when sources and sinks, such as streams, dry up.
When evaluating sustainable pumping, it may be sufficient to calculate the cone of depression to see whether a new steady state is attained or not. However, sustainable pumping may not be confused with sustainability, which is a much broader concept, as it includes other factors such as water quality, ecology, and socioeconomic considerations [50]. It is common practice to use mathematical models to simulate the cone of depression as well as to assess other impacts caused by a groundwater development. The first may be performed using traditional analytical models [41], whereas the latter requires advanced numerical modeling [51,52]. Therefore, our major concern is the use of the Sichardt formula [36] in environmental impact studies assessing sustainability, as the formula oversimplifies the hydraulics of well-flow.
The Sichardt formula [36] determines the radius of influence of an extraction by merely considering the aquifer conductivity and the lowering of the water level in the well. The radius of influence is defined as the boundary of the cone of depression, i.e., the radial distance from the center of the well to the point where there is no lowering of the water table or potentiometric surface [53] or beyond which drawdown is negligible or unobservable [54]. This definition implies the assumption of axial symmetry around the axis of the well. Axisymmetric models simulating flow to a well are frequently applied to analyze aquifer tests [55], in which case this assumption is justified because of the limited impact of such tests. It is also mathematically convenient, as it reduces the flow problem by one dimension.
However, in the case of permanent groundwater extractions, the assumption of axial symmetry is rarely valid, as the cone of depression is not restricted to the vicinity of the well. In reality, the part of the aquifer system impacted by a large cone of depression is not axially symmetric and neither are the streams and other sources and sinks interacting with the system. As a consequence, the area of influence corresponding to the cone of depression cannot be described by simply drawing a circle around the well in this case [53]. Moreover, the pumped aquifer mostly is part of a multi-aquifer system, i.e., a succession of aquifers separated by relatively less permeable aquitards, and a complete understanding of flow in the pumped aquifer without analyzing the multi-aquifer system as a whole is impossible [56]. These arguments may lead to the conclusion of abandoning the radius of influence concept [1], although it is a well-known and useful concept [33,57,58,59,60,61,62,63]. Moreover, approaches applying this concept to groundwater management have proven to be valuable, provided that they are theoretically justified [35,46,64].
In this paper, it is shown that the radius of influence is a parameter that can be derived from well-known one-dimensional axisymmetric models. These and other analytical models are still useful, not only in an educational context [65] but also because they have some advantages over numerical models [66]. In practice, groundwater studies are constrained by time and budget, often impeding the setup of data hungry numerical models, in which case the use of analytical models is an acceptable and inexpensive alternative [35]. Moreover, we believe sophisticated numerical models are not required in every case, and analytical models can help one decide whether to build a complex numerical model or not, as they offer valuable insights. Therefore, it is strongly recommended to perform hand calculations and to analyze simple analytical solutions before getting started with comprehensive numerical modeling [66]. The textbook written by Haitjema [67] is a good start to extend one’s analytical modeling skills, and for more advanced techniques, we refer to Bakker and Strack [68] who present analytical elements to simulate wells, infiltration areas, and streams in multi-aquifer systems, and to Bruggeman [69] who developed more than a thousand analytical solutions.
Our point of view is that the radius of influence is not an erroneous concept but rather its use is problematic in many cases, because groundwater practitioners often are unaware of the assumptions underlying frequently used equations to calculate the cone of depression. Groundwater modeling courses nowadays focus on the use of numerical models, which do not offer the same intuitions and insights that analytical models offer [66]. Therefore, several well-known one-dimensional axisymmetric models are carefully explained in this paper and suggested as valid alternatives to approaches that rely on empirical formulas. After presenting the Sichardt formula [36] and exposing its inconsistency with the Thiem equation [70], the solutions developed by de Glee [71] and Theis [72] are discussed: the former is used for steady flow in a leaky aquifer and the latter for transient flow in a confined aquifer. Based on these solutions, alternative formulas for the radius of influence are presented. In the subsequent section, the model of Hantush and Jacob [73] to simulate transient flow in a leaky aquifer is discussed to clarify the relation between the de Glee [71] and the Theis [72] equation, and rules of thumb are derived to distinguish between them.
Finally, the steady state solution for well-flow in a phreatic aquifer with recharge and drainage developed by Ernst [74] is discussed. The assumptions underlying this model are the same as those underlying the de Glee solution [71], except for the head-dependent boundary condition at the top, which is linear in the latter, whereas it is non-linear in the first, as it is restricted to drain water from the aquifer. The asymptotic solution for zero resistance surprisingly yields the formula to determine the radius of influence by balancing pumping and infiltration rate, which is contested by some authors [41,48]. Apparently, this formula is valid in heavily drained areas with an excess of precipitation, which are common in Flanders and the Netherlands.
To see the relation between the Theis model [72] and the Ernst model [74], the transient state solution of the latter is developed applying the Laplace transform and verified against the finite-difference model MAxSym [75]. Appendix A gives the detailed derivation of this semi-analytical solution, for which the same assumptions hold as for the Hantush and Jacob model [73], except for the non-linear head-dependent boundary condition at the top. In fact, all one-dimensional radial flow solutions presented in this paper are related, as they are all solutions to the same differential equation. This is shown by examining the total storage change.
2. The Sichardt Formula
As already mentioned in the introduction, the Sichardt formula first appears in a document written in German by Kyrieleis and Sichardt [36], who present it as empirically derived by Sichardt, yet not being published, only valid for steady state, and formulated as , with s the drawdown in m, K the hydraulic conductivity in m/s, and R the radius of influence in m. Kyrieleis and Sichardt [36] do not provide further explanation. To be consistent with other solutions presented below, we reformulate the formula with K in m/d. As drawdown s is a function of radial distance r (m) to the center of the well, we explicitly indicate that drawdown at the well face is meant in the Sichardt formula [36]:
with rw (m) the well radius.
To simulate the cone of depression due to pumping at constant rate Q (m3/d), Equation (1) is introduced into the Dupuit equation [76] for steady well-flow in a homogeneous unconfined aquifer [4,5,6]:
with h0 (m) the constant initial head, which defines the saturated thickness of the aquifer before the extraction starts. Since drawdown is positive in Sichardt’s formula [36] (1), pumping rate Q in (2) is positive.
If drawdown is small with respect to the saturated thickness, the following series expansion may be applied to (2): if . If x < 0.2 is taken, then drawdown must be smaller than 10% of the initial saturated thickness. Applying the approximation, the well-known Thiem equation [70] for steady well-flow in a homogeneous confined aquifer is obtained:
In (3), it is assumed the saturated thickness is constant and equal to D (m). In practice, the initial head h0 at the well is taken if the aquifer is phreatic. Note that distance R according to Sichardt’s formula [36] (1) sometimes is defined as the distance to the well face, in which case rw must be subtracted from R. At distance R, a constant-head boundary is defined in (2) and (3). Since drawdown is zero at R, this distance is the radius of influence according to the Dupuit [76] and Thiem [70] Equations (2) and (3), respectively.
Discussing the use of the Sichardt formula [36] (1) with geotechnical engineers, we learned it mainly serves as a rule of thumb to estimate the initial pumping rate of a dewatering well. In this case, the dewatering requires a lowering of the water table; hence, drawdown at the well face is known and the radius of influence is calculated using Sichardt’s formula [36] (1). Introducing the obtained radius of influence into Dupuit’s [76] Equation (2) gives an estimate of the unknown discharge. Some authors recommend the use of the formula only during the first 5 days of the dewatering [2,5]. This is in contrast with the assumption of steady state mentioned in the original work of Kyrieleis and Sichardt [36], as initially, water is exclusively removed from aquifer storage [40]. In a subsequent section, we will discuss the transient version of the radius of influence derived from the Theis solution [72] and compare it with the Sichardt Formula (1) [36].
Although we believe there exist models that are more reliable to quantify the size of a dewatering construction [77,78,79,80,81,82,83], discussing this matter is out of scope. Our concern lies with the use of the Sichardt Formula (1) [36] in assessing the environmental impact of permanent extractions [4]. In this case, the discharge is known, and the cone of depression must be estimated. Mathematically, this comes down to solving the system of two equations, consisting of the Sichardt Formula (1) [36] and the Dupuit Equation (2) [76] for r = rw, to find the two unknown variables: drawdown at the well face and the radius of influence. For the sake of simplicity, we replace the Dupuit Equation (2) [76] by the Thiem Equation (3) [70]. Multiplying each side of (3) by , and dividing both sides of the Sichardt Formula (1) [36] by rw, gives:
with dimensionless drawdown at the well face , dimensionless discharge , and dimensionless radius of influence . If R in Sichardt’s formula [36] (1) is interpreted as the distance to the well face, then the following system of equations must be solved:
Both (4) and (5) are solved by writing R* as a function of s* using the first equation, and introducing the result into the second equation, which gives and , respectively.
Figure 1 shows both solutions. In the case of (4), radius of influence R cannot be smaller than the well radius rw; hence, dimensionless drawdown (dotted line) cannot be smaller than 1, as it equals the dimensionless radius of influence. The minimum of the curve is found by solving , which gives . Hence, there is no solution if dimensionless discharge is smaller than 1/e, exactly one solution if and two solutions otherwise. In the case of (5), dimensionless discharge virtually equals 1 when dimensionless drawdown (solid line) is smaller than 0.1, as if . There is no solution if dimensionless discharge is smaller than 1.
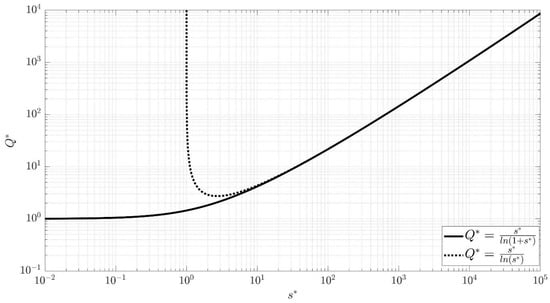
Figure 1.
Dimensionless discharge Q* as a function of dimensionless drawdown s* resulting from combining the Sichardt formula and the Thiem equation. The dimensionless parameters are defined in the text. Solid and dotted lines give the solution in which the radius of influence according to the Sichardt formula equals the distance to the well face and to the center of the well, respectively.
The Thiem Equation (3) [70] is a solution to the differential equation governing steady one-dimensional radial flow (see Appendix A), which combines Darcy’s law and the law of mass conservation [69]: two fundamental laws in physics. It is also required to formulate the finite-difference approximation of the two-dimensional radial flow equation [75]. Since it expresses the fundamental laws of groundwater flow, the Sichardt formula [36] must be consistent with the Thiem equation [70]. However, Figure 1 shows that small yet realistic pumping rates do not yield a solution. Therefore, we strongly discourage its use. The next two sections present two valid alternatives, based on the solutions of de Glee [71] and Theis [72]. The former solves the differential equation for steady flow and the latter for transient flow.
3. The de Glee Equation
Although examining the historical context in which the Sichardt formula [36] was developed and applied is out of scope, it is not unthinkable that German engineers at that time were struggling with the constant-head boundary condition that is required to apply the equations of Dupuit (2) [76] and Thiem (3) [70]. According to Zhai et al. [1], this constant-head boundary condition has been misinterpreted indeed by several authors. Nowadays, we understand the cone of depression is mathematically determined by the change of aquifer storage and the boundary conditions, but these principles were not known until they were stated first by Theis [42] in 1940.
In the Netherlands, Kooper [84] solved the problem in 1914 by assuming a constant-head resistance layer on top of the aquifer [85]. This leaky aquifer solution is known as the de Glee formula, as de Glee applied Kooper’s formula in 1930 in his dissertation [71] to evaluate field data, and he also extended it to a partially penetrating well [85]. In the English literature, the same solution was published by Jacob in 1946 [86]:
with c(d) the resistance of the constant-head layer. Function K0 is the zero-order modified Bessel function of the second kind.
The underlying steady state model assumes the leaky aquifer has an impermeable base and is homogeneous with constant saturated thickness D. The well is fully penetrating, an assumption which is justified when evaluating the extent of the cone of depression, as the effect of a partially penetrating well is observed only in a small zone around the well [87]. The system is linear; hence, drawdown according to (6) may be superimposed on the initial heads, which are assumed steady. Initial flow in the aquifer is allowed. Appendix A shows how Solution (6) is derived.
The upper boundary condition may be interpreted as an overlying homogeneous aquitard characterized by resistance c, in which a uniform head occurs that supplies the leakage [71,86]. This is the case when the aquitard is continuously being replenished by rainfall, a condition that is found in polder areas of The Netherlands and Flanders. In a more common interpretation, the aquitard is in turn overlain by an aquifer with constant head [56,86]. Flow in the pumped aquifer is strictly horizontal, whereas flow in the aquitard is strictly vertical.
In both interpretations, the extracted groundwater is balanced by the leakage through the overlying aquitard. Hence, the cone of depression covers an area in which the total leakage equals the pumping rate. Mathematically, this area is infinitely large; in practice, the following rule of thumb is applicable [64]:
where is called the leakage factor (m). Formula (7) defines a cylindrical zone around the well with radius R in which the leakage is significant. Outside this zone, the vertical flow in the overlying aquitard is negligibly small; hence, drawdown in the pumped layer is also negligibly small. Therefore, R according to (7) may be interpreted as the radius of influence. Mathematically, the outer constant-head boundary is at infinity, which avoids the use of empirical formulas. Moreover, the radius of influence according to (7) has a physical interpretation, which is consistent with the fundamental hydrological principles stated by Theis [42].
The de Glee equation [71,86] (6) is related to Thiem’s equation [70] (3). As if [88], we may approximate (6) as:
with the Euler constant equal to 0.57721. Comparing (8) with the Thiem [70] Equation (3), it is seen that the radius of influence according to (8) is [89]. However, Equation (8) is valid only for small distances and/or large leakage factor; hence, it is safer to use (7).
A less common interpretation of the de Glee solution (6) [71,86] is well-flow in a phreatic aquifer overlain by a dense network of ditches and canals interacting with the aquifer [74]. This interpretation is valid in humid areas, where these ditches drain the excess of water from rainfall. The extraction of groundwater in the aquifer causes a reduced drainage or even induces infiltration from the surface water. This interpretation is equivalent to defining a river boundary condition in each cell of the top layer of a MODFLOW model. It is also possible to define a boundary condition that only drains water, equivalent to MODFLOW drains. Definition of MODFLOW river and drain boundary conditions is given in [90]. The analytical solution that considers a drain-only boundary condition was developed by Ernst [74] and will be discussed below. First, the well-known equation derived by Theis [72] is discussed, who solved the problem of transient flow to a well in a confined aquifer.
4. The Theis Equation
We have already mentioned Narasimhan [38] who states that Weber [39] made the first successful attempt to analyze non-steady flow towards a well. However, without any notion of aquifer storativity, and hence, without knowing how to mathematically describe the elastic aquifer response, this statement probably should be nuanced. Indeed, the concept of aquifer storativity was not known until 1935, when Theis [72] developed his well-known equation with the aid of the mathematician Lubin [91]. The Theis equation is [72]:
with t the time in days, and S the storage coefficient, which is dimensionless and equals SsD, with Ss the specific elastic storage (m−1). Several approaches may be followed to derive (9) [92,93,94]. Appendix A shows how (9) is derived using the Laplace transform. In hydrogeological literature, function W is called the Theis’ well function; in mathematics, it is called the exponential integral [88]:
We may also apply the well-known Cooper and Jacob approximation [95]: for small values of u, the infinite summation in the right-hand side of (10) may be omitted, resulting into the following approximation of the Theis Equation (9) [72]:
Cooper and Jacob [95] suggest u < 0.02, whereas Jacob [96] proposes u < 0.05. Comparing (11) with the Thiem [70] Equation (3), the transient radius of influence according to the Theis model [72] is obtained [97]:
The Theis model [72] assumes a fully penetrating well with infinitesimal well radius in a homogeneous confined aquifer. Flow in the aquifer is strictly horizontal. Like the Thiem Equation (3) [70], the Theis Equation (9) [72] may be applied to simulate flow to a well in a phreatic aquifer, if drawdown is relatively small with respect to the aquifer’s saturated thickness. In this case, storage coefficient S is replaced by the specific yield Sy, which is also dimensionless. Like the de Glee Equation (6) [71,86], the Theis solution [72] (9) allows superposition if initial heads are steady.
There is no interaction with sources and sinks; hence, the aquifer storage entirely yields the extracted groundwater. Mathematically, this is accomplished by defining the outer constant-head boundary at an infinitely large distance from the well. Therefore, the Theis model [72] is best suited to simulate the initial flow to the well, when the capture is negligibly small. Equation (12) shows that the cone of depression expands with time at a pace determined by the aquifer properties: it expands more rapidly if the aquifer is transmissive (high K) and stores less groundwater (small S). In case of small K and high S, the cone of depression is deeper. Because the model is linear and the outer boundary is at infinity, the aquifer can be depleted indefinitely. In reality, the aquifer goes dry after a finite time of pumping if the cone of depression does not reach sources and/or sinks from which water can be captured to sustain the pumping.
In the case of the de Glee model [71,86], this water comes from the upper boundary condition, which represents leakage through an overlying aquitard or uniformly distributed surface water interaction. Consequently, the models of de Glee [71,86] and Theis [72] may be combined, where the latter is used at the beginning of the extraction, when capture is negligibly small, until its radius of influence (12) equals the radius of influence (7) derived from the de Glee equation [71,86] (6). The corresponding time is the time to full capture, at which a new state of equilibrium is attained and for which the de Glee solution [71,86] (6) is valid. This transition to steady state may be simulated accurately applying the model of Hantush and Jacob [73].
5. The Hantush-Jacob Model
The solution developed by Hantush and Jacob [73] may be seen as the transient version of the de Glee equation [71,86] (6) or the leaky version of the Theis equation [72] (9). If a fully penetrating well with infinitesimal radius extracts water at constant rate Q from a homogeneous leaky aquifer of infinite extent, then drawdown s as a function of radial distance r and time t is calculated as [73]:
Appendix A shows how (13) is derived applying the Laplace transform. Like the de Glee Equation (6) [71,86] and the Theis Equation (9) [72], Solution (13) allows superposition, if initial heads are steady. Hantush and Jacob [73] assume the overlying aquitard is incompressible, which means its storage is neglected. Solutions that consider storage effects in the aquitard also exist [98,99], and the well-known solution of Neuman and Witherspoon [100] even accounts for drawdown in the unpumped aquifer overlying the bounding aquitard.
Function W in (13) is the Hantush well function:
The Hantush well function (14) may be evaluated by performing a numerical inversion of the Laplace transform of W, e.g., by using the Stehfest algorithm [101] or by applying Gaussian quadrature [102]. Veling and Maas [103] give an overview of existing analytical and numerical methods to calculate or approximate the Hantush well function. Comparing (14) with Definition (10) of the Theis well function shows that both are identical if v = 0. Indeed, if c is infinitely large, then the aquifer is confined, and Solution (13) must be equal to the Theis equation [72] (9). The following relation between functions W and K0 holds [103]:
From (15) it follows that the Hantush-Jacob solution [73] (13) equals the de Glee equation [71,86] (6) if steady state is attained. Thus, the Theis solution [72] (9) and the de Glee equation [71,86] (6) are asymptotic solutions of the Hantush-Jacob model [73].
Examining the total storage change dV/dt (m3/d) gives a better idea when leakage becomes relevant and when it is maximal:
Appendix A shows how (16) is derived. If time t is zero, storage change equals pumping rate; if t is infinitely large, then storage change is zero. As e−x approximates 1 if x < 0.01 and 0 if x > 10, the Theis equation [72] (9) may be used if t < 0.01Sc and the de Glee equation [71,86] (6) if t > 10Sc. These are also useful rules of thumb to verify if estimating the radius of influence using (12) or (7), respectively, is justified. Figure 2 compares these approximations of the radius of influence with the radius of influence according to the Sichardt Formula (1) [36]. It is seen that the latter tends to underestimate the extent of the cone of depression after a period of pumping, and therefore, its use in assessing the environmental impact of permanent extractions must be avoided at all costs.
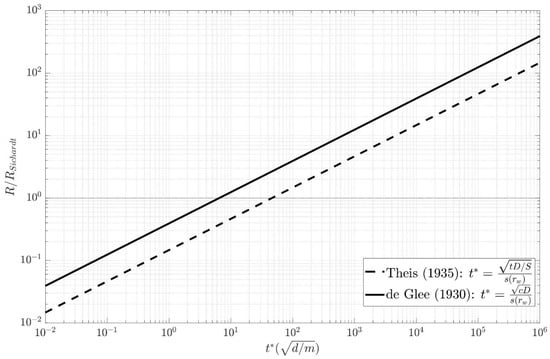
Figure 2.
Plot showing the ratio of the radius of influence R approximated using the Theis or the de Glee equations and the radius of influence RSichardt according to the empirical Sichardt formula as a function of parameter t*, which is defined in the figure’s legend. Parameter t is the time, D is the saturated thickness, S is the storage coefficient, c is the resistance, and s(rw) is the drawdown at the face of the well with radius rw. See text for definitions. The Sichardt radius of influence underestimates the hydraulic impact of the extraction if the ratio is larger than 1, i.e., above the horizontal dotted line. See text for a more detailed explanation.
6. The Ernst Model
In the model of de Glee [71,86] and the model of Hantush and Jacob [73], the upper boundary condition is linear, which implies it is an infinite source of water. In reality, the hydraulic head in a layer overlying a pumped aquifer or water levels in surface water bodies draining this aquifer also decrease after a period of pumping, at risk of going dry. This is accounted for in the model of Ernst [74] by excluding this upper boundary condition at distances where the head drops below a given level. The same assumptions underlying the model of de Glee [71,86] also hold for the model of Ernst [74], except that the constant-head layer is only allowed to drain water from the pumped aquifer. Hence, a proximal zone around the pumping well is considered without drainage, whereas the distal part of the aquifer is still being drained. As already mentioned, this draining condition is equivalent to defining a drain boundary condition in each cell of the top layer of a MODFLOW model.
Since the drainage boundary condition depends on the hydraulic head in the aquifer, the model is non-linear. As a consequence, the superposition principle is not valid, and infiltration at the top of the aquifer cannot be ignored. Ernst [74] assumes a constant infiltration rate N (m/d) and shows that the initial head before pumping is (see Appendix A):
where c is the drainage resistance. Infiltration flux N is positive if water is added to the aquifer. Initial heads (17) are relative to the steady drainage levels. For convenience, the latter are set to zero, which is allowed as the aquifer’s saturated thickness D is assumed constant. Recall that the aquifer has an infinite extent. If water at constant rate Q > 0 is extracted from a well with negligibly small radius, then drawdown s is:
Appendix A shows how (18) is derived. Function K1 is the first order modified Bessel function of the second kind. Distance rd is the boundary between the proximal zone without drainage and the distal zone with drainage. This means s1 in (18) is the drawdown in the proximal zone, whereas s2 in (18) is the drawdown in the distal zone. Boundary rd is found by solving equation s2(rd) = Nc, which is straightforward applying a non-linear solver. The left plot in Figure 3 is a graphical representation of the solution of this equation, and the right plot shows drawdown according to (18) expressed in dimensionless form.
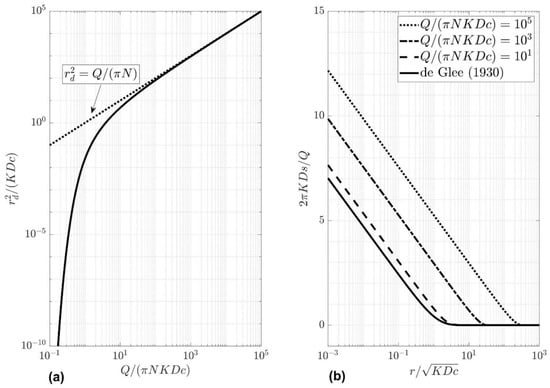
Figure 3.
Solution of the Ernst model. (a) Dimensionless extent of the no-drainage zone rd/(KDc)1/2 versus dimensionless pumping rate Q/(πNKDc). The dotted line is the asymptotic solution for zero resistance. (b) Dimensionless drawdown (2πKDs)/Q versus dimensionless distance r/(KDc)1/2 for different values of dimensionless pumping rate Q/(πNKDc). The solid line is the de Glee solution. K is the aquifer conductivity, D the saturated thickness, c the drainage resistance, N the infiltration flux, Q the pumping rate, s the drawdown, r the radial distance, and rd the boundary between the zones without and with drainage. See text for definitions and a more detailed explanation.
If drainage is perfect, then resistance c is zero, in which case s2 in (18) is zero, and s1 is reduced to the well-known solution for a well in a circular infiltration pond with radius rd [67]:
As drawdown s2 in the distal zone is zero, the radius of influence R equals rd. The dotted straight line on the left plot in Figure 3 shows that in this case:
Formula (20) is used to estimate the extent of the capture zone [67], as it balances recharge and pumping rate. In most cases, capture zone and cone of depression do not coincide [48], but they do in this case. Returning to the underlying assumptions, we may conclude (20) is valid in flat areas with an excess of precipitation which is discharged by a dense system of drainage canals and ditches. In Flanders and the Netherlands, such areas are common. The left plot in Figure 3 shows that using (20) is justified if Q/(πNKDc) > 100. In case of gentle pumping, drainage remains active all over the aquifer, and rd is negligibly small. In this case, Solution (18) simplifies to the de Glee solution [71,86] (6), which is clearly illustrated in the right plot of Figure 3. From this plot, we may derive the rule of thumb that using the de Glee equation [71,86] (6) is justified if Q/(πNKDc) < 1.
7. Transient State Solution of the Ernst Model
Ernst [74] only treats the steady state solution. In Appendix A, the transient state solution is developed applying the Laplace transform. Figure 4 shows dimensionless drawdown as a function of dimensionless distance (left plot) and dimensionless time (right plot) for different values of dimensionless discharge. The semi-analytical solution is verified against the finite-difference solution (circles) simulated using the MAxSym code [75] that was extended with the option to include head-dependent boundary conditions similar to MODFLOW rivers and drains [90]. The finite-difference solution may also be obtained using MODFLOW by tricking it into simulating axisymmetric flow using the procedure outlined by [104]. In this case, the model grid consists of one layer, and a recharge and drain boundary condition is defined in each grid cell i. Applying this procedure, the drain conductance equals Ai/c, and the recharge flux is multiplied by Ai, where Ai (m2) is the horizontal surface area of the ring represented by cell i.
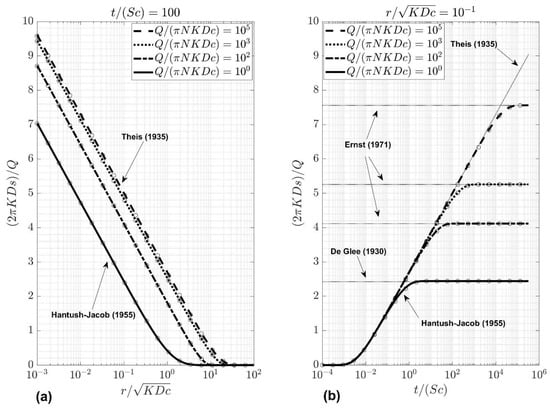
Figure 4.
Transient state solution of the Ernst model developed in this study. (a) Dimensionless drawdown (2πKDs)/Q as a function of dimensionless distance r/(KDc)1/2 for dimensionless time t/(Sc) equal to 100 and for different dimensionless pumping rates Q/(πNKDc). (b) Dimensionless drawdown (2πKDs)/Q as a function of dimensionless time t/(Sc) for dimensionless distance r/(KDc)1/2 equal to 0.1 and for different dimensionless pumping rates Q/(πNKDc). K is the aquifer conductivity, S the storativity, D the saturated thickness, c the drainage resistance, N the infiltration flux, Q the pumping rate, s the drawdown, r the radial distance, and t the time. See text for definitions. The solution is verified against the finite-difference approach (circles), and against the asymptotic solutions developed by de Glee, Theis, Hantush and Jacob, and Ernst.
The transient state solution of well-flow in an aquifer with infiltration and drainage has asymptotic solutions that correspond to the models already discussed in this paper. After a period of pumping, steady state is reached, in which case drawdown may be approximated by the Ernst solution (18) [74]. If dimensionless discharge Q/(πNKDc) < 1, then the de Glee Equation (6) [71,86] may be used. This rule of thumb may be generalized, as it also holds for transient state, in which case the solution of Hantush and Jacob (13) [73] must be used. Finally, at small values of time, drawdown may be approximated using the Theis Equation (9) [72]. The relation between the transient state solution of the Ernst model [74] and these asymptotic solutions is also shown in Figure 4.
Figure 5 also reveals the relation between the different solutions discussed in this paper. It shows the relative storage change dV/dt/Q as a function of dimensionless time t/(Sc) and dimensionless pumping rate Q/(πNKDc). Figure 5 was plotted using MAxSym, since the finite-difference approach is more convenient to calculate volumetric budgets. The exact Laplace space formulation of storage change is given in Appendix A. The left side of the contour plot is the transient part; in the right side, steady state solutions are valid. In the upper part of the plot, drainage resistance is negligibly small and infiltration is relevant; in the lower part, infiltration may be ignored. Solution (19) may be used if both storage change and resistance are negligibly small, which is in the upper right part of the plot. The dotted lines are not strict boundaries; they only indicate the rules of thumb derived in this paper that may be used to switch from one solution to another. Under the assumption of a homogeneous phreatic aquifer, infiltrated at constant rate, and discharged by area covering drainage, radius of influence (12) derived from the Theis Equation (9) [72] is applicable in the left part, radius of influence (7) derived from the de Glee equation [71,86] (6) in the lower right part, and radius of influence (20) determined by balancing pumping and infiltration rate in the upper right part.
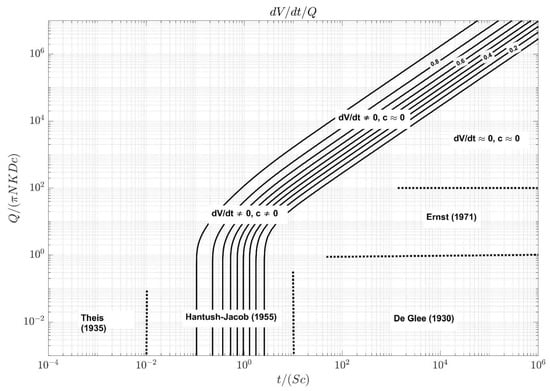
Figure 5.
Contour plot of dimensionless storage change dV/dt/Q as a function of dimensionless time t/(Sc) and dimensionless pumping rate Q/(πNKDc) for the transient state solution of the Ernst model developed in this study, with dV/dt the storage change, Q the pumping rate, t the time, S the storage coefficient, c the drainage resistance, N the infiltration flux, K the aquifer conductivity, and D the saturated thickness. See text for definitions. The dotted lines indicate the rules of thumb derived in this paper.
8. Discussion
We complete this paper by discussing the use and reliability of the formulas that were derived to calculate the cone of depression and the corresponding radius of influence. Table 1 summarizes the assumptions underlying the one-dimensional analytical models discussed in this paper. Each of these models simulates drawdown in the extracted aquifer only and assumes there is no drawdown in the adjacent layers. The aquifer base is assumed impervious and the aquifer top may be impervious, leaky, or draining. The models of Thiem [70] and Theis [72] have an impervious upper boundary, the models of de Glee [71,86] and Hantush-Jacob [73] have a leaky top, and the upper boundary in the Ernst [74] model is draining. In the latter, there is also a constant infiltration flux.
In the Dupuit solution [76], the saturated thickness of the aquifer equals the hydraulic head; hence, the upper boundary is interpreted as the water table. In all other models, the saturated thickness is constant. Therefore, the single layer is mostly interpreted as a confined aquifer in the Thiem [70] and Theis [72] models and as a semi-confined aquifer in the de Glee [71,86] and Hantush-Jacob [73] models. The bounding aquitard in the latter models is assumed incompressible and has a uniform head because it is continuously being replenished by rainfall or it is overlain by an aquifer with constant head.
Alternatively, a phreatic aquifer may be assumed using the models of Thiem [70], Theis [72], de Glee [71,86], and Hantush-Jacob [73], if drawdown is small compared to the initial saturated thickness. Implicitly, the phreatic aquifer may be recharged by a constant infiltration flux, which is canceled out in the drawdown solutions, since the governing differential equation is linear. If the aquifer is phreatic, the leaky top in the de Glee [71,86] and Hantush-Jacob [73] models is interpreted as surface water interaction similar to MODFLOW rivers. This interpretation also holds for the Ernst [74] model, although in this model, the upper boundary condition is restricted to draining water from the phreatic aquifer. Since this is a non-linear condition similar to MODFLOW drains, recharge is not canceled out in the governing equation, and therefore, the constant infiltration flux is defined explicitly.
The aquifer in these models is assumed horizontal, homogeneous, and isotropic. As a consequence, the flow to the pumping well is axially symmetric. Moreover, the well is fully penetrating; hence, flow is assumed strictly horizontal. In each of these models, the well extracts water at a constant pumping rate. The well also has an infinitesimal radius, which means wellbore storage is neglected. The outer boundary in each of these models is a constant head. In the models of Dupuit [76] and Thiem [70], this boundary is at finite distance from the well. Because drawdown is zero at the outer boundary, it corresponds to the radius of influence. In the other models, this outer boundary is defined at an infinitely large distance. Therefore, the derived formulas for calculating the radius of influence correspond to a distance from the well at which drawdown is negligibly small. These equations are given in the last column of Table 1.

Table 1.
Summary of the analytical models discussed in the paper applied to simulate axisymmetric flow towards a fully penetrating well with infinitesimal radius and constant pumping rate in a homogeneous aquifer with impervious base. From the solutions of these models, equations and rules of thumb are derived to estimate the radius of influence R, with KD the transmissivity, c the resistance, S the storage coefficient, N the infiltration flux, Q the pumping rate, and t the time. See text for explanation and definitions.
Table 1.
Summary of the analytical models discussed in the paper applied to simulate axisymmetric flow towards a fully penetrating well with infinitesimal radius and constant pumping rate in a homogeneous aquifer with impervious base. From the solutions of these models, equations and rules of thumb are derived to estimate the radius of influence R, with KD the transmissivity, c the resistance, S the storage coefficient, N the infiltration flux, Q the pumping rate, and t the time. See text for explanation and definitions.
| Model | Flow Regime | Outer Boundary | Upper Boundary | Initial Flow | Super-Position | Radius of Influence R |
|---|---|---|---|---|---|---|
| Dupuit [76] | Steady | Finite | Water table | None | No4 | Outer boundary (=input parameter) |
| Thiem [70] | Steady | Finite | Impervious 1 | Steady | Yes | Outer boundary (=input parameter) |
| de Glee [71,86] | Steady | Infinite | Leaky 2 | Steady | Yes | |
| Theis [72] | Transient | Infinite | Impervious 1 | Steady | Yes | |
| Hantush-Jacob [73] | Transient | Infinite | Leaky 2 | Steady | Yes | |
| Ernst [74] | Steady | Infinite | Drainage + Recharge | None 3 | No 4 | |
| Transient Ernst (Appendix A) | Transient | Infinite | Drainage + Recharge | None 3 | No 4 | See Figure 5 |
1 Or water table if drawdown is less than 10% of initial saturated thickness. 2 Leakage through incompressible aquitard or linear surface water interaction (cfr. MODFLOW river). 3 Initial heads equal to Nc are relative to the steady drainage levels, which are set to zero for convenience. 4 Unless the solution may be approximated by its corresponding linear equation.
The models of Dupuit [76] and Ernst [74] are non-linear: in the first, the saturated aquifer thickness depends on the hydraulic head, whereas the draining boundary condition is non-linear in the latter. Because of this non-linearity, superposition is not applicable, and the initial heads must be constant. This implies there is no initial flow in the aquifer, although the constant initials heads in the Ernst [74] model are relative to the drainage levels that are steady but not necessarily constant. This means the Ernst [74] solution may be superimposed on the initial heads that are the result of this steady but non-uniform drainage in the aquifer. The other models are linear and therefore allow initial steady flow in the aquifer, since the superposition principle is valid. Recall that under certain conditions the Dupuit [76] and Ernst [74] solutions may be approximated by the linear equations of Thiem [70] and de Glee [71,86], respectively. Superposition is explained in many hydrogeology textbooks [54,55,67]. It states that the drawdowns induced by individual constant-discharge wells can be summed to obtain the total drawdown caused by these extractions. Superposition may also be applied to simulate variable-discharge pumping.
The assumptions underlying the discussed models also hold for the derived formulas to estimate the radius of influence summarized in the last column of Table 1. These assumptions oversimplify the process of groundwater flow to a pumping well in many aspects. Therefore, assessing the environmental impact of a groundwater extraction by merely calculating the radius of influence must be avoided at all costs. These kinds of studies mostly require advanced numerical modeling, as estimating the extent of the cone of depression is not sufficient to evaluate the effects on groundwater flow and on sources and sinks. The impact on water quality and ecology, and other considerations, must also be taken into account, which may even require additional models besides a calibrated groundwater flow model.
To check whether the pumping is sustainable or not, it may suffice to estimate the area of influence. As already discussed in the introduction, this area rarely is a circle, and in most cases, the pumped aquifer is part of a multi-aquifer system. Still, a first approach that applies one-dimensional axisymmetric solutions assuming a single aquifer could be useful, as they give an idea of the extent of the cone of depression and offer insight into the sensitivity of the hydraulic parameters. If drawdowns in the unpumped layers of a multi-aquifer system are not negligibly small, axisymmetric multi-aquifer solutions can be applied [105,106,107,108,109,110], which are implemented in user-friendly Matlab and Python codes [75,111].
In many real-world cases, reliable parameter values are not available, and examining a range of realistic values is a pragmatic way to get an idea of the worst-case impact. Because of the low computational cost, axisymmetric single- and multi-layer models are well-suited to perform these kinds of calculations. Using the de Glee Equation (6) [71,86] and the Theis Equation (9) [72], respectively, it is even possible to determine the maximum radius of influence Rmax, which is independent of the aquifer transmissivity KD:
Formulas (21) and (22) only depend on pumping rate Q and the maximum allowable drawdown smax at distance Rmax. Additionally, Formula (21) derived from the de Glee equation [71,86] (6), requires resistance c, whereas Formula (22) derived from the Theis equation [72] (9), requires storage coefficient S. The latter is also time dependent. Appendix B explains how these formulas are derived.
The maximum allowable drawdown smax is necessary in (21) and (22), because the model of de Glee [71,86] and the model of Theis [72] have a boundary condition at infinity. Only at this boundary condition, drawdown is exactly zero, by definition, whereas drawdown is nonzero at all other distances from the well. Mathematically, the radius of influence is thus infinitely large. Recall that Formulas (7) and (12) estimating the radius of influence are approximations that ensure drawdown is zero at distance R. The error induced by these approximations is proportional to Q/(KD) [63].
This maximum allowable drawdown is the subject of many discussions between groundwater practitioners in Flanders, who range its optimal value from 1 mm to 10 cm. Although these discussions are necessary from an ecological point of view, they are pointless if a radius of influence approach is used as a substitute for a sophisticated mathematical model. Hence, we believe it is more meaningful to discuss model assumptions and reliability of input data. The formulas presented in this paper may be helpful in these discussions, as they show which parameter combinations are relevant. Results calculated using these formulas, however, may never be interpreted as ground truth data.
9. Conclusions
The radius of influence myth refers to the use of empirical formulas to assess the environmental impact of groundwater extractions. As an example, the frequently used Sichardt formula [36] was examined, which estimates the radius of influence merely considering the aquifer conductivity and drawdown in the pumping well. It is shown that the Sichardt formula [36] is not consistent with the fundamental Thiem equation [70]. It also tends to underestimate the extent of the cone of depression, and therefore, its use must be discouraged.
A distinction must be made between sustainable pumping and sustainability [50], the latter being a much broader concept that in many cases requires advanced numerical modelling. Concerning sustainable pumping, the fundamental hydrological principles that were stated first by Theis [42] must be kept in mind. The extraction causes a cone of depression, which is determined by the change of aquifer storage and the sources and sinks from which water is captured. As a consequence, the assumption of axial symmetry only holds close to the well, and therefore, the radius of influence rarely is an accurate measure of the extent of the cone of depression.
On the other hand, we agree with Haitjema [66] who advocates for the use of simple formulas derived from one-dimensional models. These formulas have minimum data requirements and may help set up the right numerical model. Therefore, alternatives to the Sichardt formula [36] were derived from existing one-dimensional analytical solutions: de Glee [71,86], Theis [72], and Ernst [74]. An asymptotic solution to the latter yields the contested formula to determine the radius of influence by balancing pumping and infiltration rate. Considering the assumptions underlying the Ernst model [74], it is concluded that this formula is valid in humid areas that are heavily drained.
The model of Hantush and Jacob [73] was also discussed to see the relation between the solutions of de Glee [71,86] and Theis [72]. The transient state solution of the Ernst model [74] was developed applying the Laplace transform. This solution includes drainage instead of leakage at the top of the aquifer. Examining drawdown curves and total storage change as a function of dimensionless parameters revealed the relation between the presented one-dimensional radial flow solutions, from which some useful rules of thumb were derived.
Although the derived formulas are better alternatives to frequently used empirical formulas, they may not be considered as methods to accurately estimate the cone of depression of an extraction, as they rely on oversimplifying assumptions. They are not intended as a substitute for comprehensive numerical models, although they may be useful in setting up these models, as they offer valuable insights on relevant parameter combinations.
Author Contributions
Conceptualization, A.L., A.V., D.L., M.V.C. and K.W.; methodology, A.L.; software, A.L.; validation, A.L. and A.V.; formal analysis, A.L.; investigation, A.L.; resources, A.L., A.V., D.L., M.V.C. and K.W.; data curation, A.L.; writing—original draft preparation, A.L.; writing—review and editing, A.V., D.L., M.V.C. and K.W.; visualization, A.L.; supervision, K.W.; project administration, K.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors greatly appreciate the helpful and constructive review comments from the anonymous reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Deriving the Transient State Solution of the Ernst Model
Solution (18) of the Ernst model [74] combines the solutions of two one-dimensional axisymmetric models. The first model calculates drawdown in the proximal zone without drainage (r ≤ rd). It simulates flow in a bounded homogeneous aquifer with constant thickness and infiltration at the top. The second model calculates drawdown in the distal zone where drainage is still active (r > rd). It simulates flow in a homogeneous leaky aquifer with constant thickness and infiltration at the top. The inner boundary condition in the first model defines a constant discharge equal to the pumping rate at the well, whereas the outer boundary is a constant-head equal to the drainage level. The latter is set to zero; hence, the drawdown is equal to the initial head h0 = Nc. This outer boundary coincides with the inner boundary of the second model. Therefore, drawdown in both models must be the same at this boundary, and continuity of flow requires that the inflow to the first model must be equal to the outflow from the second model. The latter determines the constant flux at the inner boundary of the second model. The outer boundary condition in the second model is a constant head at an infinite large distance.
The transient solution is found in the same way. However, in this case, the boundary between both models is time dependent. In both steady and transient case, the first as well as the second model are governed by the same partial differential equation:
with h(r,t) the hydraulic head [L] in the aquifer, which is a function of radial distance r [L] and time t [T]. A homogeneous aquifer is considered with constant transmissivity T = KD [L2/T] and constant storativity S [–]. The aquifer is recharged at the top by a constant flux N [L/T]. This flux is positive in case of infiltration. The leaky top and bottom boundary have constant heads [L] htop and hbot and hydraulic resistances [L] ctop and cbot, respectively. The inner boundary is a well with radius rw [L] from which water is extracted at constant pumping rate Q [L3/T]:
If water is extracted, then Q > 0. The outer boundary at distance rout [L] has a constant head hout [L]:
The initial condition is:
The steady state problem is also treated by Equation (A1) with , subject to boundary conditions (A2) and (A3).
In case of transient flow, the Laplace transform is applied. The Laplace transform of head h is denoted by :
with p the frequency variable [T−1]. The Laplace transform of the constants is:
Equation (A1) is transformed into:
Boundary conditions (A2) and (A3) are transformed into, respectively:
Both steady state and the Laplace transformed transient problem are described by an ordinary differential equation of the form:
subject to the following boundary conditions:
If transient flow is considered, then:
If steady flow is considered, then:
The general solution of (A10) is:
with and arbitrary constants. Note that a = 0 if flow is steady and if the aquifer is confined. In this case, b = N/T.
A particular solution is found by introducing (A15) into boundary conditions (A11) and (A12), which gives the following expressions for constants and , respectively:
where f’, g’, and z’ are the derivatives of f, g, and z, respectively, with respect to r.
If a = 0, the constants are:
and the solution simplifies to:
Recall that in this case flow is steady and the aquifer is confined. If N = 0 and h according to (A20) is subtracted from hout, then the Thiem equation [70] (3) is obtained. If Q = 0 and rw = 0, then (A20) gives the solution for a circular infiltration area. If rw = 0, hout = 0, and rout = rd, then Equation (18a) is obtained by subtracting (A20) from h0 = Nc, and setting c to zero gives (19).
If a ≠ 0, the constants are:
If , expressions (A21) and (A22) reduce to, respectively:
If , expressions (A21) and (A22) reduce to, respectively:
If and , then .
In general, the steady state solution is:
with a, b, q, and yout given by (A14). If and the lower boundary is confined, i.e., cbot = ∞, the steady state solution is:
If htop = 0 and Q = 0, then (A28) simplifies to expression (17) with ctop = c. If , , and N = 0, then (A28) simplifies to the de Glee solution [71,86]:
If h according to (A29) is subtracted from htop, then Equation (6) is obtained, with c = ctop. The generalized equation for an aquifer with leaky top and bottom layer is:
In general, the transient state solution in Laplace space is:
with a, b, q, and yout given by (A13). This solution may be inverted numerically applying the Stehfest [101] algorithm. If , , and N = 0, and if the system is confined, i.e., ctop = cbot = ∞, the following transient state solution in Laplace space is obtained:
Inverting (A32) analytically [92,112] gives the well-known Theis equation [72]:
In (A33), function W is the Theis well function (10). If h according to (A33) is subtracted from h0, then Equation (9) is obtained. If , , N = 0, and if the system is leaky with h0 = htop and cbot = ∞, the following transient state solution in Laplace space is obtained:
It is possible to invert Equation (A34) analytically [112], which gives the solution of Hantush and Jacob [73]:
In (A35), function W is the Hantush well function (14). If h according to (A35) is subtracted from h0, then Equation (13) is obtained, with c = ctop.
The radial discharge [L3/T] is the amount of water per unit of time that flows horizontally through the cylindrical surface with radius r, at time t:
In case of steady flow, and if the aquifer is leaky, i.e., a ≠ 0, (A27) is used to evaluate (A36):
with and given by (A21) and (A22), respectively, and a, b, q, and yout given by (A14). If the aquifer is confined, then a = 0, and (A37) simplifies to:
Solution (18b) is obtained by subtracting h according to (A29) from h0 = Nc, with htop = 0 and c = ctop, after which rw is substituted by rd, and Q by Qr(rd) according to (A38), with rw = 0.
In case of transient flow, the Laplace transform of (A36) is evaluated:
with and given by (A21) and (A22), respectively, and a, b, q, and yout given by (A13). Expression (A39) may be inverted numerically. In case of transient flow, the storage change is defined as the amount of water per unit of time released by or stored in the ring determined by radii r1 and r2 at time t:
The Laplace transform of (A40) is:
Introducing (A23) into (A41):
with and given by (A21) and (A22), respectively, and a, b, q, and yout given by (A13). Expression (A42) may be inverted numerically. Total storage change dV/dt is equal to . In case of the Theis model [72], this simplifies to Q/p, which is inverted to Q. To find expression (16), i.e., the total storage change in case of the Hantush and Jacob model [73], expression (A42) is evaluated for r1 = 0 and r2 = ∞. This simplifies to Q/(p+1/S/c), which is inverted to [112]:
Now that the problem of one-dimensional axisymmetric flow has been stated in general, we are able to develop the transient version of the model of Ernst [74]. The Laplace transform of transient head and in the proximal zone without drainage and the distal zone with drainage, respectively, is given by (A31). In the proximal zone, cbot = ctop = ∞, rout = rd, hout = 0, and h0 = Nc, whereas in the distal zone, cbot = ∞, ctop = c, rw = rd, htop = hout = 0, and h0 = Nc. Using (A13), the exact solution in Laplace space is:
with and . Note that in the transient case, the boundary rd between the proximal and the distal zone is time dependent. However, it is not transformed, as radial distance r is not transformed either. It is assumed and , hence, constants and are given by (A23) and (A24), respectively, and constant by (A26):
Note that , according to (A25). The pumping rate in (A47) is replaced by the inflow at the outer boundary of the proximal zone, which is given by (A39):
The unknown radius rd is found by solving h2(rd,t) = 0 using a non-linear solver. To find the head h2 at distan rd, according to (A44) is evaluated using the Stehfest algorithm [101]. The non-linear solver finds the value of rd that corresponds to the root of this numerically inverted equation. Note that the logarithm of rd is evaluated to avoid negative values. Once rd is found, drawdown s1 and s2 in the proximal and distal zone are found by numerically inverting (A44), and subtracting the calculated head h from the initial head h0 = Nc. As rd is time dependent, this routine must be applied for each time t.
Total storage change dV/dt at a given time t is found by numerically inverting , or:
If , then and , and total storage change approximates Q. If , then , and total storage change is negligibly small.
Appendix B. Finding the Maximum Radius of Influence
The De Glee solution (6) [71,86] and the Theis solution (9) [72] are expressed by an equation of the following form:
with s the drawdown [L], Q the pumping rate [L3/T], T = KD the transmissivity [L2/T], r the radial distance [L], and Pi an independent variable or hydraulic parameter. In case of the de Glee equation [71,86] (6), function f is defined as with K0 the zero-order modified Bessel function of the second kind, whereas f is the Theis Well function W in case of the Theis equation [72] (9).
Defining dimensionless drawdown and dimensionless transmissivity , Equation (A50) is written in dimensionless form:
Function g reaches its maximum in point . This point is found by numerically solving , after which maximum distance rmax is found for a given maximum drawdown smax using the definition of dimensionless drawdown s*:
The corresponding transmissivity Tmax is found using the definition of dimensionless transmissivity T* and substituting rmax by (A52):
In case of the de Glee equation [71,86] (6), and . The maximum radius of influence Rmax given a maximum allowable drawdown smax is:
with c the hydraulic resistance [T]. The corresponding maximum transmissivity is:
In the case of the Theis equation [72] (9), and . The maximum radius of influence Rmax given a maximum allowable drawdown smax at time t [L] is:
with S the storage coefficient [–]. The corresponding maximum transmissivity is:
References
- Zhai, Y.; Cao, X.; Jiang, Y.; Sun, K.; Hu, L.; Teng, Y.; Wang, J.; Li, J. Further Discussion on the Influence Radius of a Pumping Well: A Parameter with Little Scientific and Practical Significance That Can Easily Be Misleading. Water 2021, 13, 2050. [Google Scholar] [CrossRef]
- Janssen, G.J.M. Bemaling van Bouwputten; Van Marken Delft Drukkers: Delft, The Netherlands, 2003. (In Dutch) [Google Scholar]
- Bot, B. Grondwaterzakboekje, 2nd ed.; Bot Raadgevend Ingenieur: Rotterdam, The Netherlands, 2016. (In Dutch) [Google Scholar]
- Willems, E.; Monseré, T.; Dierckx, J. Geactualiseerd Richtlijnenboek Milieueffectrapportage–Basisrichtlijnen per Activiteitengroep–Landbouwdieren; Dienst MER, Afdeling Milieu-, Natuur- en Energiebeleid, Departement Leefmilieu, Natuur en Energie: Brussels, Belgium, 2009. (In Dutch) [Google Scholar]
- VMM. Richtlijnen Bemalingen Ter Bescherming van Het Milieu; Vlaamse Milieumaatschappij: Aalst, Belgium, 2019. (In Dutch) [Google Scholar]
- VMM. Handleiding Berekeningsinstrument Bemalingen; Vlaamse Milieumaatschappij: Aalst, Belgium, 2020. (In Dutch) [Google Scholar]
- OVAM. Standaardprocedure Bodemsaneringsproject; Openbare Vlaamse Afvalstoffenmaatschappij: Mechelen, Belgium, 2018. (In Dutch) [Google Scholar]
- Mansur, C.I.; Kaufman, R.I. Chapter 3–Dewatering. In Foundation Engineering; Leonards, G.A., Ed.; McGraw-Hill: New York, NY, USA, 1962; pp. 241–350. [Google Scholar]
- Fruco and Associates Inc. Dewatering and Groundwater Control for Deep Excavations. NAVFAC Manual; Department of the Navy: Washington, DC, USA, 1971.
- Powers, J.P. Construction Dewatering: New Methods and Applications, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1992. [Google Scholar]
- Powers, J.P. Construction Dewatering–A Guide to Theory and Practice; John Wiley & Sons: New York, NY, USA, 1981. [Google Scholar]
- Powers, J.P.; Corwin, A.B.; Schmall, P.C.; Kaeck, W.E. Construction Dewatering and Groundwater Control: New Methods and Applications; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- Sanglerat, G.; Olivari, G.; Cambou, B. Practical Problems in Soil Mechanics and Foundation Engineering, 1–Developments in Geotechnical Engineering; Elsevier Science Publishers B.V.: Amsterdam, The Netherlands, 1984; Volume 34A. [Google Scholar]
- Punmia, B.C.; Ashok, K.J.; Arun, K.J. Water Supply Engineering, 2nd ed.; Laxmi Publications (P) LTD.: New Delhi, India, 1995. [Google Scholar]
- Dachroth, W. Handbuch Der Baugeologie Und Geotechnik; Springer: Berlin/Heidelberg, Germany, 2017. (In German) [Google Scholar]
- Puller, M. Deep Excavations: A Practical Manual; Thomas Telford: London, UK, 2003. [Google Scholar]
- Merkl, G. Technik Der Wasserversorgung: Praxisgrundlagen Für Führungskräfte; Deutscher Industrieverlag: Oldenbourg, Germany, 2008. (In German) [Google Scholar]
- Smoltczyk, U. Ground Dewatering. In Geotechnical Engineering Handbook; Smoltczyk, U., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2003; Volume 2, pp. 365–398. [Google Scholar]
- Powrie, W. Soil Mechanics: Concepts and Applications, 2nd ed.; Taylor & Francis: New York, NY, USA, 2004. [Google Scholar]
- Coduto, D.P.; Yeung, M.R.; Kitch, W.A. Geotechnical Engineering: Principles & Practices, 2nd ed.; Pearson Prentice Hall: New York, NY, USA, 2011. [Google Scholar]
- Cashman, P.M.; Preene, M. Groundwater Lowering in Construction–A Practical Guide to Dewatering. Volume 6 of Applied Geotechnics, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Desodt, C.; Reiffsteck, P. Géotechnique-Excercices et Problèmes Corrigés de Mécanique Des Sols, Avec Rappels de Cours, 2nd ed.; Dunod: Malakoff, France, 2020. (In French) [Google Scholar]
- Ergun, M.U.; Nalçakan, M.S. Dewatering of a Large Excavation Pit by Wellpoints. In Proceedings of the Third International Conference on Case Histories in Geotechnical Engineering, St. Louis, MO, USA, 1–5 June 1993; pp. 707–711. [Google Scholar]
- Kumar, B.A.; Sudip, B.; Prabir, M. An Innovative Methodology for Groundwater Management with Reference to Saline Water Intrusion. IOSR J. Eng. 2012, 2, 1473–1486. [Google Scholar] [CrossRef]
- Rabie, M.H. Comparative Study between Predicted and Observed Records of Implementation Dewatering Systems at Abu Qir Intake Power Plant, Alexandria. J. Am. Sci. 2013, 9, 106–114. [Google Scholar]
- Yihdego, Y. Engineering and Enviro-Management Value of Radius of Influence Estimate from Mining Excavation. J. Appl. Water Eng. Res. 2018, 6, 329–337. [Google Scholar] [CrossRef]
- Yihdego, Y.; Paffard, A. Predicting Open Pit Mine Inflow and Recovery Depth in the Durvuljin Soum, Zavkhan Province, Mongolia. Mine Water Environ. 2017, 36, 114–123. [Google Scholar] [CrossRef]
- Yihdego, Y.; Drury, L. Mine Dewatering and Impact Assessment in an Arid Area: Case of Gulf Region. Environ. Monit. Assess. 2016, 188, 634. [Google Scholar] [CrossRef]
- De Filippi, F.M.; Iacurto, S.; Ferranti, F.; Sappa, G. Hydraulic Conductivity Estimation Using Low-Flow Purging Data Elaboration in Contaminated Sites. Water 2020, 12, 898. [Google Scholar] [CrossRef]
- Khadka, D.B. Experimental Design of Physical Unconfined Aquifer for Evaluation of Well Abstraction Effects: Laboratory Approach. J. Eng. Res. Rep. 2021, 20, 90–102. [Google Scholar] [CrossRef]
- Niu, W.; Wang, Z.; Chen, F.; Li, H. Settlement Analysis of a Confined Sand Aquifer Overlain by a Clay Layer Due to Single Well Pumping. Math. Probl. Eng. 2013, 2013, 789853. [Google Scholar] [CrossRef]
- Masoud, M. Groundwater Resources Management of the Shallow Groundwater Aquifer in the Desert Fringes of El Beheira Governorate, Egypt. Earth Syst. Environ. 2020, 4, 147–165. [Google Scholar] [CrossRef]
- Bair, E.S.; O’Donnell, T.P. Uses of Numerical Modeling in the Design and Licensing of Dewatering and Depressurizing Systems. Ground Water 1983, 21, 411–420. [Google Scholar] [CrossRef]
- Moh, Z.-C.; Chuay, H.-Y.; Hwang, R.N. Large Scale Pumping Test and Hydraulic Characteristics of Chingmei Gravels. In Proceedings of the Twelfth Southeast Asian Geotechnical Conference and the Fourt International Conference on Tropcial Soils, Kuala Lumpur, Malaysia, 6–10 May 1996; Volume 1, pp. 119–124. [Google Scholar]
- Fileccia, A. Some Simple Procedures for the Calculation of the Influence Radius and Well Head Protection Areas (Theoretical Approach and a Field Case for a Water Table Aquifer in an Alluvial Plain). Acque Sotter. Ital. J. Groundw. 2015, 4, 3. [Google Scholar] [CrossRef]
- Kyrieleis, W.; Sichardt, W. Grundwasserabsenkung Bei Fundierungsarbeiten; Springer: Berlin/Heidelberg, Germany, 1930. (In German) [Google Scholar]
- Sichardt, W. Das Fassungsvermögen von Rohrbrunnen Und Seine Bedeutung Für Die Grundwasserabsenkung, Insbesondere Für Größere Absenkungstiefen; Springer: Berlin/Heidelberg, Germany, 1928. (In German) [Google Scholar]
- Narasimhan, T.N. Hydraulic Characterization of Aquifers, Reservoir Rocks, and Soils: A History of Ideas. Water Resour. Res. 1998, 34, 33–46. [Google Scholar] [CrossRef]
- Weber, H. Die Reichweite von Grundwasserabsenkungen Mittels Rohrbrunnen; Springer: Berlin/Heidelberg, Germany, 1928. (In German) [Google Scholar]
- Bredehoeft, J.D.; Papadopulos, S.S.; Cooper, H.H., Jr. The Water Budget Myth. In Scientific Basis of Water Resources Management Studies in Geophysics; National Academy Press: Washington, DC, USA, 1982; pp. 51–57. [Google Scholar]
- Bredehoeft, J.D. The Water Budget Myth Revisited: Why Hydrogeologists Model. Ground Water 2002, 40, 340–345. [Google Scholar] [CrossRef] [PubMed]
- Theis, C.V. The Source of Water Derived from Wells: Essential Factors Controlling the Response of an Aquifer to Development. Civ. Eng. 1940, 10, 277–280. [Google Scholar]
- Konikow, L.F.; Leake, S.A. Depletion and Capture: Revisiting “The Source of Water Derived from Wells”. Groundwater 2014, 52, 100–111. [Google Scholar] [CrossRef]
- Lohman, S.W. Definitions of Selected Ground Water Terms–Revisions and Conceptual Refinements; USGS Water Supply Paper 1988; U.S. Government Printing Office: Washington, DC, USA, 1972.
- Bredehoeft, J.; Durbin, T. Ground Water Development-The Time to Full Capture Problem. Ground Water 2009, 47, 506–514. [Google Scholar] [CrossRef]
- Seward, P.; Xu, Y.; Turton, A. Investigating a Spatial Approach to Groundwater Quantity Management Using Radius of Influence with a Case Study of South Africa. Water SA 2015, 41, 71–78. [Google Scholar] [CrossRef]
- Barlow, P.M.; Leake, S.A.; Fienen, M.N. Capture Versus Capture Zones: Clarifying Terminology Related to Sources of Water to Wells. Groundwater 2018, 56, 694–704. [Google Scholar] [CrossRef]
- Brown, R.H. The Cone of Depression and the Area of Diversion around a Discharging Well in an Infinite Strip Aquifer Subject to Uniform Recharge. In Shortcuts and Special Problems in Aquifer Tests; USGS Water-Supply Paper 1545C; U.S. Government Printing Office: Washington, DC, USA, 1963; pp. C69–C85. [Google Scholar]
- Sophocleous, M. Retracted: On Understanding and Predicting Groundwater Response Time. Groundwater 2012, 50, 528–540. [Google Scholar] [CrossRef]
- Devlin, J.F.; Sophocleous, M. The Persistence of the Water Budget Myth and Its Relationship to Sustainability. Hydrogeol. J. 2005, 13, 549–554. [Google Scholar] [CrossRef]
- Kalf, F.R.P.; Woolley, D.R. Applicability and Methodology of Determining Sustainable Yield in Groundwater Systems. Hydrogeol. J. 2005, 13, 295–312. [Google Scholar] [CrossRef]
- Zhou, Y. A Critical Review of Groundwater Budget Myth, Safe Yield and Sustainability. J. Hydrol. 2009, 370, 207–213. [Google Scholar] [CrossRef]
- Hansen, C.V. Description and Evaluation of Selected Methods Used to Delineate Wellhead-Protection Areas around Public-Supply Wells near Mt. Hope, Kansas; USGS Water-Resources Investigations Report 90-4102; U.S. Geological Survey: Denver, CO, USA, 1991. [CrossRef]
- Bear, J. Hydraulics of Groundwater; McGraw-Hill Series in Water Resources and Environmental Engineering; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Kruseman, G.P.; de Ridder, N.A. Analysis and Evaluation of Pumping Test Data, 2nd ed.; ILRI Publication 47: Wageningen, The Netherlands, 1990. [Google Scholar]
- Neuman, S.P.; Witherspoon, P.A. Applicability of Current Theories of Flow in Leaky Aquifers. Water Resour. Res. 1969, 5, 817–829. [Google Scholar] [CrossRef]
- MacDonald, T.R.; Kitanidis, P.K. Modeling the Free Surface of an Unconfined Aquifer Near a Recirculation Well. Ground Water 1993, 31, 774–780. [Google Scholar] [CrossRef]
- Gefell, M.J.; Thomas, G.M.; Rossello, S.J. Maximum Water-Table Drawdown at a Fully Penetrating Pumping Well. Ground Water 1994, 32, 411–419. [Google Scholar] [CrossRef]
- Chu, S.T. Transient Radius of Influence Model. J. Irrig. Drain. Eng. 1994, 120, 964–969. [Google Scholar] [CrossRef]
- Soni, A.K.; Sahoo, L.K.; Ghosh, U.K.; Khond, M.V. Importance of Radius of Influence and Its Estimation in a Limestone Quarry. J. Inst. Eng. India Ser. D 2015, 96, 77–83. [Google Scholar] [CrossRef]
- Castellazzi, P.; Martel, R.; Galloway, D.L.; Longuevergne, L.; Rivera, A. Assessing Groundwater Depletion and Dynamics Using GRACE and InSAR: Potential and Limitations. Groundwater 2016, 54, 768–780. [Google Scholar] [CrossRef]
- Bresciani, E.; Shandilya, R.N.; Kang, P.K.; Lee, S. Well Radius of Influence and Radius of Investigation: What Exactly Are They and How to Estimate Them? J. Hydrol. 2020, 583, 124646. [Google Scholar] [CrossRef]
- Dragoni, W. Some Considerations Regarding the Radius or Influence or a Pumping Well. Hydrogéologie 1998, 3, 21–25. [Google Scholar]
- Zhou, Y. Sources of Water, Travel Times and Protection Areas for Wells in Semi-Confined Aquifers. Hydrogeol. J. 2011, 19, 1285–1291. [Google Scholar] [CrossRef]
- Pfannkuch, H.-O.; Mooers, H.D.; Siegel, D.I.; Quinn, J.J.; Rosenberry, D.O.; Alexander, S.C. Review: “Jacob’s Zoo”—How Using Jacob’s Method for Aquifer Testing Leads to More Intuitive Understanding of Aquifer Characteristics. Hydrogeol. J. 2021, 29, 2001–2015. [Google Scholar] [CrossRef]
- Haitjema, H. The Role of Hand Calculations in Ground Water Flow Modeling. Ground Water 2006, 44, 786–791. [Google Scholar] [CrossRef]
- Haitjema, H. Analytic Element Modeling of Groundwater Flow; Academic Press: San Diego, CA, USA, 1995. [Google Scholar]
- Bakker, M.; Strack, O.D.L. Analytic Elements for Multiaquifer Flow. J. Hydrol. 2003, 271, 119–129. [Google Scholar] [CrossRef]
- Bruggeman, G.A. Analytical Solutions of Geohydrological Problems. Developments in Water Science 46; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Thiem, G. Hydrologische Methoden; Gebhardt: Leipzig, Germany, 1906. (In German) [Google Scholar]
- De Glee, G.J. Over Grondwaterstroomingen Bij Wateronttrekking Door Middel van Putten. Ph.D. Thesis, Technische Universiteit Delft, Delft, The Netherlands, 1930. (In Dutch). [Google Scholar]
- Theis, C.V. The Relation between the Lowering of the Piezometric Surface and the Rate and Duration of Discharge of a Well Using Ground-Water Storage. Trans. Am. Geophys. Union 1935, 16, 519–524. [Google Scholar] [CrossRef]
- Hantush, M.S.; Jacob, C.E. Non-Steady Radial Flow in an Infinite Leaky Aquifer. Trans. Am. Geophys. Union 1955, 36, 95–100. [Google Scholar] [CrossRef]
- Ernst, L.F. Analysis of Groundwater Flow to Deep Wells in Areas with a Non-Linear Function for the Subsurface Drainage. J. Hydrol. 1971, 14, 158–180. [Google Scholar] [CrossRef]
- Louwyck, A.; Vandenbohede, A.; Bakker, M.; Lebbe, L. Simulation of Axi-Symmetric Flow towards Wells: A Finite-Difference Approach. Comput. Geosci. 2012, 44, 136–145. [Google Scholar] [CrossRef]
- Dupuit, J. Etude Théoriques et Pratiques Sur Le Mouvement Des Eaux Dans Les Canaux Découverts et à Travers Les Terrains Perméables; Dunot: Paris, France, 1863. (In French) [Google Scholar]
- Wang, X.-W.; Yang, T.-L.; Xu, Y.-S.; Shen, S.-L. Evaluation of Optimized Depth of Waterproof Curtain to Mitigate Negative Impacts during Dewatering. J. Hydrol. 2019, 577, 123969. [Google Scholar] [CrossRef]
- Wu, Y.-X.; Shen, S.-L.; Lyu, H.-M.; Zhou, A. Analyses of Leakage Effect of Waterproof Curtain during Excavation Dewatering. J. Hydrol. 2020, 583, 124582. [Google Scholar] [CrossRef]
- Zheng, Y.; Lei, J.; Wang, F.; Xiang, L.; Yang, J.; Xue, Q. Investigation on Dewatering of a Deep Shaft in Strong Permeable Sandy Pebble Strata on the Bank of the Yellow River. Geofluids 2021, 2021, 9994477. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X.; Xu, Y. Influence of Filter Tube of Pumping Well on Groundwater Drawdown during Deep Foundation Pit Dewatering. Water 2021, 13, 3297. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Wang, S.; Xue, X.-L.; Zheng, G.; Mei, G.-X. Evolution of Deep Ground Settlement Subject to Groundwater Drawdown during Dewatering in a Multi-Layered Aquifer-Aquitard System: Insights from Numerical Modelling. J. Hydrol. 2021, 603, 127078. [Google Scholar] [CrossRef]
- Lyu, H.-M.; Shen, S.-L.; Wu, Y.-X.; Zhou, A.-N. Calculation of Groundwater Head Distribution with a Close Barrier during Excavation Dewatering in Confined Aquifer. Geosci. Front. 2021, 12, 791–803. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Zheng, G.; Xue, X.-L. Responses of Deep Soil Layers to Combined Recharge in a Leaky Aquifer. Eng. Geol. 2019, 260, 105263. [Google Scholar] [CrossRef]
- Kooper, J. Beweging van Het Water in Den Bodem Bij Onttrekking Door Bronnen. De Ingenieur 1914, 29, 697–716. (In Dutch) [Google Scholar]
- Hemker, C.J. Groundwater Flow in Layered Aquifer Systems. Ph.D. Thesis, Vrije Universiteit Amsterdam, Amsterdam, The Netherlands, 2000. [Google Scholar]
- Jacob, C.E. Radial Flow in a Leaky Artesian Aquifer. Trans. Am. Geophys. Union 1946, 27, 198–208. [Google Scholar] [CrossRef]
- Bakker, M. An Analytic, Approximate Method for Modeling Steady, Three-Dimensional Flow to Partially Penetrating Wells. Water Resour. Res. 2001, 37, 1301–1308. [Google Scholar] [CrossRef][Green Version]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. In Dover Books on Advanced Mathematics; Abramowitz, M., Stegun, I.A., Eds.; Dover Publications: New York, NY, USA, 1965. [Google Scholar]
- De Smedt, F. Groundwater Hydrology; Department of Hydrology and Hydraulic Engineering, Faculty of Applied Sciences, Free University Brussels: Brussels, Germany, 2006. [Google Scholar]
- Harbaugh, A.W. MODFLOW-2005, the U.S. Geological Survey Modular Ground-Water Model-the Ground-Water Flow Process; USGS Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2005. [CrossRef]
- Bredehoeft, J.D. An Interview with C.V. Theis. Hydrogeol. J. 2008, 16, 5. [Google Scholar] [CrossRef]
- Loàiciga, H.A. Derivation Approaches for the Theis (1935) Equation. Ground Water 2010, 48, 2–5. [Google Scholar] [CrossRef]
- Perina, T. Derivation of the Theis (1935) Equation by Substitution. Ground Water 2010, 48, 6–7. [Google Scholar] [CrossRef]
- Masoodi, R.; Ghanbari, R.N. Derivation of the Theis (1935) Equation by Substitution. Ground Water 2012, 50, 8–9. [Google Scholar] [CrossRef]
- Cooper, H.H.; Jacob, C.E. A Generalized Graphical Method for Evaluating Formation Constants and Summarizing Well-Field History. Trans. Am. Geophys. Union 1946, 27, 526–534. [Google Scholar] [CrossRef]
- Jacob, C.E. Flow of Groundwater. In Engineering Hydraulics; Rouse, H., Ed.; Wiley: New York, NY, USA, 1950; pp. 321–386. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier Publishing Company: New York, NY, USA, 1972. [Google Scholar]
- Hantush, M.S. Modification of the Theory of Leaky Aquifers. J. Geophys. Res. 1960, 65, 3713–3725. [Google Scholar] [CrossRef]
- De Smedt, F. Constant-Rate Pumping Test in a Leaky Aquifer with Water Release from Storage in the Aquitard. Groundwater 2020, 58, 487–491. [Google Scholar] [CrossRef]
- Neuman, S.P.; Witherspoon, P.A. Theory of Flow in a Confined Two Aquifer System. Water Resour. Res. 1969, 5, 803–816. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368: Numerical Inversion of Laplace Transforms [D5]. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Shampine, L.F. Vectorized Adaptive Quadrature in MATLAB. J. Comput. Appl. Math. 2008, 211, 131–140. [Google Scholar] [CrossRef]
- Veling, E.J.M.; Maas, C. Hantush Well Function Revisited. J. Hydrol. 2010, 393, 381–388. [Google Scholar] [CrossRef][Green Version]
- Louwyck, A.; Vandenbohede, A.; Bakker, M.; Lebbe, L. MODFLOW Procedure to Simulate Axisymmetric Flow in Radially Heterogeneous and Layered Aquifer Systems. Hydrogeol. J. 2014, 22, 1217–1226. [Google Scholar] [CrossRef]
- Hemker, C.J. Steady Groundwater Flow in Leaky Multiple-Aquifer Systems. J. Hydrol. 1984, 72, 355–374. [Google Scholar] [CrossRef]
- Hemker, C.J. Transient Well Flow in Leaky Multiple-Aquifer Systems. J. Hydrol. 1985, 81, 111–126. [Google Scholar] [CrossRef]
- Hunt, B. Flow to a Well in a Multiaquifer System. Water Resour. Res. 1985, 21, 1637–1641. [Google Scholar] [CrossRef]
- Hunt, B. Solutions for Steady Groundwater Flow in Multi-Layer Aquifer Systems. Transp. Porous Media 1986, 1, 419–429. [Google Scholar] [CrossRef]
- Maas, C. The Use of Matrix Differential Calculus in Problems of Multiple-Aquifer Flow. J. Hydrol. 1986, 88, 43–67. [Google Scholar] [CrossRef]
- Hemker, C.J.; Maas, C. Unsteady Flow to Wells in Layered and Fissured Aquifer Systems. J. Hydrol. 1987, 90, 231–249. [Google Scholar] [CrossRef]
- Bakker, M. Semi-Analytic Modeling of Transient Multi-Layer Flow with TTim. Hydrogeol. J. 2013, 21, 935–943. [Google Scholar] [CrossRef]
- Hantush, M.S. Hydraulics of Wells. In Advances in Hydroscience; Chow, V.T., Ed.; Academic Press: New York, NY, USA; London, UK, 1964; Volume 1, pp. 281–432. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).