Micro-Climate Computed Machine and Deep Learning Models for Prediction of Surface Water Temperature Using Satellite Data in Mundan Water Reservoir
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
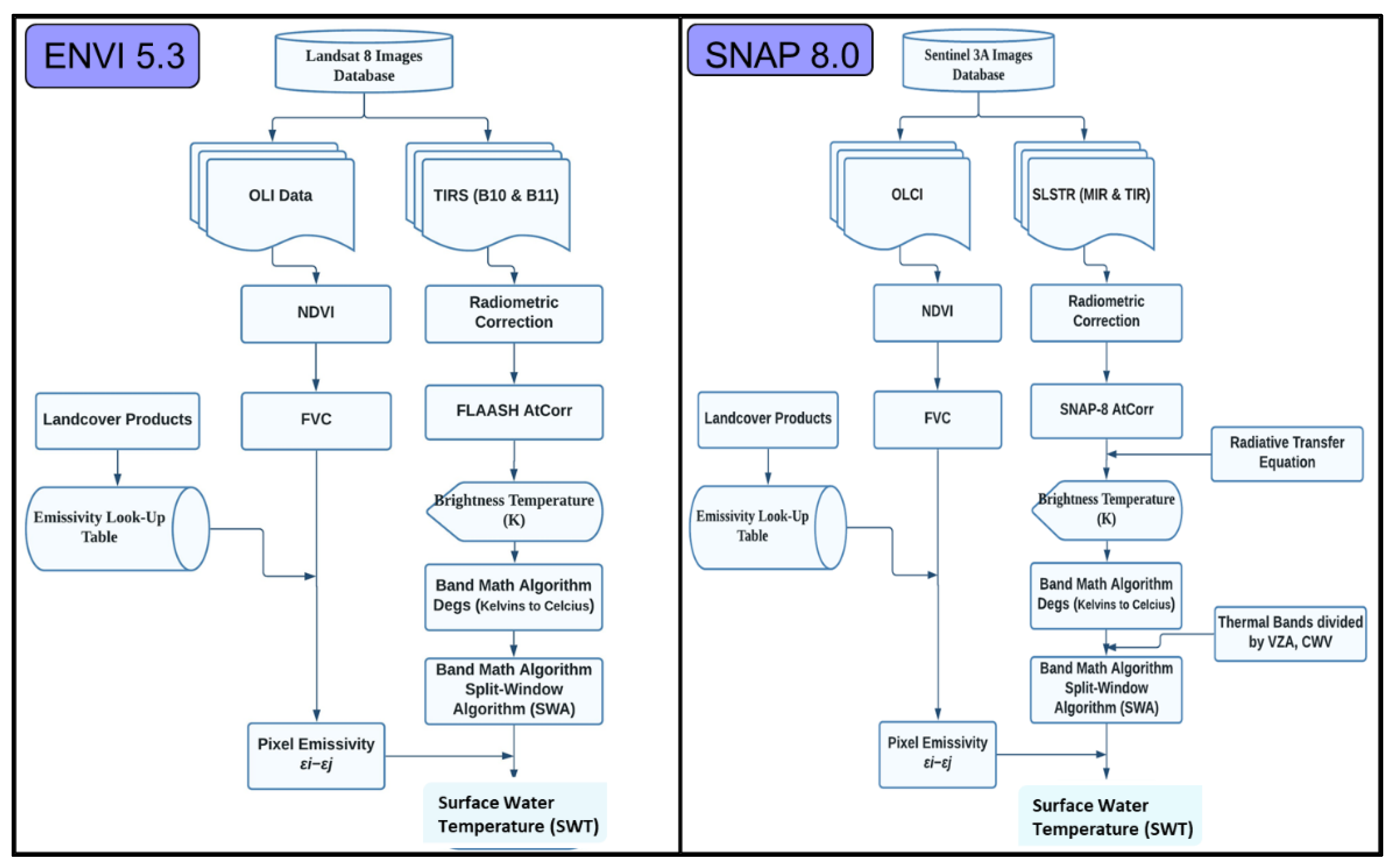
2.2. Data Collection and Image Preprocessing
2.3. Machine and Deep Learning Algorithms Applied for Regression
- I.
- Gaussian Process Regression (GPR)
- II.
- Support Vector Machine (SVM)
- III.
- Artificial Neural Network (ANN)
- IV.
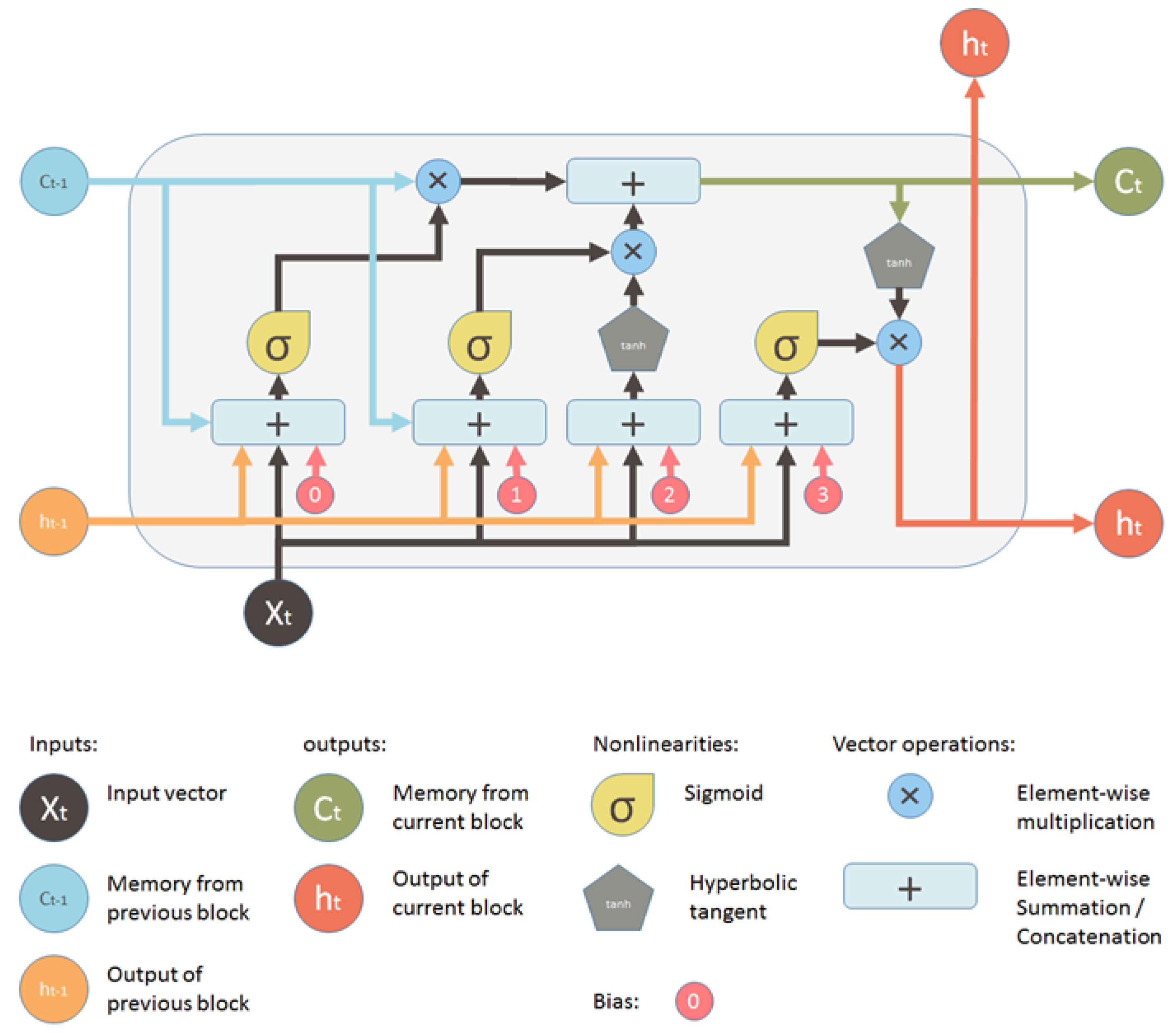
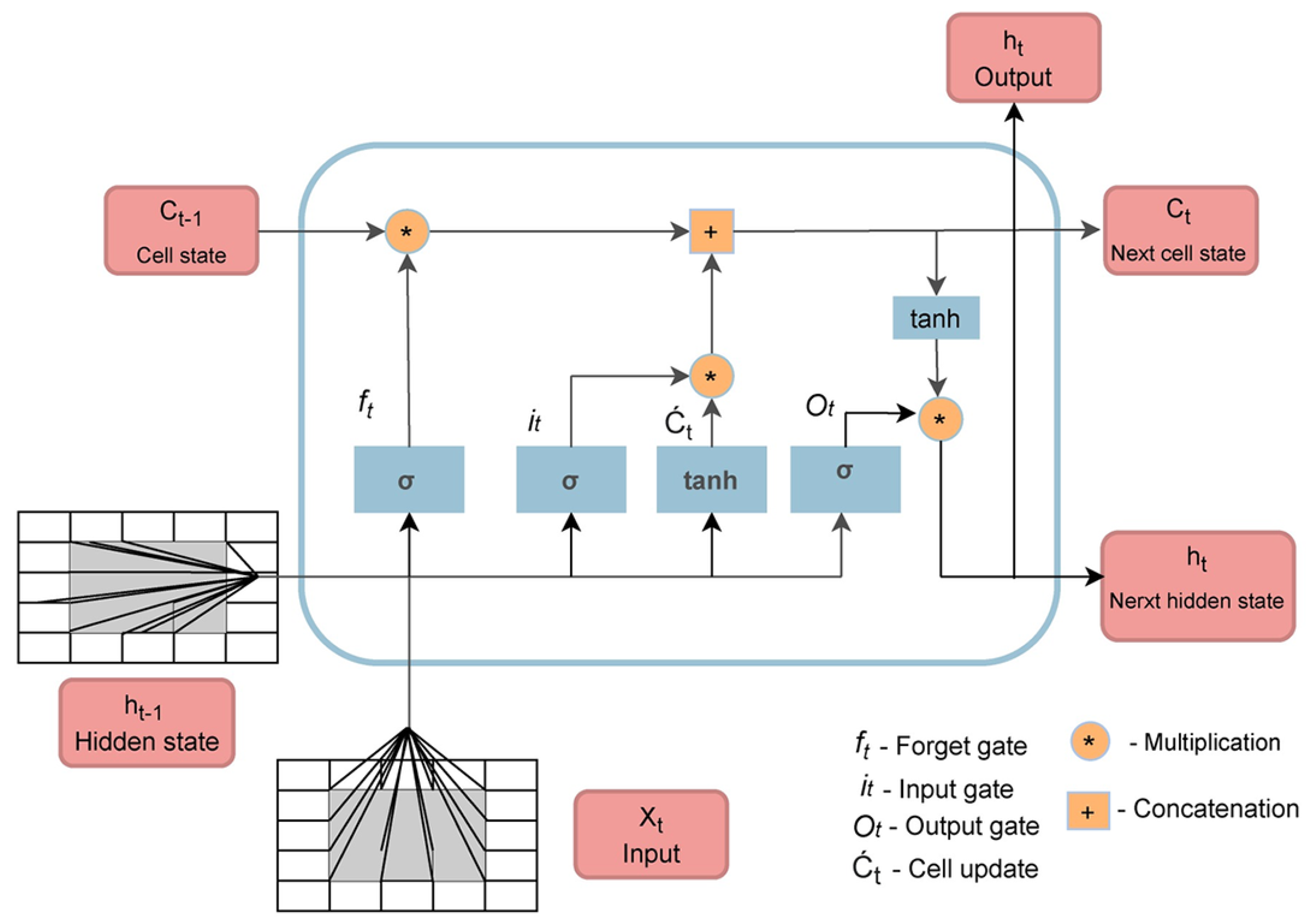
- Long Short Term Memory (LSTM)
- V.
- Convolutional Long Short Term Memory (Conv-LSTM)
2.4. Sliding Window Time Series Cross-Validation and Model Evaluation Metrics
2.5. Performance Evaluation Metrics
2.6. Hypothesis Testing (Two-Factor ANOVA) and Post-Hoc Scheffe
3. Results
3.1. Descriptive Statistics
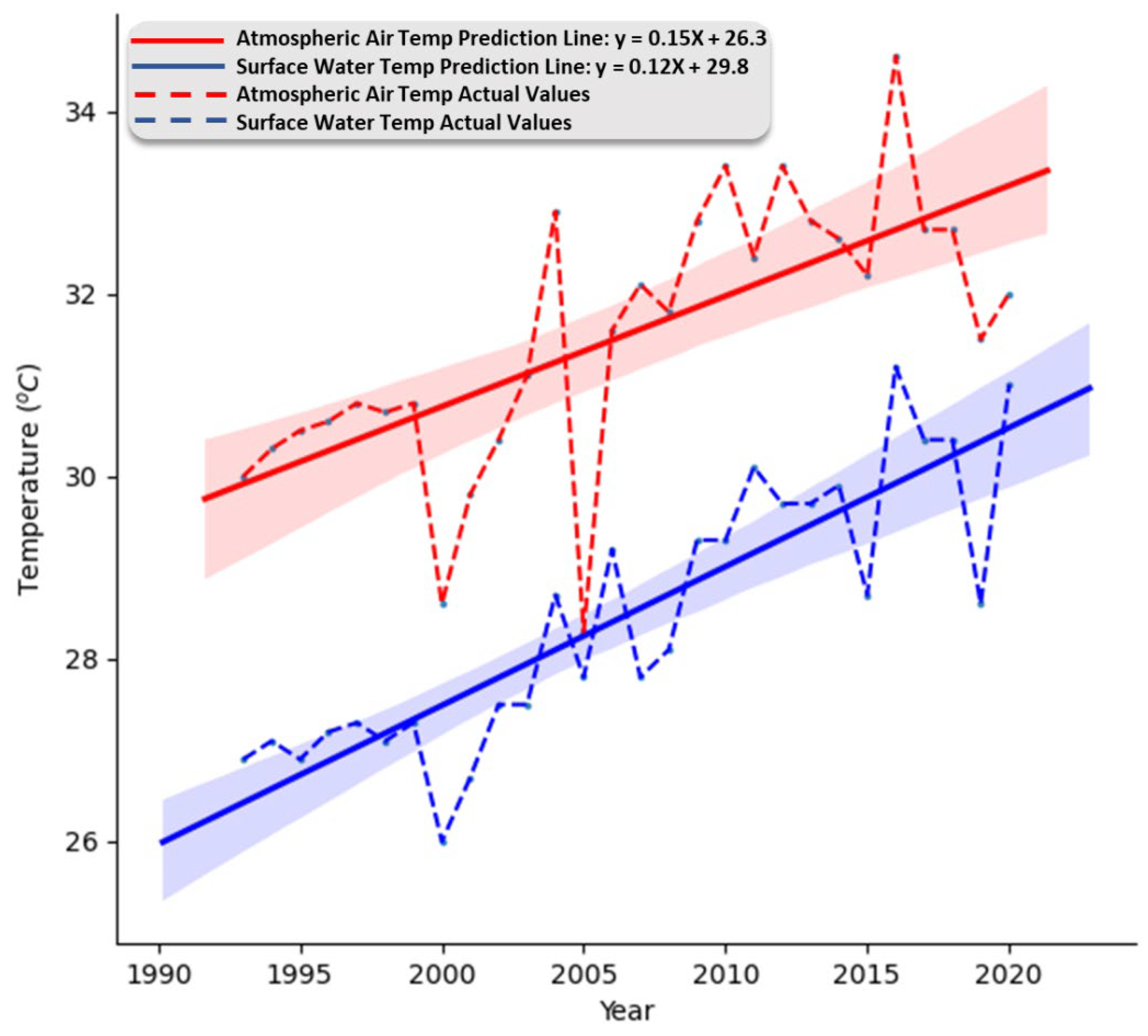
3.2. Long Term Atmospheric Air and Surface Water Temperature Trends for Mundan Water Reservoir (1993–2020)
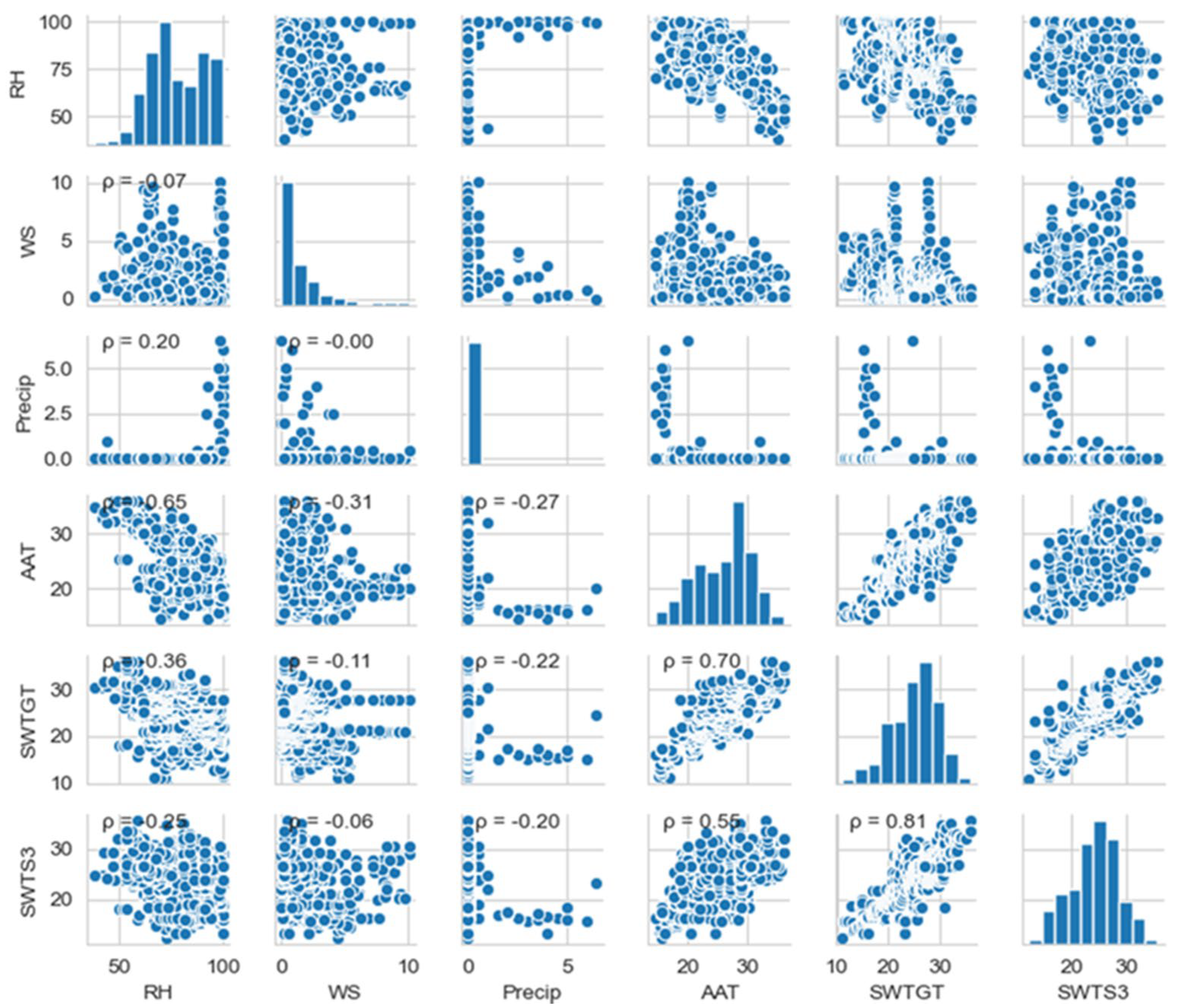
3.3. Exploratory Data Analysis–Correlation between Different Variables
3.4. Machine Learning Models
4. Discussion
4.1. Factors Affecting the Accuracy of SWT Predictions
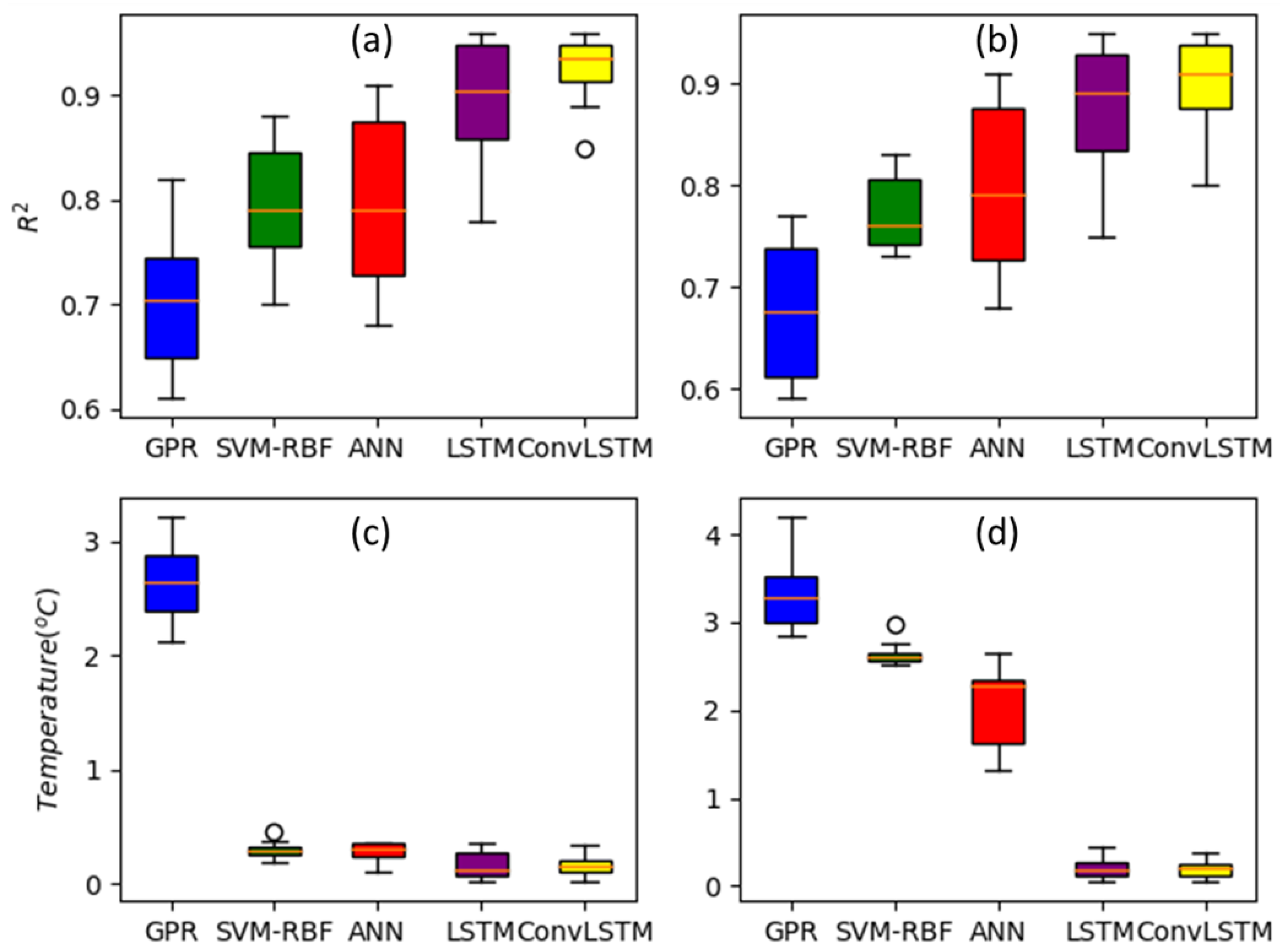
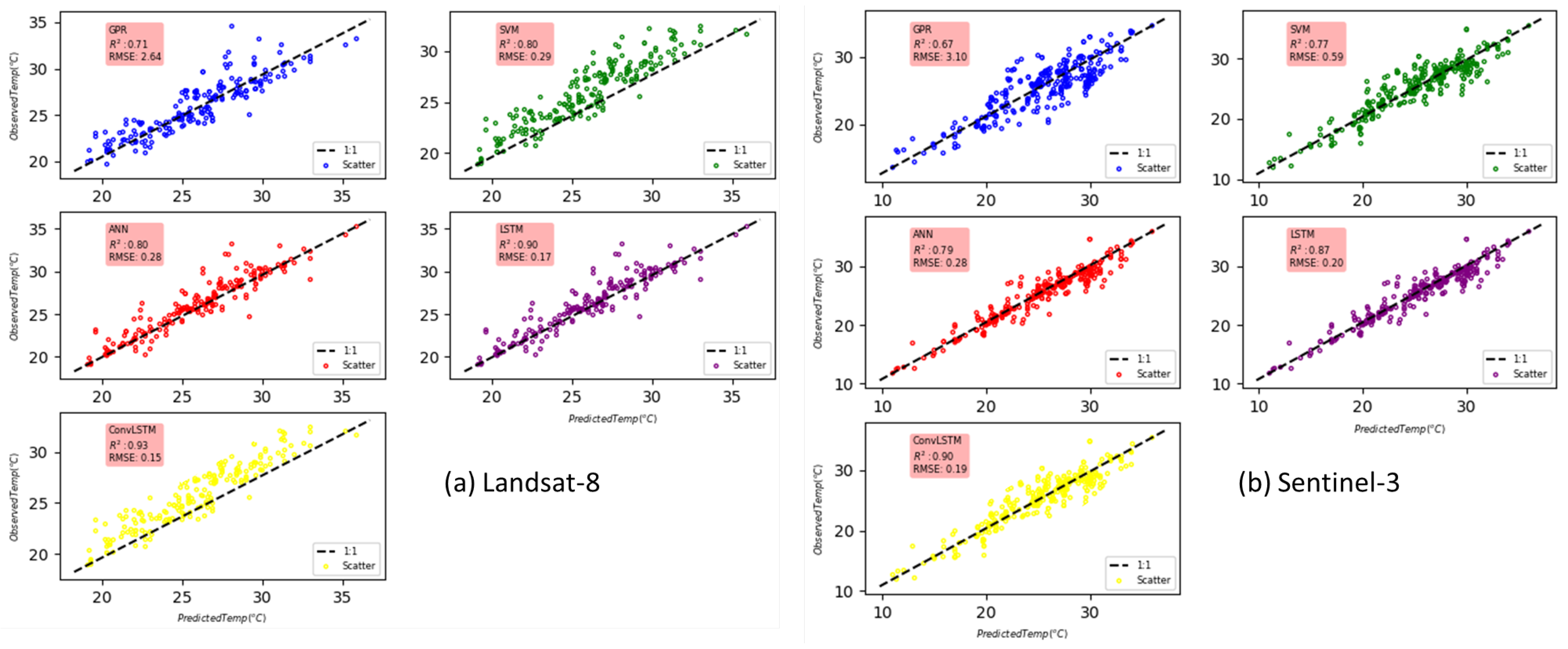
- The five models tested performed well on both the test and training sets (accuracy > 0.67 for S3 and >0.71 for L8). Refer to Figure 8;
- DL models outperformed all other models in terms of greater R2 and as well as lower RMSE values when comparing the five generated models, achieving the highest accuracy in testing data. In terms of R2 and RMSE, 1D-ConvLSTM performed ahead of every other model for both satellites following the descending order: 1D-ConvLSTM > LSTM > ANN > SVM > GPR (Figure 8);
- Two deep-learning architectures (LSTM and 1D-ConvLSTM) performed relatively better than conventional and simple ANN architectures on test data used to evaluate different models. LSTM layers provide an added advantage over conventional model architecture when working with time series data since they are made up of memory cell blocks (known as hidden units in simple hidden layers). The hidden memory cell blocks can store information for longer time interval [58]. Deep-learning architectures needed more time to train than basic ML structures despite having superior predictive accuracy because they had more trainable parameters. Although adopting techniques, such as transfer learning or graphics processing unit (GPU) computing, can help to reduce training times;
- For all the evaluated models, the median R2 values ranged from 0.67 to 0.92, while the median RMSE scores ranged from 0.16 to 3.4 °C. In addition, L8 models performed better than their S3 corresponding models. It is also important to note that for both satellites, DL models performed better than conventional ML techniques. Similarly, this trend is also observed for the RMSE metric.
- Furthermore, the results of the two sample t-tests confirm the null hypothesis (H0), which states that the average RMSE score for Landsat-8 is assumed to be less than or equal to the average of Sentinel-3’s RMSE score, with equal or pooled variance (p-value = 0.9453, (p(x ≤ T) = 0.05). This means that the probability of a type I error, which involves rejecting the correct H0, is too high: 94.53% for the 50 samples. This is further evidence that L8 SWT estimates are more precise than S3 estimates;
- These sensor performances may be attributed to the following factors: sensor characteristics, L8 has a higher spatial resolution compared to S3, data processing, season, day-night changes (in the case of Sentinel-3), and atmospheric correction.
4.2. Hypothesis Testing: Two-Factor ANOVA
- Type of ML/DL main effect (F = 17.4607, p = 4.001 × 10−12 ***);
- The satellite type main effect (F = 15.4478, p = 0.0001208 ***);
- Interaction effect (satellite type × type of ML/DL) (F = 3.5325, p = 0.008399 ***);
- The results indicate that both factors and their interaction have an impact on model performance;
- An increasing effect based on the factorial analysis of variance using effect size estimates () was observed in the following descending order: type of ML/DL > interaction > type of satellite;
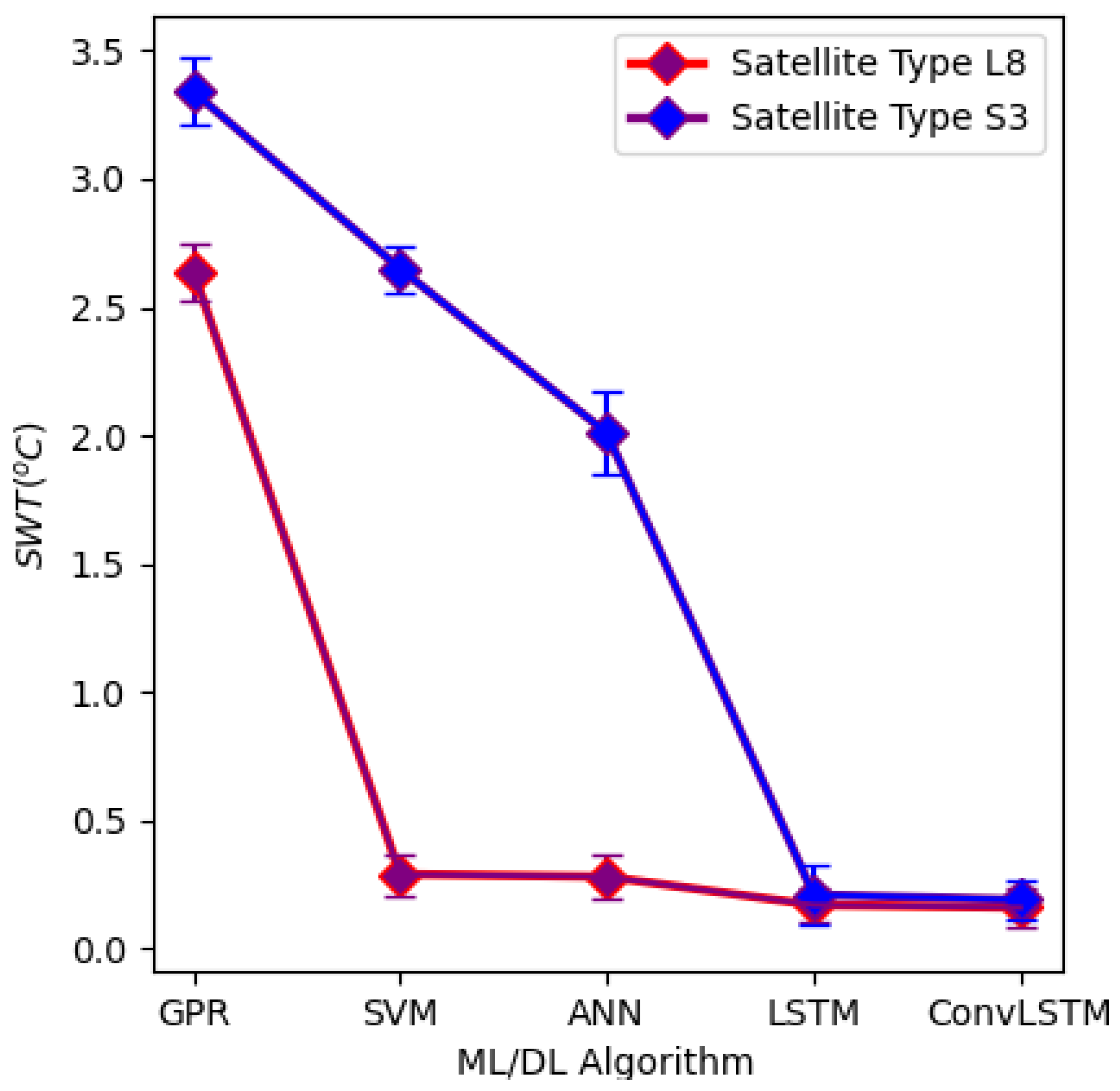
- According to the two-factor ANOVA design approach, the selection of ML/DL is therefore more significant than the type of satellite used. The model score for S3 is improved by using DL models as shown by diverging or crossing lines, which shows evidence of interaction between the two factors (Figure 10);
4.3. Hypothesis Testing: Scheffe’s Post-Hoc Multiple Comparison
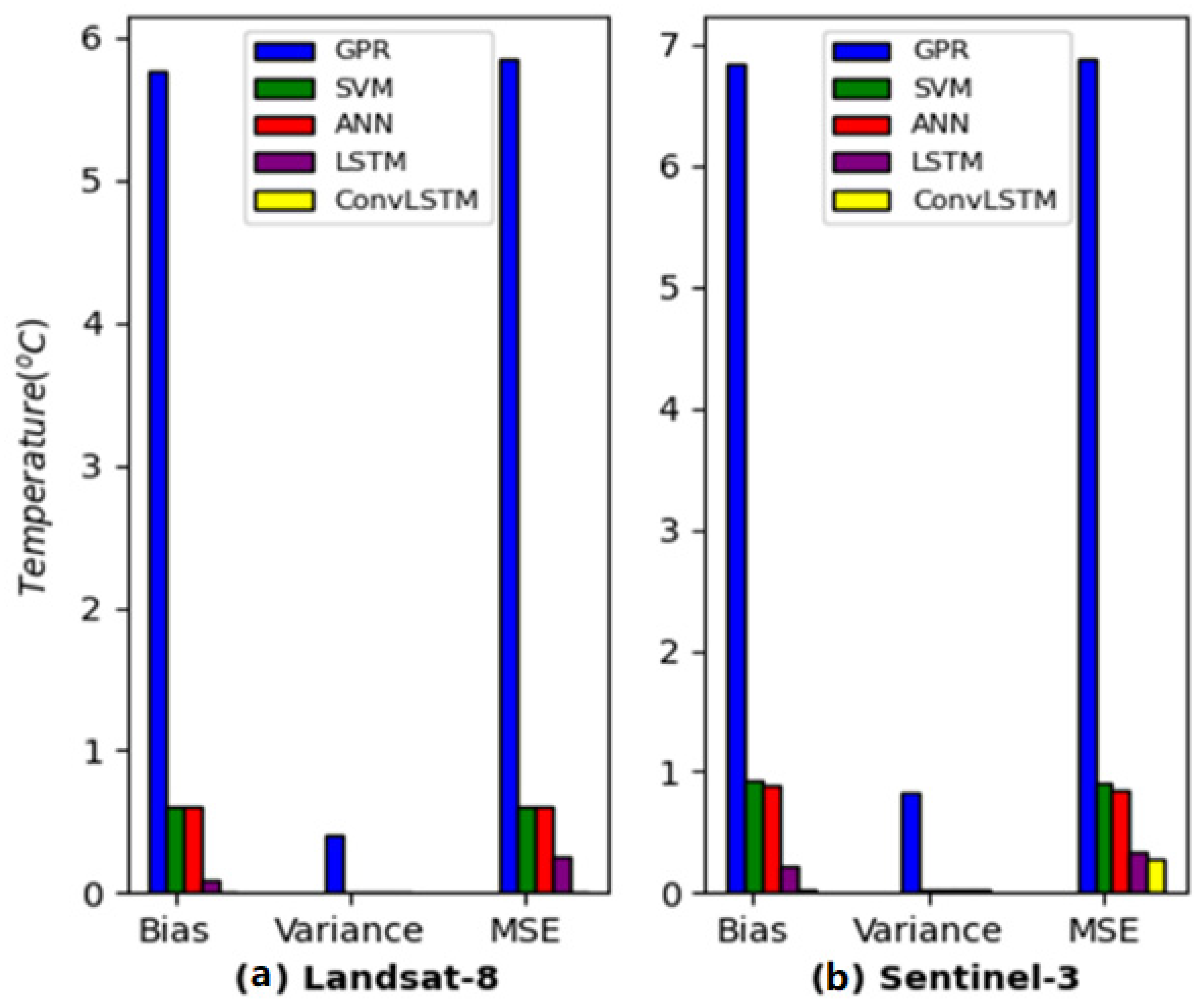
4.4. Bias-Variance Trade-off for the ML/DL Models
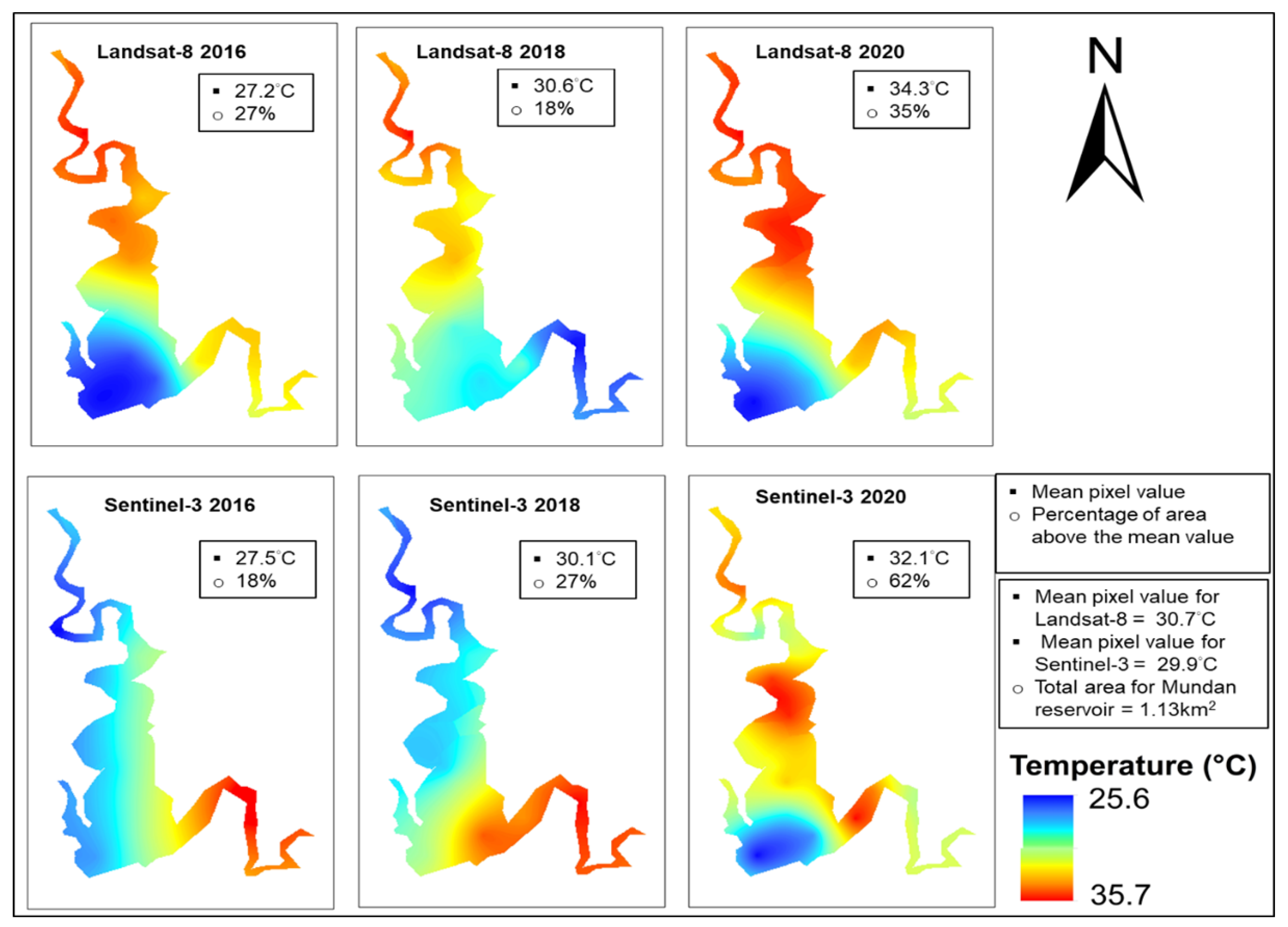
4.5. Spatio-Temoporary Variation Thermal Maps for Mundan
5. Conclusions
- (1)
- The ANOVA result demonstrated that the ML/DL model used had a more significant impact on estimation accuracy than the type of satellite used. However, it demonstrates that both factors had a significant impact in improving SWT’s estimation accuracy;
- (2)
- To further support this, DL models applied to low resolution satellites performed significantly well;
- (3)
- The considered important evaluation metrics for estimation of SWT were R2, RMSE, and bias-variance trade-off evaluators;
- (4)
- The maximum prediction accuracy was achieved by the ConvLSTM based on L8-TIRS data, with R2 = 0.93, RMSE = 0.15 °C.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mansourmoghaddam, M.; Ghafarian Malamiri, H.R.; Rousta, I.; Olafsson, H.; Zhang, H. Assessment of Palm Jumeirah Island’s construction effects on the surrounding water quality and surface temperatures during 2001–2020. Water 2022, 14, 634. [Google Scholar] [CrossRef]
- Suzuki, H.; Nakatsugawa, M.; Ishiyama, N. Climate change impacts on stream water temperatures in a snowy cold region according to geological conditions. Water 2022, 14, 2166. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Stewart, I.T.; Maurer, E.P. Effects of climate change on stream temperature, dissolved oxygen, and sediment concentration in the sierra Nevada in California. Water Resour. Res. 2013, 49, 2765–2782. [Google Scholar] [CrossRef]
- Ho, J.C.; Michalak, A.M.; Pahlevan, N. Widespread global increase in intense lake phytoplankton blooms since the 1980s. Nature 2019, 574, 667–670. [Google Scholar] [CrossRef]
- Findlay, H.S.; Turley, C. Ocean acidification and climate change. In Climate Change; Elsevier: Amsterdam, The Netherlands, 2021; pp. 251–279. [Google Scholar] [CrossRef]
- The Food and Agriculture Organization of the United Nations (FAO); The International Water Management Institute (IWMI). Water Pollution from Agriculture: A global Review. FAO: Rome, Italy; International Water Management Institute (IWMI): Colombo, Sri Lanka. CGIAR Research Program on Water, Land and Ecosystems 2017, (WLE). Available online: https://www.fao.org/3/i7754e/i7754e.pdf (accessed on 20 June 2021).
- Damania, R.; Desbureaux, S.; Rodella, A.-S.; Russ, J.; Zaveri, E. Quality Unknown: The Invisible Water Crisis; World Bank Publications: Washington, DC, USA, 2019. [Google Scholar] [CrossRef]
- Cherif, E.K.; Mozetič, P.; Francé, J.; Flander-Putrle, V.; Faganeli-Pucer, J.; Vodopivec, M. Comparison of in-situ chlorophyll-a time series and sentinel-3 ocean and land color instrument data in Slovenian National Waters (gulf of trieste, Adriatic Sea). Water 2021, 13, 1903. [Google Scholar] [CrossRef]
- Zhu, W.-D.; Qian, C.-Y.; He, N.-Y.; Kong, Y.-X.; Zou, Z.-Y.; Li, Y.-W. Research on chlorophyll-a concentration retrieval based on BP neural network model—case study of Dianshan Lake, China. Sustainability 2022, 14, 8894. [Google Scholar] [CrossRef]
- Seidel, M.; Hutengs, C.; Oertel, F.; Schwefel, D.; Jung, A.; Vohland, M. Underwater use of a hyperspectral camera to estimate optically active substances in the water column of Freshwater Lakes. Remote Sens. 2020, 12, 1745. [Google Scholar] [CrossRef]
- Yang, H.; Kong, J.; Hu, H.; Du, Y.; Gao, M.; Chen, F. A review of remote sensing for Water Quality Retrieval: Progress and challenges. Remote Sens. 2022, 14, 1770. [Google Scholar] [CrossRef]
- Malakar, N.K.; Hulley, G.C.; Hook, S.J.; Laraby, K.; Cook, M.; Schott, J.R. An operational land surface temperature product for landsat thermal data: Methodology and validation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5717–5735. [Google Scholar] [CrossRef]
- Kumar, C.; Podestá, G.; Kilpatrick, K.; Minnett, P. A machine learning approach to estimating the error in satellite sea surface temperature retrievals. Remote Sens. Environ. 2021, 255, 112227. [Google Scholar] [CrossRef]
- Ai, B.; Wen, Z.; Jiang, Y.; Gao, S.; Lv, G. Sea surface temperature inversion model for infrared remote sensing images based on Deep Neural Network. Infrared Phys. Technol. 2019, 99, 231–239. [Google Scholar] [CrossRef]
- Sammartino, M.; Buongiorno Nardelli, B.; Marullo, S.; Santoleri, R. An artificial neural network to infer the Mediterranean 3D chlorophyll-a and temperature fields from remote sensing observations. Remote Sens. 2020, 12, 4123. [Google Scholar] [CrossRef]
- Jung, S.; Yoo, C.; Im, J. High-resolution seamless daily sea surface temperature based on satellite data fusion and machine learning over Kuroshio Extension. Remote Sens. 2022, 14, 575. [Google Scholar] [CrossRef]
- Barth, A.; Alvera-Azcárate, A.; Licer, M.; Beckers, J.-M. DINCAE 1.0: A convolutional neural network with error estimates to reconstruct sea surface temperature satellite observations. Geosci. Model Dev. 2020, 13, 1609–1622. [Google Scholar] [CrossRef]
- Hafeez, S.; Wong, M.S.; Abbas, S.; Asim, M. Evaluating landsat-8 and sentinel-2 data consistency for high spatiotemporal inland and coastal water quality monitoring. Remote Sens. 2022, 14, 3155. [Google Scholar] [CrossRef]
- Pan, Y.; Bélanger, S.; Huot, Y. Evaluation of atmospheric correction algorithms over lakes for high-resolution multispectral imagery: Implications of adjacency effect. Remote Sens. 2022, 14, 2979. [Google Scholar] [CrossRef]
- Malenovský, Z.; Rott, H.; Cihlar, J.; Schaepman, M.E.; García-Santos, G.; Fernandes, R.; Berger, M. Sentinels for science: Potential of sentinel-1, -2, and -3 missions for scientific observations of ocean, cryosphere, and land. Remote Sens. Environ. 2012, 120, 91–101. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.Ö.; Floury, N.; Brown, M.; et al. Gmes sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Kravitz, J.; Matthews, M.; Lain, L.; Fawcett, S.; Bernard, S. Potential for high fidelity global mapping of common inland water quality products at high spatial and temporal resolutions based on a synthetic data and machine learning approach. Front. Environ. Sci. 2021, 9, 587660. [Google Scholar] [CrossRef]
- Caballero, I.; Roca, M.; Santos-Echeandía, J.; Bernárdez, P.; Navarro, G. Use of the Sentinel-2 and Landsat-8 Satellites for Water Quality Monitoring: An Early Warning Tool in the Mar Menor Coastal Lagoon. Remote Sens. 2022, 14, 2744. [Google Scholar] [CrossRef]
- Dorji, P.; Fearns, P. Impact of the spatial resolution of satellite remote sensing sensors in the quantification of total suspended sediment concentration: A case study in turbid waters of northern Western Australia. PLoS ONE 2017, 12, e0175042. [Google Scholar] [CrossRef] [PubMed]
- Al-Kharusi, E.S.; Tenenbaum, D.E.; Abdi, A.M.; Kutser, T.; Karlsson, J.; Bergström, A.-K.; Berggren, M. Large-scale retrieval of coloured dissolved organic matter in Northern Lakes using sentinel-2 data. Remote Sens. 2020, 12, 157. [Google Scholar] [CrossRef]
- Yu, Z.; Yang, K.; Luo, Y.; Shang, C.; Zhu, Y. Lake surface water temperature prediction and changing characteristics analysis—a case study of 11 natural lakes in Yunnan-Guizhou Plateau. J. Clean. Prod. 2020, 276, 122689. [Google Scholar] [CrossRef]
- Yang, L.; Driscol, J.; Sarigai, S.; Wu, Q.; Lippitt, C.D.; Morgan, M. Towards Synoptic Water Monitoring Systems: A Review of AI Methods for Automating Water Body Detection and Water Quality Monitoring Using Remote Sensing. Sensors 2022, 22, 2416. [Google Scholar] [CrossRef]
- Du, C.; Ren, H.; Qin, Q.; Meng, J.; Zhao, S. A practical split-window algorithm for estimating land surface temperature from Landsat 8 data. Remote Sens. 2015, 7, 647–665. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Li, Z.-L.; Stoll, M.P.; Becker, F. Multi-channel and multi-angle algorithms for estimating sea and land surface temperature with ATSR data. Int. J. Remote Sens. 1996, 17, 2089–2114. [Google Scholar] [CrossRef]
- Cui, T.; Pagendam, D.; Gilfedder, M. Gaussian process machine learning and Kriging for groundwater salinity interpolation. Environ. Model. Softw. 2021, 144, 105170. [Google Scholar] [CrossRef]
- Ewusi, A.; Ahenkorah, I.; Aikins, D. Modelling of total dissolved solids in water supply systems using regression and supervised machine learning approaches. Appl. Water Sci. 2021, 11, 13. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Gaussian processes in machine learning. Adv. Lect. Mach. Learn. 2004, 3176, 63–71. [Google Scholar] [CrossRef]
- Mamun, M.; Lee, S.-J.; An, K.-G. Temporal and spatial variation of nutrients, suspended solids, and chlorophyll in Yeongsan Watershed. J. Asia-Pac. Biodivers. 2018, 11, 206–216. [Google Scholar] [CrossRef]
- Mamun, M.; Kim, J.-J.; Alam, M.A.; An, K.-G. Prediction of algal chlorophyll-a and water clarity in monsoon-region reservoir using machine learning approaches. Water 2019, 12, 30. [Google Scholar] [CrossRef]
- Cho, K.H.; Sthiannopkao, S.; Pachepsky, Y.A.; Kim, K.-W.; Kim, J.H. Prediction of contamination potential of groundwater arsenic in Cambodia, Laos, and Thailand using Artificial Neural Network. Water Res. 2011, 45, 5535–5544. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Cho, K.H.; Park, J.; Cha, S.M.; Kim, J.H. Development of early-warning protocol for predicting chlorophyll-a concentration using machine learning models in freshwater and estuarine reservoirs, Korea. Science of The Total Environment 2015, 502, 31–41. [Google Scholar] [CrossRef]
- Zhang, Z.; Pan, X.; Jiang, T.; Sui, B.; Liu, C.; Sun, W. Monthly and Quarterly Sea Surface Temperature Prediction Based on Gated Recurrent Unit Neural Network. J. Mar. Sci. Eng. 2020, 8, 249. [Google Scholar] [CrossRef]
- Yang, Y.; Dong, J.; Sun, X.; Lima, E.; Mu, Q.; Wang, X. A CFCC-LSTM model for sea surface temperature prediction. IEEE Geosci. Remote Sens. Lett. 2018, 15, 207–211. [Google Scholar] [CrossRef]
- Ye, W.; Zhang, F.; Du, Z. Machine Learning in Extreme Value Analysis, an Approach to Detecting Harmful Algal Blooms with Long-Term Multisource Satellite Data. Remote Sens. 2022, 14, 3918. [Google Scholar] [CrossRef]
- Jia, X.; Ji, Q.; Han, L.; Liu, Y.; Han, G.; Lin, X. Prediction of Sea Surface Temperature in the East China Sea Based on LSTM Neural Network. Remote Sens. 2022, 14, 3300. [Google Scholar] [CrossRef]
- Yan, S. Understanding LSTM and Its Diagrams. Medium. Available online: https://blog.mlreview.com/understanding-lstm-and-its-diagrams-37e2f46f1714 (accessed on 5 September 2022).
- Su, H.; Jiang, J.; Wang, A.; Zhuang, W.; Yan, X.-H. Subsurface Temperature Reconstruction for the Global Ocean from 1993 to 2020 Using Satellite Observations and Deep Learning. Remote Sens. 2022, 14, 3198. [Google Scholar] [CrossRef]
- Song, T.; Wei, W.; Meng, F.; Wang, J.; Han, R.; Xu, D. Inversion of Ocean Subsurface Temperature and Salinity Fields Based on Spatio-Temporal Correlation. Remote Sens. 2022, 14, 2587. [Google Scholar] [CrossRef]
- Iskandaryan, D.; Ramos, F.; Trilles, S. Bidirectional convolutional LSTM for the prediction of nitrogen dioxide in the city of Madrid. PLoS ONE 2022, 17, e0269295. [Google Scholar] [CrossRef] [PubMed]
- Kaastra, I.; Boyd, M. Designing a neural network for forecasting financial and Economic Time Series. Neurocomputing 1996, 10, 215–236. [Google Scholar] [CrossRef]
- Mozaffari, L.; Mozaffari, A.; Azad, N.L. Vehicle speed prediction via a sliding-window time series analysis and an evolutionary least learning machine: A case study on san francisco urban roads. Eng. Sci. Technol. Int. J. 2015, 18, 150–162. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J. Predicting inflow rate of the Soyang River Dam using Deep learning techniques. Water 2021, 13, 2447. [Google Scholar] [CrossRef]
- McCombie, A.M. Some relations between air temperatures and the surface water temperatures of Lakes. Limnol. Oceanogr. 1959, 4, 252–258. [Google Scholar] [CrossRef]
- Webb, B.W.; Zhang, Y. Spatial and seasonal variability in the components of the river heat budget. Hydrol. Processes 1997, 11, 79–101. [Google Scholar] [CrossRef]
- Mohseni, O.; Stefan, H.G. Stream temperature/air temperature relationship: A physical interpretation. J. Hydrol. 1999, 218, 128–141. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Luo, Y.; Stewart, I.T.; Maurer, E.P. Development and application of a hydroclimatological stream temperature model within the soil and water assessment tool. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
- Hafeez, S.; Wong, M.; Ho, H.; Nazeer, M.; Nichol, J.; Abbas, S.; Tang, D.; Lee, K.; Pun, L. Comparison of machine learning algorithms for retrieval of water quality indicators in case-II waters: A case study of hong kong. Remote Sens. 2019, 11, 617. [Google Scholar] [CrossRef]
- Ewuzie, U.; Bolade, O.P.; Egbedina, A.O. Application of deep learning and machine learning methods in water quality modeling and prediction: A Review. In Current Trends and Advances in Computer-Aided Intelligent Environmental Data Engineering; Elsevier: Amsterdam, The Netherlands, 2022; pp. 185–218. [Google Scholar] [CrossRef]
- Arias-Rodriguez, L.F.; Duan, Z.; Sepúlveda, R.; Martinez-Martinez, S.I.; Disse, M. Monitoring water quality of Valle de Bravo Reservoir, Mexico, using entire lifespan of Meris data and machine learning approaches. Remote Sens. 2020, 12, 1586. [Google Scholar] [CrossRef]
- Bande, P.; Adam, E.; Elbasit, M.A.A.; Adelabu, S. Comparing Landsat 8 and sentinel-2 in mapping water quality at Vaal dam. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 22–27. [Google Scholar]
- Windle, A.E.; Evers-King, H.; Loveday, B.R.; Ondrusek, M.; Silsbe, G.M. Evaluating atmospheric correction algorithms applied to olci sentinel-3 data of Chesapeake Bay Waters. Remote Sens. 2022, 14, 1881. [Google Scholar] [CrossRef]
- Baek, S.-S.; Pyo, J.; Chun, J.A. Prediction of water level and water quality using a CNN-LSTM combined deep learning approach. Water 2020, 12, 3399. [Google Scholar] [CrossRef]
- Schaeffer, B.A.; Iiames, J.; Dwyer, J.; Urquhart, E.; Salls, W.; Rover, J.; Seegers, B. An initial validation of Landsat 5 and 7 derived surface water temperature for U.S. lakes, reservoirs, and estuaries. Int. J. Remote Sens. 2018, 39, 7789–7805. [Google Scholar] [CrossRef]
- Pizani, F.M.; Maillard, P.; Ferreira, A.F.; de Amorim, C.C. Estimation of water quality in a reservoir from sentinel-2 MSI and landsat-8 oli sensors. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, V-3-2020, 401–408. [Google Scholar] [CrossRef]
- Yadav, S.; Yamashiki, Y.; Susaki, J.; Yamashita, Y.; Ishikawa, K. Chlorophyll estimation of lake water and coastal water using landsat-8 and sentinel-2a satellite. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-3/W7, 77–82. [Google Scholar] [CrossRef]
- Zarei, A.; Shah-Hosseini, R.; Ranjbar, S.; Hasanlou, M. Validation of non-linear split window algorithm for land surface temperature estimation using sentinel-3 satellite imagery: Case study; Tehran Province, Iran. Adv. Space Res. 2021, 67, 3979–3993. [Google Scholar] [CrossRef]
- Piñeiro, G.; Perelman, S.; Guerschman, J.P.; Paruelo, J.M. How to evaluate models: Observed vs. predicted or predicted vs. observed? Ecol. Model. 2008, 216, 316–322. [Google Scholar] [CrossRef]
- Ali, K.A.; Moses, W.J. Application of a PLS-augmented ANN model for retrieving chlorophyll-a from hyperspectral data in case 2 waters of the western basin of Lake Erie. Remote Sens. 2022, 14, 3729. [Google Scholar] [CrossRef]
- Seegers, B.N.; Stumpf, R.P.; Schaeffer, B.A.; Loftin, K.A.; Werdell, P.J. Performance metrics for the assessment of Satellite Data Products: An ocean color case study. Opt. Express 2018, 26, 7404. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Sathyendranath, S.; Müller, D.; Brockmann, C.; Deschamps, P.-Y.; Devred, E.; Doerffer, R.; Fomferra, N.; Franz, B.; Grant, M.; et al. The Ocean Colour Climate Change Initiative: III. A round-robin comparison on in-water bio-optical algorithms. Remote Sens. Environ. 2015, 162, 271–294. [Google Scholar] [CrossRef]
- Fisher, T.; Gibson, H.; Liu, Y.; Abdar, M.; Posa, M.; Salimi-Khorshidi, G.; Hassaine, A.; Cai, Y.; Rahimi, K.; Mamouei, M. Uncertainty-aware interpretable deep learning for slum mapping and monitoring. Remote Sens. 2022, 14, 3072. [Google Scholar] [CrossRef]
- Hu, C. A novel ocean color index to detect floating algae in the global oceans. Remote Sens. Environ. 2009, 113, 2118–2129. [Google Scholar] [CrossRef]
- Shen, M.; Chen, J.; Zhuan, M.; Chen, H.; Xu, C.-Y.; Xiong, L. Estimating uncertainty and its temporal variation related to global climate models in quantifying climate change impacts on hydrology. J. Hydrol. 2018, 556, 10–24. [Google Scholar] [CrossRef]


| Landsat-8 Data Set | ||||||
|---|---|---|---|---|---|---|
| Index | RH (%) | WS (m/s) | Precip (mm) | AAT (°C) | SWTL8 (°C) | SWTGT (°C) |
| Count (N) | 882 | 882 | 882 | 882 | 882 | 882 |
| Mean | 66.8 | 1.42 | 0.10 | 27.4 | 27.7 | 26.0 |
| Std. Dev | 19.6 | 1.34 | 0.66 | 4.31 | 3.69 | 3.75 |
| Min | 10 | 0 | 0 | 17 | 19.1 | 19.1 |
| First Quartile | 57.3 | 0.3 | 0 | 23.6 | 24.7 | 23 |
| Median | 69 | 1 | 0 | 27.6 | 27 | 25.9 |
| Third Quartile | 80 | 2.4 | 0 | 31 | 30.3 | 28.7 |
| Max | 99 | 7.7 | 5 | 36.9 | 37.6 | 36.3 |
| Sentinel-3 Data Set | ||||||
| Index | RH (%) | WS (m/s) | Precip (mm) | AAT (°C) | SWTS3 (°C) | SWTGT (°C) |
| Count (N) | 1050 | 1050 | 1050 | 1050 | 1050 | 1050 |
| Mean | 77.9 | 1.39 | 0.07 | 26.0 | 24.1 | 25.1 |
| Std. Dev | 13.3 | 1.82 | 0.49 | 4.73 | 4.23 | 4.55 |
| Min | 38 | 0 | 0 | 14.4 | 12.4 | 11 |
| First Quartile | 67 | 0.1 | 0 | 22 | 21.2 | 21.7 |
| Median | 76 | 0.8 | 0 | 27.0 | 24.4 | 25.5 |
| Third Quartile | 90 | 1.9 | 0 | 29.1 | 27 | 28.2 |
| Max | 100 | 10.1 | 6.5 | 36 | 35.5 | 36 |
| Model | Hyper-Parameter Name | Hyperparameter Description | Grid Search Parameter Values | Optimal Hyper-Parameter Value |
| GPR | length_scale | The length-scale of the respective feature dimension is specified. | 0.5, 1, 2, 3 | 1 |
| Kernel function | Transforms data that is linearly inseparable into data that is linearly separable and specifies the kernel type to be used in the algorithm. | RBF, Constant, and exponential | RBF | |
| n_restarts_optimizer | The number of optimizer restarts required to find the kernel parameters that maximize the log-marginal likelihood. | 5, 7, 9, 11, 13 | 9 | |
| SVM | Cost (C) | Regularization parameter | 0.1, 1, 10, 100, 1000 | 10 |
| gamma | Kernel coefficient for RBF, poly and Sigmoid | 0.0001, 0.001, 0.01, 0.1, 1 | 0.0001 | |
| Kernel function | Transformation of linearly inseparable data to linearly separable ones and specifying the kernel type to be used in the algorithm | RBF, Sigmoid, Linear, and Polynomial | RBF | |
| epsilon (ε) | Defines a tolerance margin in which errors are not penalized. | 0.01, 0.1, 1, 1.5 | 0.1 | |
| ANN | Activation functions | The activation function compute the input values of a layer into output values | ReLU, Sigmoid, Softplus, and tanh | Sigmoid–hidden layers and ReLU–output layer |
| Optimizer | The optimizer changes the learning rate and weights of neurons in the neural network to achieve lowest loss function | Adam, SGD, RMSprop, and Adagrad | Adam | |
| Learning rate | Learning rate manipulates the step size for a model to attain the minimum loss function | 0.001, 1 | 0.01 | |
| Neurons | The number of neurons in every layer is set to be the same and should be adjusted to the solution complexity | 10, 100 | 65 | |
| Epochs | The number of times a whole dataset is passed through the neural network model | 20, 100 | 100 | |
| Batch size | Batch size is the number of training data sub-samples for the input. | 50, 500 | 100 | |
| Drop out | Dropout is another regularization layer. The dropout layer, randomly drops a certain number of neurons in a layer | 0, 2 | 0.9 | |
| Dropout rate | The rate of how much percentage of neurons to drop is set in the dropout rate | 0, 0.5 | 0.15 | |
| Batch Normalization | The batch normalization layer normalizes the values passed to it for every batch. This is similar to standard scaler in conventional Machine Learning | 0, 1 | 0.90 | |
| LSTM | Learning rate | Learning rate controls the step size for a model to reach the minimum loss function | 0.001, 1 | 10−3 |
| Epochs | The number of times a whole dataset is passed through the neural network model | 20, 100 | 100 | |
| Batch size | Batch size is the number of training data sub-samples for the input. | 50, 500 | 100 | |
| Drop out | The dropout layer is another name for the regularization layer, which randomly drops a set number of neurons in a layer. | 0, 2 | 0.5 | |
| ConvLSTM | Learning rate | Learning rate controls the step size for a model to reach the minimum loss function | 0.001, 1 | 10−3 |
| Epochs | The number of times an entire dataset is processed through the neural network model. | 20, 100 | 100 | |
| Batch size | Batch size is the number of training data sub-samples for the input. | 50, 500 | 100 | |
| Drop out | The dropout layer is another name for the regularization layer, which randomly drops a set number of neurons in a layer. | 0, 2 | 0.5 |
| L8 | L8 | L8 | L8 | L8 | L8 | S3 | S3 | S3 | S3 | S3 | S3 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SLT | ML/DL | GPR | SVM-RBF | SVM-Lin | ANN | LSTM | ConvLSTM | GPR | SVM-RBF | SVM-Lin | ANN | LSTM | ConvLSTM |
| L8 | GPR | ||||||||||||
| L8 | SVM-RBF | 0.001 | |||||||||||
| L8 | SVM-Lin | 0.001 | 1.00000 | ||||||||||
| L8 | ANN | 0.001 | 0.8999947 | 1.00000 | |||||||||
| L8 | LSTM | 0.001 | 0.8999947 | 1.00000 | 0.8999947 | ||||||||
| L8 | ConvLSTM | 0.001 | 0.8999947 | 1.00000 | 0.8999947 | 0.8999947 | |||||||
| S3 | GPR | 0.001 | 0.001 | 0.00000 | 0.001 | 0.001 | 0.001 | ||||||
| S3 | SVM-RBF | 0.8999947 | 0.001 | 0.000000 | 0.001 | 0.001 | 0.001 | 0.001 | |||||
| S3 | SVM-Lin | 0.8999947 | 0.001 | 0.000000 | 0.001 | 0.001 | 0.001 | 0.001 | 0.00000 | ||||
| S3 | ANN | 0.001 | 0.01 | 0.01 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 1.00000 | |||
| S3 | LSTM | 0.001 | 0.8999947 | 0.8999947 | 0.8999947 | 0.8999947 | 0.8999947 | 0.001 | 0.001 | 0.999781 | 0.001 | ||
| S3 | ConvLSTM | 0.001 | 0.8999947 | 0.8999947 | 0.8999947 | 0.8999947 | 0.8999947 | 0.001 | 0.001 | 0.999974 | 0.001 | 0.8999947 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukonza, S.S.; Chiang, J.-L. Micro-Climate Computed Machine and Deep Learning Models for Prediction of Surface Water Temperature Using Satellite Data in Mundan Water Reservoir. Water 2022, 14, 2935. https://doi.org/10.3390/w14182935
Mukonza SS, Chiang J-L. Micro-Climate Computed Machine and Deep Learning Models for Prediction of Surface Water Temperature Using Satellite Data in Mundan Water Reservoir. Water. 2022; 14(18):2935. https://doi.org/10.3390/w14182935
Chicago/Turabian StyleMukonza, Sabastian Simbarashe, and Jie-Lun Chiang. 2022. "Micro-Climate Computed Machine and Deep Learning Models for Prediction of Surface Water Temperature Using Satellite Data in Mundan Water Reservoir" Water 14, no. 18: 2935. https://doi.org/10.3390/w14182935