Designing Efficient and Sustainable Predictions of Water Quality Indexes at the Regional Scale Using Machine Learning Algorithms
Abstract
:1. Introduction
2. Materials and Methods
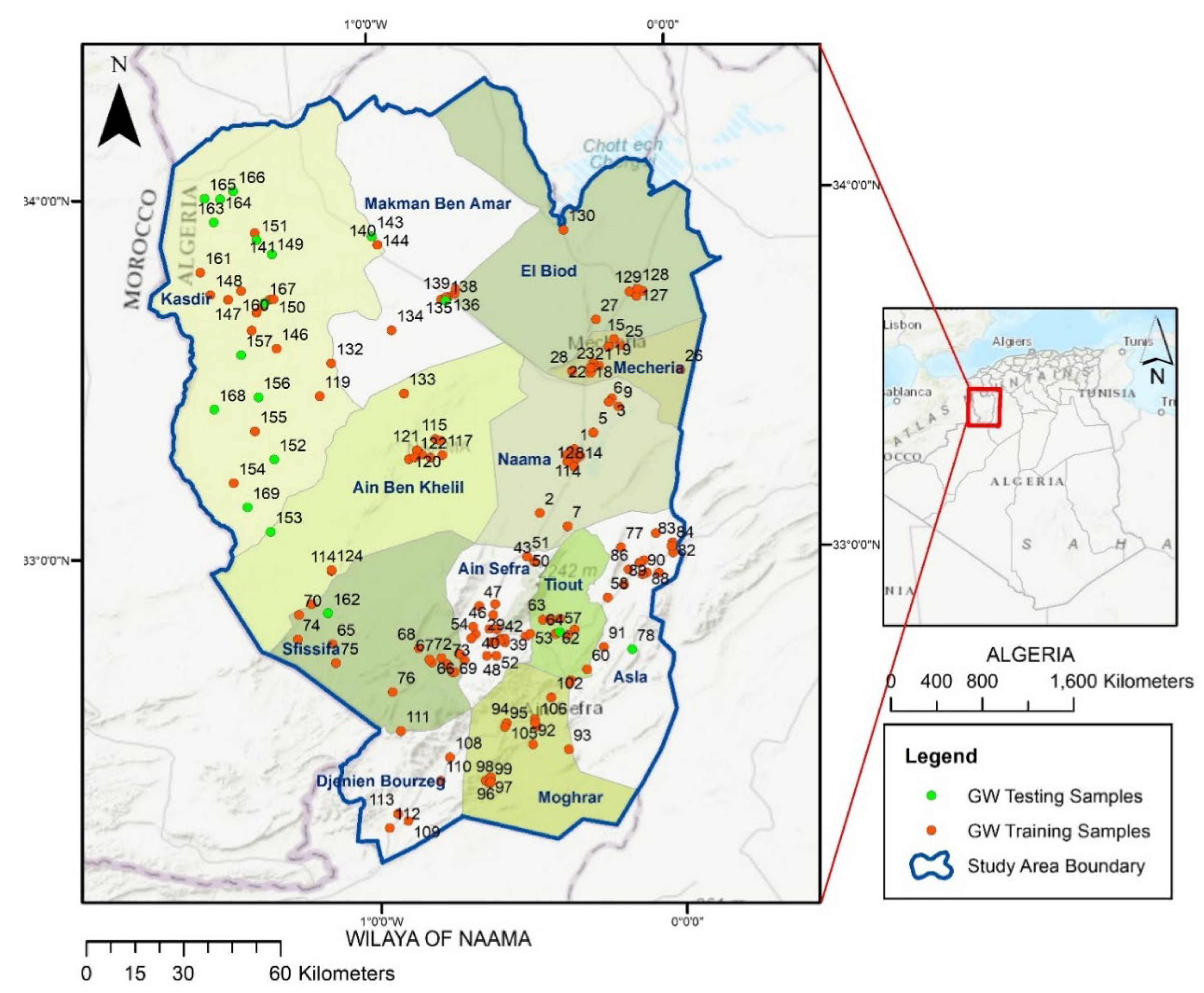
2.1. Description of the Study Area and Data Collection
2.2. Data Collection, Analysis, Sampling, Preprocessing and Water Quality Index Calculation
2.3. Data Classification
2.4. Data Standardization
2.5. Classification Techniques
2.5.1. Decision Tree
2.5.2. Ensemble Tree
2.5.3. K Nearest Neighbors (KNN)
2.5.4. Discrimination Analysis (DA) Classifier
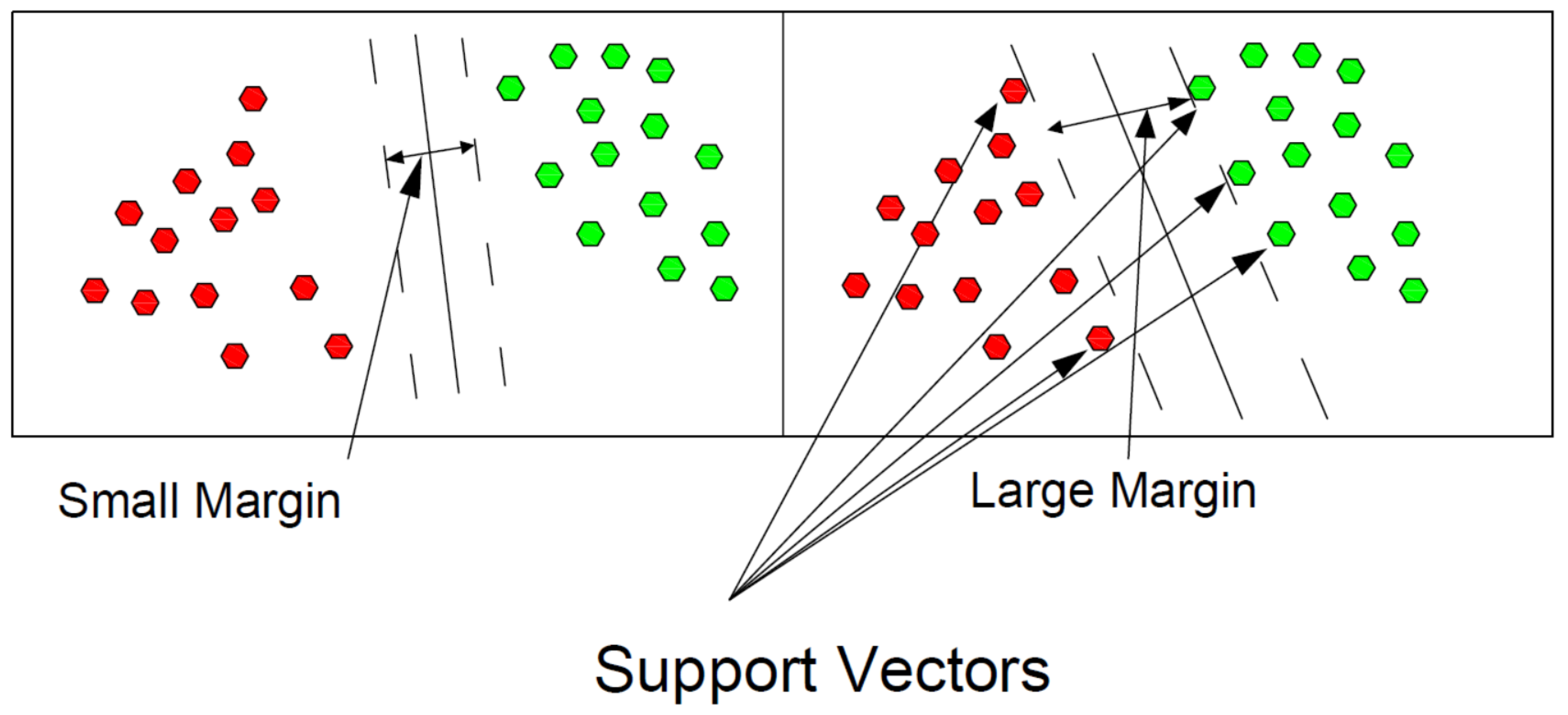
2.5.5. Support Vector Machine (SVM)
3. Results
3.1. Description of the Physicochemical Analysis of the Sampling Points
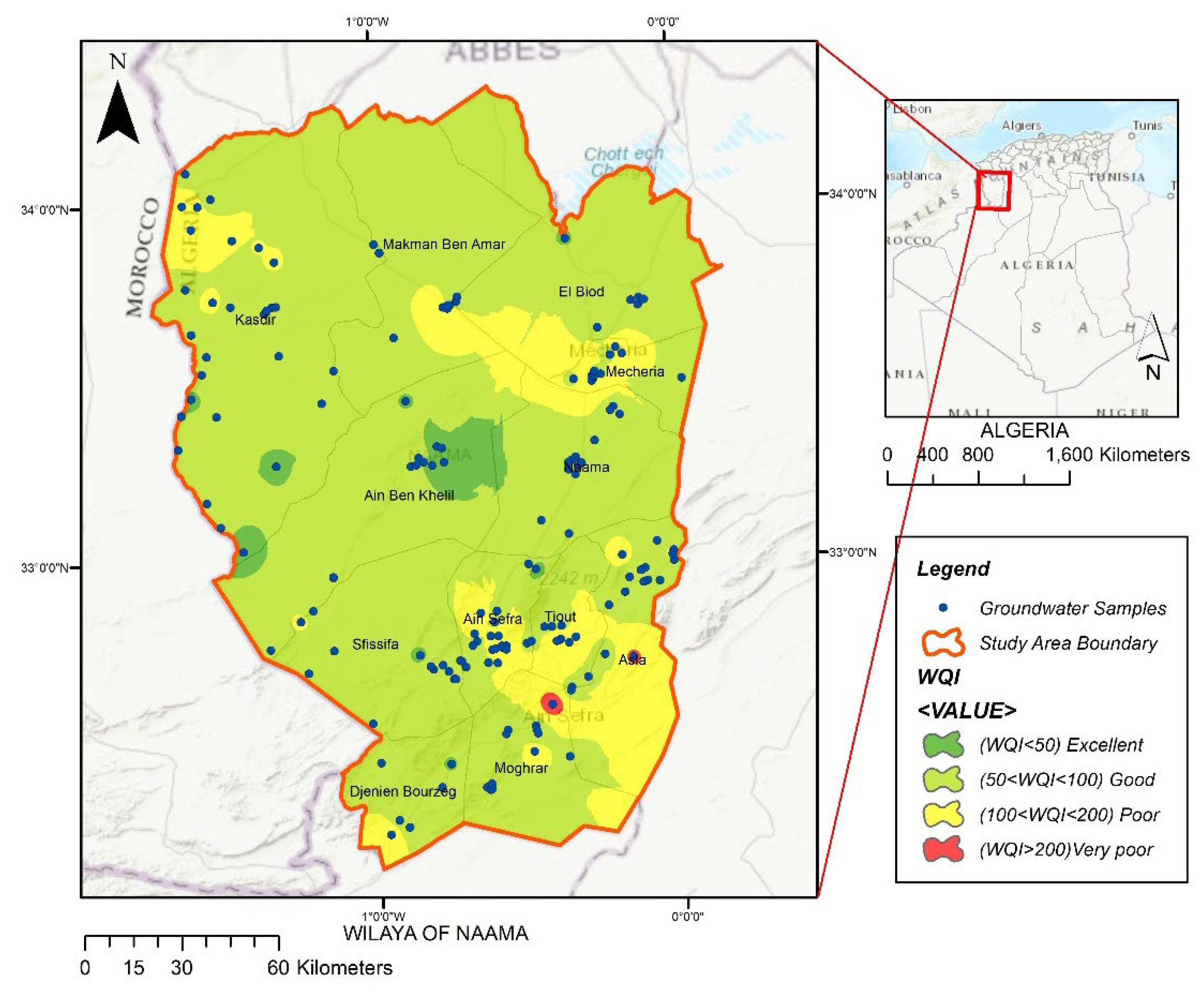
3.2. Water Quality Index Assessment
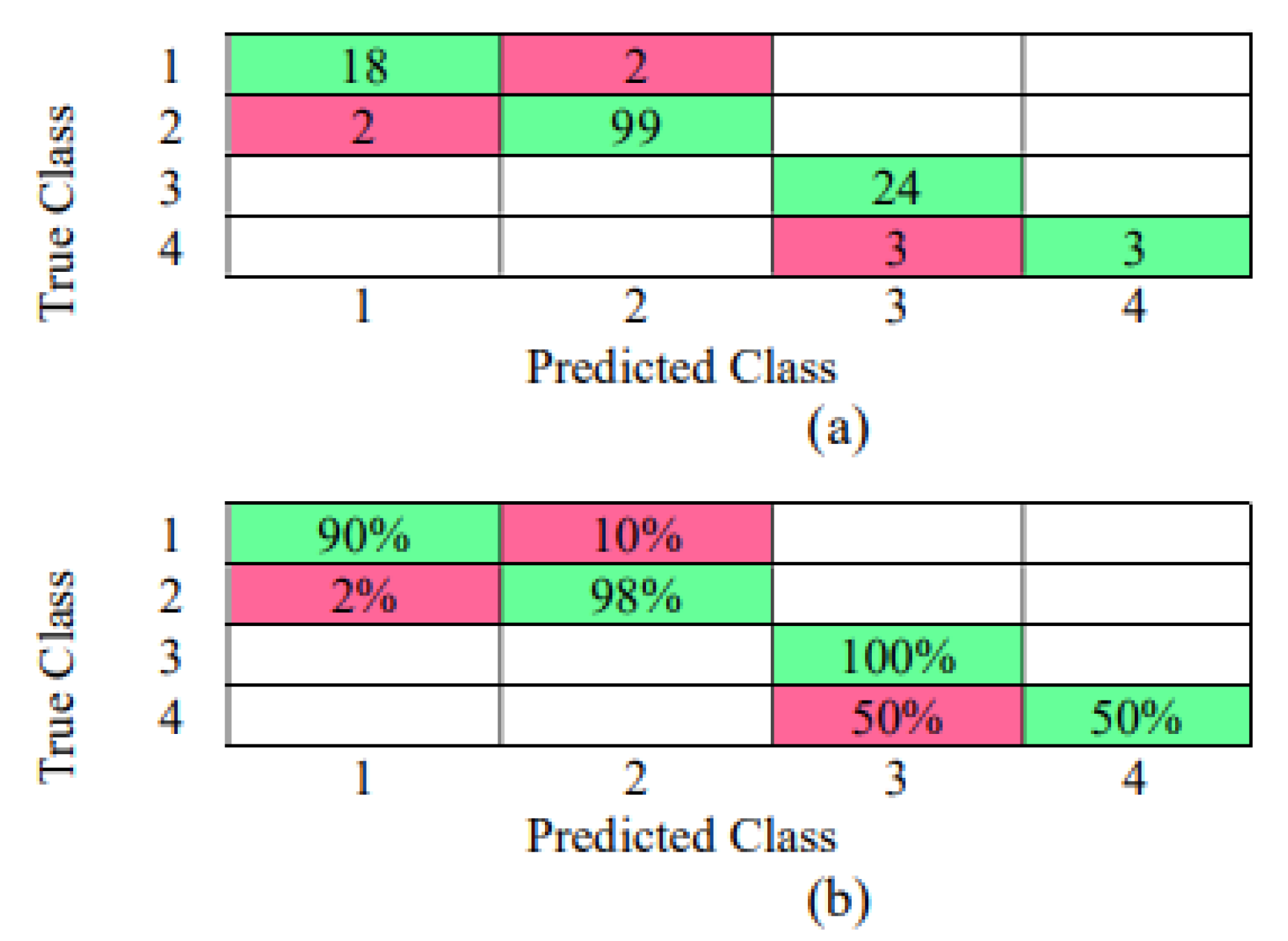
3.3. Results with Raw Data
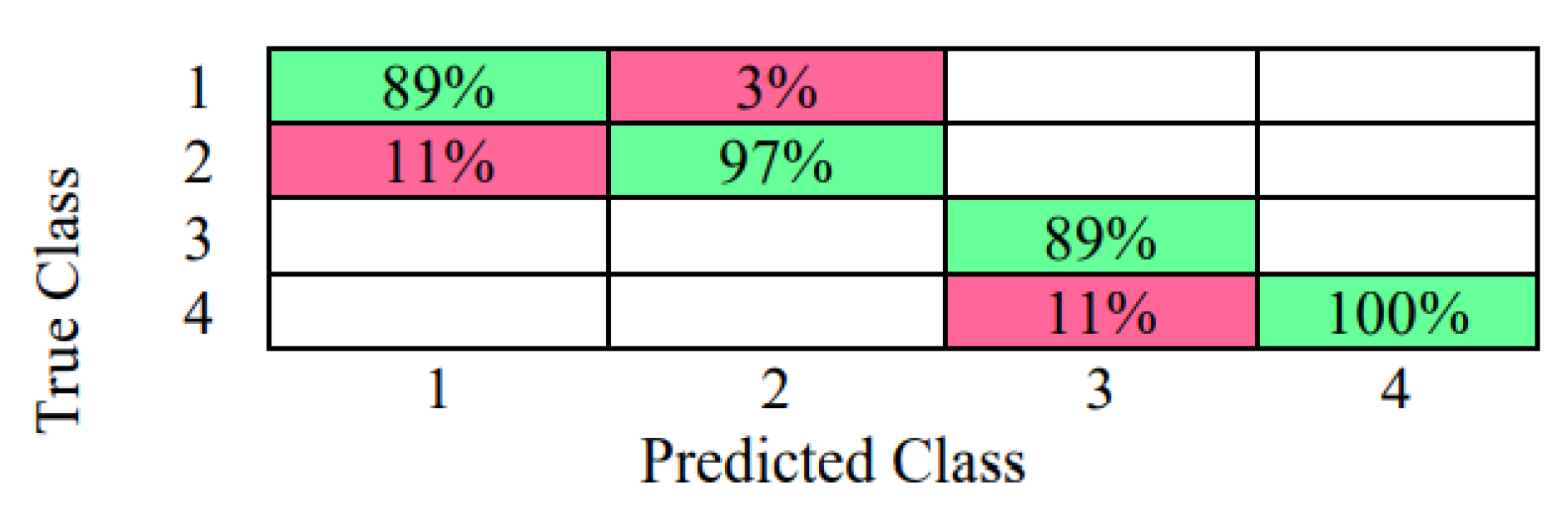
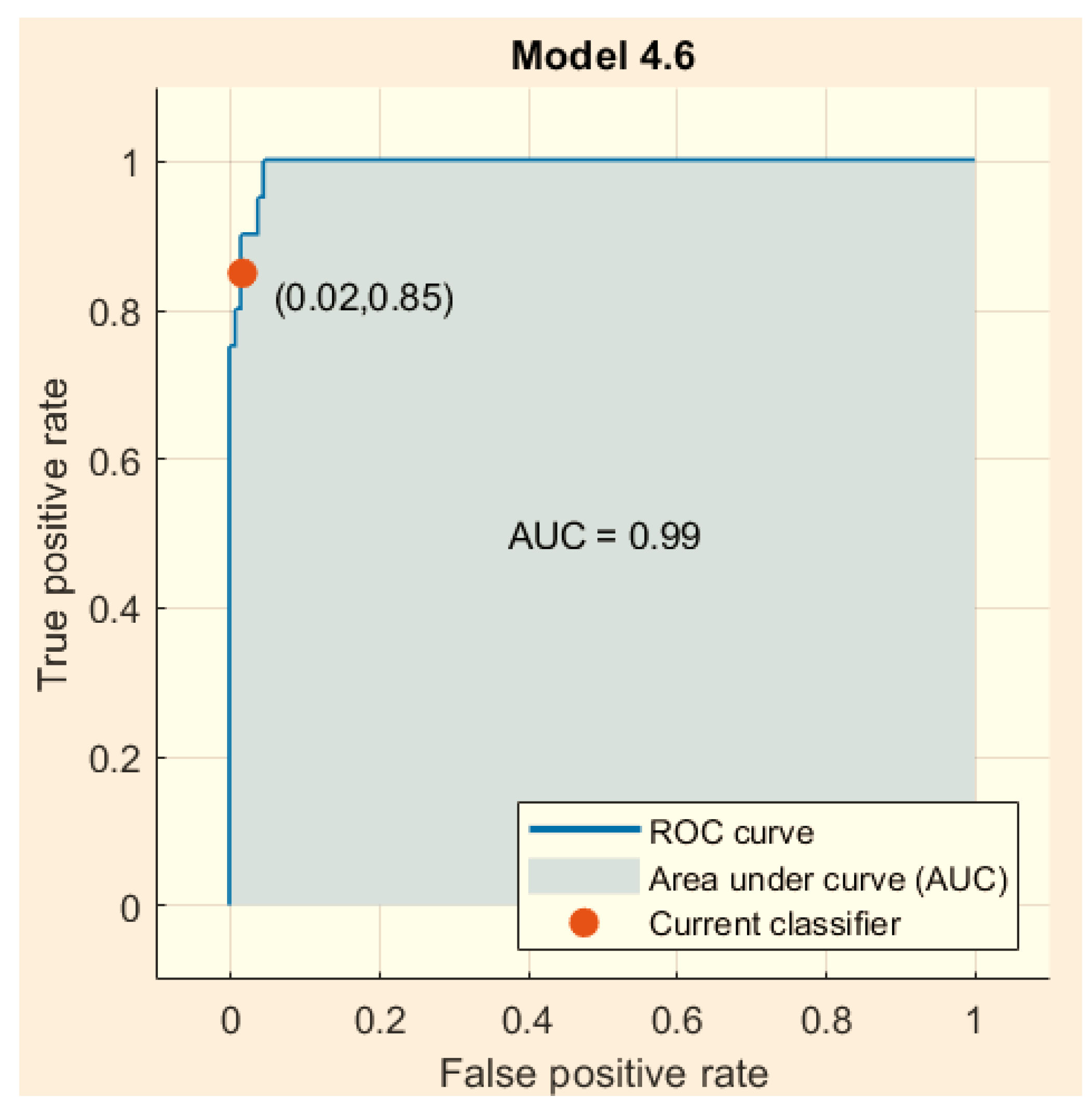
3.4. Results with Standardization of the Data [(X − μ)/σ] Linear SVM
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Keesstra, S.D.; Geissen, V.; Mosse, K.; Piiranen, S.; Scudiero, E.; Leistra, M.; van Schaik, L. Soil as a filter for groundwater quality. J. Curr. Opin. Environ. Sustain. 2012, 4, 507–516. [Google Scholar] [CrossRef]
- Pulido, M.; Barrena-González, J.; Alfonso-Torreño, A.; Robina-Ramírez, R.; Keesstra, S. The problem of water use in rural areas of Southwestern Spain: A local perspective. Water 2019, 11, 1311. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Ortega-Martorell, S.; Al-Bugharbee, H.; Olier, I.; Hashim, K.S.; Gharghan, S.K.; Kot, P.; Al-Khaddar, R. Urban water demand prediction for a city that suffers from climate change and population growth: Gauteng province case study. Water 2020, 12, 1885. [Google Scholar] [CrossRef]
- WHO. UN-Water Global Analysis and Assessment of Sanitation and Drinking-Water (GLAAS) 2014 in Report: Investing in Water and Sanitation: Increasing Access, Reducing Inequalities; World Health Organization: Geneva, Switzerland, 2014.
- Sorenson, S.B.; Morssink, C.; Campos, P.A. Safe access to safe water in low income countries: Water fetching in current times. Soc. Sci. Med. 2011, 72, 1522–1526. [Google Scholar] [CrossRef] [PubMed]
- Downing, J.A.; Polasky, S.; Olmstead, S.M.; Newbold, S.C. Protecting local water quality has global benefits. Nat. Commun. 2021, 12, 2709. [Google Scholar] [CrossRef] [PubMed]
- Luvhimbi, N.; Tshitangano, T.G.; Mabunda, J.T.; Olaniyi, F.C.; Edokpayi, J.N. Water quality assessment and evaluation of human health risk of drinking water from source to point of use at Thulamela municipality, Limpopo Province. Sci. Rep. 2022, 12, 6059. [Google Scholar] [CrossRef]
- Uddin, G.; Nash, S.; Olbert, A.I. A review of water quality index models and their use for assessing surface water quality. Ecol. Indic. 2020, 122, 107218. [Google Scholar] [CrossRef]
- Lumb, A.; Sharma, T.C.; Bibeault, J.-F. A review of genesis and evolution of water quality index (WQI) and some future directions. Water Qual. Expo. Health 2011, 3, 11–24. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, P.; Qian, H. Groundwater quality assessment using improved water quality index (WQI) and human health risk (HHR) evaluation in a semi-arid region of northwest China. Expo. Health 2020, 12, 487–500. [Google Scholar] [CrossRef]
- Akter, T.; Jhohura, F.T.; Akter, F.; Chowdhury, T.R.; Mistry, S.K.; Dey, D.; Barua, M.K.; Islam, A.; Rahman, M. Water Quality Index for measuring drinking water quality in rural Bangladesh: A cross-sectional study. J. Health Popul. Nutr. 2016, 35, 4. [Google Scholar] [CrossRef] [Green Version]
- Abba, S.I.; Pham, Q.B.; Saini, G.; Linh, N.T.T.; Ahmed, A.N.; Mohajane, M.; Khaledian, M.; Abdulkadir, R.A.; Bach, Q.-V. Implementation of data intelligence models coupled with ensemble machine learning for prediction of water quality index. Environ. Sci. Pollut. Res. 2020, 27, 41524–41539. [Google Scholar] [CrossRef]
- Mohammadpour, R.; Shaharuddin, S.; Chang, C.K.; Zakaria, N.A.; Ab Ghani, A.; Chan, N.W. Prediction of water quality index in constructed wetlands using support vector machine. Environ. Sci. Pollut. Res. 2014, 22, 6208–6219. [Google Scholar] [CrossRef]
- Singh, K.P.; Basant, N.; Gupta, S. Support vector machines in water quality management. Anal. Chim. Acta 2011, 703, 152–162. [Google Scholar] [CrossRef]
- Safavi, H.R.; Esmikhani, M. Conjunctive use of surface water and groundwater: Application of support vector machines (SVMs) and genetic algorithms. Water Resour. Manag. 2013, 27, 2623–2644. [Google Scholar] [CrossRef]
- Gakii, C.; Jepkoech, J. A classification model for water quality analysis using decision tree. Eur. J. Comput. Sci. Inf. Technol. 2019, 7, 1–8. [Google Scholar]
- Jeihouni, M.; Toomanian, A.; Mansourian, A. Decision tree-based data mining and rule induction for identifying high quality groundwater zones to water supply management: A novel hybrid use of data mining and GIS. Water Resour. Manag. 2019, 34, 139–154. [Google Scholar] [CrossRef]
- Chen, K.; Chen, H.; Zhou, C.; Huang, Y.; Qi, X.; Shen, R.; Liu, F.; Zuo, M.; Zou, X.; Wang, J.; et al. Comparative analysis of surface water quality prediction performance and identification of key water parameters using different machine learning models based on big data. Water Res. 2019, 171, 115454. [Google Scholar] [CrossRef]
- Zhang, C.; Ma, Y. Ensemble Machine Learning: Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Xin, X.; Lu, W.-X.; Gong, L. Discriminant analysis method application in water quality assessment: Take Yinma River as example. In Proceedings of the 2010 4th International Conference on Bioinformatics and Biomedical Engineering, Chengdu, China, 18–20 June 2010. [Google Scholar]
- Lei, L. Assessment of Water Quality Using Multivariate Statistical Techniques in the Ying River Basin, China. Master Thesis, University of Michigan, Ann Arbor, MI, USA, April 2014. Available online: https://deepblue.lib.umich.edu/bitstream/handle/2027.42/106539/final%20draft_Lei%20Lei.pdf?sequence= (accessed on 29 July 2022).
- Al-Adhaileh, M.H.; Alsaade, F.W. Modelling and prediction of water quality by using artificial intelligence. Sustainability 2021, 13, 4259. [Google Scholar] [CrossRef]
- Li, Y.; Khan, M.Y.A.; Jiang, Y.; Tian, F.; Liao, W.; Fu, S.; He, C. CART and PSO+KNN algorithms to estimate the impact of water level change on water quality in Poyang Lake, China. Arab. J. Geosci. 2019, 12, 287. [Google Scholar] [CrossRef]
- Egbueri, J.C.; Agbasi, J.C. Data-driven soft computing modeling of groundwater quality parameters in southeast Nigeria: Comparing the performances of different algorithms. Environ. Sci. Pollut. Res. 2022, 29, 38346–38373. [Google Scholar] [CrossRef]
- Pham, T.L.; Tran, T.H.Y.; Tran, T.T.; Ngo, X.Q.; Nguyen, X.D. Assessment of surface water quality in a drinking water supply reservoir in Vietnam: A combination of different indicators. Rend. Lincei. Sci. Fis. E Nat. 2022, 1–10. Available online: https://link.springer.com/article/10.1007/s12210-022-01086-5 (accessed on 29 July 2022). [CrossRef]
- He, B.; Shi, Y.; Wan, Q.; Zhao, X. Prediction of customer attrition of commercial banks based on SVM model. Procedia Comput. Sci. 2014, 31, 423–430. [Google Scholar] [CrossRef]
- Samantaray, S.; Sahoo, A.; Ghose, D.K. Assessment of sediment load concentration using SVM, SVM-FFA and PSR-SVM-FFA in arid watershed, India: A Case Study. KSCE J. Civ. Eng. 2020, 24, 1944–1957. [Google Scholar] [CrossRef]
- Kurniawan, I.; Hayder, G.; Mustafa, H.M. Predicting water quality parameters in a complex river system. J. Ecol. Eng. 2021, 22, 250–257. [Google Scholar] [CrossRef]
- Koranga, M.; Pant, P.; Pant, D.; Bhatt, A.K.; Pant, R.P.; Ram, M.; Kumar, T. SVM Model to Predict the Water Quality Based on Physicochemical Parameters. Int. J. Math. Eng. Manag. Sci. 2021, 6, 645–659. [Google Scholar] [CrossRef]
- Tan, G.; Yan, J.; Gao, C.; Yang, S. Prediction of water quality time series data based on least squares support vector machine. Procedia Eng. 2012, 31, 1194–1199. [Google Scholar] [CrossRef]
- Ladjal, M.; Bouamar, M.; Djerioui, M.; Brik, Y. Performance evaluation of ANN and SVM multiclass models for intelligent water quality classification using Dempster-Shafer Theory. In Proceedings of the 2016 International Conference on Electrical and Information Technologies (ICEIT), Tangiers, Morocco, 4–7 May 2016. [Google Scholar]
- Kouadri, S.; Elbeltagi, A.; Islam, A.R.M.T.; Kateb, S. Performance of machine learning methods in predicting water quality index based on irregular data set: Application on Illizi region (Algerian southeast). Appl. Water Sci. 2021, 11, 190. [Google Scholar] [CrossRef]
- Boudibi, S.; Sakaa, B.; Benguega, Z.; Fadlaoui, H.; Othman, T.; Bouzidi, N. Spatial prediction and modeling of soil salinity using simple cokriging, artificial neural networks, and support vector machines in El Outaya plain, Biskra, southeastern Algeria. Acta Geochim. 2021, 40, 390–408. [Google Scholar] [CrossRef]
- Dilmi, S.; Ladjal, M. A novel approach for water quality classification based on the integration of deep learning and feature extraction techniques. Chemom. Intell. Lab. Syst. 2021, 214, 104329. [Google Scholar] [CrossRef]
- Ghoneim, S. Determination of Transformers’ Insulating Paper State Based on Classification Techniques. Processes 2021, 9, 427. [Google Scholar] [CrossRef]
- Bouarfa, S.; Bellal, S.A. Assessment of the Aeolian sand dynamics in the region of Ain Sefra (Western Algeria), using wind data and satellite imagery. Arab. J. Geosci. 2018, 11, 56. [Google Scholar] [CrossRef]
- Hadjadj, K.; Guerine, L.; Derdour, A. Flore des populations de frêne dimorphe (fraxinus dimorpha coss. & durieu) dans l’Atlas Saharien (Monts des Ksours, Algérie). J. Lejeunia Rev. De Bot. 2021. [Google Scholar] [CrossRef]
- Derdour, A.; Guerine, l.; Allali, M. Assessment of drinking and irrigation water quality using WQI and SAR method in Maâder sub-basin, Ksour Mountains, Algeria. J. Sustain. Water Resour. Manag. 2021, 7, 8. [Google Scholar] [CrossRef]
- Derdour, A.; Ali, M.M.M.; Sari, S.M.C. Evaluation of the quality of groundwater for its appropriateness for drinking purposes in the watershed of Naama, SW of Algeria, by using water quality index (WQI). SN Appl. Sci. 2020, 2, 1951. [Google Scholar] [CrossRef]
- Benaradj, A.; Boucherit, H.; Merzougui, T. Water Resources, State of Play, and Development Prospects in the Steppe Region of Naâma (Western Algeria), in Water Resources in Algeria-Part II; Springer: Berlin/Heidelberg, Germany, 2020; pp. 253–283. [Google Scholar]
- Derdour, A.; Bouanani, A. Coupling HEC-RAS and HEC-HMS in rainfall–runoff modeling and evaluating floodplain inundation maps in arid environments: Case study of Ain Sefra city, Ksour Mountain. SW of Algeria. Environ. Earth Sci. 2019, 78, 586. [Google Scholar]
- Guerine, L.; Belgourari, M.; Guerinik, H. Cartography and diachronic study of the naama sabkha (Southwestern Algeria) remotely sensed vegetation index and soil properties. J. Rangel. Sci. 2020, 10, 172–187. [Google Scholar]
- Rahmani, A.; Bouanani, A.; Kacemi, A.; Hamed, K.B. Contribution of GIS for the survey and the management of water resources in the basin “Benhandjir–Tirkount” (Ain Sefra)–mounts of Ksour-Saharian Atlas–Algeria. J. Fundam. Appl. Sci. 2017, 9, 829–846. [Google Scholar] [CrossRef]
- Varol, S.; Davraz, A. Evaluation of the groundwater quality with WQI (Water Quality Index) and multivariate analysis: A case study of the Tefenni plain (Burdur/Turkey). Environ. Earth Sci. 2014, 73, 1725–1744. [Google Scholar] [CrossRef]
- Bora, M.; Goswami, D.C. Water quality assessment in terms of water quality index (WQI): Case study of the Kolong River, Assam, India. Appl. Water Sci. 2016, 7, 3125–3135. [Google Scholar] [CrossRef]
- Ramakrishnaiah, C.R.; Sadashivaiah, C.; Ranganna, G. Assessment of water quality index for the groundwater In Tumkur Taluk, Karnataka State, India. E J. Chem. 2009, 6, 523–530. [Google Scholar] [CrossRef]
- Hassan, A.N.; El-Hag, A. Two-layer ensemble-based soft voting classifier for transformer oil interfacial tension prediction. Energies 2020, 13, 1735. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Qiao, L.; Chen, S.; Liu, S.; Liu, J. Fault diagnosis of power transformer based on tree ensemble model. IOP Conf. Ser. Mater. Sci. Eng. 2020, 715, 012032. [Google Scholar] [CrossRef]
- Kherif, O.; Benmahamed, Y.; Teguar, M.; Boubakeur, A.; Ghoneim, S.S.M. accuracy improvement of power transformer faults diagnostic using KNN classifier with decision tree principle. IEEE Access 2021, 9, 81693–81701. [Google Scholar] [CrossRef]
- Silva, A.; Stam, A. Discriminant Analysis; Reading and understanding multivariate statistics; Grimm, L.G., Yarnold, P.R., Eds.; APA Books: Washington, DC, USA, 1995; pp. 277–318. [Google Scholar]
- Yazdani-Asrami, M.; Taghipour-Gorjikolaie, M.; Song, W.; Zhang, M.; Yuan, W. Prediction of nonsinusoidal AC loss of superconducting tapes using artificial intelligence-based models. IEEE Access 2020, 8, 207287–207297. [Google Scholar] [CrossRef]
- Benmahamed, Y.; Kherif, O.; Teguar, M.; Boubakeur, A.; Ghoneim, S. Accuracy improvement of transformer faults diagnostic based on DGA data using SVM-BA classifier. Energies 2021, 14, 2970. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Fan, X.; Liu, J.; Zhang, H. Moisture prediction of transformer oil-immersed polymer insulation by applying a support vector machine combined with a genetic algorithm. Polymers 2020, 12, 1579. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Zhu, X.; Pedrycz, W.; Li, Z. A design of information granule-based under-sampling method in imbalanced data classification. Soft Comput. 2020, 24, 17333–17347. [Google Scholar] [CrossRef]
- Tharwat, A.; Hassanien, A.E.; Elnaghi, B.E. A BA-based algorithm for parameter optimization of Support Vector Machine. Pattern Recognit. Lett. 2017, 93, 13–22. [Google Scholar] [CrossRef]
- WHO (World Health Organization). Guidelines for Drinking-Water Quality: First Addendum to the Fourth Edition; World Health Organization: Geneva, Switzerland, 2017.
- Taha, I.B.; Mansour, D.-E.A.; Ghoneim, S.S.; Elkalashy, N.I. Conditional probability-based interpretation of dissolved gas analysis for transformer incipient faults. IET Gener. Transm. Distrib. 2017, 11, 943–951. [Google Scholar] [CrossRef]
- Rapant, S.; Cvečková, V.; Fajčíková, K.; Sedláková, D.; Stehlíková, B. Impact of calcium and magnesium in groundwater and drinking water on the health of inhabitants of the Slovak Republic. Int. J. Environ. Res. Public Health 2017, 14, 278. [Google Scholar] [CrossRef]
- Ismail, E.; Abdelhalim, A.; Heleika, M.A. Hydrochemical characteristics and quality assessment of groundwater aquifers northwest of Assiut District, Egypt. J. Afr. Earth Sci. 2021, 181, 104260. [Google Scholar] [CrossRef]
- Ganyaglo, S.Y.; Gibrilla, A.; Teye, E.M.; Owusu-Ansah, E.D.-G.J.; Tettey, S.; Diabene, P.Y.; Asimah, S. Groundwater fluoride contamination and probabilistic health risk assessment in fluoride endemic areas of the Upper East Region, Ghana. Chemosphere 2019, 233, 862–872. [Google Scholar] [CrossRef]
- Ntanganedzeni, B.; Elumalai, V.; Rajmohan, N. Coastal aquifer contamination and geochemical processes evaluation in tugela catchment, South Africa—Geochemical and statistical approaches. Water 2018, 10, 687. [Google Scholar] [CrossRef] [Green Version]
- Osiakwan, G.M.; Appiah-Adjei, E.K.; Kabo-Bah, A.T.; Gibrilla, A.; Anornu, G. Assessment of groundwater quality and the controlling factors in coastal aquifers of Ghana: An integrated statistical, geostatistical and hydrogeochemical approach. J. Afr. Earth Sci. 2021, 184, 104371. [Google Scholar] [CrossRef]
- Dassi, L. Use of chloride mass balance and tritium data for estimation of groundwater recharge and renewal rate in an unconfined aquifer from North Africa: A case study from Tunisia. Environ. Earth Sci. 2010, 60, 861–871. [Google Scholar] [CrossRef]
- Leong, W.C.; Bahadori, A.; Zhang, J.; Ahmad, Z. Prediction of water quality index (WQI) using support vector machine (SVM) and least square-support vector machine (LS-SVM). Int. J. River Basin Manag. 2019, 19, 149–156. [Google Scholar] [CrossRef]
- Chia, S.L.; Chia, M.Y.; Koo, C.H.; Huang, Y.F. Integration of advanced optimization algorithms into least-square support vector machine (LSSVM) for water quality index prediction. Water Supply 2021, 22, 1951–1963. [Google Scholar] [CrossRef]
- Kamyab-Talesh, F.; Mousavi, S.-F.; Khaledian, M.; Yousefi-Falakdehi, O.; Norouzi-Masir, M. Prediction of water quality index by support vector machine: A case study in the Sefidrud Basin, Northern Iran. Water Resour. 2019, 46, 112–116. [Google Scholar] [CrossRef]
- Kulisz, M.; Kujawska, J.; Przysucha, B.; Cel, W. Forecasting water quality index in groundwater using artificial neural network. Energies 2021, 14, 5875. [Google Scholar] [CrossRef]
- Abera, K.A.; Gebreyohannes, T.; Abrha, B.; Hagos, M.; Berhane, G.; Hussien, A.; Belay, A.S.; Van Camp, M.; Walraevens, K. Vulnerability Mapping of Groundwater Resources of Mekelle City and Surroundings, Tigray Region, Ethiopia. Water 2022, 14, 2577. [Google Scholar] [CrossRef]
- Giao, N.T.; Dan, T.H.; Van Ni, D.; Anh, P.K.; Nhien, H.T.H. Spatiotemporal Variations in Physicochemical and Biological Properties of Surface Water Using Statistical Analyses in Vinh Long Province, Vietnam. Water 2022, 14, 2200. [Google Scholar] [CrossRef]
- Abuzaid, A.S.; Jahin, H.S. Combinations of multivariate statistical analysis and analytical hierarchical process for indexing surface water quality under arid conditions. J. Contam. Hydrol. 2022, 248, 104005. [Google Scholar] [CrossRef] [PubMed]
- Braga, F.H.R.; Dutra, M.L.S.; Lima, N.S.; Silva, G.M.; Miranda, R.C.M.; Firmo, W.C.A.; Moura, A.R.L.; Monteiro, A.S.; Silva, L.C.N.; Silva, D.F.; et al. Study of the Influence of Physicochemical Parameters on the Water Quality Index (WQI) in the Maranhão Amazon, Brazil. Water 2022, 14, 1546. [Google Scholar] [CrossRef]

| PC-Parameters | Units | Permissible Limits | Weight (Wi) | Relative Weight (Wi) |
|---|---|---|---|---|
| pH | 8.5 | 4 | 0.118 | |
| Electrical Conductivity | µδ/cm | 2800 | 4 | 0.118 |
| Mineralization | mg/L | 2000 | 4 | 0.118 |
| Magnesium | mg/L | 50 | 1 | 0.029 |
| Calcium | mg/L | 200 | 2 | 0.059 |
| Potassium | mg/L | 12 | 2 | 0.059 |
| Sodium | mg/L | 200 | 2 | 0.059 |
| Chlorides | mg/L | 500 | 3 | 0.088 |
| Sulphates | mg/L | 400 | 4 | 0.118 |
| Nitrates | mg/L | 50 | 5 | 0.147 |
| Bicarbonates | mg/L | 120 | 3 | 0.088 |
| 34 | 1 |
| Samples | Excellent (1) | Good (2) | Poor (3) | Very Poor or Unsafe (4) | Total |
|---|---|---|---|---|---|
| Training | 20 | 101 | 24 | 6 | 151 |
| Testing | 5 | 5 | 5 | 3 | 18 |
| Total | 25 | 106 | 29 | 9 | 169 |
| Min Value | Max Value | Mean Value | Standard Values [56] | Standard Deviation | Coefficient of Variation (%) | |
|---|---|---|---|---|---|---|
| Ca++ | 12.00 | 832.00 | 137.69 | 75–200 | 122.50 | 88.97 |
| Mg++ | 3.00 | 560.00 | 76.03 | 50 | 68.85 | 90.56 |
| Na+ | 5.00 | 2967.00 | 186.40 | 200 | 315.33 | 169.17 |
| K+ | 1.00 | 59.00 | 8.97 | 12 | 8.47 | 94.38 |
| Cl− | 10.00 | 443.00 | 118.95 | 250 | 62.90 | 52.88 |
| SO42− | 38.00 | 2370.00 | 376.78 | 250 | 437.83 | 116.20 |
| HCO3− | 20.00 | 529.00 | 237.85 | 120 | 63.92 | 26.87 |
| NO3− | 1.00 | 390.00 | 26.82 | 50 | 36.85 | 137.40 |
| Cond. | 290.00 | 8660.00 | 1556.82 | 1500 | 1306.60 | 83.93 |
| Miner. | 186.00 | 5493.00 | 1076.67 | - | 877.30 | 81.48 |
| pH | 6.58 | 10.60 | 7.71 | 6.5–8.5 | 0.51 | 6.64 |
| Classes | Type | Number of Samples | % |
|---|---|---|---|
| I | Excellent | 25 | 14.8 |
| II | Good | 106 | 62.7 |
| III | Poor | 29 | 17.2 |
| IV | Unsafe | 9 | 5.3 |
| Classifier | Training Data | |
|---|---|---|
| Raw Data | Standardization | |
| 1. Decision Tree (DT) | ||
| Fine tree | 83.4 | 75.5 |
| Medium tree | 83.4 | 75.5 |
| Coarse tree | 81.5 | 76.8 |
| Linear discriminant | 88.7 | 88.7 |
| Quadratic discriminant | Fail | Fail |
| 2. Support Vector Machine (SVM) | ||
| Linear SVM | 94.7 | 95.4 |
| Quadratic SVM | 93.4 | 93.4 |
| Cubic SVM | 90.7 | 91.4 |
| Fine Gaussian SVM | 66.9 | 67.5 |
| Medium Gaussian SVM | 90.1 | 91.1 |
| Coarse Gaussian SVM | 74.8 | 74.2 |
| 3. K-Nearest Neighbors (KNN) | ||
| Fine KNN | 86.1 | 84.1 |
| Medium KNN | 81.5 | 83.4 |
| Coarse KNN | 66.9 | 66.9 |
| Cosine KNN | 72.8 | 78.8 |
| Cubic KNN | 80.8 | 80.1 |
| Weighted KNN | 83.4 | 84.1 |
| 4. Ensemble Trees | ||
| Ensemble boosted trees | 66.9 | 66.9 |
| Ensemble bagged trees | 86.8 | 88.1 |
| Ensemble subspace Discriminant | 83.4 | 83.4 |
| Ensemble subspace KNN | 82.8 | 88.7 |
| Ensemble RUSBoosted trees | 75.5 | 78.8 |
| 5. Discrimination Analysis (DA) | ||
| Linear Discrimination | 90.7% | 90.1 |
| Quadratic Discrimination | Failed | Failed |
| Ca++ | Mg++ | Na+ | K+ | Cl− | SO4−− | HCO3− | NO3− | Cond. | Miner. | pH | WQI Results | Quality | Pred. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 72 | 46 | 55 | 4 | 104 | 154 | 173 | 10 | 900 | 618 | 8.4 | 49.48 | Excellent | Good |
| 59 | 50 | 44 | 4 | 61 | 184 | 223 | 4 | 760 | 544 | 7.27 | 48.44 | Excellent | Excellent |
| 33 | 29 | 16 | 3 | 21 | 64 | 169 | 3 | 290 | 223 | 7.67 | 33.32 | Excellent | Excellent |
| 72 | 32 | 48 | 3 | 63 | 136 | 224 | 17 | 712 | 510 | 7.37 | 49.66 | Excellent | Excellent |
| 68 | 28 | 46 | 4 | 56 | 132 | 198 | 7 | 587 | 420 | 7.39 | 43.62 | Excellent | Excellent |
| 60 | 68 | 322 | 4 | 150 | 172 | 271 | 6 | 1980 | 1503 | 7.32 | 80.06 | Good | Good |
| 118 | 64 | 74 | 3 | 142 | 228 | 258 | 27 | 1186 | 900 | 7.53 | 67.70 | Good | Good |
| 73 | 59 | 41 | 2 | 78 | 219 | 217 | 12 | 867 | 658 | 7.34 | 52.77 | Good | Good |
| 116 | 48 | 37 | 2 | 36 | 363 | 203 | 8 | 945 | 717 | 7.22 | 55.10 | Good | Good |
| 91 | 56 | 35 | 4 | 99 | 146 | 284 | 4 | 890 | 676 | 6.94 | 54.36 | Good | Good |
| 101 | 99 | 444 | 17 | 139.6 | 908 | 106 | 8 | 2730 | 2073 | 7.34 | 108.02 | Poor | Poor |
| 128 | 124 | 311 | 12 | 152.5 | 546 | 201 | 10 | 2470 | 1875 | 7.5 | 100.95 | Poor | Poor |
| 506 | 290 | 140 | 19 | 184 | 2370 | 113 | 39 | 3520 | 2672 | 7.34 | 178.91 | Poor | Poor |
| 222 | 159 | 120 | 11 | 205 | 1020 | 193 | 25 | 2050 | 1556 | 7.29 | 107.86 | Poor | Poor |
| 303 | 211 | 85 | 12 | 116 | 1495 | 173 | 34 | 2290 | 1738 | 7.25 | 128.38 | Poor | Poor |
| 112.2 | 331 | 472 | 19 | 265.8 | 1536 | 182 | 44 | 4600 | 2852 | 8 | 241.26 | Very Poor | Very Poor |
| 451 | 95 | 1277 | 38 | 200 | 1320 | 127 | 1 | 6400 | 3968 | 8.1 | 220.54 | Very Poor | Poor |
| 160 | 452 | 978 | 26.1 | 172.1 | 1872 | 288 | 9 | 6200 | 5270 | 8 | 365.72 | Very Poor | Very Poor |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Derdour, A.; Jodar-Abellan, A.; Pardo, M.Á.; Ghoneim, S.S.M.; Hussein, E.E. Designing Efficient and Sustainable Predictions of Water Quality Indexes at the Regional Scale Using Machine Learning Algorithms. Water 2022, 14, 2801. https://doi.org/10.3390/w14182801
Derdour A, Jodar-Abellan A, Pardo MÁ, Ghoneim SSM, Hussein EE. Designing Efficient and Sustainable Predictions of Water Quality Indexes at the Regional Scale Using Machine Learning Algorithms. Water. 2022; 14(18):2801. https://doi.org/10.3390/w14182801
Chicago/Turabian StyleDerdour, Abdessamed, Antonio Jodar-Abellan, Miguel Ángel Pardo, Sherif S. M. Ghoneim, and Enas E. Hussein. 2022. "Designing Efficient and Sustainable Predictions of Water Quality Indexes at the Regional Scale Using Machine Learning Algorithms" Water 14, no. 18: 2801. https://doi.org/10.3390/w14182801
APA StyleDerdour, A., Jodar-Abellan, A., Pardo, M. Á., Ghoneim, S. S. M., & Hussein, E. E. (2022). Designing Efficient and Sustainable Predictions of Water Quality Indexes at the Regional Scale Using Machine Learning Algorithms. Water, 14(18), 2801. https://doi.org/10.3390/w14182801










