Future Projections and Uncertainties of CMIP6 for Hydrological Indicators and Their Discrepancies from CMIP5 over South Korea
Abstract
:1. Introduction
2. Methodology
3. Results and Discussions
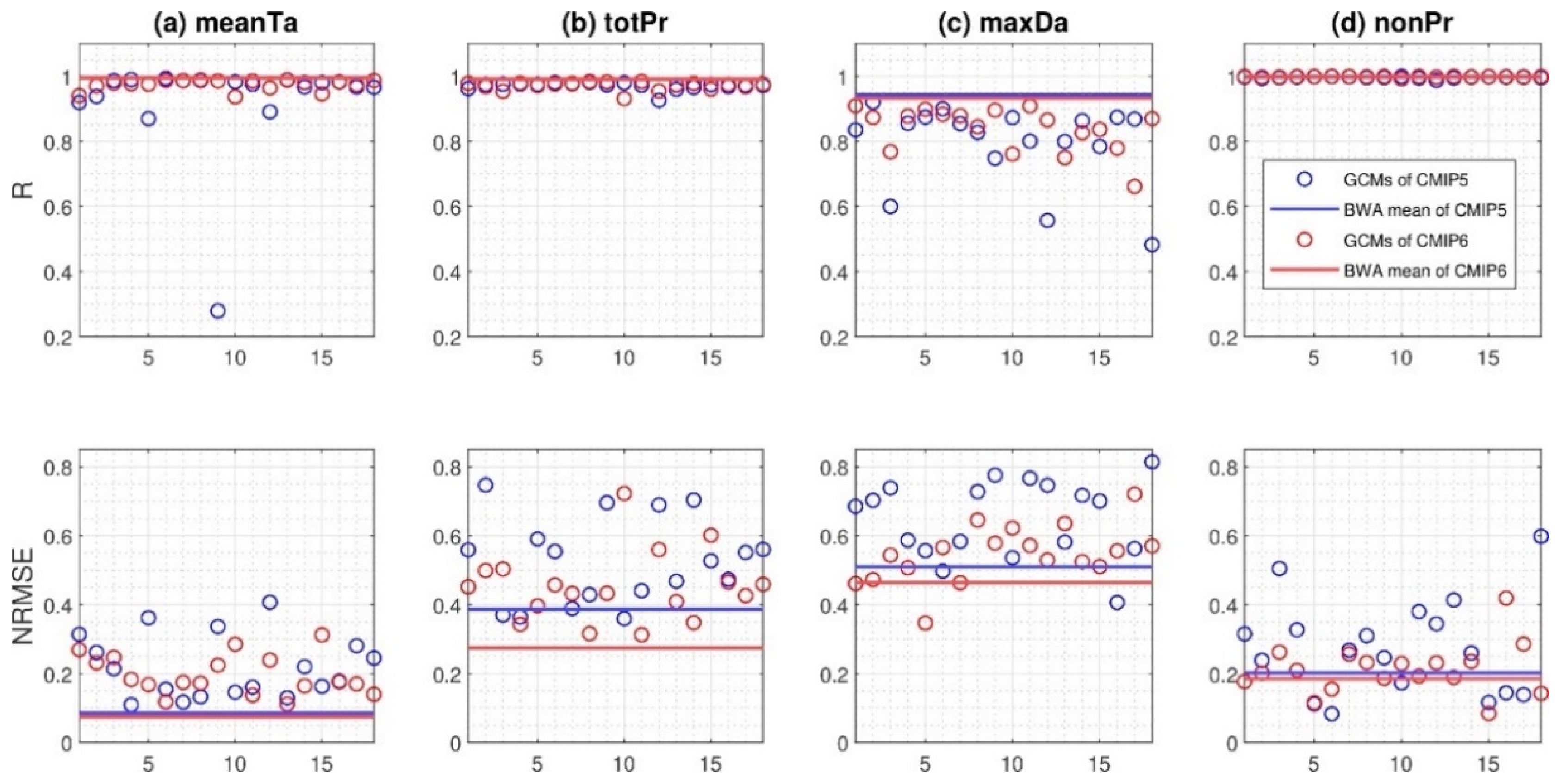
3.1. Comparison of the BWA Mean and Individual GCMs for the Control Period
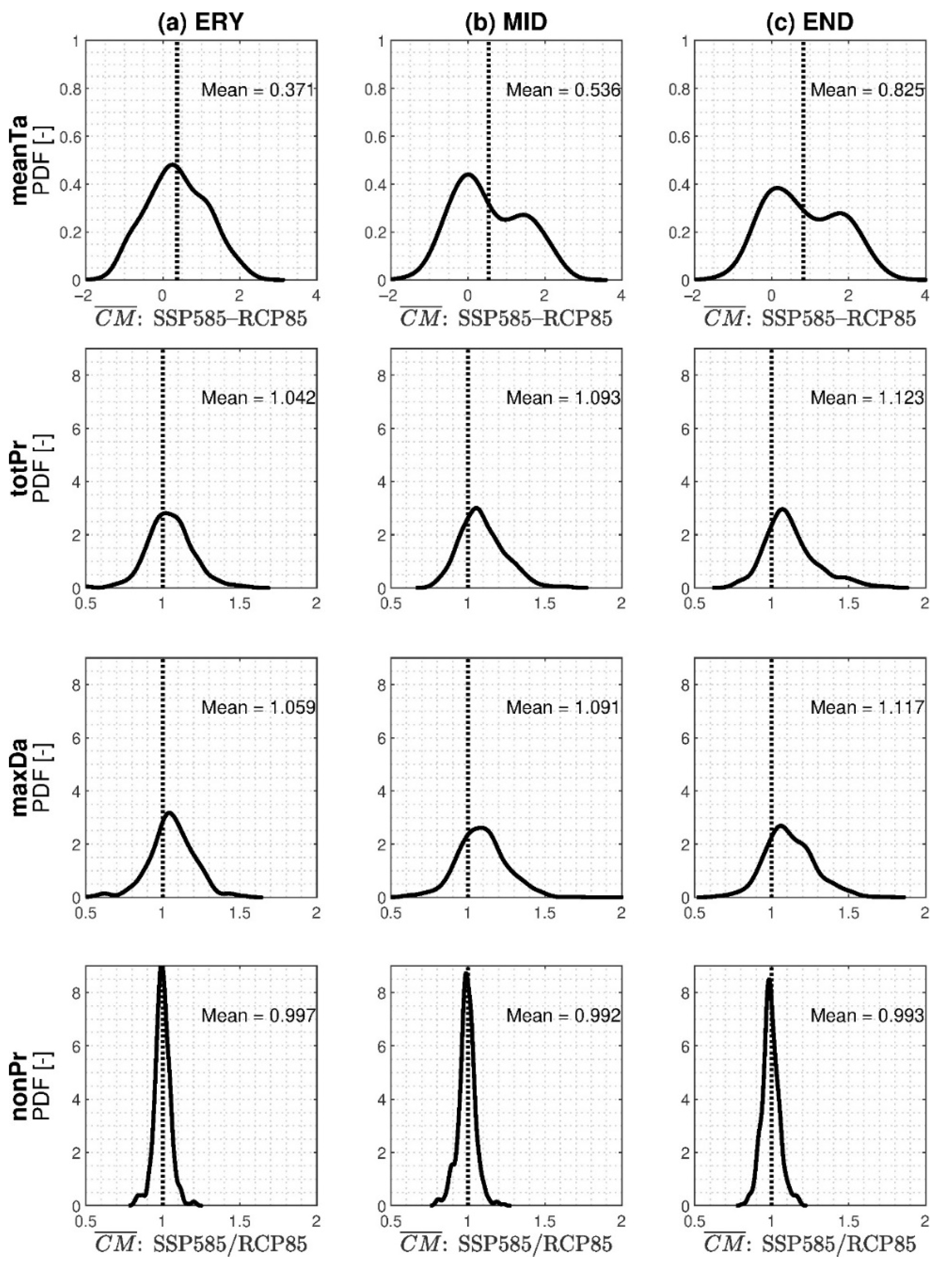
3.2. Future Projection from the CMIP5 and CMIP6 Databases
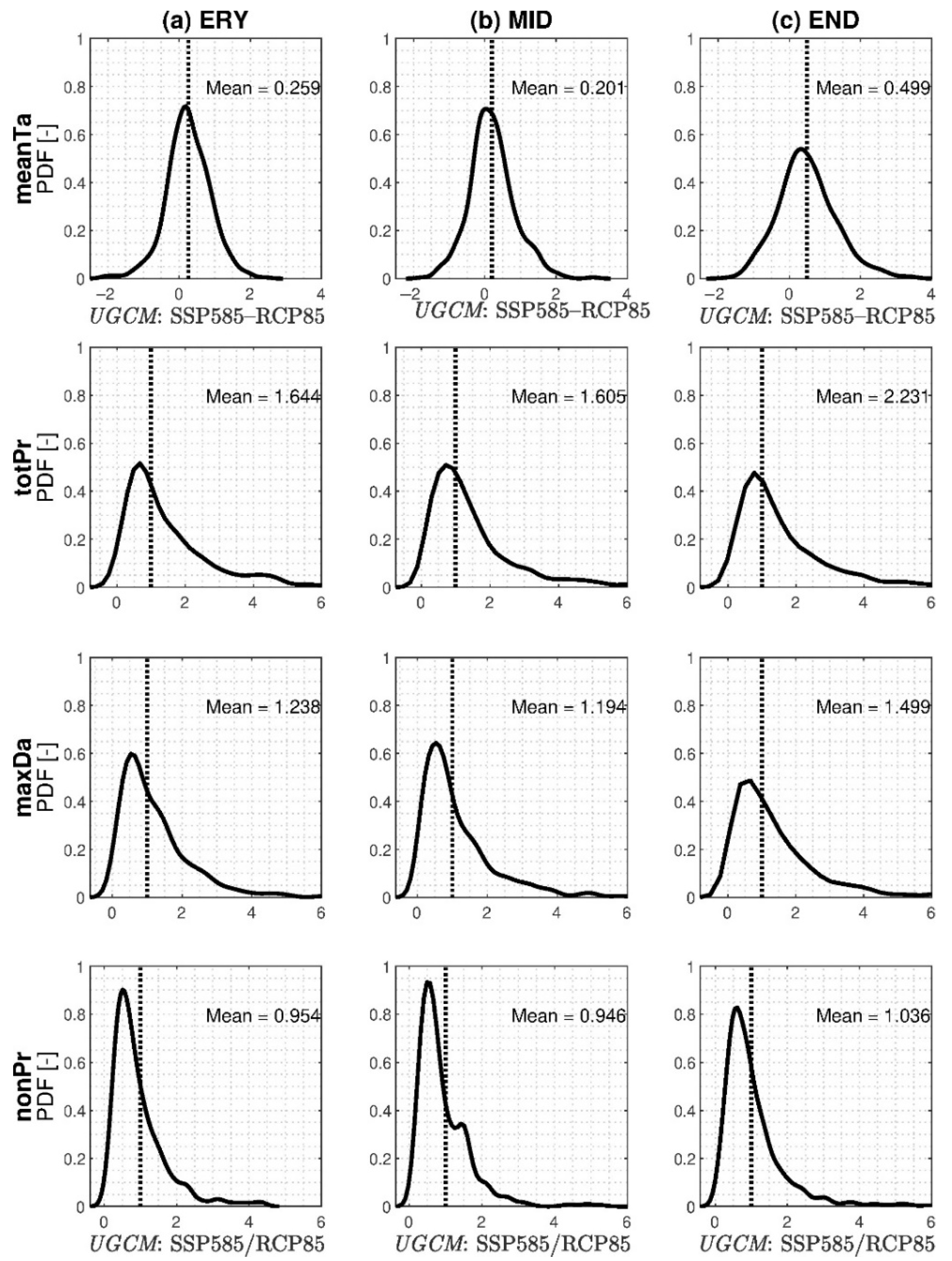
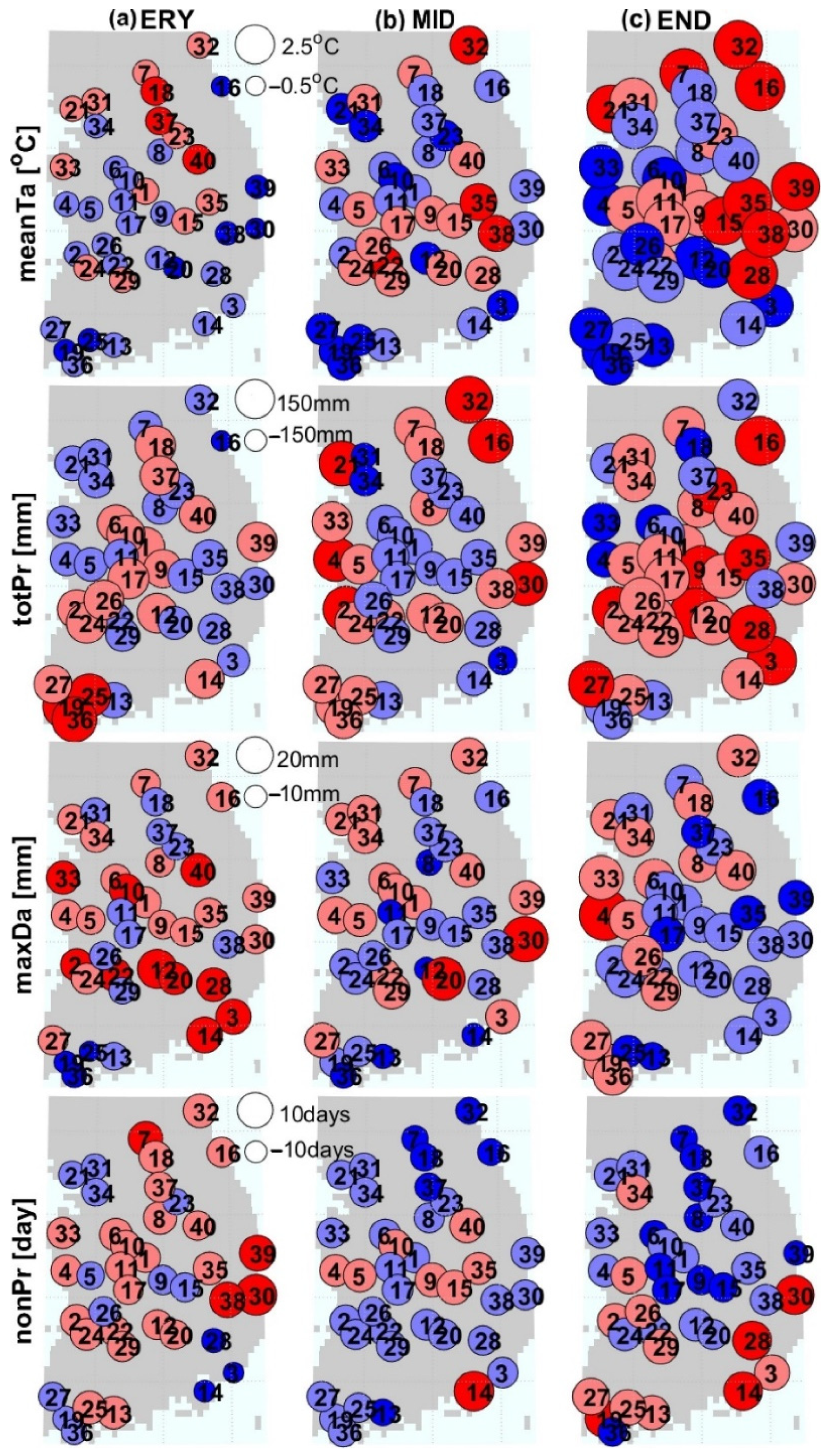
3.3. GCM Uncertainty in the CMIP6 Database and its Differences from CMIP5
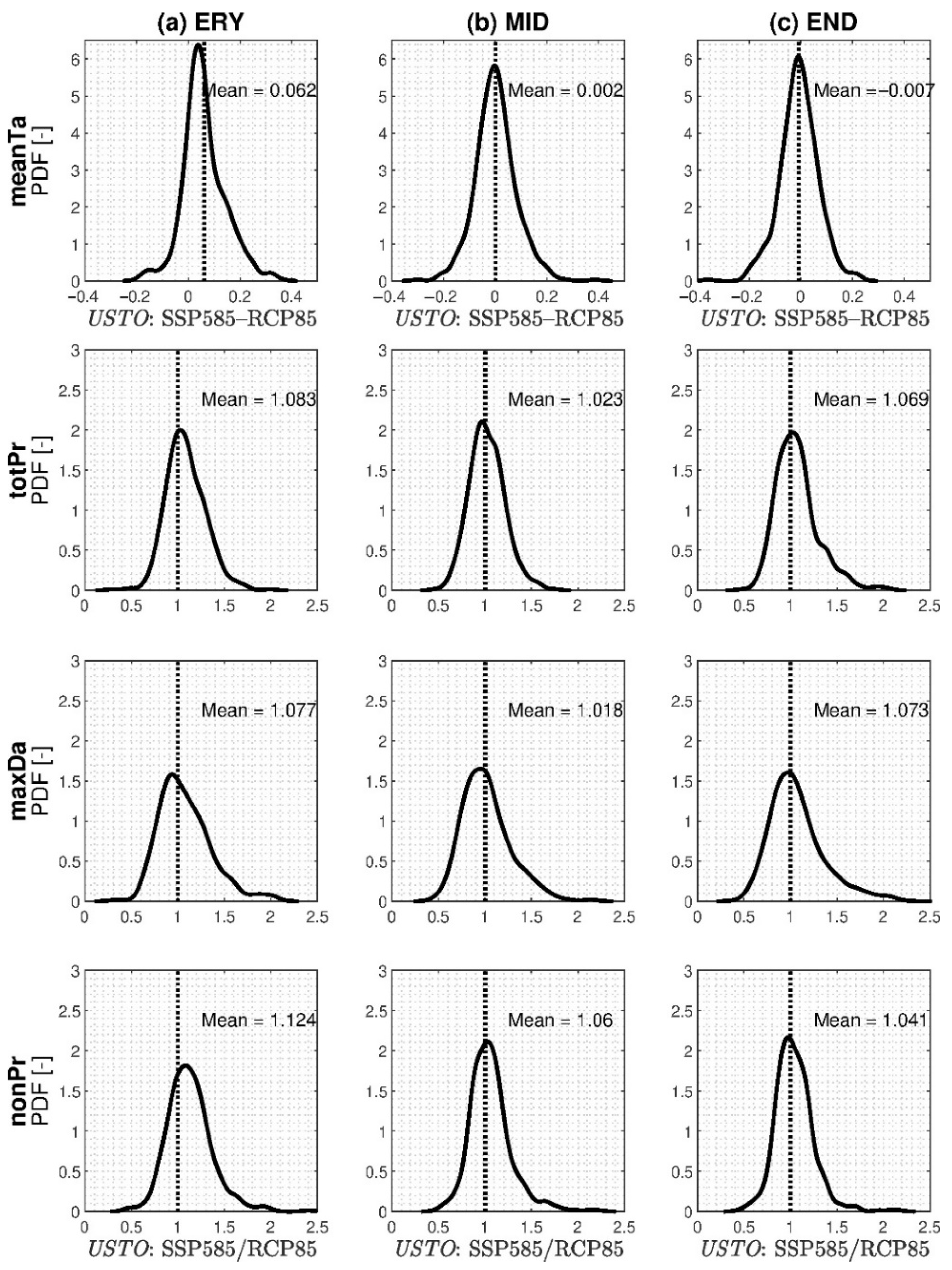
3.4. Stochastic Uncertainty in the CMIP6 Database and Its Difference from CMIP5
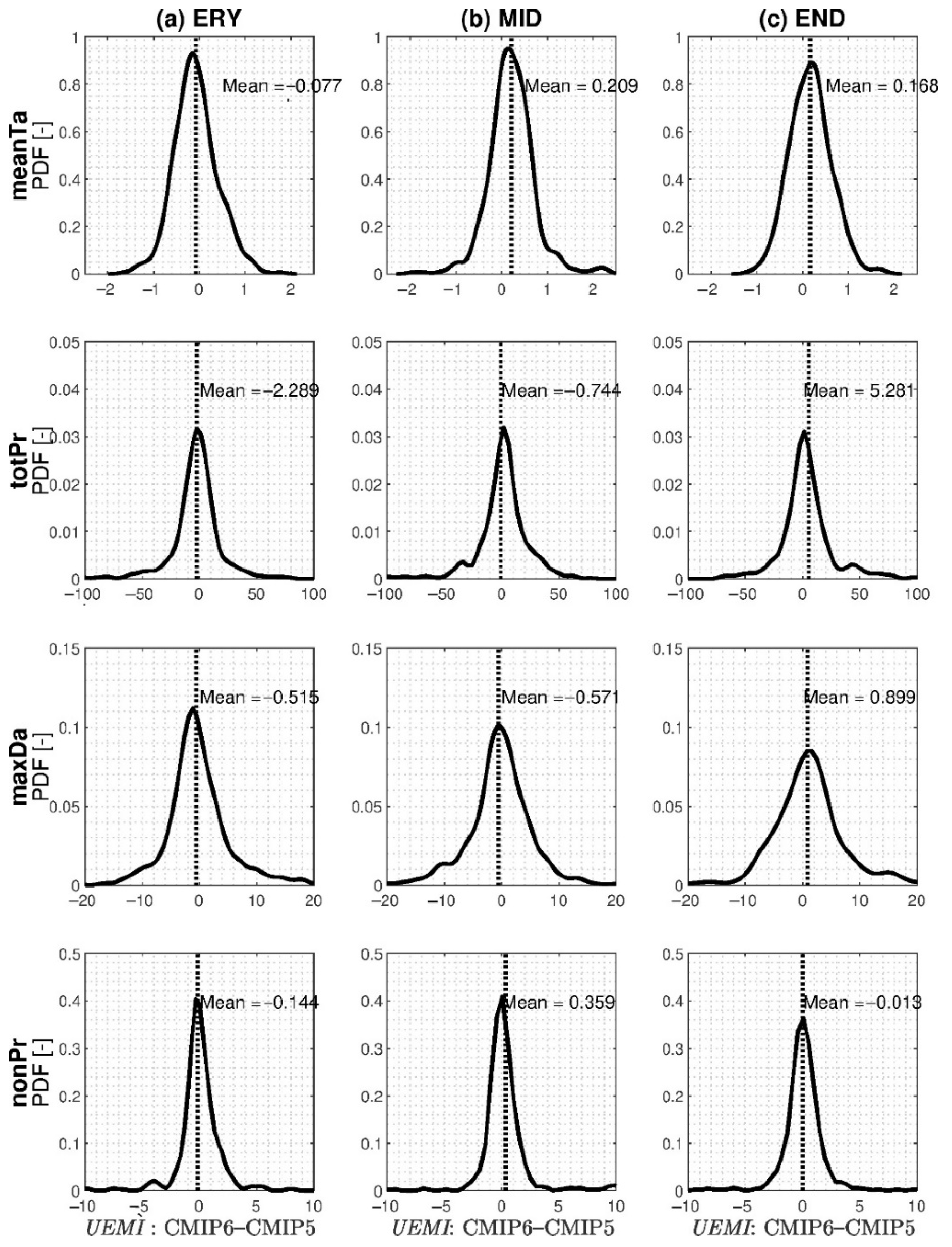
3.5. Emission Scenario Uncertainty in the CMIP6 Database and Its Difference from CMIP5
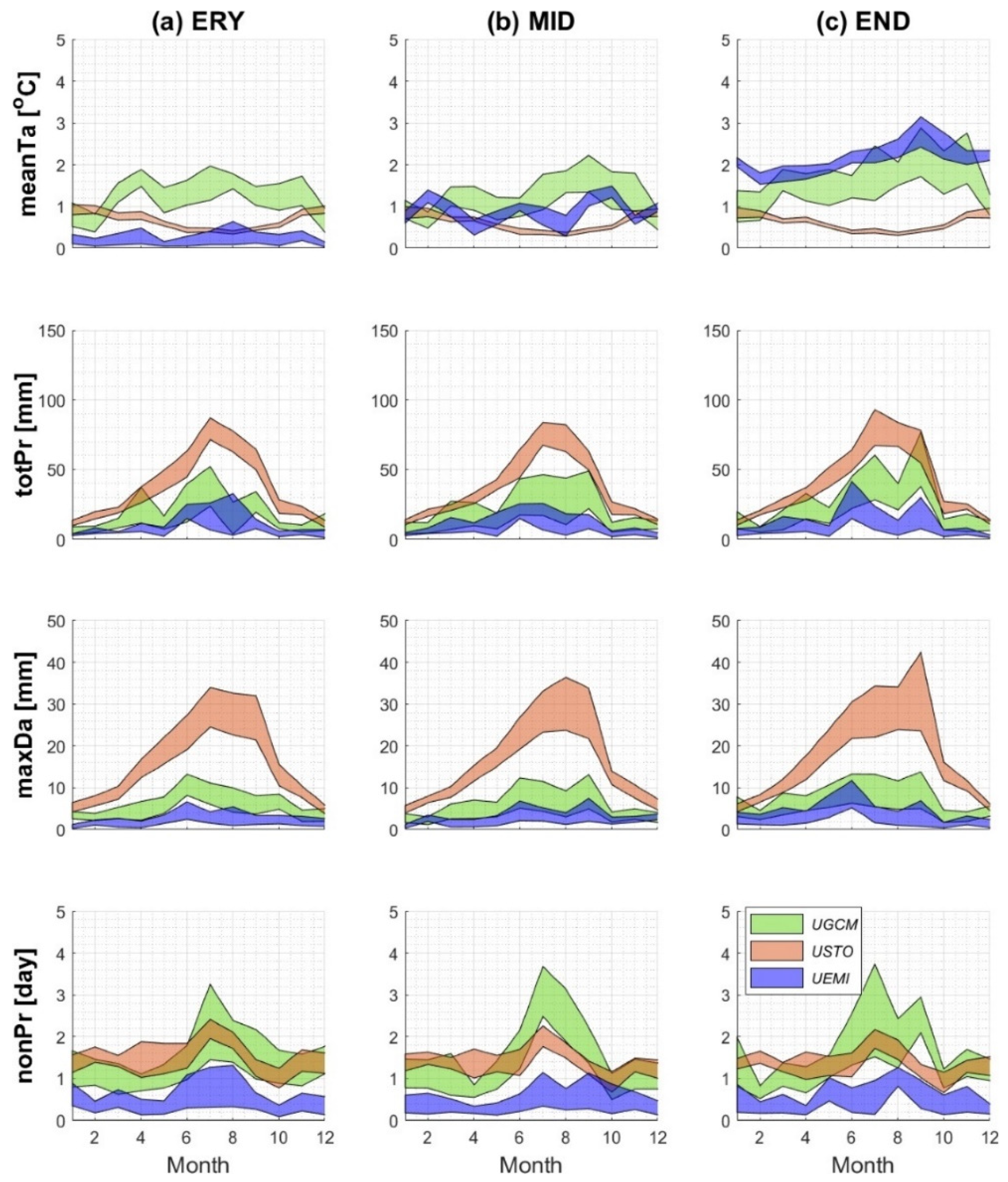
3.6. Relative Contributions of Three Uncertainty Sources
3.7. Implications for Stakeholders
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; 1535p. [Google Scholar]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Kim, M.K.; Yu, D.G.; Oh, J.S.; Byun, Y.H.; Boo, K.O.; Chung, I.U.; Park, J.S.; Park, D.S.R.; Min, S.K.; Sung, H.M. Performance Evaluation of CMIP5 and CMIP6 Models on Heatwaves in Korea and Associated Teleconnection Patterns. J. Geophys. Res. Atmos. 2020, 125, e2020JD032583. [Google Scholar] [CrossRef]
- Bracegirdle, T.J.; Holmes, C.R.; Hosking, J.S.; Marshall, G.J.; Osman, M.; Patterson, M.; Rackow, T. Improvements in Circumpolar Southern Hemisphere Extratropical Atmospheric Circulation in CMIP6 Compared to CMIP5. Earth Space Sci. 2020, 7, e2019EA001065. [Google Scholar] [CrossRef]
- Kim, Y.-H.; Min, S.-K.; Zhang, X.; Sillmann, J.; Sandstad, M. Evaluation of the CMIP6 multi-model ensemble for climate extreme indices. Weather. Clim. Extrem. 2020, 29, 100269. [Google Scholar] [CrossRef]
- Zhu, H.; Jiang, Z.; Li, J.; Li, W.; Sun, C.; Li, L. Does CMIP6 Inspire More Confidence in Simulating Climate Extremes over China? Adv. Atmos. Sci. 2020, 37, 1119–1132. [Google Scholar] [CrossRef]
- Ayugi, B.; Zhihong, J.; Zhu, H.; Ngoma, H.; Babaousmail, H.; Rizwan, K.; Dike, V. Comparison of CMIP6 and CMIP5 models in simulating mean and extreme precipitation over East Africa. Int. J. Climatol. 2021, 41, 6474–6496. [Google Scholar] [CrossRef]
- Wang, B.; Jin, C.; Liu, J. Understanding Future Change of Global Monsoons Projected by CMIP6 Models. J. Clim. 2020, 33, 6471–6489. [Google Scholar] [CrossRef]
- Scoccimarro, E.; Gualdi, S. Heavy Daily Precipitation Events in the CMIP6 Worst-Case Scenario: Projected Twenty-First-Century Changes. J. Clim. 2020, 33, 7631–7642. [Google Scholar] [CrossRef]
- Agel, L.; Barlow, M. How Well Do CMIP6 Historical Runs Match Observed Northeast U.S. Precipitation and Extreme Precipitation–Related Circulation? J. Clim. 2020, 33, 9835–9848. [Google Scholar] [CrossRef]
- Wehner, M.; Gleckler, P.; Lee, J. Characterization of long period return values of extreme daily temperature and precipitation in the CMIP6 models: Part 1, model evaluation. Weather. Clim. Extrem. 2020, 30, 100283–100298. [Google Scholar] [CrossRef]
- Thorarinsdottir, T.L.; Sillmann, J.; Haugen, M.; Gissibl, N.; Sandstad, M. Evaluation of CMIP5 and CMIP6 simulations of historical surface air temperature extremes using proper evaluation methods. Environ. Res. Lett. 2020, 15, 124041–124054. [Google Scholar] [CrossRef]
- Wehner, M.F. Characterization of long period return values of extreme daily temperature and precipitation in the CMIP6 models: Part 2, projections of future change. Weather. Clim. Extrem. 2020, 30, 100284–100297. [Google Scholar] [CrossRef]
- Moon, S.; Ha, K.-J. Future changes in monsoon duration and precipitation using CMIP6. NPJ Clim. Atmos. Sci. 2020, 3, 45. [Google Scholar] [CrossRef]
- Perez, J.; Menendez, M.; Mendez, F.J.; Losada, I.J. Evaluating the performance of CMIP3 and CMIP5 global climate models over the north-east Atlantic region. Clim. Dyn. 2014, 43, 2663–2680. [Google Scholar] [CrossRef]
- Das, L.; Meher, J.K.; Akhter, J.; Benestad, R.E.; Mezghani, A. Performance of CMIP3 and CMIP5 GCMs to Simulate Observed Rainfall Characteristics over the Western Himalayan Region. J. Clim. 2017, 30, 7777–7799. [Google Scholar] [CrossRef]
- Grose, M.R.; Brown, J.N.; Narsey, S.; Brown, J.R.; Murphy, B.F.; Langlais, C.; Gupta, A.S.; Moise, A.F.; Irving, D.B. Assessment of the CMIP5 global climate model simulations of the western tropical Pacific climate system and comparison to CMIP3. Int. J. Climatol. 2014, 34, 3382–3399. [Google Scholar] [CrossRef]
- Scoccimarro, E.; Gualdi, S.; Bellucci, A.; Zampieri, M.; Navarra, A. Heavy Precipitation Events in a Warmer Climate: Results from CMIP5 Models. J. Clim. 2013, 26, 7902–7911. [Google Scholar] [CrossRef]
- Ogata, T.; Ueda, H.; Inoue, T.; Hayasaki, M.; Yoshida, A.; Watanabe, S.; Kira, M.; Ooshiro, M.; Kumai, A. Projected Future Changes in the Asian Monsoon: A Comparison of CMIP3 and CMIP5 Model Results. J. Meteorol. Soc. Jpn. Ser. II 2014, 92, 207–225. [Google Scholar] [CrossRef]
- Chen, H.; Sun, J.; Lin, W.; Xu, H. Comparison of CMIP6 and CMIP5 models in simulating climate extremes. Sci. Bull. 2020, 65, 1415–1418. [Google Scholar] [CrossRef]
- Almazroui, M.; Saeed, F.; Saeed, S.; Islam, M.N.; Ismail, M.; Klutse, N.A.B.; Siddiqui, M.H. Projected Change in Temperature and Precipitation Over Africa from CMIP6. Earth Syst. Environ. 2020, 4, 455–475. [Google Scholar] [CrossRef]
- Grose, M.R.; Narsey, S.; Delage, F.P.; Dowdy, A.J.; Bador, M.; Boschat, G.; Chung, C.; Kajtar, J.B.; Rauniyar, S.; Freund, M.B.; et al. Insights from CMIP6 for Australia’s Future Climate. Earth’s Future 2020, 8, e2019EF001469. [Google Scholar] [CrossRef]
- Stefanidis, S. Ability of Different Spatial Resolution Regional Climate Model to Simulate Air Temperature in a Forest Ecosystem of Central Greece. J. Environ. Prot. Ecol. 2021, 22, 1488–1495. [Google Scholar]
- Tolika, K.; Anagnostopoulou, C.; Velikou, K.; Vagenas, C. A comparison of the updated very high resolution model RegCM3_10 km with the previous version RegCM3_25 km over the complex terrain of Greece: Present and future projections. Theor. Appl. Climatol. 2016, 126, 715–726. [Google Scholar] [CrossRef]
- Song, Y.H.; Chung, E.S.; Shahid, S. Spatiotemporal differences and uncertainties in projections of precipitation and temperature in South Korea from CMIP6 and CMIP5 general circulation models. Int. J. Climatol. 2021, 41, 5899–5919. [Google Scholar] [CrossRef]
- Monerie, P.-A.; Wainwright, C.M.; Sidibe, M.; Akinsanola, A.A. Model uncertainties in climate change impacts on Sahel precipitation in ensembles of CMIP5 and CMIP6 simulations. Clim. Dyn. 2020, 55, 1385–1401. [Google Scholar] [CrossRef]
- Zamani, Y.; Hashemi Monfared, S.A.; Azhdari Moghaddam, M.; Hamidianpour, M. A comparison of CMIP6 and CMIP5 projections for precipitation to observational data: The case of Northeastern Iran. Theor. Appl. Climatol. 2020, 142, 1613–1623. [Google Scholar] [CrossRef]
- Hawkins, E.; Sutton, R. The Potential to Narrow Uncertainty in Regional Climate Predictions. Bull. Am. Meteorol. Soc. 2009, 90, 1095–1108. [Google Scholar] [CrossRef]
- Lafaysse, M.; Hingray, B.; Mezghani, A.; Gailhard, J.; Terray, L. Internal variability and model uncertainty components in future hydrometeorological projections: The Alpine Durance basin. Water Resour. Res. 2014, 50, 3317–3341. [Google Scholar] [CrossRef]
- Hingray, B.; Said, M. Partitioning Internal Variability and Model Uncertainty Components in a Multimember Multimodel Ensemble of Climate Projections. J. Clim. 2014, 27, 6779–6798. [Google Scholar] [CrossRef]
- Hawkins, E.; Sutton, R. The potential to narrow uncertainty in projections of regional precipitation change. Clim. Dyn. 2010, 37, 407–418. [Google Scholar] [CrossRef]
- Beobide-Arsuaga, G.; Bayr, T.; Reintges, A.; Latif, M. Uncertainty of ENSO-amplitude projections in CMIP5 and CMIP6 models. Clim. Dyn. 2021, 56, 3875–3888. [Google Scholar] [CrossRef]
- Fatichi, S.; Ivanov, V.Y.; Paschalis, A.; Peleg, N.; Molnar, P.; Rimkus, S.; Kim, J.; Burlando, P.; Caporali, E. Uncertainty partition challenges the predictability of vital details of climate change. Earth’s Future 2016, 4, 240–251. [Google Scholar] [CrossRef]
- Kim, J.; Ivanov, V.Y.; Fatichi, S. Climate change and uncertainty assessment over a hydroclimatic transect of Michigan. Stoch. Environ. Res. Risk Assess. 2016, 30, 923–944. [Google Scholar] [CrossRef]
- Hawkins, E.; Smith, R.S.; Gregory, J.M.; Stainforth, D.A. Irreducible uncertainty in near-term climate projections. Clim. Dyn. 2015, 46, 3807–3819. [Google Scholar] [CrossRef]
- Monerie, P.-A.; Sanchez-Gomez, E.; Pohl, B.; Robson, J.; Dong, B. Impact of internal variability on projections of Sahel precipitation change. Environ. Res. Lett. 2017, 12, 114003. [Google Scholar] [CrossRef]
- Olonscheck, D.; Notz, D. Consistently Estimating Internal Climate Variability from Climate Model Simulations. J. Clim. 2017, 30, 9555–9573. [Google Scholar] [CrossRef]
- Tebaldi, C.; Smith, R.L.; Nychka, D.; Mearns, L.O. Quantifying uncertainty in projections of regional climate change: A Bayesian approach to the analysis of multimodel ensembles. J. Clim. 2005, 18, 1524–1540. [Google Scholar] [CrossRef]
- Ivanov, V.Y.; Bras, R.L.; Curtis, D.C. A weather generator for hydrological, ecological, and agricultural applications. Water Resour. Res. 2007, 43, 1–21. [Google Scholar] [CrossRef]
- Fatichi, S.; Ivanov, V.Y.; Caporali, E. Simulation of future climate scenarios with a weather generator. Adv. Water Resour. 2011, 34, 448–467. [Google Scholar] [CrossRef]
- Kim, J.; Tanveer, M.E.; Bae, D.-H. Quantifying climate internal variability using an hourly ensemble generator over South Korea. Stoch. Environ. Res. Risk Assess. 2018, 32, 3037–3051. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Tebaldi, C.; van Vuuren, D.P.; Eyring, V.; Friedlingstein, P.; Hurtt, G.; Knutti, R.; Kriegler, E.; Lamarque, J.-F.; Lowe, J.; et al. The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 2016, 9, 3461–3482. [Google Scholar] [CrossRef]
- Wu, T.; Lu, Y.; Fang, Y.; Xin, X.; Li, L.; Li, W.; Jie, W.; Zhang, J.; Liu, Y.; Zhang, L.; et al. The Beijing Climate Center Climate System Model (BCC-CSM): The main progress from CMIP5 to CMIP6. Geosci. Model Dev. 2019, 12, 1573–1600. [Google Scholar] [CrossRef]
- Swart, N.C.; Cole, J.N.S.; Kharin, V.V.; Lazare, M.; Scinocca, J.F.; Gillett, N.P.; Anstey, J.; Arora, V.; Christian, J.R.; Hanna, S.; et al. The Canadian Earth System Model version 5 (CanESM5.0.3). Geosci. Model Dev. 2019, 12, 4823–4873. [Google Scholar] [CrossRef]
- Cherchi, A.; Fogli, P.G.; Lovato, T.; Peano, D.; Iovino, D.; Gualdi, S.; Masina, S.; Scoccimarro, E.; Materia, S.; Bellucci, A.; et al. Global mean climate and main patterns of variability in the CMCC-CM2 coupled model. J. Adv. Model. Earth Syst. 2018, 11, 185–209. [Google Scholar] [CrossRef]
- Voldoire, A.; Saint-Martin, D.; Sénési, S.; Decharme, B.; Alias, A.; Chevallier, M.; Colin, J.; Guérémy, J.F.; Michou, M.; Moine, M.P.; et al. Evaluation of CMIP6 DECK Experiments With CNRM-CM6-1. J. Adv. Model. Earth Syst. 2019, 11, 2177–2213. [Google Scholar] [CrossRef]
- Ziehn, T.; Chamberlain, M.A.; Law, R.M.; Lenton, A.; Bodman, R.W.; Dix, M.; Stevens, L.; Wang, Y.P.; Srbinovsky, J. The Australian Earth System Model: ACCESS-ESM1. 5. J. South. Hemisph. Earth Syst. Sci. 2020, 70, 193–214. [Google Scholar] [CrossRef]
- Bi, D.H.; Dix, M.; Marsland, S.; O’Farrell, S.; Sullivan, A.; Bodman, R.; Law, R.; Harman, I.; Srbinovsky, J.; Rashid, H.A.; et al. Configuration and spin-up of ACCESS-CM2, the new generation Australian Community Climate and Earth System Simulator Coupled Model. J. South. Hemisph. Earth Syst. Sci. 2020, 70, 225–251. [Google Scholar] [CrossRef]
- Song, Y.H.; Nashwan, M.S.; Chung, E.S.; Shahid, S. Advances in CMIP6 INM-CM5 over CMIP5 INM-CM4 for precipitation simulation in South Korea. Atmos. Res. 2021, 247, 105261. [Google Scholar] [CrossRef]
- Volodin, E.M.; Mortikov, E.V.; Kostrykin, S.V.; Galin, V.Y.; Lykossov, V.N.; Gritsun, A.S.; Diansky, N.A.; Gusev, A.V.; Iakovlev, N.G. Simulation of the present-day climate with the climate model INMCM5. Clim. Dyn. 2017, 49, 3715–3734. [Google Scholar] [CrossRef]
- Boucher, O.; Servonnat, J.; Albright, A.L.; Aumont, O.; Balkanski, Y.; Bastrikov, V.; Bekki, S.; Bonnet, R.; Bony, S.; Bopp, L.; et al. Presentation and Evaluation of the IPSL-CM6A-LR Climate Model. J. Adv. Model. Earth Syst. 2020, 12, e2019MS002010. [Google Scholar] [CrossRef]
- Li, L.J.; Yu, Y.Q.; Tang, Y.L.; Lin, P.F.; Xie, J.B.; Song, M.R.; Dong, L.; Zhou, T.J.; Liu, L.; Wang, L.; et al. The Flexible Global Ocean-Atmosphere-Land System Model Grid-Point Version 3 (FGOALS-g3): Description and Evaluation. J. Adv. Model. Earth Syst. 2020, 12, e2019MS002012. [Google Scholar] [CrossRef]
- Tatebe, H.; Ogura, T.; Nitta, T.; Komuro, Y.; Ogochi, K.; Takemura, T.; Sudo, K.; Sekiguchi, M.; Abe, M.; Saito, F.; et al. Description and basic evaluation of simulated mean state, internal variability, and climate sensitivity in MIROC6. Geosci. Model Dev. 2019, 12, 2727–2765. [Google Scholar] [CrossRef]
- Roberts, M.J.; Baker, A.; Blockley, E.W.; Calvert, D.; Coward, A.; Hewitt, H.T.; Jackson, L.C.; Kuhlbrodt, T.; Mathiot, P.; Roberts, C.D.; et al. Description of the resolution hierarchy of the global coupled HadGEM3-GC3.1 model as used in CMIP6 HighResMIP experiments. Geosci. Model Dev. 2019, 12, 4999–5028. [Google Scholar] [CrossRef]
- Müller, W.A.; Jungclaus, J.H.; Mauritsen, T.; Baehr, J.; Bittner, M.; Budich, R.; Bunzel, F.; Esch, M.; Ghosh, R.; Haak, H.; et al. A Higher-resolution Version of the Max Planck Institute Earth System Model (MPI-ESM1.2-HR). J. Adv. Model. Earth Syst. 2018, 10, 1383–1413. [Google Scholar] [CrossRef]
- Yukimoto, S.; Kawai, H.; Koshiro, T.; Oshima, N.; Yoshida, K.; Urakawa, S.; Tsujino, H.; Deushi, M.; Tanaka, T.; Hosaka, M.; et al. The Meteorological Research Institute Earth System Model Version 2.0, MRI-ESM2.0: Description and Basic Evaluation of the Physical Component. J. Meteorol. Soc. Jpn. Ser. II 2019, 97, 931–965. [Google Scholar] [CrossRef]
- Feng, R.; Otto-Bliesner, B.L.; Brady, E.C.; Rosenbloom, N. Increased Climate Response and Earth System Sensitivity from CCSM4 to CESM2 in Mid-Pliocene Simulations. J. Adv. Model. Earth Syst. 2020, 12, e2019MS002033. [Google Scholar] [CrossRef]
- Danabasoglu, G.; Lamarque, J.F.; Bacmeister, J.; Bailey, D.A.; DuVivier, A.K.; Edwards, J.; Emmons, L.K.; Fasullo, J.; Garcia, R.; Gettelman, A.; et al. The Community Earth System Model Version 2 (CESM2). J. Adv. Model. Earth Syst. 2020, 12, e2019MS001916. [Google Scholar] [CrossRef]
- Seland, Ø.; Bentsen, M.; Olivié, D.; Toniazzo, T.; Gjermundsen, A.; Graff, L.S.; Debernard, J.B.; Gupta, A.K.; He, Y.-C.; Kirkevåg, A.; et al. Overview of the Norwegian Earth System Model (NorESM2) and key climate response of CMIP6 DECK, historical, and scenario simulations. Geosci. Model Dev. 2020, 13, 6165–6200. [Google Scholar] [CrossRef]
- Dunne, J.P.; Horowitz, L.W.; Adcroft, A.J.; Ginoux, P.; Held, I.M.; John, J.G.; Krasting, J.P.; Malyshev, S.; Naik, V.; Paulot, F.; et al. The GFDL Earth System Model Version 4.1 (GFDL-ESM 4.1): Overall Coupled Model Description and Simulation Characteristics. J. Adv. Model. Earth Syst. 2020, 12, e2019MS002015. [Google Scholar] [CrossRef]
- Rong, X.; Li, J.; Chen, H.; Xin, Y.; Su, J.; Hua, L.; Zhou, T.; Qi, Y.; Zhang, Z.; Zhang, G.; et al. The CAMS Climate System Model and a Basic Evaluation of Its Climatology and Climate Variability Simulation. J. Meteorol. Res. 2019, 32, 839–861. [Google Scholar] [CrossRef]
- Cao, J.; Wang, B.; Yang, Y.-M.; Ma, L.; Li, J.; Sun, B.; Bao, Y.; He, J.; Zhou, X.; Wu, L. The NUIST Earth System Model (NESM) version 3: Description and preliminary evaluation. Geosci. Model Dev. 2018, 11, 2975–2993. [Google Scholar] [CrossRef]
- Fatichi, S.; Ivanov, V.Y.; Caporali, E. Assessment of a stochastic downscaling methodology in generating an ensemble of hourly future climate time series. Clim. Dyn. 2013, 40, 1841–1861. [Google Scholar] [CrossRef]
- Doi, M.V.; Kim, J. Projections on climate internal variability and climatological mean at fine scales over South Korea. Stoch. Environ. Res. Risk Assess. 2020, 34, 1037–1058. [Google Scholar] [CrossRef]
- Doi, M.V.; Kim, J. Addressing Climate Internal Variability on Future Intensity-Duration-Frequency Curves at Fine Scales across South Korea. Water 2021, 13, 2828. [Google Scholar] [CrossRef]
- Kim, J.; Ivanov, V.Y. A holistic, multi-scale dynamic downscaling framework for climate impact assessments and challenges of addressing finer-scale watershed dynamics. J. Hydrol. 2015, 522, 645–660. [Google Scholar] [CrossRef]
- Tran, V.N.; Kim, J. Quantification of predictive uncertainty with a metamodel: Toward more efficient hydrologic simulations. Stoch. Environ. Res. Risk Assess. 2019, 33, 1453–1476. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, T.; Zhang, L.; Chen, X.; Zhang, W.; Jiang, J. Global Land Monsoon Precipitation Changes in CMIP6 Projections. Geophys. Res. Lett. 2020, 47, e2019GL086902. [Google Scholar] [CrossRef]
- Ha, K.J.; Moon, S.; Timmermann, A.; Kim, D. Future Changes of Summer Monsoon Characteristics and Evaporative Demand Over Asia in CMIP6 Simulations. Geophys. Res. Lett. 2020, 47, e2020GL087492. [Google Scholar] [CrossRef]
- Jin, C.; Wang, B.; Liu, J. Future Changes and Controlling Factors of the Eight Regional Monsoons Projected by CMIP6 Models. J. Clim. 2020, 33, 9307–9326. [Google Scholar] [CrossRef]
- Sung, H.M.; Kim, J.; Shim, S.; Seo, J.-b.; Kwon, S.-H.; Sun, M.-A.; Moon, H.; Lee, J.-H.; Lim, Y.-J.; Boo, K.-O.; et al. Climate Change Projection in the Twenty-First Century Simulated by NIMS-KMA CMIP6 Model Based on New GHGs Concentration Pathways. Asia-Pac. J. Atmos. Sci. 2021, 57, 851–862. [Google Scholar] [CrossRef]
- Shin, Y.; Shin, Y.; Hong, J.; Kim, M.-K.; Byun, Y.-H.; Boo, K.-O.; Chung, I.-U.; Park, D.-S.R.; Park, J.-S. Future Projections and Uncertainty Assessment of Precipitation Extremes in the Korean Peninsula from the CMIP6 Ensemble with a Statistical Framework. Atmosphere 2021, 12, 97. [Google Scholar] [CrossRef]
- Almazroui, M.; Saeed, S.; Saeed, F.; Islam, M.N.; Ismail, M. Projections of Precipitation and Temperature over the South Asian Countries in CMIP6. Earth Syst. Environ. 2020, 4, 297–320. [Google Scholar] [CrossRef]
- Jiang, J.; Zhou, T.; Chen, X.; Zhang, L. Future changes in precipitation over Central Asia based on CMIP6 projections. Environ. Res. Lett. 2020, 15, 054009. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Shahid, S.; Islam, A.R.M.T.; Hwang, S.; Cho, J.; Zaman, M.A.U.; Ahmed, M.; Rahman, M.M.; Hossain, M.B. Comparison of CMIP6 and CMIP5 model performance in simulating historical precipitation and temperature in Bangladesh: A preliminary study. Theor. Appl. Climatol. 2021, 145, 1385–1406. [Google Scholar] [CrossRef]
- Tebaldi, C.; Debeire, K.; Eyring, V.; Fischer, E.; Fyfe, J.; Friedlingstein, P.; Knutti, R.; Lowe, J.; O’Neill, B.; Sanderson, B.; et al. Climate model projections from the Scenario Model Intercomparison Project (ScenarioMIP) of CMIP6. Earth Syst. Dyn. 2021, 12, 253–293. [Google Scholar] [CrossRef]
- Stouffer, R.J.; Eyring, V.; Meehl, G.A.; Bony, S.; Senior, C.; Stevens, B.; Taylor, K.E. CMIP5 Scientific Gaps and Recommendations for CMIP6. Bull. Am. Meteorol. Soc. 2017, 98, 95–105. [Google Scholar] [CrossRef]
- Kim, J.; Ivanov, V.Y.; Fatichi, S. Soil erosion assessment—Mind the gap. Geophys. Res. Lett. 2016, 43, 12446–12456. [Google Scholar] [CrossRef]
- Tran, V.N.; Kim, J. A robust surrogate data assimilation approach to real-time forecasting using polynomial chaos expansion. J. Hydrol. 2021, 598, 126367. [Google Scholar] [CrossRef]
- Tran, V.N.; Kim, J. Robust and efficient uncertainty quantification for extreme events that deviate significantly from the training dataset using polynomial chaos-kriging. J. Hydrol. 2022, 609, 127716. [Google Scholar] [CrossRef]

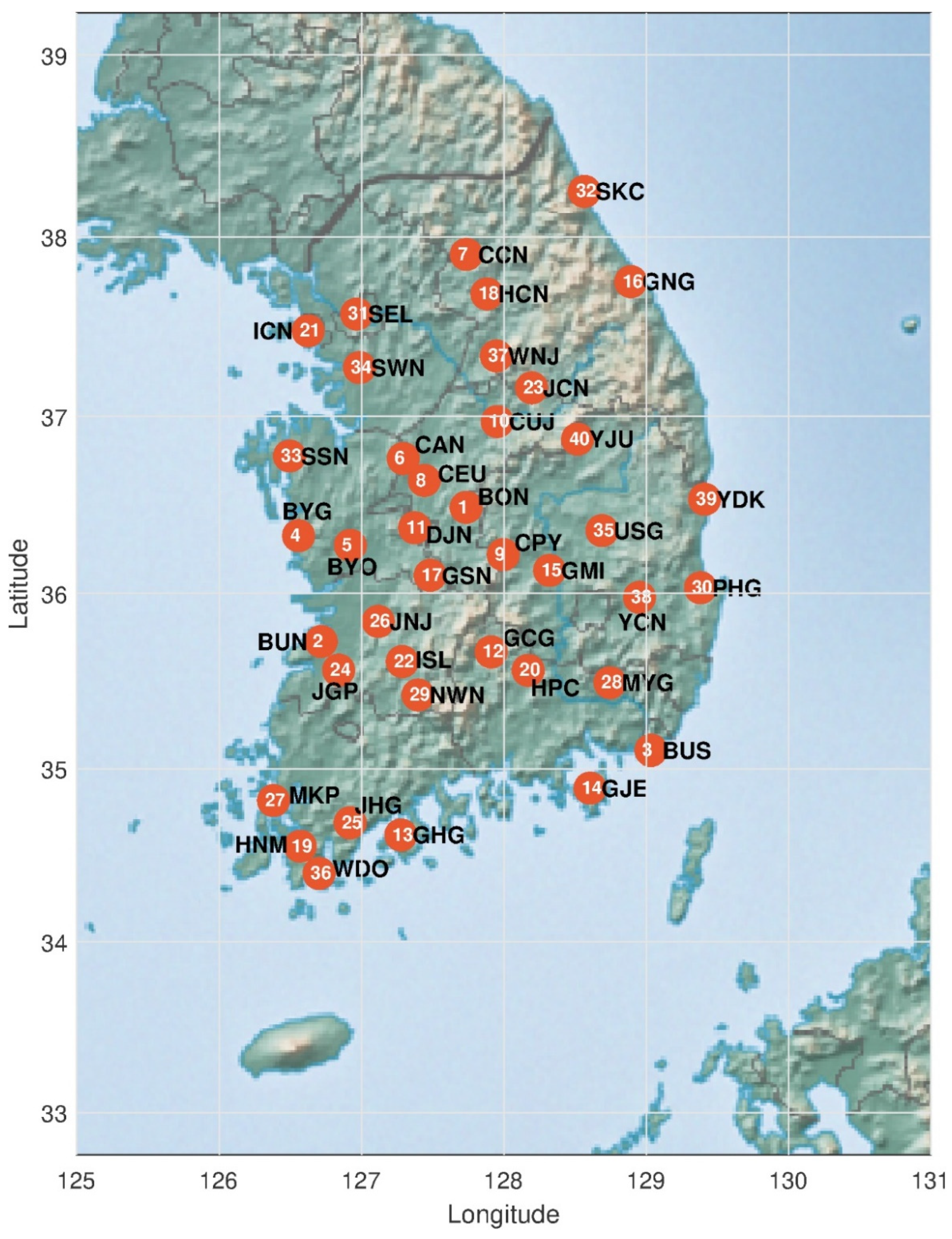
| No. | CMIP5 | CMIP6 | Ref. | ||||
|---|---|---|---|---|---|---|---|
| Institute | Model Name | Lon × Lat | Institute | Model Name | Lon × Lat | ||
| 1 | BCC | BCC-CSM1-1 | 128 × 128 | BCC | BCC-CSM2-MR | 320 × 160 | [44] |
| 2 | CCCMA | CanESM2 | 128 × 64 | CCCMA | CanESM5 | 128 × 64 | [45] |
| 3 | CMCC | CMCC-CM | 480 × 480 | CMCC | CMCC-CM2-SR5 | 288 × 192 | [46] |
| 4 | CNRM | CNRM-CM5 | 256 × 128 | CNRM-CERFACS | CNRM-CM6-1 | 256 × 128 | [47] |
| 5 | CSIRO-BOM | ACCESSS1-0 | 288 × 192 | CSIRO | ACCESS-ESM1-5 | 192 × 145 | [48] |
| 6 | CSIRO-QCCE | CSIRO-Mk3-6-0 | 192 × 96 | CSIRO-ARCCSS | ACCESS-CM2 | 192 × 144 | [49] |
| 7 | INM | INM-CM-4 | 180 × 120 | INM | INM-CM-5 | 180 × 120 | [50,51] |
| 8 | IPSL | IPSL-CM5A-LR | 96 × 96 | IPSL | IPSL-CM6A-LR | 144 × 143 | [52] |
| 9 | LASG-CESS | FGOALS-g2 | 128 × 128 | CAS | FGOALS-g3 | 180 × 90 | [53] |
| 10 | MIROC | MIROC5 | 256 × 256 | MIROC | MIROC6 | 256 × 256 | [54] |
| 11 | MOHC | HadGEM2-ES | 192 × 145 | MOHC | HadGEM3-GC31-LL | 192 × 145 | [55] |
| 12 | MPI-M | MPI-ESM-MR | 192 × 192 | MPI-M | MPI-ESM1-2-HR | 384 × 192 | [56] |
| 13 | MRI | MRI-CGCM3 | 320 × 160 | MRI | MRI-ESM2-0 | 320 × 160 | [57] |
| 14 | NCAR | CCSM4 | 288 × 192 | NCAR | CESM2 | 288 × 192 | [58,59] |
| 15 | NCC | NorESM1-M | 144 × 96 | NCC | NorESM2-LM | 144 × 96 | [60] |
| 16 | NOAA-GFDL | GFDL-ESM2G | 180 × 180 | NOAA-GFDL | GFDL-ESM4 | 360 × 180 | [61] |
| 17 | BNU | BNU-ESM | 128 × 128 | CAMS | CAMS-CSM1-0 * | 360 × 200 | [62] |
| 18 | NSF-DOE | CESM1-CAM5 | 382 × 288 | NUIST | NESM3 * | 192 × 96 | [63] |
| Index | R | NRMSE | ||
|---|---|---|---|---|
| BWA Mean | GCMs | BWA Mean | GCMs | |
| meanTa (°C) | 0.995 | 0.278–0.993 | 0.085 | 0.109–0.407 |
| 0.994 | 0.936–0.987 | 0.074 | 0.111–0.312 | |
| totPr (mm) | 0.989 | 0.926–0.981 | 0.385 | 0.359–0.474 |
| 0.990 | 0.931–0.984 | 0.274 | 0.312–0.722 | |
| maxDa (mm) | 0.943 | 0.482–0.920 | 0.509 | 0.406–0.814 |
| 0.932 | 0.661–0.908 | 0.464 | 0.346–0.721 | |
| nonPr (day) | 0.998 | 0.987–0.999 | 0.201 | 0.112–0.598 |
| 0.999 | 0.992–0.999 | 0.185 | 0.084–0.419 | |
| Index | CTL | ERY | MID | END |
|---|---|---|---|---|
| meanTa (°C) | 9.8–14.2 | 11.2–15.6 | 12.8–17.2 | 14.5–18.7 |
| 10.4–15.0 | 11.7–15.8 | 13.1–17.7 | 15.6–19.9 | |
| totPr (mm) | 959.6–1299.5 | 995.9–1388.9 | 1112.8–1467.5 | 1128.7–1466.9 |
| 1034.3–1452.7 | 1143.5–1474.1 | 1083.0–1505.6 | 1148.7–1523.6 | |
| maxDa (mm) | 66.9–93.1 | 75.0–97.1 | 81.8–109.7 | 82.6–112.0 |
| 75.1–112.9 | 81.5–100.6 | 82.3–107.8 | 80.9–123.2 | |
| nonPr (day) | 238–270 | 242–270 | 237–271 | 240–269 |
| 250–264 | 246–265 | 250–265 | 249–264 |
| Index | CTL | ERY | MID | END |
|---|---|---|---|---|
| meanTa (°C) | 0.49–1.87 | 0.40–1.57 | 0.44–1.66 | 0.62–1.68 |
| 0.55–1.98 | 0.60–2.65 | 0.63–2.24 | 0.69–2.60 | |
| totPr (mm) | 22.62–278.02 | 6.77–252.66 | 5.78–260.79 | 33.75–256.91 |
| 6.28–248.50 | 10.24–248.42 | 21.59–245.88 | 11.27–305.46 | |
| maxDa (mm) | 1.18–41.43 | 2.52–31.52 | 5.02–50.85 | 1.47–71.74 |
| 1.63–22.28 | 0.71–19.41 | 0.71–25.43 | 1.94–25.84 | |
| nonPr (day) | 2–40 | 3–33 | 2–47 | 3–33 |
| 1–15 | 1–21 | 1–15 | 1–21 |
| Index | CTL | ERY | MID | END |
|---|---|---|---|---|
| meanTa (°C) | 0.77–1.28 | 0.77–1.27 | 0.77–1.26 | 0.77–1.26 |
| 0.78–1.28 | 0.77–1.25 | 0.77–1.27 | 0.77–1.27 | |
| totPr (mm) | 239.7–497.5 | 206.7–487.8 | 205.8–558.7 | 238.1–544.3 |
| 239.7–497.5 | 199.3–480.9 | 216.5–474.5 | 264.5–556.7 | |
| maxDa (mm) | 41.2–105.00 | 43.2–115.3 | 48.1–110.5 | 48.6–110.1 |
| 41.2–105.00 | 38.7–105.4 | 42.6–116.5 | 47.9–132.3 | |
| nonPr (day) | 8–10 | 7–9 | 7–9 | 7–10 |
| 8–10 | 7–10 | 8–10 | 7–9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doi, M.V.; Kim, J. Future Projections and Uncertainties of CMIP6 for Hydrological Indicators and Their Discrepancies from CMIP5 over South Korea. Water 2022, 14, 2926. https://doi.org/10.3390/w14182926
Doi MV, Kim J. Future Projections and Uncertainties of CMIP6 for Hydrological Indicators and Their Discrepancies from CMIP5 over South Korea. Water. 2022; 14(18):2926. https://doi.org/10.3390/w14182926
Chicago/Turabian StyleDoi, Manh Van, and Jongho Kim. 2022. "Future Projections and Uncertainties of CMIP6 for Hydrological Indicators and Their Discrepancies from CMIP5 over South Korea" Water 14, no. 18: 2926. https://doi.org/10.3390/w14182926




