Hydraulic Transient Simulation of Pipeline-Open Channel Coupling Systems and Its Applications in Hydropower Stations
Abstract
:1. Introduction
2. Mathematical Model and Verifications
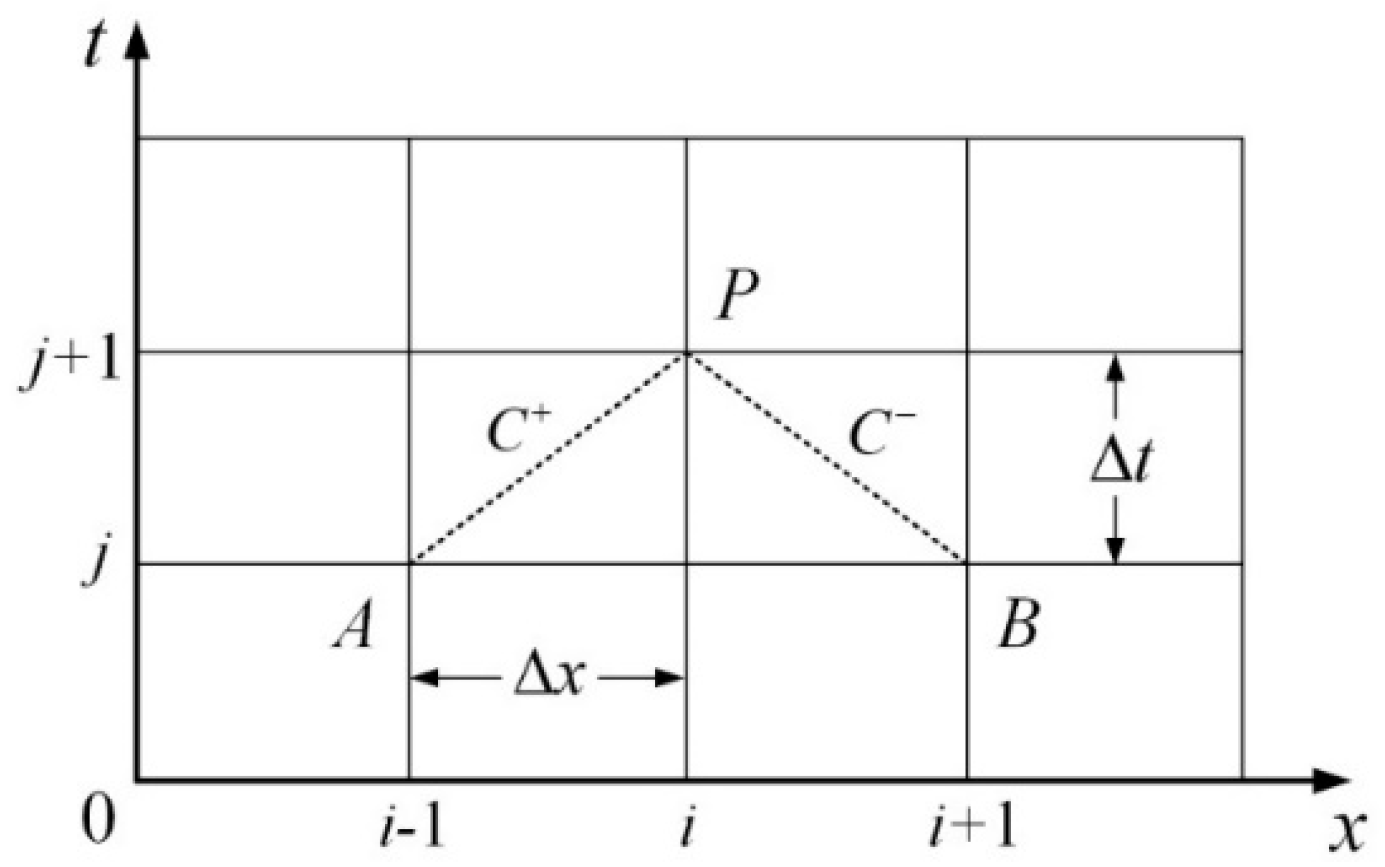
2.1. Transient Modelling of Pipeline Flow
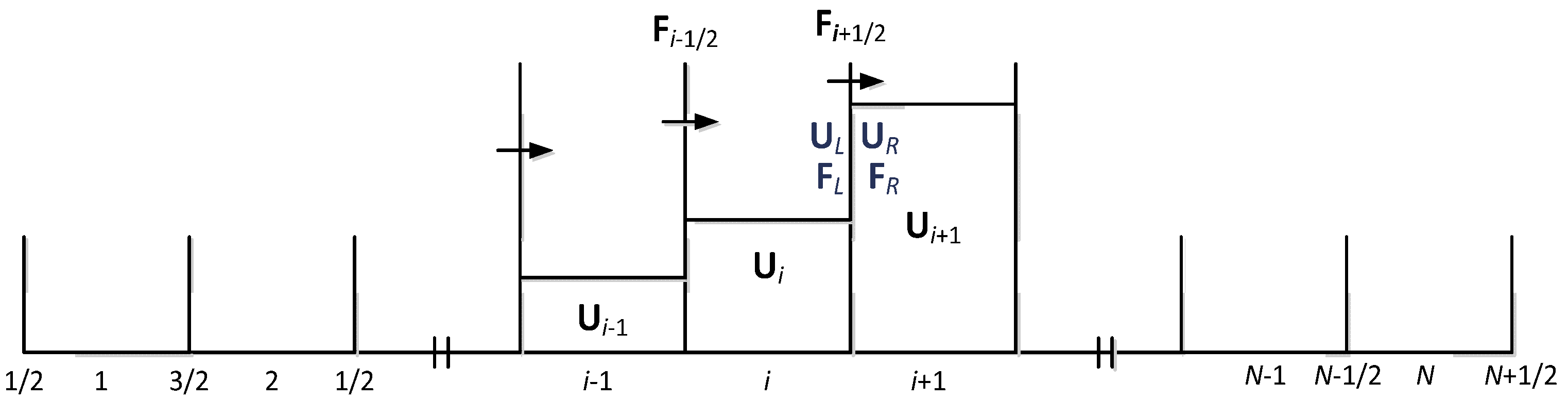
2.2. Modelling of Open Channel Flow
2.3. Boundary Condition Based on Riemann Invariants
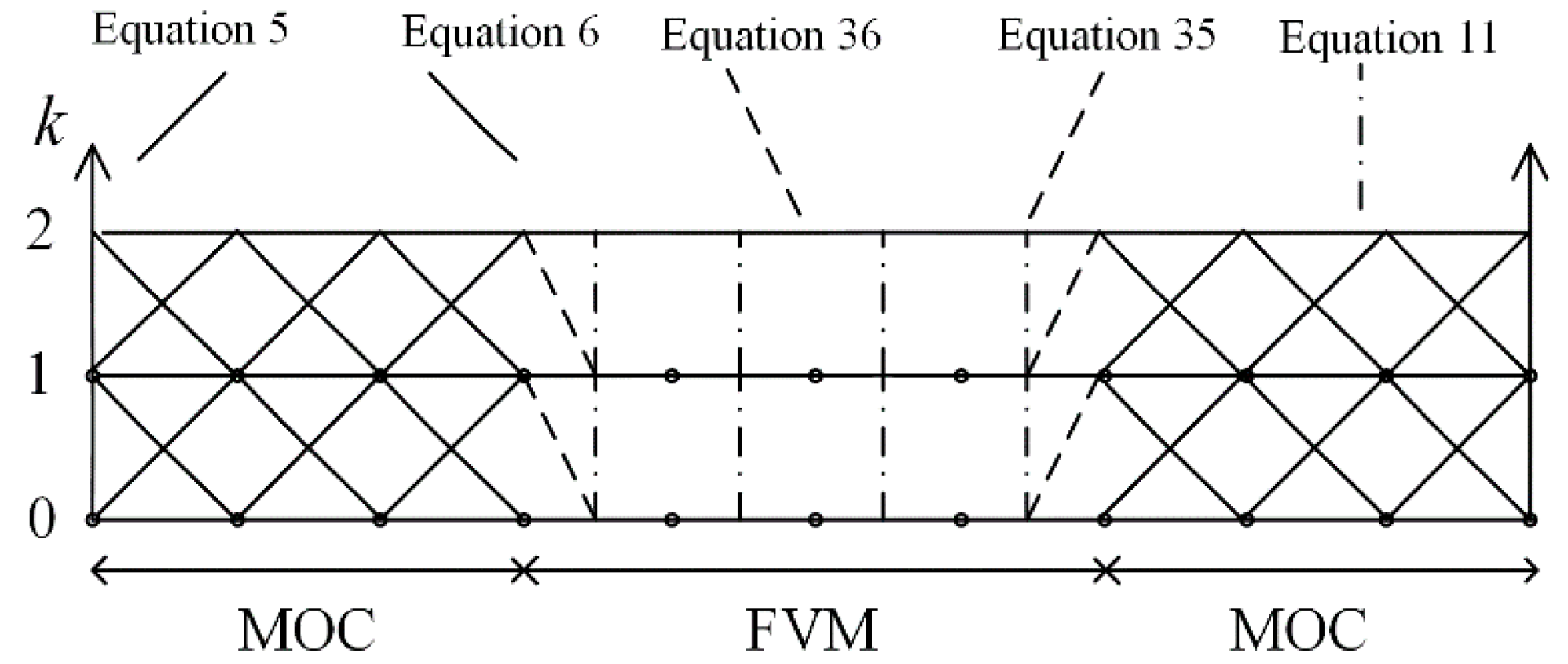
2.4. The Simulation Process
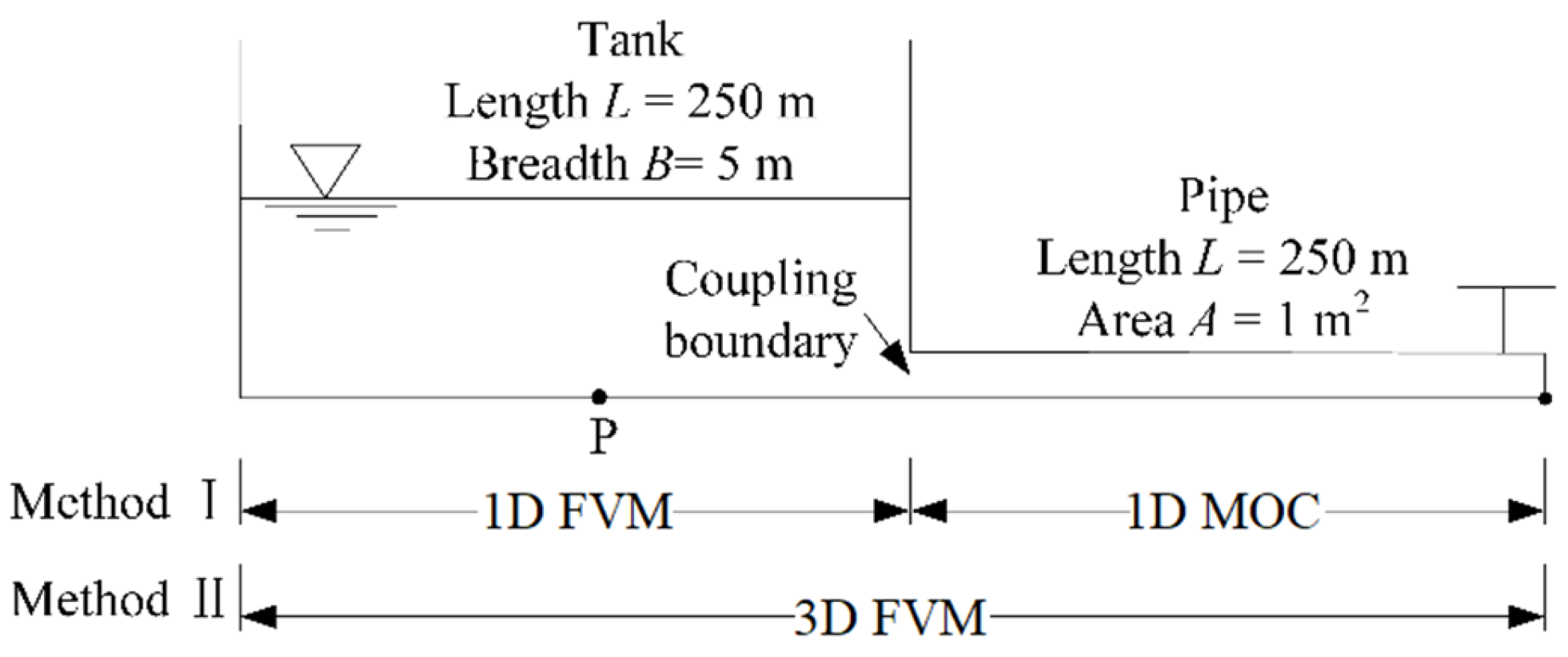
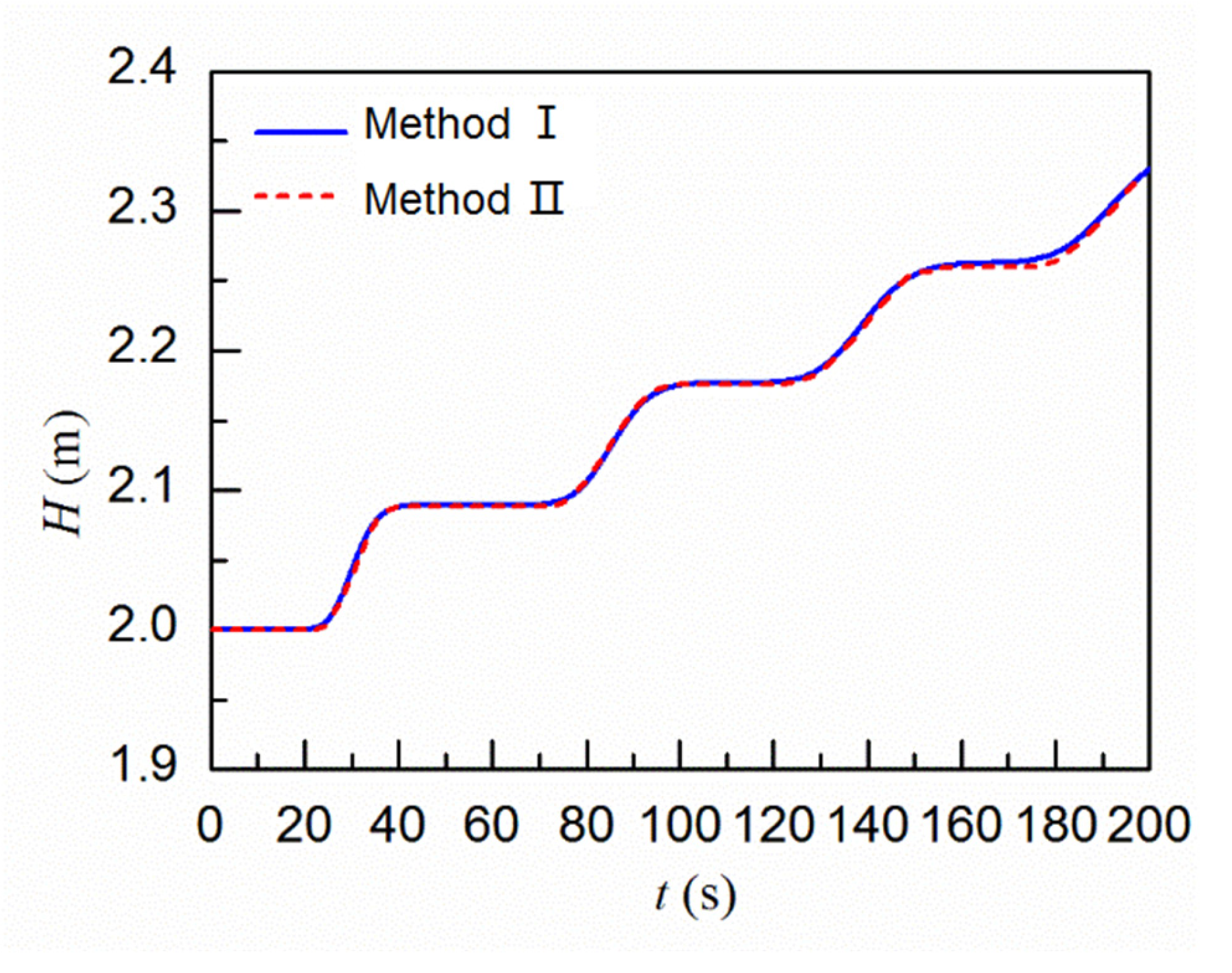
3. Numerical Validations
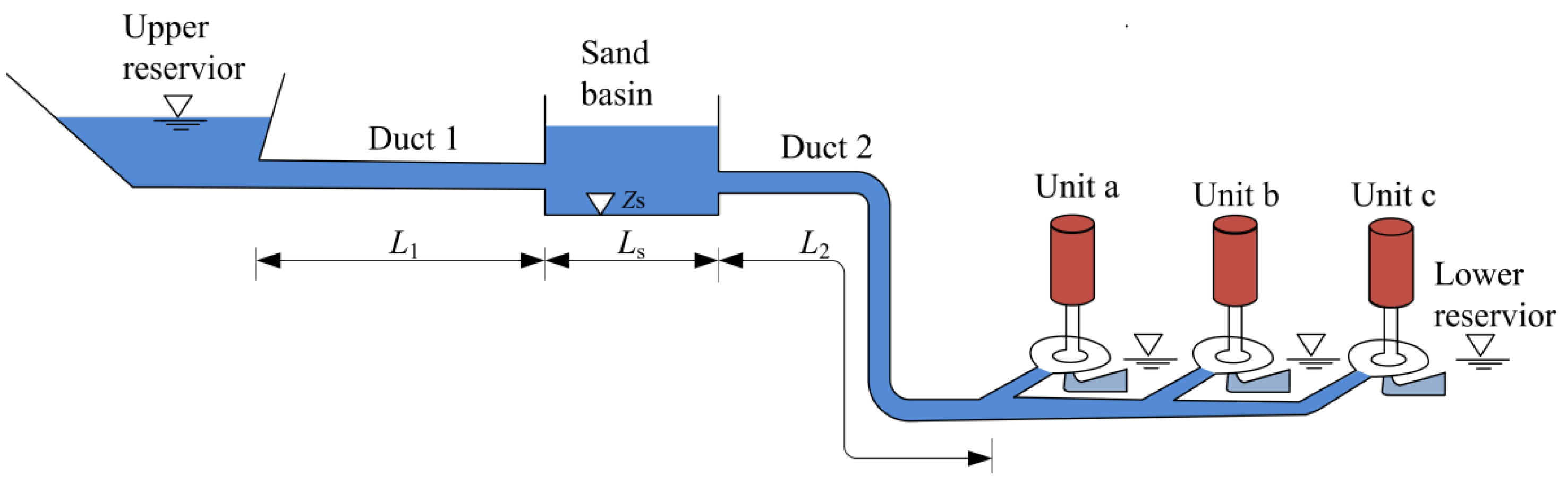
4. Transient Simulation of a Hydropower Station with a Sand Basin
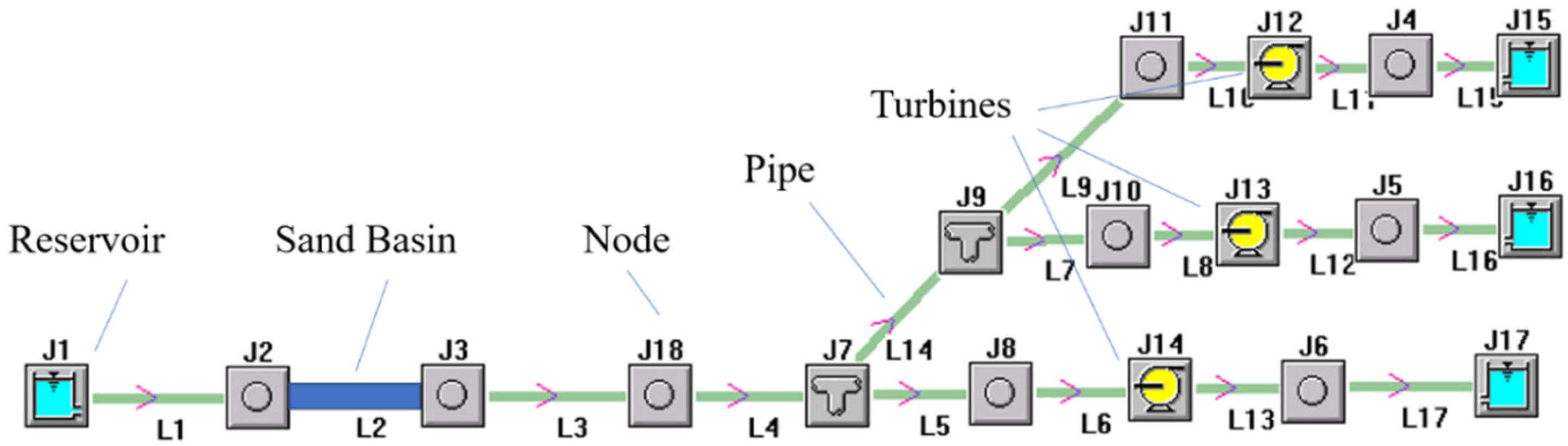
4.1. System Configuration and Modelling
4.2. Full Load-Rejection
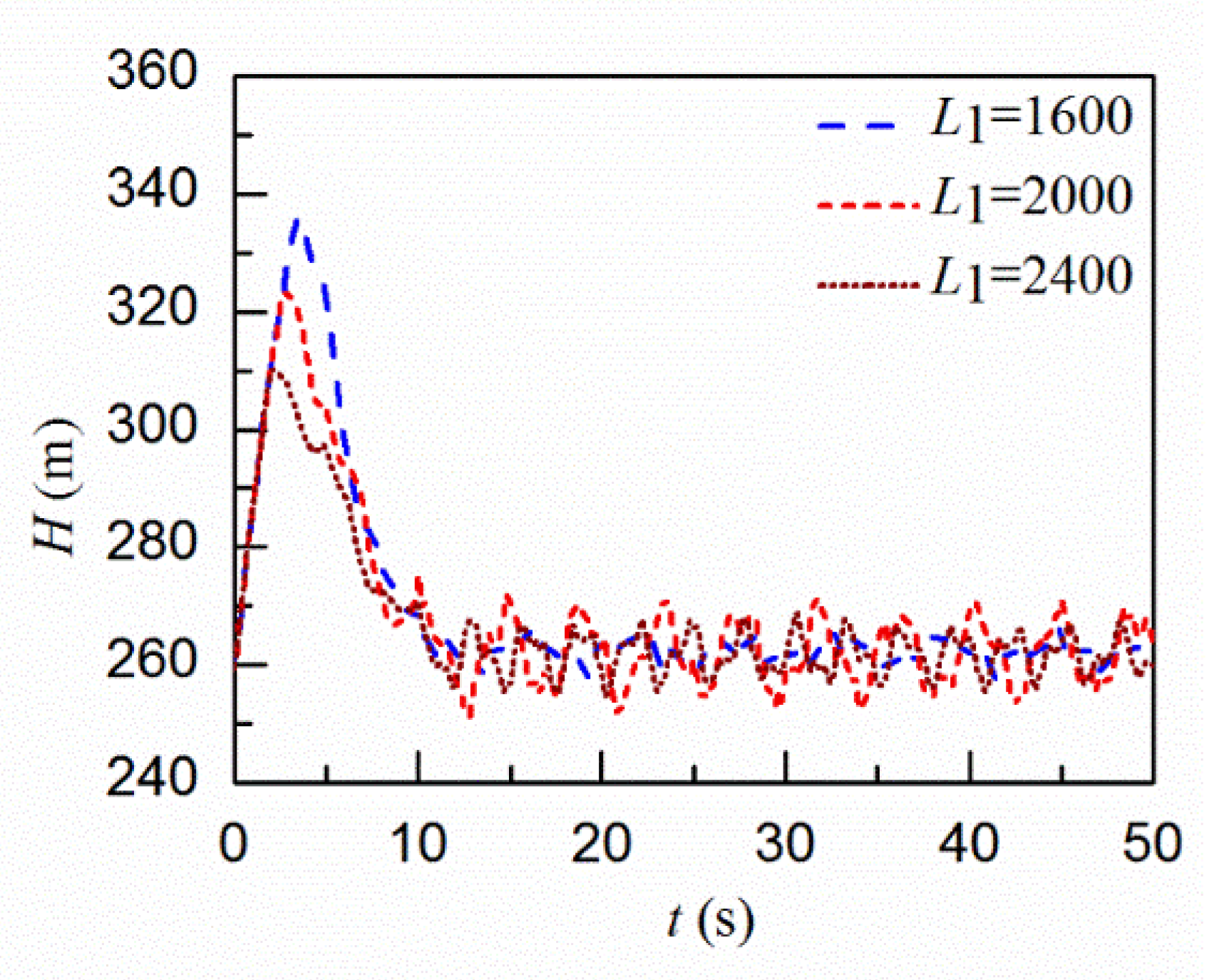
4.2.1. Simulation Results
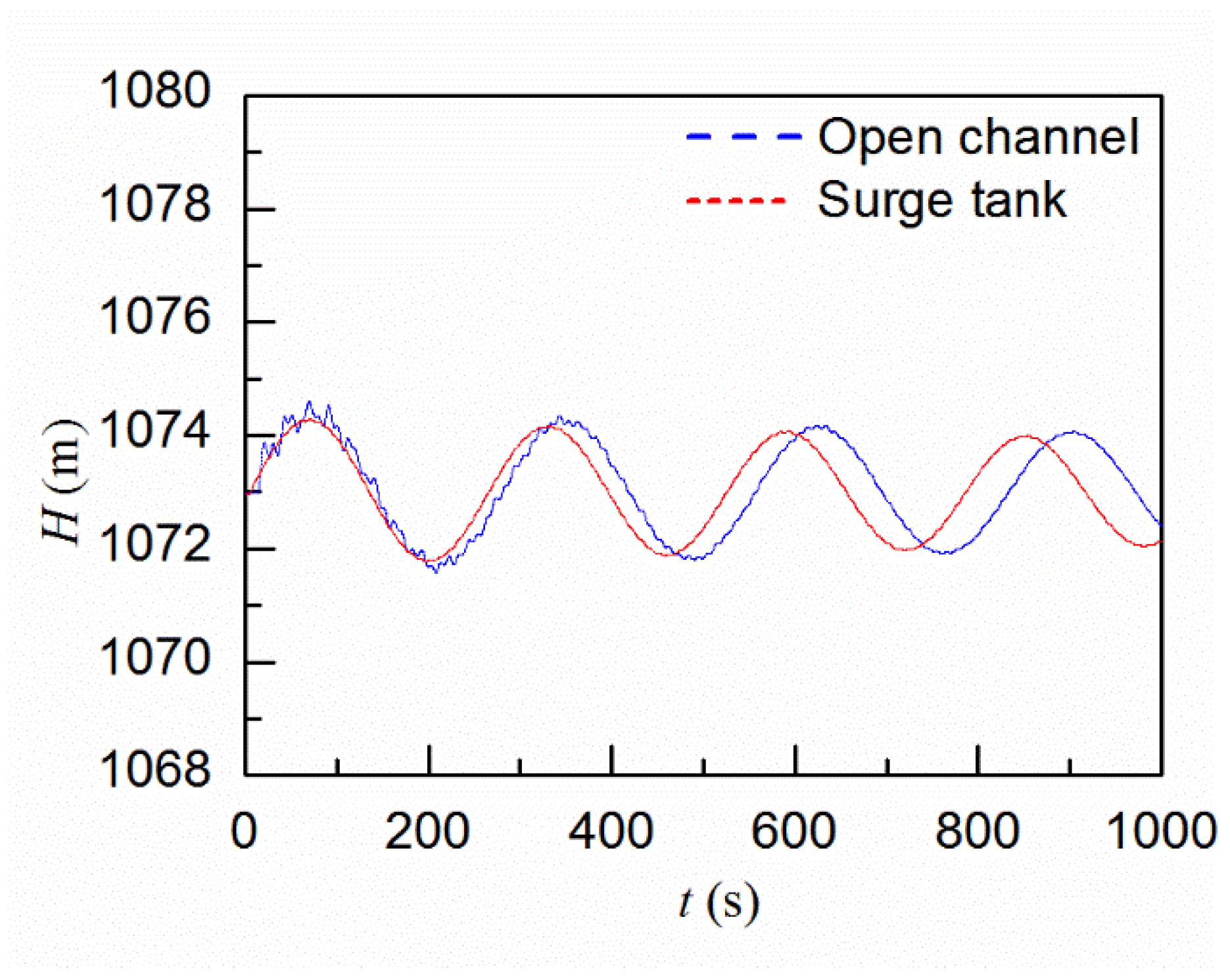
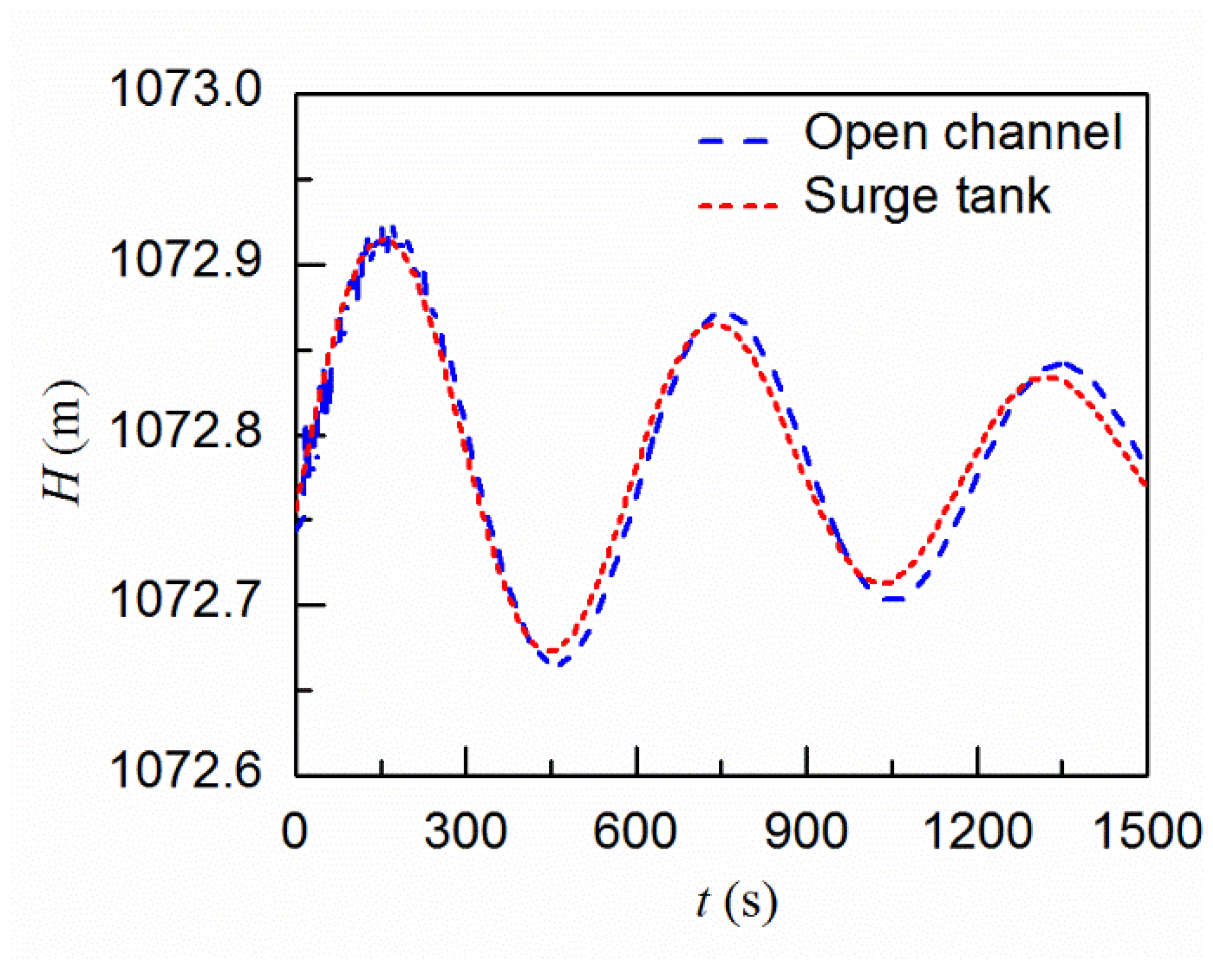
4.2.2. Comparison with the Results by Modelling the Basin Tank as a Surge Tank
4.3. 5% Load-Rejection with Frequency Regulation
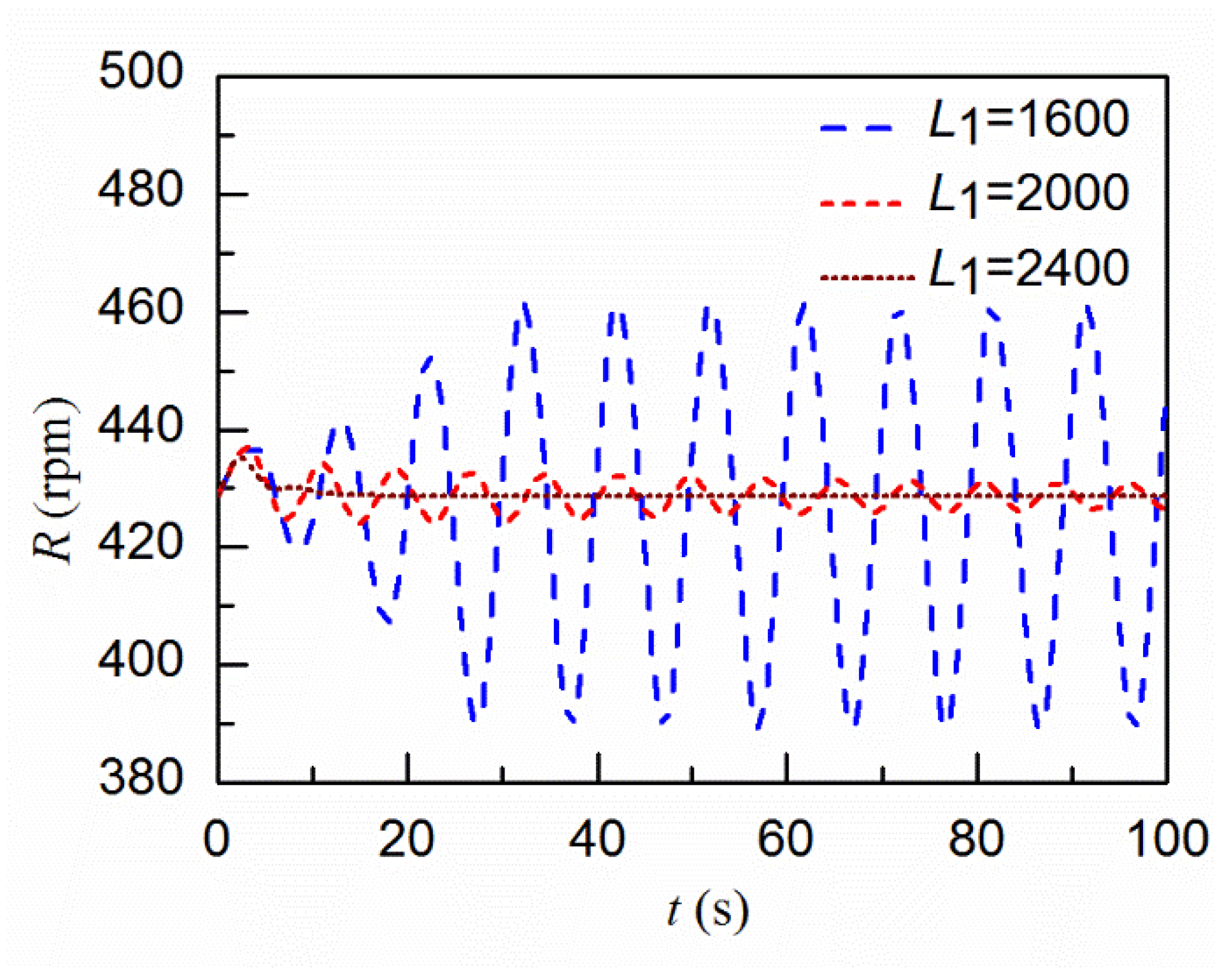
4.3.1. Simulation Results
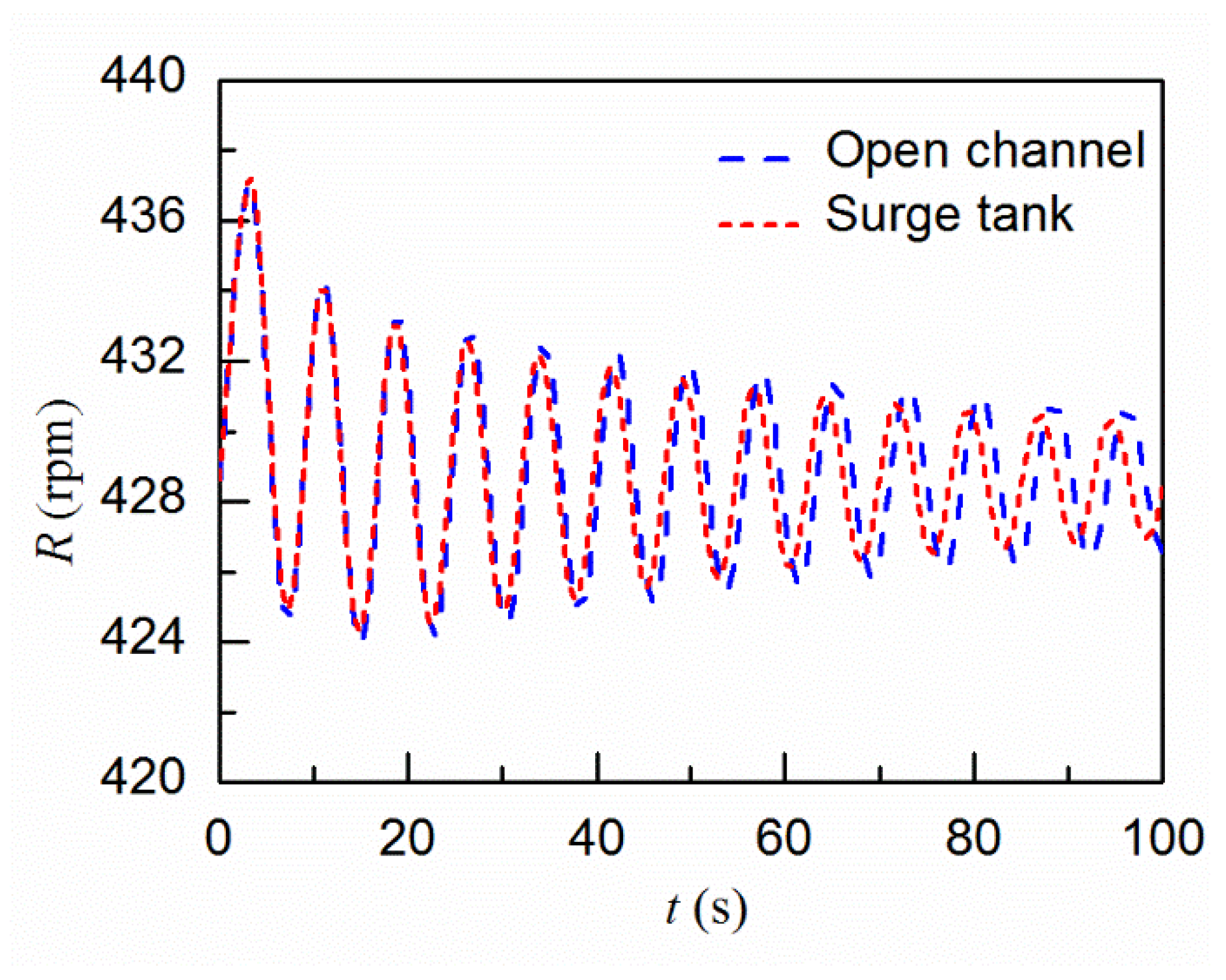
4.3.2. Comparison with the Results by Modelling the Basin Tank as a Surge Tank
5. Conclusions
- The MOC-FVM coupling method can accurately simulate the pipeline-open channel coupling transient flow with the simulated parameters transmitted successfully at the coupling boundaries.
- The coupling method has been successfully applied to a hydropower station with a sand basin constructed between the upstream reservoir and turbines. The sand basin can be modelled as an open channel.
- The effects of the sand basin on the transient process are similar to a surge tank which can relieve water hammer pressures during load rejection scenarios and can benefit the frequency regulation process. By modelling the sand basin as an open channel, the flow velocity and the friction in the horizontal direction, which are neglected when modelling the sand basin as a surge tank, can be considered, and thus more reliable and accurate results can be obtained.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, S.-G.; Lee, K.-B.; Kim, K.-Y. Water hammer in the pump-rising pipeline system with an air chamber. J. Hydrodyn. 2014, 26, 960–964. [Google Scholar] [CrossRef]
- Zhang, K.; Zeng, W.; Simpson, A.R.; Zhang, S.; Wang, C. Water Hammer Simulation Method in Pressurized Pipeline with a Moving Isolation Device. Water 2021, 13, 1794. [Google Scholar] [CrossRef]
- Yang, W.; Yang, J.; Guo, W.; Zeng, W.; Wang, C.; Saarinen, L.; Norrlund, P. A Mathematical Model and Its Application for Hydro Power Units under Different Operating Conditions. Energies 2015, 8, 10260–10275. [Google Scholar] [CrossRef]
- Karpenko, M.; Bogdevicius, M. Investigation into the hydrodynamic processes of fitting connections for determining pressure losses of transport hydraulic drive. Transport 2020, 35, 108–120. [Google Scholar] [CrossRef]
- Wylie, E.B.; Streeter, V.L. Fluid Transients in Systems; Prentice Hall Inc.: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Urbanowicz, K. Modern Modeling of Water Hammer. Pol. Marit. Res. 2017, 24, 68–77. [Google Scholar] [CrossRef]
- Chaudhry, M.H. Applied Hydraulic Transients, 3rd ed.; Springer: New York, NY, USA, 2014. [Google Scholar]
- Nicolet, C. Hydroacoustic Modelling and Numerical Simulation of Unsteady Operation of Hydroelectric Systems. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2007. [Google Scholar]
- Tijsseling, A.S. Fluid-structure interaction in liquid-filled pipe systems: A review. J. Fluids Struct. 1996, 10, 109–146. [Google Scholar] [CrossRef]
- Covas, D.; Stoianov, I.; Mano, J.F.; Ramos, H.; Graham, N.; Maksimovic, C. The dynamic effect of pipe-wall viscoelasticity in hydraulic transients. Part I—Experimental analysis and creep characterization. J. Hydraul. Res. 2004, 42, 516–530. [Google Scholar] [CrossRef]
- Vardy, A.E.; Brown, J.M.B. Transient, turbulent, smooth pipe friction. J. Hydraul. Res. 1995, 33, 435–456. [Google Scholar] [CrossRef]
- Lai, W.; Khan, A.A. Numerical solution of the Saint-Venant equations by an efficient hybrid finite-volume/finite-difference method. J. Hydrodyn. 2018, 30, 189–202. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, R.-X.; Duan, Y.-L.; Li, Y. A Characteristic-Based Finite Volume Scheme for Shallow Water Equations. J. Hydrodyn. 2009, 21, 531–540. [Google Scholar] [CrossRef]
- Yin, C.-C.; Zeng, W.; Yang, J.-D. Transient simulation and analysis of the simultaneous load rejection process in pumped storage power stations using a 1-D-3-D coupling method. J. Hydrodyn. 2021, 33, 979–991. [Google Scholar] [CrossRef]
- Wang, C.; Nilsson, H.; Yang, J.; Petit, O. 1D–3D coupling for hydraulic system transient simulations. Comput. Phys. Commun. 2017, 210, 1–9. [Google Scholar] [CrossRef]
- Zhang, X.-X.; Cheng, Y.-G.; Yang, J.-D.; Xia, L.-S.; Lai, X. Simulation of the load rejection transient process of a francis turbine by using a 1-D-3-D coupling approach. J. Hydrodyn. 2014, 26, 715–724. [Google Scholar] [CrossRef]
- Zhang, X.-X.; Cheng, Y.-G. Simulation of Hydraulic Transients in Hydropower Systems Using the 1-D-3-D Coupling Approach. J. Hydrodyn. 2012, 24, 595–604. [Google Scholar] [CrossRef]
- Yang, J.; Yang, J. 1-D MOC simulation software for hydraulic transients: TOPsys. Proc. IOP Conf. Ser. Earth Environ. Sci. 2018, 163, 12081. [Google Scholar] [CrossRef]
- Zeng, W.; Yang, J.; Hu, J. Pumped storage system model and experimental investigations on S-induced issues during transients. Mech. Syst. Signal Pract. 2017, 90, 350–364. [Google Scholar] [CrossRef]
- Hu, J.; Yang, J.; Zeng, W.; Yang, J. Transient Pressure Analysis of a Prototype Pump Turbine: Field Tests and Simulation. J. Fluids Eng. 2018, 140, 71102. [Google Scholar] [CrossRef]
- Wang, C.; Yang, J.-D. Water Hammer Simulation Using Explicit-Implicit Coupling Methods. J. Hydraul. Eng. 2015, 141, 4014086. [Google Scholar] [CrossRef]
- Toro, E.F. Shock-Capturing Methods for Free-Surface Shallow Flows; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
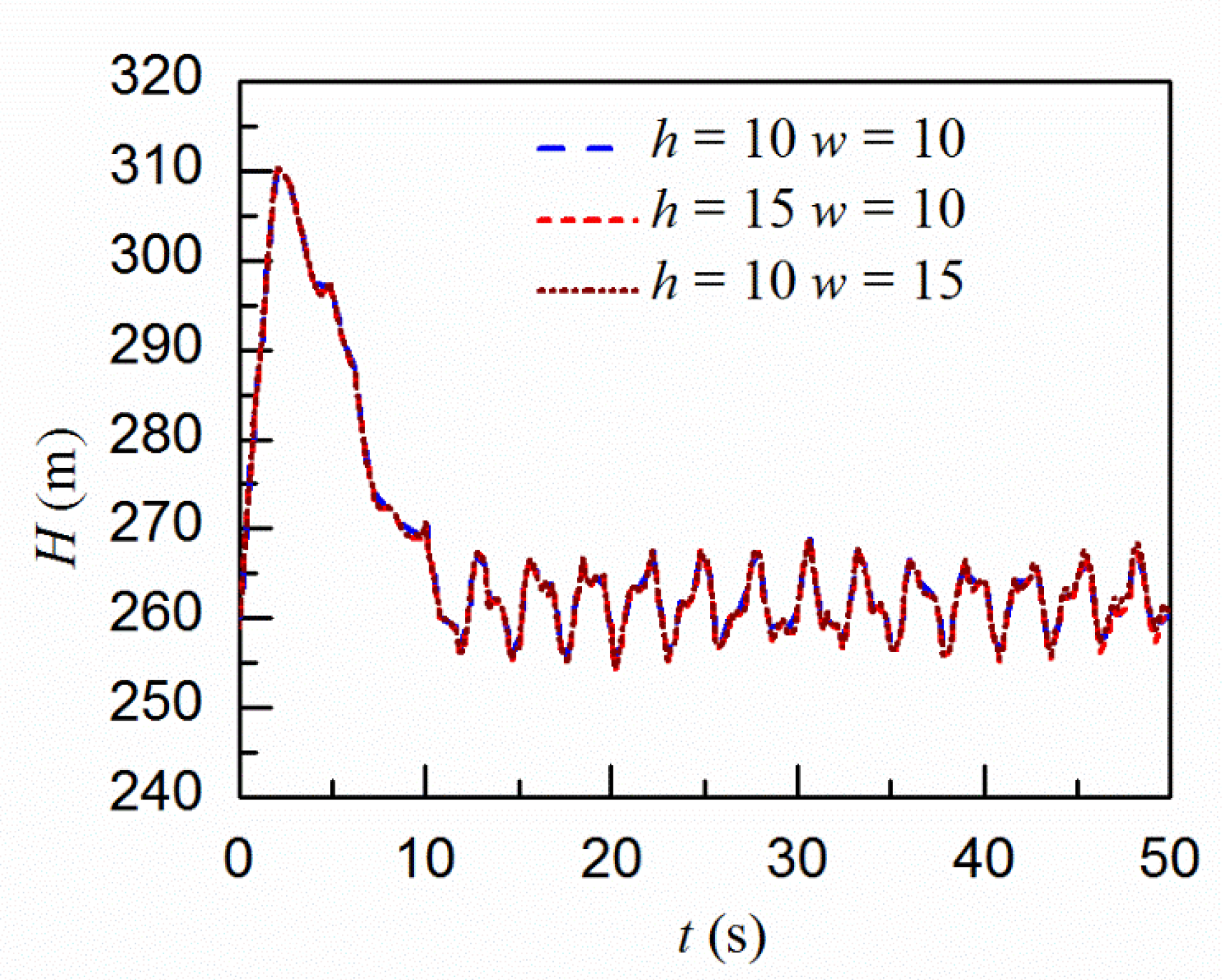
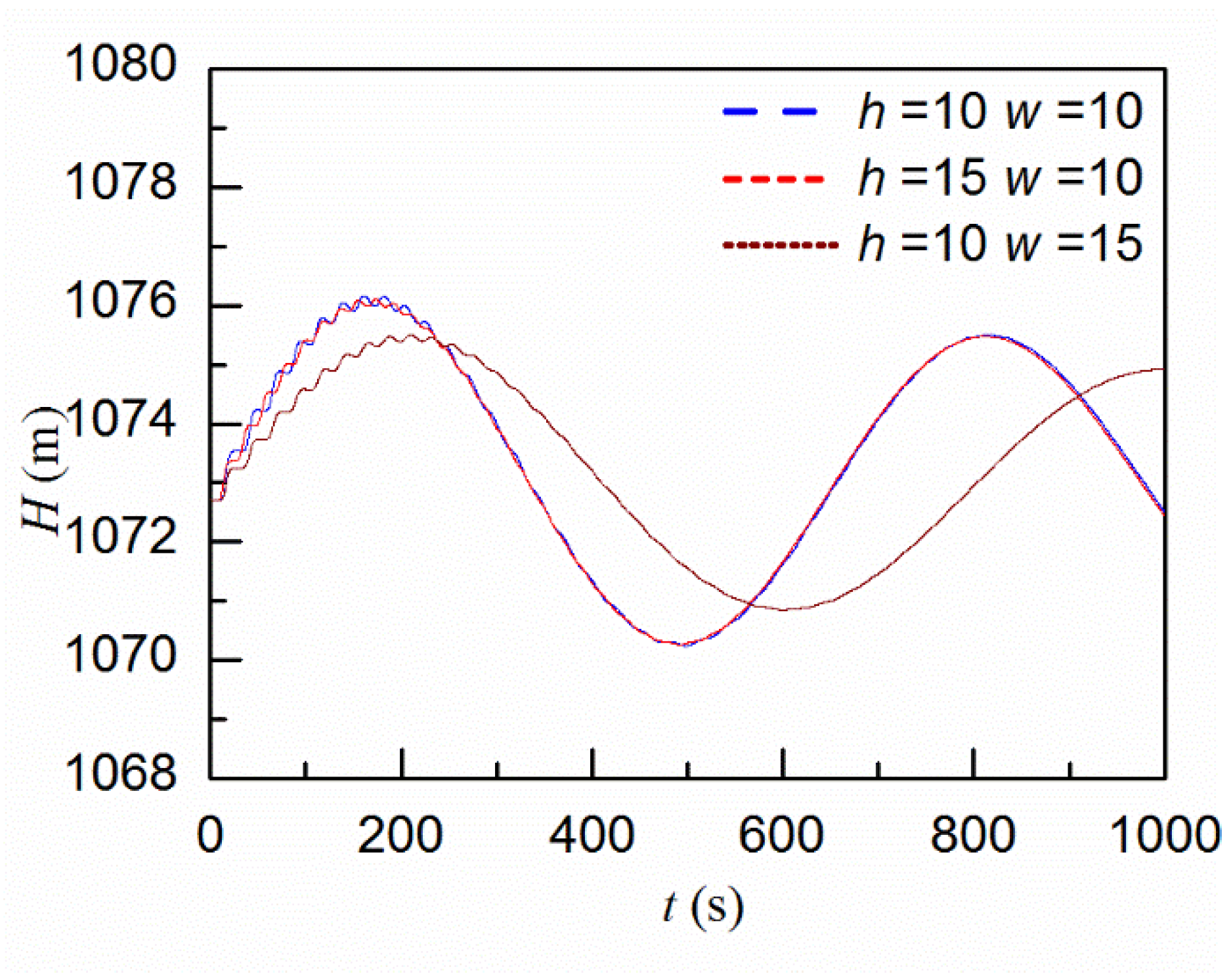
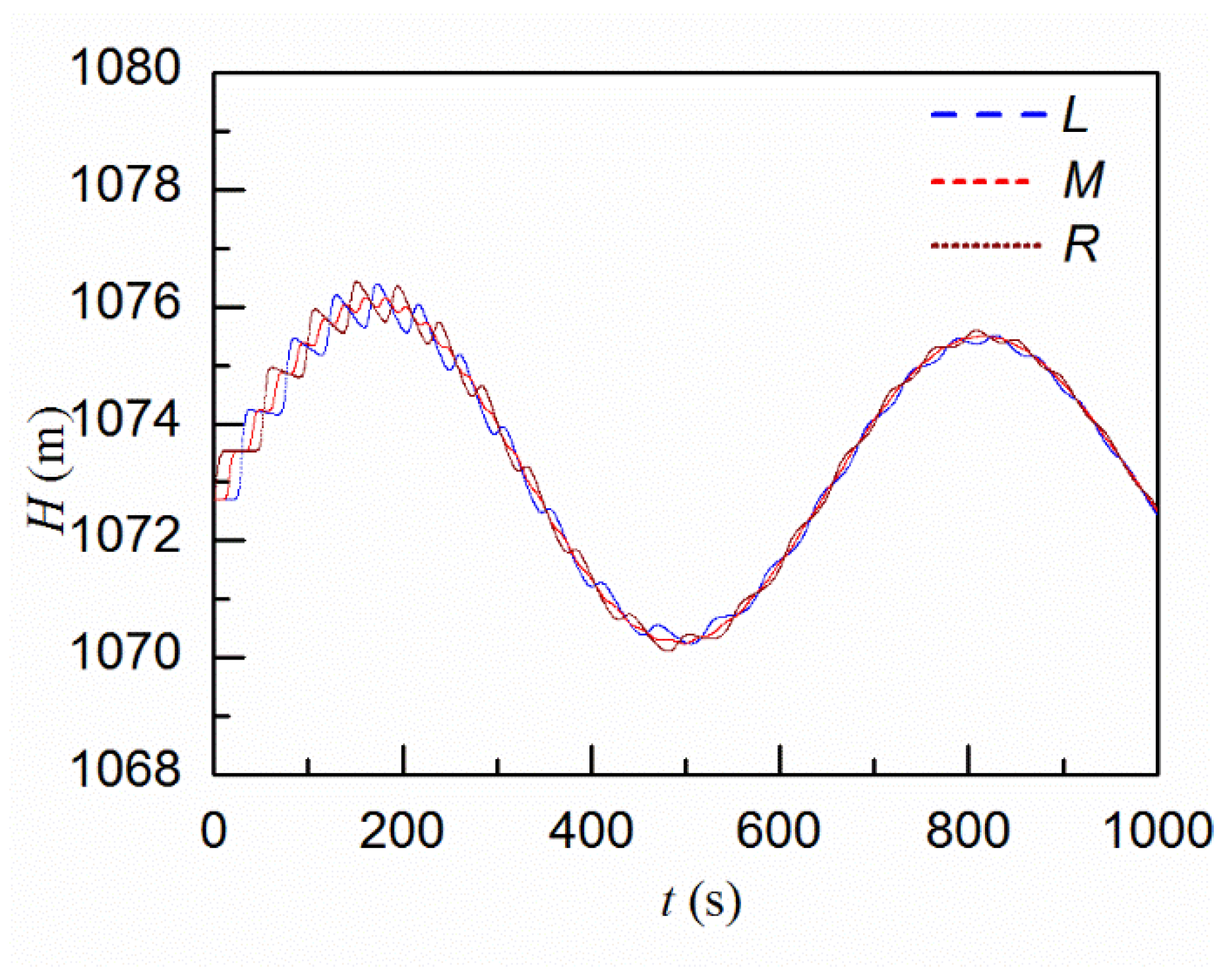
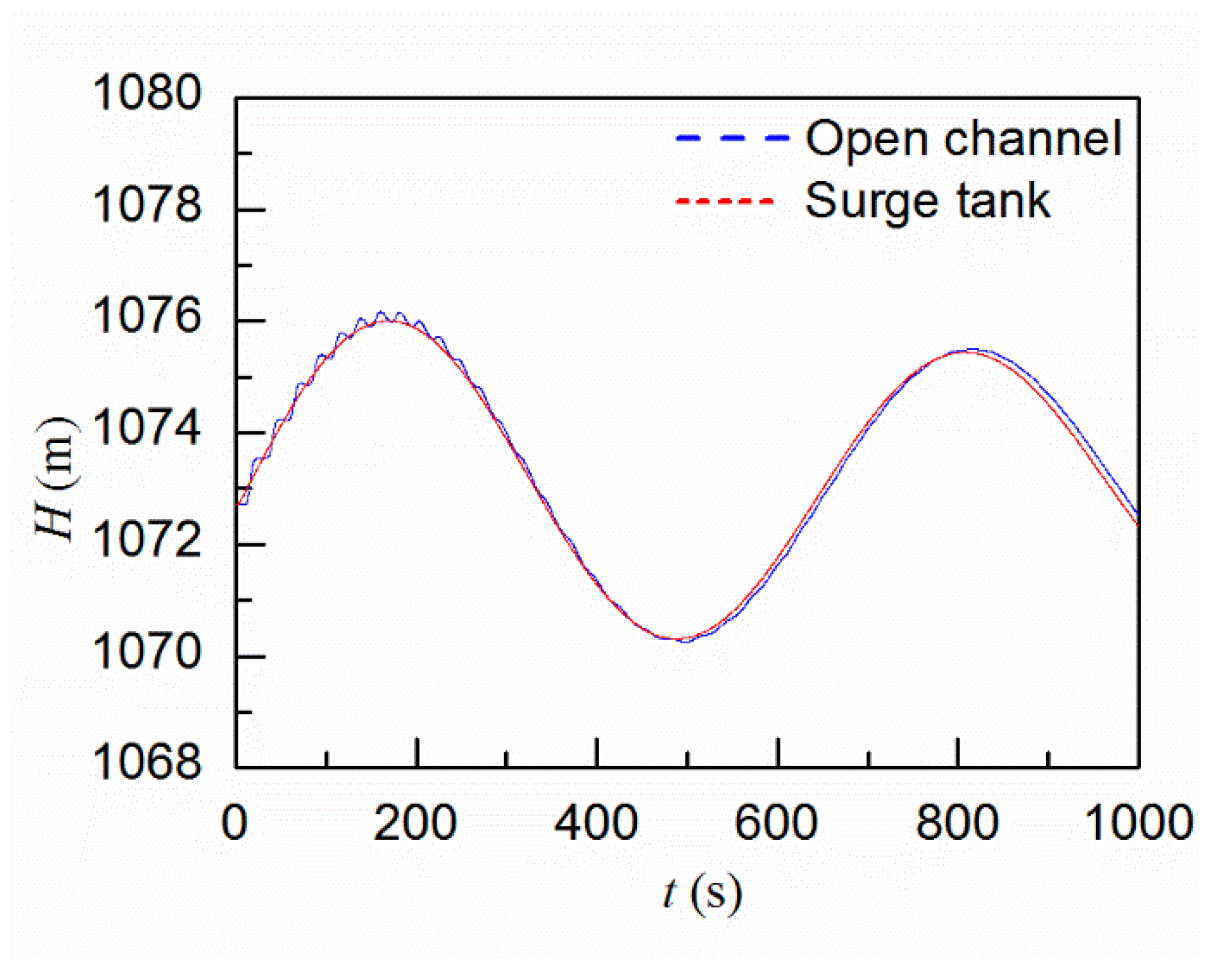

| Runner Inlet Diameter (m) | Guide Vane Height (m) | Upstream Water Level (m) | Downstream Water Level (m) | Rated Rotational Speed (rpm) | Rated Output (Mw) | Rated Flow Rate (m3/s) | Rotational Inertia (t.m2) |
|---|---|---|---|---|---|---|---|
| 2.3 | 0.7 | 1073 | 829 | 429.6 | 10.54 | 29 | 726 |
| Temporary Droop | Differential Time Constant | Time Lag in Servomotor | Dashpot Time Constant |
|---|---|---|---|
| 0.3 | 0.3 s | 0.05 s | 5.0 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, W.; Wang, C.; Yang, J. Hydraulic Transient Simulation of Pipeline-Open Channel Coupling Systems and Its Applications in Hydropower Stations. Water 2022, 14, 2897. https://doi.org/10.3390/w14182897
Zeng W, Wang C, Yang J. Hydraulic Transient Simulation of Pipeline-Open Channel Coupling Systems and Its Applications in Hydropower Stations. Water. 2022; 14(18):2897. https://doi.org/10.3390/w14182897
Chicago/Turabian StyleZeng, Wei, Chao Wang, and Jiandong Yang. 2022. "Hydraulic Transient Simulation of Pipeline-Open Channel Coupling Systems and Its Applications in Hydropower Stations" Water 14, no. 18: 2897. https://doi.org/10.3390/w14182897







