Land-Use and Land Cover Is Driving Factor of Runoff Yield: Evidence from A Remote Sensing-Based Runoff Generation Simulation
Abstract
:1. Introduction
2. Materials and Methods
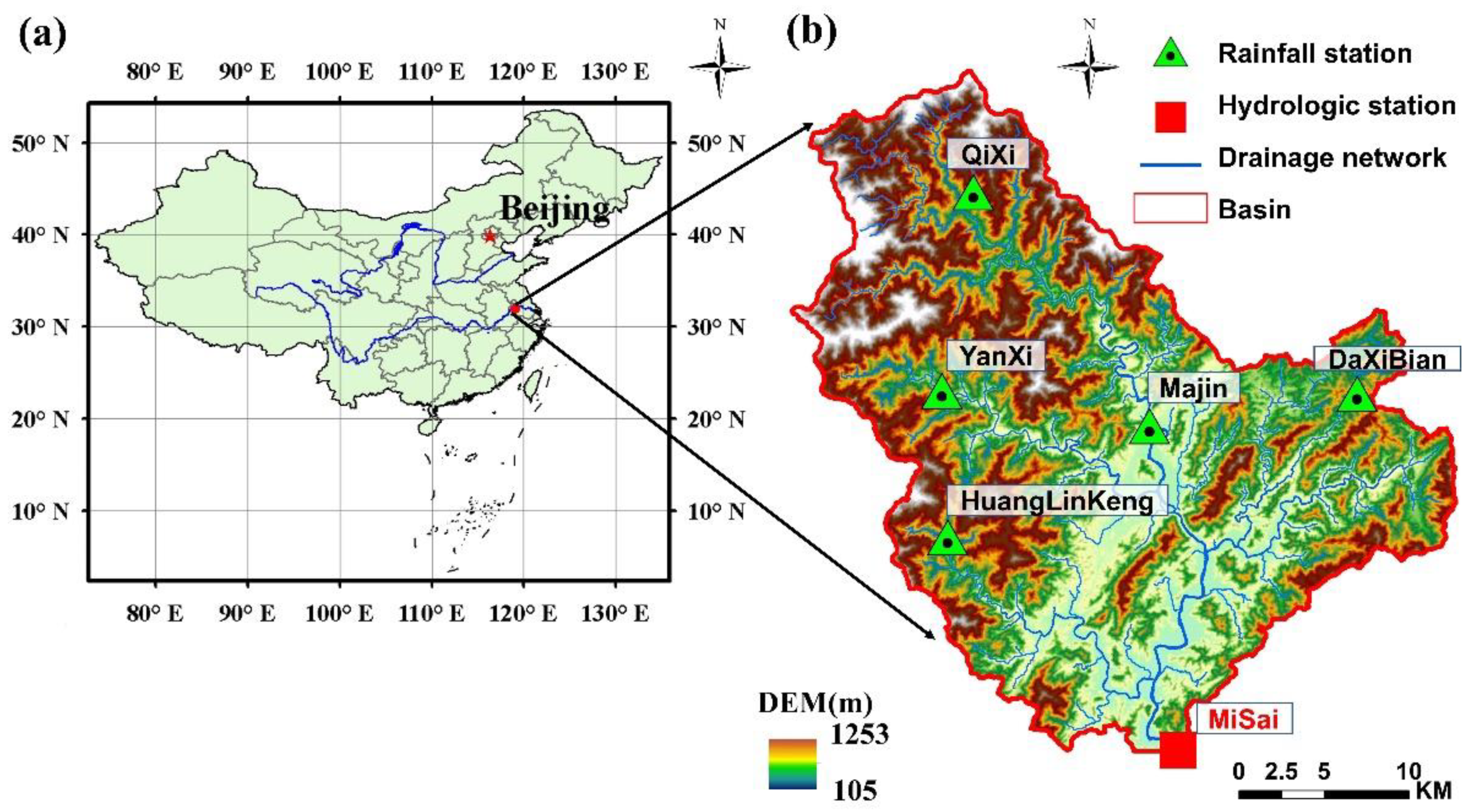
2.1. Study Area and Data Collection
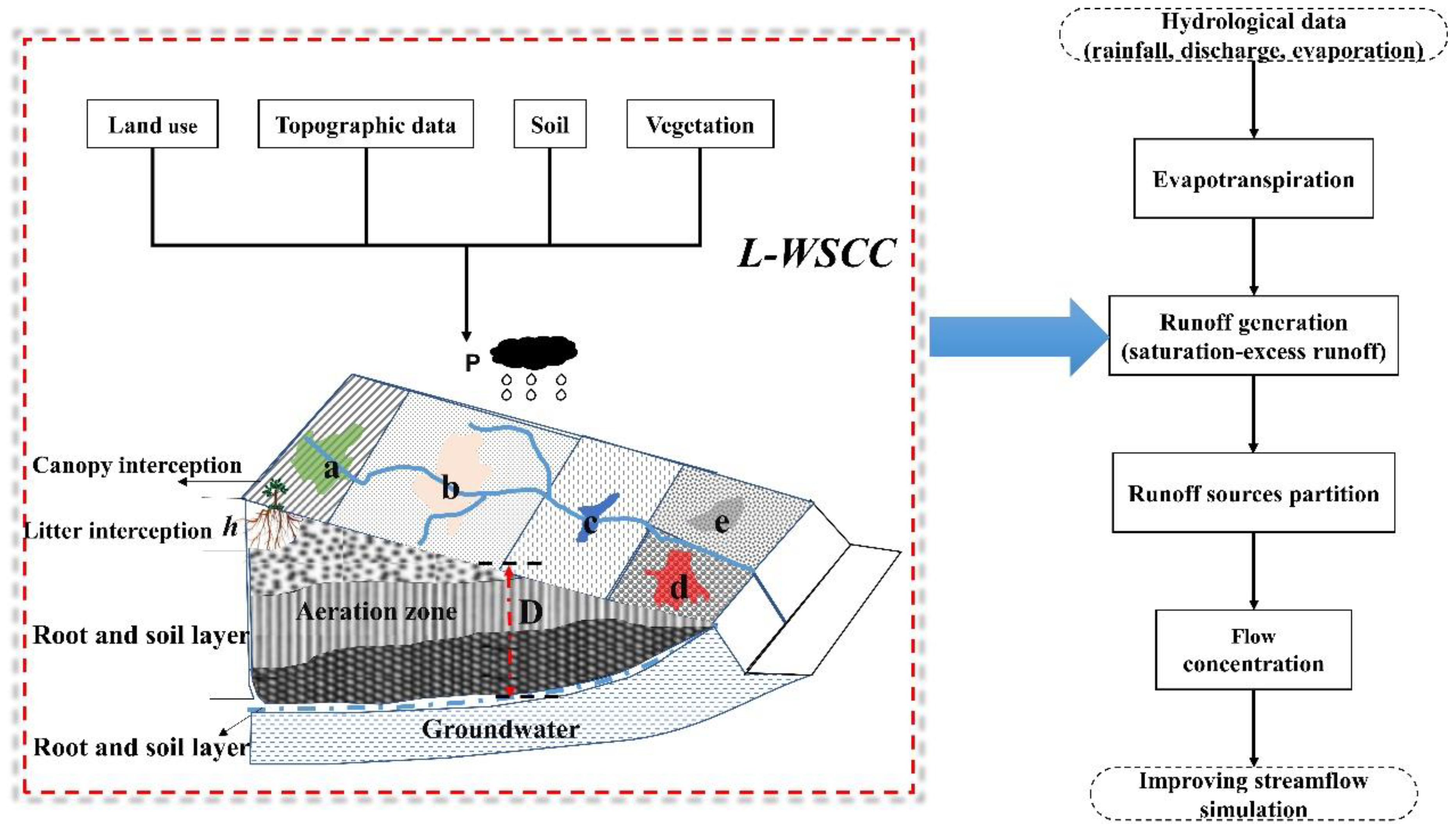
2.2. WSCC and L-WSCC
2.3. Data Preprocessing and Model Setting
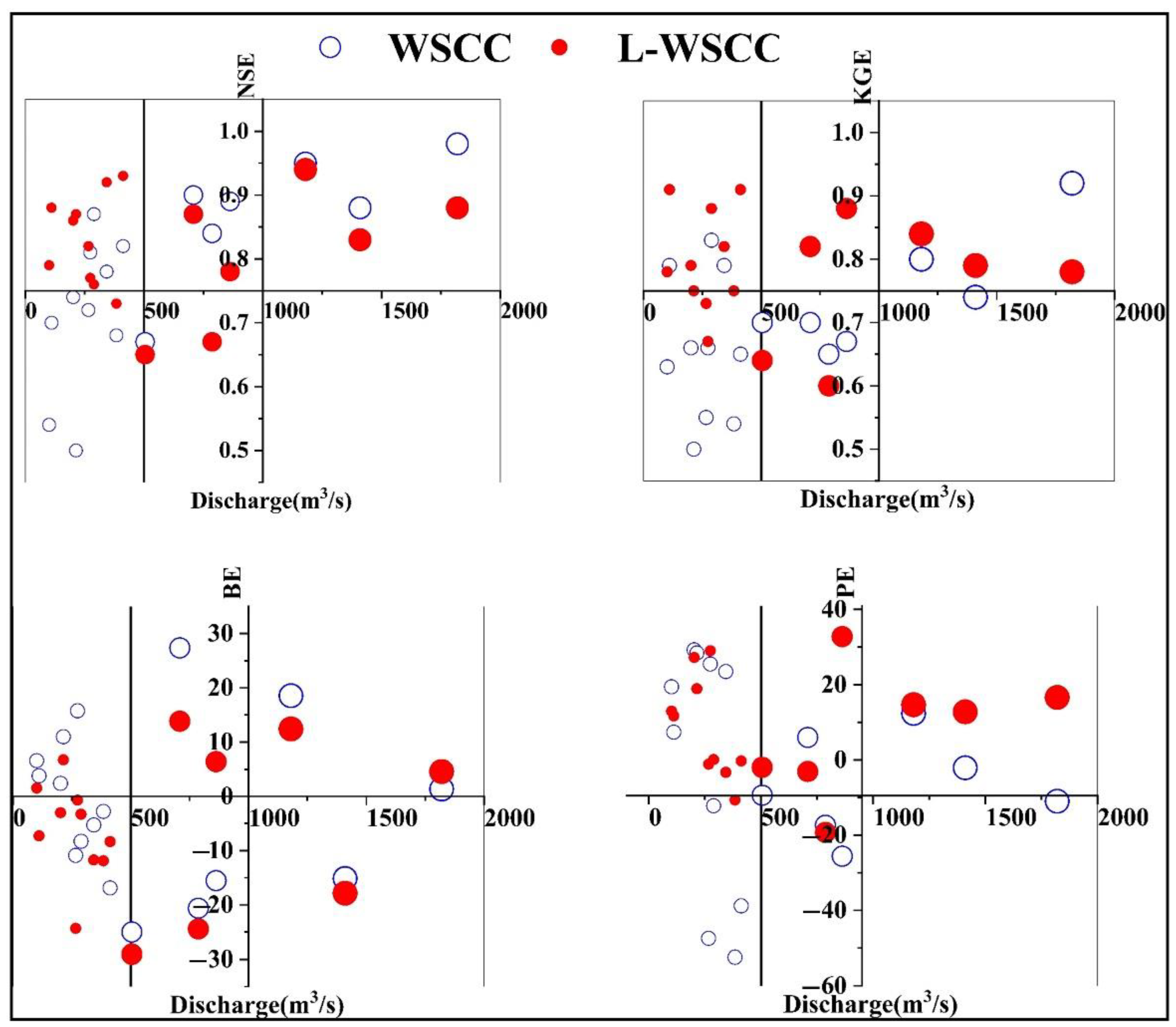
2.4. Evaluation Criteria
3. Results and Discussion
3.1. Results on Land-Use Change
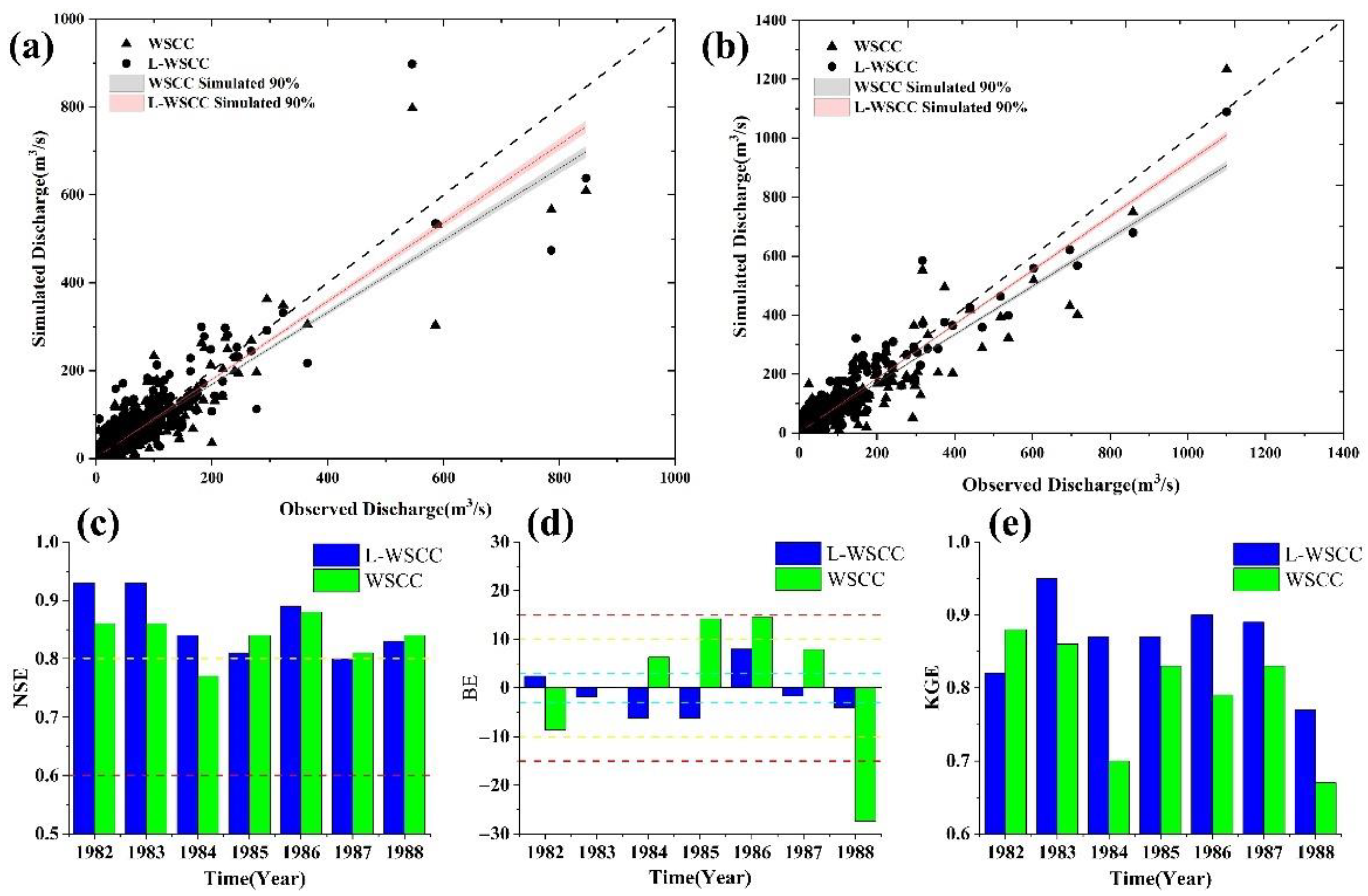
3.2. Calibration and Validation on Different Time-Scales
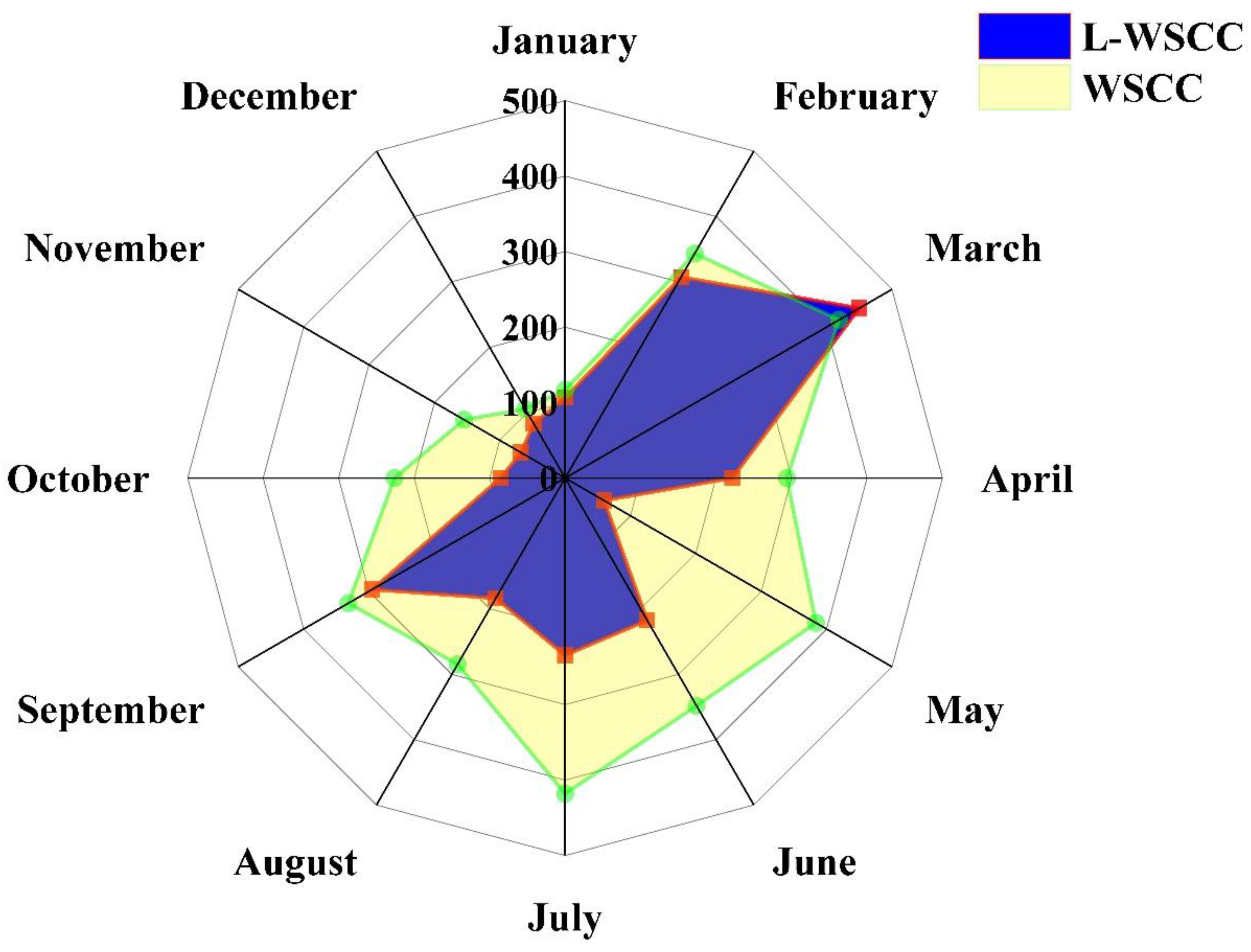
3.3. Seasonal Variation of Simulation
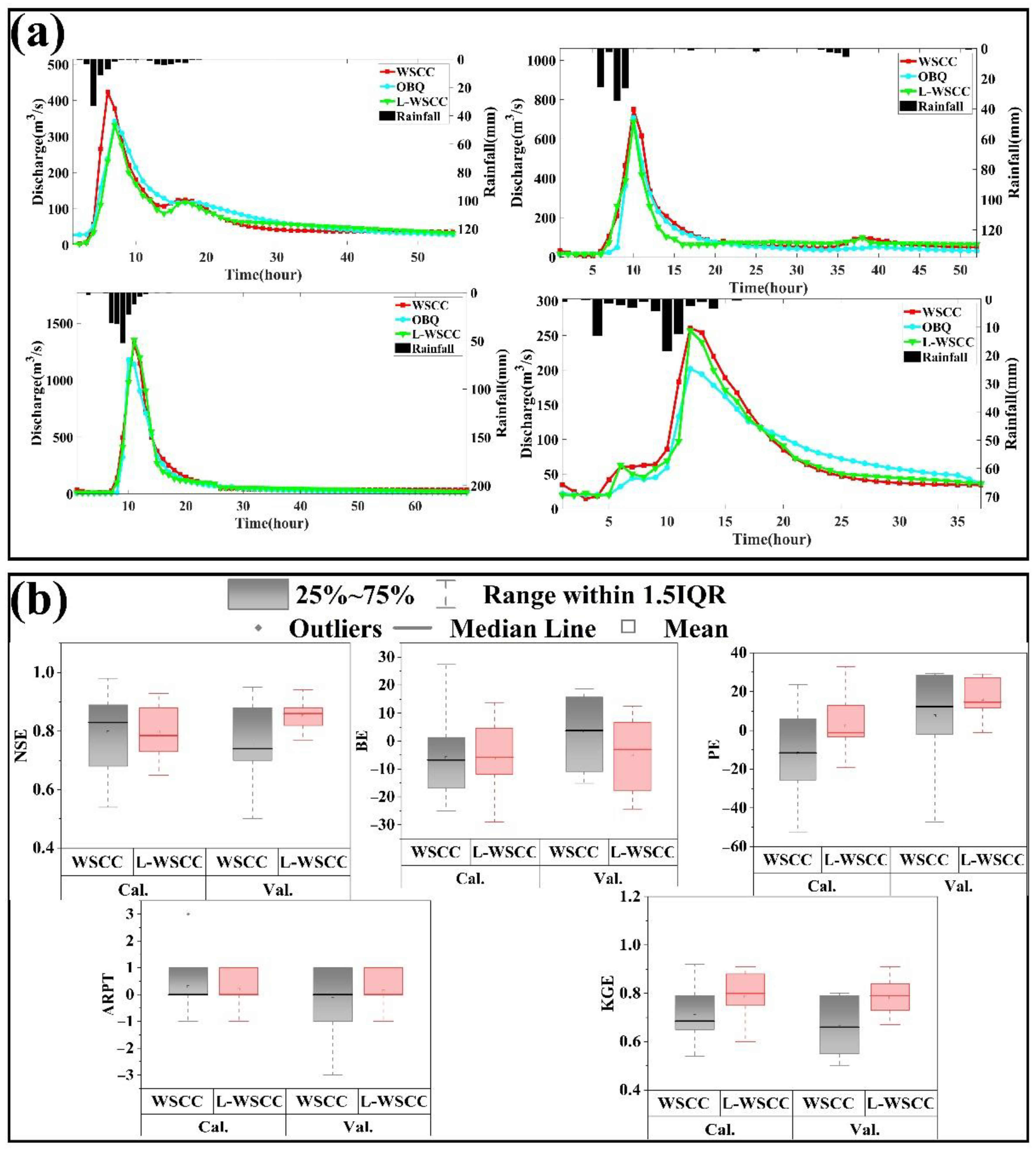
3.4. Simulation in Different Flood Types
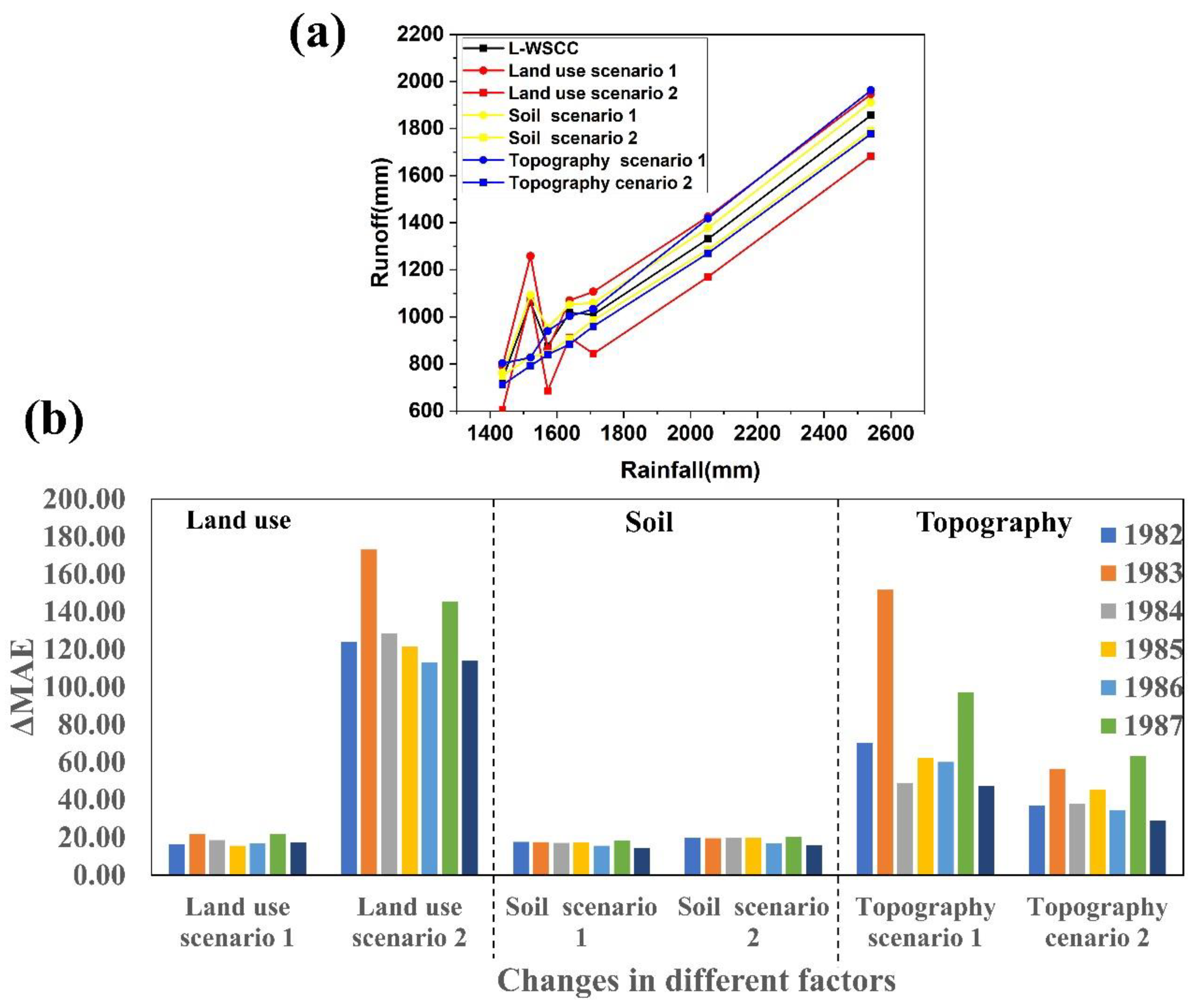
3.5. The Local Sensitivity Analysis of Different Driving Factors
3.6. Strength and Recommendations for Future Studies
4. Conclusions
- (1)
- The application of L-WSCC in Misai basin demonstrated that the method proposed in this article performed well in hydrological simulating at the different timescales (mean NSE: 0.86 for daily scale, 0.82 for hourly scale; mean BE: 4.34% for daily scale, 11.02% for hourly scale). The results have proven to be robust and reliable, which were powerful evidence for the reasonability of the construction process of L-WSCC.
- (2)
- The contrasting results confirmed that L-WSCC performed favorably compared to the empirical WSCC method and identified novel L-WSCC with high confidence in flood simulation (mean NSE increased from 0.78 to 0.82, mean PE decreased from 21.66% to 12.74%, mean RE decreased from 12.18% to 11.02%). These results indicated that the L-WSCC can derive a set of feasible values for the runoff generation.
- (3)
- The correction of hydrologic responses resulting from L-WSCC is more obvious for relatively small flood event (increased by 15.96% of small floods in terms of mean NSE). The proposed method can more accurately capture the runoff process of small flood events according to various remote sensing factors, thereby improving the ability of WSCC to simulate small floods. Thus, the newly proposed model may better represent runoff generation that previously have been beyond the scope of the traditional WSCC method (which is considered to work well for large flood events simulation).
- (4)
- The results of sensitivity analysis showed that land-use and land cover (especially the change of vegetation) have the greatest impact on yield (mean ΔMAE: 131.38%), which demonstrated that land-use have a predominant control on runoff yield in the short term.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.T.; Chen, A.S.; Fu, G.T.; Djordjevic, S.; Zhang, C.; Savic, D.A. An integrated framework for high-resolution urban flood modelling considering multiple information sources and urban features. Environ. Modell. Softw. 2018, 107, 85–95. [Google Scholar] [CrossRef]
- Dou, Y.H.; Ye, L.; Gupta, H.V.; Zhang, H.R.; Behrangi, A.; Zhou, H.C. Improved Flood Forecasting in Basins with No Precipitation Stations: Constrained Runoff Correction Using Multiple Satellite Precipitation Products. Water Resour. Res. 2021, 57, 29682. [Google Scholar] [CrossRef]
- Toosi, A.S.; Calbimonte, G.H.; Nouri, H.; Alaghmand, S. River basin-scale flood hazard assessment using a modified multi-criteria decision analysis approach: A case study. J. Hydrol. 2019, 574, 660–671. [Google Scholar] [CrossRef]
- Sugianto, S.; Deli, A.; Miswar, E.; Rusdi, M.; Irham, M. The Effect of Land Use and Land Cover Changes on Flood Occurrence in Teunom Watershed, Aceh Jaya. Land 2022, 11, 1271. [Google Scholar] [CrossRef]
- Li, X.G. A new method to evaluate floodwater for control/use in high-sediment rivers of Northwest China. Sci. Rep. 2017, 7, 17219. [Google Scholar] [CrossRef]
- Archer, D.R.; Fowler, H.J. Characterising flash flood response to intense rainfall and impacts using historical information and gauged data in Britain. J. Flood Risk Manag. 2018, 11, S121–S133. [Google Scholar] [CrossRef]
- Zhou, Q.Q.; Leng, G.Y.; Feng, L.Y. Predictability of state-level flood damage in the conterminous United States: The role of hazard, exposure and vulnerability. Sci. Rep. 2017, 7, 5334. [Google Scholar] [CrossRef]
- Breinl, K.; Lun, D.; Muller-Thomy, H.; Bloschl, G. Understanding the relationship between rainfall and flood probabilities through combined intensity-duration-frequency analysis. J. Hydrol. 2021, 602, 126759. [Google Scholar] [CrossRef]
- Liu, W.M.; Carling, P.A.; Hu, K.H.; Wang, H.; Zhou, Z.; Zhou, L.Q.; Liu, D.Z.; Lai, Z.P.; Zhang, X.B. Outburst floods in China: A review. Earth Sci. Rev. 2019, 197, 102859. [Google Scholar] [CrossRef]
- Zhang, W.Y. Application of NRCS-CN method for estimation of watershed runoff and disaster risk. Geomat. Nat. Hazards Risk 2019, 10, 2220–2238. [Google Scholar] [CrossRef] [Green Version]
- Oladotun, O.M. Assessment of Runoff Potential for Disaster Risk Reduction Using Geospatial Technology in Opa Watershed, Southwestern Nigeria. S. Afr. J. Geomat. 2021, 10, 90–100. [Google Scholar] [CrossRef]
- Guan, M.F.; Sillanpaa, N.; Koivusalo, H. Storm runoff response to rainfall pattern, magnitude and urbanization in a developing urban catchment. Hydrol. Process 2016, 30, 543–557. [Google Scholar] [CrossRef]
- Erena, S.H.; Worku, H. Dynamics of land use land cover and resulting surface runoff management for environmental flood hazard mitigation: The case of Dire Daw city, Ethiopia. J. Hydrol. Reg. Stud. 2019, 22, 100598. [Google Scholar] [CrossRef]
- Zhao, R.J. The Xinanjiang Model Applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar] [CrossRef]
- Alazzy, A.A.; Lu, H.S.; Zhu, Y.H. Assessing the Uncertainty of the Xinanjiang Rainfall-Runoff Model: Effect of the Likelihood Function Choice on the GLUE Method. J. Hydrol. Eng. 2015, 20, 1943–5584. [Google Scholar] [CrossRef]
- Gong, J.F.; Yao, C.; Li, Z.J.; Chen, Y.F.; Huang, Y.C.; Tong, B.X. Improving the flood forecasting capability of the Xinanjiang model for small- and medium-sized ungauged catchments in South China. Nat. Hazards 2021, 106, 2077–2109. [Google Scholar] [CrossRef]
- Liao, S.L.; Li, G.; Sun, Q.Y.; Li, Z.F. Real-time correction of antecedent precipitation for the Xinanjiang model using the genetic algorithm. J. Hydroinform. 2016, 18, 803–815. [Google Scholar] [CrossRef]
- Yao, C.; Zhang, K.; Yu, Z.B.; Li, Z.J.; Li, Q.L. Improving the flood prediction capability of the Xinanjiang model in ungauged nested catchments by coupling it with the geomorphologic instantaneous unit hydrograph. J. Hydrol. 2014, 517, 1035–1048. [Google Scholar] [CrossRef]
- Gao, H.K.; Cai, H.Y.; Duan, Z. Understanding the impacts of catchment characteristics on the shape of the storage capacity curve and its influence on flood flows. Hydrol. Res. 2018, 49, 90–106. [Google Scholar] [CrossRef]
- Tran, Q.Q.; De Niel, J.; Willems, P. Spatially Distributed Conceptual Hydrological Model Building: A Genetic top-Down Approach Starting From Lumped Models. Water Resour. Res. 2018, 54, 8064–8085. [Google Scholar] [CrossRef] [Green Version]
- Badjana, H.M.; Fink, M.; Helmschrot, J.; Diekkruger, B.; Kralisch, S.; Afouda, A.A.; Wala, K. Hydrological system analysis and modelling of the Kara River basin (West Africa) using a lumped metric conceptual model. Hydrolog. Sci. J. 2017, 62, 1094–1113. [Google Scholar] [CrossRef]
- Chen, X.; Chen, Y.D.; Xu, C.Y. A distributed monthly hydrological model for integrating spatial variations of basin topography and rainfall. Hydrol. Process. 2007, 21, 242–252. [Google Scholar] [CrossRef]
- Jayawardena, A.W.; Zhou, M.C. A modified spatial soil moisture storage capacity distribution curve for the Xinanjiang model. J. Hydrol. 2000, 227, 93–113. [Google Scholar] [CrossRef]
- Zhuo, L.; Han, D.W. Misrepresentation and amendment of soil moisture in conceptual hydrological modelling. J. Hydrol. 2016, 535, 637–651. [Google Scholar] [CrossRef]
- Bartlett, M.S.; Parolari, A.J.; McDonnell, J.J.; Porporato, A. Beyond the SCS-CN method: A theoretical framework for spatially lumped rainfall-runoff response. Water Resour. Res. 2016, 52, 4608–4627. [Google Scholar] [CrossRef]
- Bartlett, M.S.; Daly, E.; McDonnell, J.J.; Parolari, A.J.; Porporato, A. Stochastic rainfall-runoff model with explicit soil moisture dynamics. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20150389. [Google Scholar] [CrossRef]
- Shi, P.F.; Yang, T.; Xu, C.Y.; Yong, B.; Huang, C.S.; Li, Z.Y.; Qin, Y.W.; Wang, X.Y.; Zhou, X.D.; Li, S. Rainfall-Runoff Processes and Modelling in Regions Characterized by Deficiency in Soil Water Storage. Water 2019, 11, 1858. [Google Scholar] [CrossRef]
- Guo, W.J.; Wang, C.H.; Zeng, X.M.; Ma, T.F.; Yang, H. Subgrid Parameterization of the Soil Moisture Storage Capacity for a Distributed Rainfall-Runoff Model. Water 2015, 7, 2691–2706. [Google Scholar] [CrossRef]
- Sivapalan, M.; Woods, R.A. Evaluation of the Effects of General-Circulation Models Subgrid Variability and Patchiness of Rainfall and Soil-Moisture on Land-Surface Water-Balance Fluxes. Hydrol. Process. 1995, 9, 697–717. [Google Scholar] [CrossRef]
- Yao, C.; Li, Z.J.; Bao, H.J.; Yu, Z.B. Application of a Developed Grid-Xinanjiang Model to Chinese Watersheds for Flood Forecasting Purpose. J. Hydrol. Eng. 2009, 14, 923–934. [Google Scholar] [CrossRef]
- Meng, C.Q.; Zhou, J.Z.; Zhong, D.Y.; Wang, C.; Guo, J. An Improved Grid-Xinanjiang Model and Its Application in the Jinshajiang Basin, China. Water 2018, 10, 1265. [Google Scholar] [CrossRef]
- Yao, C.; Li, Z.J.; Yu, Z.B.; Zhang, K. A priori parameter estimates for a distributed, grid-based Xinanjiang model using geographically based information. J. Hydrol. 2012, 468, 47–62. [Google Scholar] [CrossRef]
- Fowler, K.J.A.; Peel, M.C.; Western, A.W.; Zhang, L.; Peterson, T.J. Simulating runoff under changing climatic conditions: Revisiting an apparent deficiency of conceptual rainfall-runoff models. Water Resour. Res. 2016, 52, 1820–1846. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. A dynamic TOPMODEL. Hydrol. Process. 2001, 15, 1993–2011. [Google Scholar] [CrossRef]
- Chang, B.X.; Wherley, B.; Aitkenhead-Peterson, J.A.; McInnes, K.J. Effects of urban residential landscape composition on surface runoff generation. Sci. Total Environ. 2021, 783, 146977. [Google Scholar] [CrossRef]
- Ren, L.L.; Wang, G.Z.; Fang, L.U. Application of spatially varying storage capacity model for runoff parameterization in semi-arid catchment. Water Sci. Eng. 2009, 2, 1–10. [Google Scholar] [CrossRef]
- Yuan, F.; Ren, L. Application of the Xinanjiang vegetation-hydrology model to streamflow simulation over the Hanjiang River basin, China. Hydrol. Mt. Reg. Obs. Process. Dyn. 2009, 82, 2273–2278. [Google Scholar] [CrossRef]
- Feng, X.M.; Sun, G.; Fu, B.J.; Su, C.H.; Liu, Y.; Lamparski, H. Regional effects of vegetation restoration on water yield across the Loess Plateau, China. Hydrol. Earth Syst. Sci. 2012, 16, 2617–2628. [Google Scholar] [CrossRef]
- Cerda, A.; Lucas-Borja, M.E.; Franch-Pardo, I.; Ubeda, X.; Novara, A.; Lopez-Vicente, M.; Popovic, Z.; Pulido, M. The role of plant species on runoff and soil erosion in a Mediterranean shrubland. Sci. Total Environ. 2021, 799, 149218. [Google Scholar] [CrossRef]
- Crosson, W.L.; Limaye, A.S.; Laymon, C.A. Parameter sensitivity of soil moisture retrievals from airborne C- and X-band radiometer measurements in SMEX02. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2842–2853. [Google Scholar] [CrossRef]
- Crave, A.; GascuelOdoux, C. The influence of topography on time and space distribution of soil surface water content. Hydrol. Process. 1997, 11, 203–210. [Google Scholar] [CrossRef]
- Western, A.W.; Grayson, R.B.; Bloschl, G.; Willgoose, G.R.; McMahon, T.A. Observed spatial organization of soil moisture and its relation to terrain indices. Water Resour. Res. 1999, 35, 797–810. [Google Scholar] [CrossRef]
- Wilson, D.J.; Western, A.W.; Grayson, R.B. A terrain and data-based method for generating the spatial distribution of soil moisture. Adv. Water Resour. 2005, 28, 43–54. [Google Scholar] [CrossRef]
- Zhao, Q.; Gong, H.L.; Deng, W.; Wang, S.Y.; Zhao, W.J.; An, X.S.; Gong, Z.N.; Zhang, Z.Q. Using DEM to quantify spatial variability of soil storage capacity: A semi-distribtited hydrological model for northern China. Int. Geosci. Remote Sens. Symp. 2005, 6, 4429–4432. [Google Scholar]
- Sivapalan, M.; Woods, R.A.; Kalma, J.D. Variable bucket representation of TOPMODEL and investigation of the effects of rainfall heterogeneity. Hydrol. Process. 1997, 11, 1307–1330. [Google Scholar] [CrossRef]
- Gao, H.K.; Birkel, C.; Hrachowitz, M.; Tetzlaff, D.; Soulsby, C.; Savenije, H.H.G. A simple topography-driven and calibration-free runoff generation module. Hydrol. Earth Syst. Sci. 2019, 23, 787–809. [Google Scholar] [CrossRef]
- Mu, W.B.; Yu, F.L.; Li, C.Z.; Xie, Y.B.; Tian, J.Y.; Liu, J.; Zhao, N.N. Effects of Rainfall Intensity and Slope Gradient on Runoff and Soil Moisture Content on Different Growing Stages of Spring Maize. Water 2015, 7, 2990–3008. [Google Scholar] [CrossRef]
- Defersha, M.B.; Melesse, A.M. Effect of rainfall intensity, slope and antecedent moisture content on sediment concentration and sediment enrichment ratio. Catena 2012, 90, 47–52. [Google Scholar] [CrossRef]
- Schneiderman, E.M.; Steenhuis, T.S.; Thongs, D.J.; Easton, Z.M.; Zion, M.S.; Neal, A.L.; Mendoza, G.F.; Walter, M.T. Incorporating variable source area hydrology into a curve-number-based watershed model. Hydrol. Process. 2007, 21, 3420–3430. [Google Scholar] [CrossRef]
- Penna, D.; Tromp-van Meerveld, H.J.; Gobbi, A.; Borga, M.; Dalla Fontana, G. The influence of soil moisture on threshold runoff generation processes in an alpine headwater catchment. Hydrol. Earth Syst. Sci. 2011, 15, 689–702. [Google Scholar] [CrossRef]
- Barling, R.D.; Moore, I.D.; Grayson, R.B. A Quasi-Dynamic Wetness Index for Characterizing the Spatial-Distribution of Zones of Surface Saturation and Soil-Water Content. Water Resour. Res. 1994, 30, 1029–1044. [Google Scholar] [CrossRef]
- Brammer, D.D.; Mcdonnell, J.J. An evolving perceptual model of hillslope flow at the Maimai catchment. Adv. Hillslope Process. 1996, 1, 35–60. [Google Scholar]
- Bell, V.A.; Kay, A.L.; Jones, R.G.; Moore, R.J.; Reynard, N.S. Use of soil data in a grid-based hydrological model to estimate spatial variation in changing flood risk across the UK. J. Hydrol. 2009, 377, 335–350. [Google Scholar] [CrossRef]
- Moore, R.J.; Cole, S.J.; Bell, V.A.; Jones, D.A. Issues in flood forecasting: Ungauged basins, extreme floods and uncertainty. Front. Flood Res. 2006, 305, 103–122. [Google Scholar]
- Zhang, X.J.; Liu, P.; Cheng, L.; Xie, K.; Han, D.Y.; Zhou, L.T. The temporal variations in runoff-generation parameters of the Xinanjiang model due to human activities: A case study in the upper Yangtze River Basin, China. J. Hydrol. Reg. Stud. 2021, 37, 100910. [Google Scholar] [CrossRef]
- Wang, D.B. A new probability density function for spatial distribution of soil water storage capacity leads to the SCS curve number method. Hydrol. Earth Syst. Sci. 2018, 22, 6567–6578. [Google Scholar] [CrossRef]
- Guo, W.J.; Wang, C.H.; Ma, T.F. A distributed Grid-Xinanjiang model with integration of subgrid variability of soil storage capacity. Water Sci. Eng. 2016, 9, 97–105. [Google Scholar] [CrossRef]
- Xia, F.; Liu, X.M.; Xu, J.M.; Wang, Z.G.; Huang, J.F.; Brookes, P.C. Trends in the daily and extreme temperatures in the Qiantang River basin, China. Int. J. Climatol. 2015, 35, 57–68. [Google Scholar] [CrossRef]
- Zhang, X.J.; Xu, Y.P.; Fu, G.T. Uncertainties in SWAT extreme flow simulation under climate change. J. Hydrol. 2014, 515, 205–222. [Google Scholar] [CrossRef]
- Gao, C.; He, Z.G.; Pan, S.L.; Xuan, W.D.; Xu, Y.P. Effects of climate change on peak runoff and flood levels in Qu River Basin, East China. J. Hydro Environ. Res. 2020, 28, 34–47. [Google Scholar] [CrossRef]
- Li, H.X.; Zhang, Y.Q.; Chiew, F.H.S.; Xu, S.G. Predicting runoff in ungauged catchments by using Xinanjiang model with MODIS leaf area index. J. Hydrol. 2009, 370, 155–162. [Google Scholar] [CrossRef]
- Wigmosta, M.S.; Vail, L.W.; Lettenmaier, D.P. A Distributed Hydrology-Vegetation Model for Complex Terrain. Water Resour. Res. 1994, 30, 1665–1679. [Google Scholar] [CrossRef]
- Zhao, J.; Xu, Z.; Singh, V. Estimation of root zone storage capacity at the catchment scale using improved Mass Curve Technique. J. Hydrol. 2016, 540, 959–972. [Google Scholar] [CrossRef]
- Zhou, Q.W.; Keith, D.M.; Zhou, X.; Cai, M.Y.; Cui, X.F.; Wei, X.C.; Luo, Y.X. Comparing the Water-holding Characteristics of Broadleaved, Coniferous, and Mixed Forest Litter Layers in a Karst Region. Mt. Res. Dev. 2018, 38, 220–229. [Google Scholar] [CrossRef]
- Xie, J.J.; Su, D.R. Water-Holding Characteristics of Litter in Meadow Steppes with Different Years of Fencing in Inner Mongolia, China. Water 2020, 12, 2374. [Google Scholar] [CrossRef]
- Bulcock, H.H.; Jewitt, G.P.W. Modelling canopy and litter interception in commercial forest plantations in South Africa using the Variable Storage Gash model and idealised drying curves. Hydrol. Earth Syst. Sci. 2012, 16, 4693–4705. [Google Scholar] [CrossRef]
- Xie, J.; He, J.; Su, D.; Lyu, S.; Qiang, W. A dynamic model of litter interception that can be applied to the management of semi-arid meadow steppe with prohibition of grazing. Ecohydrol. Hydrobiol. 2021, 22, 75–84. [Google Scholar] [CrossRef]
- Kirkby, M.J.; Beven, K.J. A physically based, variable contributing area model of basin hydrology. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The Future of Distributed Models-Model Calibration and Uncertainty Prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Dejong, R.; Zentner, R.P. Assessment of the Spaw Model for Semi-Arid Growing Conditions with Minimal Local Calibration. Agric. Water Manag. 1985, 10, 31–46. [Google Scholar] [CrossRef]
- Chanzy, A.; Mumen, M.; Richard, G. Accuracy of top soil moisture simulation using a mechanistic model with limited soil characterization. Water Resour. Res. 2008, 44, W03420. [Google Scholar] [CrossRef]
- van Emmerik, T.H.M.; Li, Z.; Sivapalan, M.; Pande, S.; Kandasamy, J.; Savenije, H.H.G.; Chanan, A.; Vigneswaran, S. Socio-hydrologic modeling to understand and mediate the competition for water between agriculture development and environmental health: Murrumbidgee River basin, Australia. Hydrol. Earth Syst. Sci. 2014, 18, 4239–4259. [Google Scholar] [CrossRef]
- Payan, J.L.; Perrin, C.; Andreassian, V.; Michel, C. How can man-made water reservoirs be accounted for in a lumped rainfall-runoff model? Water Resour. Res. 2008, 44, W03420. [Google Scholar] [CrossRef]
- Hansen, M.C.; Defries, R.S.; Townshend, J.R.G.; Sohlberg, R. Global land cover classification at 1km spatial resolution using a classification tree approach. Int. J. Remote Sens. 2000, 21, 1331–1364. [Google Scholar] [CrossRef]
- Wang-Erlandsson, L.; Bastiaanssen, W.G.M.; Gao, H.; Jagermeyr, J.; Senay, G.B.; van Dijk, A.I.J.M.; Guerschman, J.P.; Keys, P.W.; Gordon, L.J.; Savenije, H.H.G. Global root zone storage capacity from satellite-based evaporation. Hydrol. Earth Syst. Sci. 2016, 20, 1459–1481. [Google Scholar] [CrossRef]
- Gao, H.; Hrachowitz, M.; Schymanski, S.J.; Fenicia, F.; Sriwongsitanon, N.; Savenije, H.H.G. Climate controls how ecosystems size the root zone storage capacity at catchment scale. Geophys. Res. Lett. 2014, 41, 7916–7923. [Google Scholar] [CrossRef]
- Hahmann, A.N. Representing spatial subgrid-scale precipitation variability in a GCM. J. Hydrometeorol. 2003, 4, 891–900. [Google Scholar] [CrossRef]
- Kumar, R.; Samaniego, L.; Attinger, S. Implications of distributed hydrologic model parameterization on water fluxes at multiple scales and locations. Water Resour. Res. 2013, 49, 360–379. [Google Scholar] [CrossRef]
- Moore, R.J. The PDM rainfall-runoff model. Hydrol. Earth Syst. Sci. 2007, 11, 483–499. [Google Scholar] [CrossRef]
- Goegebeur, M.; Pauwels, V.R.N. Improvement of the PEST parameter estimation algorithm through Extended Kalman Filtering. J. Hydrol. 2007, 337, 436–451. [Google Scholar] [CrossRef]
- Li, X.H.; Zhang, Q.; Shao, M.; Li, Y.L. A comparison of parameter estimation for distributed hydrological modelling using automatic and manual methods. Adv. Mater. Res. 2012, 356–360, 2372–2375. [Google Scholar] [CrossRef]
- Wang, J.L.; Wang, C.; Rao, V.; Orr, A.; Yan, E.; Kotamarthi, R. A parallel workflow implementation for PEST version 13.6 in high-performance computing for WRF-Hydro version 5.0: A case study over the midwestern United States. Geosci. Model Dev. 2019, 12, 3523–3539. [Google Scholar] [CrossRef]
- Soltani, M.; Laux, P.; Mender, M.; Kunstmann, H. Inverse distributed modelling of streamflow and turbulent fluxes: A sensitivity and uncertainty analysis coupled with automatic optimization. J. Hydrol. 2019, 571, 856–872. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and Water Quality Models: Performance Measures and Evaluation Criteria. Am. Soc. Agric. Biol. Eng. 2015, 58, 1763–1785. [Google Scholar]
- Pijanowski, B.C.; Robinson, K.D. Rates and patterns of land use change in the Upper Great Lakes States, USA: A framework for spatial temporal analysis. Landsc. Urban Plan. 2011, 102, 102–116. [Google Scholar] [CrossRef]
- Jodar, J.; Carpintero, E.; Martos-Rosillo, S.; Ruiz-Constan, A.; Marin-Lechado, C.; Cabrera-Arrabal, J.A.; Navarrete-Mazariegos, E.; Gonzalez-Ramon, A.; Lamban, L.J.; Herrera, C.; et al. Combination of lumped hydrological and remote-sensing models to evaluate water resources in a semi-arid high altitude ungauged watershed of Sierra Nevada (Southern Spain). Sci. Total Environ. 2018, 625, 285–300. [Google Scholar] [CrossRef]
- Sun, W.C.; Ishidaira, H.; Bastola, S. Calibration of hydrological models in ungauged basins based on satellite radar altimetry observations of river water level. Hydrol. Process. 2012, 26, 3524–3537. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F. One-dimensional statistical dynamic representation of subgrid spatial variability of precipitation in the two-layer variable infiltration capacity model. J. Geophys. Res. Atmos. 1996, 101, 21403–21422. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andreassian, V. Does a large number of parameters enhance model performance? Comparative assessment of common catchment model structures on 429 catchments. J. Hydrol. 2001, 242, 275–301. [Google Scholar] [CrossRef]
- Zhang, R.; Cuartas, L.A.; Carvalho, L.V.D.; Leal, K.R.D.; Mendiondo, E.M.; Abe, N.; Birkinshaw, S.; Mohor, G.S.; Seluchi, M.E.; Nobre, C.A. Season-based rainfall-runoff modelling using the probability-distributed model (PDM) for large basins in southeastern Brazil. Hydrol. Process. 2018, 32, 2217–2230. [Google Scholar] [CrossRef]
- Todini, E. The ARNO rainfall-runoff model. J. Hydrol. 1996, 175, 339–382. [Google Scholar] [CrossRef]
- Geris, J.; Tetzlaff, D.; Seibert, J.; Vis, M.; Soulsby, C. Conceptual Modelling to Assess Hydrological Impacts and Evaluate Environmental Flow Scenarios in Montane River Systems Regulated for Hydropower. River Res. Appl. 2015, 31, 1066–1081. [Google Scholar] [CrossRef]
- Wang, X.Y.; Yang, T.; Yong, B.; Krysanova, V.; Shi, P.F.; Li, Z.Y.; Zhou, X.D. Impacts of climate change on flow regime and sequential threats to riverine ecosystem in the source region of the Yellow River. Environ. Earth Sci. 2018, 77, 465. [Google Scholar] [CrossRef]
| Year | 1982 | 1983 (%) | 1984 (%) | 1985 (%) | 1986 (%) | 1987 (%) | 1988 (%) | |
|---|---|---|---|---|---|---|---|---|
| Land Use | ||||||||
| Cultivated land | - | −18.41 | 26.00 | 2.53 | −42.42 | 23.12 | 12.83 | |
| Forest land | - | 2.31 | −8.03 | −0.01 | 16.00 | −8.04 | 7.05 | |
| Grass land | - | 753.00 | −14.39 | 1.48 | 26.52 | 51.92 | −99.42 | |
| Water | - | 1.67 | −0.96 | −2.57 | 1.88 | 2.42 | −0.73 | |
| Urban land | - | −38.15 | 110.17 | −45.90 | 14.29 | 14.17 | −45.83 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Fu, H.; Yang, J.; Gao, C. Land-Use and Land Cover Is Driving Factor of Runoff Yield: Evidence from A Remote Sensing-Based Runoff Generation Simulation. Water 2022, 14, 2854. https://doi.org/10.3390/w14182854
Xu C, Fu H, Yang J, Gao C. Land-Use and Land Cover Is Driving Factor of Runoff Yield: Evidence from A Remote Sensing-Based Runoff Generation Simulation. Water. 2022; 14(18):2854. https://doi.org/10.3390/w14182854
Chicago/Turabian StyleXu, Chaowei, Hao Fu, Jiashuai Yang, and Chan Gao. 2022. "Land-Use and Land Cover Is Driving Factor of Runoff Yield: Evidence from A Remote Sensing-Based Runoff Generation Simulation" Water 14, no. 18: 2854. https://doi.org/10.3390/w14182854







