ORGANICS: A QGIS Plugin for Simulating One-Dimensional Transport of Dissolved Substances in Surface Water
Abstract
:1. Introduction
2. Materials and Methods
2.1. Software Development
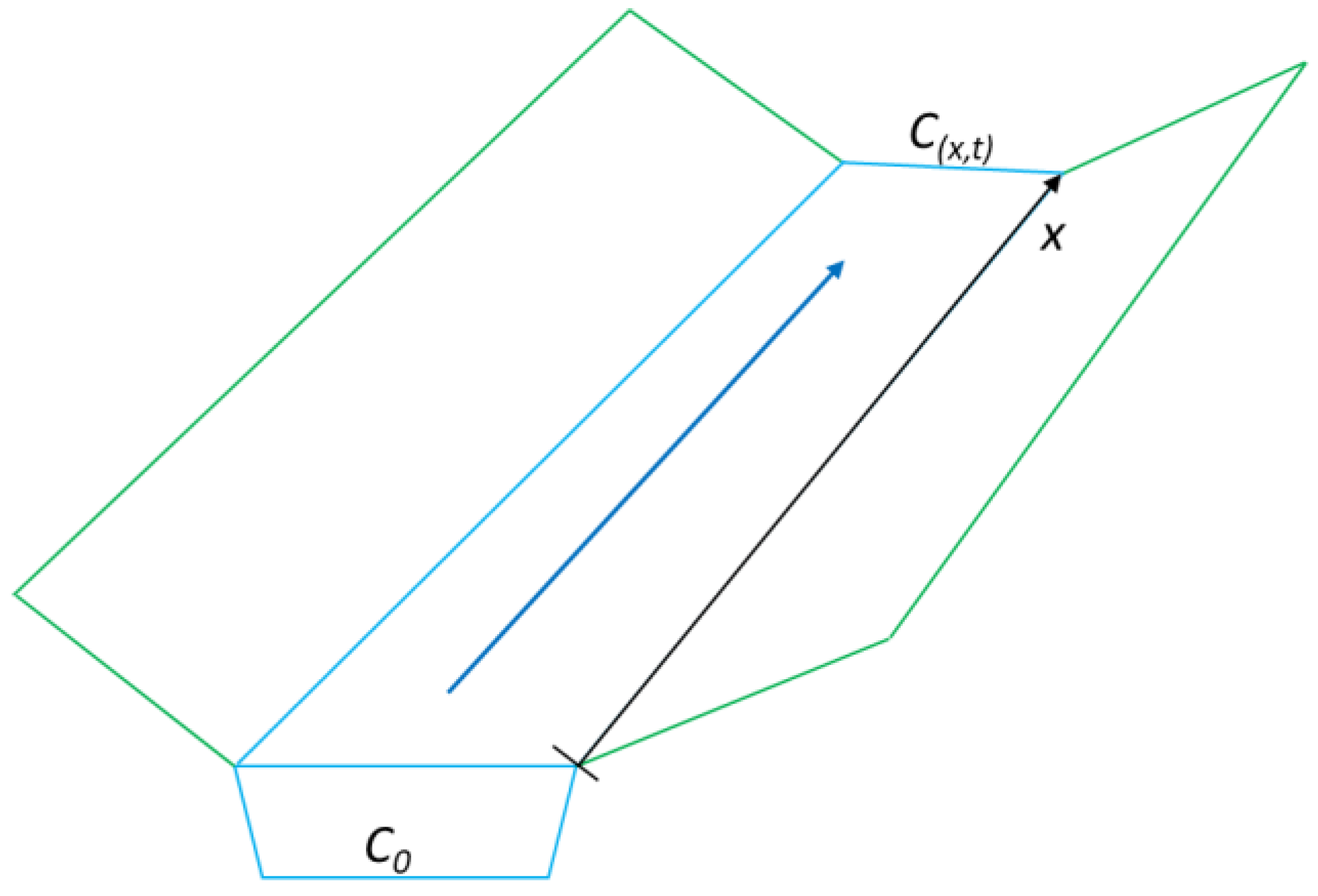
2.2. Data Needs
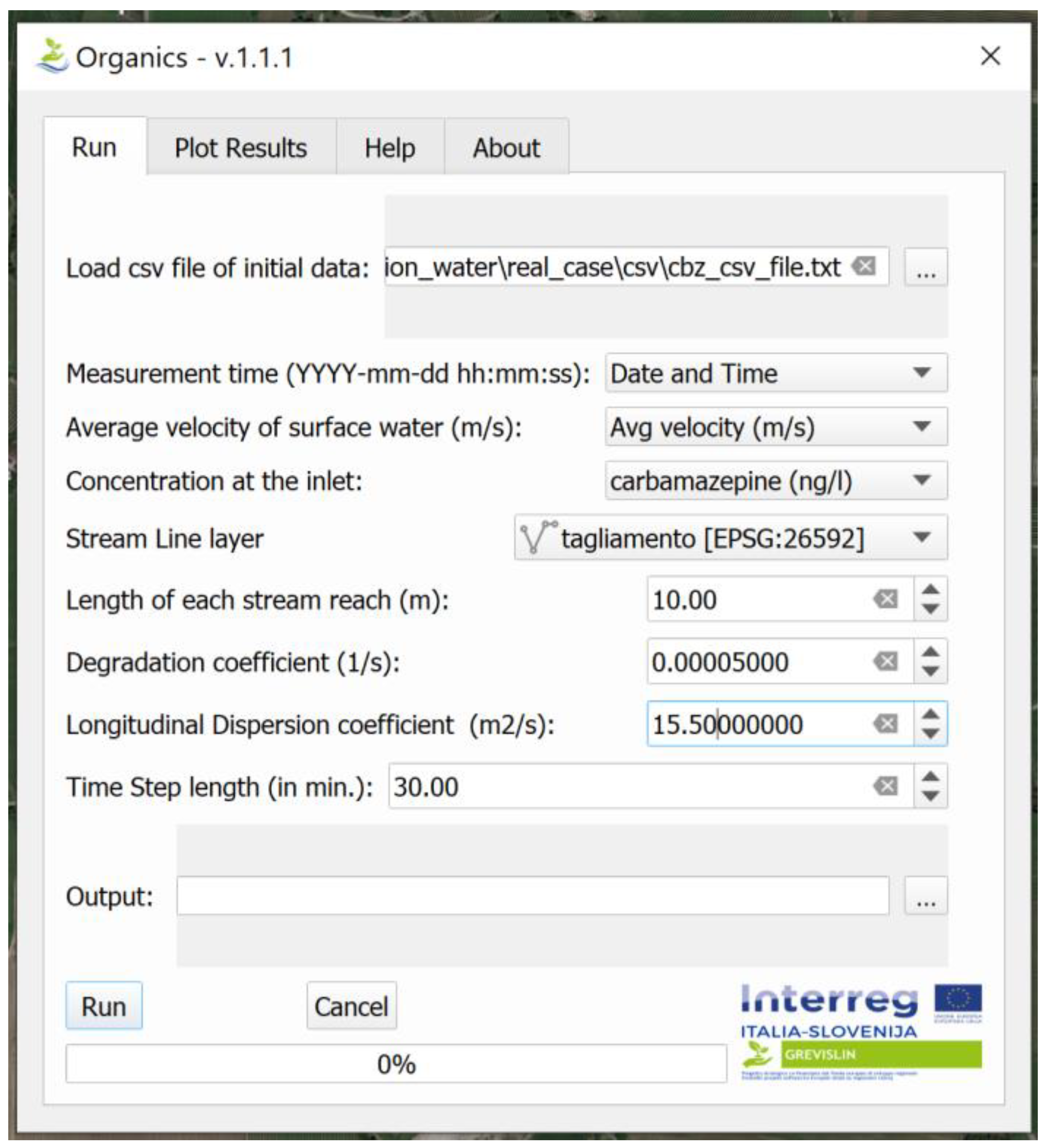
- a *.csv file specifying the water average longitudinal velocity (U) and concentration values at the inlet of the watercourse (constant concentration boundary condition), and the time these data refer to. The file must comply with the template format defined for the plugin. In particular, the file must contain data relating to (at least) one dataset, specifying:
- -
- starting date and time, in YYYY-MM-DD HH: MM: SS format;
- -
- average flow velocity in the surface water body, in m · s−1. This value will be used at all the node of the surface water body;
- -
- the concentration of the source at the inlet point.
- an ESRI linear Shapefile representing the surface water body. The file may consist of one or more segments. The line must be digitized towards the flow direction. When more segments are used, the topology must be respected (all the lines must be connected).
2.3. Model Implementation and Run
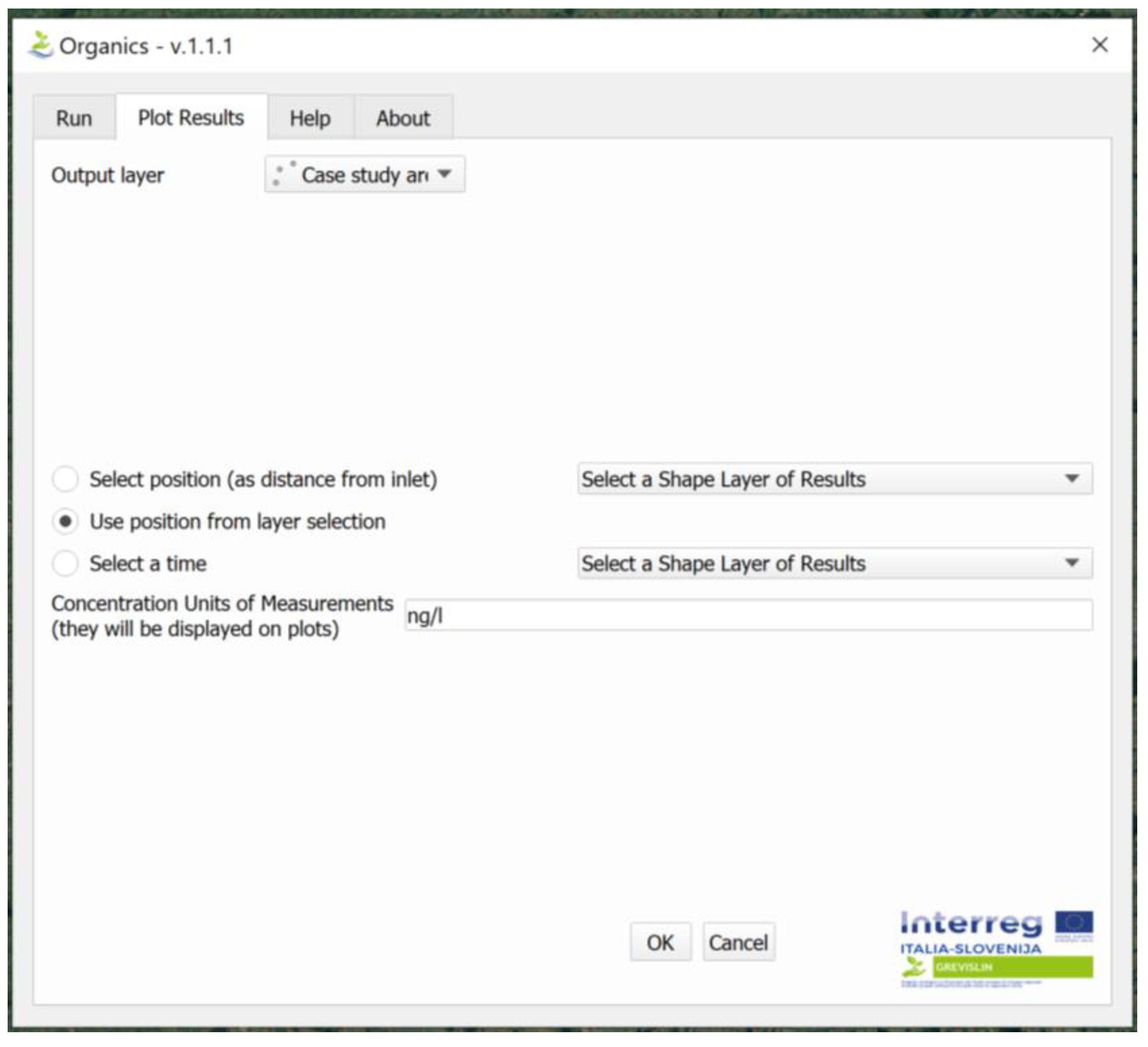
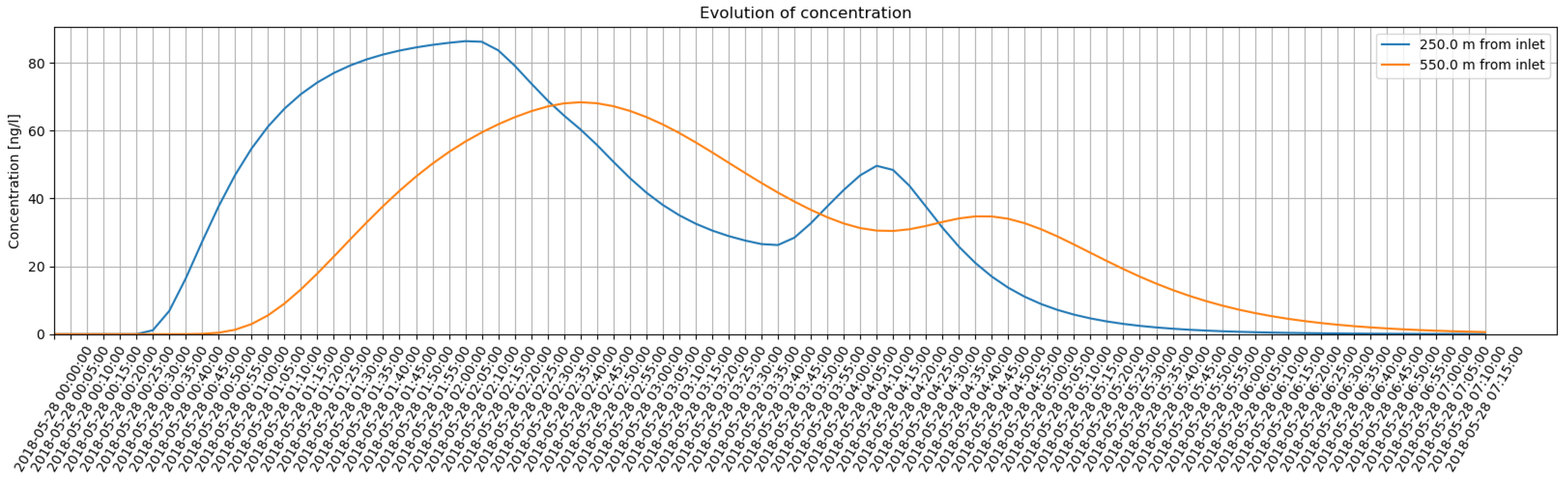
- Select a position (distance in m from the entry point): this option will create a graph displaying the concentration trend in a point defined by the user at a certain distance from the starting point, as a function of time (Figure 4);
- Use the selected position on the layer: this option allows to view the same result as above, but in this case the position is provided by selecting, using the classic selection tools on the map, one or more points of the output layer (Figure 5);
- Select a time: this graph will display the concentration values, at a given simulated time, as a function of the distance from the inlet (Figure 6). The times available for selection correspond to the discretization obtained with the time step chosen in input by the user.
3. Results and Discussion
3.1. Model Validation
3.2. Example Problem
3.2.1. C0 Mass Injection, Constant over Time
3.2.2. Time-Limited Pulse C0 Mass Injection
3.2.3. C0 Mass Input, Variable over Time (Multi-Pulse Boundary Condition)
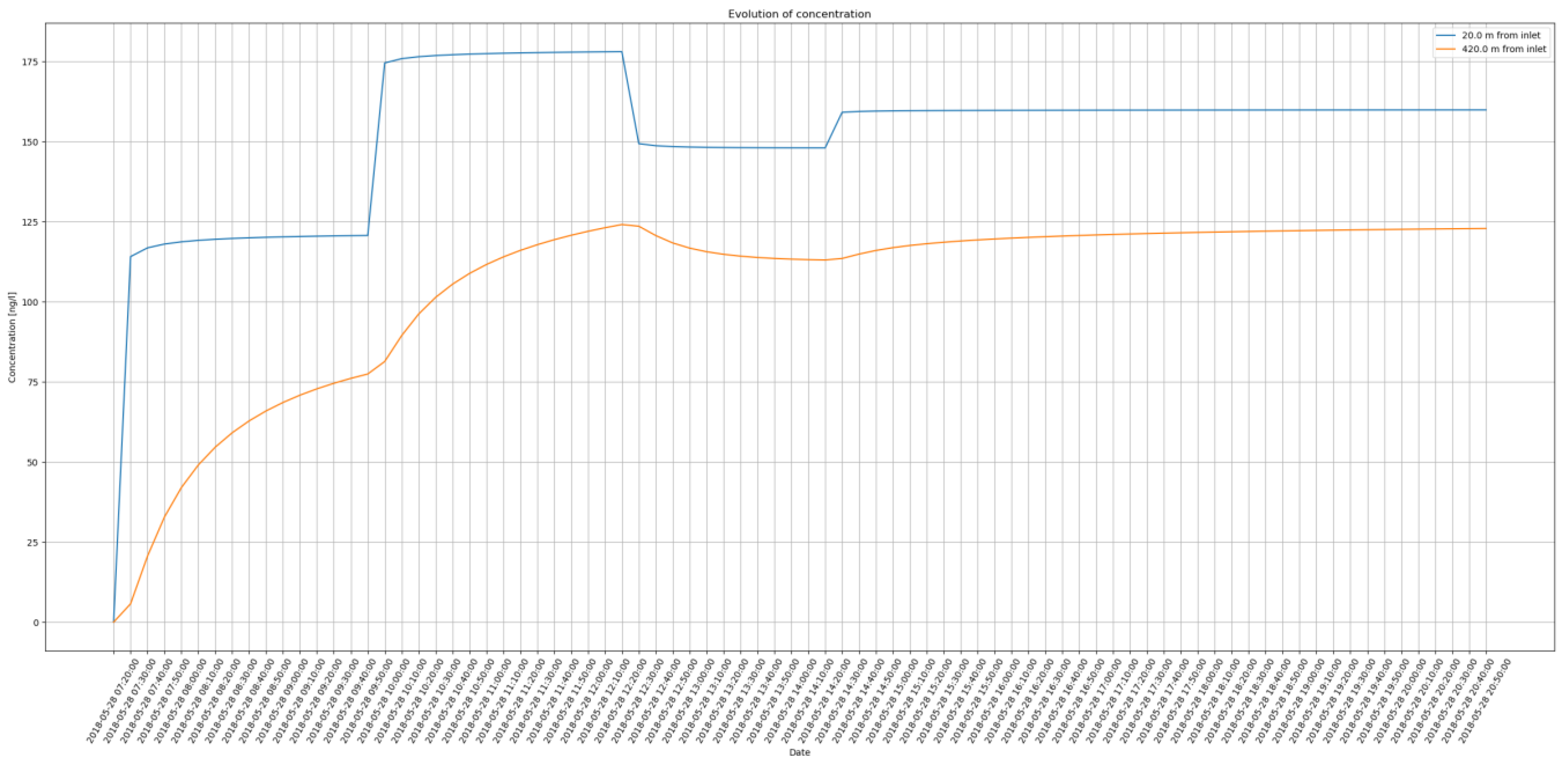
3.3. Case Study Application
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Walker, D.B.; Baumgartner, D.J.; Gerba, C.P.; Fitzsimmons, K. Chapter 16—Surface water pollution. In Environmental and Pollution Science, 3rd ed.; Mark, L.B., Ian, L.P., Charles, P.G., Eds.; Academic Press: Cambridge, MA, USA, 2019; pp. 261–292. ISBN 978-0-12-814719-1. [Google Scholar] [CrossRef]
- Montuori, P.; De Rosa, E.; Di Duca, F.; Provvisiero, D.P.; Sarnacchiaro, P.; Nardone, A.; Triassi, M. Estimation of Polycyclic Aromatic Hydrocarbons Pollution in Mediterranean Sea from Volturno River, Southern Italy: Distribution, Risk Assessment and Loads. Int. J. Environ. Res. Public Health 2021, 18, 1383. [Google Scholar] [CrossRef] [PubMed]
- Beermann, A.J.; Elbrecht, V.; Karnatz, S.; Ma, L.; Matthaei, C.D.; Piggott, J.J.; Leese, F. Multiple-stressor effects on stream macroinvertebrate communities: A mesocosm experiment manipulating salinity, fine sediment and flow velocity. Sci. Total Environ. 2018, 610–611, 961–971. [Google Scholar] [CrossRef] [PubMed]
- Jackson, M.C.; Loewen, C.J.G.; Vinebrooke, R.D.; Chimimba, C.T. Net effects of multiple stressors in freshwater ecosystems: A meta-analysis. Glob. Chang. Biol. 2016, 22, 180–189. [Google Scholar] [CrossRef] [PubMed]
- Bavumiragira, J.P.; Ge, J.; Yin, H. Fate and transport of pharmaceuticals in water systems: A processes review. Sci. Total Environ. 2022, 823, 153635. [Google Scholar] [CrossRef]
- Pistocchi, C.; Silvestri, N.; Rossetto, R.; Sabbatini, T.; Guidi, M.; Baneschi, I.; Bonari, E.; Trevisan, D. A simple model to assess nitrogen and phosphorus contamination in ungauged surface drainage networks: Application to the Massaciuccoli Lake Catchment. Italy. J. Environ. Qual. 2012, 41, 544–553. [Google Scholar] [CrossRef]
- Anderson, E.J.; Phanikumar, M.S. Surface storage dynamics in large rivers: Comparing three-dimensional particle transport, one-dimensional fractional derivative, and multirate transient storage models. Water Resour. Res. 2011, 47, W09511. [Google Scholar] [CrossRef]
- De Wit, M.; Pebesma, E.J. Nutrient fluxes at the river basin scale. II: The balance between data availability and model complexity. Hydrol. Processes 2001, 15, 761–775. [Google Scholar] [CrossRef]
- Runkel, R.L. One-Dimensional Transport with Inflow and Storage (OTIS): A Solute Transport Model for Streams and Rivers; USGS Water Resources Investigations Report 98-4018; U.S. Geological Survey: Denver, CO, USA, 1998. Available online: http://co.water.usgs.gov/otis/ (accessed on 1 July 2022).
- Van Genuchten, M.T.; Leij, F.J.; Skaggs, T.H.; Toride, N.; Bradford, S.A.; Pontedeiro, E.M. Exact analytical solutions for contaminant transport in rivers 1. The equilibrium advection-dispersion equation. J. Hydrol. Hydromech. 2013, 61, 146–160. [Google Scholar] [CrossRef]
- De Smedt, F.; Brevis, W.; Debels, P. Analytical solution for solute transport resulting from instantaneous injection in streams with transient storage. J. Hydrol. 2005, 315, 25–39. [Google Scholar] [CrossRef]
- Šimůnek, J.; Van Genuchten, M.T.; Sejna, M.; Toride, N.; Leij, F.J. The STANMOD Computer Software for Evaluating Solute Transport in Porous Media Using Analytical Solutions of Convection-Dispersion Equation; Version 2.0, IGWMC-TPS-71; International Ground Water Modeling Center (IGWMC), Colorado School of Mines: Golden, CO, USA, 2000; p. 32. Available online: http://www.pc-progress.com/en/Default.aspx?stanmod (accessed on 1 July 2022).
- Ince, D.C.; Hatton, L.; Graham-Cumming, J. The case for open computer programs. Nature 2012, 482, 485. [Google Scholar] [CrossRef]
- Brovelli, M.A.; Minghini, M.; Moreno-Sanchez, R.; Oliveira, R. 2017. Free and open source software for geospatial applications (FOSS4G) to support Future Earth. Int. J. Digit. Earth 2017, 10, 386–404. [Google Scholar] [CrossRef]
- Communication to the Commission, Open Source Software Strategy 2020–2023; Think Open: Brussels, Belgium, 2020.
- Coetzee, S.; Ivánová, I.; Mitasova, H.; Brovelli, M.A. Open Geospatial Software and Data: A Review of the Current State and A Perspective into the Future. ISPRS Int. J. Geo-Inf. 2020, 9, 90. [Google Scholar] [CrossRef]
- Kresic, N.; Mikszewski, A. Hydrogeological Conceptual Site Models: Data Analysis and Visualization; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Rossetto, R.; De Filippis, G.; Triana, F.; Ghetta, M.; Borsi, I.; Schmid, W. Software tools for management of conjunctive use of surface-and ground-water in the rural environment: Integration of the Farm Process and the Crop Growth Module in the FREEWAT platform. Agric. Water Manag. 2019, 223, 105717. [Google Scholar] [CrossRef]
- Foglia, L.; Borsi, I.; Mehl, S.; de Filippis, G.; Cannata, M.; Vasquez-Sune, E.; Criollo, R.; Rossetto, R. FREEWAT, a Free and Open Source, GIS-Integrated, Hydrological Modeling Platform. Groundwater 2018, 56, 521–523. [Google Scholar] [CrossRef] [PubMed]
- Rosas-Chavoya, M.; Gallardo-Salazar, J.L.; López-Serrano, P.M.; Alcántara-Concepción, P.C.; León-Miranda, A.K. QGIS a constantly growing free and open-source geospatial software contributing to scientific development. Cuad. Investig. Geográfica 2022, 48, 197–213. [Google Scholar] [CrossRef]
- Vieux, B.E. Geographic information systems and non-point source water quality and quantity modelling. Hydrol. Processes 1991, 5, 101–113. [Google Scholar] [CrossRef]
- Olivera, F.; Valenzuela, M.; Srinivasan, R.; Choi, J.; Cho, H.; Koka, S.; Agrawal, A. ArcGIS-SWAT: A geodata model and GIS interface for SWAT. J. Am. Water Resour. Assoc. 2006, 42, 295–309. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R.; King, K.W. Soil and Water Assessment Tool (SWAT): Theoretical Documentation; Version 2000; TWRI Report TR-191; TexasWater Resources Institute: College Station, TX, USA, 2002. [Google Scholar]
- Becker, M.W.; Jiang, Z. Flux-based contaminant transport in a GIS environment. J. Hydrol. 2007, 343, 203–210. [Google Scholar] [CrossRef]
- Akbar, T.A.; Lin, H.; DeGroote, J. Development and evaluation of GIS-based ArcPRZM-3 system for spatial modeling of groundwater vulnerability to pesticide contamination. Comput. Geosci. 2011, 37, 822–830. [Google Scholar] [CrossRef]
- Rossetto, R.; Borsi, I.; Schifani, C.; Bonari, E.; Mogorovich, P.; Primicerio, M. SID&GRID: Integrating hydrological modeling in GIS environment. Rend. Online Soc. Geol. Ital. 2013, 24, 282–283. [Google Scholar]
- Anguix, A.; Díaz, L. gvSIG: A GIS desktop solution for an open SDI. J. Geogr. Reg. Plan. 2008, 1, 41–48. [Google Scholar]
- Oliveira, M.M.; Martins, T.N. A methodology for the preliminary characterization of the river boundary condition in finite difference groundwater flow numerical models. Acque Sotter. Ital. J. Groundw. 2019, 8, 21–27. [Google Scholar] [CrossRef]
- Harbaugh, A.W. MODFLOW-2005, the U.S. Geological Survey Modular Groundwater Model—The Ground-water Flow Process; U.S. Geological Survey, Techniques and Methods 6–A16; U.S. Geological Survey: Reston, VA, USA, 2005.
- Bittner, D.; Rychlik, A.; Klöffel, T.; Leuteritz, A.; Disse, M.; Chiogna, G. A GIS-based model for simulating the hydrological effects of land use changes on karst systems—The integration of the LuKARS model into FREEWAT. Environ. Model. Softw. 2020, 127, 104682. [Google Scholar] [CrossRef]
- QGIS A Free and Open Source Geographic Information System. Open Source. Geospatial Foundation Project. 2009. Available online: http://qgis.osgeo.org (accessed on 1 July 2022).
- Nielsen, A.; Bolding, K.; Hu, F.; Trolle, D. An open source QGIS-based workflow for model application and experimentation with aquatic ecosystems. Environ. Model. Softw. 2017, 95, 358–364. [Google Scholar] [CrossRef]
- Ellsäßer, F.; Röll, A.; Stiegler, C.; Hendrayanto Hölscher, D. Introducing QWaterModel, a QGIS plugin for predicting evapotranspiration from land surface temperatures. Environ. Model. Softw. 2020, 130, 104739. [Google Scholar] [CrossRef]
- Dile, Y.T.; Daggupati, P.; George, C.; Srinivasan, R.; Arnold, J. Introducing a new open source GIS user interface for the SWAT model. Environ. Model. Softw. 2016, 85, 129–138. [Google Scholar] [CrossRef]
- Criollo, R.; Velasco, V.; Nardi, A.; De Vries, L.M.; Riera, C.; Scheiber, L.; Jurado, A.; Brouyère, S.; Pujades, E.; Rossetto, R.; et al. AkvaGIS: An open source tool for water quantity and quality management. Comput. Geosci. 2019, 127, 123–132. [Google Scholar] [CrossRef]
- De Filippis, G.; Ercoli, L.; Rossetto, R. A Spatially Distributed, Physically-Based Modeling Approach for Estimating Agricultural Nitrate Leaching to Groundwater. Hydrology 2021, 8, 8. [Google Scholar] [CrossRef]
- Benedini, M.; Tsakiris, G. Water quality modelling for rivers and streams. In Water Science and Technology Library; Springer: Berlin/Heidelberg, Germany, 2013; Volume 70. [Google Scholar]
- Python Software Foundation. Python 3 Release. Available online: https://www.python.org/download/releases/3.0/ (accessed on 1 July 2022).
- Qt5 Library. One framework. One codebase. Any platform. Available online: https://www.qt.io/ (accessed on 1 July 2022).
- QGIS. QGIS Python API. Available online: https://qgis.org/pyqgis/3.10/ (accessed on 1 July 2022).
- Pullar, D.; Springer, D. Towards integrating GIS and catchment models. Environ. Model. Softw. 2000, 15, 451–459. [Google Scholar] [CrossRef]
- Wang, L.; Jackson, C.R.; Pachocka, M.; Kingdon, A. A seamlessly coupled GIS and distributed groundwater flow model. Environ. Model. Softw. 2016, 82, 1–6. [Google Scholar] [CrossRef]
- Toride, N.; Leij, F.J.; van Genuchten, M.T. The CXTFIT Code for Estimating Transport Parameters from Laboratory or Field Tracer Experiments; Version 2.0. Research Report No. 137; U.S. Salinity Laboratory, USDA, ARS: Riverside, CA, USA, 1995.
- Van Genuchten, M.T.; Alves, W.J. Analytical Solutions of the One-Dimensional Convective Dispersive Solute Transport Equations; Technical Bulletin No. 1661; U.S. Department of Agriculture: Washington, DC, USA, 1982.
- Tixier, C.; Singer, H. Occurrence and fate of carbamazepine, clofibric acid, diclofenac, ibuprofen, ketoprofen, and naproxen in surface waters. Environ. Sci. Technol. 2003, 37, 1061–1068. [Google Scholar] [CrossRef] [PubMed]
- Barbagli, A.; Jensen, B.N.; Raza, M.; Schueth, C.; Rossetto, R. Assessment of soil buffer capacity on nutrients and pharmaceuticals in nature-based solution applications. Environ. Sci. Pollut. Res. 2019, 26, 759–774. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Geißen, S.U.; Gal, C. Carbamazepine and diclofenac: Removal in wastewater treatment plants and occurrence in water bodies. Chemosphere 2008, 73, 1151–1161. [Google Scholar] [CrossRef]
- Cardini, A.; Pellegrino, E.; Ercoli, L. Predicted and Measured Concentration of Pharmaceuticals in Surface Water of Areas with Increasing Anthropic Pressure: A Case Study in the Coastal Area of Central Italy. Water 2021, 13, 2807. [Google Scholar] [CrossRef]
- Julínek, T.; Říha, J. Longitudinal dispersion in an open channel determined from a tracer study. Environ. Earth Sci. 2017, 76, 592. [Google Scholar] [CrossRef]
- Liu, Y.; Zarfl, C.; Basu, N.B.; Cirpka, O.A. Modeling the fate of pharmaceuticals in a fourth-order river under competing assumptions of transient storage. Water Resour. Res. 2020, 56, e2019WR026100. [Google Scholar] [CrossRef]
- Acuña, V.; von Schiller, D.; García-Galán, M.J.; Rodríguez-Mozaz, S.; Corominas, L.; Petrovic, M.; Poch, M.; Barceló, D.; Sabater, S. Occurrence and in-stream attenuation of wastewater-derived pharmaceuticals in Iberian rivers. Sci. Total Environ. 2015, 503–504, 133–141. [Google Scholar] [CrossRef]
- Piacentini, S.M.; Rossetto, R. Attitude and Actual Behaviour towards Water-Related Green Infrastructures and Sustainable Drainage Systems in Four North-Western Mediterranean Regions of Italy and France. Water 2020, 12, 1474. [Google Scholar] [CrossRef]
- Rossetto, R.; Barbagli, A.; Borsi, I.; Mazzanti, G.; Vienken, T.; Bonari, E. Site investigation and design of the monitoring system at the Sant’Alessio Induced RiverBank Filtration plant (Lucca, Italy). Rend. Online Soc. Geol. Ital. 2015, 35, 248–251. [Google Scholar]
- Luo, L.; Lan, J.; Wang, Y.; Li, H.; Wu, Z.; McBridge, C.; Zhou, H.; Liu, F.; Zhang, R.; Gong, F.; et al. A Novel Early Warning System (EWS) for Water Quality, Integrating a High-Frequency Monitoring Database with Efficient Data Quality Control Technology at a Large and Deep Lake (Lake Qiandao), China. Water 2022, 14, 602. [Google Scholar] [CrossRef]
- Liu, J.; Wang, P.; Jiang, D.; Nan, J.; Zhu, W. An integrated data-driven framework for surface water quality anomaly detection and early warning. J. Clean. Prod. 2020, 251, 119145. [Google Scholar] [CrossRef]
- Robles, G.; Steinmacher, I.; Adams, P.; Treude, C. Twenty Years of Open Source Software: From Skepticism to Mainstream. IEEE Softw. 2019, 36, 12–15. [Google Scholar] [CrossRef]
- Hanamoto, S.; Nakada, N.; Yamashita, N.; Tanaka, H. Modeling the photochemical attenuation of down-the-drain chemicals during river transport by stochastic methods and field measurements of pharmaceuticals and personal care products. Environ. Sci. Technol. 2013, 47, 13571–13577. [Google Scholar] [CrossRef]
- Guillet, G.; Knapp, J.L.A.; Merel, S.; Cirpka, O.A.; Grathwohl, P.; Zwiener, C.; Schwientek, M. Fate of wastewater contaminants in rivers: Using conservative-tracer based transfer functions to assess reactive transport. Sci. Total Environ. 2019, 656, 1250–1260. [Google Scholar] [CrossRef] [PubMed]


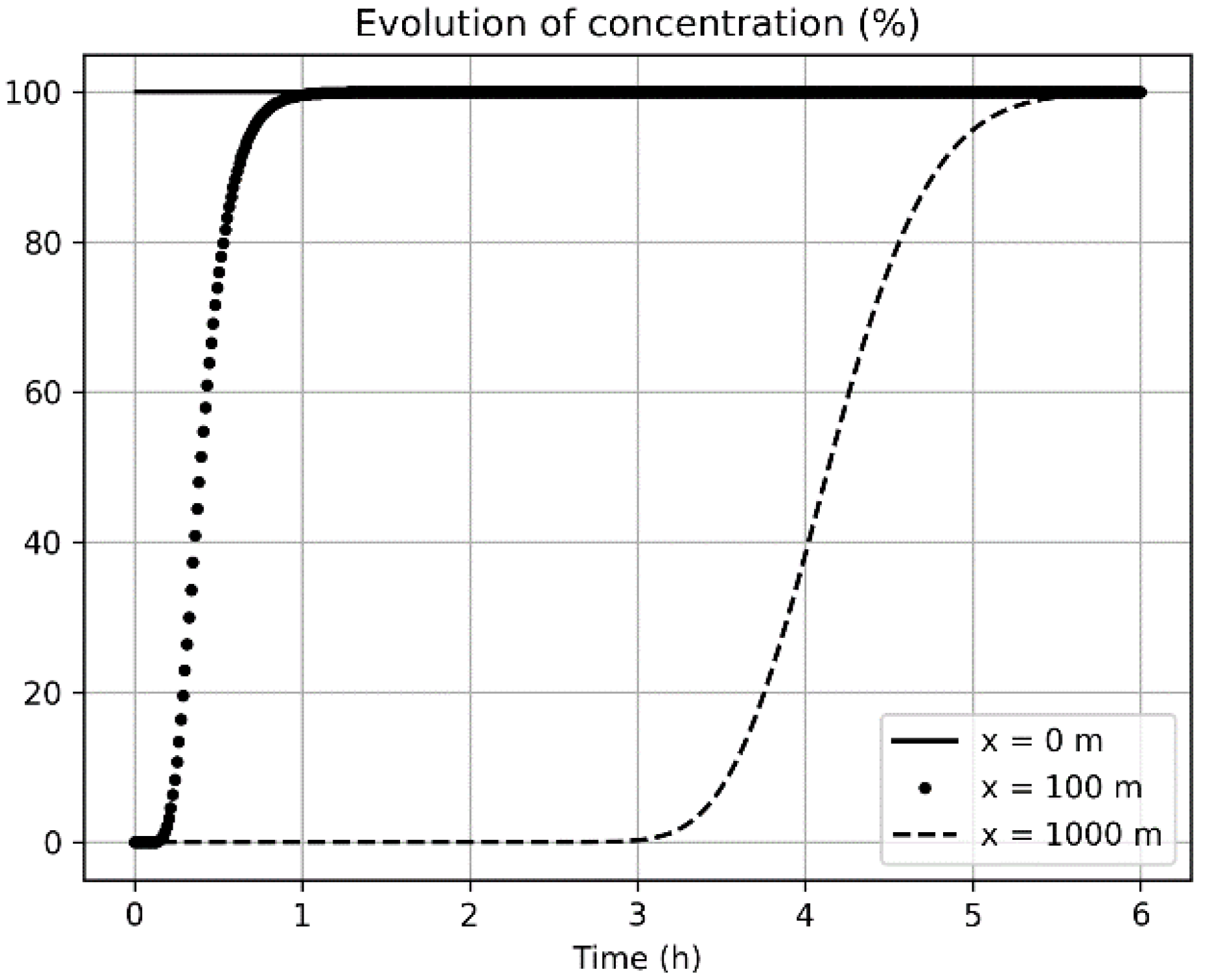
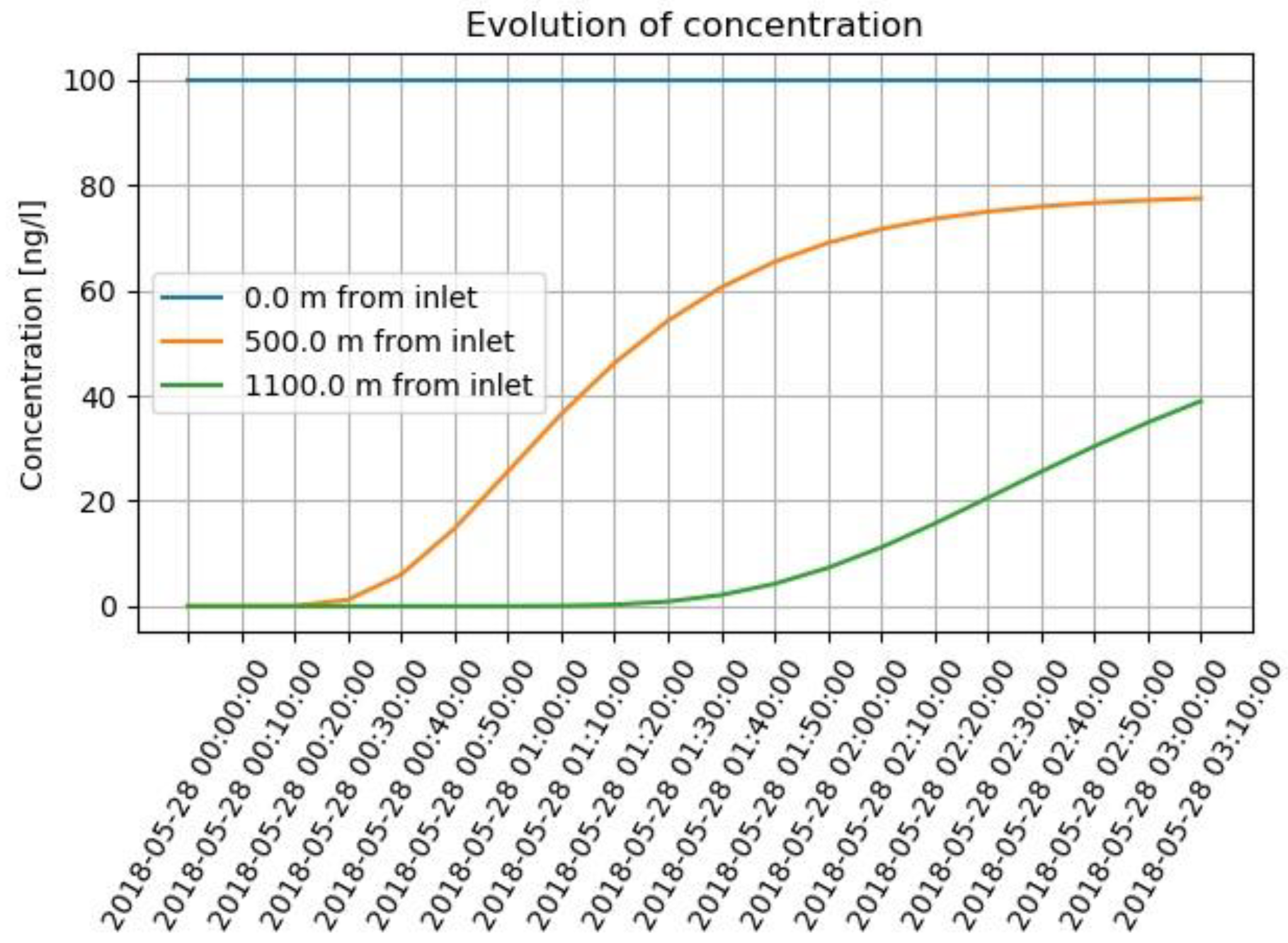
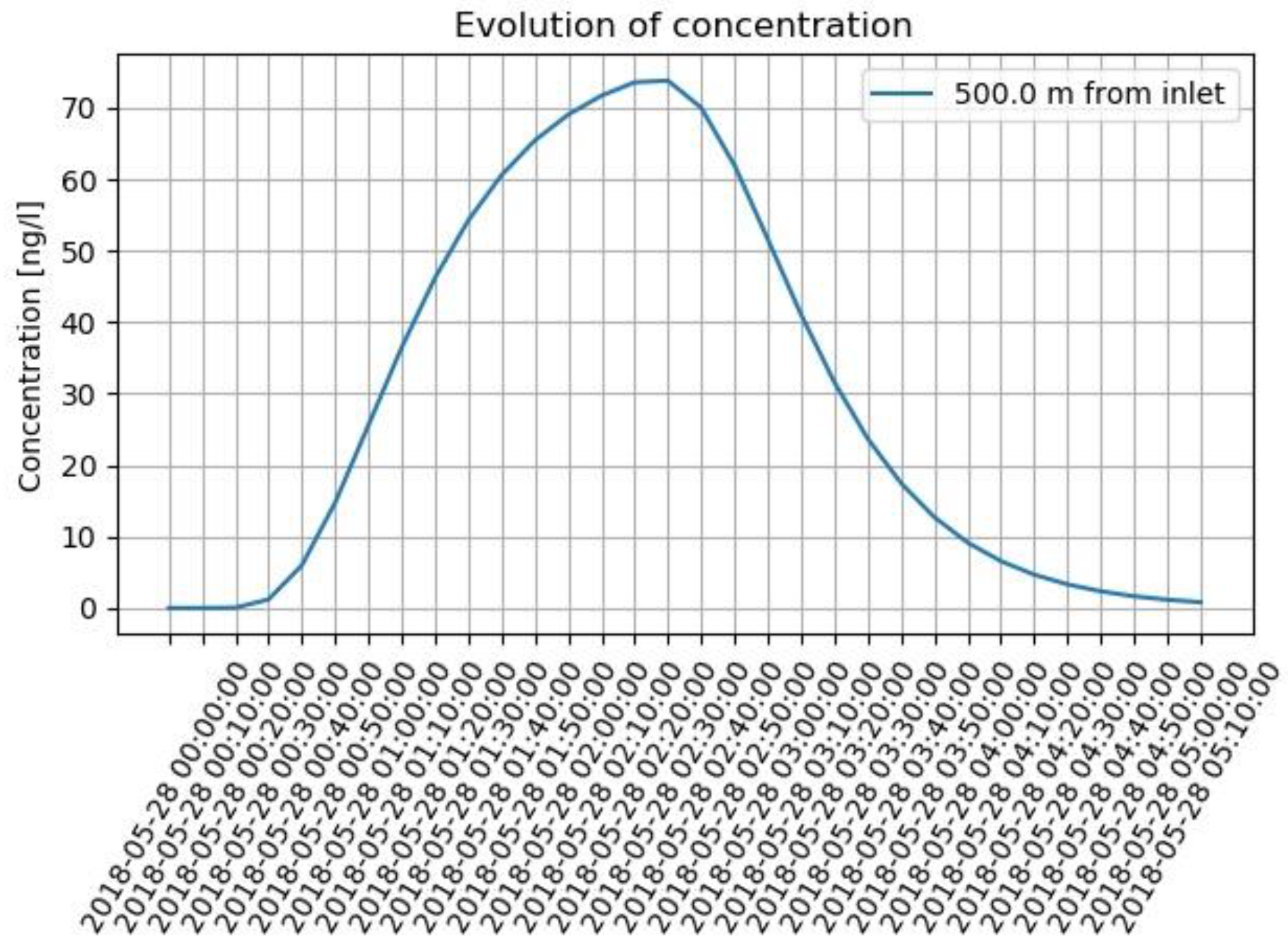

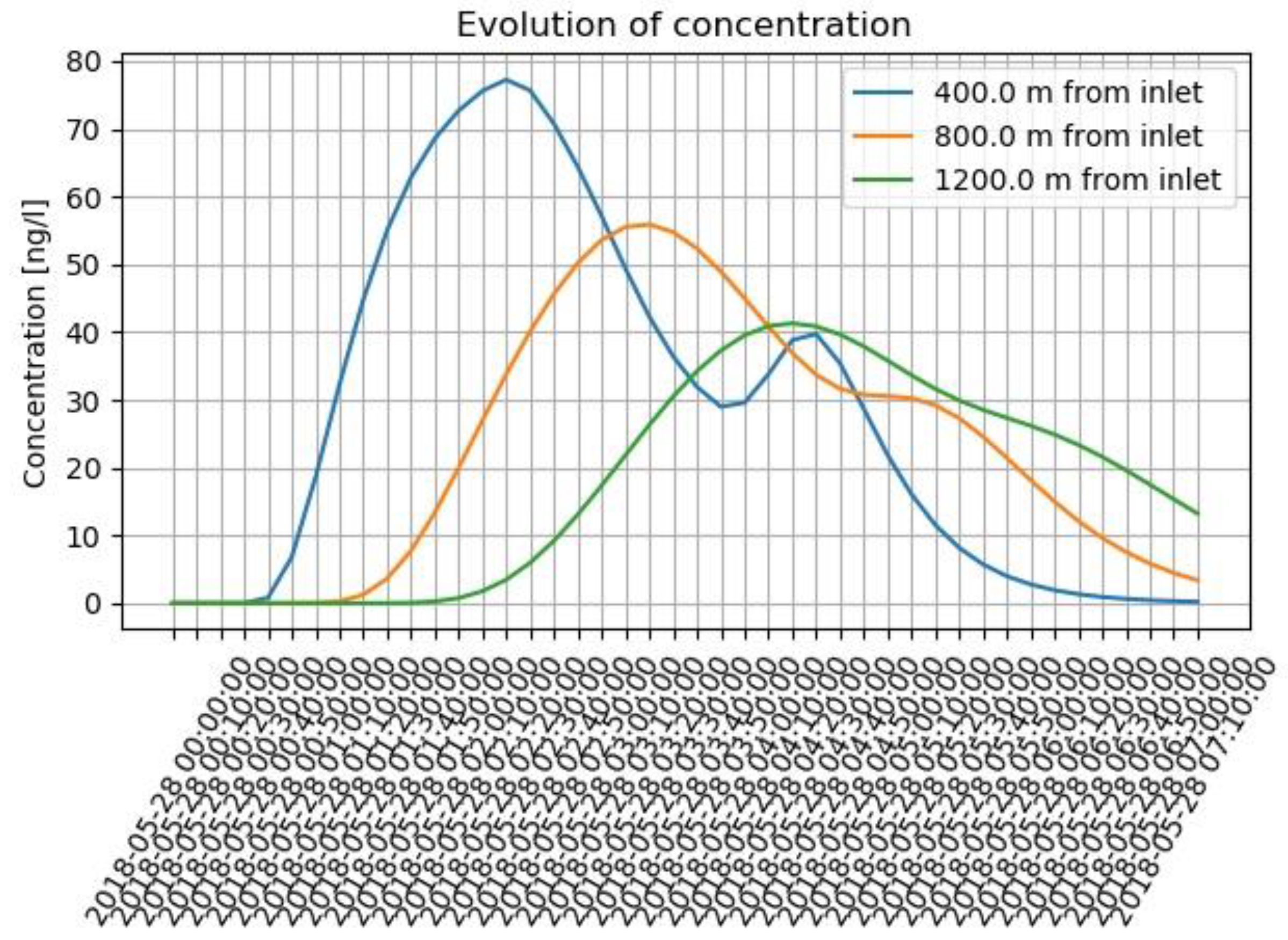
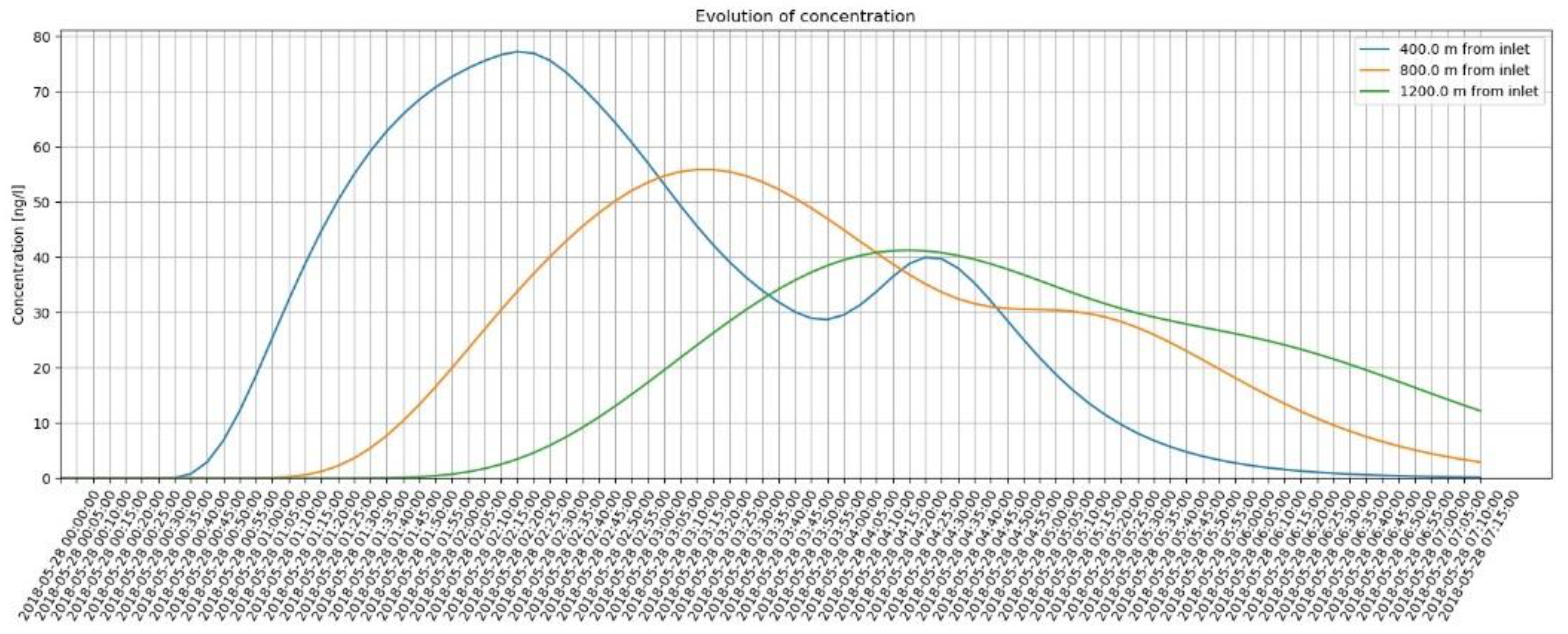

| Parameter | Value | Units |
|---|---|---|
| Total length of the reach | 1200 | m |
| Simulation length | 50 | m |
| Time step | 10 | min |
| Velocity (U) | 0.1 | m/s |
| First order decay rate (k) | 0.00005 | s−1 |
| Longitudinal dispersion (E) | 5.0 | m2/s |
| Initial time | 28 May 2018 00:00 | dd/mm/yyyy hh:mm |
| Date and Time | C0 (ng/L) |
|---|---|
| 28 May 2018 0:00 | 0 |
| 28 May 2018 0:20 | 100 |
| 28 May 2018 2:00 | 50 |
| 28 May 2018 2:30 | 25 |
| 28 May 2018 3:30 | 75 |
| 28 May 2018 4:00 | 0 |
| Time | Inlet (PSMw) (ng/L) | Outlet (PSMz)(ng/L) | Flow Velocity (m/s) | Simulated Value (PSMz_sim) (ng/L) |
|---|---|---|---|---|
| 07:20 | 123 | - | 0.025 | - |
| 09:50 | 181 | - | 0.026 | - |
| 11:00 | - | 105 | - | 112 |
| 12:20 | 162 | - | 0.026 | - |
| 13:10 | - | 112 | - | 116 |
| 14:20 | 162 | - | 0.021 | - |
| 15:40 | - | 115 | - | 119 |
| 16:50 | 150 | - | 0.029 | - |
| 18:00 | - | 125 | - | 122 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rossetto, R.; Cisotto, A.; Dalla Libera, N.; Braidot, A.; Sebastiani, L.; Ercoli, L.; Borsi, I. ORGANICS: A QGIS Plugin for Simulating One-Dimensional Transport of Dissolved Substances in Surface Water. Water 2022, 14, 2850. https://doi.org/10.3390/w14182850
Rossetto R, Cisotto A, Dalla Libera N, Braidot A, Sebastiani L, Ercoli L, Borsi I. ORGANICS: A QGIS Plugin for Simulating One-Dimensional Transport of Dissolved Substances in Surface Water. Water. 2022; 14(18):2850. https://doi.org/10.3390/w14182850
Chicago/Turabian StyleRossetto, Rudy, Alberto Cisotto, Nico Dalla Libera, Andrea Braidot, Luca Sebastiani, Laura Ercoli, and Iacopo Borsi. 2022. "ORGANICS: A QGIS Plugin for Simulating One-Dimensional Transport of Dissolved Substances in Surface Water" Water 14, no. 18: 2850. https://doi.org/10.3390/w14182850






