Investigation of Shock Wave Pressure Transmission Patterns and Influencing Factors Caused by Underwater Drilling Blasting
Abstract
:1. Introduction
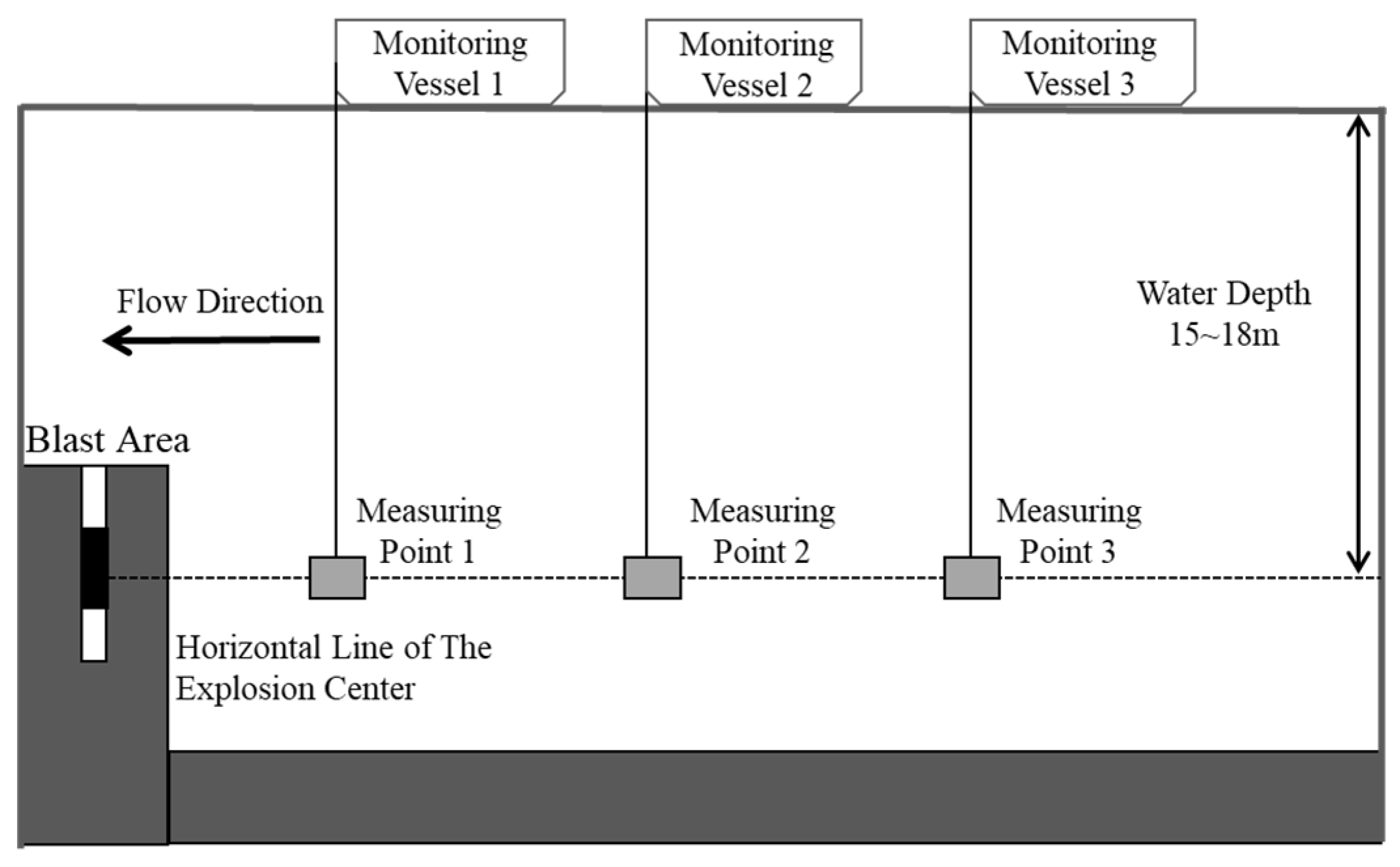
2. Blast Shock Wave Monitoring Scheme
3. Results and Analysis of the Field Monitoring of Shock Waves
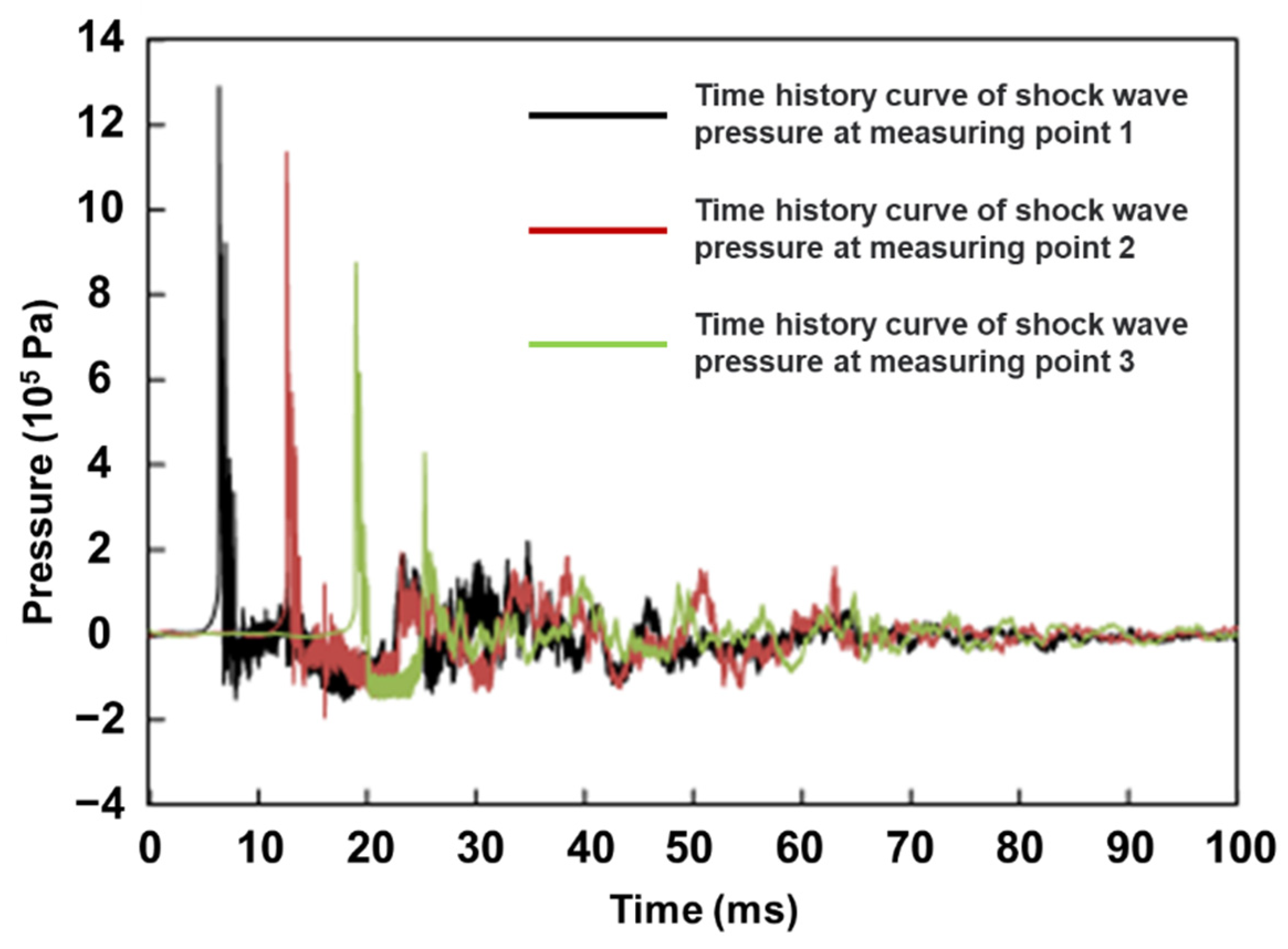
3.1. Field Monitoring Results
3.2. Underwater Attenuation Characteristics of Shock Waves
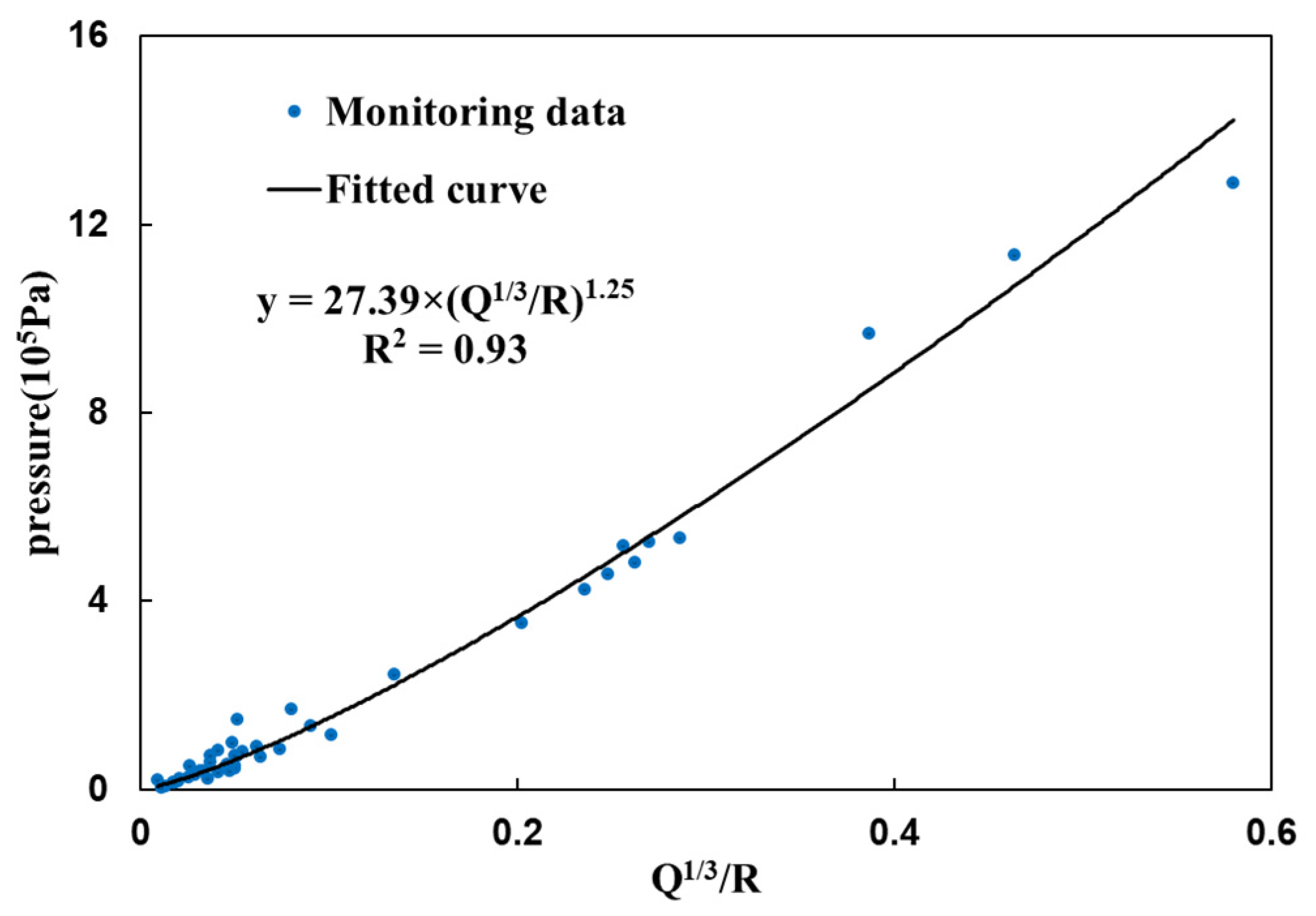
3.3. Fitting of the Shock Wave Monitoring Data
4. Numerical Simulation of Underwater Blast Shock Waves
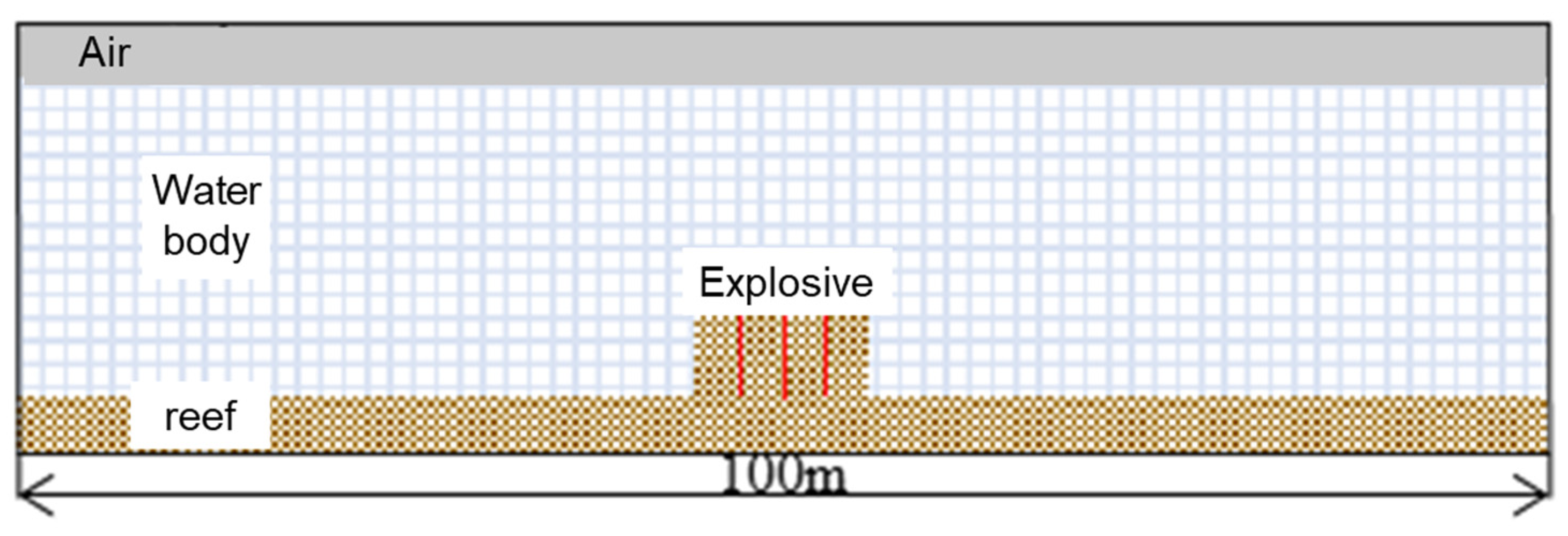
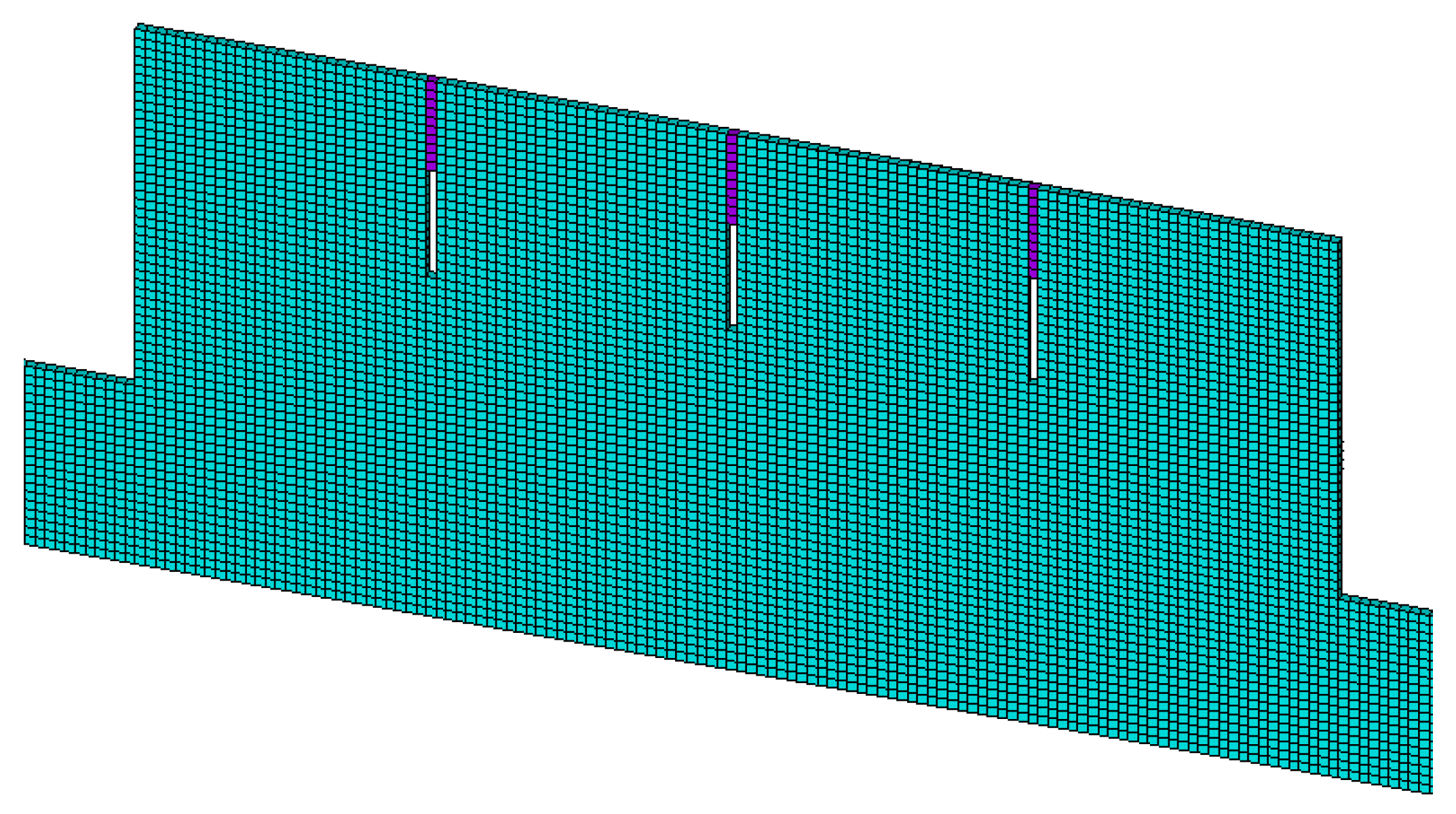
4.1. Modeling
4.2. Material Model and Parameters
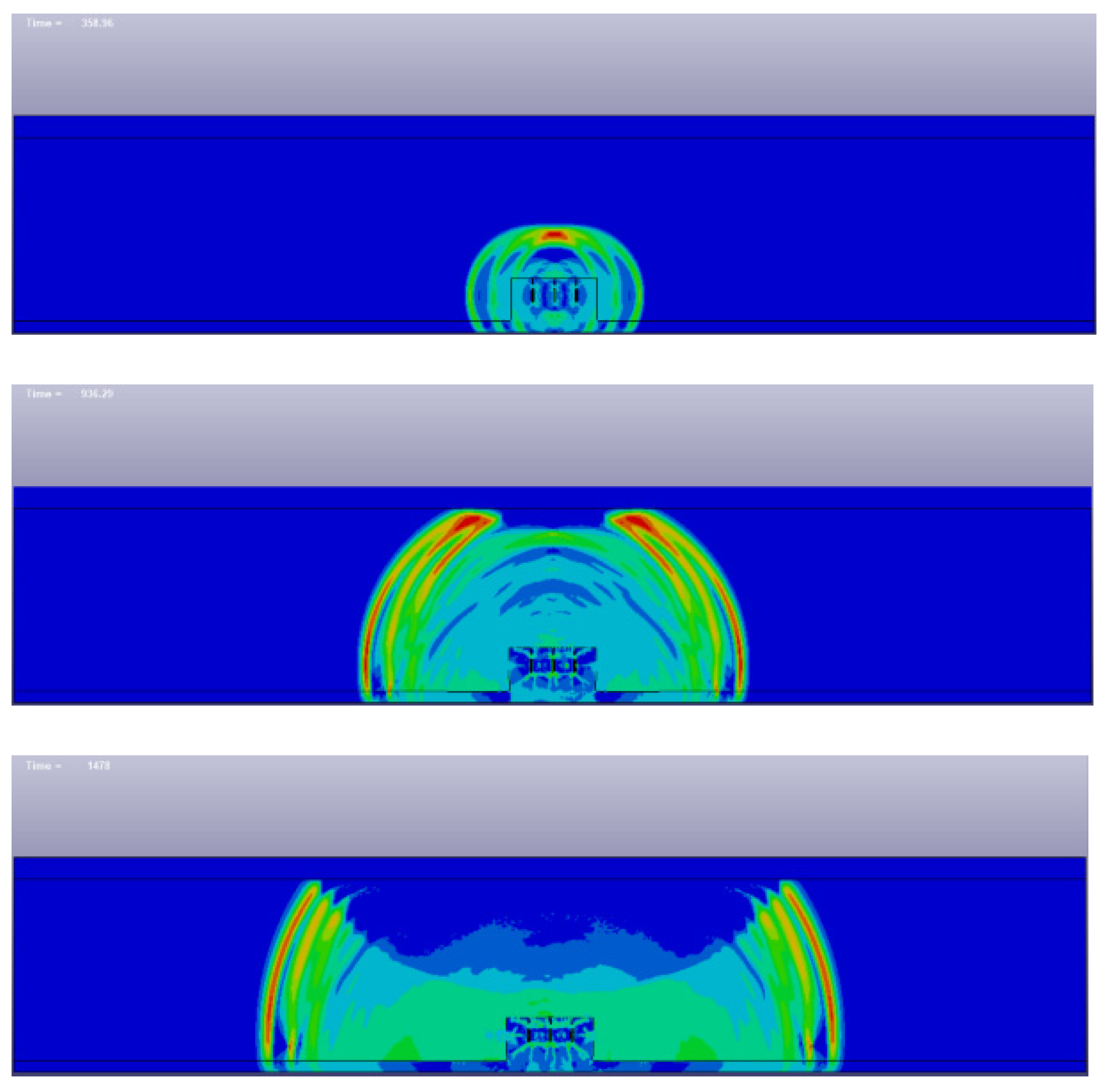
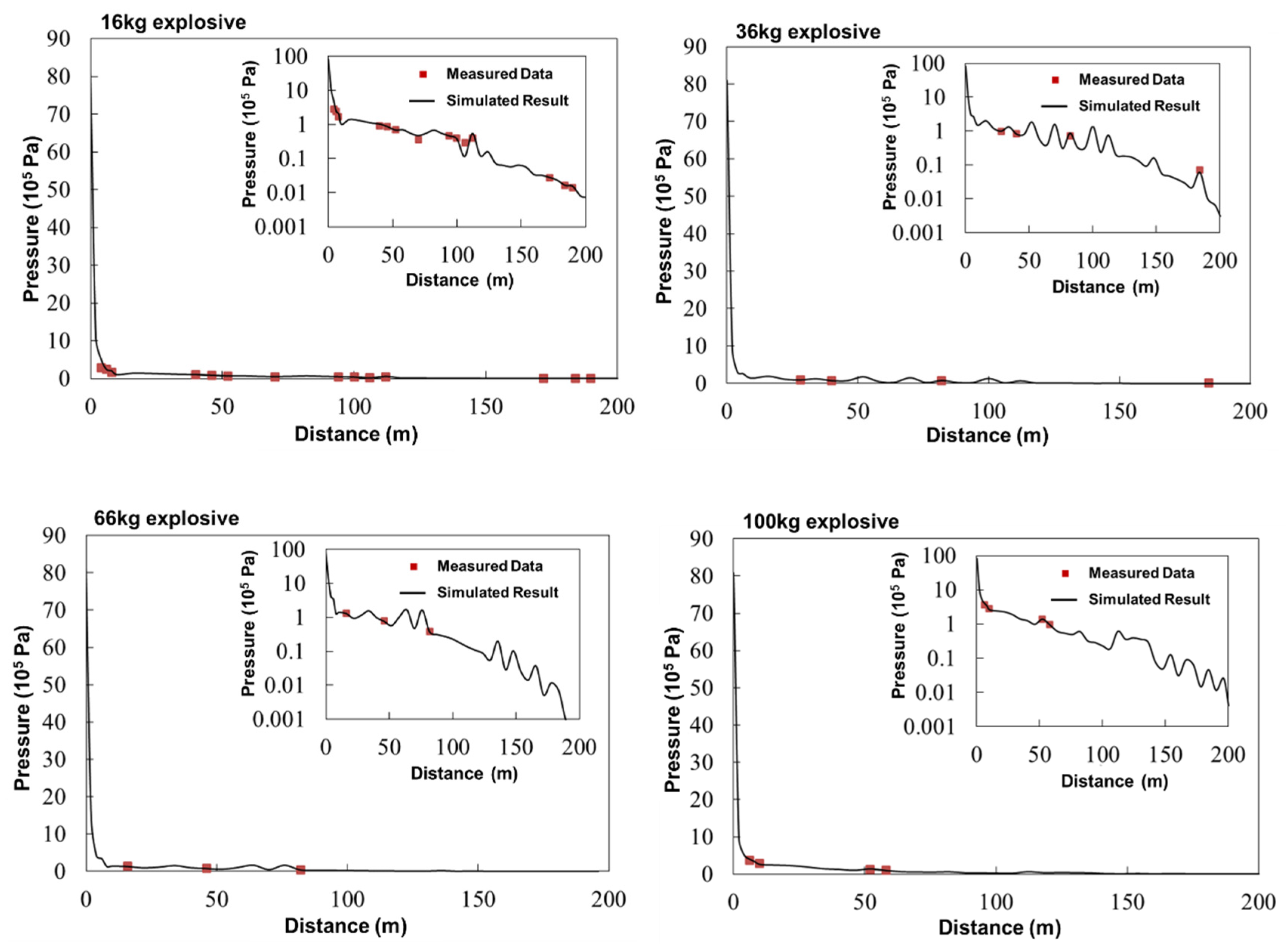
4.3. Analysis and Verification of the Simulation Results
4.4. Factors Influencing the Blast Shock Wave Transmission Characteristics
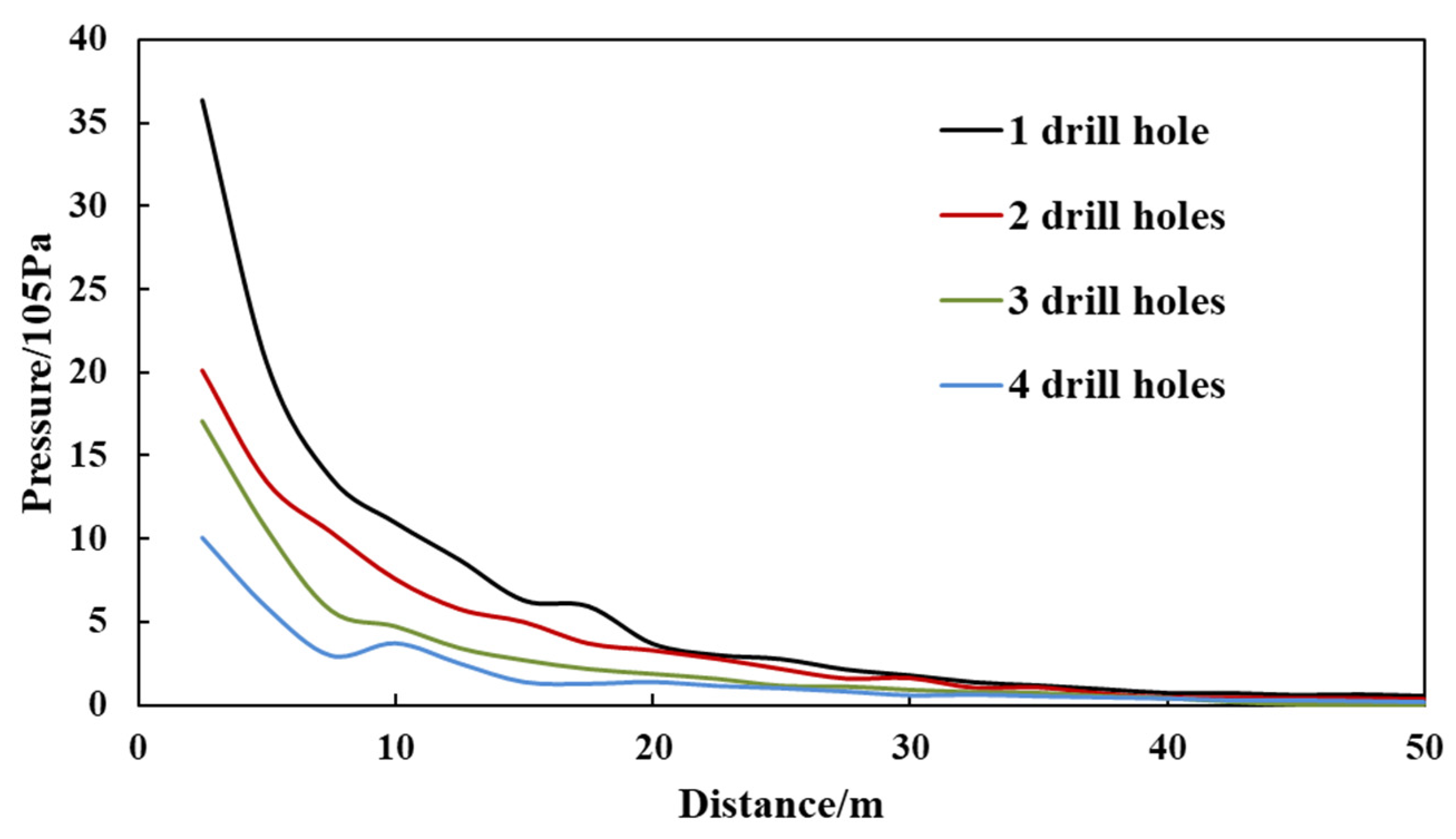
4.4.1. Number of Blastholes
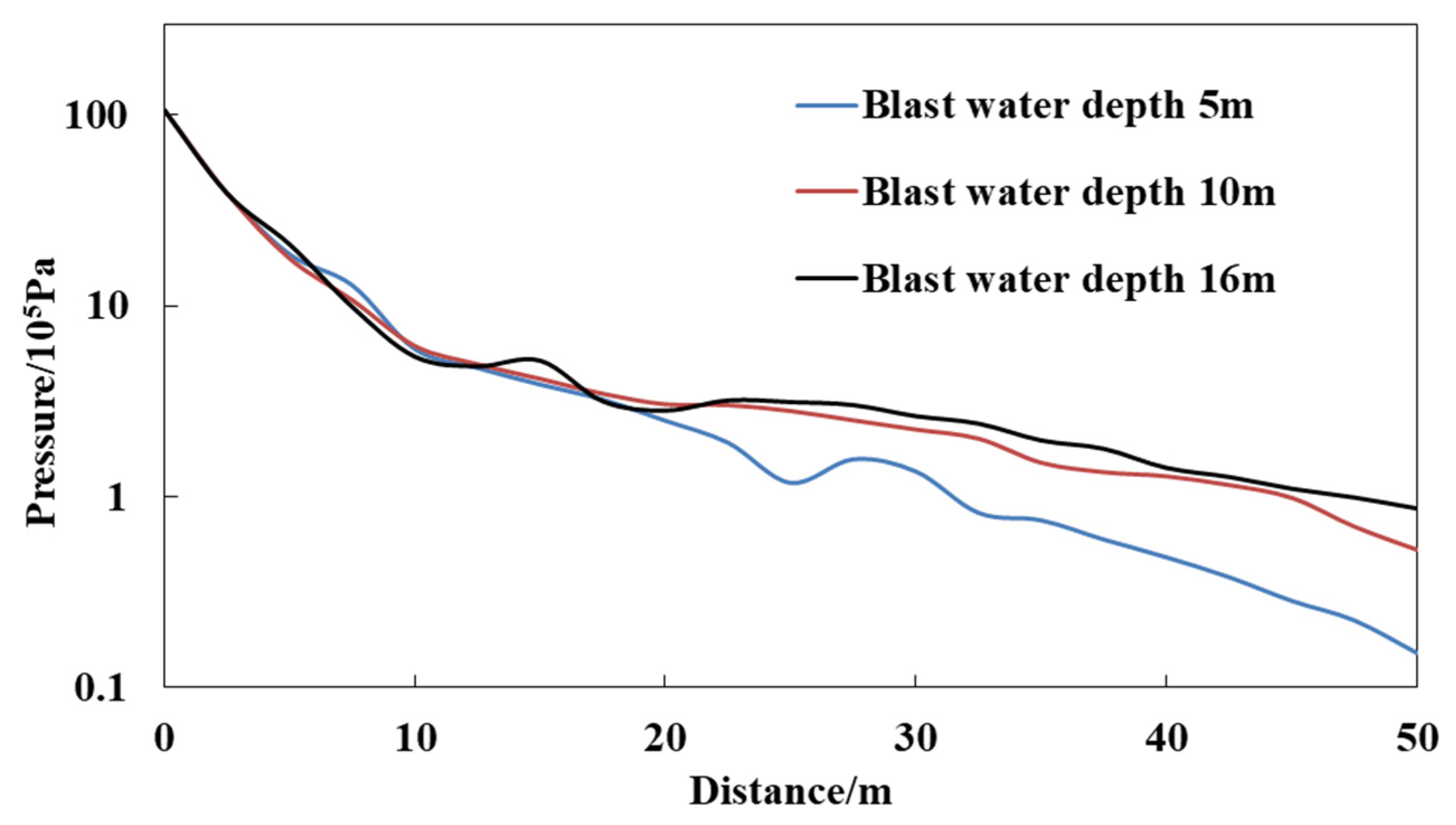
4.4.2. Water Depth
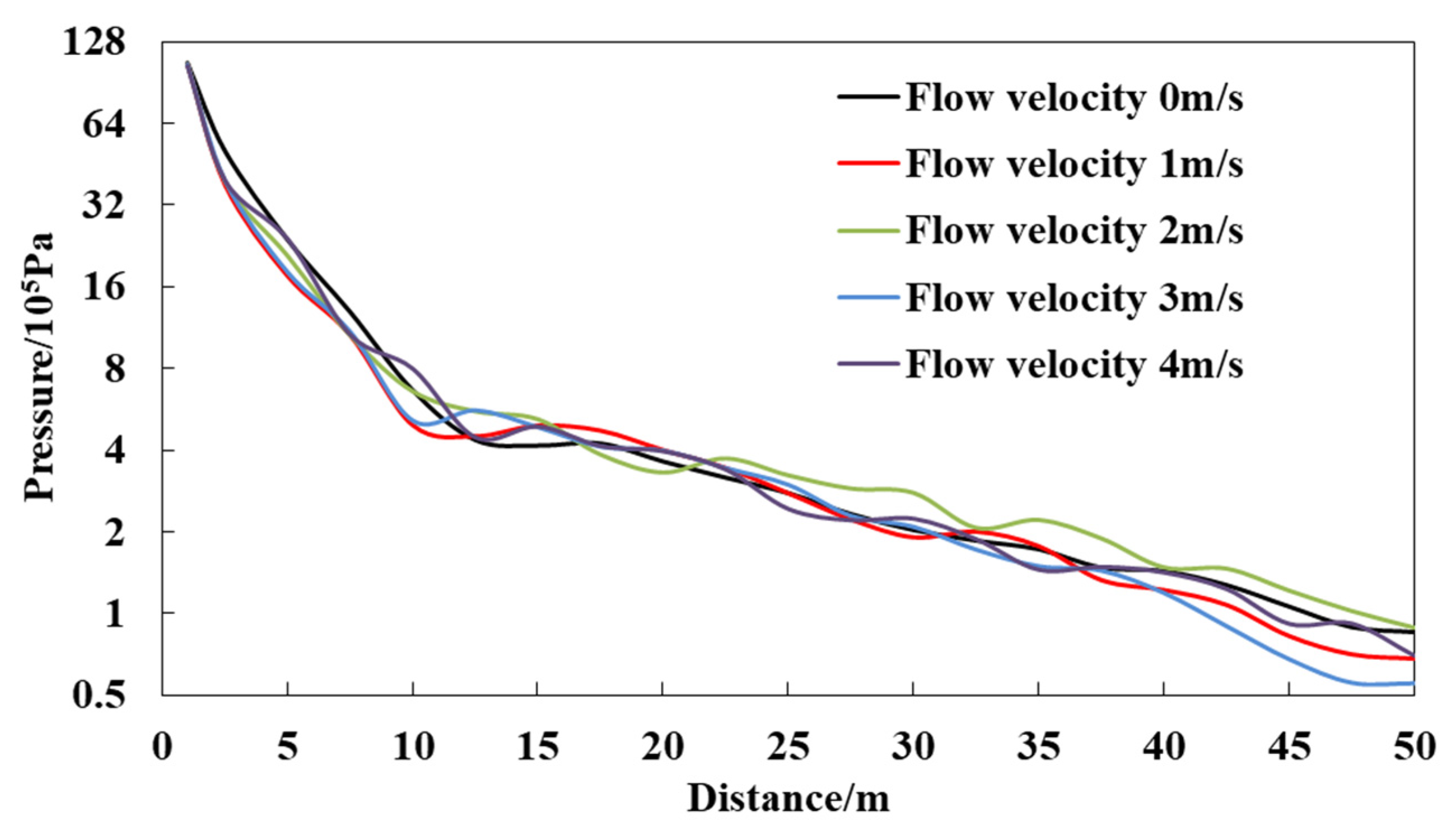
4.4.3. Water Velocity
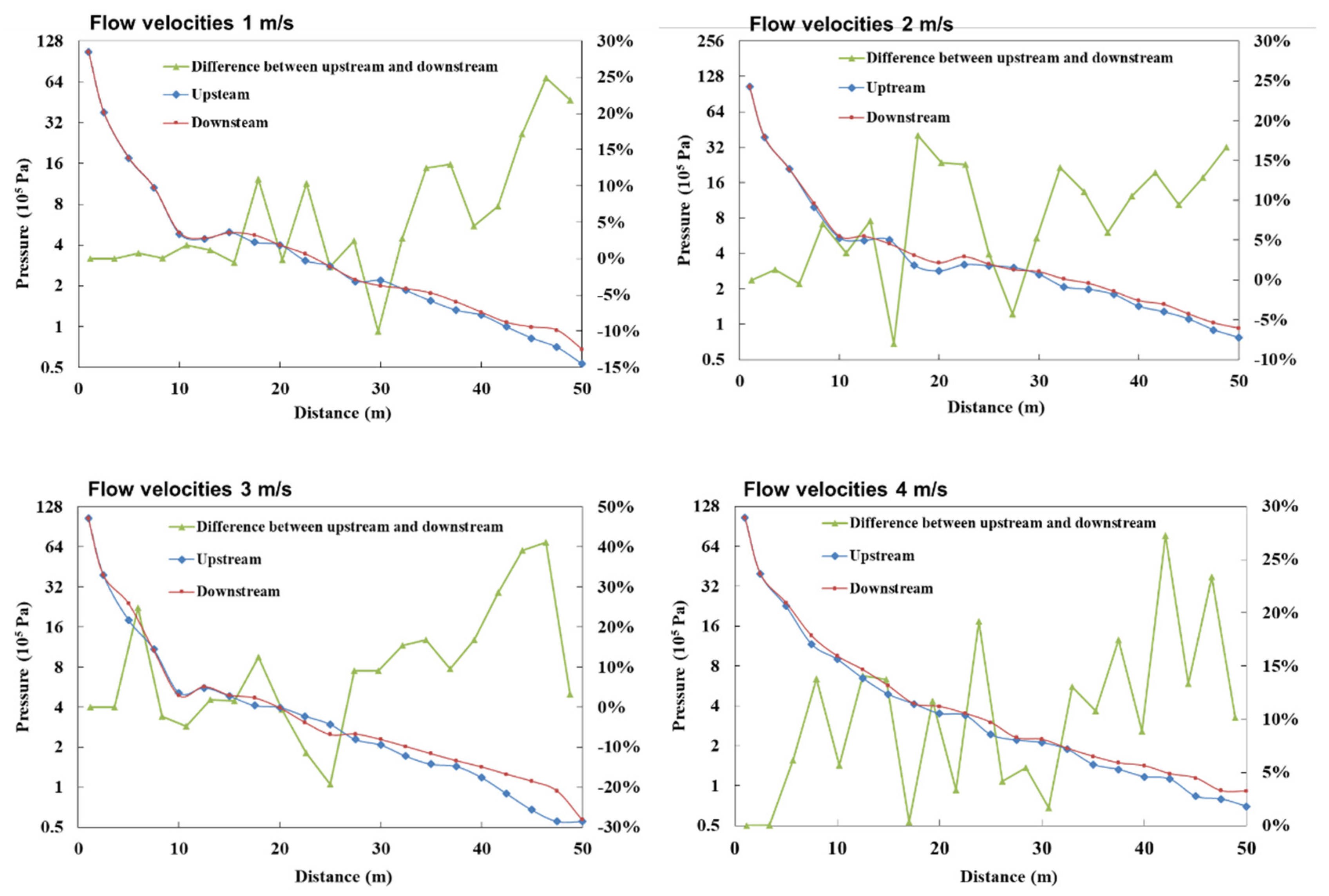
4.4.4. Flow Direction
5. Conclusions
- (1)
- Based on the field monitoring data, an accurate empirical equation for the peak pressure of the underwater drilling blasting shock wave was fitted as P = 27.39 × (Q1/3/R)1.25, which is accurate in estimating the shock wave pressure with different explosive weights and blast source distances in underwater drilling blasting projects.
- (2)
- The transmission characteristics of the drilling blasting shock wave in water were numerically simulated using the software ANSYS/LS-DYNA. The results showed that the shock wave propagates into the surrounding water in a spherical form and reflects when reaching the water surface, and the reflected wave has a significant weakening effect on the incident wave.
- (3)
- The numerical simulation results showed the following: With a fixed weight of explosive, the more blastholes there are, the smaller the peak pressure of the shock wave; the smaller the blast water depth is, the more quickly the peak pressure of the shock wave is attenuated; the flow velocity has little influence on the shock wave transmission, while the flow direction has a certain influence, where the pressure of the shock wave is slightly lower in the upstream direction than in the downstream direction, and the higher the flow velocity is, the greater the difference and the more pronounced the degree of decrease with increasing distance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gu, W.; Wang, Z.; Liu, J.; Xu, J.; Liu, X.; Cao, T. Water-Depth-Based Prediction Formula for the Blasting Vibration Velocity of Lighthouse Caused by Underwater Drilling Blasting. Shock Vib. 2017, 2017, 7340845. [Google Scholar] [CrossRef]
- Peng, Y.; Wu, L.; Chen, C.; Zhu, B.; Jia, Q. Study on the Robust Regression of the Prediction of Vibration Velocity in Underwater Drilling and Blasting. Arab. J. Sci. Eng. 2018, 43, 5541–5549. [Google Scholar] [CrossRef]
- Bach, L.; Nielsen, M.H.; Bollwerk, S.M. Environmental Impact of Submarine Rock Blasting and Dredging Operations in an Arctic Harbor Area: Dispersal and Bioavailability of Sediment-Associated Heavy Metals. Water Air Soil Pollut. 2017, 228, 198. [Google Scholar] [CrossRef]
- Wang, Z.-X.; Gu, W.-B.; Liang, T.; Zhao, S.-T.; Chen, P.; Yu, L.-F. Monitoring and Prediction of the Vibration Intensity of Seismic Waves Induced in Underwater Rock by Underwater Drilling and Blasting. Def. Technol. 2022, 18, 109–118. [Google Scholar] [CrossRef]
- Peng, Y.; Wu, L.; Su, Y.; Zhu, B.; Chen, C.; Li, B. Review of research on safety control of seismic wave and shock wave induced by underwater blasting. Geosystem Eng. 2017, 20, 172–179. [Google Scholar] [CrossRef]
- Seo, S.-I.; Sagong, M.; Son, S.-W. Global response of submerged floating tunnel against underwater explosion. KSCE J. Civ. Eng. 2015, 19, 2029–2034. [Google Scholar] [CrossRef]
- Tatlısuluoğlu, A.; Beji, S. Blast Pressure Measurements of an Underwater Detonation in the Sea. J. Mar. Sci. Appl. 2021, 20, 706–713. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, C.; Wang, P.; Zhu, J.; Zhou, X. Blast Vibration Control in A Hydropower Station for the Safety of Adjacent Structure. Appl. Sci. 2020, 10, 6195. [Google Scholar] [CrossRef]
- Ge, S.; Zu, Y.C.; Yuan, L.; Ming, S.Z.; Jian, Y.W. Experimental and numerical investigation of the centrifugal model for underwater explosion shock wave and bubble pulsation. Ocean Eng. 2017, 142, 523–531. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, G.; Wang, C.; Pang, B.; Du, C. Numerical simulation of failure modes of concrete gravity dams subjected to underwater explosion. Eng. Fail. Anal. 2014, 36, 49–64. [Google Scholar] [CrossRef]
- Schiffer, A.; Tagarielli, V.L. The response of circular composite plates to underwater blast: Experiments and modelling. J. Fluids Struct. 2015, 52, 130–144. [Google Scholar] [CrossRef]
- Koli, S.; Chellapandi, P.; Rao, L.B.; Sawant, A. Study on JWL equation of state for the numerical simulation of near-field and far-field effects in underwater explosion scenario. Eng. Sci. Technol. 2020, 23, 758–768. [Google Scholar] [CrossRef]
- Moradloo, A.J.; Adib, A.; Pirooznia, A. Damage analysis of arch concrete dams subjected to underwater explosion. Appl. Math. Model. 2019, 75, 709–734. [Google Scholar] [CrossRef]
- Wang, G.; Wang, Y.; Lu, W.; Zhou, W.; Chen, M.; Yan, P. On the determination of the mesh size for numerical simulations of shock wave propagation in near field underwater explosion. Appl. Ocean Res. 2016, 59, 1–9. [Google Scholar] [CrossRef]
- Wang, T.; Guo, X.; Fu, H.; Guo, Y.; Peng, X.; Wu, Y.; Li, J.; Xia, Y. Effects of Water Depth and Ice Thickness on Ice Cover Blasting for Ice Jam Flood Prevention: A Case Study on the Heilong River, China. Water 2018, 10, 700. [Google Scholar] [CrossRef]
- Li, X.F.; Li, H.B.; Zhang, G.K. Damage assessment and blast vibrations controlling considering rock properties of underwater blasting. Int. J. Rock Mech. Min. 2019, 121, 104045. [Google Scholar] [CrossRef]
- Balakrishnan, V.; Pradhan, M.; Dhekne, P.Y. Investigating rock fragmentation in distributed spherical air-gap blasting technique. Powder Technol. 2020, 362, 101–110. [Google Scholar] [CrossRef]
- Nakagawa, A.; Manley, G.T.; Gean, A.D.; Ohtani, K.; Armonda, R.; Tsukamoto, A.; Yamamoto, H.; Takayama, K.; Tominaga, T. Mechanisms of Primary Blast-Induced Traumatic Brain Injury: Insights from Shock-Wave Research. J. Neurotrauma 2011, 28, 1101–1119. [Google Scholar] [CrossRef]
- Chemin, A.; Fawaz, M.W.; Amans, D. Investigation of the blast pressure following laser ablation at a solid–fluid interface using shock waves dynamics in air and in water. Appl. Surf. Sci. 2022, 574, 151592. [Google Scholar] [CrossRef]
- Cole, R.H.; Weller, R. Underwater explosions. Phys. Today. 1948, 1, 35. [Google Scholar] [CrossRef]
- Zhang, P.; Ye, X.; Gu, W.; Liu, W.; Yang, T.; Cui, Y. Testing and analysis of shock waves from explosion of spherical charges at shallow water bottom. Eng. Blasting 2000, 1, 15–20. [Google Scholar]
- Li, H.; Zhao, L.; Ning, Y.; Li, B.; Ju, X.; Zhang, Y.; Chen, G. Testing and analyzing pressure product by submarine explosion with spherical charges. Eng. Blasting 2005, 1, 16–21. [Google Scholar]
- Sun, Y.; Long, Y.; Shao, L.; Xie, X.B. Experimental investigation of shock wave in water of underwater drilling blasting. Eng. Blasting 2007, 13, 15–19. [Google Scholar]
- Chen, X.; Xu, L.; Zhu, Q. Mechanical behavior and damage evolution for concrete subjected to multiple impact loading. KSCE J. Civ. Eng. 2017, 21, 2351–2359. [Google Scholar] [CrossRef]
- Jing, L.; Wang, Z.; Zhao, L. Dynamic response of cylindrical sandwich shells with metallic foam cores under blast loading—numerical simulations. Compos. Struct. 2013, 99, 213–223. [Google Scholar] [CrossRef]
- Xue, Y.; Si, H.; Chen, G. The fragmentation mechanism of coal impacted by water jets and abrasive jets. Powder Technol. 2020, 361, 849–859. [Google Scholar] [CrossRef]
- Sugiyama, Y.; Tanaka, T.; Matsuo, A.; Homae, T.; Wakabayashi, K.; Matsumura, T.; Nakayama, Y. Numerical simulation of blast wave mitigation achieved by water inside a subsurface magazine model. J. Loss Prevent. Proc. 2016, 43, 521–528. [Google Scholar] [CrossRef]
- Ohl, C.D. Cavitation inception following shock wave passage. Phys. Fluids 2002, 14, 3512–3521. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, Y.; Hao, H. Numerical Investigation of Effects of Water Saturation on Blast Wave Propagation in Soil Mass. J. Eng. Mech. 2004, 130, 551–561. [Google Scholar] [CrossRef]
- Hempen, G.L. Air-Screen Reduction of Water-Borne Energy from Underwater Blasting; University of Missouri-Rolla: Rolla, MO, USA, 1993. [Google Scholar]
| Number of Monitoring | Monitoring Points | Total Amount of Explosive (kg) | Distance from the Blasting (m) | Hole Number | Depth of Water (m) | Pressure (105 Pa) |
|---|---|---|---|---|---|---|
| 1 | 1 | 6 | 70 | 1 | 12.8 | 0.49 |
| 2 | 6 | 90 | 1 | 12.8 | 0.16 | |
| 3 | 6 | 100 | 1 | 12.8 | 0.13 | |
| 2 | 1 | 8 | 39 | 1 | 12.8 | 1.48 |
| 2 | 8 | 70 | 1 | 12.8 | 0.30 | |
| 3 | 8 | 222 | 1 | 12.8 | 0.21 | |
| 3 | 1 | 12 | 50 | 1 | 15.0 | 0.52 |
| 2 | 12 | 90 | 1 | 15.0 | 0.24 | |
| 3 | 12 | 110 | 1 | 15.0 | 0.23 | |
| 4 | 1 | 16 | 34 | 2 | 12.8 | 0.86 |
| 2 | 16 | 50 | 2 | 12.8 | 0.69 | |
| 3 | 16 | 80 | 2 | 12.8 | 0.39 | |
| 5 | 1 | 20 | 30 | 3 | 15.0 | 1.34 |
| 2 | 20 | 50 | 3 | 15.0 | 0.80 | |
| 3 | 20 | 80 | 3 | 15.0 | 0.38 | |
| 6 | 1 | 20 | 34 | 3 | 12.8 | 1.71 |
| 2 | 20 | 44 | 3 | 12.8 | 0.92 | |
| 3 | 20 | 56 | 3 | 12.8 | 0.47 | |
| 7 | 1 | 34 | 67 | 5 | 20.0 | 0.98 |
| 2 | 34 | 87 | 5 | 20.0 | 0.59 | |
| 3 | 34 | 90 | 5 | 20.0 | 0.23 | |
| 8 | 1 | 36 | 80 | 5 | 9.0 | 0.82 |
| 2 | 36 | 90 | 5 | 9.0 | 0.71 | |
| 3 | 36 | 252 | 5 | 9.0 | 0.07 | |
| 9 | 1 | 38 | 67 | 7 | 13.9 | 0.50 |
| 2 | 38 | 67 | 7 | 13.9 | 0.71 | |
| 3 | 38 | 67 | 7 | 13.9 | 0.43 | |
| 10 | 1 | 44 | 86 | 5 | 20.0 | 0.35 |
| 2 | 44 | 207 | 5 | 20.0 | 0.14 | |
| 3 | 44 | 323 | 5 | 20.0 | 0.04 | |
| 11 | 1 | 48 | 57 | 4 | 6.2 | 0.69 |
| 2 | 48 | 77 | 4 | 6.2 | 0.38 | |
| 3 | 48 | 200 | 4 | 6.2 | 0.15 | |
| 12 | 1 | 66 | 20 | 5 | 15.0 | 3.53 |
| 2 | 66 | 30 | 5 | 15.0 | 2.45 | |
| 3 | 66 | 40 | 5 | 15.0 | 1.16 | |
| 13 | 1 | 100 | 8 | 8 | 15.0 | 12.89 |
| 2 | 100 | 10 | 8 | 15.0 | 11.35 | |
| 3 | 100 | 12 | 8 | 15.0 | 9.69 | |
| 14 | 1 | 105 | 18 | 9 | 20.0 | 4.82 |
| 2 | 105 | 19 | 9 | 20.0 | 4.58 | |
| 3 | 105 | 20 | 9 | 20.0 | 4.23 | |
| 15 | 1 | 115 | 17 | 12 | 20.0 | 5.33 |
| 2 | 115 | 18 | 12 | 20.0 | 5.25 | |
| 3 | 115 | 19 | 12 | 20.0 | 5.18 |
| Coefficient | Blasting Pattern | |
|---|---|---|
| K | α | |
| 415~555 | 1.05~1.15 | Blasting in water |
| 203~319 | 1.21~1.34 | A single charge blasting in water |
| 31.0~51.0 | 1.10~2.00 | Underwater drilling blasting |
| Material | Density ρ (g·cm−3) | Elasticity Modulus E (GPa) | Compressive Strength σ (MPa) | Tensile Strength σmtl (MPa) | Poisson Ratio v |
|---|---|---|---|---|---|
| Reef | 2.65 | 68.69 | 160 | 5.6 | 0.25 |
| Hole stemming | 1.75 | 0.00016 | 5.00 | 0.30 | 0.20 |
| Parameter | Density ρ (g·cm−3) | Explosive Velocity (m·s−1) | A (GPa) | B (GPa) | R1 | R2 | ω | E0 (GJ·m−3) | Pcj (GPa) |
|---|---|---|---|---|---|---|---|---|---|
| Value | 1.63 | 4500 | 216.7 | 0.184 | 4.2 | 0.9 | 0.15 | 4.1 | 18.5 |
| Material | ρ0 (kg·m−3) | C (km·s−1) | S1 | S2 | S3 | μ (10−4) | γ0 | E0 |
|---|---|---|---|---|---|---|---|---|
| Water | 1.02 | 1.647 | 1.92 | −0.096 | 0 | 8.9 | 0.35 | 0 |
| Air | 0.00129 | 0.344 | 0 | 0 | 0 | 0.18 | 1.40 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, Y.; Li, W.; Du, H.; Yang, X. Investigation of Shock Wave Pressure Transmission Patterns and Influencing Factors Caused by Underwater Drilling Blasting. Water 2022, 14, 2837. https://doi.org/10.3390/w14182837
Wan Y, Li W, Du H, Yang X. Investigation of Shock Wave Pressure Transmission Patterns and Influencing Factors Caused by Underwater Drilling Blasting. Water. 2022; 14(18):2837. https://doi.org/10.3390/w14182837
Chicago/Turabian StyleWan, Yu, Wenjie Li, Hongbo Du, and Xiao Yang. 2022. "Investigation of Shock Wave Pressure Transmission Patterns and Influencing Factors Caused by Underwater Drilling Blasting" Water 14, no. 18: 2837. https://doi.org/10.3390/w14182837







