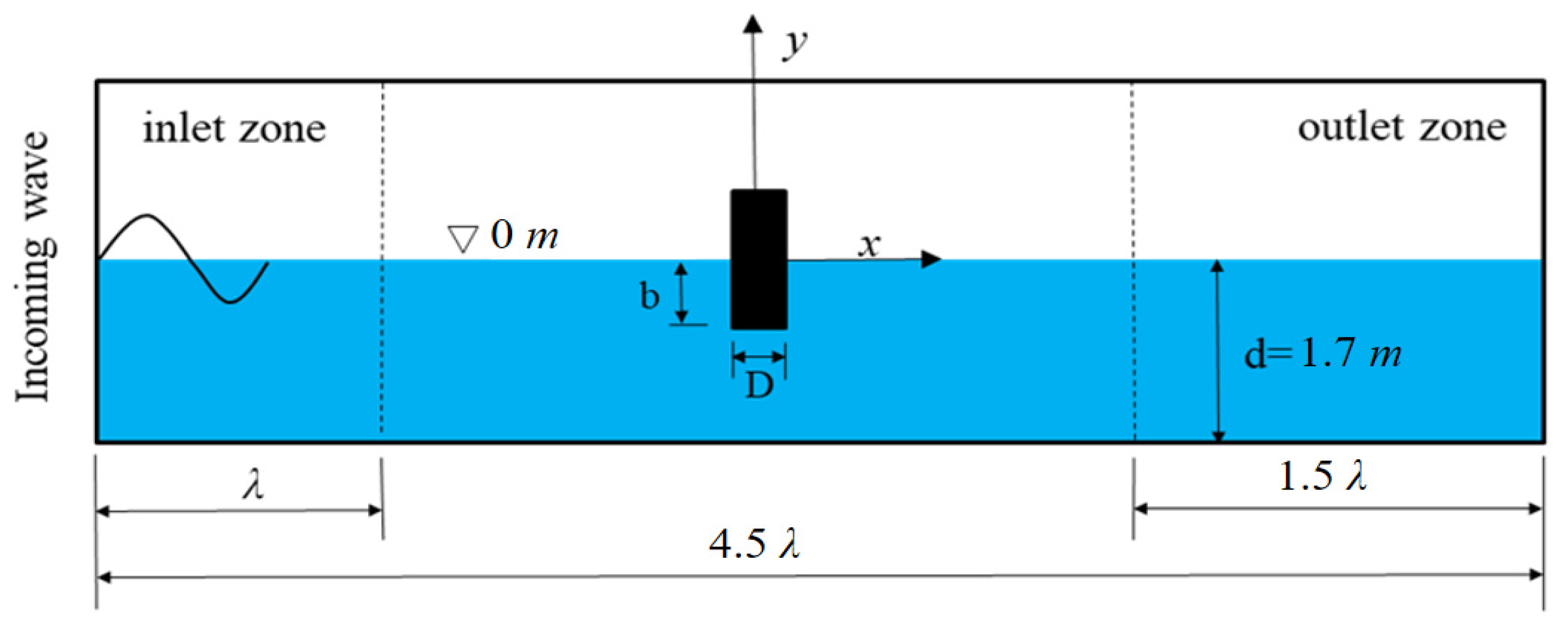
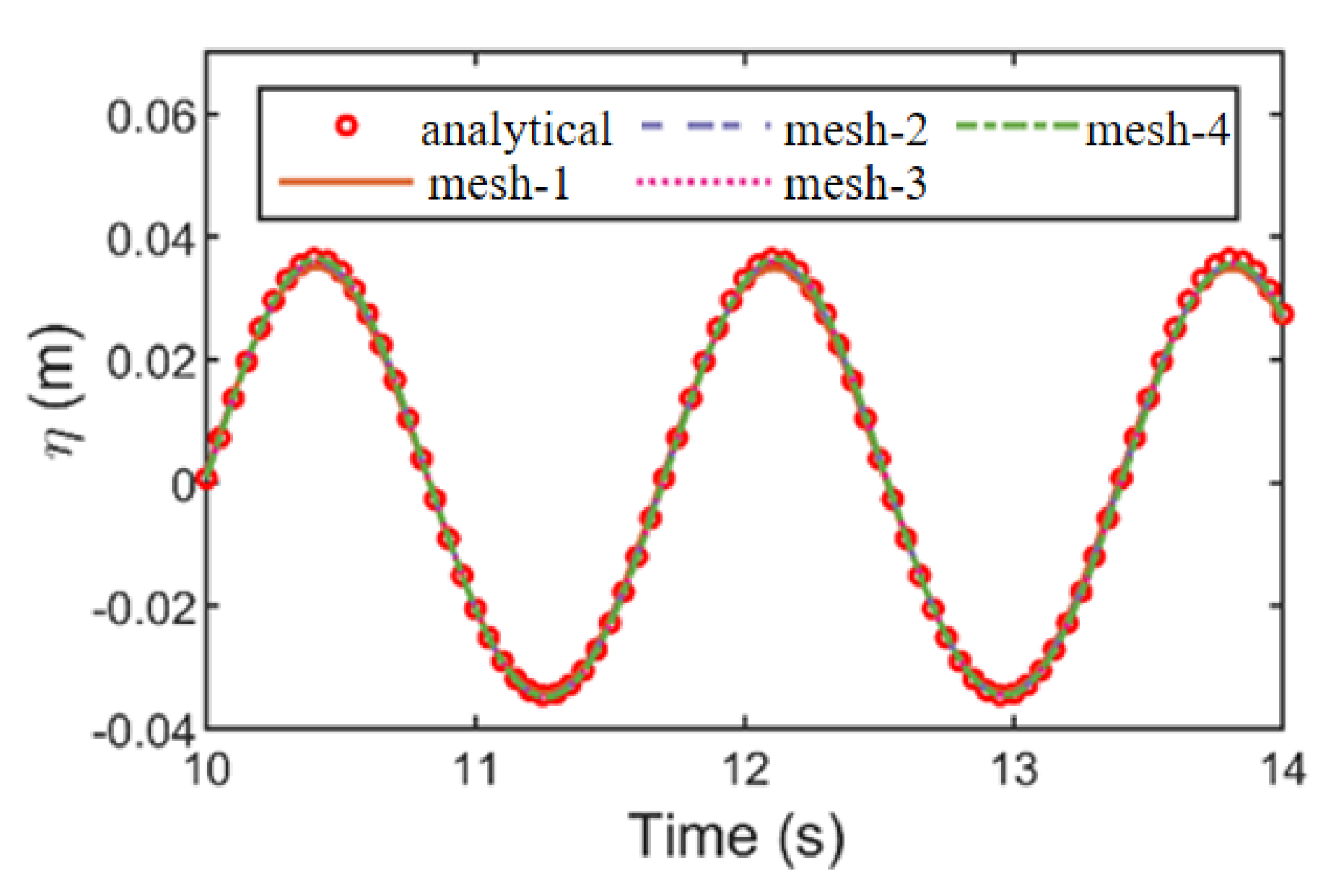
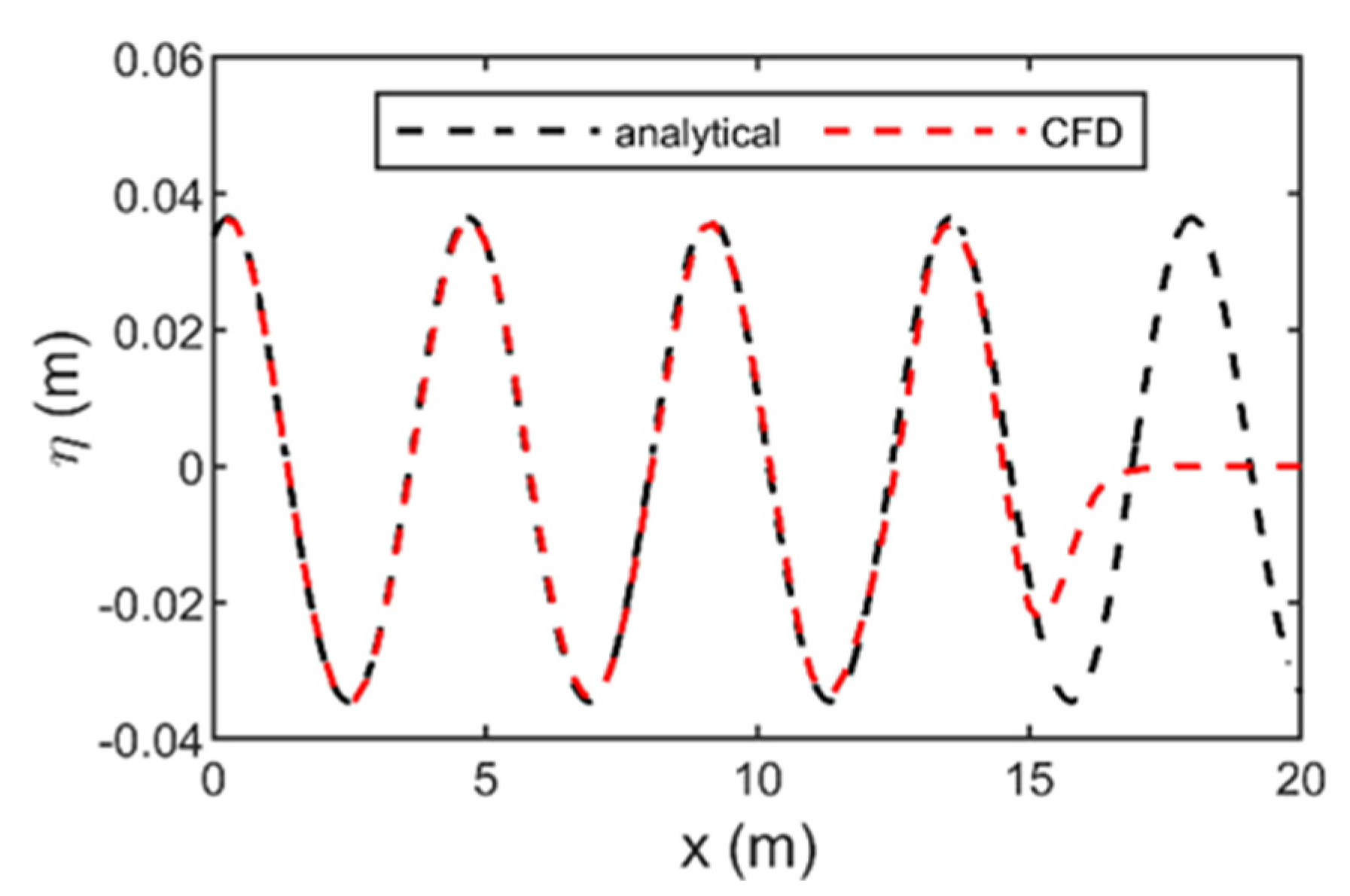
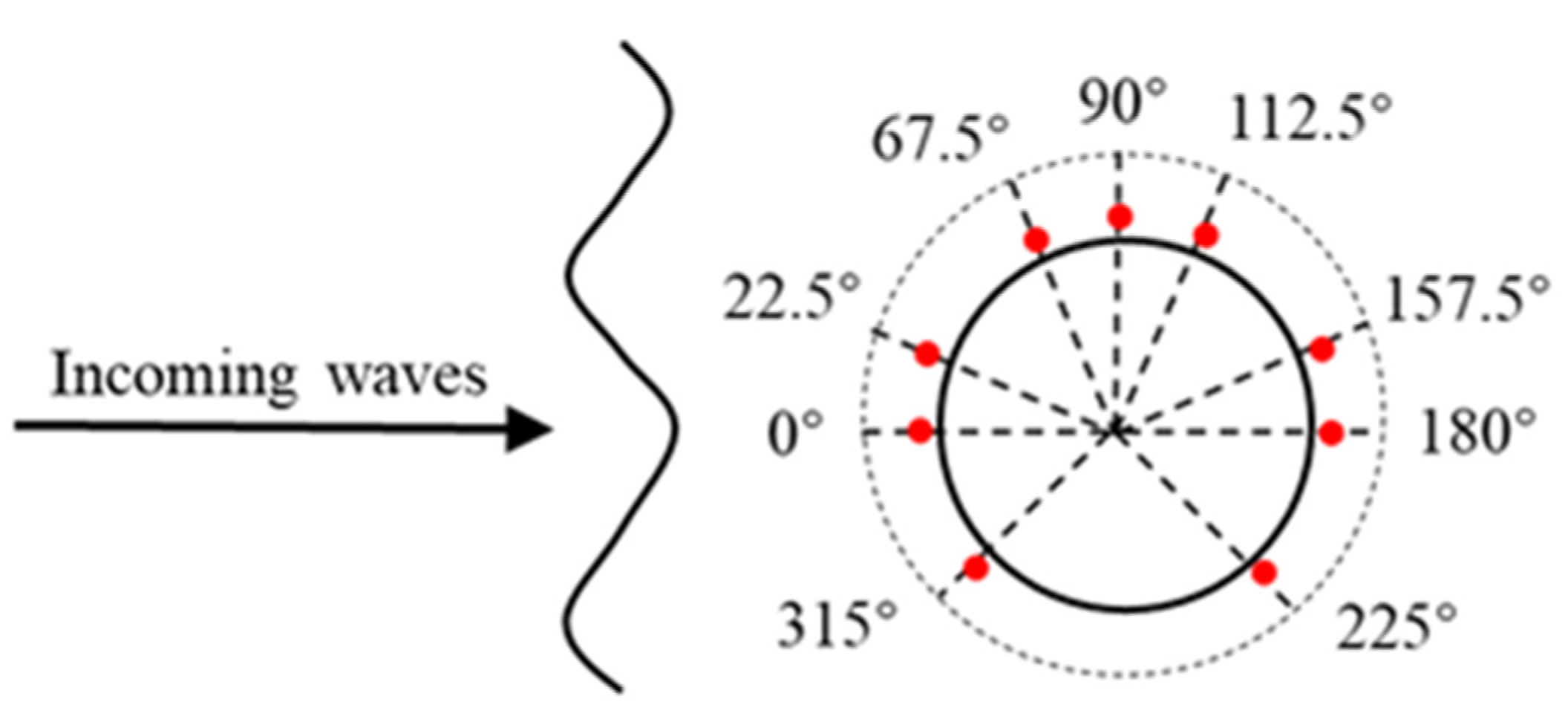
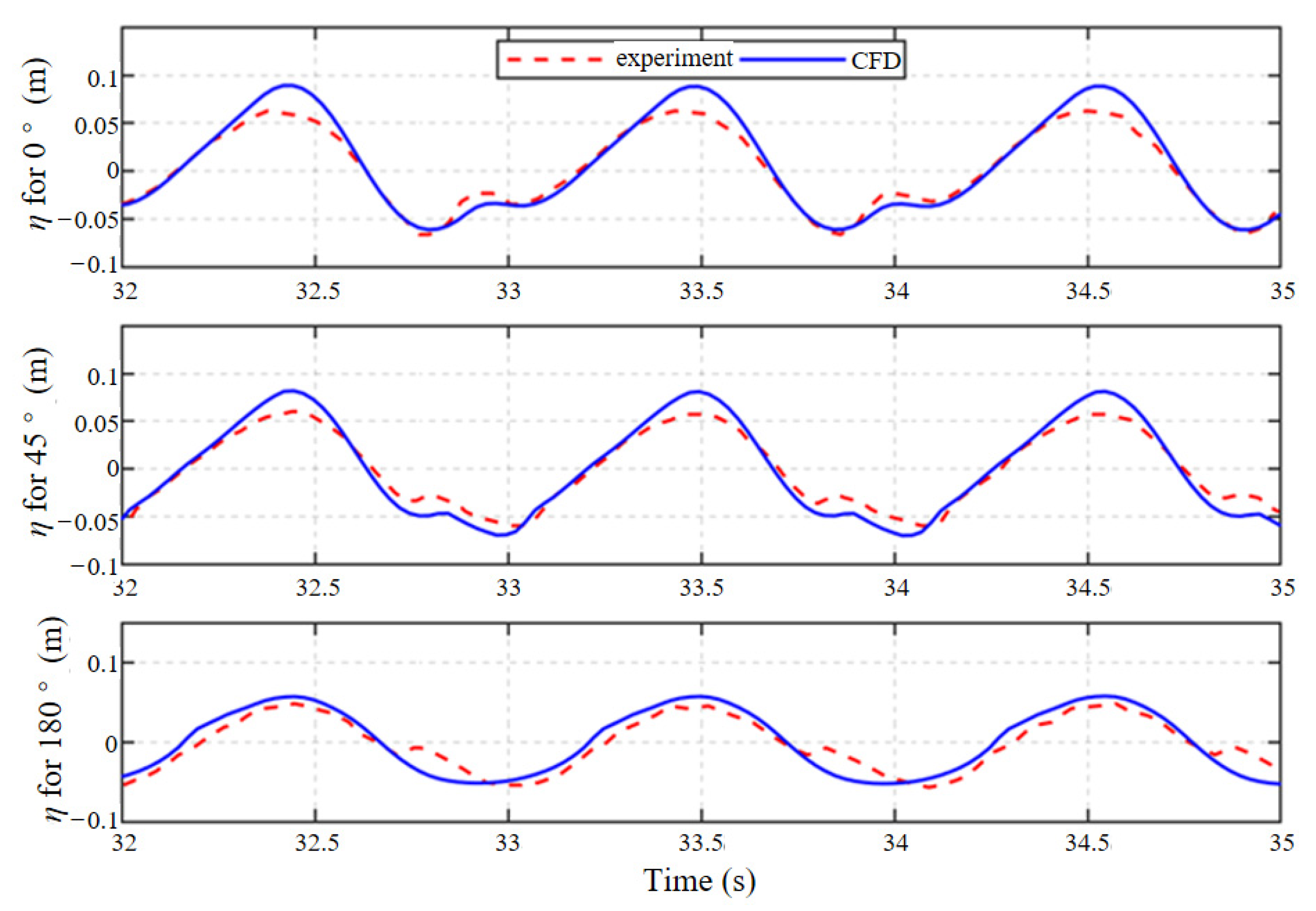
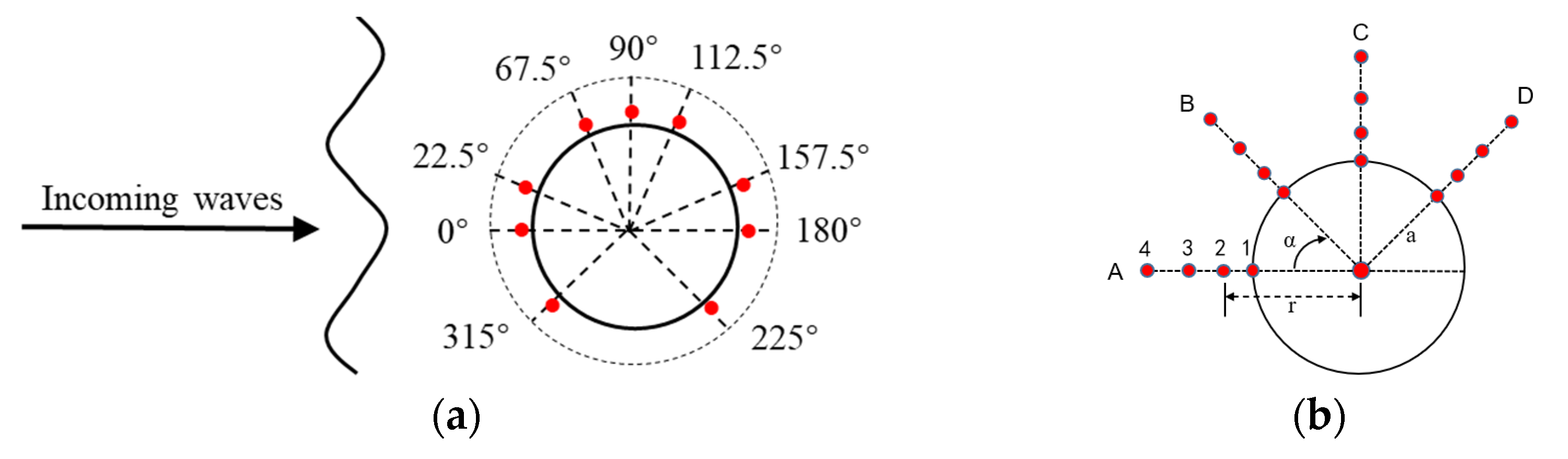
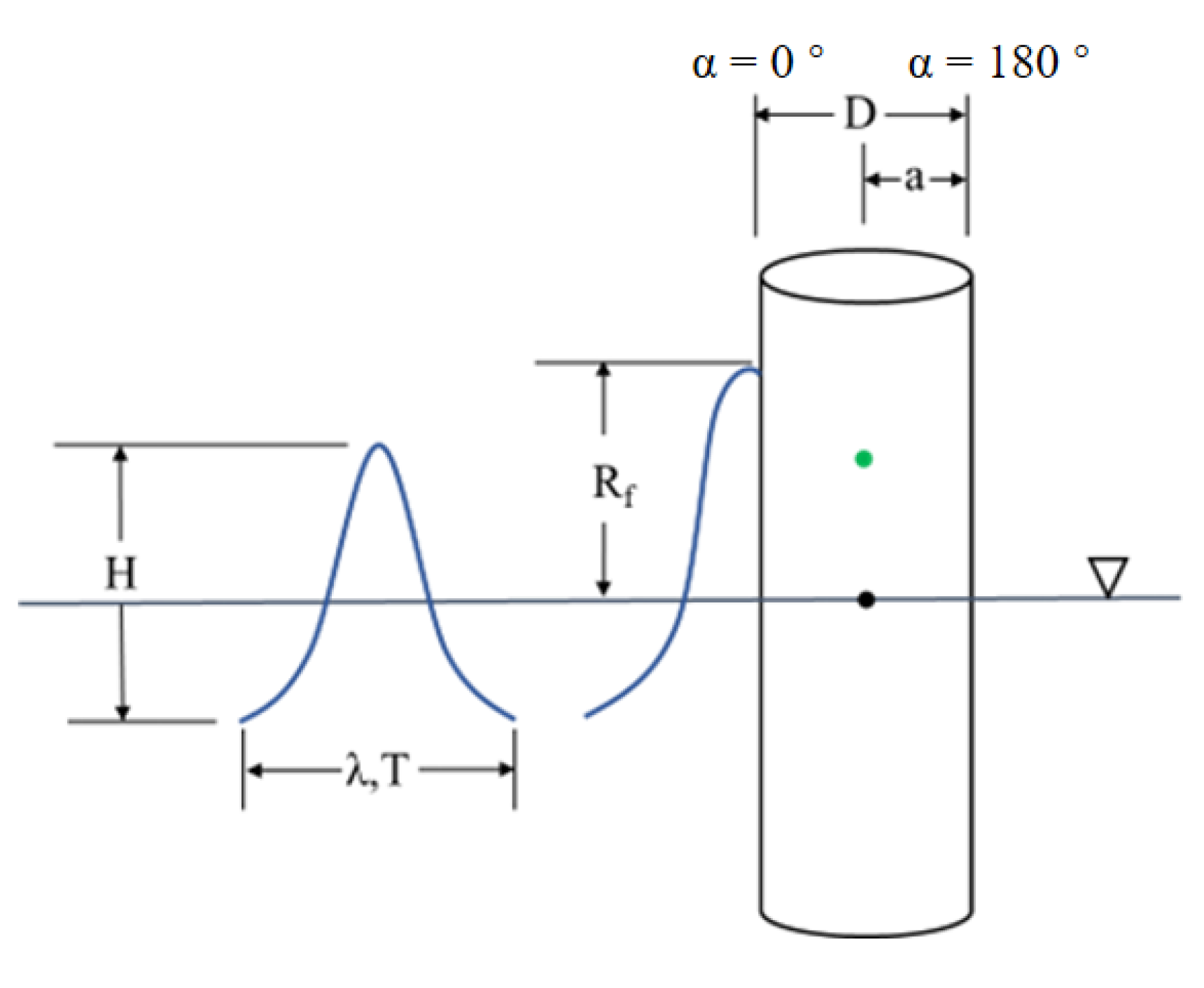
1. Introduction
Wave run-up and wave load of offshore structures are important factors that need to be considered in the design of offshore structures. For example, regarding offshore oil platforms and wind turbines, it is necessary to accurately evaluate the wave run-up amplification height around the structure caused by incident waves, so as to avoid the impact of waves on deck or wind turbine appendages, and thus prevent structural failure. Past works have revealed that amplification of incident waves (regular or irregular) may cause the water body to slap the structure, generating large horizontal forces, uplift forces, and overturning moments [
1,
2,
3]. Especially for the platform supported by the column, the wave run-up effect along the wave facing surface of the column will greatly increase the risk of strong nonlinear slamming or even green water. In order to avoid potential damage, a variety of load conditions should be considered in the design of the structure. For the floating structure, both horizontal and vertical wave forces should be paid attention. For the fixed cylinder, the horizontal wave force is much larger than the vertical wave force, which shows an order of magnitude difference [
4,
5]. Therefore, only the horizontal wave force of the fixed cylinder structure is studied in this paper.
Interaction between waves and simple structures can be solved by analytical or semi-analytical solutions. Based on the linear diffraction theory, McCamy and Fuchs [
6] investigated the wave field around the vertical monopile, but the linear diffraction theory is only highly effective for little wave steepness. Kim and Hue [
7], Kriebel [
8], and Martin et al. [
9] extended the theory of linear diffraction to second order, increasing the accuracy of the model. Model tests and numerical simulations are needed to analyze the interaction between waves and complex structures, such as high order problems. Hallermeier [
10] assumed that the water particle was forced to rise above the wave crest about
along the surface of the cylinder (wherein
is the maximum horizontal velocity of the water quality point at the wave crest, and
is the acceleration of gravity), and the kinetic energy was converted into potential energy. Based on this, a semi-empirical formula for the velocity stagnation head was proposed to estimate the maximum wave run-up height of the cylinder. This formula was then corrected by a series of wave run-up tests for a fixed vertical cylinder [
11]. Bonakdar et al. [
12] used relative water depth, relative wave height, and slenderness ratio as the control parameters of relative wave run-up ratio, integrated multiple sets of experimental data, and used an M5 model tree and nonlinear regressive technique to fit the single pile run-up formula under wide range wave conditions (shallow water, medium water depth, and deep water). Limited by experimental conditions, the numerical model of the wave–structure interaction based on potential flow theory has been widely used in ocean engineering. Through frequency domain and time domain analysis, the time series of wave surface elevation and wave force of wave–structure interaction can be quickly obtained. Liu et al. [
13] used the three-dimensional high order boundary element method to simulate the interaction between second order wave flow and a three-dimensional floating body. Wang and Wu [
14] investigated the second order wave diffraction of wave and cylindrical array by the finite element method in the time domain. Ohl et al. [
15] analyzed the diffraction problem of regular wave and cylindrical array, and compared the experimental, theoretical, and numerical simulation results. Abbasnia and Ghiasi [
16] established the two-dimensional fully nonlinear numerical wave flume based on the NURBS (non-uniform rational B-spline) high-order finite element method to simulate the interaction between regular waves and multiple horizontal fixed cylinders. Bai et al. [
17] investigated the nonlinear properties of the near-trapping phenomenon caused by regular waves interacting with cylindrical arrays using a fully nonlinear time domain model.
An important factor to be considered in the simulation of wave–structure interaction is the viscous effect. Potential flow theory ignores the existence of a fluid viscous effect, but the viscous effect cannot be ignored in some cases. For example, the potential flow solver overpredicts the local free surface height in the near collapse problem of multiple cylinders [
18]. For the potential flow solver, the simulation of the highly nonlinear wave-structure interaction and the large deformation motion of the free surface have always been a great challenge, but the computational fluid dynamics (CFD) solver can well solve the above problems and obtain more accurate predictions. Xiang et al. [
19] investigated the assessment of extreme wave impact on coastal decks with different geometries via the arbitrary Lagrangian–Eulerian method, and the results revealed that the ratio of the wavelength-to-deck width governs the loads on a deck, and the loads do not change after a certain value of this ratio is exceeded. Istrati et al. [
20] presented a simplified methodology for the tsunami design of skewed bridges, and the performance criteria for bridges in tsunami-prone areas via the finite element method. Westphalen et al. [
21] simulated interaction between a regular wave and a fixed horizontal cylinder via particle-based methods, and the numerical results showed good agreement with physical experiments. Hasanpour et al. [
22] investigated the impact of Tsunami-Borne large debris flow on coastal structures via coupled particle-mesh methods (SPH-FEM). In recent years, the CFD software package OpenFOAM has become more and more popular in ocean engineering due to its open source and optional expansion, although the solving may require considerable computational resources [
23]. Lara et al. [
24] used OpenFOAM software and IHFOAM to simulate the interaction of a single pile, multi-pile, and a wave. The wave run-up height and force of the multi-pile and single pile were compared, and the difference in hydrodynamic force of the incident wave and the nonlinear interaction between the wave and structure were pointed out. Sun et al. [
18] investigated the nonlinear interaction between regular waves and a single truncated cylinder by using the second-order frequency domain solver and CFD software OpenFOAM. The free surface elevation around the cylinder and wave force were compared with the experimental data. The accuracy and computational efficiency of the potential flow solver and the CFD solver were evaluated and compared. It is pointed out that the potential flow solver has the problem of inaccurate prediction of wave height at large wave steepness. Mohseni et al. [
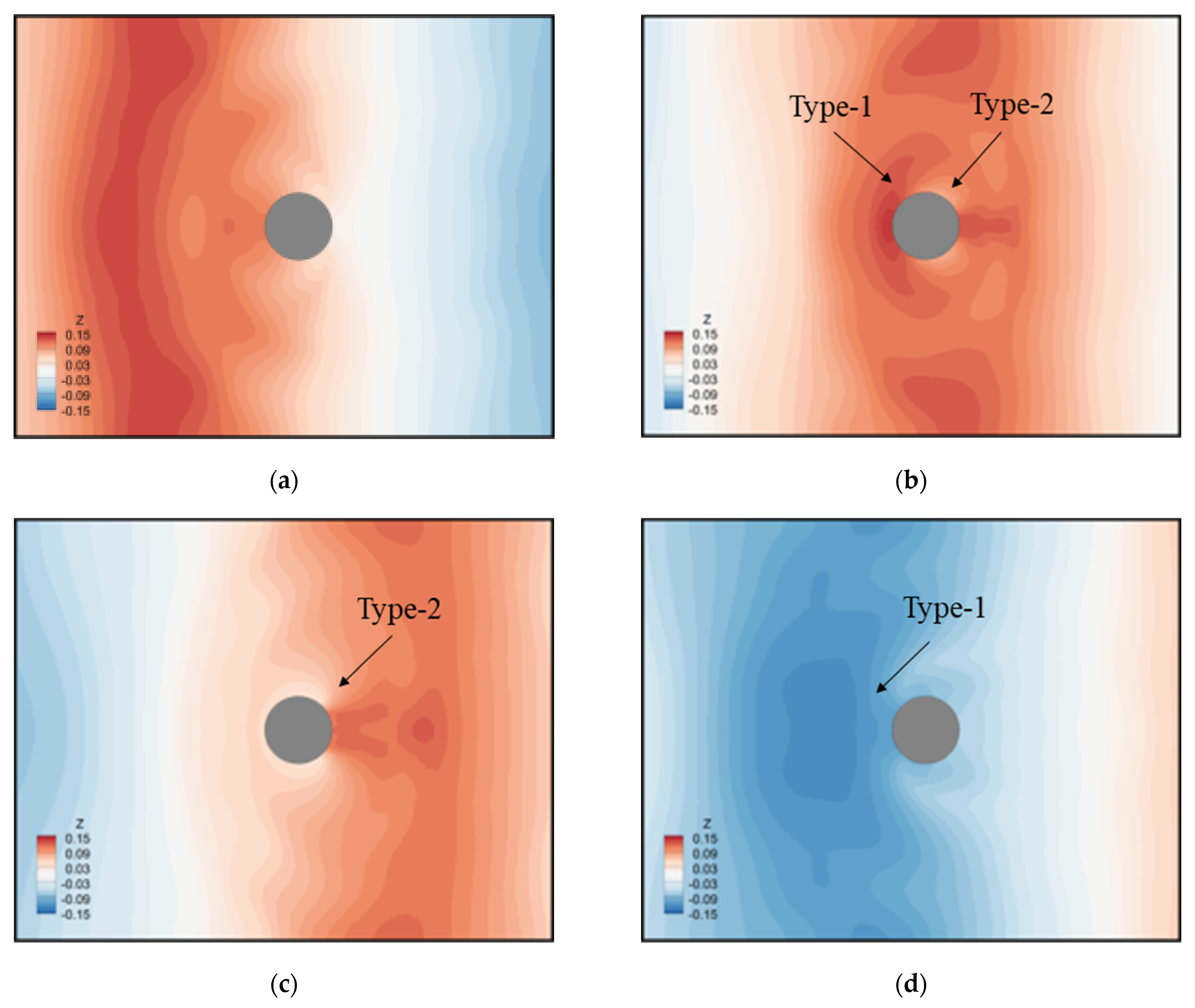
25] established a three-dimensional numerical wave flume based on OpenFOAM, and investigated the importance of Type-1 and Type-2 scattering waves in nonlinear amplification of wave height around a vertical fixed cylinder under different wave steepness and wave fields. Cao and Wan [
26] established the viscous numerical wave flume based on OpenFOAM to simulate the wave run-up of a fixed vertical cylinder under solitary waves.
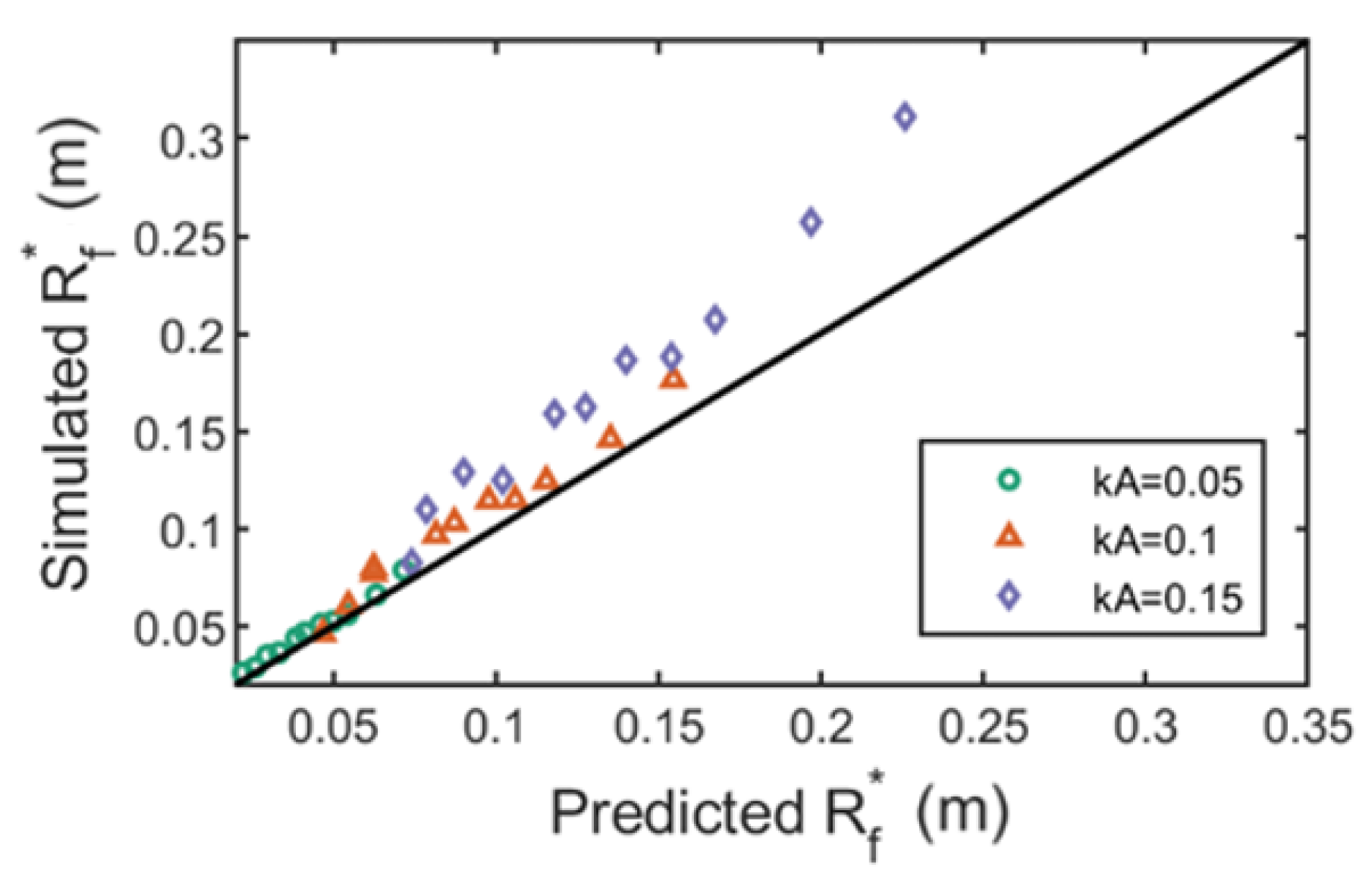
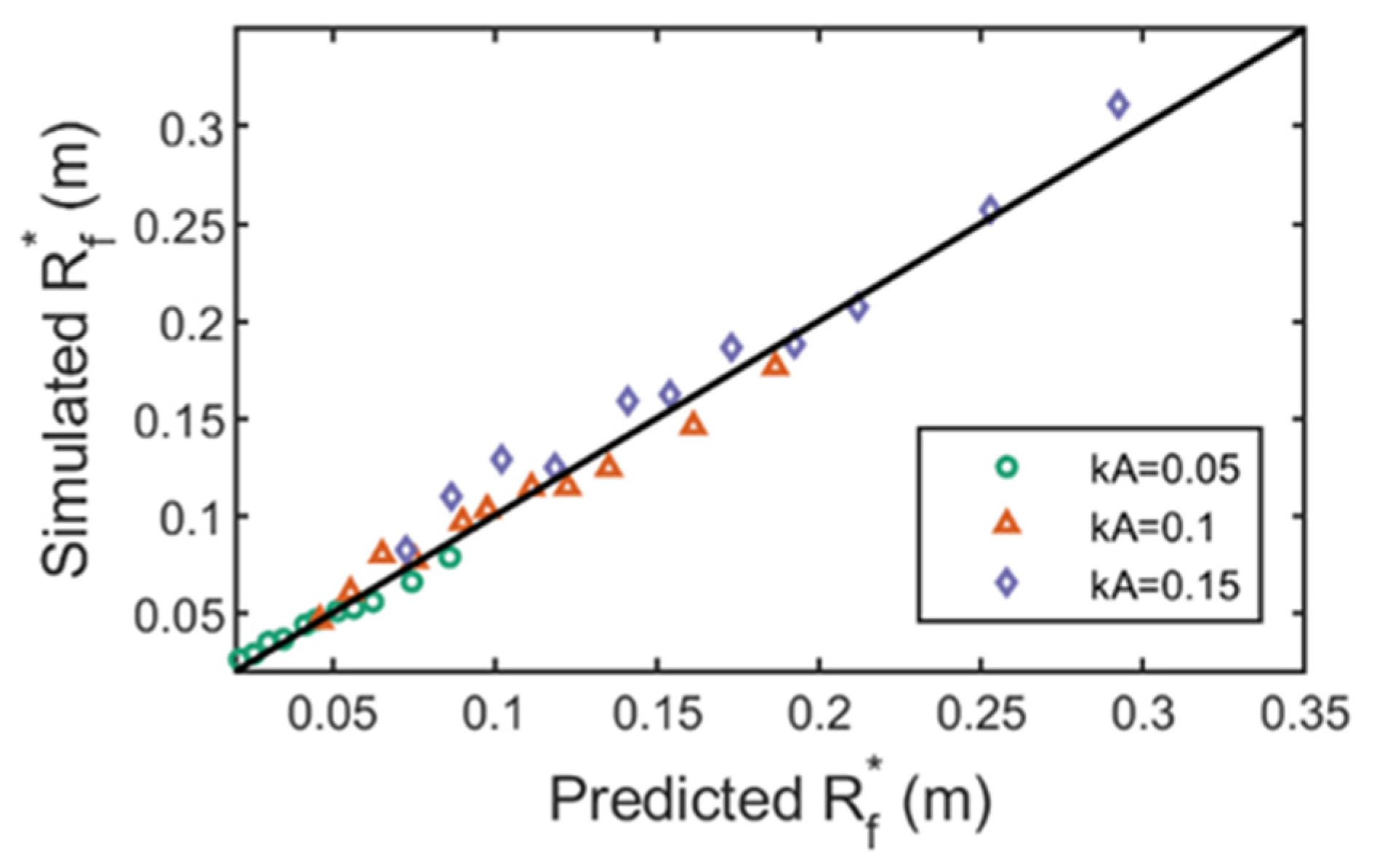
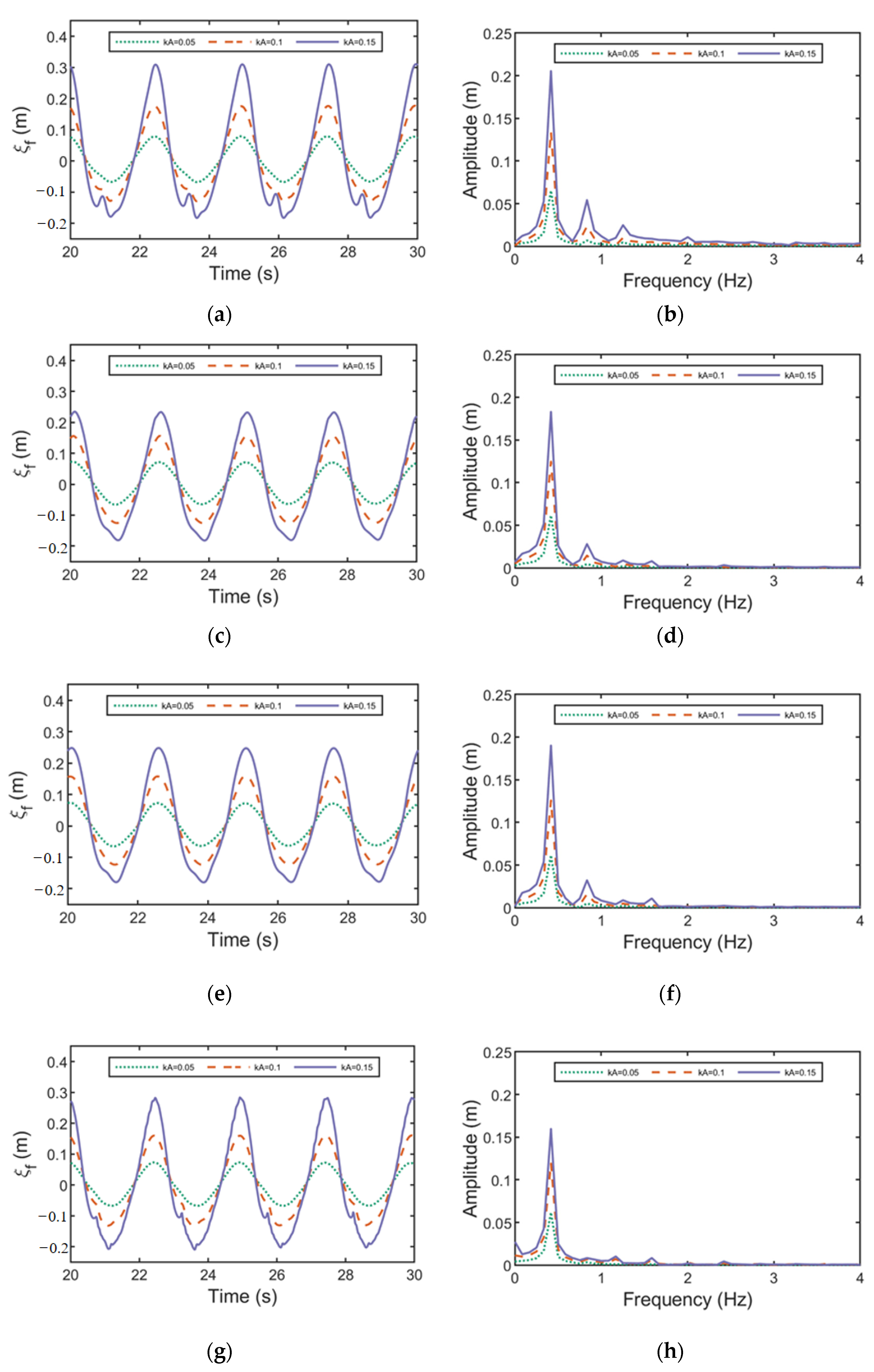
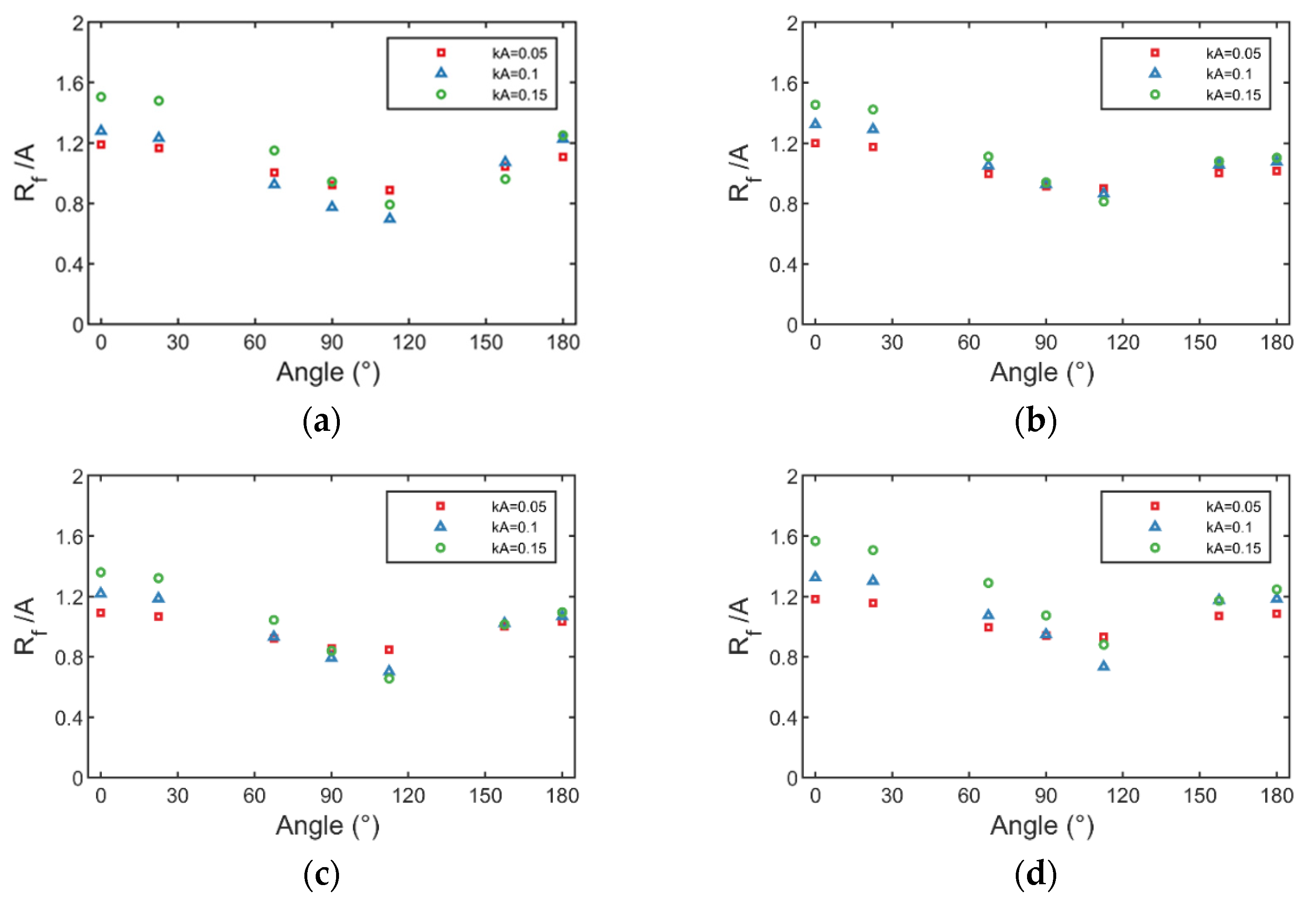
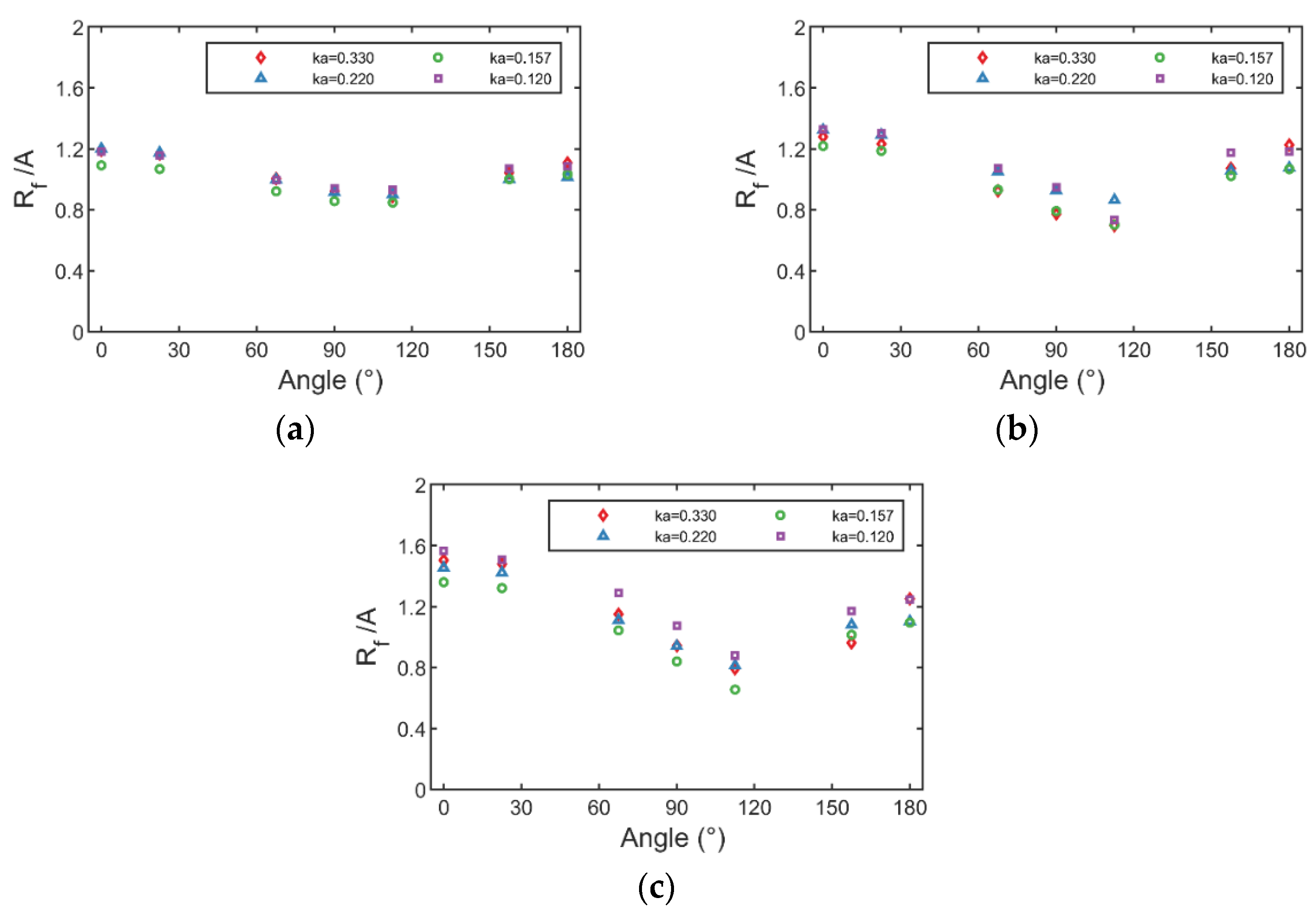
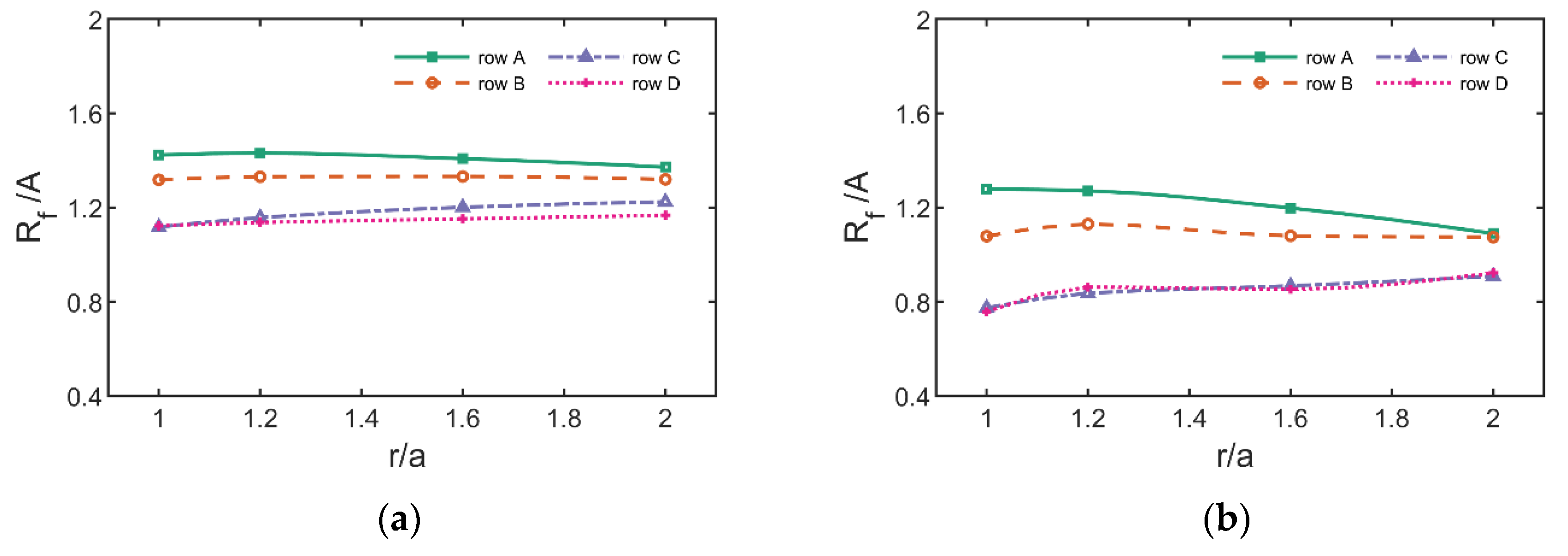
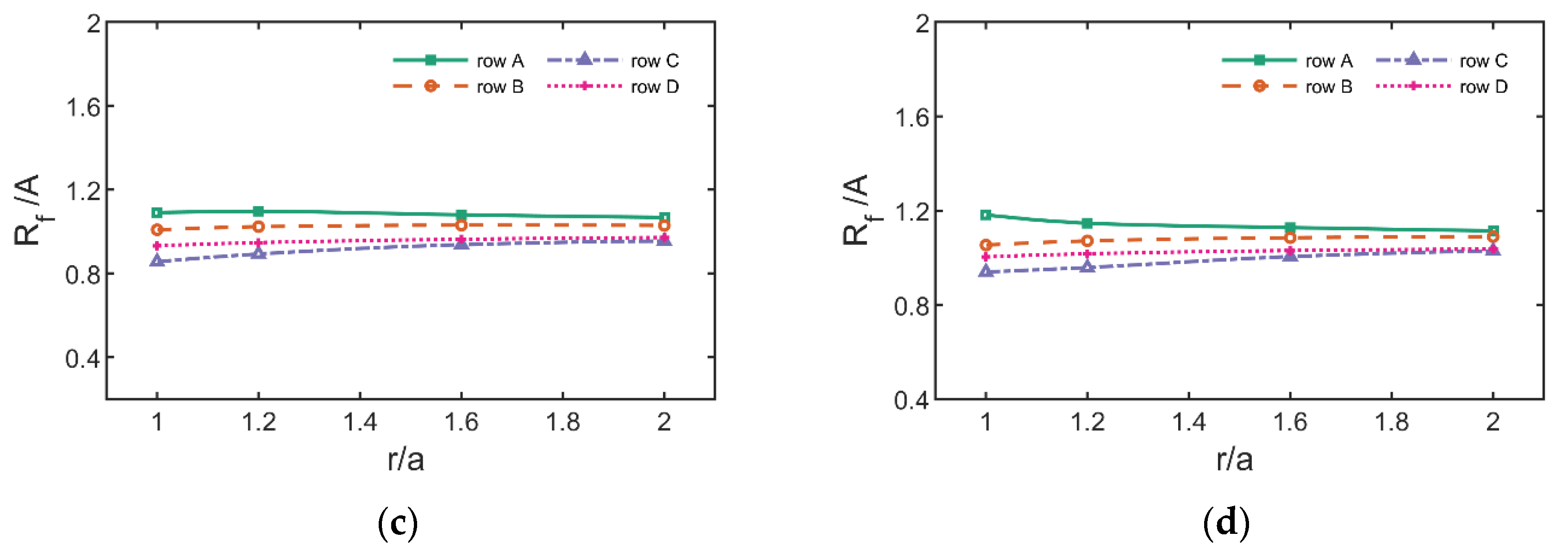
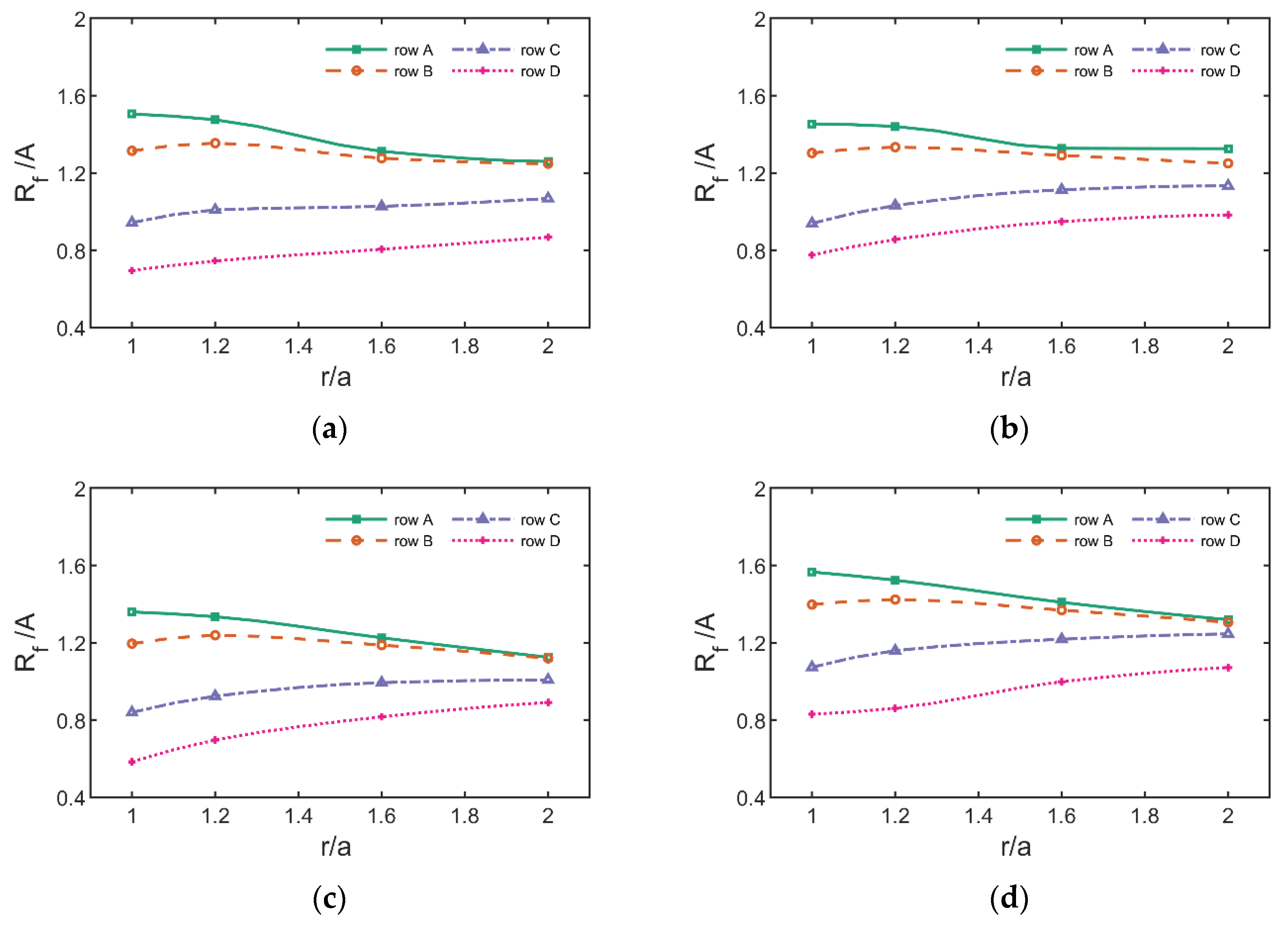
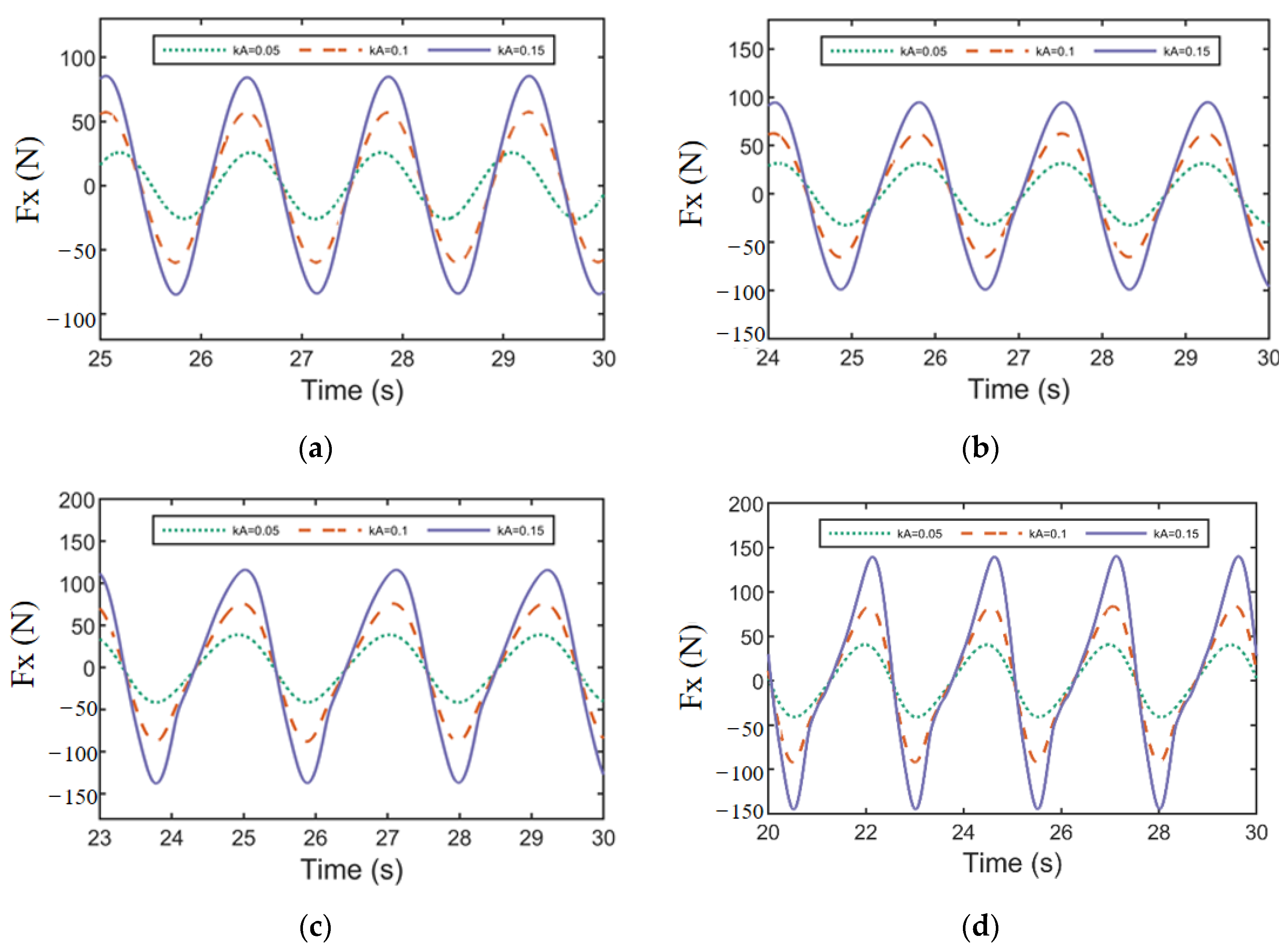
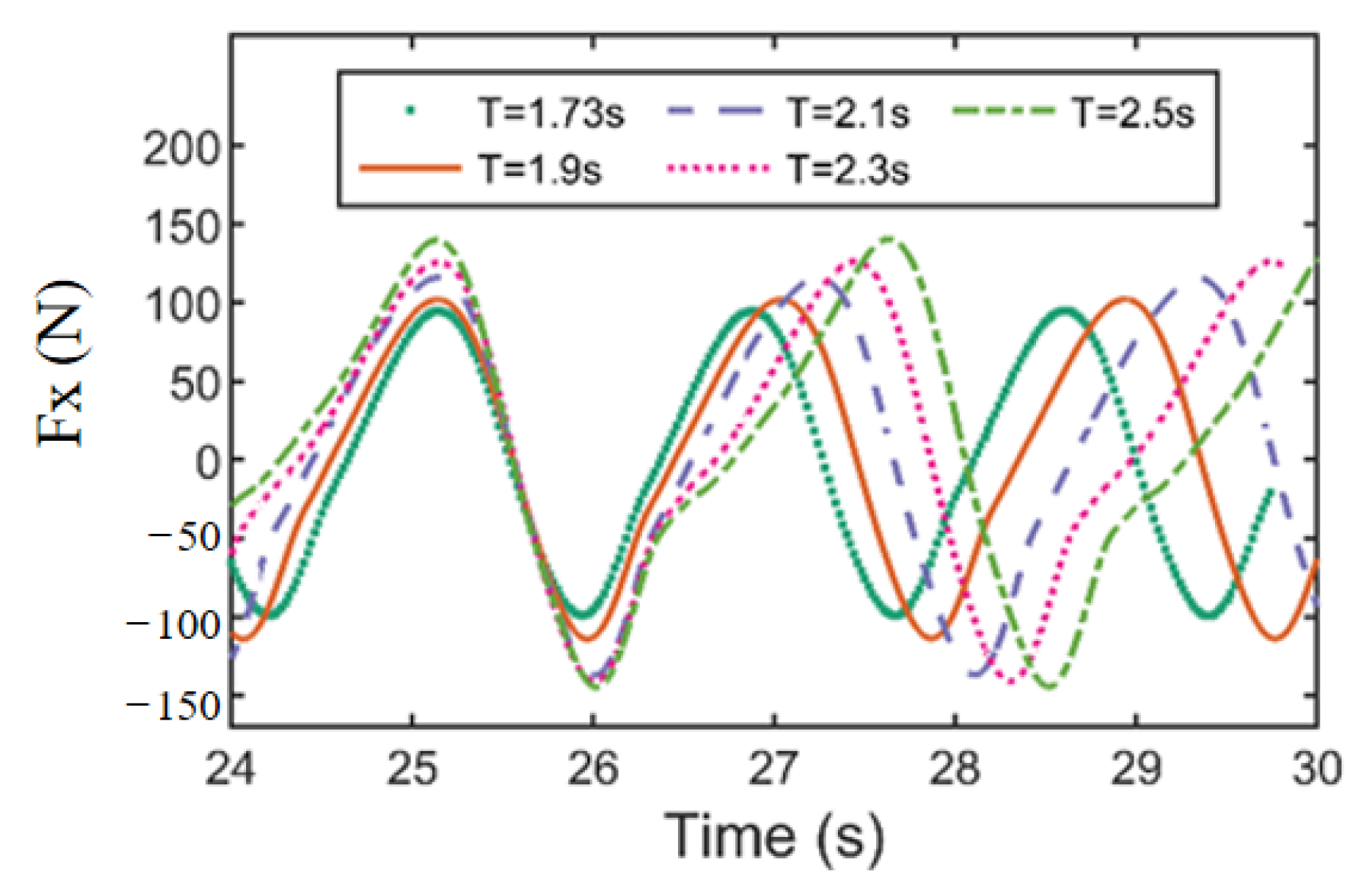
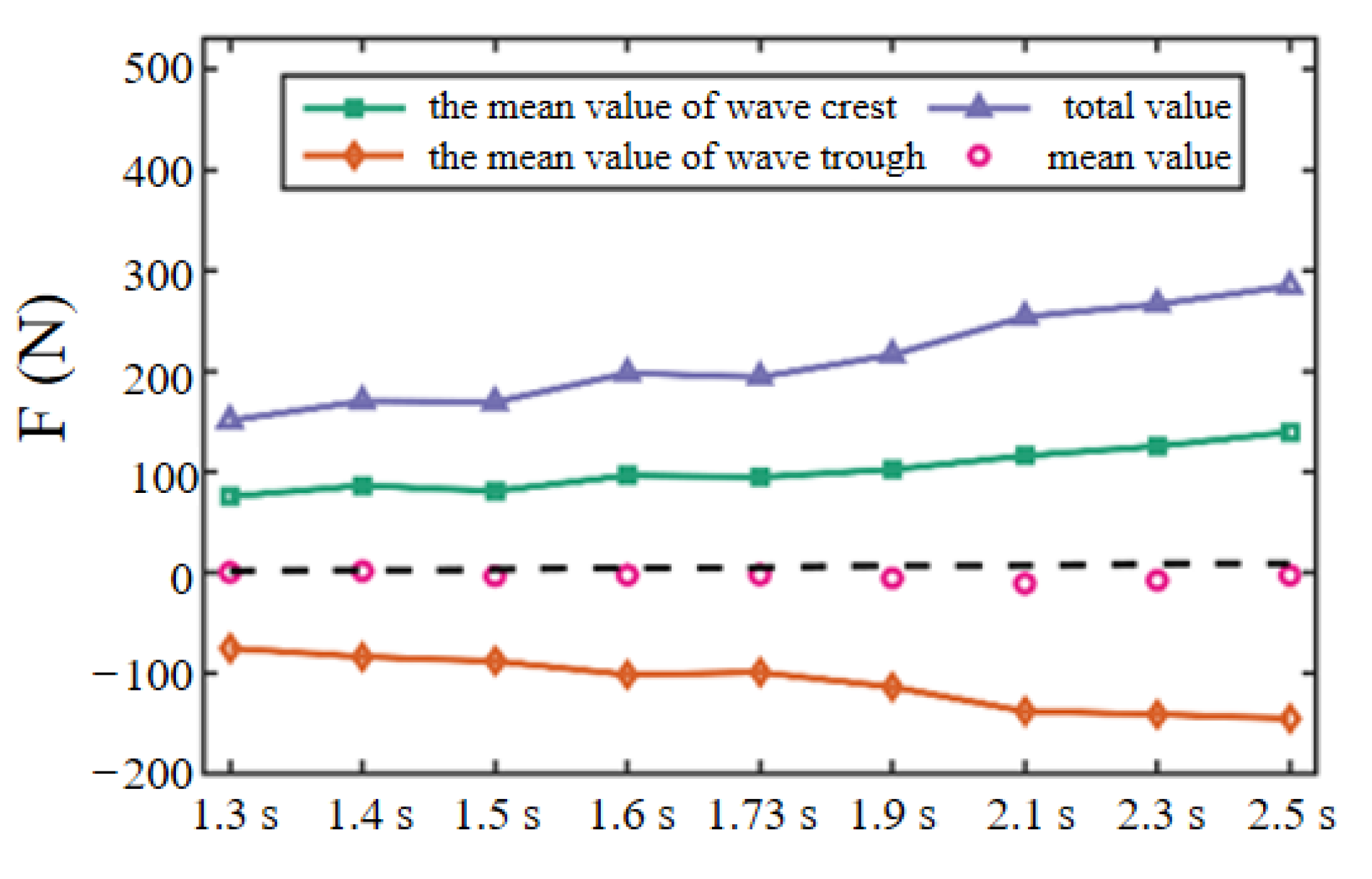
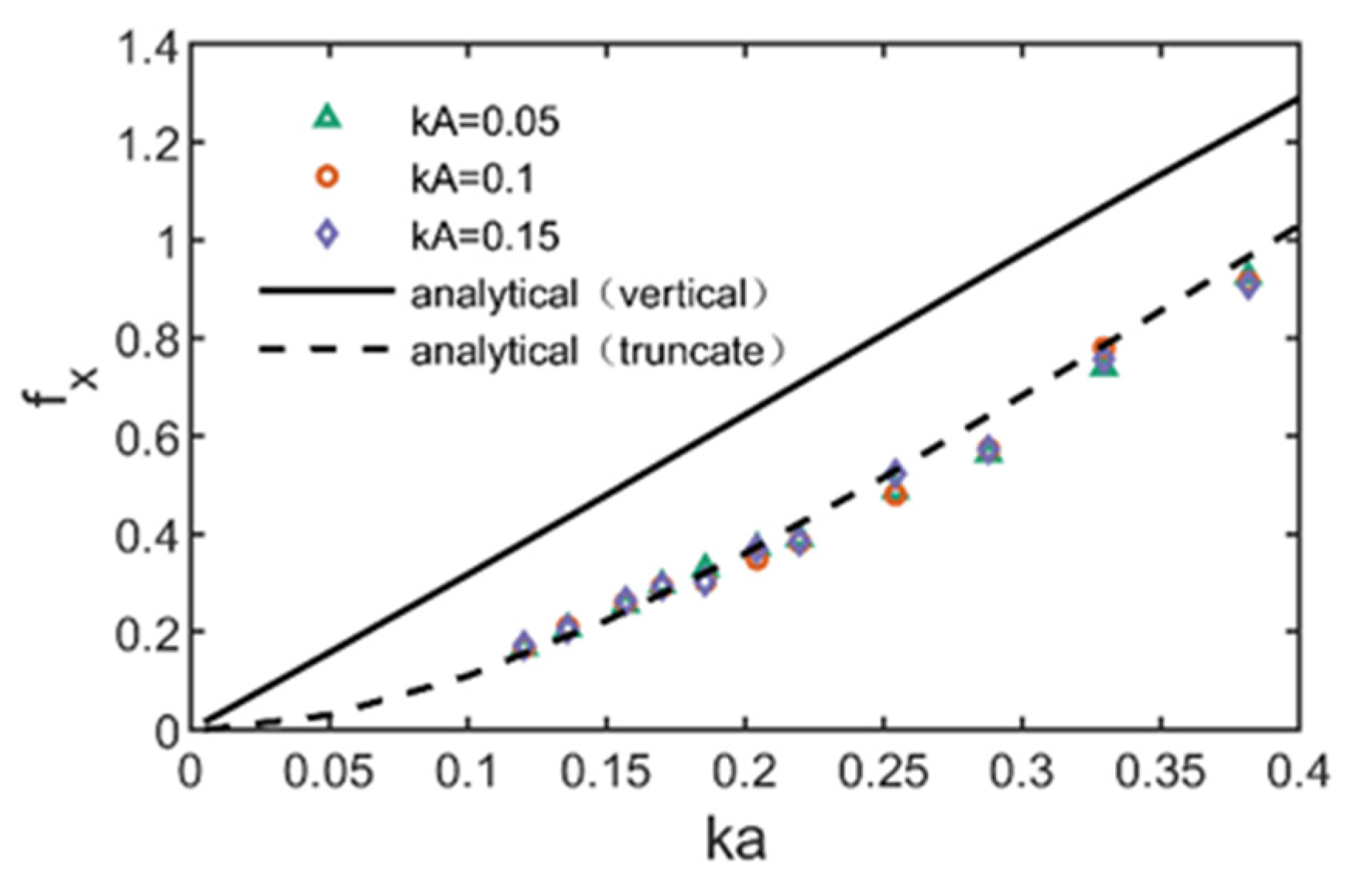
In view of the above research, this paper establishes a refined numerical wave flume based on OpenFOAM to simulate the interaction between regular waves and a fixed truncated cylinder, and investigates the variation of the maximum run-up height of a fixed truncated cylinder under regular waves and its difference with the estimation formula, the distribution of thee wave field around the cylinder, and the variation of horizontal wave force. The organization of this paper is as follows. The literature review is shown in
Section 1. Numerical theory, CFD model establishment, and model validation are presented in
Section 2.
Section 3 presents the analysis and discussion of simulation results. The main conclusions are presented in
Section 4. The future works are presented in
Section 5.