Numerical Investigation of Wave Run-Up and Load on Fixed Truncated Cylinder Subjected to Regular Waves Using OpenFOAM
Abstract
:1. Introduction
2. Numerical Model and Its Validation
2.1. Governing Equation
2.2. Model Validation
2.2.1. Mesh Convergence Validation
2.2.2. Validation of the Established Model
2.3. Model Setup
3. Results Analysis
3.1. Analysis of Maximum Wave Run-Up Height
3.1.1. Maximum Run-Up Height Change
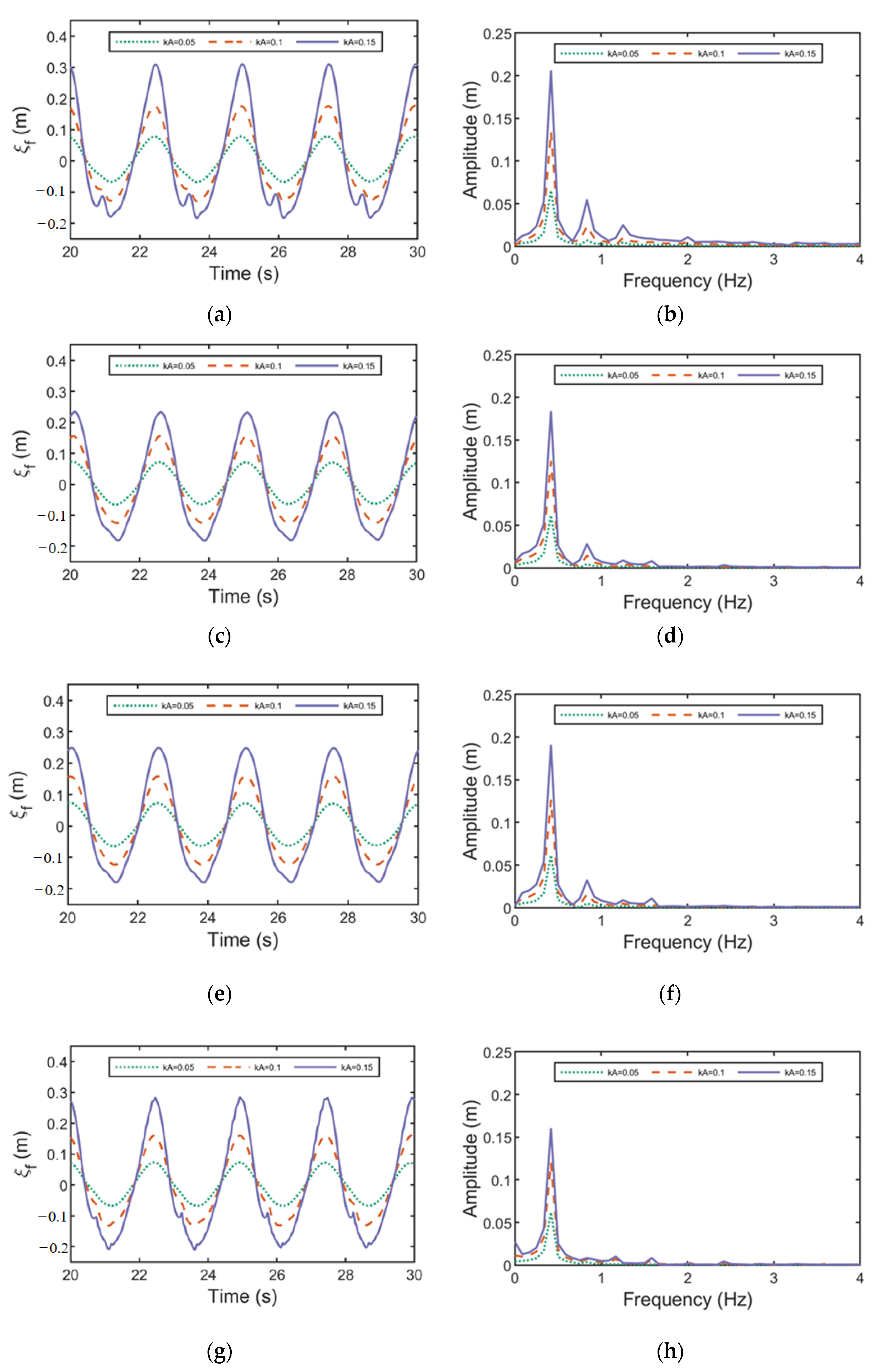
3.1.2. Wave Surface Time Series Curve and Fourier Analysis
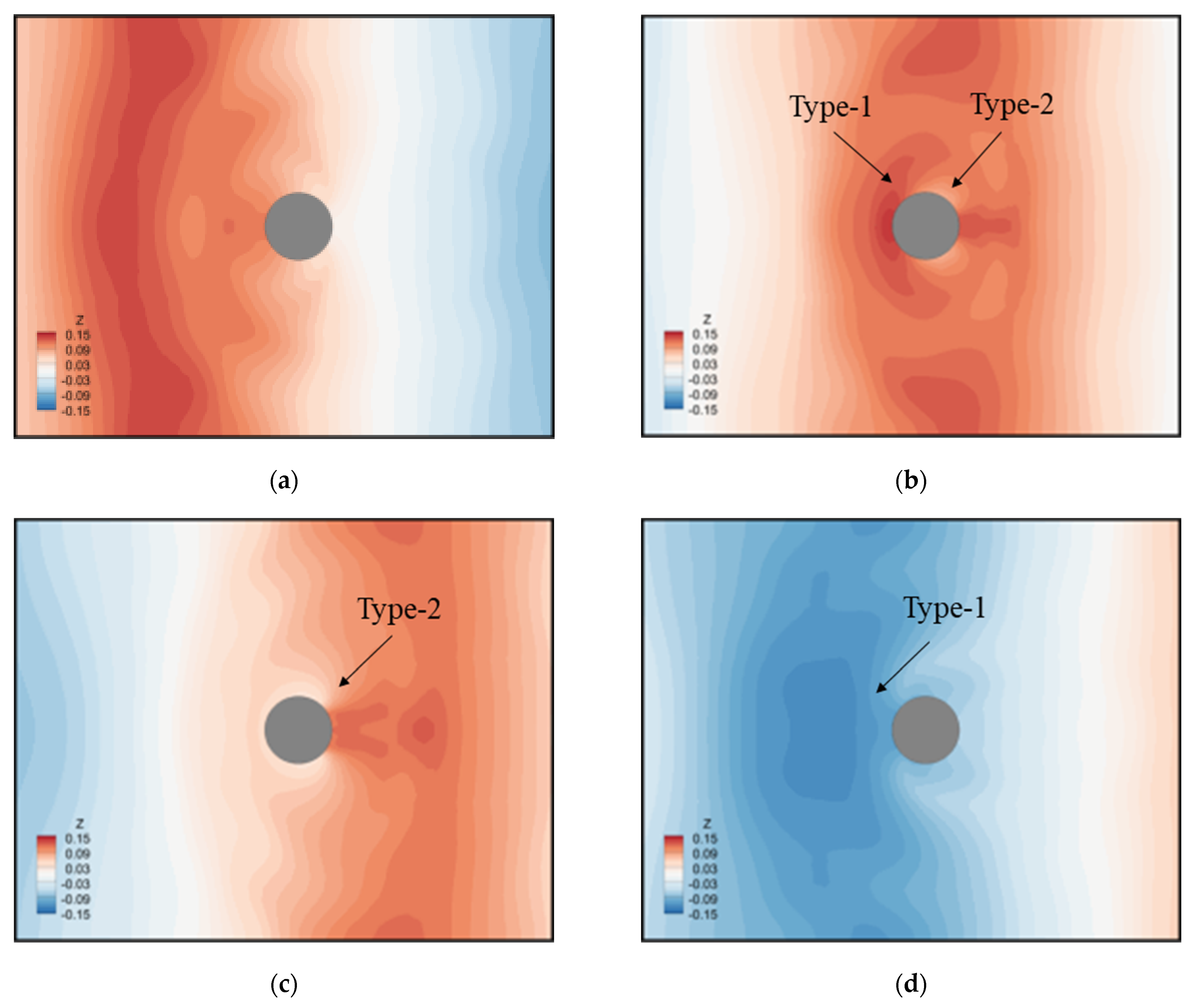
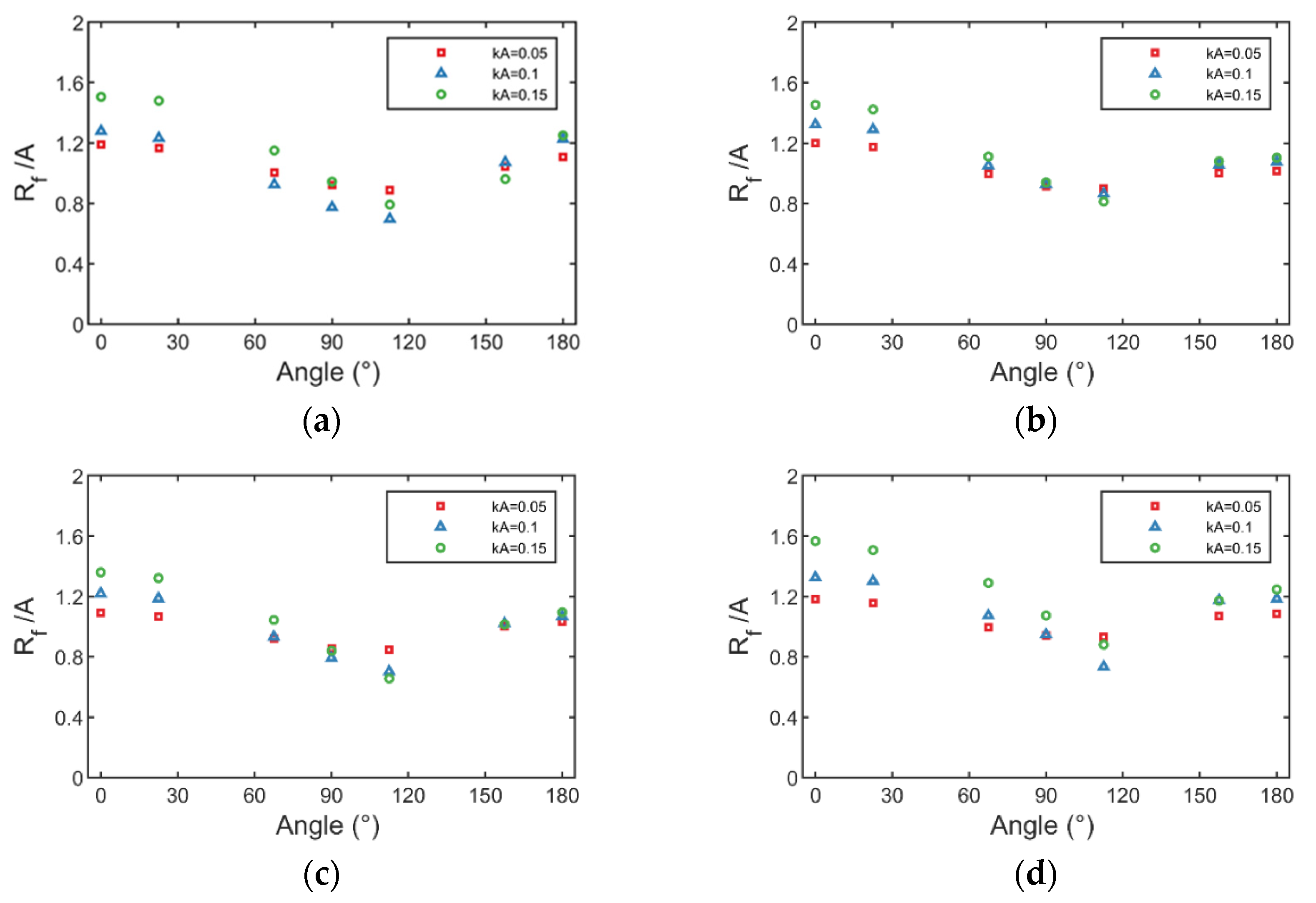
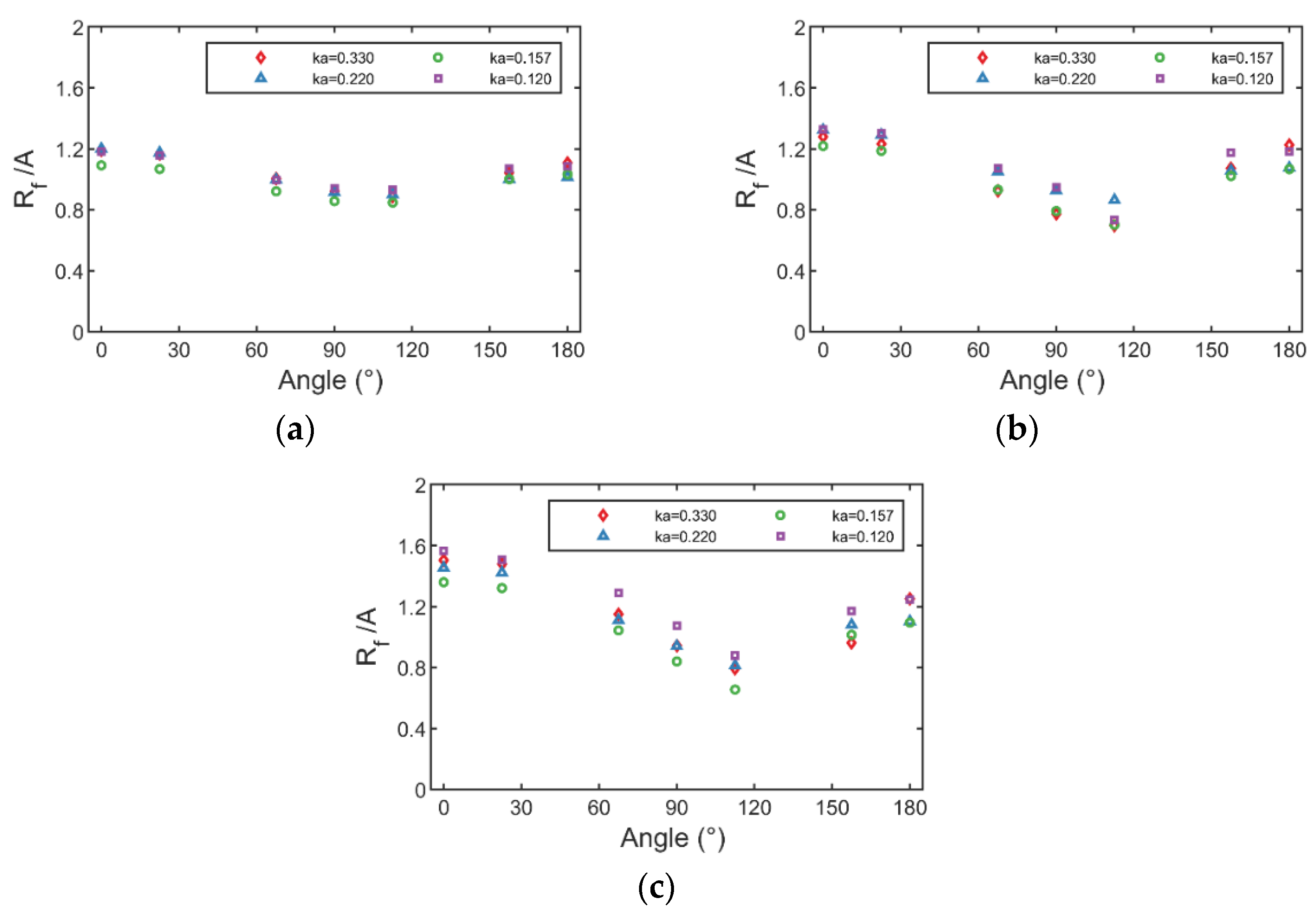
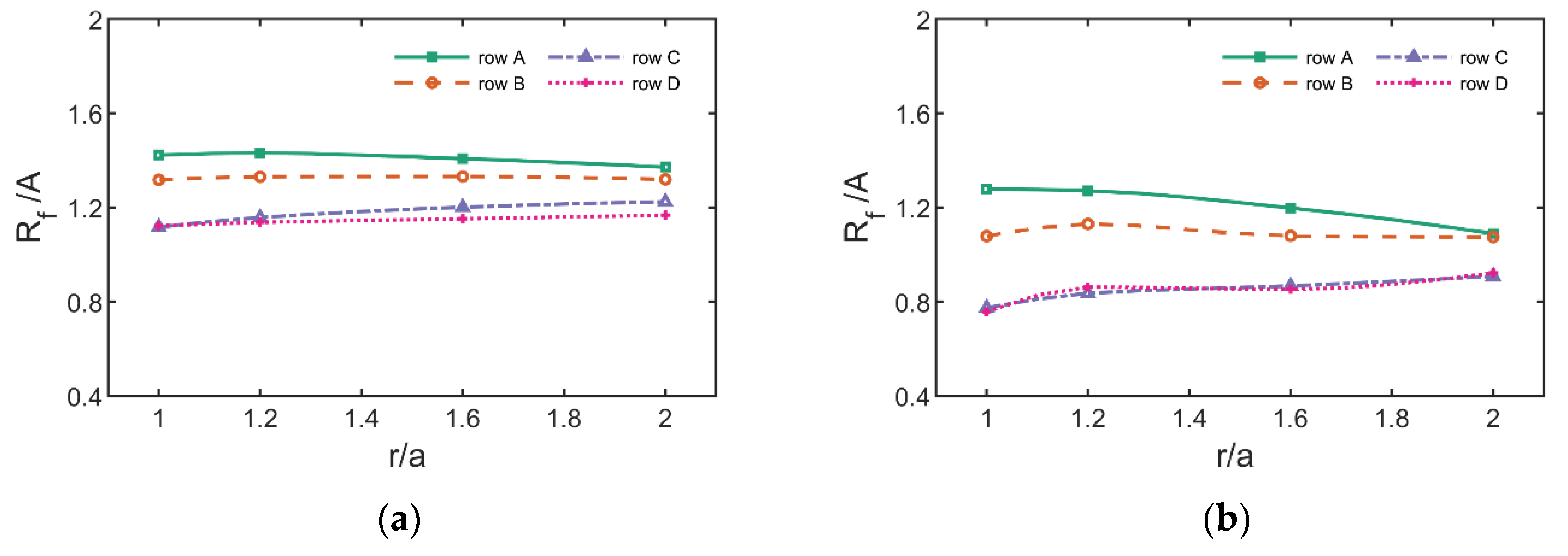
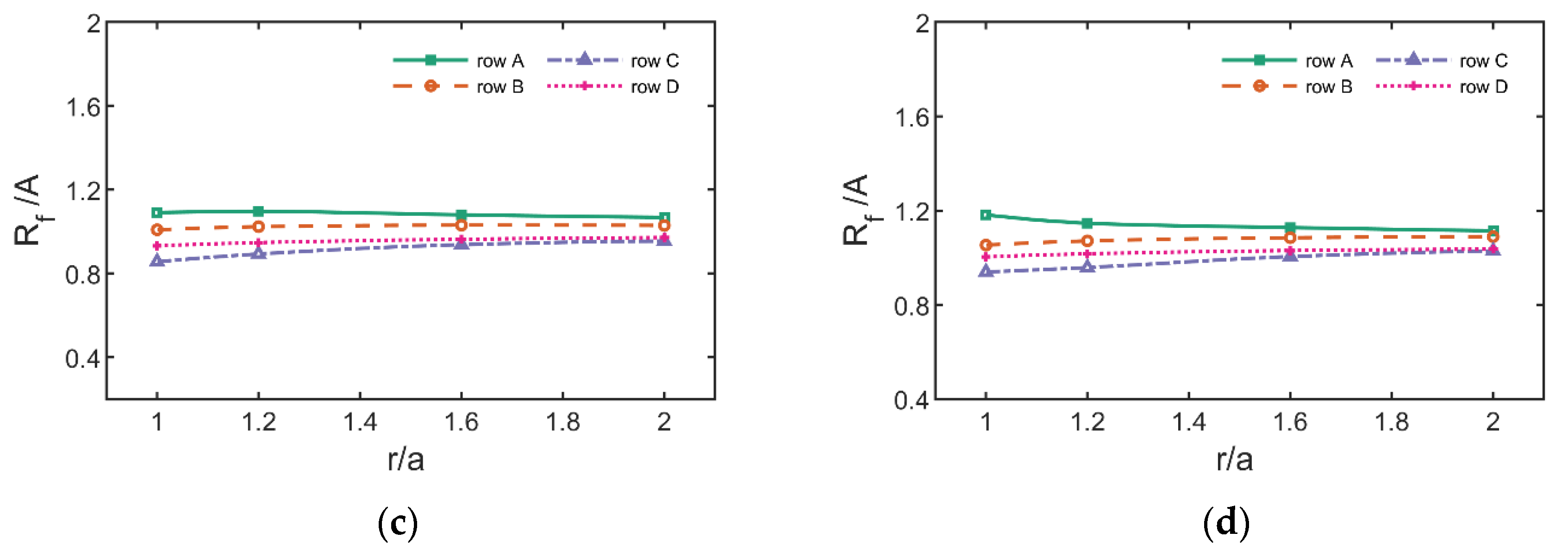
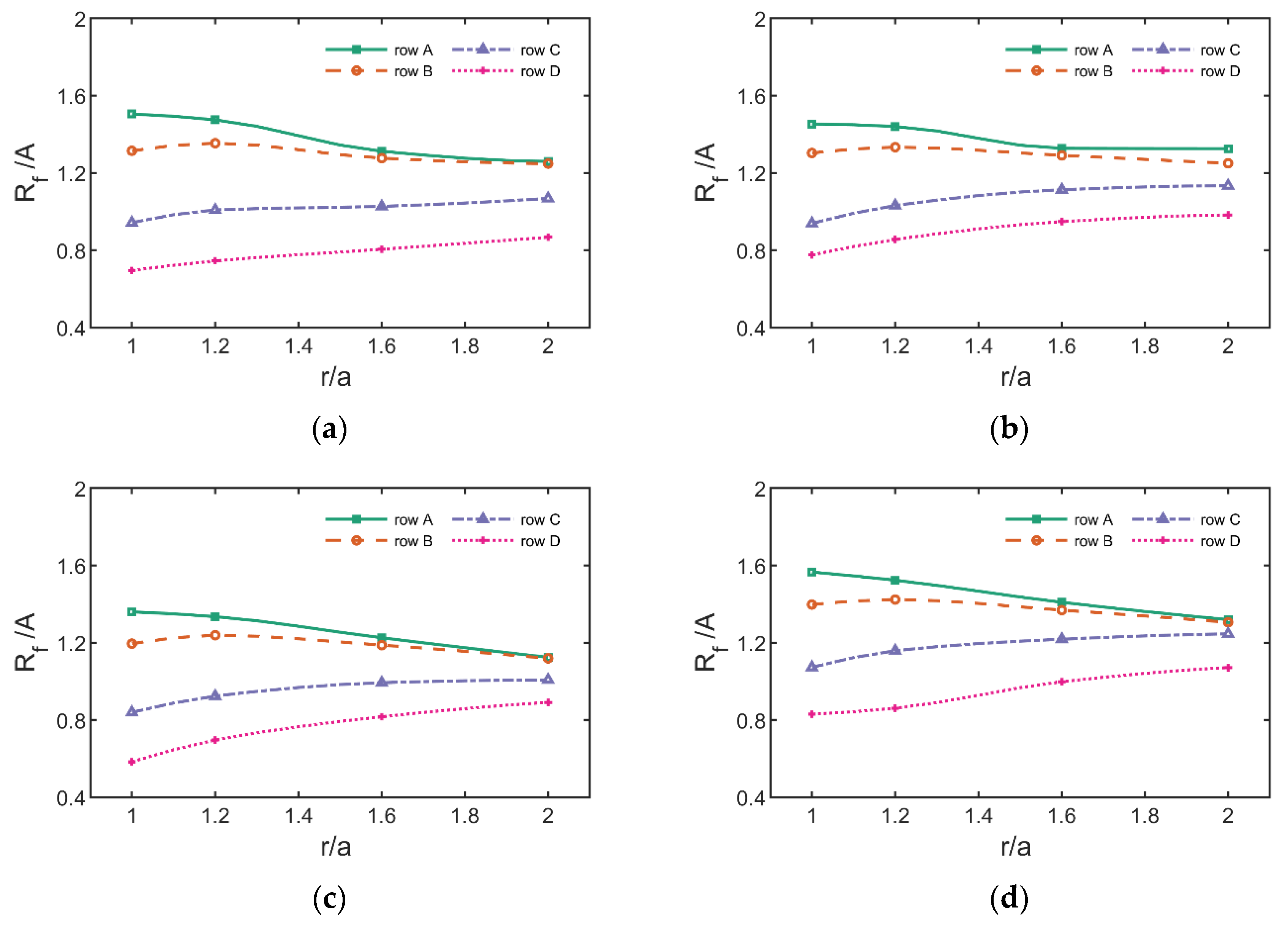
3.2. Spatial Distribution of Wave Run-Up
3.2.1. Circumferential Run-Up Height Distribution
3.2.2. Radial Run-Up Height Distribution
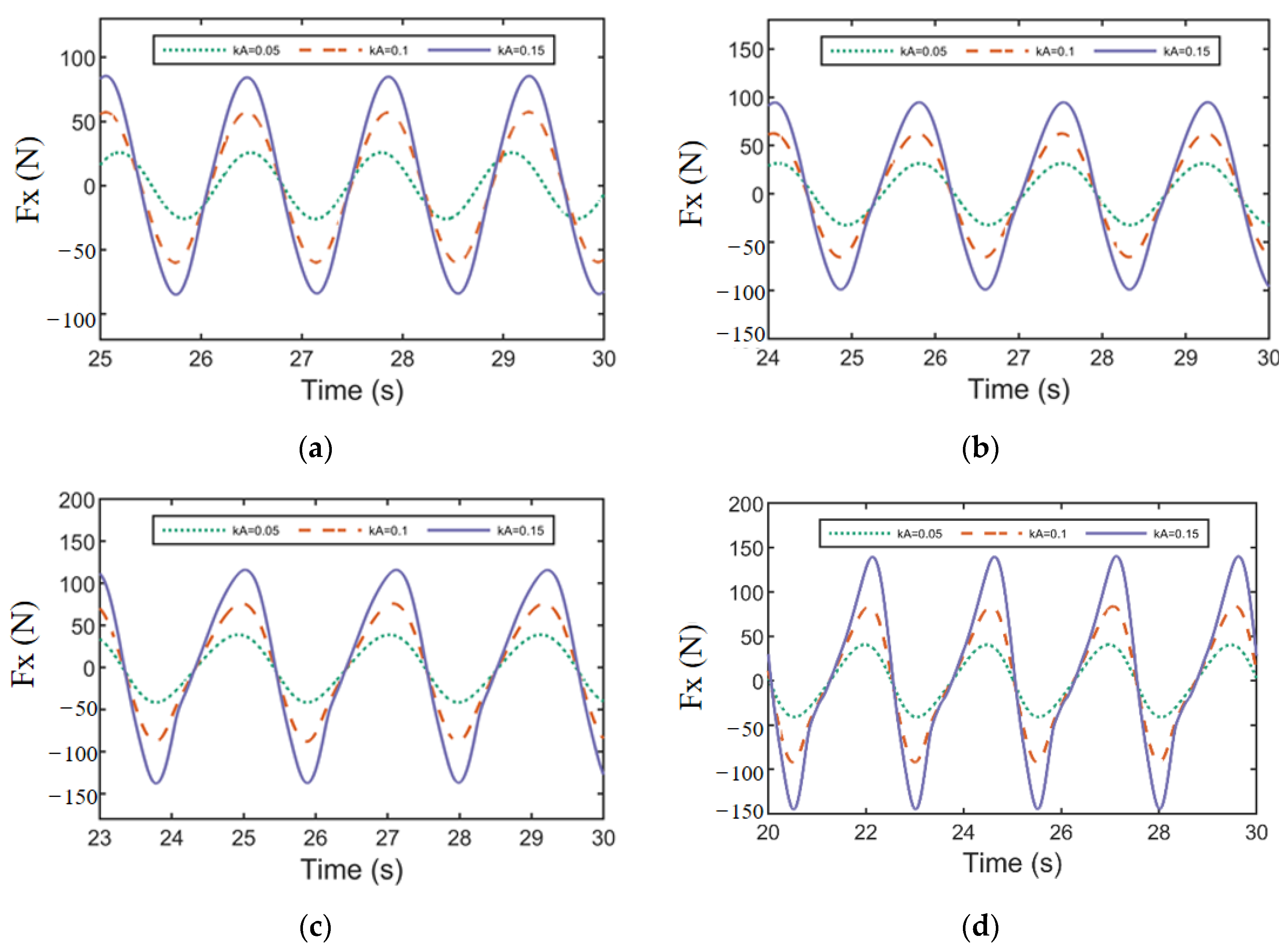
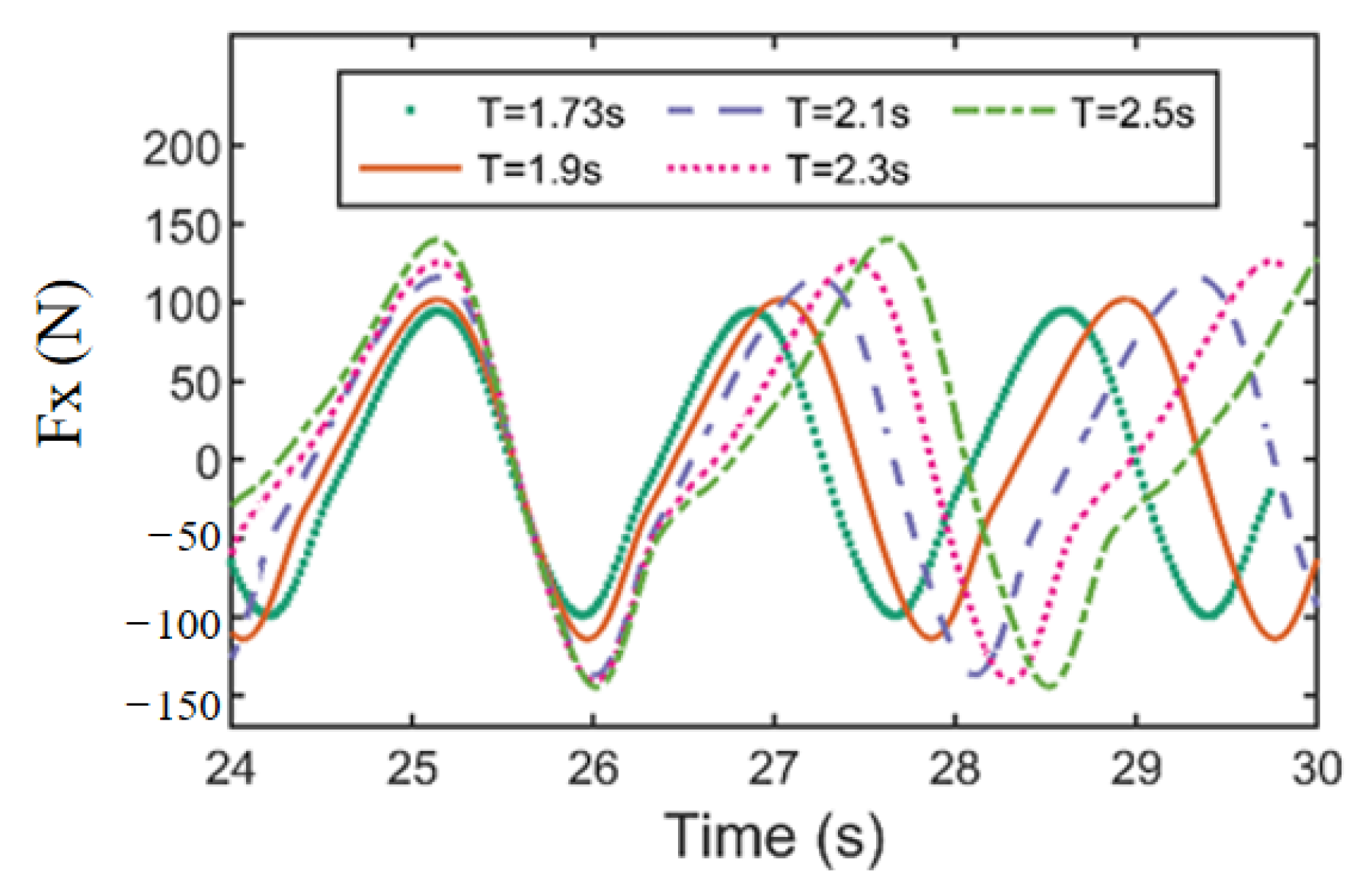
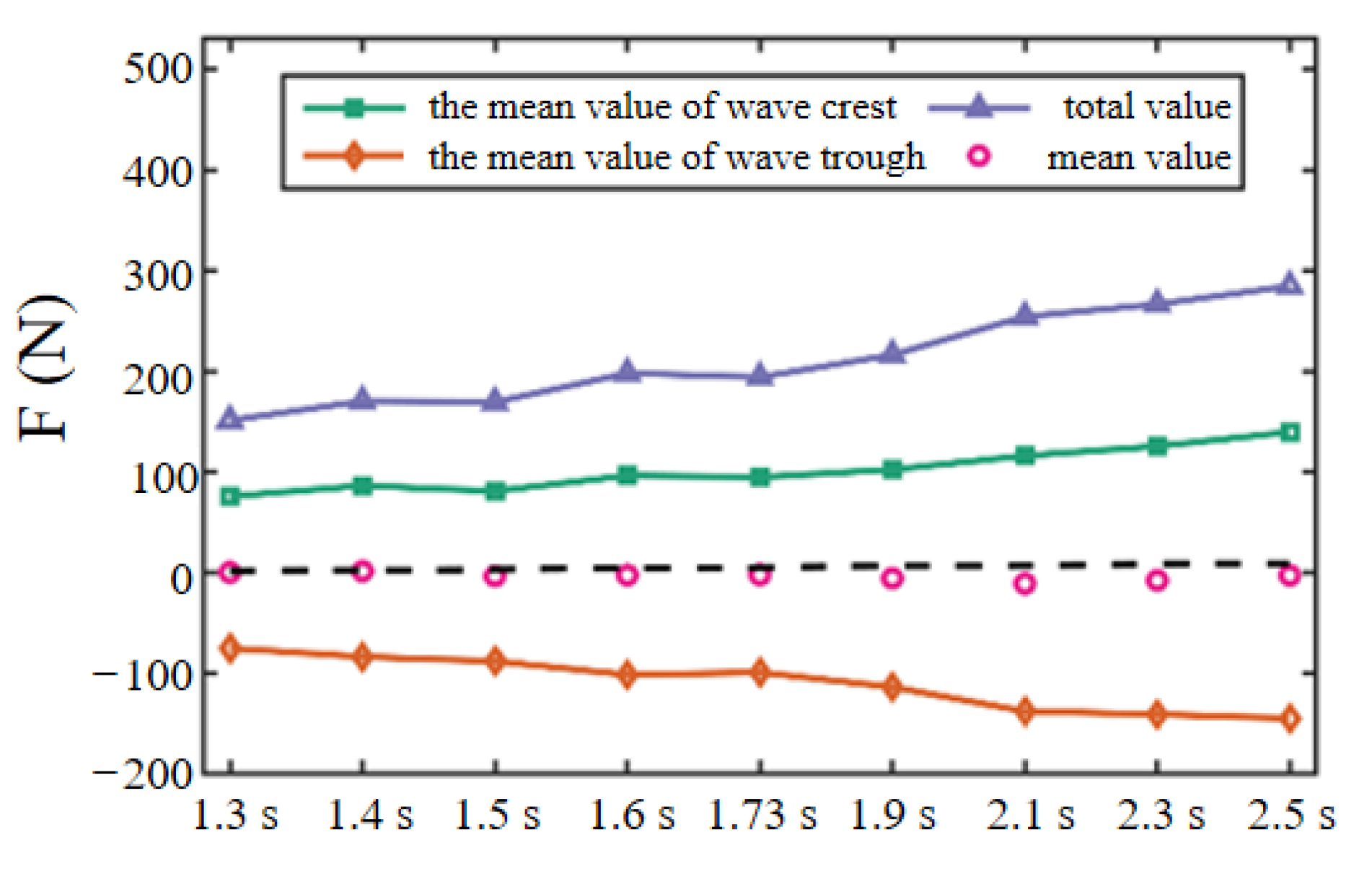
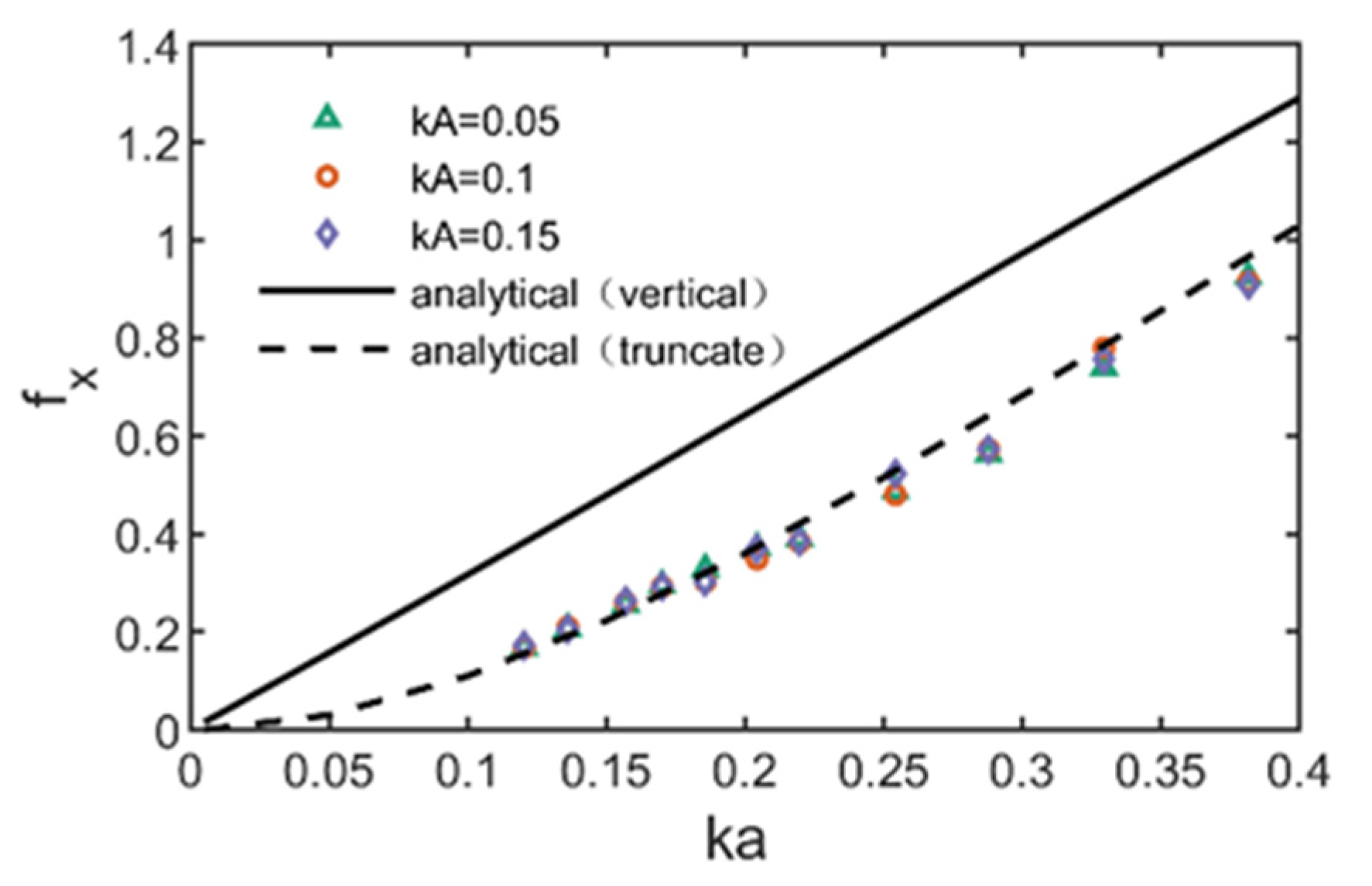
3.3. The Variation of Horizontal Wave Force with Scattering Parameters
4. Conclusions
- (1)
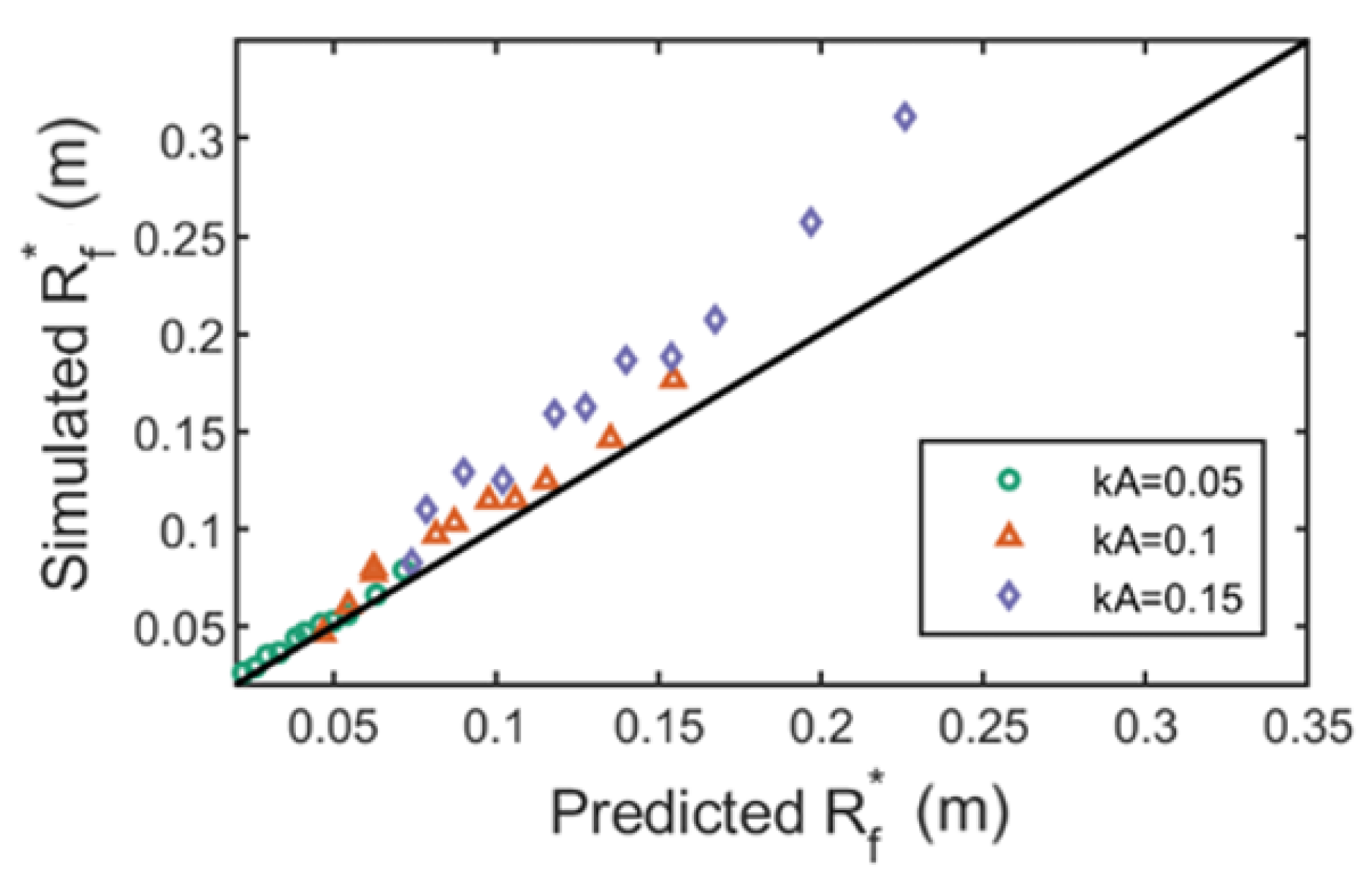
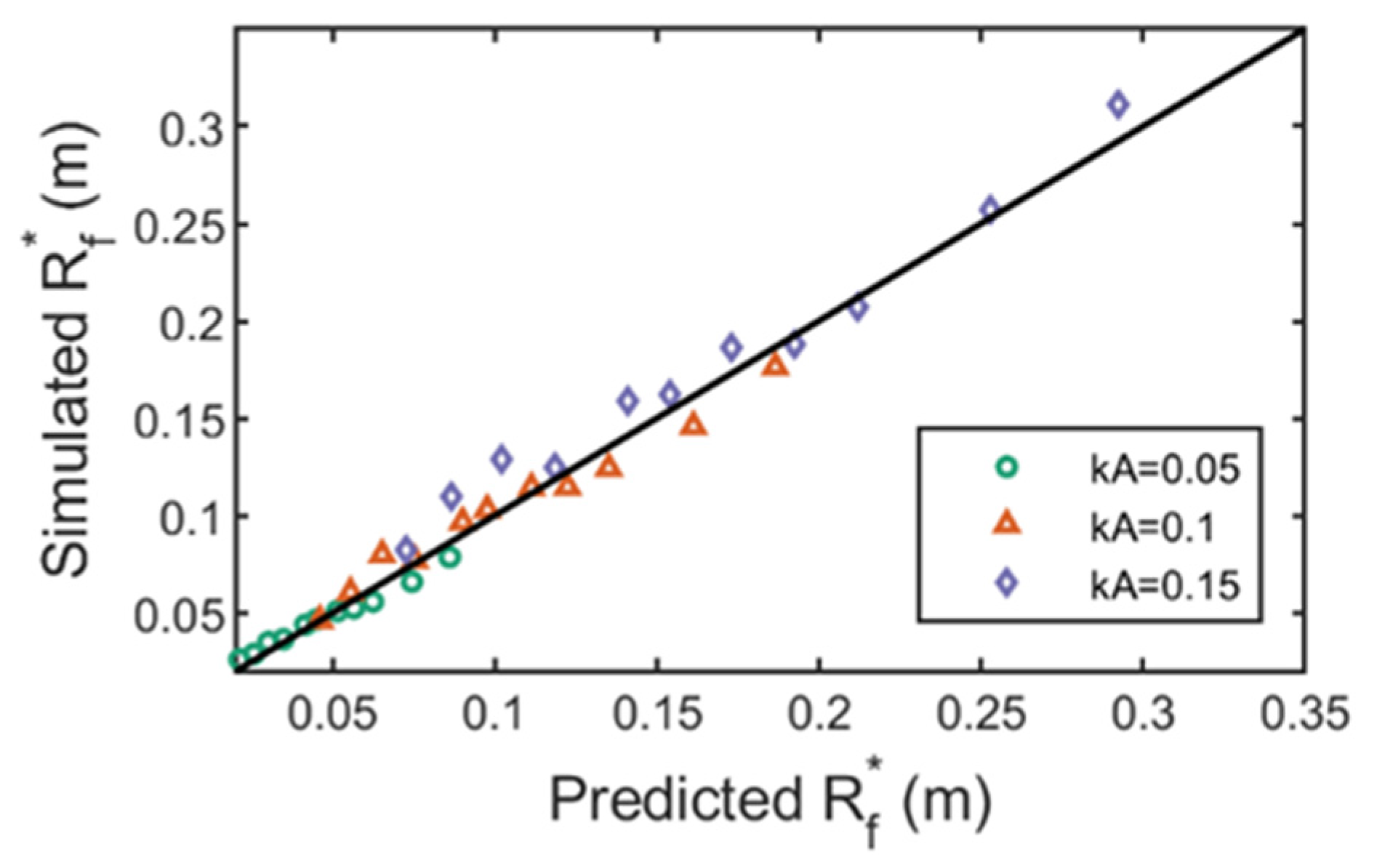
- The fixed cylinder draft has little effect on the maximum wave run-up height, but has a significant effect on the horizontal wave force. The maximum wave run-up height of a fixed truncated cylinder can be predicted theoretically by a fixed vertical cylinder run-up height estimation formula. The estimation formula proposed by Vos et al. [11] has good prediction at low wave steepness, but it will be underestimated with the increase of wave steepness, while the estimation formula proposed by Bonakdar et al. [12] can predict the wave run-up height well.
- (2)
- At the same wave steepness, the radial dimensionless run-up height increases with the increase of scattering parameters. The radial run-up height distribution gradually decreases in the upstream along the radial direction of the cylinder, and increases in the downstream, indicating that before the wave propagates to the cylinder, there is a large wave surface uplift in the upstream due to the scattering of the cylinder. At the same time, the increase of wave steepness will also lead to the increase of run-up height in the upstream region of the cylinder, and the decrease of run-up height in the corresponding downstream region.
- (3)
- Under the same wave number, the average amplitude of horizontal wave force increases linearly with the increase of incident wave radiation. Under the wave parameters and structural parameters simulated in this paper, the dimensionless horizontal wave force increases nonlinearly with the increase of scattering parameters, and the wave steepness parameter is not the significant influence parameter. When the scattering parameter is small, the theoretical value is consistent with the simulation results. With the increase of scattering parameters, the linear diffraction theory will overestimate the horizontal wave force.
5. Future Work
- (1)
- The effects of larger wave steepness on the wave run-up and wave load could be considered.
- (2)
- The wave conditions in practical engineering applications are irregular, such as solitary waves, extreme waves, etc., and wave breaking occurs when waves interact with structures. When the extreme waves break, water and air will react violently, and there will be an obvious turbulence effect, which will have a strong impact on structures, and are different from the effects caused by unbroken waves [34]. Therefore, the effects of extreme waves on the wave run-up and wave load could be considered.
- (3)
- There are many factors that affect the wave run-up, such as the scattering parameters, the wave steepness, the wavelength to diameter ratio, the water depth, etc. This paper mainly focuses on the effects of scattering parameters and wave steepness on the wave run-up and wave load; the effects of other parameters could be studied in further investigations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Allsop, W.; Cuomo, G.; Tirindelli, M. New prediction method for wave-in-deck loads on exposed piers/jetties/bridges. In Proceedings of the 30th International Conference, San Diego, CA, USA, 3–8 September 2006. [Google Scholar] [CrossRef]
- Xiang, T.; Istrati, D.; Yim, S.C.; Buckle, I.G.; Lomonaco, P. Tsunami Loads on a Representative Coastal Bridge Deck: Experimental Study and Validation of Design Equations. J. Waterw. Port Coastal Ocean Eng. 2020, 146, 04020022. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I.; Lomonaco, P.; Yim, S. Deciphering the Tsunami Wave Impact and Associated Connection Forces in Open-Girder Coastal Bridges. J. Mar. Sci. Eng. 2018, 6, 148. [Google Scholar] [CrossRef]
- Zhao, H.; Teng, B.; Li, G.; Lin, Y. An experimental study of first—harmonic wave force on vertical truncated cylinder. China Offshore Platf. 2003, 18, 12–17. [Google Scholar]
- Boo, S. Measurements of higher harmonic wave forces on a vertical truncated circular cylinder. Ocean Eng. 2006, 33, 219–233. [Google Scholar] [CrossRef]
- MacCamy, R.; Fuchs, R. Wave Forces on Piles: A Diffraction Theory; US Beach Erosion Board: New York, NY, USA, 1954. [Google Scholar]
- Kim, M.-H.; Yue, D.K.P. The complete second-order diffraction solution for an axisymmetric body Part 1. Monochromatic incident waves. J. Fluid Mech. 1989, 200, 235–264. [Google Scholar] [CrossRef]
- Kriebel, D. Nonlinear wave interaction with a vertical circular cylinder. Part I: Diffraction theory. J. Waterw. Port Coast. Ocean. Eng. 1990, 17, 345–377. [Google Scholar] [CrossRef]
- Martin, A.; Easson, W.; Bruce, T. Runup on columns in steep, deep water regular waves. J. Waterw. Port Coast. Ocean. Eng. 2001, 127, 26–32. [Google Scholar] [CrossRef]
- Hallermeier, R.J. Nonlinear Flow of Wave Crests Past a Thin Pile. J. Waterw. Harb. Coast. Eng. Div. 1976, 102, 365–377. [Google Scholar] [CrossRef]
- De Vos, L.; Frigaard, P.; De Rouck, J. Wave run-up on cylindrical and cone shaped foundations for offshore wind turbines. Coast. Eng. 2007, 54, 17–29. [Google Scholar] [CrossRef]
- Bonakdar, L.; Oumeraci, H.; Etemad-Shahidi, A. Run-up on vertical piles due to regular waves: Small-scale model tests and prediction formulae. Coast. Eng. 2016, 118, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Teng, B.; Ning, D.-Z.; Gou, Y. Wave-Current Interactions with Three-Dimensional Floating Bodies. J. Hydrodyn. 2010, 22, 229–241. [Google Scholar] [CrossRef]
- Wang, C.; Wu, G. Time domain analysis of second-order wave diffraction by an array of vertical cylinders. J. Fluids Struct. 2007, 23, 605–631. [Google Scholar] [CrossRef]
- Ohl, C.O.G.; Taylor, R.E.; Taylor, P.H.; Borthwick, A.G.L. Water wave diffraction by a cylinder array. Part 1. Regular waves. J. Fluid Mech. 2001, 442, 1–32. [Google Scholar] [CrossRef]
- Abbasnia, A.; Ghiasi, M. A fully nonlinear wave interaction with an array of submerged cylinders by NURBS numerical wave tank and acceleration potential. Ships Offshore Struct. 2014, 9, 404–417. [Google Scholar] [CrossRef]
- Bai, W.; Feng, X.; Taylor, R.E.; Ang, K. Fully nonlinear analysis of near-trapping phenomenon around an array of cylinders. Appl. Ocean Res. 2013, 44, 71–81. [Google Scholar] [CrossRef]
- Sun, L.; Zang, J.; Chen, L.; Taylor, R.E.; Taylor, P. Regular waves onto a truncated circular column: A comparison of experiments and simulations. Appl. Ocean Res. 2016, 59, 650–662. [Google Scholar] [CrossRef]
- Xiang, T.; Istrati, D. Assessment of extreme wave impact on coastal decks with different geometries via the arbitrary lagran-gian-eulerian method. J. Mar. Sci. Eng. 2021, 9, 1342. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I.G. Tsunami Loads on Straight and Skewed Bridges–Part 2: Numerical Investigation and Design Recom-Mendations. Oregon. Dept. of Transportation. Research Section. 2021. Available online: https://trid.trb.org/view/1778885 (accessed on 7 September 2022).
- Westphalen, J.; Greaves, D.M.; Raby, A.; Hu, Z.Z.; Causon, D.M.; Mingham, C.G.; Omidvar, P.; Stansby, P.K.; Rogers, B.D. Investigation of Wave-Structure Interaction Using State of the Art CFD Techniques. Open J. Fluid Dyn. 2014, 04, 18–43. [Google Scholar] [CrossRef]
- Hasanpour, A.; Istrati, D.; Buckle, I. Coupled SPH–FEM Modeling of Tsunami-Borne Large Debris Flow and Impact on Coastal Structures. J. Mar. Sci. Eng. 2021, 9, 1068. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.L.; Losada, I.J. Simulating coastal engineering processes with OpenFOAM®. Coast. Eng. 2013, 71, 119–134. [Google Scholar] [CrossRef]
- Lara, J.; Higuera, P.; Guanche, R.; Losada, I.J. Wave interaction with piled structures: Application with IH-FOAM. In Proceedings of the 32nd International Conference on Offshore Mechanics and Arctic Engineering, Nantes, France, 9–14 September 2013. [Google Scholar]
- Mohseni, M.; Esperanca, P.T.; Sphaier, S.H. Numerical study of wave run-up on a fixed and vertical surface-piercing cylinder subjected to regular, non-breaking waves using OpenFOAM. Appl. Ocean. Res. 2018, 79, 228–252. [Google Scholar] [CrossRef]
- Cao, H.-J.; Wan, D.-C. RANS-VOF solver for solitary wave run-up on a circular cylinder. China Ocean Eng. 2015, 29, 183–196. [Google Scholar] [CrossRef]
- Larsen, B.E.; Fuhrman, D.R. On the over-production of turbulence beneath surface waves in Reynolds-averaged Navier–Stokes models. J. Fluid Mech. 2018, 853, 419–460. [Google Scholar] [CrossRef]
- Larsen, B.E.; Fuhrman, D.R. Tutorial for "multiphaseStabilizedTurbulence" in OpenFOAM®—v1912. 27 April 2020. Available online: https://doi.org/10.11583/DTU.12154713 (accessed on 27 April 2020).
- Jacobsen, N.G.; Fuhrman, D.R.; Fredsøe, J. A wave generation toolbox for the open-source CFD library: OpenFoam®. Int. J. Numer. Methods Fluids 2012, 70, 1073–1088. [Google Scholar] [CrossRef]
- Devolder, B.; Rauwoens, P.; Troch, P. Application of a buoyancy-modified k-ω SST turbulence model to simulate wave run-up around a monopile subjected to regular waves using OpenFOAM ®. Coast. Eng. 2017, 125, 81–94. [Google Scholar] [CrossRef]
- Qiao, D.; Feng, C.; Yan, J.; Liang, H.; Ning, D.; Li, B. Numerical simulation and experimental analysis of wave interaction with a porous plate. Ocean Eng. 2020, 218, 108106. [Google Scholar] [CrossRef]
- Swan, C.; Sheikh, R. The interaction between steep waves and a surface-piercing column. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2015, 373, 20140114. [Google Scholar] [CrossRef]
- Rainey, R.C.T. Weak or strong nonlinearity: The vital issue. J. Eng. Math. 2007, 58, 229–249. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I. Role of Trapped Air on the Tsunami-Induced Transient Loads and Response of Coastal Bridges. Geosciences 2019, 9, 191. [Google Scholar] [CrossRef] [Green Version]
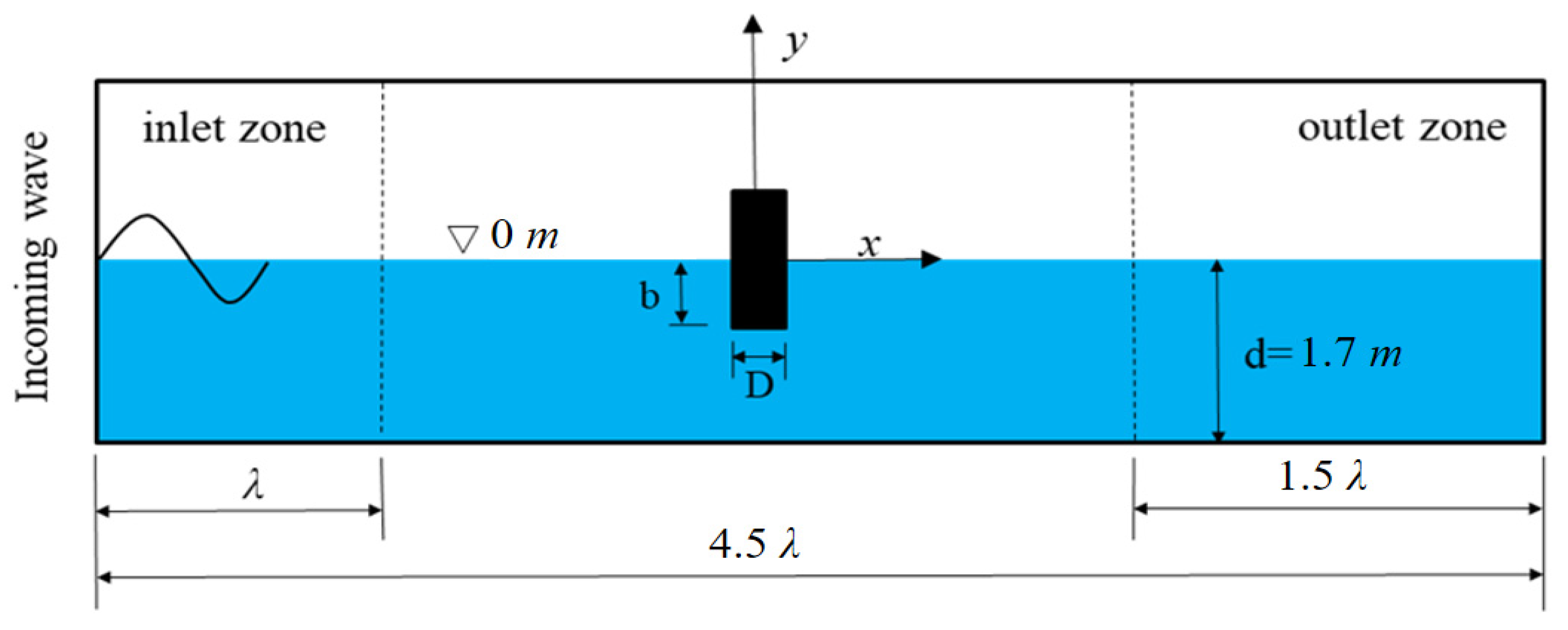
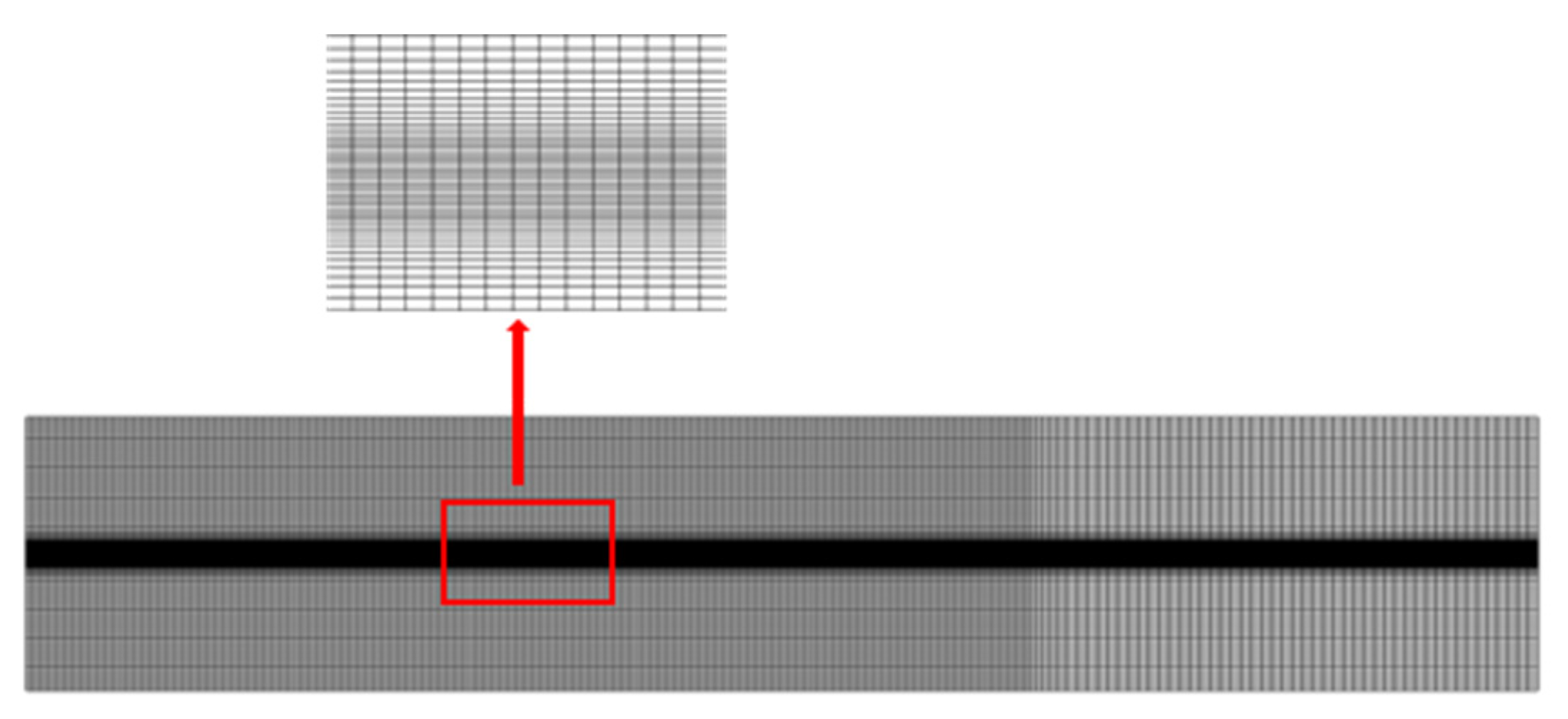
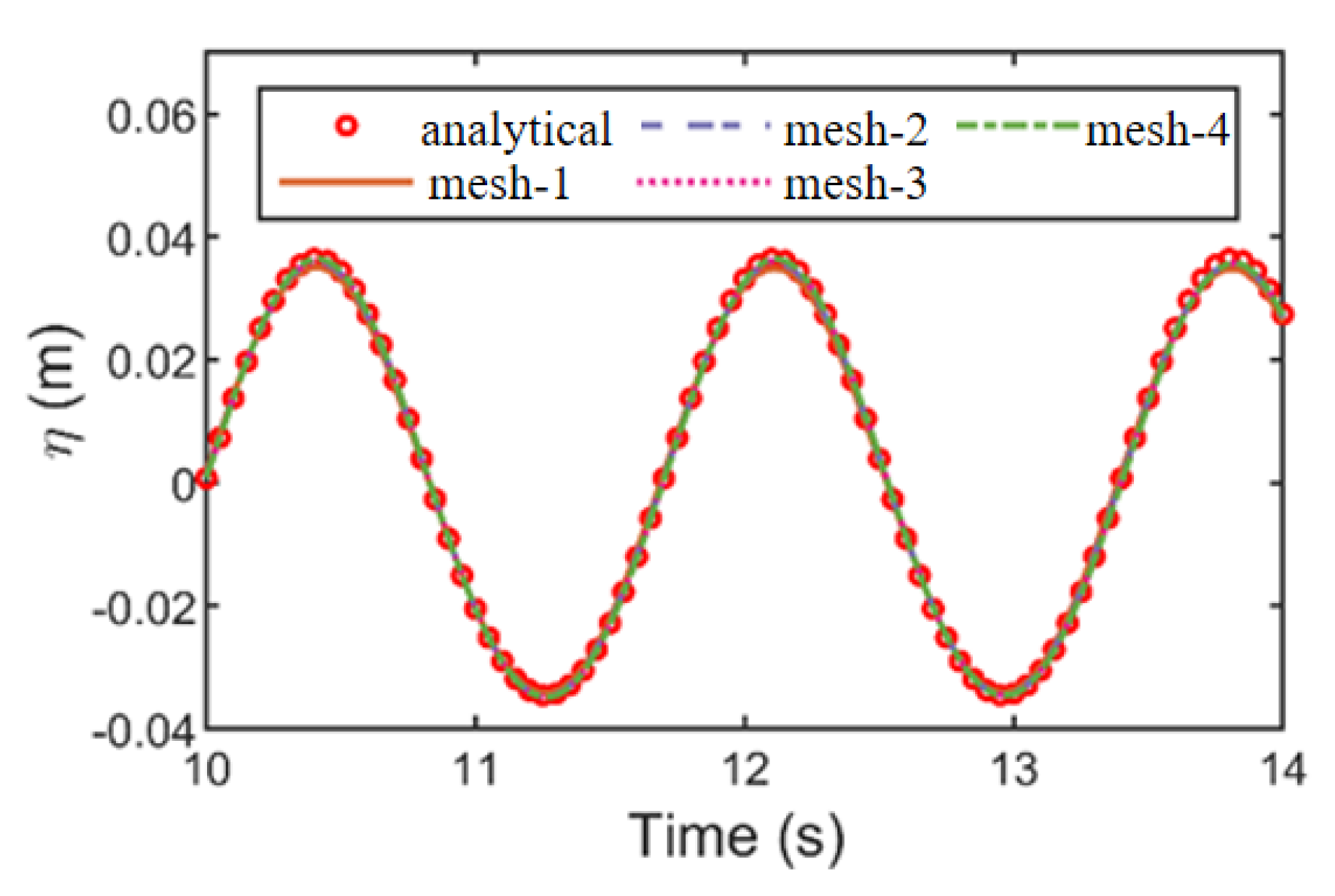
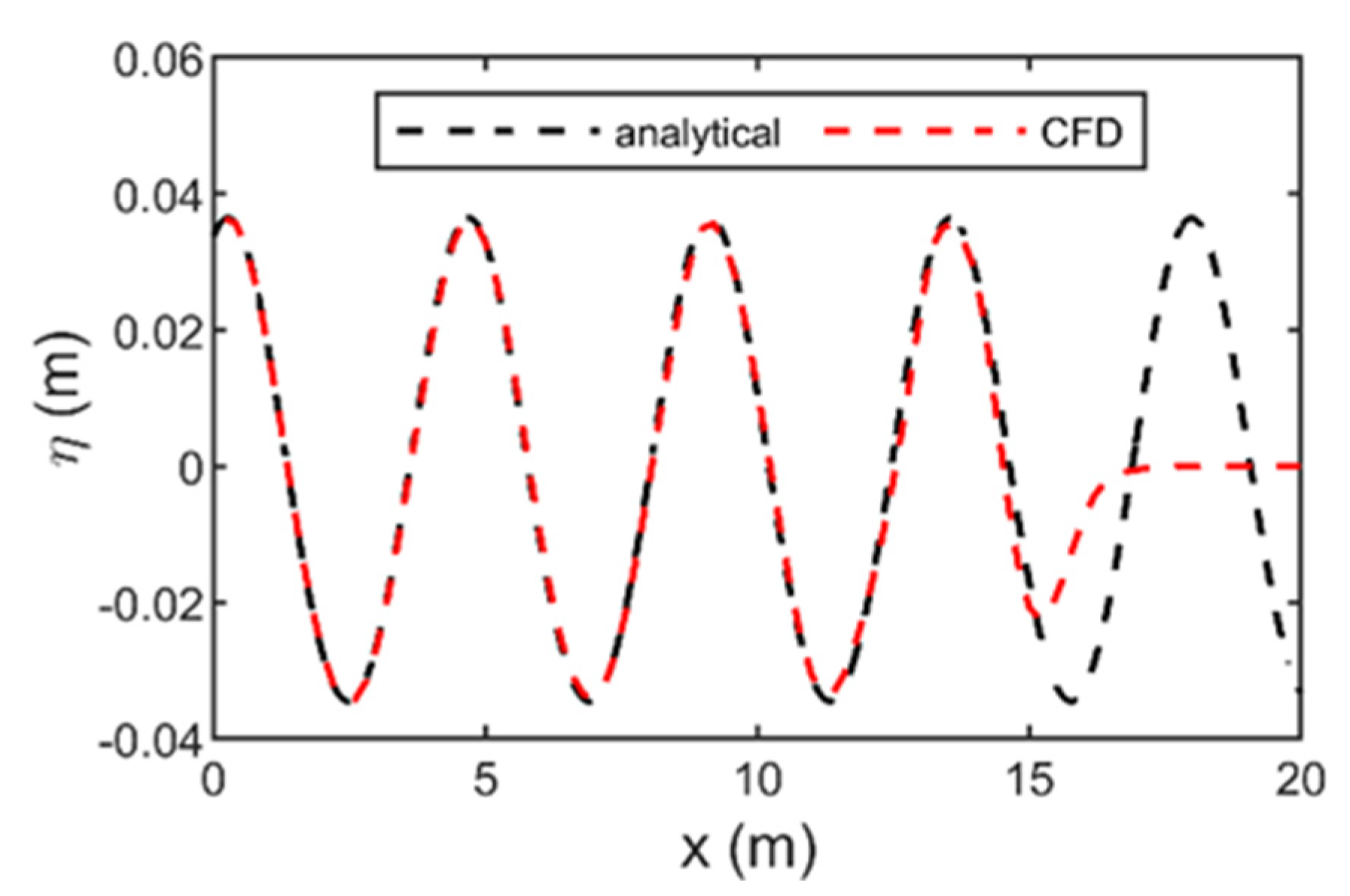

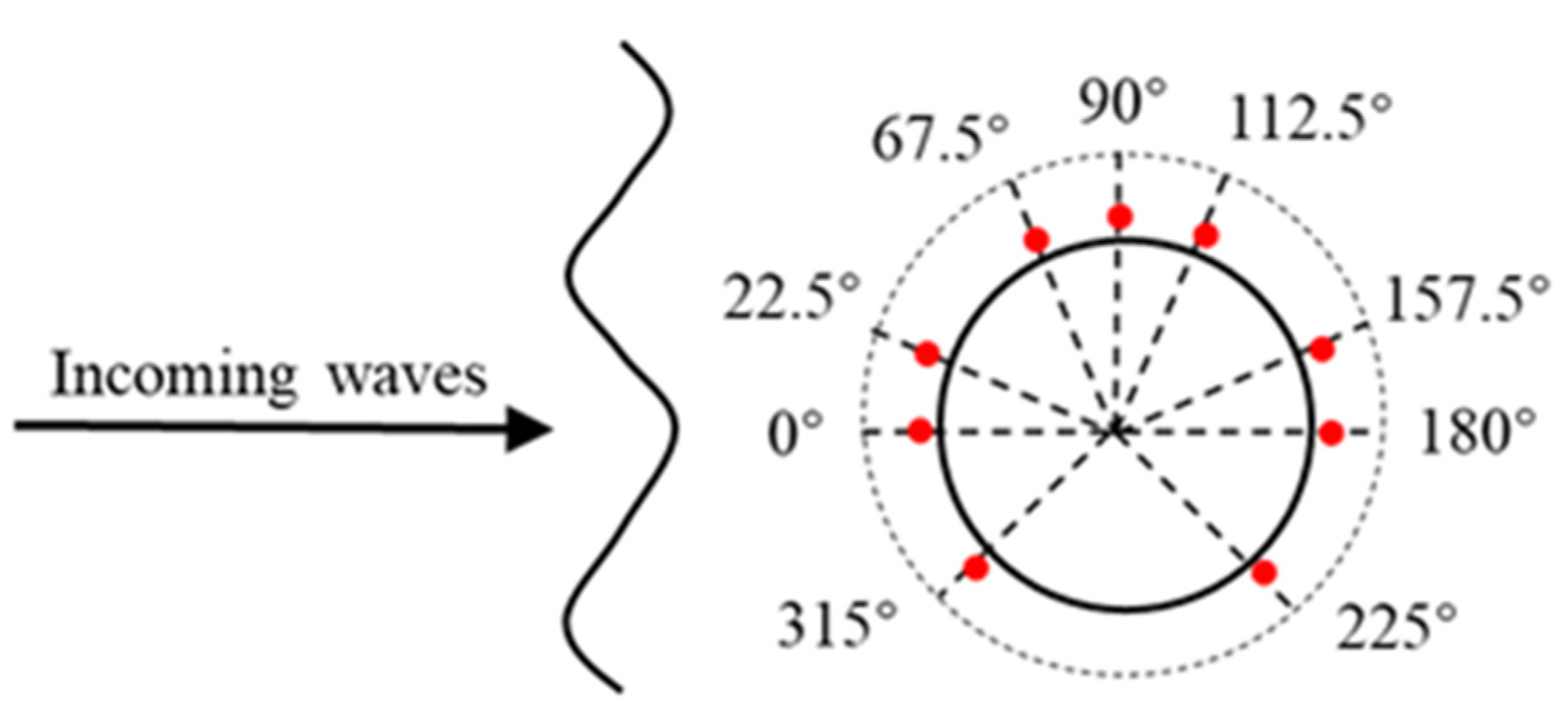
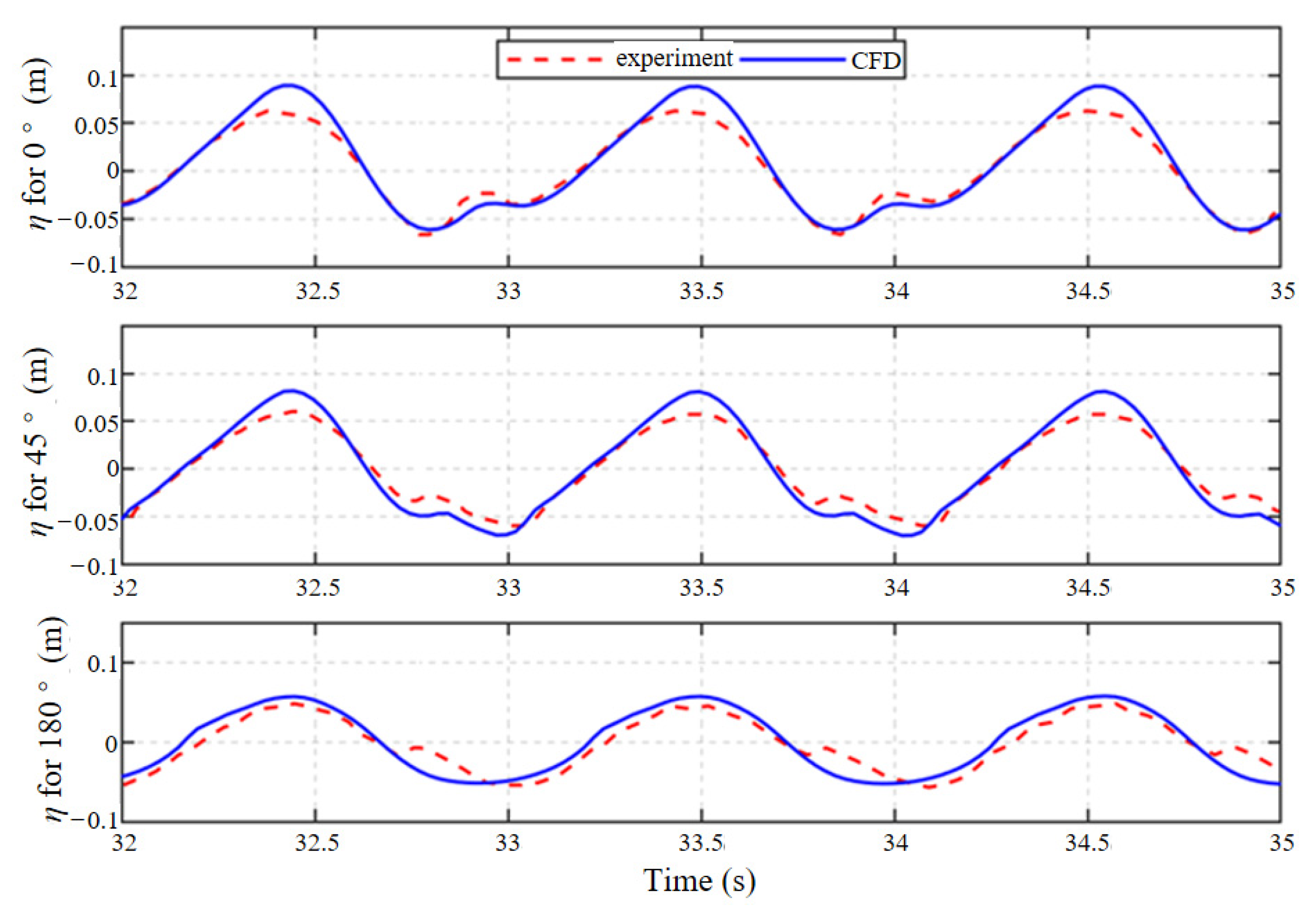
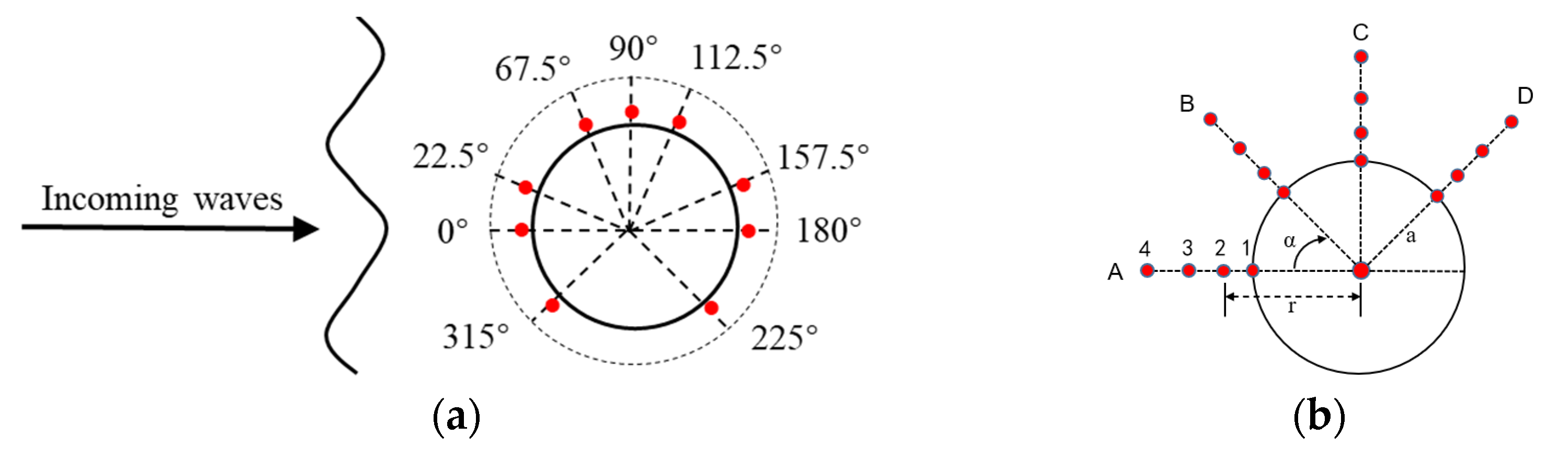

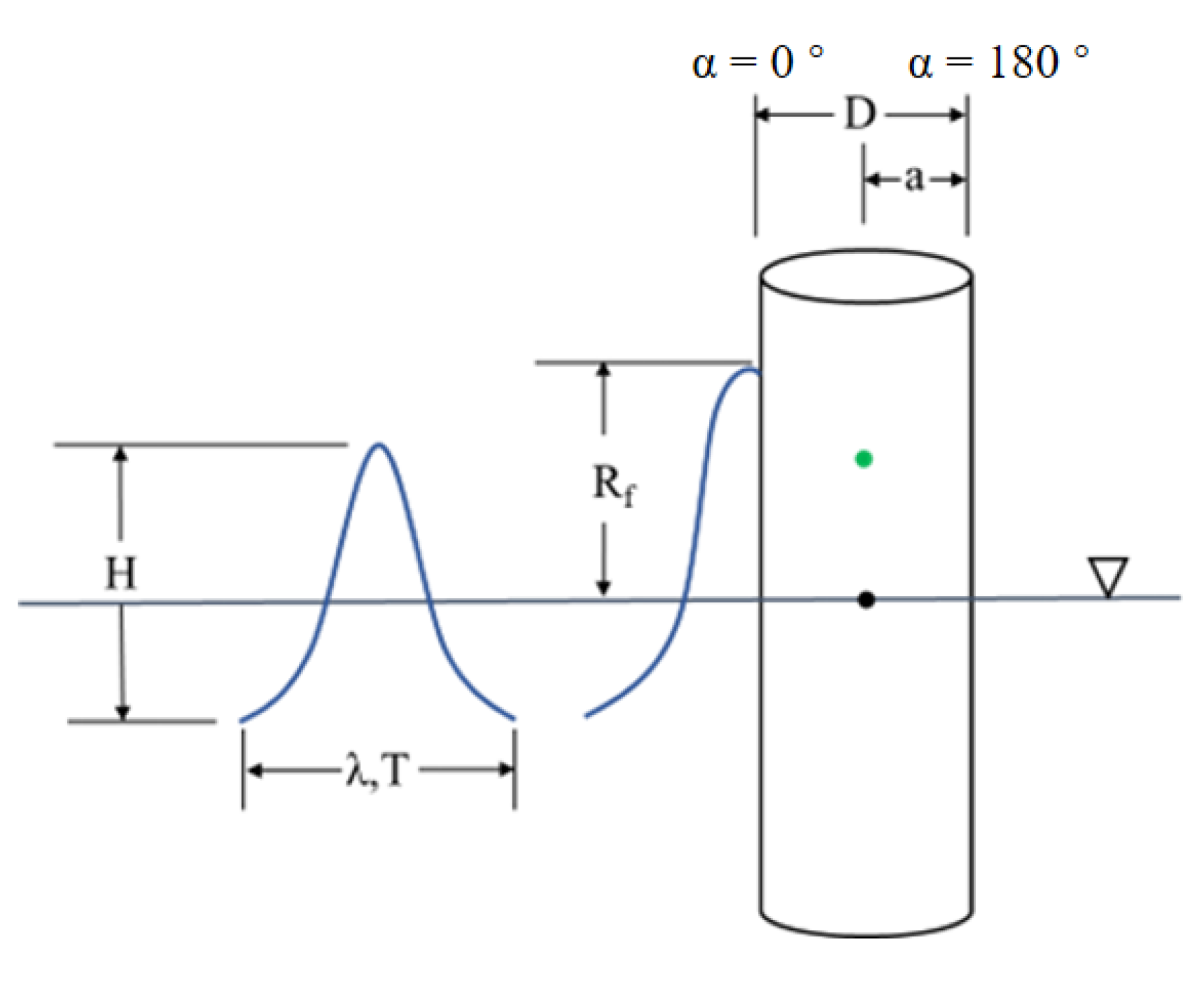
| Mesh Type | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| H/Δy | 5 | 10 | 15 | 20 |
| λ/Δx | 40 | 80 | 120 | 160 |
| Δy (m) | 0.0142 | 0.0071 | 0.0047 | 0.0036 |
| Δx (m) | 0.1108 | 0.0554 | 0.0369 | 0.0277 |
| Δx/Δy | 7.8 | 7.8 | 7.8 | 7.8 |
| Mesh Type | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| height(m) | 0.0690 | 0.0706 | 0.0706 | 0.0708 |
| relative error | −2.86% | −0.89% | −0.61% | −0.28% |
| Name of Wave Probes | ||
|---|---|---|
| A1–A4 | 0 | a,1.2a,1.6a,2a |
| B1–B4 | 45 | a,1.2a,1.6a,2a |
| C1–C4 | 90 | a,1.2a,1.6a,2a |
| D1–D4 | 135 | a,1.2a,1.6a,2a |
| Number | |||||
|---|---|---|---|---|---|
| F1 | 1.3 | 0.042 | 0.084 | 0.126 | 0.3815 |
| F2 | 1.4 | 0.049 | 0.098 | 0.146 | 0.3295 |
| F3 | 1.5 | 0.056 | 0.112 | 0.167 | 0.2879 |
| F4 | 1.6 | 0.063 | 0.126 | 0.189 | 0.2543 |
| F5 | 1.7 | 0.073 | 0.146 | 0.218 | 0.2197 |
| F6 | 1.8 | 0.078 | 0.156 | 0.235 | 0.2044 |
| F7 | 1.9 | 0.087 | 0.174 | 0.258 | 0.1857 |
| F8 | 2.0 | 0.094 | 0.188 | 0.282 | 0.1701 |
| F9 | 2.1 | 0.102 | 0.204 | 0.305 | 0.1570 |
| F10 | 2.3 | 0.118 | 0.236 | 0.353 | 0.1361 |
| F11 | 2.5 | 0.133 | 0.266 | 0.398 | 0.1204 |
| Estimation Formula | Estimation Formula | ||||
|---|---|---|---|---|---|
| Vos | 0.0188 | 0.9474 | 0.9771 | 30.13 | Vos |
| Bonakdar | 0.0031 | 0.9941 | 0.979 | 9.76 | Bonakdar |
| Wave Probes | 0° | 157.5° | 180° | 225° | |||||
|---|---|---|---|---|---|---|---|---|---|
| Second Order | Third Order | Second Order | Third Order | Second Order | Third Order | Second Order | Third Order | ||
| T = 1.4 s | kA = 0.05 | 0.107 | — | 0.048 | — | 0.071 | — | 0.028 | — |
| kA = 0.1 | 0.310 | — | 0.118 | — | 0.189 | — | 0.077 | — | |
| kA = 0.15 | 0.320 | — | 0.142 | — | 0.265 | — | 0.210 | — | |
| T = 1.73 s | kA = 0.05 | — | — | — | — | — | — | — | — |
| kA = 0.1 | 0.144 | 0.027 | 0.052 | — | 0.077 | — | 0.029 | 0.047 | |
| kA = 0.15 | 0.211 | 0.029 | 0.075 | 0.014 | 0.112 | 0.02 | 0.072 | 0.089 | |
| T = 2.1 s | kA = 0.05 | — | — | — | — | — | — | — | — |
| kA = 0.1 | 0.178 | 0.06 | 0.097 | — | 0.105 | 0.031 | 0.07 | 0.075 | |
| kA = 0.15 | 0.252 | 0.112 | 0.111 | — | 0.12 | 0.035 | 0.124 | 0.121 | |
| T = 2.5 s | kA = 0.05 | 0.104 | — | 0.074 | — | 0.08 | — | 0.053 | — |
| kA = 0.1 | 0.176 | 0.074 | 0.116 | — | 0.127 | — | 0.057 | 0.058 | |
| ka = 0.15 | 0.264 | 0.121 | 0.153 | 0.048 | 0.169 | 0.046 | 0.052 | 0.063 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Li, Y.; Wu, F.; Gao, S.; Yan, J. Numerical Investigation of Wave Run-Up and Load on Fixed Truncated Cylinder Subjected to Regular Waves Using OpenFOAM. Water 2022, 14, 2830. https://doi.org/10.3390/w14182830
Wang B, Li Y, Wu F, Gao S, Yan J. Numerical Investigation of Wave Run-Up and Load on Fixed Truncated Cylinder Subjected to Regular Waves Using OpenFOAM. Water. 2022; 14(18):2830. https://doi.org/10.3390/w14182830
Chicago/Turabian StyleWang, Bin, Yu Li, Fei Wu, Shan Gao, and Jun Yan. 2022. "Numerical Investigation of Wave Run-Up and Load on Fixed Truncated Cylinder Subjected to Regular Waves Using OpenFOAM" Water 14, no. 18: 2830. https://doi.org/10.3390/w14182830
APA StyleWang, B., Li, Y., Wu, F., Gao, S., & Yan, J. (2022). Numerical Investigation of Wave Run-Up and Load on Fixed Truncated Cylinder Subjected to Regular Waves Using OpenFOAM. Water, 14(18), 2830. https://doi.org/10.3390/w14182830





