Combined Districting and Main Line Routing—A Method to Implement a Basic Drinking Water Supply Infrastructure in Informal Settlements
Abstract
:1. Introduction
2. State of the Art
2.1. Upgrading Areas in Informal Settlements
- Insecure residence status;
- Inadequate access to safe water;
- Inadequate access to sanitation and other infrastructure;
- Poor structural quality of housing;
- Overcrowding.
2.2. Districting: Introduction and Basics
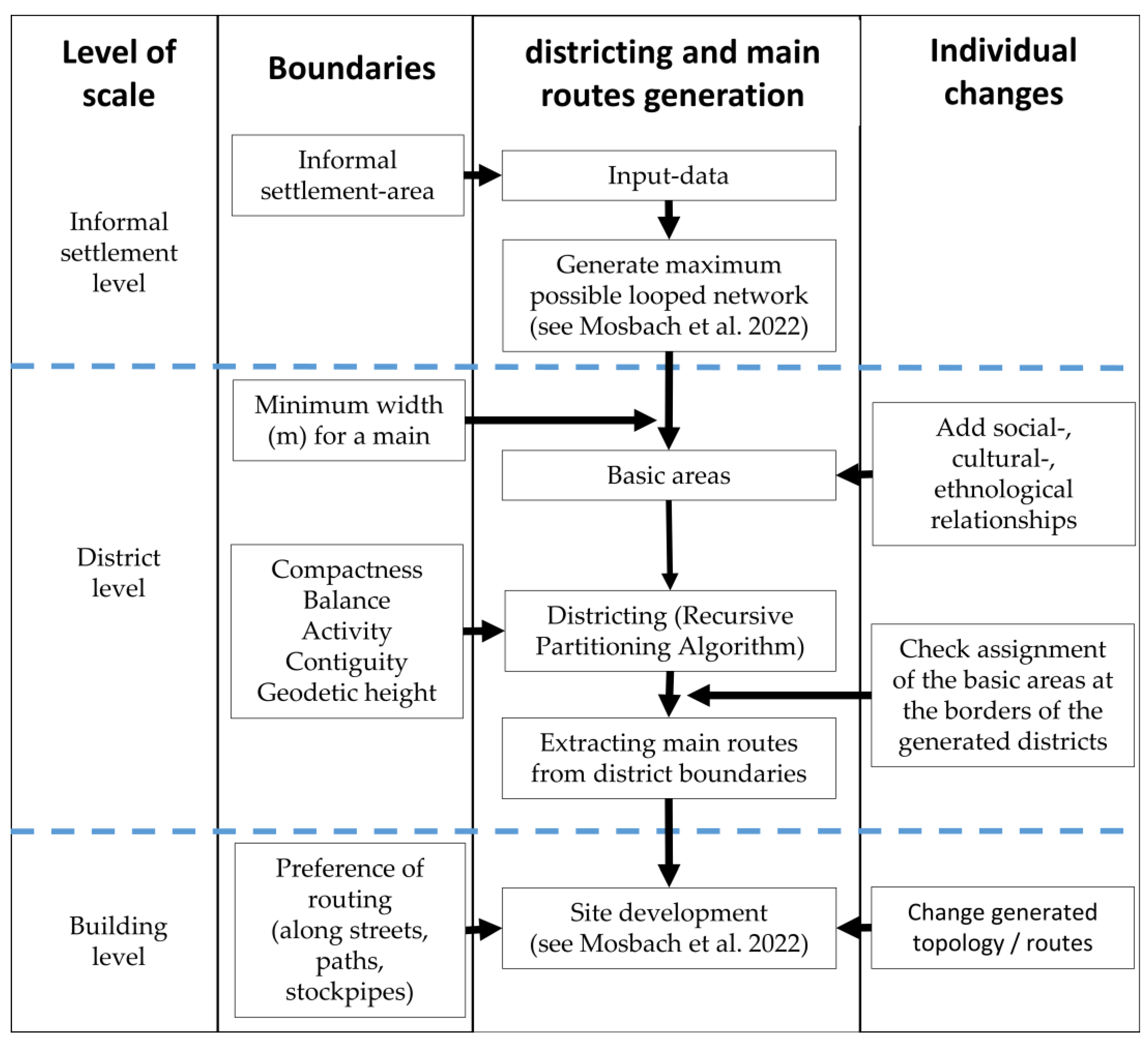
3. Materials and Methods
- A superordinate main pipeline layout for a pipe-based water supply is searched.
- The routing should run along existing roads/trails or between houses that are at least 10 m apart from each other.
- The individual districts should approximately be equal in size (area).
- Geographical compactness. Compactness makes the districts easier to manage and economical to operate [9] so that pipeline lengths are mostly minimized.
- Elevation compactness (to prevent multiple pressure zones within a district).
3.1. Software and Data
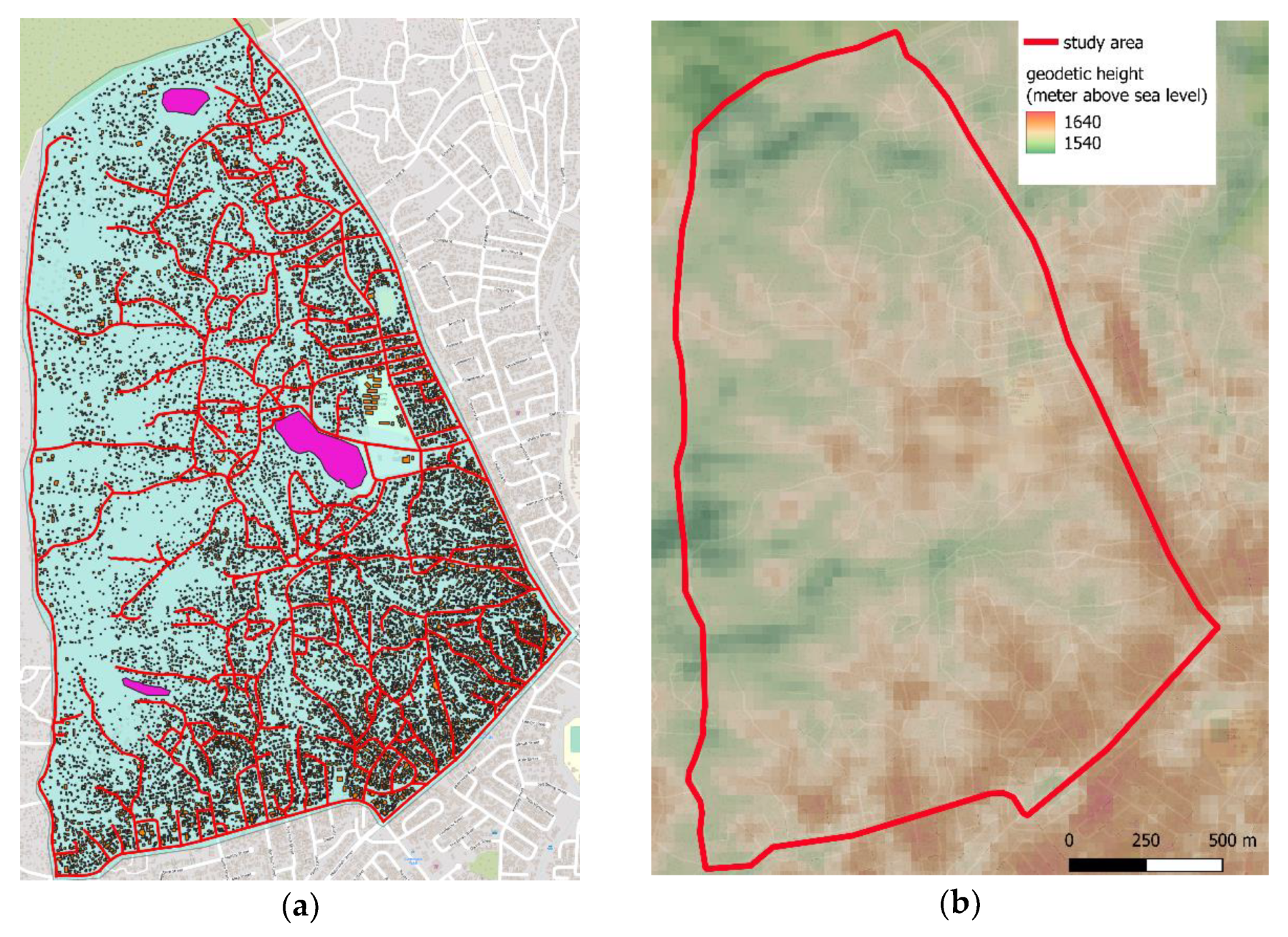
3.2. Informal Settlement Level: Area under Consideration, Data Import and Maximum Network Creation
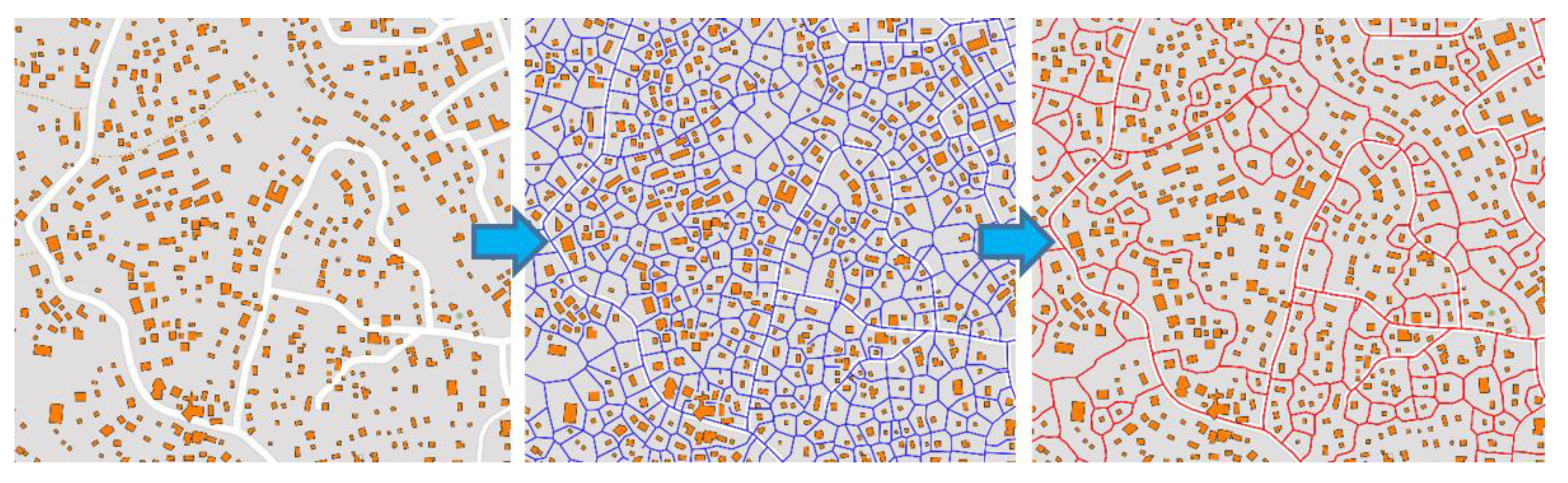
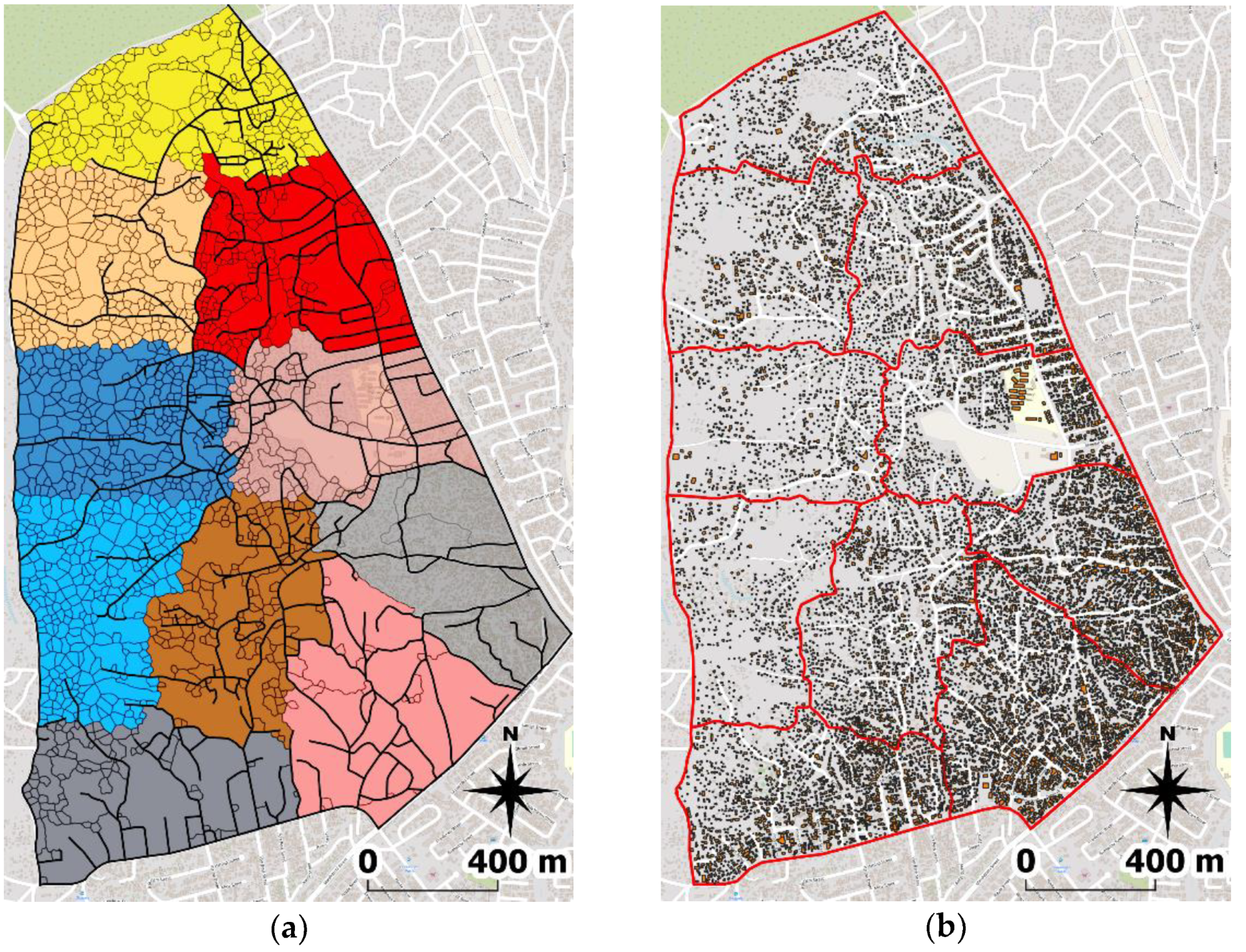
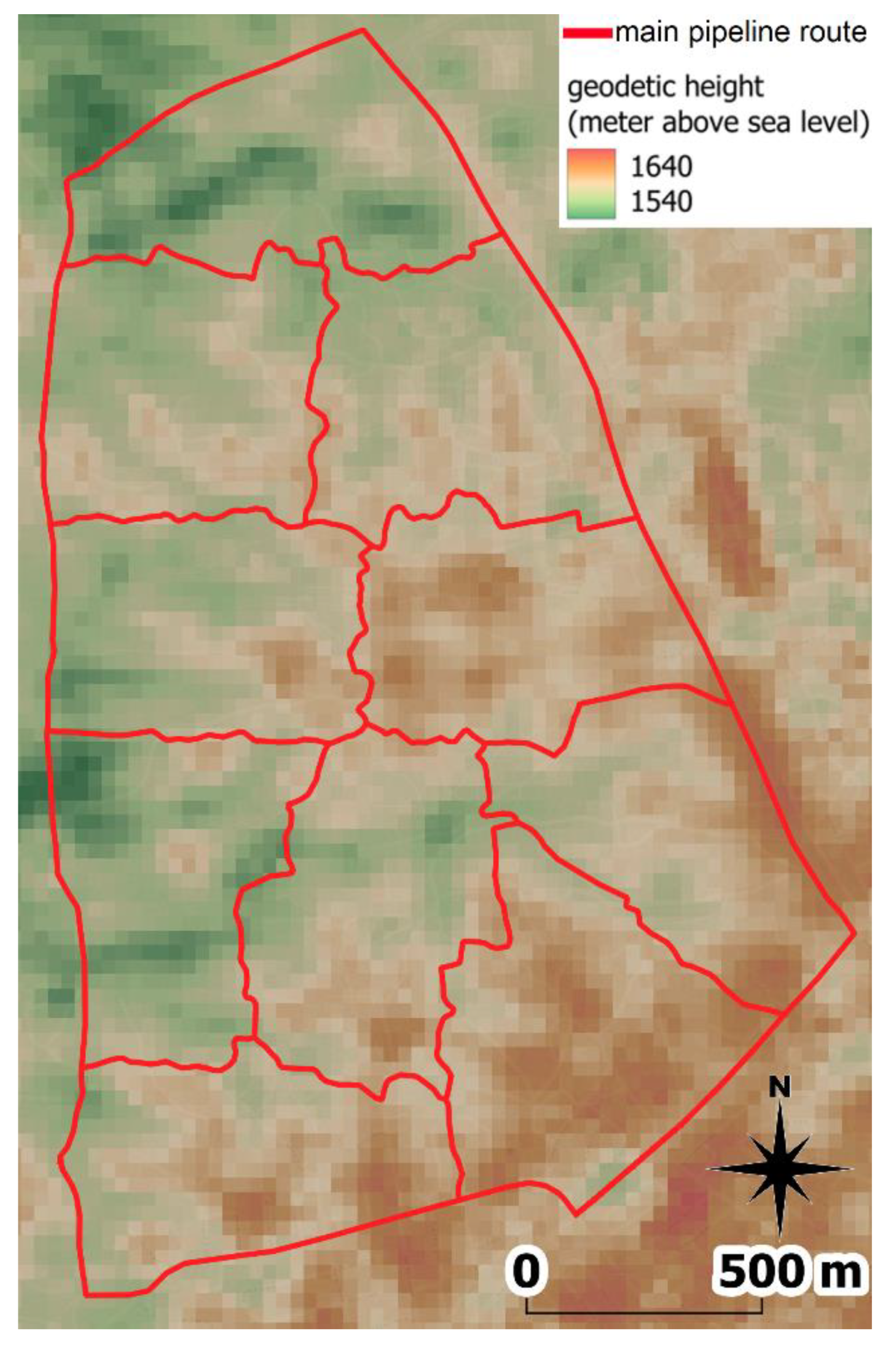
3.3. District Level: Districting
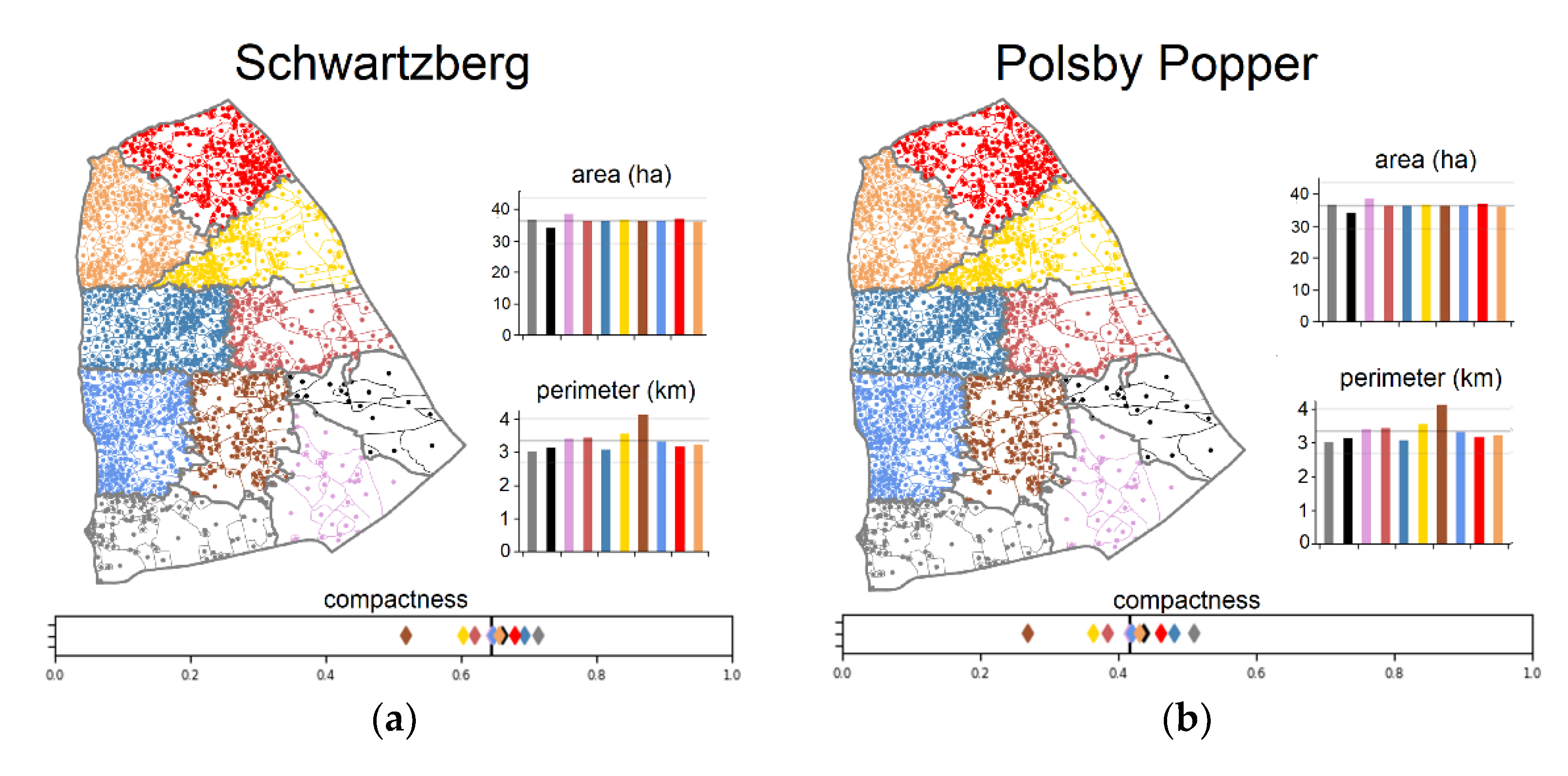
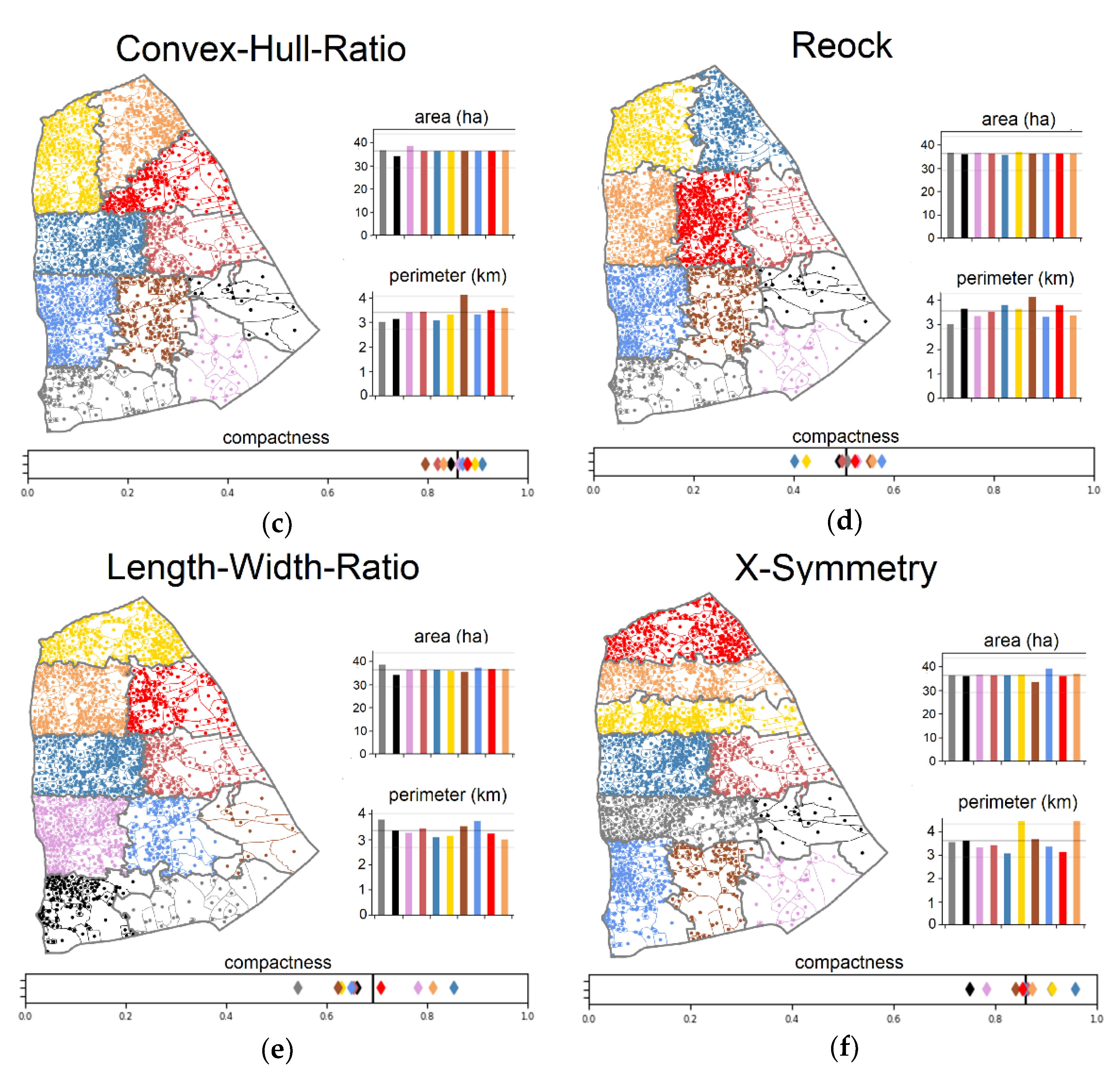
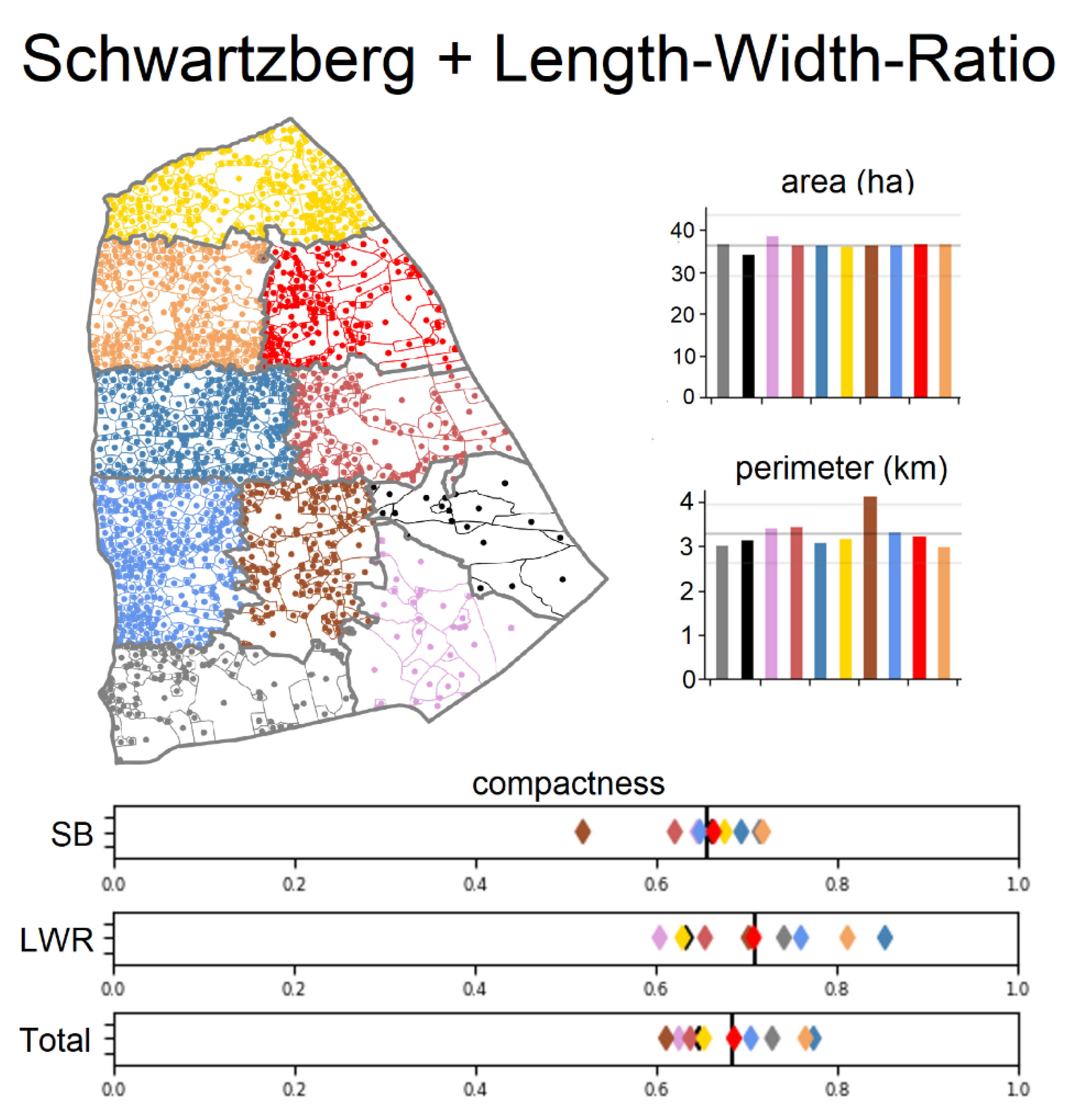
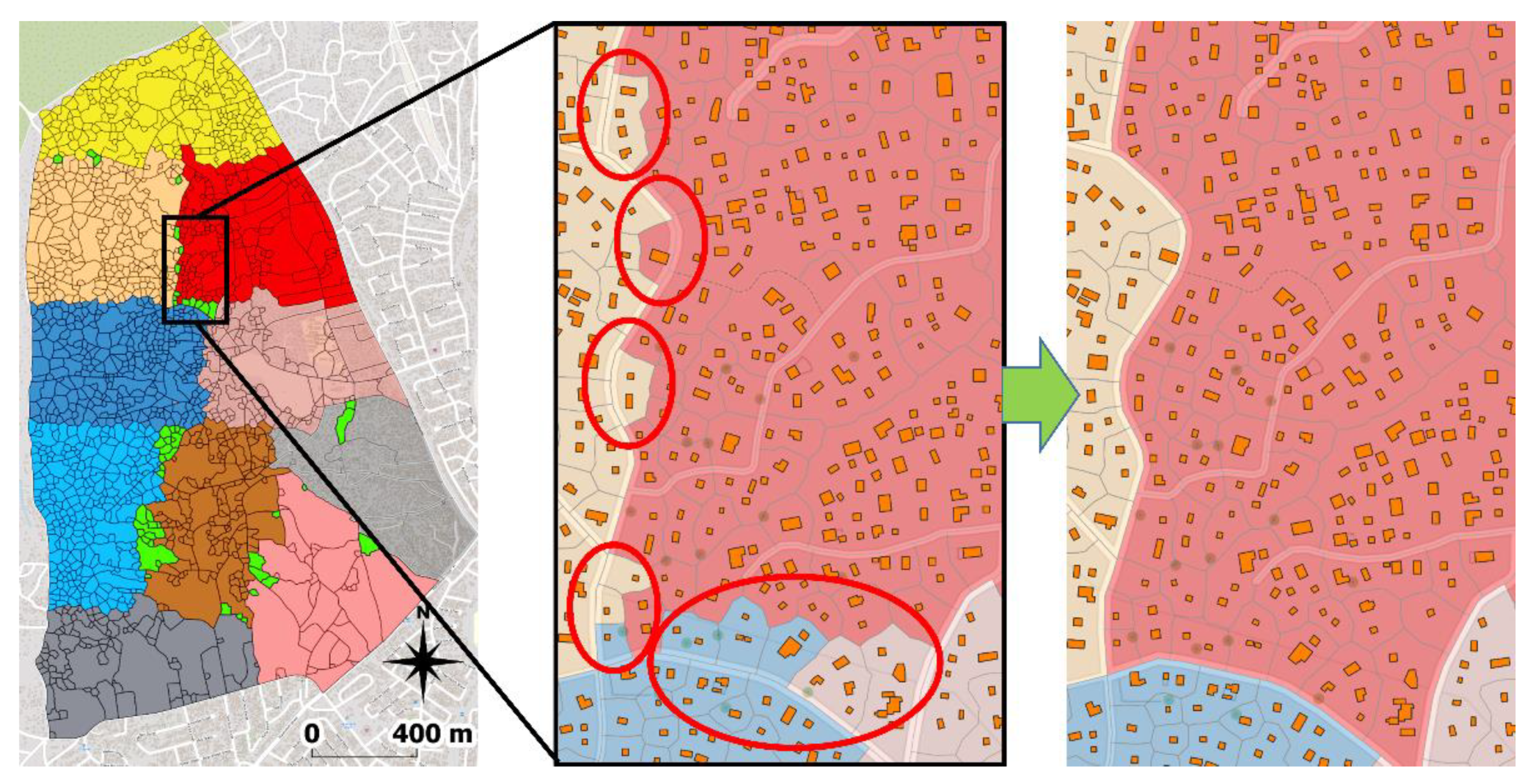
4. Results
5. Discussion
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- United Nations. The World’s Cities in 2018: Data Booklet ST/ESA/SER.A/417. 2018. Available online: https://www.un.org/en/events/citiesday/assets/pdf/the_worlds_cities_in_2018_data_booklet.pdf (accessed on 21 October 2021).
- United Nations. Special Edition: Progress towards the Sustainable Development Goals: Report of the Secretary-General E/2019/68; United Nations: New York, NY, USA, 2019. [Google Scholar]
- Abbott, J. An analysis of informal settlement upgrading and critique of existing methodological approaches. Habitat Int. 2002, 26, 303–315. [Google Scholar] [CrossRef]
- Amado, M.; Poggi, F.; Martins, A.; Vieira, N.; Amado, A.R. Transforming Cape Vert Informal Settlements. Sustainability 2018, 10, 2571. [Google Scholar] [CrossRef]
- Ohls Aigbavboa, C.; Thwala, W.D. Lessons learned from in situ upgrading and eradication of informal settlement in Gauteng Province in South Africa. Int. J. Hous. Mark. Anal. 2010, 3, 233–244. [Google Scholar] [CrossRef]
- Brown-Luthango, M.; Reyes, E.; Gubevu, M. Informal settlement upgrading and safety: Experiences from Cape Town, South Africa. J. Hous. Built. Environ. 2017, 32, 471–493. [Google Scholar] [CrossRef]
- United Nations Human Settlements Programme. Streets as Tools for Urban Transformation in Slums: A Street-Led Approach to Citywide Slum Upgrading; United Nations Human Settlements Programme: Nairobi, Kenya, 2012. [Google Scholar]
- World Health Organization. Domestic Water Quantity, Service Level and Health, 2nd ed.; World Health Organization: Geneva, Switzerland, 2020; ISBN 978-92-4-001524-1.
- Kalcsics, J.; Nickel, S.; Schröder, M. Towards a unified territorial design approach—Applications, algorithms and GIS integration. Top 2005, 13, 1–56. [Google Scholar] [CrossRef]
- United Nations. Glossary of Environment Statistics; Series, F., Ed.; United Nations: New York, NY, USA, 1997; ISBN 92-1-161386-8. [Google Scholar]
- Park, C. A Dictionary of Environment and Conservation; Oxford University Press: London, UK, 2007; ISBN 9780198609957. [Google Scholar]
- United Nations Human Settlements Programme. Expert Group Meeting on Urban Indicators: Secure Tenure, Slums and Global Sample of Cities; United Nations Human Settlements Programme: Nairobi, Kenya, 2002; Available online: https://www.citiesalliance.org/sites/default/files/expert-group-meeting-urban-indicators%5B1%5D.pdf (accessed on 14 August 2022).
- Abbott, J. The use of GIS in informal settlement upgrading: Its role and impact on the community and on local government. Habitat Int. 2003, 27, 575–593. [Google Scholar] [CrossRef]
- Weber, B.; Mendelsohn, J. Informal Settlements in Namibia: Their Nature and Growth; Development Workshop (DW) Namibia: Windhoek, Namibia, 2016; ISBN 978-99945-85-81-6. [Google Scholar]
- Curdes, G. Stadtstruktur und Stadtgestaltung, 2nd ed.; Verlag W. Kohlhammer: Stuttgart, Germany, 1997; ISBN 3-17-014294-1. [Google Scholar]
- van Horen, B. Informal Settlement Upgrading: Bridging the Gap Between the de Facto and the de Jure. J. Plan. Educ. Res. 2000, 19, 389–400. [Google Scholar] [CrossRef]
- Brelsford, C.; Martin, T.; Hand, J.; Bettencourt, L.M.A. Toward cities without slums: Topology and the spatial evolution of neighborhoods. Sci. Adv. 2018, 4, eaar4644. [Google Scholar] [CrossRef]
- Kohli, D.; Sliuzas, R.; Kerle, N.; Stein, A. An ontology of slums for image-based classification. Comput. Environ. Urban Syst. 2012, 36, 154–163. [Google Scholar] [CrossRef]
- Kuffer, M.; Pfeffer, K.; Sliuzas, R. Slums from Space—15 Years of Slum Mapping Using Remote Sensing. Remote Sens. 2016, 8, 455. [Google Scholar] [CrossRef] [Green Version]
- Wurm, M.; Taubenböck, H. Detecting social groups from space—Assessment of remote sensing-based mapped morphological slums using income data. Remote Sens. Lett. 2018, 9, 41–50. [Google Scholar] [CrossRef]
- Kalcsics, J.; Ríos-Mercado, R.Z. Districting Problems. In Location Science, 2nd ed.; Laporte, G., Nickel, S., Saldanha da Gama, F., Eds.; Springer International Publishing: Cham, Switzerland, 2019; ISBN 978-3-030-32176-5. [Google Scholar]
- Fleischmann, B.; Paraschis, J.N. Solving a large scale districting problem: A case report. Comput. Oper. Res. 1988, 15, 521–533. [Google Scholar] [CrossRef]
- Butsch, A. Districting Problems—New Geometrically Motivated Approaches. Ph.D. Thesis, Karlsruher Institut für Technologie, Karlsruhe, Germany, 2016. [Google Scholar]
- Caro, F.; Shirabe, T.; Guignard, M.; Weintraub, A. School redistricting: Embedding GIS tools with integer programming. J. Oper. Res. Soc. 2004, 55, 836–849. [Google Scholar] [CrossRef]
- Ferland, J.A.; Guénette, G. Decision Support System for the School Districting Problem. Oper. Res. 1990, 38, 15–21. [Google Scholar] [CrossRef]
- Schoepfle, O.B.; Church, R.L. A Fast, Network-based, Hybrid Heuristic for the Assignment of Students to Schools. J. Oper. Res. Soc. 1989, 40, 1029–1040. [Google Scholar] [CrossRef]
- D’Amico, S.J.; Wang, S.-J.; Batta, R.; Rump, C.M. A simulated annealing approach to police district design. Comput. Oper. Res. 2002, 29, 667–684. [Google Scholar] [CrossRef]
- Liberatore, F.; Camacho-Collados, M.; Vitoriano, B. Police Districting Problem: Literature Review and Annotated Bibliography. In Optimal Districting and Territory Design; Ríos-Mercado, R.Z., Ed.; Springer International Publishing: Cham, Switzerland, 2020; pp. 9–29. ISBN 978-3-030-34311-8. [Google Scholar]
- Bergey, P.K.; Ragsdale, C.T.; Hoskote, M. A Simulated Annealing Genetic Algorithm for the Electrical Power Districting Problem. Ann. Oper. Res. 2003, 121, 33–55. [Google Scholar] [CrossRef]
- Ríos-Mercado, R.Z. Research Trends in Optimization of Districting Systems. In Optimal Districting and Territory Design; Ríos-Mercado, R.Z., Ed.; Springer: Cham, Switzerland, 2020; pp. 3–8. ISBN 978-3-030-34311-8. [Google Scholar]
- Young, H.P. Measuring the Compactness of Legislative Districts. Legis. Stud. Q. 1988, 13, 105–115. [Google Scholar] [CrossRef]
- Ansolabehere, S.; Palmer, M. A two-hundred year statistical history of the gerrymander. Ohio State Law J. 2016, 77, 741–762. [Google Scholar]
- Kaufman, A.R.; King, G.; Komisarchik, M. Replication Data for: How to Measure Legislative District Compactness If You Only Know It When You See It. Am. J. Political Sci. 2021, 65, 533–550. [Google Scholar] [CrossRef]
- Reock, E.C., Jr. Measuring Compactness as a Requirement of Legislative Apportionment. Midwest J. Political Sci. 1961, 5, 70–74. [Google Scholar] [CrossRef]
- Polsby, D.D.; Popper, R.D. The Third Criterion: Compactness as a Procedural Safeguard Against Partisan Gerrymandering. Yale Law Policy Rev. 1991, 9, 301–353. [Google Scholar] [CrossRef]
- Boyce, R.R.; Clark, W.A.V. The Concept of Shape in Geography. Geogr. Rev. 1964, 54, 561–572. [Google Scholar] [CrossRef]
- Schwartzberg, J.E. Reapportionment, Gerrymanders, and the Notion of Compactness. Minn. Law Rev. 1966, 50, 443. [Google Scholar]
- Bender, M.; Kalcsics, J. Multi-Period Service Territory Design. In Optimal Districting and Territory Design; Ríos-Mercado, R.Z., Ed.; Springer International Publishing: Cham, Switzerland, 2020; pp. 129–152. ISBN 978-3-030-34311-8. [Google Scholar]
- Ricca, F.; Scozzari, A.; Simeone, B. Political Districting: From classical models to recent approaches. Ann. Oper. Res. 2013, 204, 271–299. [Google Scholar] [CrossRef]
- Ulrich, T. Heuristiken für Kombinierte Standort- und Gebietsplanung mit Vorgegebenen und Zusätzlichen, frei Wählbaren Standorten. 2014. Available online: https://i11www.iti.kit.edu/_media/teaching/theses/da-ulrich-14.pdf (accessed on 12 March 2021).
- Taubenböck, H.; Kraff, N.J. The physical face of slums: A structural comparison of slums in Mumbai, India, based on remotely sensed data. J. Hous. Built Environ. 2014, 29, 15–38. [Google Scholar] [CrossRef]
- Hecht, R. Automatische Klassifizierung von Gebäudegrundrissen: Ein Beitrag zur Kleinräumigen Beschreibung der Siedlungsstruktur; Rhombos-Verl.: Berlin, Germany, 2014; ISBN 978-3-944101-63-7. [Google Scholar]
- Arlt, G.; Blum, A.; Gruhler, K.; Lehmann, I. Siedlungsraumbezogene Strukturtypen. In Typologien der Gebauten Umwelt: Modellierung und Analyse der Siedlungsentwicklung mit dem Strukturtypenansatz; Blum, A., Ed.; Shaker: Aachen, Germany, 2010; pp. 25–38. ISBN 978-3-8322-9209-6. [Google Scholar]
- Mosbach, J.; Sonnenburg, A.; Fiedler, J.E.; Urban, W. Development of a New Method to Support a Participatory Planning for Piped Water Supply Infrastructure in Informal Settlements. Water 2022, 14, 1316. [Google Scholar] [CrossRef]
- QGIS Association. QGIS Geographic Information System; QGIS.org; 2021. Available online: https://www.qgis.org/en/site/index.html (accessed on 19 October 2021).
- Hagberg, A.A.; Schult, D.A.; Swart, P.J. Exploring network structure, dynamics, and function using NetworkX. In Proceedings of the 7th Python in Science Conference (SciPy2008), Pasadena, CA, USA, 19–24 August 2008; Varoquaux, G., Vaught, T., Millman, J., Eds.; [Google Scholar]
- OpenStreetMap contributors. Available online: https://planet.openstreetmap.org/ (accessed on 29 March 2022).
- NASA Earthdata. NASADEM; NASA Earthdata: Cleveland, OH, USA, 11–21 February 2000. [Google Scholar]
- Mair, M.; Zischg, J.; Rauch, W.; Sitzenfrei, R. Where to Find Water Pipes and Sewers?—On the Correlation of Infrastructure Networks in the Urban Environment. Water 2017, 9, 146. [Google Scholar] [CrossRef]
- Rehm, I.-S.; Friesen, J.; Pouls, K.; Busch, C.; Taubenböck, H.; Pelz, P.F. A Method for Modeling Urban Water Infrastructures Combining Geo-Referenced Data. Water 2021, 13, 2299. [Google Scholar] [CrossRef]
- Hans-Martin Heck, R.B. Netzentwurf und Netzoptimierung. 2006. Available online: http://www.optiv.de/Fallbsp/05-Netzentwurf/05-Netzentwurf/05-Netzentwurf.pdf (accessed on 12 March 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mosbach, J.; Krämer, M.; Fiedler, J.E.; Sonnenburg, A.; Urban, W. Combined Districting and Main Line Routing—A Method to Implement a Basic Drinking Water Supply Infrastructure in Informal Settlements. Water 2022, 14, 2805. https://doi.org/10.3390/w14182805
Mosbach J, Krämer M, Fiedler JE, Sonnenburg A, Urban W. Combined Districting and Main Line Routing—A Method to Implement a Basic Drinking Water Supply Infrastructure in Informal Settlements. Water. 2022; 14(18):2805. https://doi.org/10.3390/w14182805
Chicago/Turabian StyleMosbach, Julian, Moritz Krämer, Justus Ernst Fiedler, Alexander Sonnenburg, and Wilhelm Urban. 2022. "Combined Districting and Main Line Routing—A Method to Implement a Basic Drinking Water Supply Infrastructure in Informal Settlements" Water 14, no. 18: 2805. https://doi.org/10.3390/w14182805




