The Future Change in Evaporation Based on the CMIP6 Merged Data Generated by Deep-Learning Method in China
Abstract
:1. Introduction
2. Materials and Methods
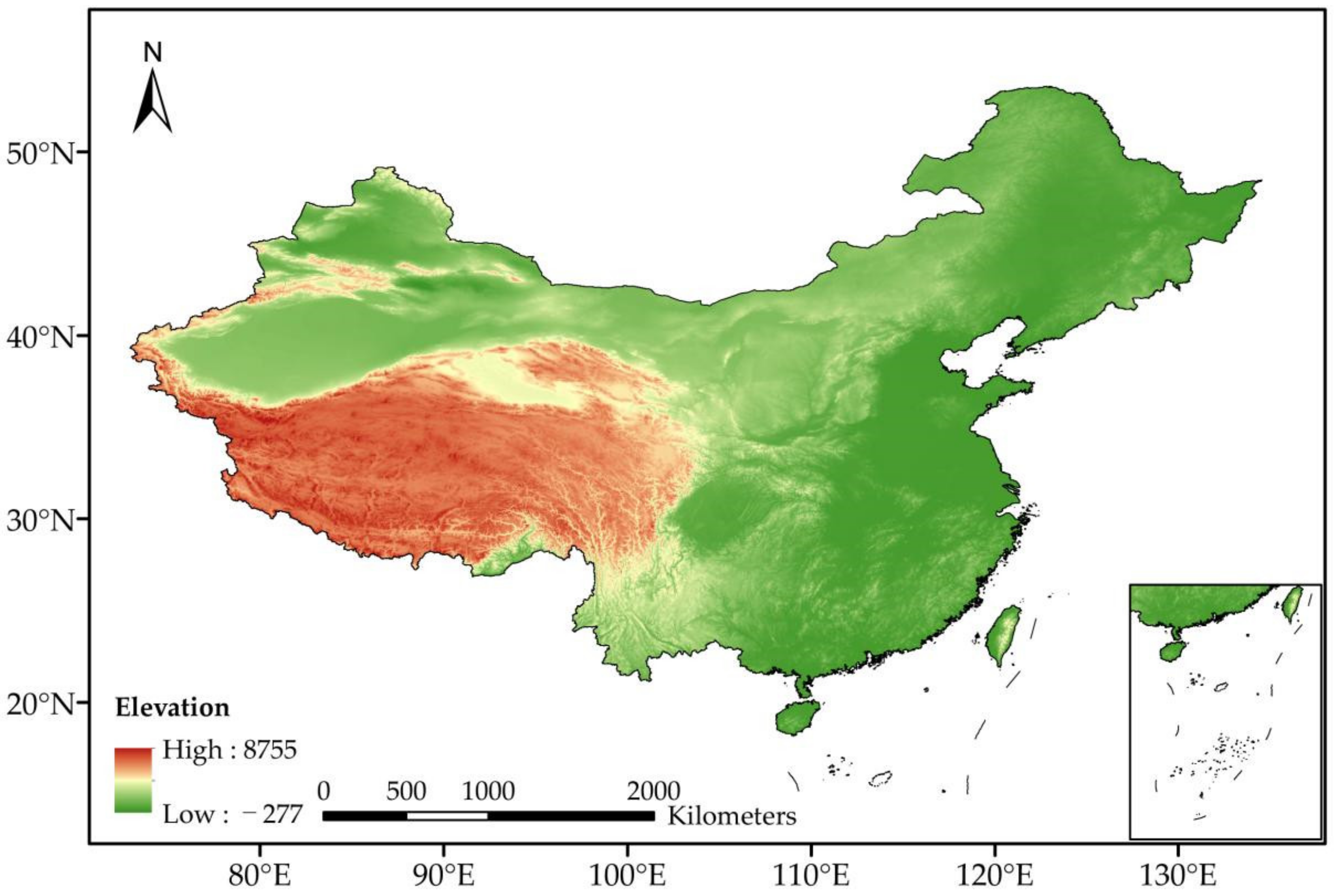
2.1. Study Region and Data
2.1.1. Evaporation Reanalysis Data
2.1.2. CMIP6 Evaporation Data
2.2. Methods
2.2.1. Deep-Learning Method
2.2.2. Evaluation Metric
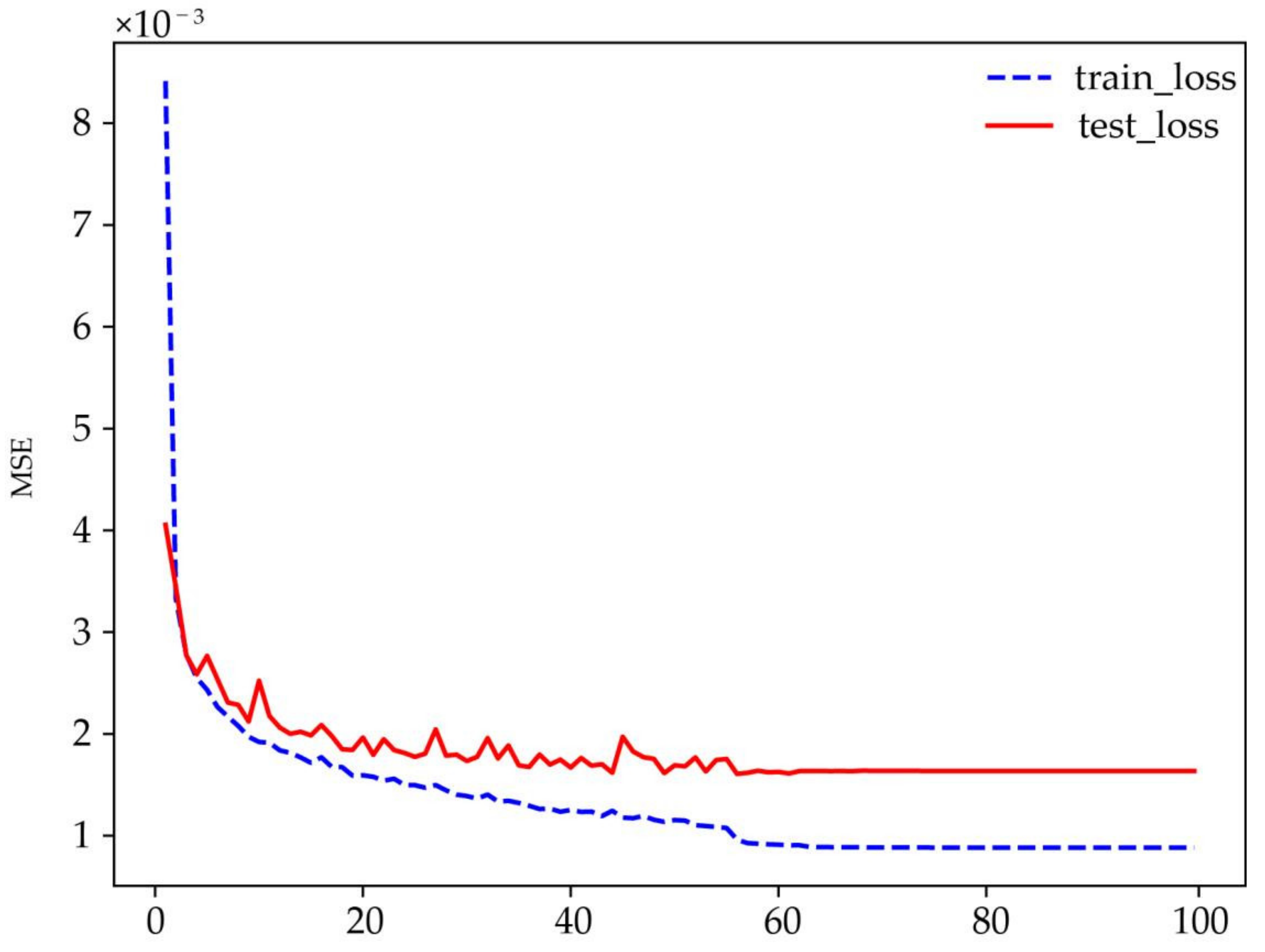
2.2.3. Training Setting and Strategy
3. Results
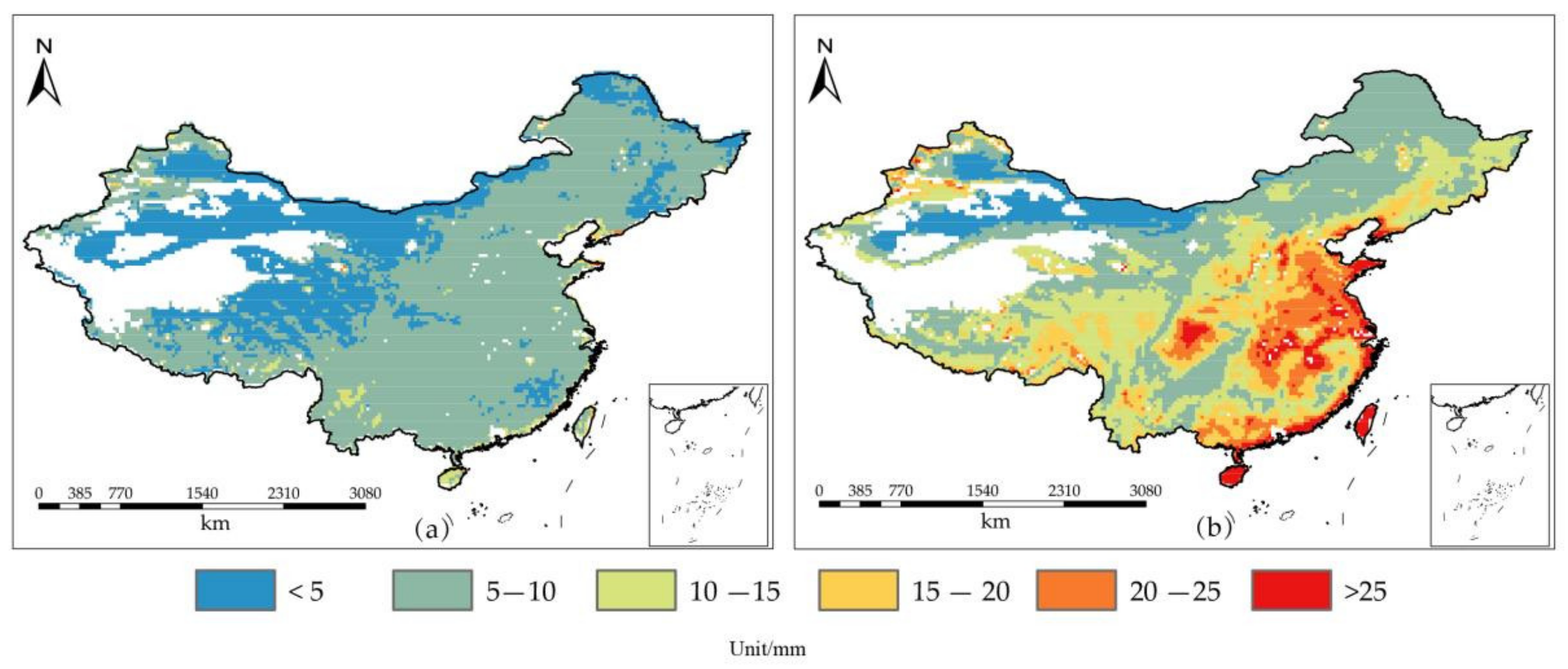
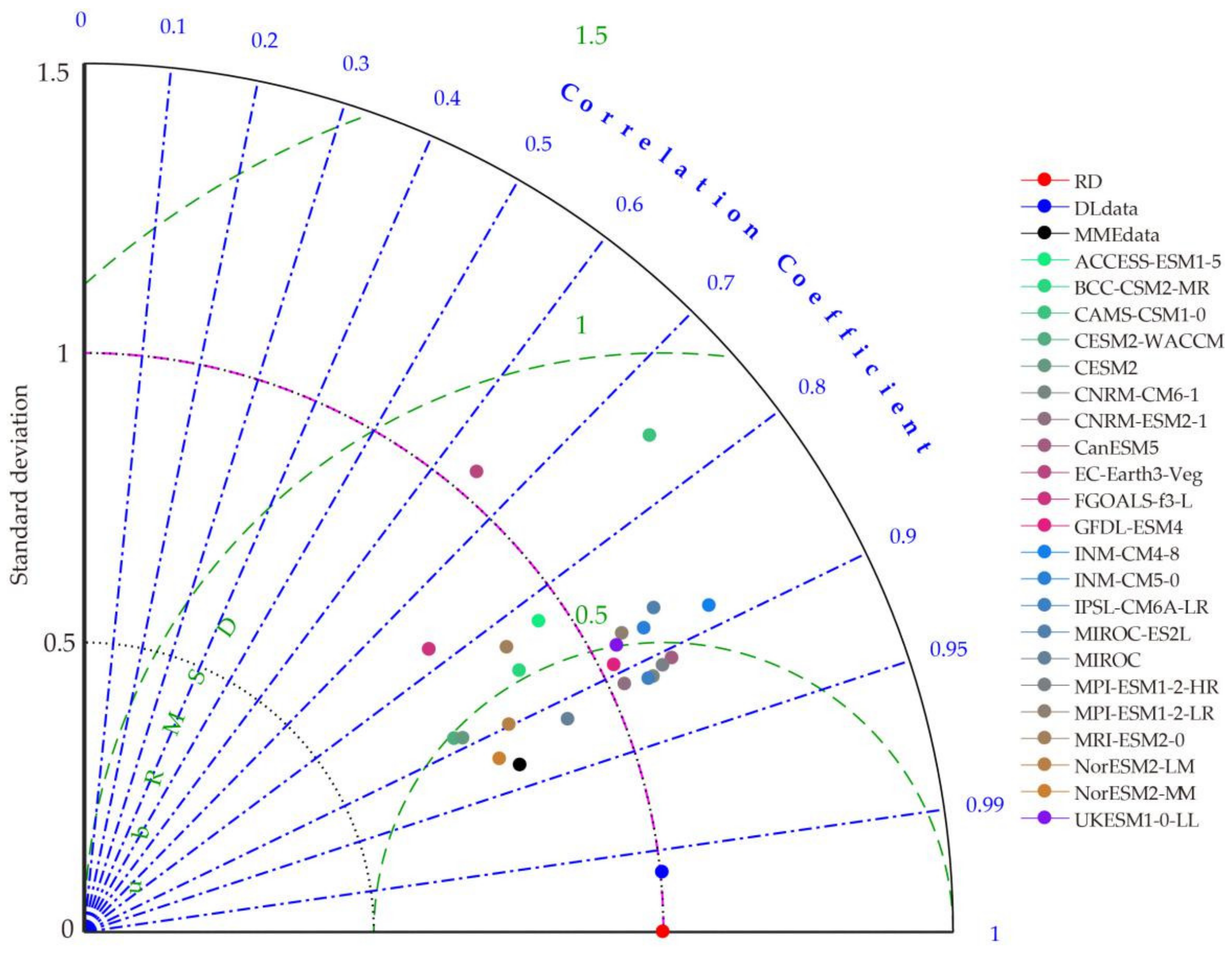
3.1. Evaluation of Merged Data
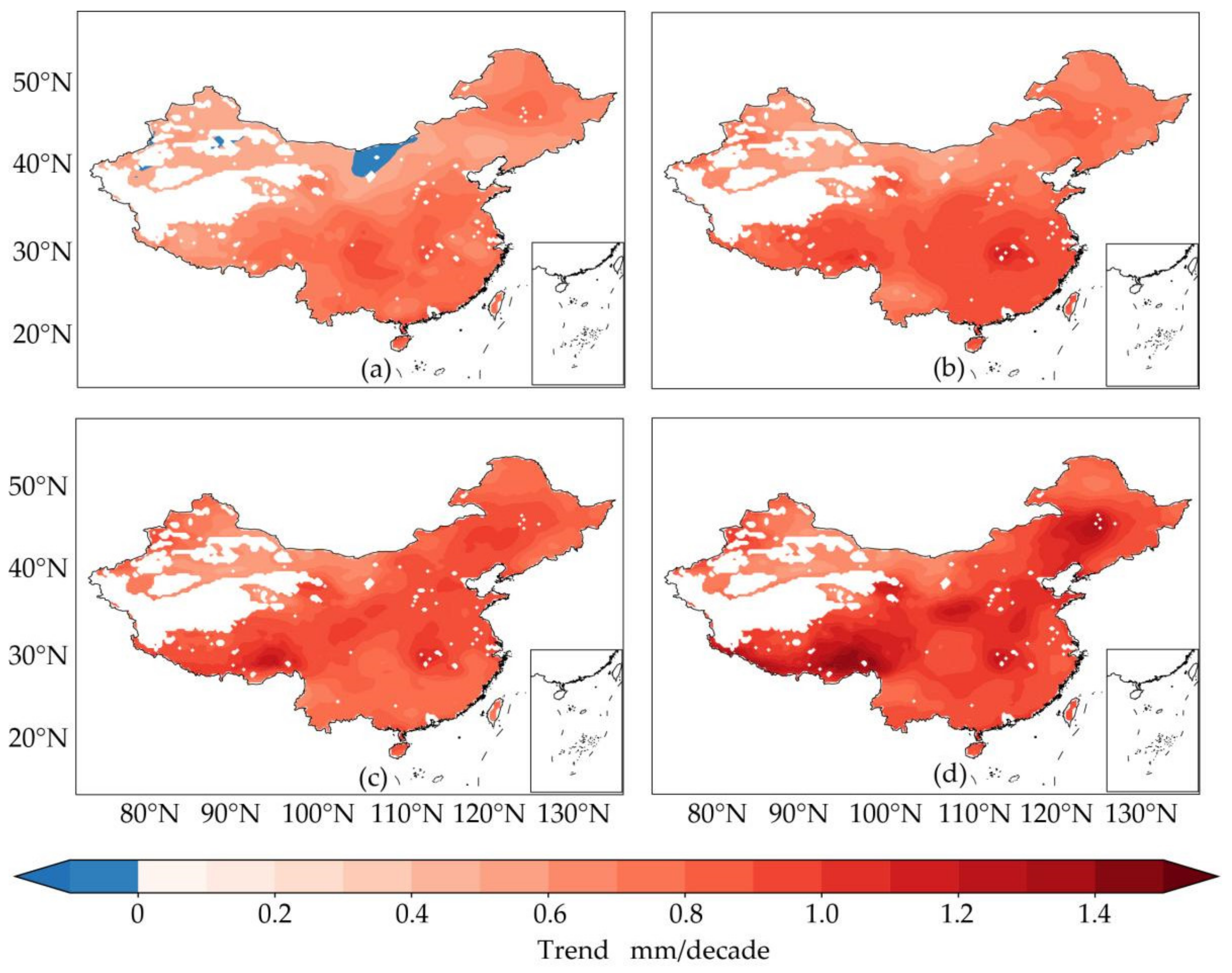
3.2. Future Evaporation Change
4. Discussion
4.1. Data Merge and Downscaling of Climate Data
4.2. Future Spatial-Temporal Changes in LET
4.3. Limitation and Prospect
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, J.; Chadwick, R.; Seo, K.H.; Dong, C.; Huang, G.; Foltz, G.R.; Jiang, J.H. Responses of the tropical atmospheric circulation to climate change and connection to the hydrological cycle. Annu. Rev. Earth Planet. Sci. 2018, 46, 549–580. [Google Scholar] [CrossRef]
- Zohaib, M.; Kim, H.; Choi, M. Evaluating the patterns of spatiotemporal trends of root zone soil moisture in major climate regions in East Asia. J. Geophys. Res. Atmos. 2017, 122, 7705–7722. [Google Scholar] [CrossRef]
- Lu, J.; Wang, G.; Li, S.; Feng, A.; Zhan, M.; Jiang, T.; Su, B.; Wang, Y. Projected Land Evaporation and Its Response to Vegetation Greening over China Under Multiple Scenarios in the CMIP6 Models. J. Geophys. Res. Biogeosci. 2021, 126, e2021JG006327. [Google Scholar] [CrossRef]
- Lu, J.; Sun, G.; McNulty, S.G.; Amatya, D.M. Modeling actual evapotranspiration from forested watersheds across the southeastern united states. JAWRA J. Am. Water Resour. Assoc. 2003, 39, 886–896. [Google Scholar] [CrossRef]
- Jun, W.; Xinhua, W.; Meihua, G.; Xuyan, X. Impact of Climate Change on Reference Crop Evapotranspiration in Chuxiong City, Yunnan Province. Procedia Earth Planet. Sci. 2012, 5, 113–119. [Google Scholar] [CrossRef]
- Montroull, N.B.; Saurral, R.I.; Camilloni, I.A. Hydrological impacts in La Plata basin under 1.5, 2 and 3 °C global warming above the pre-industrial level. Int. J. Clim. 2018, 38, 3355–3368. [Google Scholar] [CrossRef]
- Eyring, V.; Cox, P.M.; Flato, G.M.; Gleckler, P.J.; Abramowitz, G.; Caldwell, P.; Collins, W.D.; Gier, B.K.; Hall, A.D.; Hoffman, F.M.; et al. Taking climate model evaluation to the next level. Nat. Clim. Chang. 2019, 9, 102–110. [Google Scholar] [CrossRef]
- Van Vuuren, D.P.; Kriegler, E.; O’Neill, B.C.; Ebi, K.L.; Riahi, K.; Carter, T.R.; Edmonds, J.; Hallegatte, S.; Kram, T.; Mathur, R.; et al. A new scenario framework for Climate Change Research: Scenario matrix architecture. Clim. Chang. 2013, 122, 373–386. [Google Scholar] [CrossRef]
- Riahi, K.; Van Vuuren, D.P.; Kriegler, E.; Edmonds, J.; O’Neill, B.C.; Fujimori, S.; Bauer, N.; Calvin, K.; Dellink, R.; Fricko, O.; et al. The Shared Socioeconomic Pathways and their energy, land use, and greenhouse gas emissions implications: An overview. Glob. Environ. Chang. 2016, 42, 153–168. [Google Scholar] [CrossRef]
- Fricko, O.; Havlik, P.; Rogelj, J.; Klimont, Z.; Gusti, M.; Johnson, N.; Kolp, P.; Strubegger, M.; Valin, H.; Amann, M. The marker quantification of the Shared Socioeconomic Pathway 2: A middle-of-the-road scenario for the 21st century. Glob. Environ. Chang. 2017, 42, 251–267. [Google Scholar] [CrossRef] [Green Version]
- Fujimori, S.; Hasegawa, T.; Masui, T.; Takahashi, K.; Herran, D.S.; Dai, H.; Hijioka, Y.; Kainuma, M. SSP3: AIM implementation of Shared Socioeconomic Pathways. Glob. Environ. Chang. 2017, 42, 268–283. [Google Scholar] [CrossRef]
- Calvin, K.; Bond-Lamberty, B.; Clarke, L.; Edmonds, J.; Eom, J.; Hartin, C.; Kim, S.; Kyle, P.; Link, R.; Moss, R.; et al. The SSP4: A world of deepening inequality. Glob. Environ. Chang. 2017, 42, 284–296. [Google Scholar] [CrossRef]
- Kriegler, E.; Bauer, N.; Popp, A.; Humpenöder, F.; Leimbach, M.; Strefler, J.; Baumstark, L.; Bodirsky, B.L.; Hilaire, J.; Klein, D.; et al. Fossil-fueled development (SSP5): An energy and resource intensive scenario for the 21st century. Glob. Environ. Chang. 2017, 42, 297–315. [Google Scholar] [CrossRef]
- Turner, D.P.; Conklin, D.R.; Vache, K.B.; Schwartz, C.; Nolin, A.W.; Chang, H.; Watson, E.; Bolte, J.P. Assessing mechanisms of climate change impact on the upland forest water balance of the Willamette River Basin, Oregon. Ecohydrology 2017, 10, e1776. [Google Scholar] [CrossRef]
- Parsons, L.A.; Brennan, M.K.; Wills, R.C.; Proistosescu, C. Magnitudes and Spatial Patterns of Interdecadal Temperature Variability in CMIP6. Geophys. Res. Lett. 2020, 47, e2019GL086588. [Google Scholar] [CrossRef]
- Li, B.; Rodell, M.; Zaitchik, B.F.; Reichle, R.H.; Koster, R.D.; van Dam, T.M. Assimilation of GRACE terrestrial water storage into a land surface model: Evaluation and potential value for drought monitoring in western and central Europe. J. Hydrol. 2012, 446–447, 103–115. [Google Scholar] [CrossRef]
- Deser, C.; Phillips, A.; Bourdette, V.; Teng, H. Uncertainty in climate change projections: The role of internal variability. Clim. Dyn. 2012, 38, 527–546. [Google Scholar] [CrossRef]
- Zhuan, M.; Chen, J.; Xu, C.-Y.; Zhao, C.; Xiong, L.; Liu, P. A method for investigating the relative importance of three components in overall uncertainty of climate projections. Int. J. Clim. 2018, 39, 1853–1871. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, J. Uncertainty in Projection of Climate Extremes: A Comparison of CMIP5 and CMIP6. J. Meteorol. Res. 2021, 35, 646–662. [Google Scholar] [CrossRef]
- Weigel, A.P.; Liniger, M.A.; Appenzeller, C. Can multi-model combination really enhance the prediction skill of probabilistic ensemble forecasts? Q. J. R. Meteorol. Soc. 2008, 134, 241–260. [Google Scholar] [CrossRef]
- White, R.H.; Toumi, R. The limitations of bias correcting regional climate model inputs. Geophys. Res. Lett. 2013, 40, 2907–2912. [Google Scholar] [CrossRef]
- Maraun, D.; Widmann, M. Structure of statistical downscaling methods. In Statistical Downscaling and Bias Correction for Climate Research; Cambridge University Press: Cambridge, UK, 2018; pp. 135–140. [Google Scholar]
- Adachi, S.A.; Tomita, H. Methodology of the constraint condition in dynamical downscaling for regional climate evaluation: A review. J. Geophys. Res. Atmos. 2020, 125, e2019JD032166. [Google Scholar] [CrossRef]
- Zhu, J.; Huang, G.; Wang, X.; Cheng, G.; Wu, Y. High-resolution projections of mean and extreme precipitations over China through PRECIS under RCPs. Clim. Dyn. 2018, 50, 4037–4060. [Google Scholar] [CrossRef]
- Stefanidis, S. Ability of Different Spatial Resolution Regional Climate Model to Simulate Air Temperature in a Forest Ecosystem of Central Greece. J. Environ. Prot. Ecol. 2021, 22, 1488–1495. [Google Scholar]
- Xue, Y.; Janjic, Z.; Dudhia, J.; Vasic, R.; De Sales, F. A review on regional dynamical downscaling in intraseasonal to seasonal simulation/prediction and major factors that affect downscaling ability. Atmospheric Res. 2014, 147–148, 68–85. [Google Scholar] [CrossRef]
- Sachindra, D.; Ahmed, K.; Rashid, M.; Shahid, S.; Perera, B. Statistical downscaling of precipitation using machine learning techniques. Atmos. Res. 2018, 212, 240–258. [Google Scholar] [CrossRef]
- Das, L.; Akhter, J. How well are the downscaled CMIP5 models able to reproduce the monsoon precipitation over seven homogeneous zones of India? Int. J. Clim. 2019, 39, 3323–3333. [Google Scholar] [CrossRef]
- Asong, Z.; Khaliq, M.; Wheater, H. Projected changes in precipitation and temperature over the Canadian Prairie Provinces using the Generalized Linear Model statistical downscaling approach. J. Hydrol. 2016, 539, 429–446. [Google Scholar] [CrossRef]
- Miao, C.; Ashouri, H.; Hsu, K.-L.; Sorooshian, S.; Duan, Q. Evaluation of the PERSIANN-CDR Daily Rainfall Estimates in Capturing the Behavior of Extreme Precipitation Events over China. J. Hydrometeorol. 2015, 16, 1387–1396. [Google Scholar] [CrossRef]
- Ho, C.K.; Stephenson, D.B.; Collins, M.; Ferro, C.A.T.; Brown, S.J. Calibration Strategies: A Source of Additional Uncertainty in Climate Change Projections. Bull. Am. Meteorol. Soc. 2012, 93, 21–26. [Google Scholar] [CrossRef]
- Fang, G.H.; Yang, J.; Chen, Y.N.; Zammit, C. Comparing bias correction methods in downscaling meteorological variables for a hydrologic impact study in an arid area in China. Hydrol. Earth Syst. Sci. 2015, 19, 2547–2559. [Google Scholar] [CrossRef] [Green Version]
- Themeßl, M.J.; Gobiet, A.; Leuprecht, A. Empirical-statistical downscaling and error correction of daily precipitation from regional climate models. Int. J. Climatol. 2011, 31, 1530–1544. [Google Scholar] [CrossRef]
- Bruyère, C.L.; Done, J.M.; Holland, G.J.; Fredrick, S. Bias corrections of global models for regional climate simulations of high-impact weather. Clim. Dyn. 2014, 43, 1847–1856. [Google Scholar] [CrossRef]
- Colette, A.; Vautard, R.; Vrac, M. Regional climate downscaling with prior statistical correction of the global climate forcing. Geophys. Res. Lett. 2012, 39, L13707. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Ham, Y.-G.; Kim, J.-H.; Luo, J.-J. Deep learning for multi-year ENSO forecasts. Nature 2019, 573, 568–572. [Google Scholar] [CrossRef]
- Kadow, C.; Hall, D.M.; Ulbrich, U. Artificial intelligence reconstructs missing climate information. Nat. Geosci. 2020, 13, 408–413. [Google Scholar] [CrossRef]
- Tian, L.; Sun, J.; Chang, J.; Xia, J.; Zhang, Z.; Kolomenskii, A.A.; Schuessler, H.A.; Zhang, S. Retrieval of gas concentrations in optical spectroscopy with deep learning. Measurement 2021, 182, 109739. [Google Scholar] [CrossRef]
- Yoon, Y.; Jeon, H.-G.; Yoo, D.; Lee, J.-Y.; Kweon, I.S. Learning a Deep Convolutional Network for Light-Field Image Super-Resolution. In Proceedings of the 2015 IEEE International Conference on Computer Vision Workshop (ICCVW), Santiago, Chile, 7–13 December 2015; pp. 57–65. [Google Scholar] [CrossRef]
- Zhang, L.; Nie, J.; Wei, W.; Zhang, Y.; Liao, S.; Shao, L. Unsupervised Adaptation Learning for Hyperspectral Imagery Super-Resolution. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 3070–3079. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, S.; Wang, X. Learning continuous image representation with local implicit image function. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 8628–8638. [Google Scholar]
- Vandal, T.; Kodra, E.; Ganguly, S.; Michaelis, A.; Nemani, R.; Ganguly, A. Generating High Resolution Climate Change Projections through Single Image Super-Resolution. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ‘17), Halifax, NS, Canada, 13–17 August 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 1663–1672. [Google Scholar]
- Rodrigues, E.R.; Oliveira, I.; Cunha, R.; Netto, M. DeepDownscale: A deep learning strategy for high-resolution weather forecast. In Proceedings of the 2018 IEEE 14th International Conference on e-Science (e-Science), Amsterdam, The Netherlands, 29 October–1 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 415–422. [Google Scholar]
- Lu, J.; Wang, G.; Chen, T.; Li, S.; Hagan, D.F.T.; Kattel, G.; Peng, J.; Jiang, T.; Su, B. A harmonized global land evaporation dataset from model-based products covering 1980–2017. Earth Syst. Sci. Data 2021, 13, 5879–5898. [Google Scholar] [CrossRef]
- Liu, Y.; Ganguly, A.R.; Dy, J. Climate Downscaling Using YNet. In Proceedins of the 26th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Virtual Event, CA, USA, 6–10 July 2020; pp. 3145–3153. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Feng, D.; Wang, G.; Wei, X.; Amankwah, S.O.Y.; Hu, Y.; Luo, Z.; Hagan, D.F.T.; Ullah, W. Merging and Downscaling Soil Moisture Data From CMIP6 Projections Using Deep Learning Method. Front. Environ. Sci. 2022, 10. [Google Scholar] [CrossRef]
- Wang, Z.; Zhan, C.; Ning, L.; Guo, H. Evaluation of global terrestrial evapotranspiration in CMIP6 models. Arch. Meteorol. Geophys. Bioclimatol. Ser. B 2021, 143, 521–531. [Google Scholar] [CrossRef]
- Niu, Z.; Wang, L.; Chen, X.; Yang, L.; Feng, L. Spatiotemporal distributions of pan evaporation and the influencing factors in China from 1961 to 2017. Environ. Sci. Pollut. Res. 2021, 28, 68379–68397. [Google Scholar] [CrossRef] [PubMed]
- Brêda, J.P.; de Paiva, R.C.; Collischon, W.; Bravo, J.M.; Siqueira, V.A.; Steinke, E.B. Climate change impacts on South American water balance from a continental-scale hydrological model driven by CMIP5 projections. Clim. Chang. 2020, 159, 503–522. [Google Scholar] [CrossRef]
- Sullivan, R.C.; Kotamarthi, V.R.; Feng, Y. Recovering Evapotranspiration Trends from Biased CMIP5 Simulations and Sensitivity to Changing Climate over North America. J. Hydrometeorol. 2019, 20, 1619–1633. [Google Scholar] [CrossRef]
- Stefanidis, S.; Alexandridis, V. Precipitation and Potential Evapotranspiration Temporal Variability and Their Relationship in Two Forest Ecosystems in Greece. Hydrology 2021, 8, 160. [Google Scholar] [CrossRef]
- Ajjur, S.B.; Al-Ghamdi, S.G. Evapotranspiration and water availability response to climate change in the Middle East and North Africa. Clim. Chang. 2021, 166, 28. [Google Scholar] [CrossRef]
- Zhan, M.Y.; Wang, G.J.; Lu, J.; Chen, L.Q.; Zhu, C.X.; Jiang, T.; Wang, Y.J. Projected evapotranspiration and the influencing factors in the Yangtze River Basin based on CMIP6 models. Trans. Atmos. Sci. 2020, 43, 1115–1126. (In Chinese) [Google Scholar] [CrossRef]
- Wang, X.; Chan, K.C.; Yu, K.; Dong, C.; Loy, C.C. EDVR: Video Restoration with Enhanced Deformable Convolutional Networks. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Long Beach, CA, USA, 16–17 June 2019; pp. 1954–1963. [Google Scholar] [CrossRef] [Green Version]
| Institution (Country) | Model Name | Resolution (Lon × Lat) | Used Member |
|---|---|---|---|
| CSIRO (Australia) | ACCESS-CM2 | 1.875° × 1.25° | r1i1p1f1 |
| BCC (China) | BCC-CSM2-MR | 2.25° × 2.25° | r1i1p1f1 |
| CAMS (China) | CAMS-CSM1-0 | 1.125° × 1.125° | r1i1p1f1 |
| NCAR (USA) | CESM2-WACCM | 2.5° × 1.875° | r1i1p1f1 |
| CESM2 | r1i1p1f1 | ||
| CNRM-CERFACS (France) | CNRM-CM6-1-HR | 1.25° × 0.9375° | r1i1p1f2 |
| CNRM-ESM2-1 | r1i1p1f2 | ||
| CCCMA (Canada) | CanESM5 | 2.8125° × 2.8125° | r1i1p1f1 |
| EC-Earth Consortium (EU) | EC-Earth3-Veg | 0.703125° × 0.703125° | r1i1p1f1 |
| CAS (China) | FGOALS-f3-L | 2.5° × 2° | r1i1p1f1 |
| NOAA-GFDL (USA) | GFDL-ESM4 | 2.5° × 2° | r1i1p1f1 |
| INM (Russia) | INM-CM4-8 | 2° × 1.5° | r1i1p1f1 |
| INM-CM5-0 | r1i1p1f1 | ||
| IPSL (France) | IPSL-CM6A-LR | 2.5° × 1.259° | r1i1p1f1 |
| MIROC (Japan) | MIROC-ES2L | 2.8125° × 2.8125° | r1i1p1f2 |
| MIROC6 | 2.8125° × 0.703125° | r1i1p1f1 | |
| MPI-M (Germany) | MPI-ESM1-2-HR | 0.9375° × 0.9375° | r1i1p1f1 |
| MPI-ESM1-2-LR | 1.875° × 1.875° | r1i1p1f1 | |
| MRI (Japan) | MRI-ESM2-0 | 1.125° × 1.125° | r1i1p1f1 |
| NCC (Norway) | NorESM2-LM | 5° × 3.75° | r1i1p1f1 |
| NorESM2-MM | 2.5° × 1.875° | r1i1p1f1 | |
| MOHC (UK) | UKESM1-0-LL | 1.875° × 1.25° | r1i1p1f2 |
| Methods | MAE | RMSE | ubRMSD | R |
|---|---|---|---|---|
| DL data | 5.91 | 5.86 | 5.88 | 0.95 |
| MEM data | 14.63 | 21.16 | 19.01 | 0.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, X.; Wei, X.; Tian, W.; Wang, G.; Zhu, W. The Future Change in Evaporation Based on the CMIP6 Merged Data Generated by Deep-Learning Method in China. Water 2022, 14, 2800. https://doi.org/10.3390/w14182800
Niu X, Wei X, Tian W, Wang G, Zhu W. The Future Change in Evaporation Based on the CMIP6 Merged Data Generated by Deep-Learning Method in China. Water. 2022; 14(18):2800. https://doi.org/10.3390/w14182800
Chicago/Turabian StyleNiu, Xianghua, Xikun Wei, Wei Tian, Guojie Wang, and Wenhui Zhu. 2022. "The Future Change in Evaporation Based on the CMIP6 Merged Data Generated by Deep-Learning Method in China" Water 14, no. 18: 2800. https://doi.org/10.3390/w14182800





