Assessment of Net Erosion and Suspended Sediments Yield within River Basins of the Agricultural Belt of Russia
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.2.1. Relief and LS-Factor
2.2.2. Field Observations
2.2.3. Land Use
2.2.4. Precipitation
2.2.5. Soils
2.3. Methodology
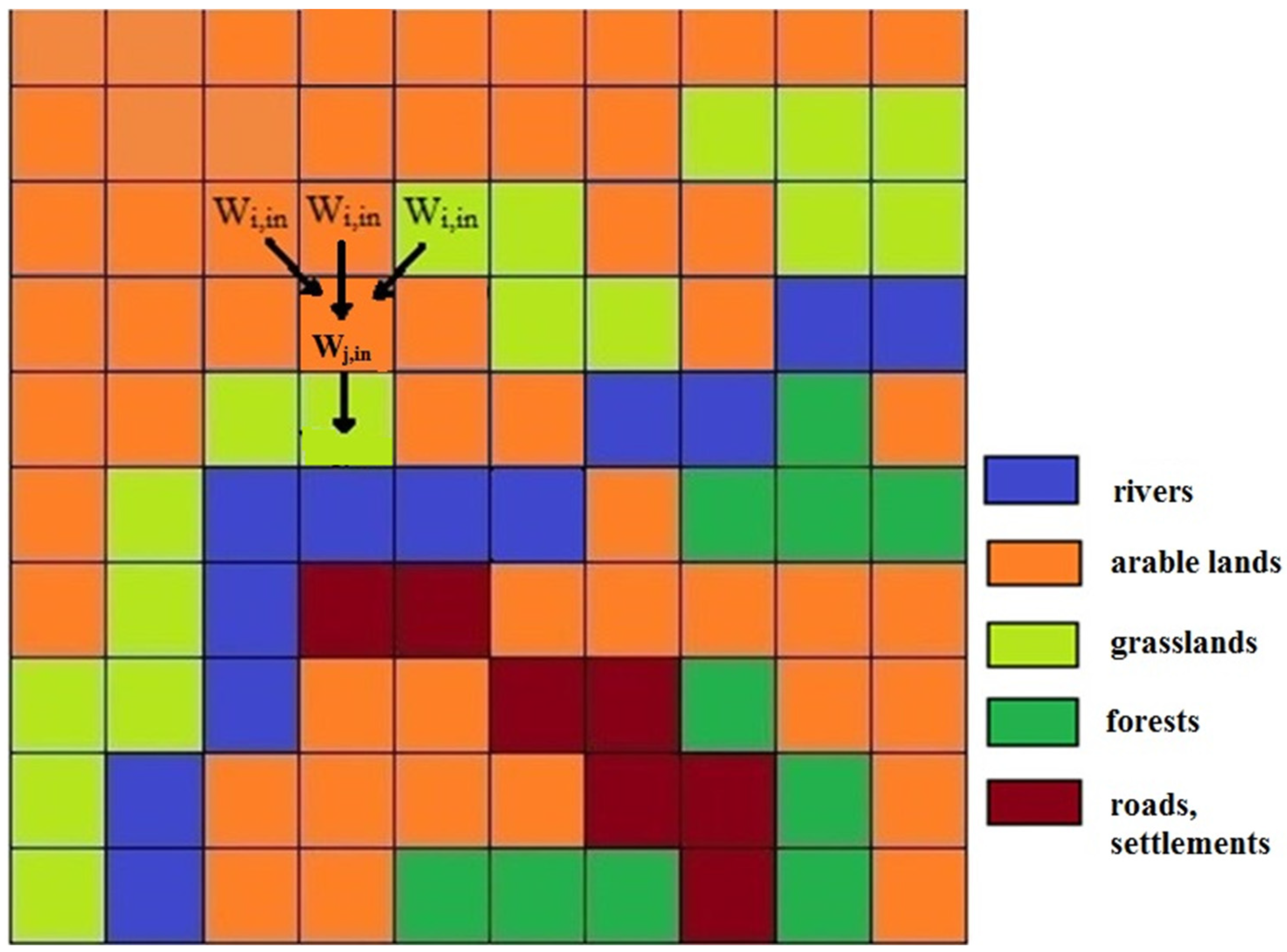
2.3.1. WATEM/SEDEM Model
2.3.2. SEA/Balance Model
2.3.3. Comparative Analysis Method
3. Results
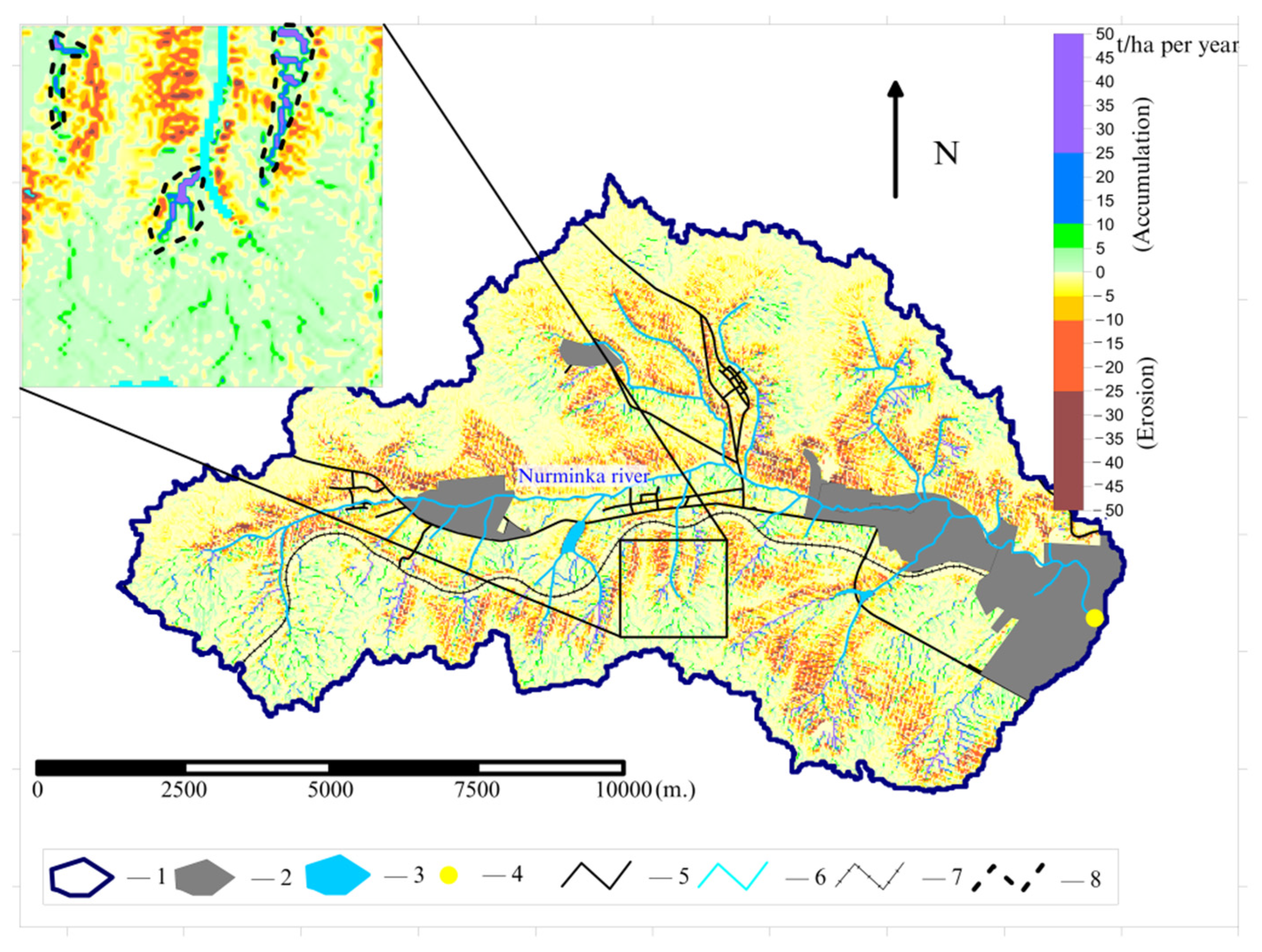
Analysis of Sediment Yield Dynamics
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Walling, D.E. The Sediment Delivery Problem. J. Hydrol. 1983, 65, 209–237. [Google Scholar] [CrossRef]
- Litvin, L.F. Geography of Soil Erosion of Agricultural Lands in Russia; Akademkniga: Moscow, Russia, 2002. [Google Scholar]
- Golosov, V.; Yermolaev, O.; Litvin, L.; Chizhikova, N.; Kiryukhina, Z.; Safina, G. Influence of Climate and Land Use Changes on Recent Trends of Soil Erosion Rates within the Russian Plain. Land Degrad. Dev. 2018, 29, 2658–2667. [Google Scholar] [CrossRef]
- Prishchepov, A.; Müller, D.; Dubinin, M.; Baumann, M.; Radeloff, V.C. Determinants of the Spatial Distribution of Abandoned Agricultural Lands in the European Part of Russia. Spat. Econ. 2013, 3, 30–62. [Google Scholar] [CrossRef]
- Ivanov, M.A.; Prishchepov, A.V.; Golosov, V.N.; Zalyaliev, R.R.; Efimov, K.V.; Kondrat’eva, A.A.; Kinyashova, A.D.; Ionova, Y.K. Method of Croplands Dynamics Mapping in River Basins of the European Part of Russia for the Period of 1985–2015. Sovr. Probl. DZZ Kosm. 2017, 14, 161–171. [Google Scholar] [CrossRef]
- Krasilnikov, P.; Makarov, O.; Alyabina, I.; Nachtergaele, F. Assessing Soil Degradation in Northern Eurasia. Geoderma Reg. 2016, 7, 1–10. [Google Scholar] [CrossRef]
- Maltsev, K.; Yermolaev, O. Assessment of Soil Loss by Water Erosion in Small River Basins in Russia. Catena 2020, 195, 104726. [Google Scholar] [CrossRef]
- Warren, S.D.; Ruzycki, T.S.; Vaughan, R.; Nissen, P.E. Validation of the Unit Stream Power Erosion and Deposition (USPED) Model at Yakima Training Center, Washington. Northwest Sci. 2019, 92, 338. [Google Scholar] [CrossRef]
- De Vente, J.; Poesen, J.; Verstraeten, G.; Van Rompaey, A.; Govers, G. Spatially Distributed Modelling of Soil Erosion and Sediment Yield at Regional Scales in Spain. Glob. Planet. Chang. 2008, 60, 393–415. [Google Scholar] [CrossRef]
- Alatorre, L.C.; Beguería, S.; García-Ruiz, J.M. Regional Scale Modeling of Hillslope Sediment Delivery: A Case Study in the Barasona Reservoir Watershed (Spain) Using WATEM/SEDEM. J. Hydrol. 2010, 391, 109–123. [Google Scholar] [CrossRef]
- Pietroń, J.; Chalov, S.R.; Chalova, A.S.; Alekseenko, A.V.; Jarsjö, J. Extreme Spatial Variability in Riverine Sediment Load Inputs Due to Soil Loss in Surface Mining Areas of the Lake Baikal Basin. Catena 2017, 152, 82–93. [Google Scholar] [CrossRef]
- Boardman, J.; Poesen, J. Soil Erosion in Europe: Major Processes, Causes and Consequences. In Soil Erosion in Europe; John Wiley & Sons, Ltd.: Chichester, UK, 2006; pp. 477–487. ISBN 978-0-470-85920-9. [Google Scholar]
- Borrelli, P.; Alewell, C.; Alvarez, P.; Anache, J.A.A.; Baartman, J.; Ballabio, C.; Bezak, N.; Biddoccu, M.; Cerdà, A.; Chalise, D.; et al. Soil Erosion Modelling: A Global Review and Statistical Analysis. Sci. Total Environ. 2021, 780, 146494. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; USDA: Washington, DC, USA, 1978; p. 67. [Google Scholar]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K. Predicting Soil Erosion by Water: A Guide to Conservation Planning With the Resived Universal Soil Loss Equation (RUSLE). In Agriculture Handbook; SSOP: Washington, DC, USA, 1997; ISBN 0-16-048938-5. [Google Scholar]
- Dabney, S.M.; Yoder, D.C.; Vieira, D.A.N. The Application of the Revised Universal Soil Loss Equation, Version 2, to Evaluate the Impacts of Alternative Climate Change Scenarios on Runoff and Sediment Yield. J. Soil Water Conserv. 2012, 67, 343–353. [Google Scholar] [CrossRef]
- Schob, A.; Schmidt, J.; Tenholtern, R. Derivation of Site-Related Measures to Minimise Soil Erosion on the Watershed Scale in the Saxonian Loess Belt Using the Model EROSION 3D. Catena 2006, 68, 153–160. [Google Scholar] [CrossRef]
- Vigiak, O.; Malagó, A.; Bouraoui, F.; Vanmaercke, M.; Poesen, J. Adapting SWAT Hillslope Erosion Model to Predict Sediment Concentrations and Yields in Large Basins. Sci. Total Environ. 2015, 538, 855–875. [Google Scholar] [CrossRef] [PubMed]
- Walling, D.E.; Russell, M.A.; Hodgkinson, R.A.; Zhang, Y. Establishing Sediment Budgets for Two Small Lowland Agricultural Catchments in the UK. Catena 2002, 47, 323–353. [Google Scholar] [CrossRef]
- Boomer, K.B.; Weller, D.E.; Jordan, T.E. Empirical Models Based on the Universal Soil Loss Equation Fail to Predict Sediment Discharges from Chesapeake Bay Catchments. J. Environ. Qual. 2008, 37, 79–89. [Google Scholar] [CrossRef]
- Baartman, J.E.M.; Masselink, R.; Keesstra, S.D.; Temme, A.J.A.M. Linking Landscape Morphological Complexity and Sediment Connectivity: Landscape morphological complexity and sediment connectivity. Earth Surf. Process. Landf. 2013, 38, 1457–1471. [Google Scholar] [CrossRef]
- Heckmann, T.; Cavalli, M.; Cerdan, O.; Foerster, S.; Javaux, M.; Lode, E.; Smetanová, A.; Vericat, D.; Brardinoni, F. Indices of Sediment Connectivity: Opportunities, Challenges and Limitations. Earth Sci. Rev. 2018, 187, 77–108. [Google Scholar] [CrossRef]
- Borselli, L.; Cassi, P.; Torri, D. Prolegomena to Sediment and Flow Connectivity in the Landscape: A GIS and Field Numerical Assessment. Catena 2008, 75, 268–277. [Google Scholar] [CrossRef]
- Zhao, G.; Gao, P.; Tian, P.; Sun, W.; Hu, J.; Mu, X. Assessing Sediment Connectivity and Soil Erosion by Water in a Representative Catchment on the Loess Plateau, China. Catena 2020, 185, 104284. [Google Scholar] [CrossRef]
- Gay, A.; Cerdan, O.; Mardhel, V.; Desmet, M. Application of an Index of Sediment Connectivity in a Lowland Area. J. Soils Sediments 2016, 16, 280–293. [Google Scholar] [CrossRef]
- López-Vicente, M.; Navas, A.; Gaspar, L.; Machín, J. Advanced Modelling of Runoff and Soil Redistribution for Agricultural Systems: The SERT Model. Agric. Water Manag. 2013, 125, 1–12. [Google Scholar] [CrossRef]
- Chartin, C.; Evrard, O.; Onda, Y.; Patin, J.; Lefèvre, I.; Ottlé, C.; Ayrault, S.; Lepage, H.; Bonté, P. Tracking the Early Dispersion of Contaminated Sediment along Rivers Draining the Fukushima Radioactive Pollution Plume. Anthropocene 2013, 1, 23–34. [Google Scholar] [CrossRef]
- Vigiak, O.; Borselli, L.; Newham, L.T.H.; McInnes, J.; Roberts, A.M. Comparison of Conceptual Landscape Metrics to Define Hillslope-Scale Sediment Delivery Ratio. Geomorphology 2012, 138, 74–88. [Google Scholar] [CrossRef]
- Ferro, V.; Porto, P. Sediment Delivery Distributed (SEDD) Model. J. Hydrol. Eng. 2000, 5, 411–422. [Google Scholar] [CrossRef]
- Bhattarai, R.; Dutta, D. A Comparative Analysis of Sediment Yield Simulation by Empirical and Process-Oriented Models in Thailand / Une Analyse Comparative de Simulations de l’exportation Sédimentaire En Thaïlande à l’aide de Modèles Empiriques et de Processus. Hydrol. Sci. J. 2008, 53, 1253–1269. [Google Scholar] [CrossRef]
- Verstraeten, G.; Prosser, I.P.; Fogarty, P. Predicting the Spatial Patterns of Hillslope Sediment Delivery to River Channels in the Murrumbidgee Catchment, Australia. J. Hydrol. 2007, 334, 440–454. [Google Scholar] [CrossRef]
- Haregeweyn, N.; Poesen, J.; Verstraeten, G.; Govers, G.; de Vente, J.; Nyssen, J.; Deckers, J.; Moeyersons, J. Assessing the performance of a spatially distributed soil erosion and sediment delivery model (watem/sedem) in northern ethiopia: Spatially distributed soil erosion and sedementation. Land Degrad. Develop. 2013, 24, 188–204. [Google Scholar] [CrossRef]
- Zhidkin, A.P.; Smirnova, M.A.; Gennadiev, A.N.; Lukin, S.V.; Zazdravnykh, Y.A.; Lozbenev, N.I. Digital Mapping of Soil Associations and Eroded Soils (Prokhorovskii District, Belgorod Oblast). Eurasian Soil Sci. 2021, 54, 13–24. [Google Scholar] [CrossRef]
- Van Rompaey, A.J.J.; Verstraeten, G.; Van Oost, K.; Govers, G.; Poesen, J. Modelling Mean Annual Sediment Yield Using a Distributed Approach. Earth Surf. Process. Landf. 2001, 26, 1221–1236. [Google Scholar] [CrossRef]
- Unified State Register of Soil Resources of Russia, Version 1.0; Institute of Soil Science: Moscow, Russian, 2014.
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
- Mal’tsev, K.A.; Golosov, V.N.; Gafurov, A.M. Digital elevation models and their use for assessing soil erosion rates on arable lands. Uch. Zap. Kazan. Univ. Ser. Estestv. Nauk. 2018, 160, 514–530. [Google Scholar]
- Ashatkin, I.A.; Maltsev, K.A.; Gainutdinova, G.F.; Usmanov, B.M.; Gafurov, A.M.; Ganieva, A.F.; Maltseva, T.S.; Gizzatullina, E.R. Analysis of Relief Morphometry by Global DEM in the Southern Part of the European Territory of Russia. Uch. Zap. Kazan. Univ. Ser. Estestv. Nauki 2020, 162, 612–628. [Google Scholar] [CrossRef]
- Lindsay, J.B. The Terrain Analysis System: A Tool for Hydro-Geomorphic Applications. Hydrol. Process. 2005, 19, 1123–1130. [Google Scholar] [CrossRef]
- Lindsay, J.B.; Creed, I.F. Removal of Artifact Depressions from Digital Elevation Models: Towards a Minimum Impact Approach. Hydrol. Process. 2005, 19, 3113–3126. [Google Scholar] [CrossRef]
- Desmet, J.J.; Govers, G. A GIS Procedure for Automatically Calculating the USLE LS Factor on Topographically Complex Landscape Units. J. Soil Water Conserv. 1996, 51, 427–433. [Google Scholar]
- Yermolaev, O.; Mukharamova, S.; Vedeneeva, E. River Runoff Modeling in the European Territory of Russia. Catena 2021, 203, 105327. [Google Scholar] [CrossRef]
- Lyuri, D.I.; Goryachkin, S.V.; Karavaeva, N.A.; Denisenko, E.A.; Nefedova, T.G. Dynamics of Agricultural Lands in Russia in the XX Century and the Postagrogenic Restoration of Vegetation and Soils; GEOS: Moscow, Russia, 2010; ISBN 978-5-89118-500-5. [Google Scholar]
- Ivanov, M.A. Changes of Cropland Area in the River Basins of the European Part of Russia for the Period 1985-2015 Years, as a Factor of Soil Erosion Dynamics. IOP Conf. Ser. Earth Environ. Sci. 2018, 107, 012010. [Google Scholar] [CrossRef]
- Litvin, L.F.; Kiryukhina, Z.P.; Krasnov, S.F.; Dobrovol’skaya, N.G. Dynamics of Agricultural Soil Erosion in European Russia. Eurasian Soil Sci. 2017, 50, 1344–1353. [Google Scholar] [CrossRef]
- Kanatieva, N.P.; Krasnov, S.F.; Litvin, L.F. Modern Change of Climate Factors of Erosion in Northern Volga Region. Soil Eros. Channel Process. 2010, 17, 14–28. [Google Scholar]
- Maltsev, K.A.; Yermolaev, O.P. Potential Soil Loss from Erosion on Arable Lands in the European Part of Russia. Eurasian Soil Sci. 2019, 52, 1588–1597. [Google Scholar] [CrossRef]
- Larionov, G.A. Eroziya I Deflyatsiya Pochv: Osnovnyye Zakonomernosti I Kolichestvennyye Otsenki (Water and Wind Erosion: Main Features and Quantitative Assessment); MSU Publishing House: Moscow, Russia, 1993; ISBN 978-5-211-02467-0. [Google Scholar]
- Rukhovich, D.I.; Koroleva, P.V.; Kalinina, N.V.; Vil’chevskaya, E.V.; Simakova, M.S.; Dolinina, E.A.; Rukhovich, S.V. State Soil Map of the Russian Federation: An ArcInfo Version. Eurasian Soil Sci. 2013, 46, 225–240. [Google Scholar] [CrossRef]
- Alekseevsky, N.I. Formirovaniye I Dvizheniye Rechnykh Nanosov (Formation and Movement of River Sediments); MSU Publishing House: Moscow, Russia, 1998. [Google Scholar]
- Dedkov, A. The Relationship between Sediment Yield and Drainage Basin Area. In Sediment Transfer through the Fluvial System, Proceedings of the Moscow International Symposium, Moscow, Russia, 2–6 August 2004; IAHS Publication: Wallingford, UK, 2004; Volume 288, pp. 197–204. [Google Scholar]
- Dedkov, A.P.; Mozzherin, V.V. Eroziya i Stok Nanosov na Zemle (Erosion and Sediment Runoff on the Earth); Kazan University: Kazan, Russia, 1984. [Google Scholar]
- Braude, I.D. Ratsionalʹnoye Ispolʹzovaniye Erodirovannykh Serykh Lesnykh Pochv Nechernozemnoy Zony RSFSR (Rational Use of Eroded Grey Forest Soils in the Non-Chernozem Zone of Russia); Lesnaya Promyshlennost Press: Moscow, Russia, 1976. [Google Scholar]
- Rozhkov, A.G. O Srednemnogoletney Velichine Smyva Pochv s Pashni v Tsentral’noy Chernozemnoy Zone (About Mean Annual Soil Erosion Rate from Cultivated Field of Central Chernozem Zone). Nauchno Tekhnicheskiy Bull. Zacshita Pochv Erozii 1977, 15, 13–18. [Google Scholar]
- Golosov, V.N. Erozionno-Akkumulyativnyye Protsessy i Balans Nanosov v Basseyne r. Protvy (Erosion-Accumulative Processes and Balance of Sediments in the Protva River Basin). Bull. Mosc. Univ. 1988, 6, 19–25. [Google Scholar]
- Ivanov, V.D.; Nazarenko, N.P. Vliyaniye Erozionnykh i Akkumulyativnykh Protsessov Na Strukturu Pochvennogo Pokrova Balochnykh Vodosborov (Influence of Erosion and Accumulation Processes on the Structure of the Soil Cover in Dry Valley Catchments). Eurasian Soil Sci. 1998, 1256–1264. [Google Scholar]
- Golosov, V.N.; Belyaev, V.R.; Markelov, M.V.; Shamshurina, E.N. Specifics of Sediment Redistribution Within a Small Arable Catchment During Different Periods of Its Cultivation (Gracheva Loschina Catchment, the Kursk Region). Geomorfologiâ 2015, 1, 25–35. [Google Scholar] [CrossRef]
- Zhidkin, A.P.; Golosov, V.N.; Svetlichny, A.A.; Pyatkova, A.V. An Assessment of Load on the Arable Slopes on the Basis of Field Methods and Mathematic Models. Geomorfologiâ 2015, 2, 41–53. [Google Scholar] [CrossRef]
- Golosov, V.N. Redistribution of Sediments on Small River Catchments of Temperate Zone. In Erosion and Sediment Yield: Global and Regional Perspectives, Proceedings of the Exeter Symposium, Exeter, UK, 15–19 July 1996; IAHS Publication: Wallingford, UK, 1996; pp. 339–346. [Google Scholar]
- Golosov, V.N. Special Considerations for Areas Affected by Chernobyl Fallout. In Handbook for the Assessment of Soil Erosion and Sedimentation Using Environmental Radionuclides; Zapata, F., Ed.; Springer: Dordrecht, The Netherlands, 2003; pp. 165–183. ISBN 978-0-306-48054-6. [Google Scholar]
- Golosov, V.N. Erozionno-Akkumulyativnyye Protsessy v Rechnykh Basseynakh Osvoyennykh Ravnin (Erosion and Deposition Processes in River Basins of Cultivated Plains); GEOS: Moscow, Russia, 2006. [Google Scholar]
- Golosov, V.N.; Panin, A.V.; Markelov, M.V. Chernobyl 137Cs Redistribution in the Small Basin of the Lokna River, Central Russia. Phys. Chem. Earth Part A Solid Earth Geod. 1999, 24, 881–885. [Google Scholar] [CrossRef]
- Panin, A.V.; Walling, D.E.; Golosov, V.N. The Role of Soil Erosion and Fluvial Processes in the Post-Fallout Redistribution of Chernobyl-Derived Caesium-137: A Case Study of the Lapki Catchment, Central Russia. Geomorphology 2001, 40, 185–204. [Google Scholar] [CrossRef]
- Golosov, V.N.; Ivanova, N.N. Sediment-Associated Chernobyl 137Cs Redistribution in the Small Basins of Central Russia. In Applied Geomorphology: Theory and Practice; Allison, R.J., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2002; pp. 165–181. [Google Scholar]
- Bezukhov, D.A.; Golosov, V.N.; Panin, A.V. Evaluation of the Sediment Delivery Ratio of Small Watersheds in the Forest-Steppe and Steppe Regions of the Russian Plain. Izv. Ross. Akad. Nauk. Seriya Geogr. 2019, 4, 73–84. (In Russian) [Google Scholar] [CrossRef]
- Golosov, V. Application of Chernobyl-Derived 137Cs for the Assessment of Soil Redistribution within a Cultivated Field. Soil Tillage Res. 2003, 69, 85–98. [Google Scholar] [CrossRef]
- Belyaev, V.; Markelov, M.V.; Golosov, V.; Bonté, P.; Ivanova, N. The Use of Cesium-137 to Assess Modern Agrogenic Transformation of Soil Cover in the Areas Subjected to Chernobyl Fallout. Eurasian Soil Sci. 2003, 36, 788–802. [Google Scholar]
- Belyaev, V.; Golosov, V.; Kislenko, K.S.; Kuznetsova, J.S.; Markelov, M.V. Combining Direct Observations, Modelling, and 137Cs Tracer for Evaluating Individual Event Contribution to Long-Term Sediment Budgets. IAHS-AISH Publ. 2008, 325, 114–122. [Google Scholar]
- Mal’tsev, K.A.; Ivanov, M.A.; Sharifullin, A.G.; Golosov, V.N. Changes in the Rate of Soil Loss in River Basins within the Southern Part of European Russia. Eurasian Soil Sci. 2019, 52, 718–727. [Google Scholar] [CrossRef]
- Walling, D.E.; Collins, A.L.; Sichingabula, H.M.; Leeks, G.J.L. Integrated Assessment of Catchment Suspended Sediment Budgets: A Zambian Example. Land Degrad. Dev. 2001, 12, 387–415. [Google Scholar] [CrossRef]
- Walling, D.E.; Collins, A.L.; Sichingabula, H.M. Using Unsupported Lead-210 Measurements to Investigate Soil Erosion and Sediment Delivery in a Small Zambian Catchment. Geomorphology 2003, 52, 193–213. [Google Scholar] [CrossRef]
- Walling, D.E. Human Impact on Land–Ocean Sediment Transfer by the World’s Rivers. Geomorphology 2006, 79, 192–216. [Google Scholar] [CrossRef]
- Blake, W.H.; Wallbrink, P.J.; Wilkinson, S.N.; Humphreys, G.S.; Doerr, S.H.; Shakesby, R.A.; Tomkins, K.M. Deriving Hillslope Sediment Budgets in Wildfire-Affected Forests Using Fallout Radionuclide Tracers. Geomorphology 2009, 104, 105–116. [Google Scholar] [CrossRef]
- Navas, A.; López-Vicente, M.; Gaspar, L.; Palazón, L.; Quijano, L. Establishing a Tracer-Based Sediment Budget to Preserve Wetlands in Mediterranean Mountain Agroecosystems (NE Spain). Sci. Total Environ. 2014, 496, 132–143. [Google Scholar] [CrossRef] [PubMed]
- Yermolaev, O.P.; Medvedeva, R.A.; Ivanov, M.A. Modern gully erosion in forest and forest-steppe landscapes of the east of the Russian Plain. Geomorphology 2021, 52, 28–41. [Google Scholar] [CrossRef]
- Butakov, G.P.; Serebrennikova, I.A.; Yusupova, V.V. The Dynamics of Gully Erosion and River at the End of the 20th Century on the Territory of the Republic of Tatarstan. In Modern and Ancient Erosion Processes; Butakov, G.P., Larionov, G.A., Eds.; Kazan University: Kazan, Russia, 2001; pp. 51–67. [Google Scholar]
- Gusarov, A.V.; Golosov, V.N.; Ivanov, M.M.; Sharifullin, A.G. Influence of Relief Characteristics and Landscape Connectivity on Sediment Redistribution in Small Agricultural Catchments in the Forest-Steppe Landscape Zone of the Russian Plain within European Russia. Geomorphology 2019, 327, 230–247. [Google Scholar] [CrossRef]
- Chalov, R.S.; Sidorchuk, A.Y.; Golosov, V.N. (Eds.) Catchment Erosion-Fluvial Systems: Monograph; INFRA-M: Moscow, Russia, 2017. [Google Scholar]
- Golosov, V.; Panin, A. Century-Scale Stream Network Dynamics in the Russian Plain in Response to Climate and Land Use Change. Catena 2006, 66, 74–92. [Google Scholar] [CrossRef]
- Park, H.; Sherstiukov, A.B.; Fedorov, A.N.; Polyakov, I.V.; Walsh, J.E. An Observation-Based Assessment of the Influences of Air Temperature and Snow Depth on Soil Temperature in Russia. Environ. Res. Lett. 2014, 9, 064026. [Google Scholar] [CrossRef]
- Petelko, A.I.; Golosov, V.N.; Belyaev, V.R. Experience of Design of System of Counter-Erosion Measures. In Proceedings of the 10th International Symposium on River Sedimentation, Moscow, Russia, 1–4 August 2007; Volume 1, pp. 311–316. [Google Scholar]
- Golosov, V.N. Erozionno-Akkumulyativnyye Protsessy Na Sklonakh v Yuzhnoy Chasti Nechernozemnoy Zony (Erosion-Accumulative Processes on Slopes in the Southern Part of the Non-Chernozem Zone). Geomorphologiya 1988, 6, 51–57. [Google Scholar]
- Barabanov, A.T.; Dolgov, S.V.; Koronkevich, N.I.; Panov, V.I.; Petel’ko, A.I. Surface Runoff and Snowmelt Infiltration into the Soil on Plowlands in the Forest-Steppe and Steppe Zones of the East European Plain. Eurasian Soil Sci. 2018, 51, 66–72. [Google Scholar] [CrossRef]
- Tsymbarovich, P.; Kust, G.; Kumani, M.; Golosov, V.; Andreeva, O. Soil Erosion: An Important Indicator for the Assessment of Land Degradation Neutrality in Russia. Int. Soil Water Conserv. Res. 2020, 8, 418–429. [Google Scholar] [CrossRef]
- Moatar, F.; Meybeck, M.; Raymond, S.; Birgand, F.; Curie, F. River Flux Uncertainties Predicted by Hydrological Variability and Riverine Material Behaviour: Predicting uncertainties when monitoring riverine material fluxes. Hydrol. Process. 2013, 27, 3535–3546. [Google Scholar] [CrossRef]


| River Basin ID | Nearest Climatic Station Name | P *—Warm Season, mm | P—Cold Season, mm | Mean Annual P, mm | T *—Warm Season, °C | T—Cold Season, °C | Mean Annual T, °C |
|---|---|---|---|---|---|---|---|
| 77194 | Kazan | 361 | 187 | 548 | 12.7 | −7.7 | 4.1 |
| 76644 | Kilmez | 389 | 153 | 542 | 11.7 | −8.8 | 3.1 |
| 77217 | Chulpanovo | 336 | 146 | 482 | 12.7 | −8.8 | 3.7 |
| 76324 | Sterlitamak | 335 | 185 | 520 | 13.1 | −9.5 | 3.7 |
| 76522 | Elabuga | 361 | 177 | 538 | 12.7 | −8.3 | 3.9 |
| 76520 | Elabuga | 361 | 177 | 538 | 12.7 | −8.3 | 3.9 |
| 75647 | Krasnoslobodsk | 359 | 180 | 539 | 12.9 | −6.9 | 4.6 |
| 78205 | Oktyabrsky Gorodok | 286 | 156 | 442 | 14.0 | −6.9 | 5.3 |
| 78157 | Rostashi | 321 | 128 | 449 | 14.1 | −6.0 | 5.7 |
| 76646 | Elabuga | 361 | 177 | 538 | 12.7 | −8.3 | 3.9 |
| 77222 | Samara | 323 | 228 | 551 | 14.5 | −7.0 | 5.6 |
| River Basin ID—River Name | Slope Angle, (deg) | Length of Slopes, (m) | Density of Dry Valley Network, (km/km2) | Density of River Network, (km/km2) | Cropland (%) of Catchment Area | Area (km2) |
|---|---|---|---|---|---|---|
| 77194—Betka river | 2.6 | 175 | 0.96 | 0.61 | 52 | 141 |
| 76644—Nurminka river | 2.3 | 133 | 0.52 | 0.57 | 69 | 96 |
| 77217—Malyy Cheremshan | 1.5 | 174 | 0.55 | 0.23 | 65 | 1254 |
| 76324—Sterlya River (1985) y. | 1.6 | 177 | - | 0.44 | 61 | 591 |
| 76324—Sterlya River (2018) y. | 1.6 | 162 | - | - | 56 | 591 |
| 76522—Menzelia river | 2.3 | 209 | 0.52 | 0.65 | 71 | 396 |
| 76520—Mellya river | 2.1 | 218 | 0.60 | 0.26 | 66 | 766 |
| 75647—Rudnya river | 2.3 | 200 | - | 0.26 | 63 | 1136 |
| 78205—Atkarka river | 1.8 | 176 | - | 0.58 | 78 | 1014 |
| 78157—Bolshoi Arkadak river | 1.5 | 142 | - | 0.12 | 73 | 1314 |
| 76646—Anzirka river | 2.5 | 182 | 0.80 | 1.55 | 56 | 226 |
| 77222—Birla river | 1.2 | 189 | 0.15 | 0.95 | 58 | 106 |
| River Basin ID | River | Observation Period | Duration (Years) |
|---|---|---|---|
| 77194 | Betka | 1946, 1963–1975 | 14 |
| 76644 | Nurminka | 1963–1985 | 22 |
| 77217 | Malyy Cheremshan | 1963–1980 | 18 |
| 76324 | Sterlya | 1986–1989, 1992–2013 | 35 |
| 76522 | Menzelia | 1963–1981 | 18 |
| 76520 | Mellya | 1964–1981 | 18 |
| 75647 | Rudnya | 1967–1984 | 15 |
| 78205 | Atkarka | 1965–1975 | 11 |
| 78157 | Bolshoi Arkadak | 1963–1975 | 13 |
| 76646 | Anzirka | 1965–1975 | 11 |
| 77222 | Birla | 1967–1982 | 11 |
| Land Category | 1985–1990 | 2013–2015 | ||
|---|---|---|---|---|
| Area, ha | Percent of the Total Area | Area, ha | Percent of the Total Area | |
| Water bodies | 39 | 0.06 | 35.1 | 0.06 |
| Forests | 4584.18 | 7.75 | 4602.6 | 7.79 |
| Meadows | 16,373.18 | 27.69 | 18,966.15 | 32.08 |
| Cropland | 36,571.01 | 61.88 | 32,924.00 | 55.67 |
| Urban areas | 1548.63 | 2.62 | 2588.15 | 4.4 |
| Total | 59,116 | 100 | 59,116 | 100 |
| Cold Period 1986–1990 (mm) | Warm Period 1986–1990 (mm) | Cold Period 1991–2013 (mm) | Warm Period 1991–2013 (mm) | |
|---|---|---|---|---|
| st. Sterlitamak—Sterlya River | 222 | 156 | 216 | 173 |
| Plan Curvature | |||||
|---|---|---|---|---|---|
| +(Concave, Convergent) | −(Convex, Divergent) | ||||
| Profile Curvature | +(concave) | Slope angle ≥ 3° | Slope angle < 3° | Slope angle ≥ 3° | Slope angle < 3° |
| 0.71 | 0.31 | 0.71 | 0.31 | ||
| −(convex) | Slope angle ≥ 3° | Slope angle < 3° | Slope angle ≥ 3° | Slope angle < 3° | |
| 0.78 | 0.59 | 0.86 | 0.32 | ||
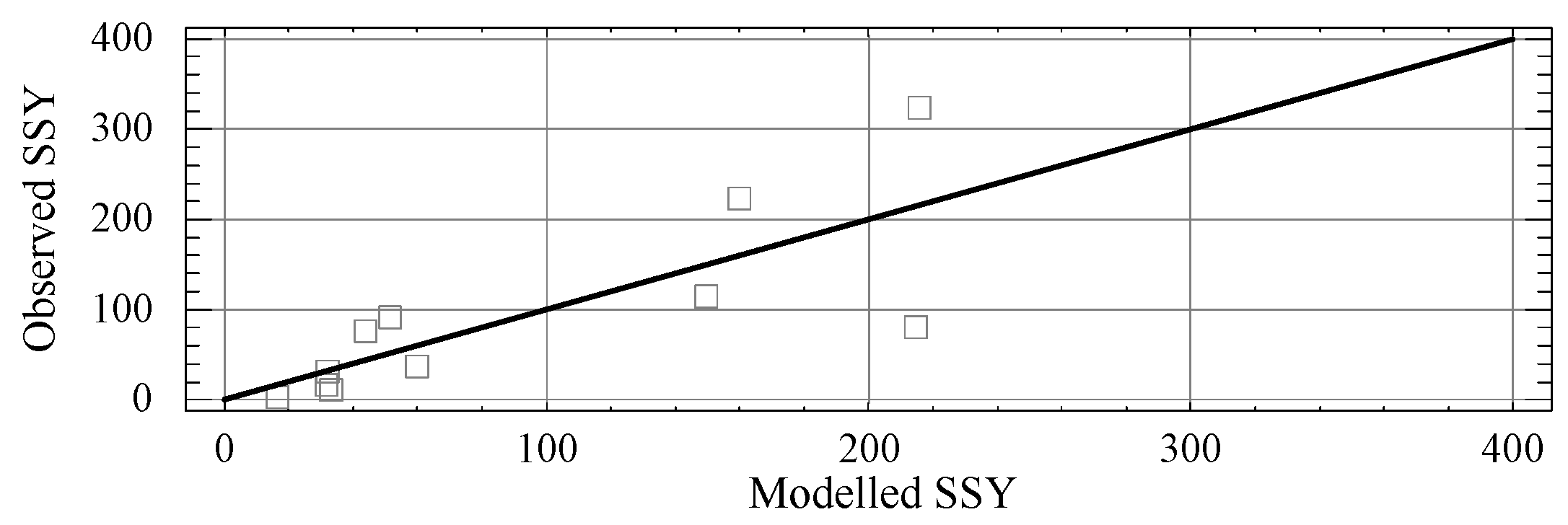
| River Basin ID | River | SSYmod1 * (t/km2 per Year) | SSYmod2 * (t/km2 per Year) | SSYobs * (t/km2 per Year) | ERRmod1 *, % | ERRmod2 *, % |
|---|---|---|---|---|---|---|
| 77194 | Betka | 323 | 341 | 365 | −12 | −7 |
| 76644 | Nurminka | 115 | 410 | 246 | −53 | +67 |
| 77217 | Malyy Cheremshan | 37 | 67 | 84 | −56 | −21 |
| 76324 | Sterlya | 16 | 42 | 33 | −51 | +28 |
| 76522 | Menzelia | 223 | 186 | 264 | −15 | −30 |
| 76520 | Mellya | 77 | 65 | 55 | +41 | +19 |
| 75647 | Rudnya | 92 | 112 | 69 | +33 | +62 |
| 78205 | Atkarka | 11 | 18 | 36 | −70 | −51 |
| 78157 | Bolshoi Arkadak | 31 | 37 | 34 | −8 | +9 |
| 76646 | Anzirka | 81 | 163 | 363 | −78 | −55 |
| 77222 | Birla | 3 | 12 | 6 | −53 | +96 |
| Factors that Changed in the Calculation for the Two Periods | 1985–1990 (t/y) | 1991–2013 (t/y) | Change, % |
|---|---|---|---|
| Change in land use | 9219 | 7502 | −19 |
| Change in precipitation | 9219 | 10,098 | +10 |
| Change in land use and precipitation | 9219 | 8232 | −11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maltsev, K.; Golosov, V.; Yermolaev, O.; Ivanov, M.; Chizhikova, N. Assessment of Net Erosion and Suspended Sediments Yield within River Basins of the Agricultural Belt of Russia. Water 2022, 14, 2781. https://doi.org/10.3390/w14182781
Maltsev K, Golosov V, Yermolaev O, Ivanov M, Chizhikova N. Assessment of Net Erosion and Suspended Sediments Yield within River Basins of the Agricultural Belt of Russia. Water. 2022; 14(18):2781. https://doi.org/10.3390/w14182781
Chicago/Turabian StyleMaltsev, Kirill, Valentin Golosov, Oleg Yermolaev, Maxim Ivanov, and Nelli Chizhikova. 2022. "Assessment of Net Erosion and Suspended Sediments Yield within River Basins of the Agricultural Belt of Russia" Water 14, no. 18: 2781. https://doi.org/10.3390/w14182781





