A Comprehensive Approach to Develop a Hydrological Model for the Simulation of All the Important Hydrological Components: The Case of the Three-River Headwater Region, China
Abstract
:1. Introduction
2. Materials and Methods
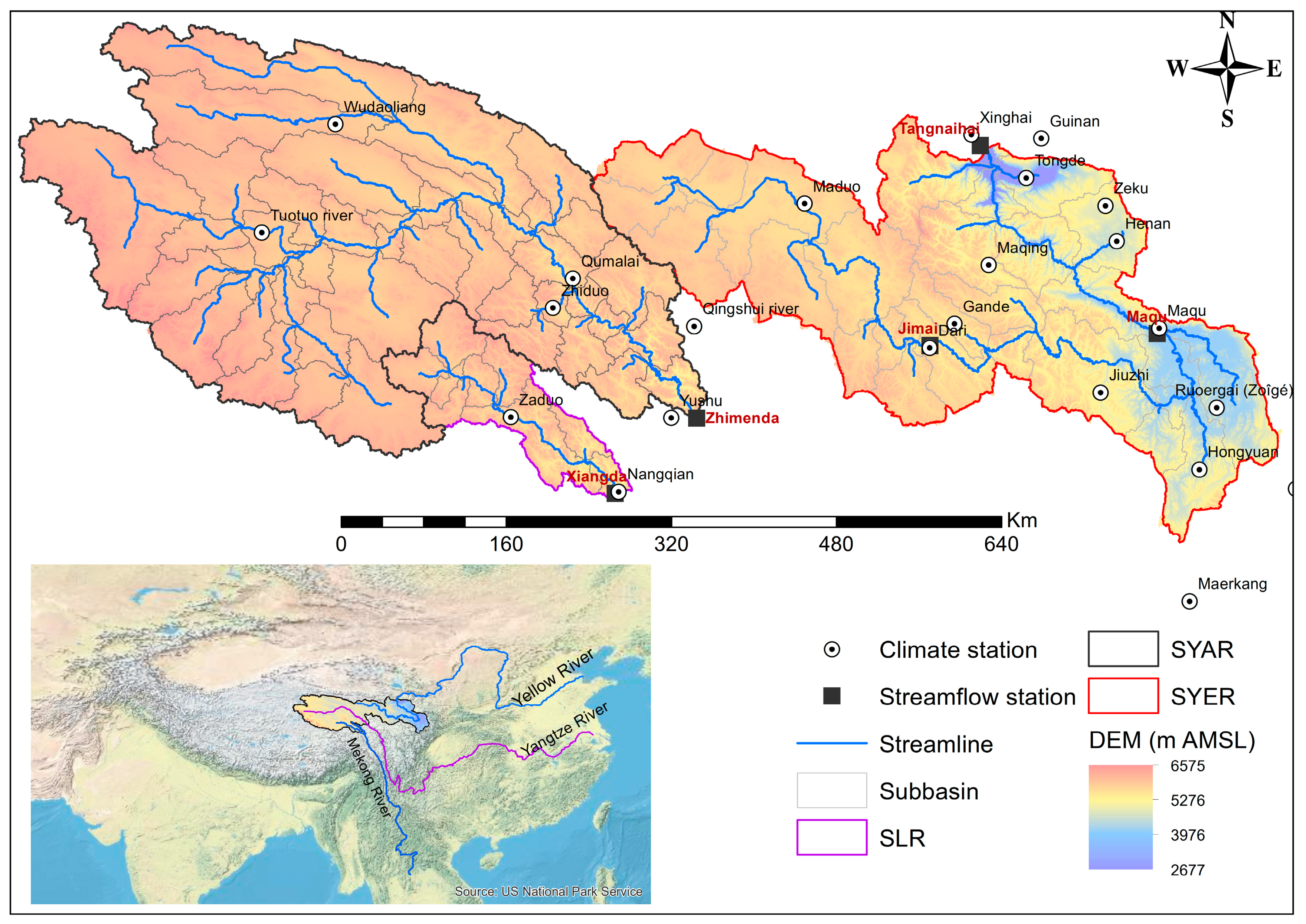
2.1. Study Area
2.2. Data Description
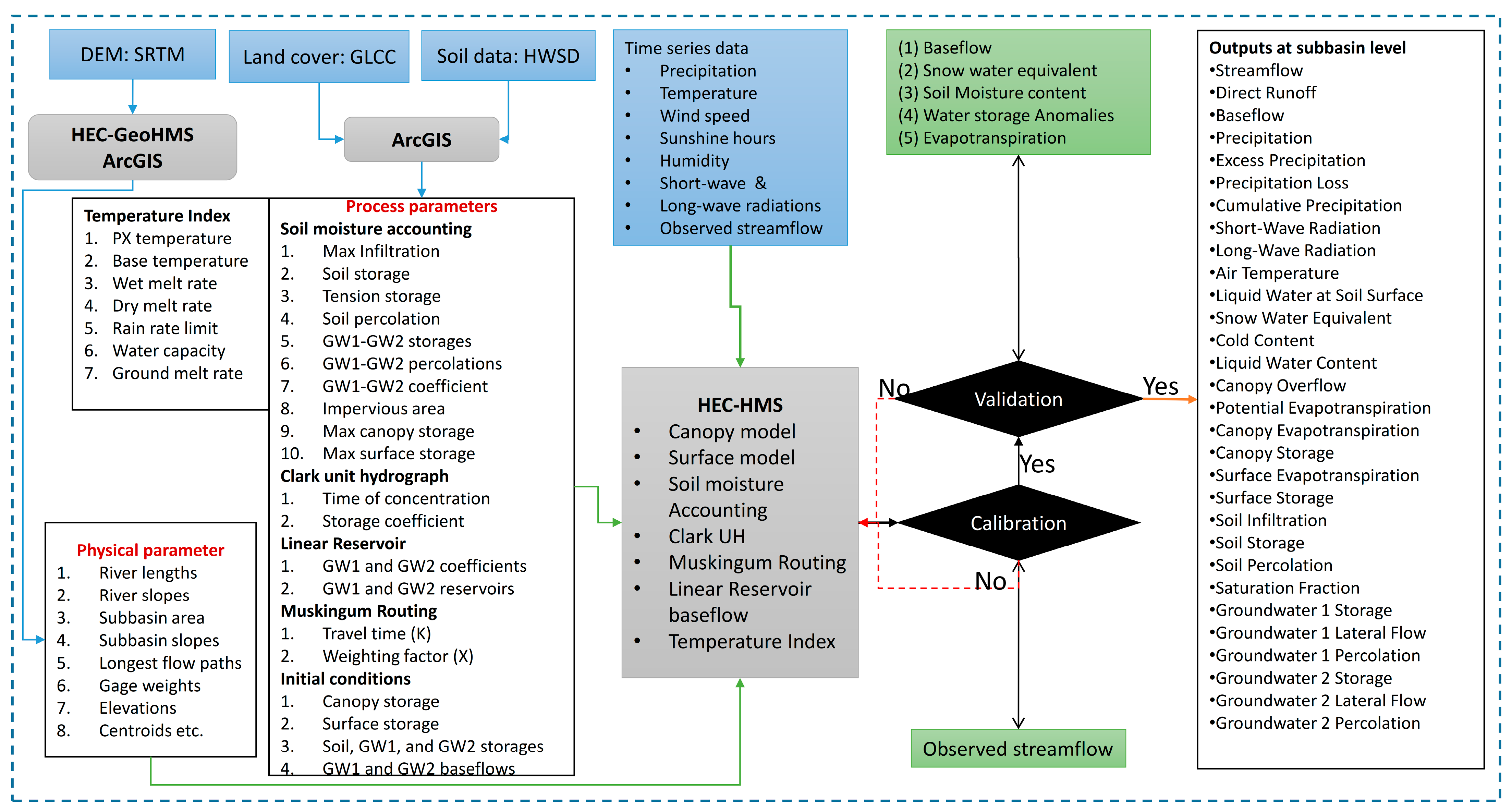
2.3. Setup of HEC-HMS
2.4. Calibration and Validation
2.4.1. Estimation of Physical Parameters
2.4.2. Estimation of Process Parameter
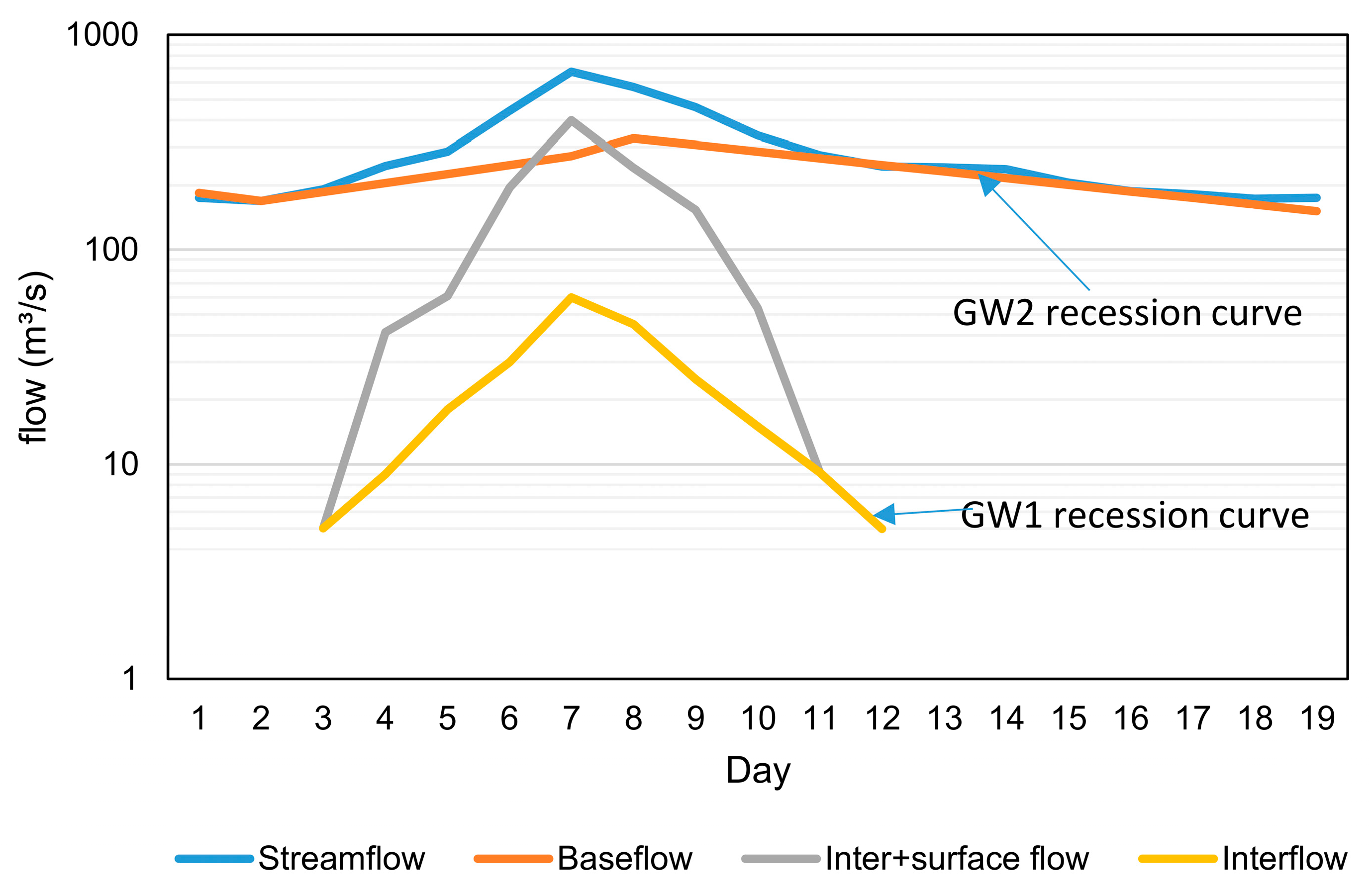
- First, search and separate single isolated storm event from streamflow time series.
- Plot a streamflow hydrograph for a single isolated storm event on a semi-logarithmic graph, as shown in Figure 4.
- Estimate the recession constant (k) for both the recession curves of baseflow and interflow. We used regression analysis on a semi-logarithmic graph. Baseflow is contributed by the deep groundwater layer (GW2) and interflow from the shallow groundwater layer (GW1) [24].
- Estimate the storage coefficient (Sc), storage capacity (St), and storage depth (St/area) with the following equations for both GW1 and GW2:
| Soil Texture | Area (km2) | % of the Total Area | Soil Depth (mm) | Porosity (cm3/cm3) | Field Capacity (cm3/cm3) | KS (mm/h) | Infiltration (mm/h) |
|---|---|---|---|---|---|---|---|
| Clay | 2481 | 2 | 1000 | 0.49 | 0.41 | 0.6 | 2 |
| Clay loam | 1926 | 2 | 1000 | 0.48 | 0.36 | 2.3 | 5 |
| Loam | 40,205 | 34 | 654 | 0.46 | 0.28 | 13.2 | 10 |
| Sand | 630 | 1 | 1000 | 0.4 | 0.1 | 210 | 25 |
| Sandy loam | 72,088 | 61 | 300 | 0.44 | 0.18 | 25.9 | 20 |
| Silt loam | 670 | 1 | 1000 | 0.49 | 0.31 | 6.8 | 7 |
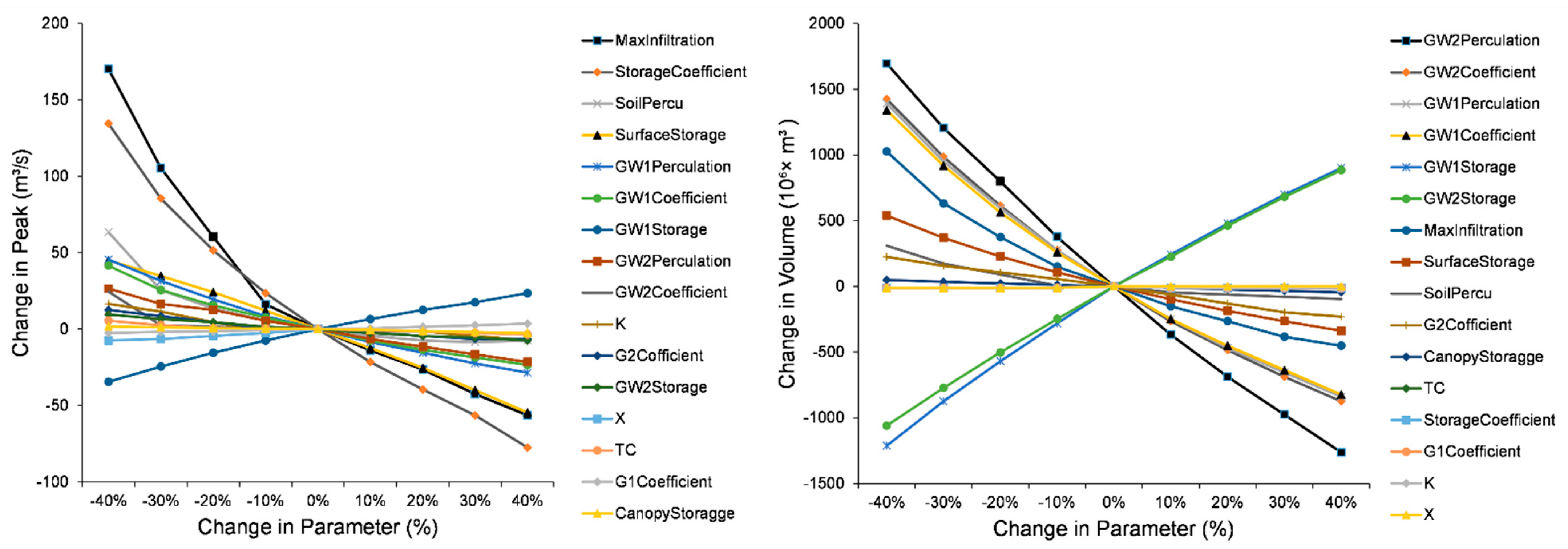
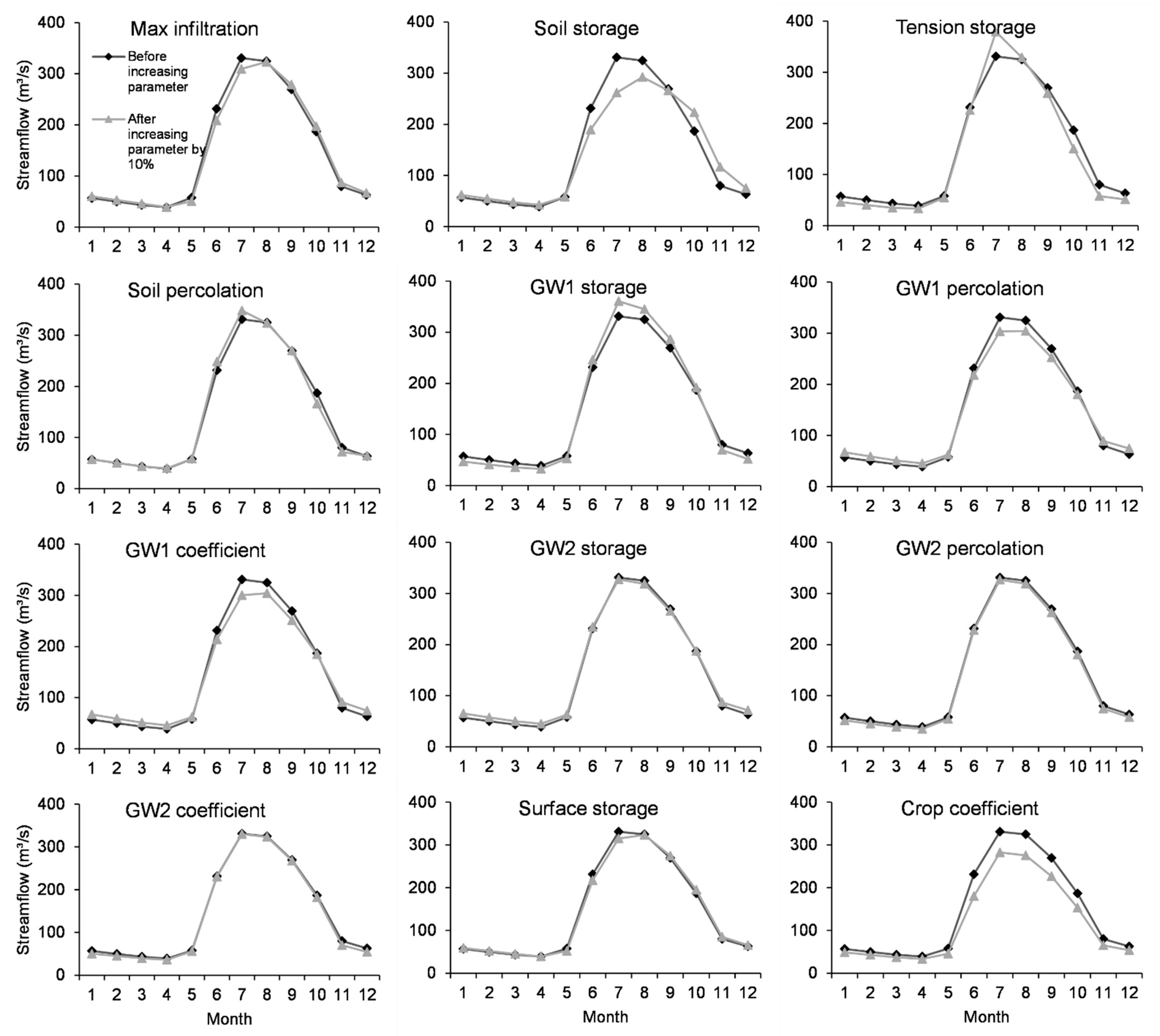
2.4.3. Sensitivity Analysis
2.5. Baseflow Separation
2.6. Terrestrial Water Storage
2.7. Actual Evapotranspiration Estimation
3. Results
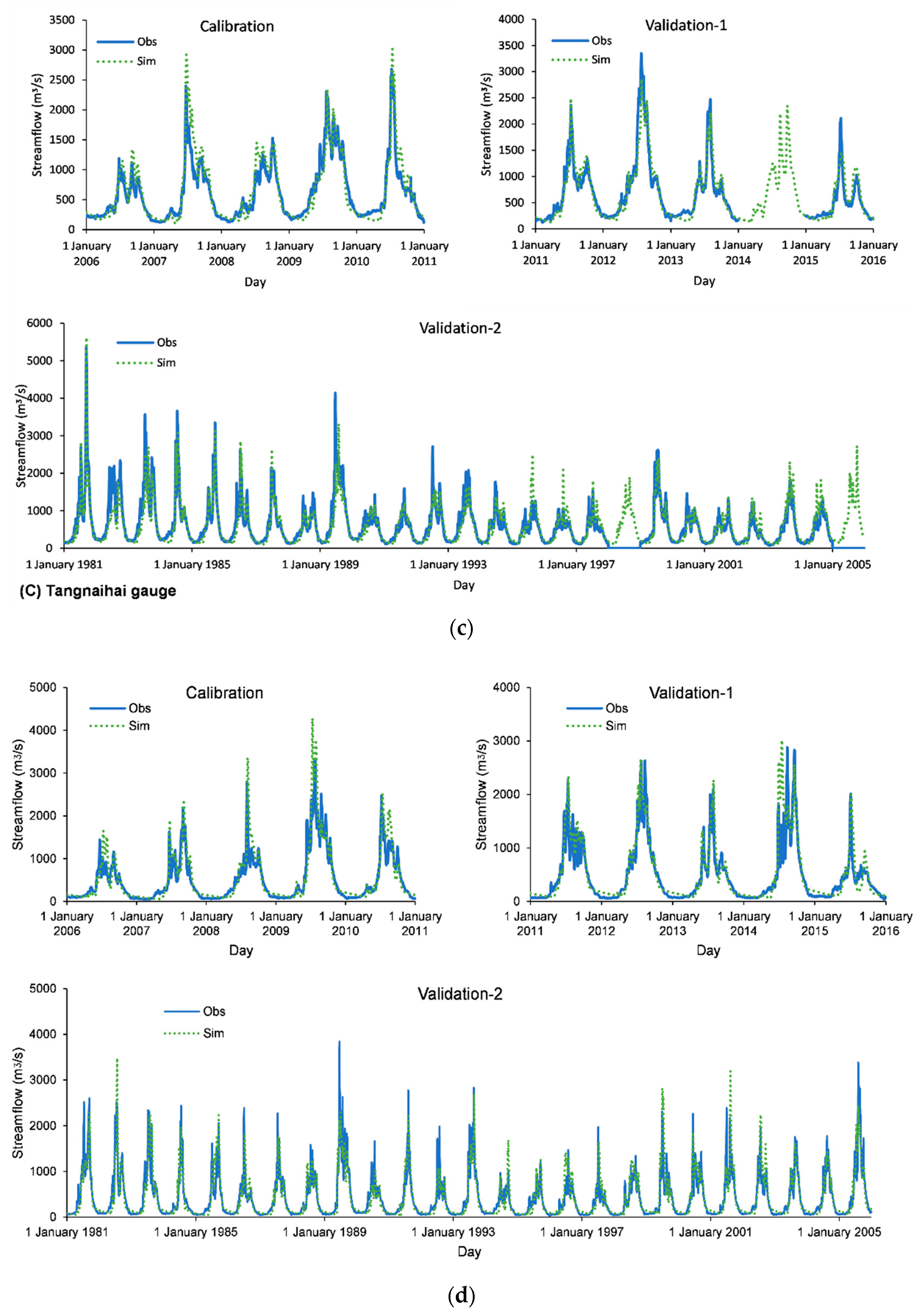
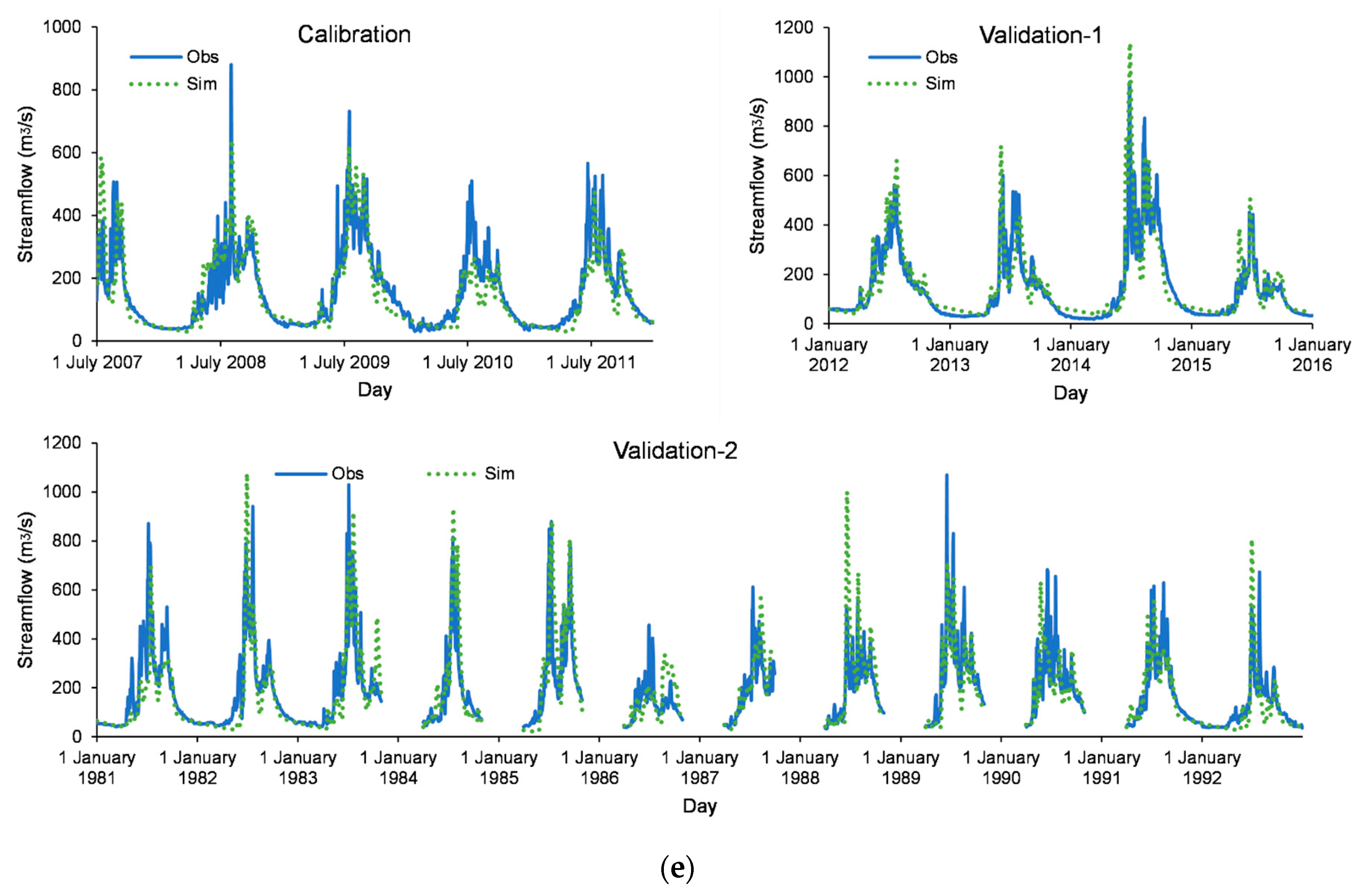
3.1. Calibration and Validation with Streamflow
3.2. Validation of Other Hydrological Components
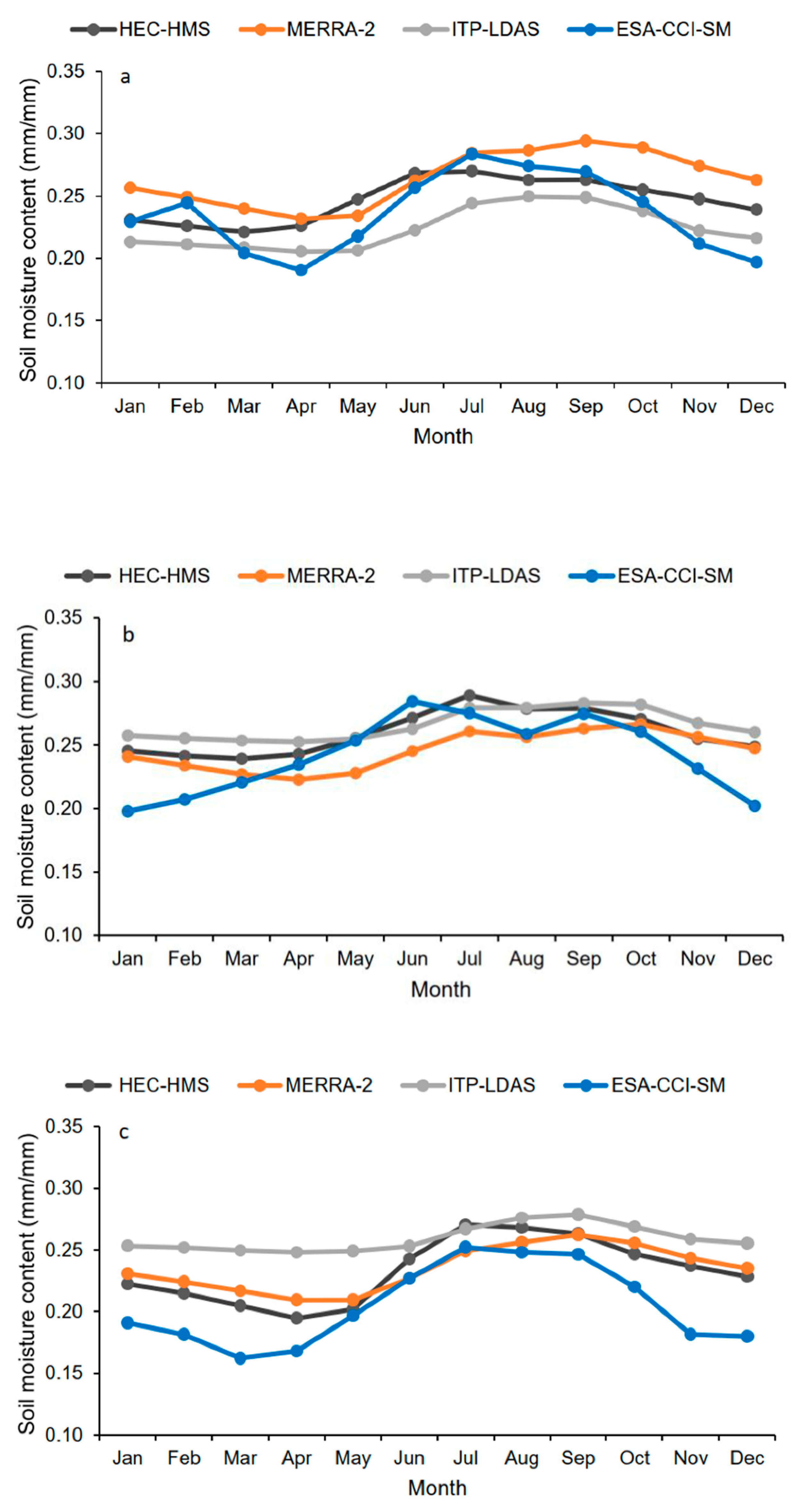
3.2.1. Soil Moisture Content
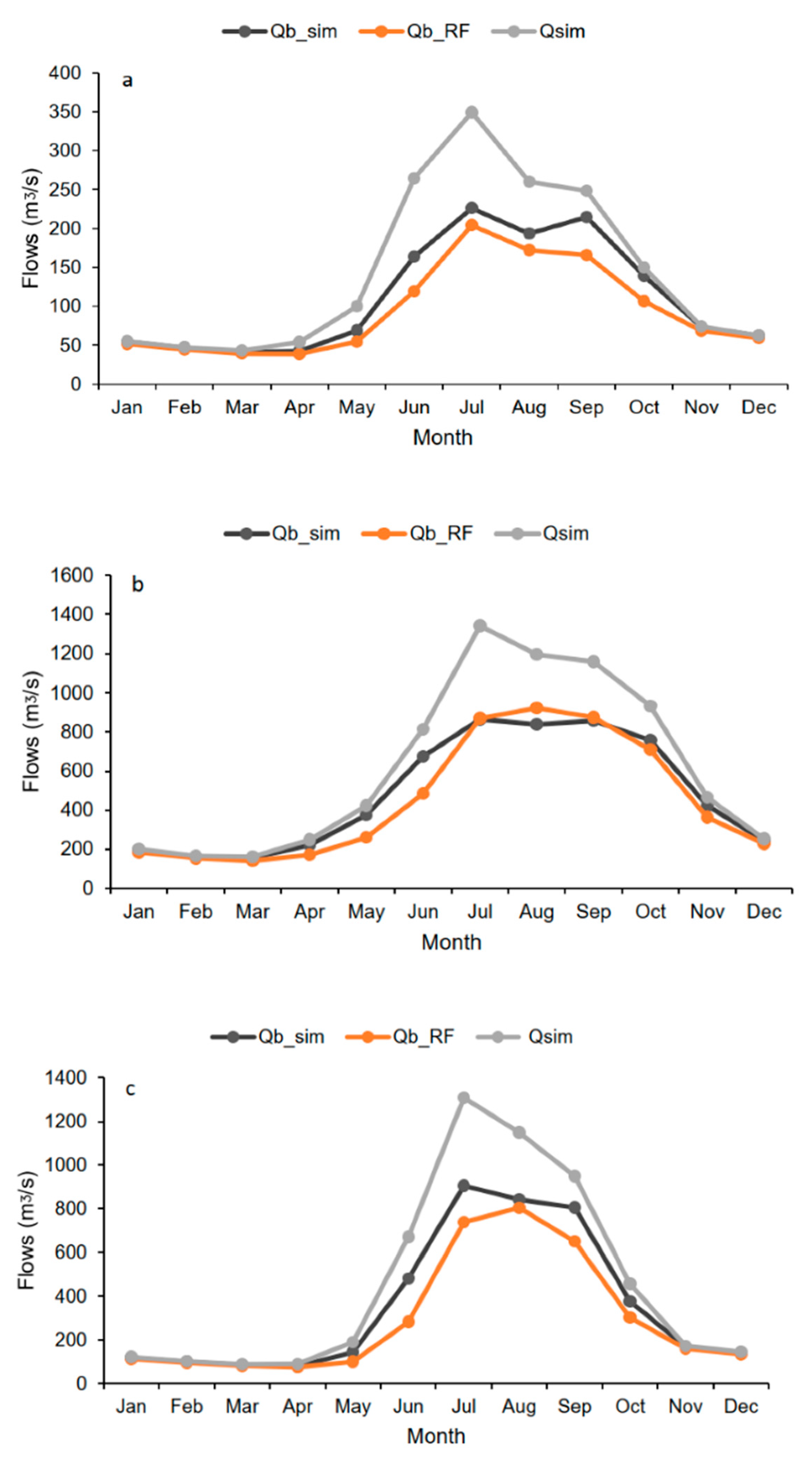
3.2.2. Baseflow
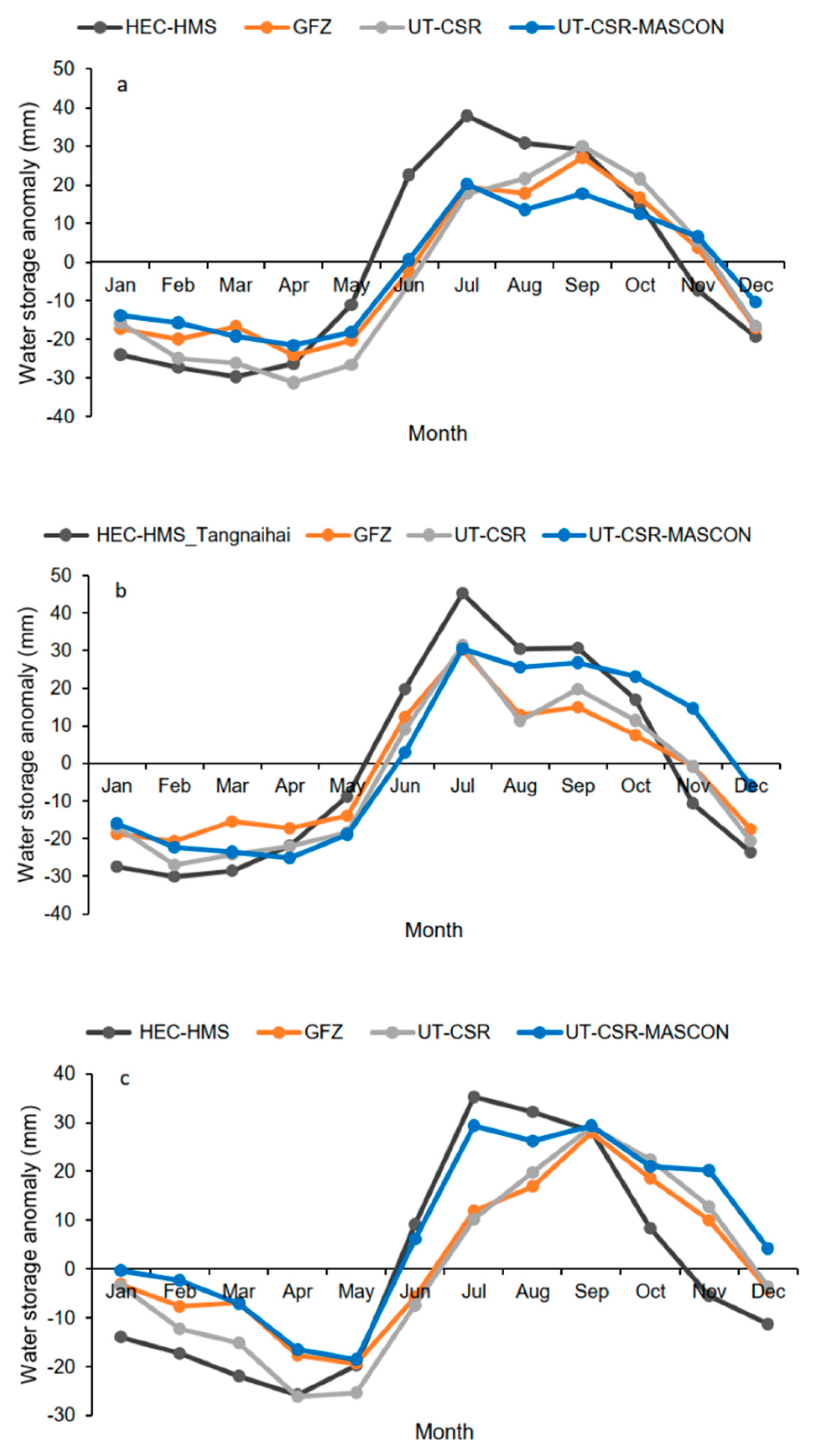
3.2.3. Terrestrial Water Storage
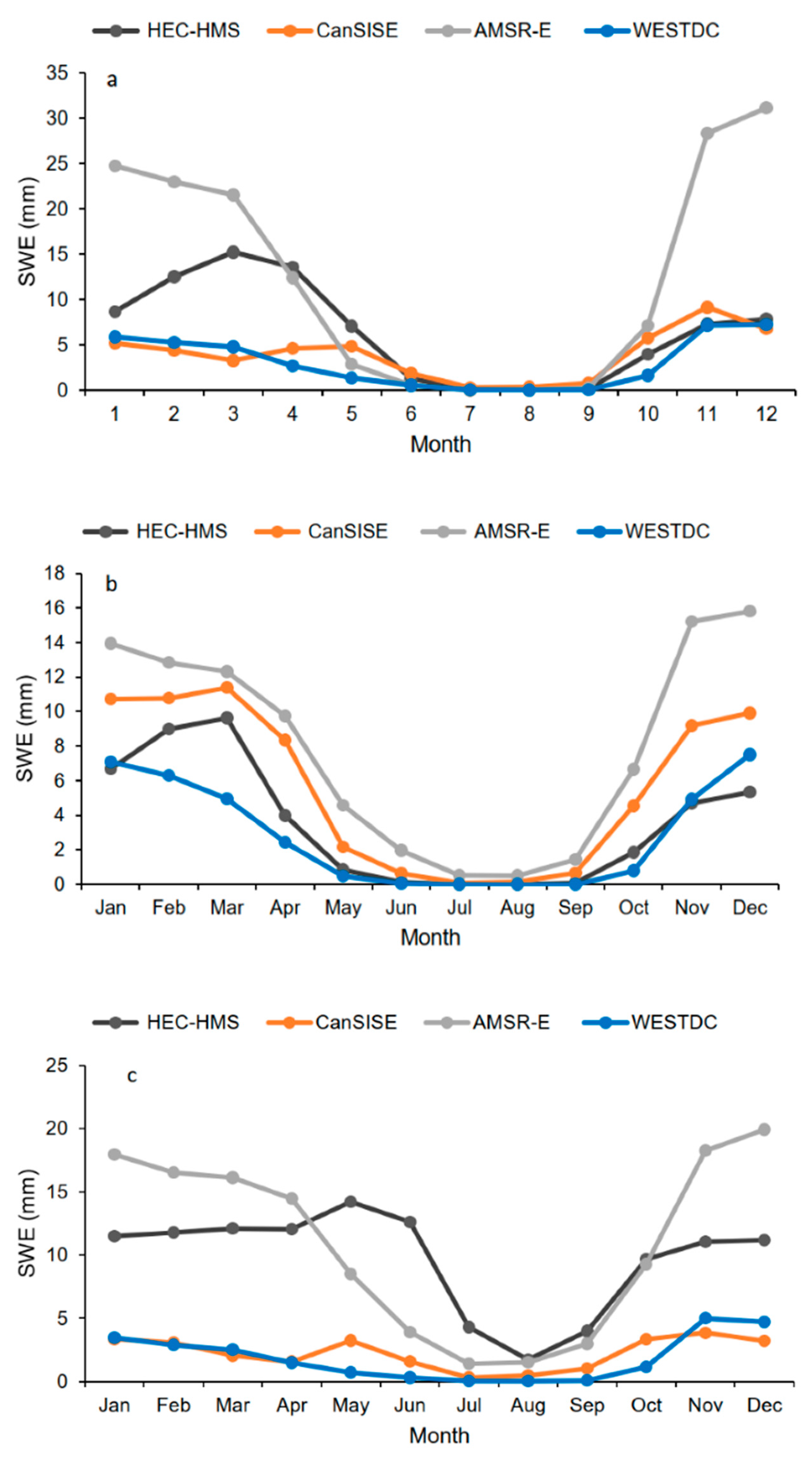
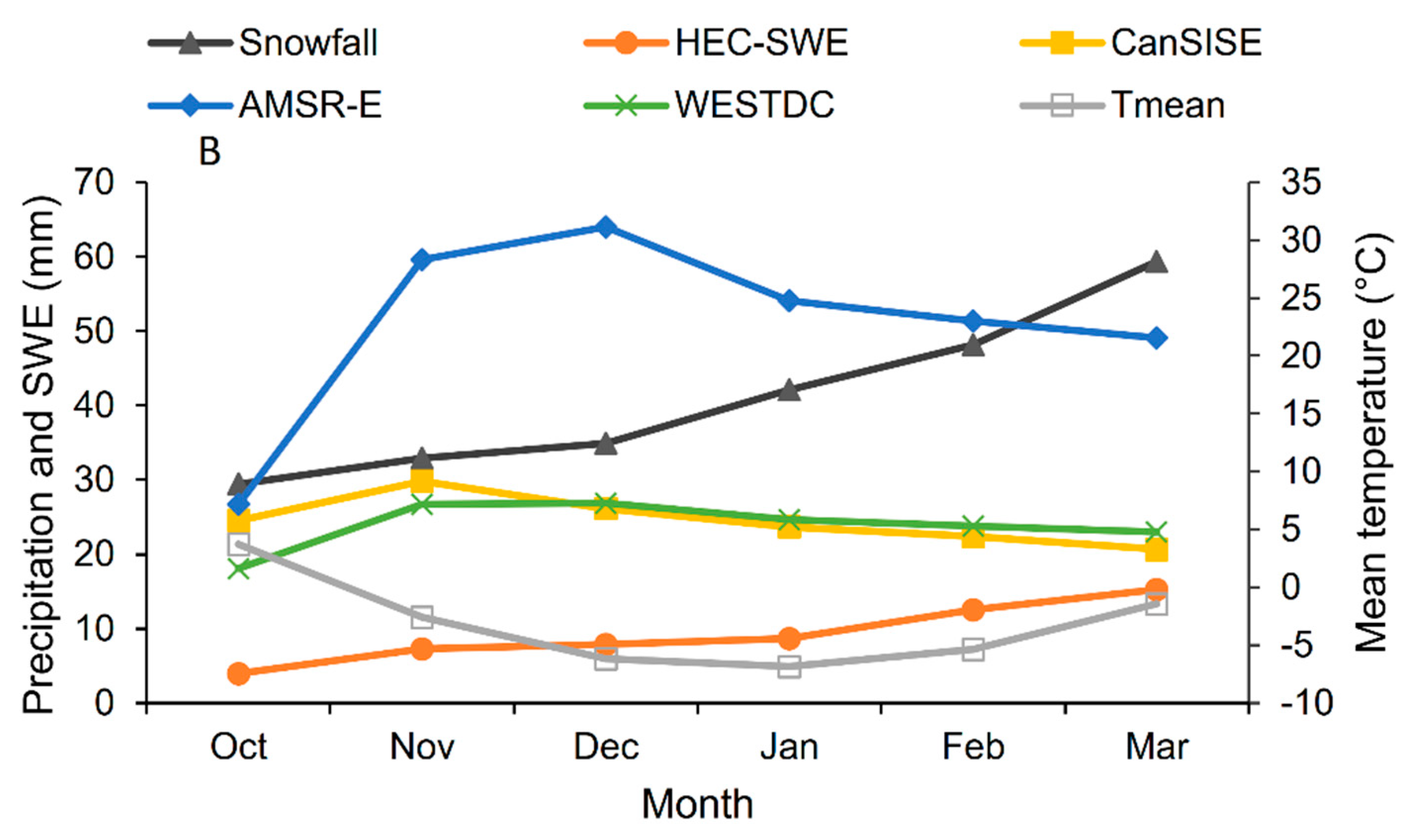
3.2.4. Snow Water Equivalent
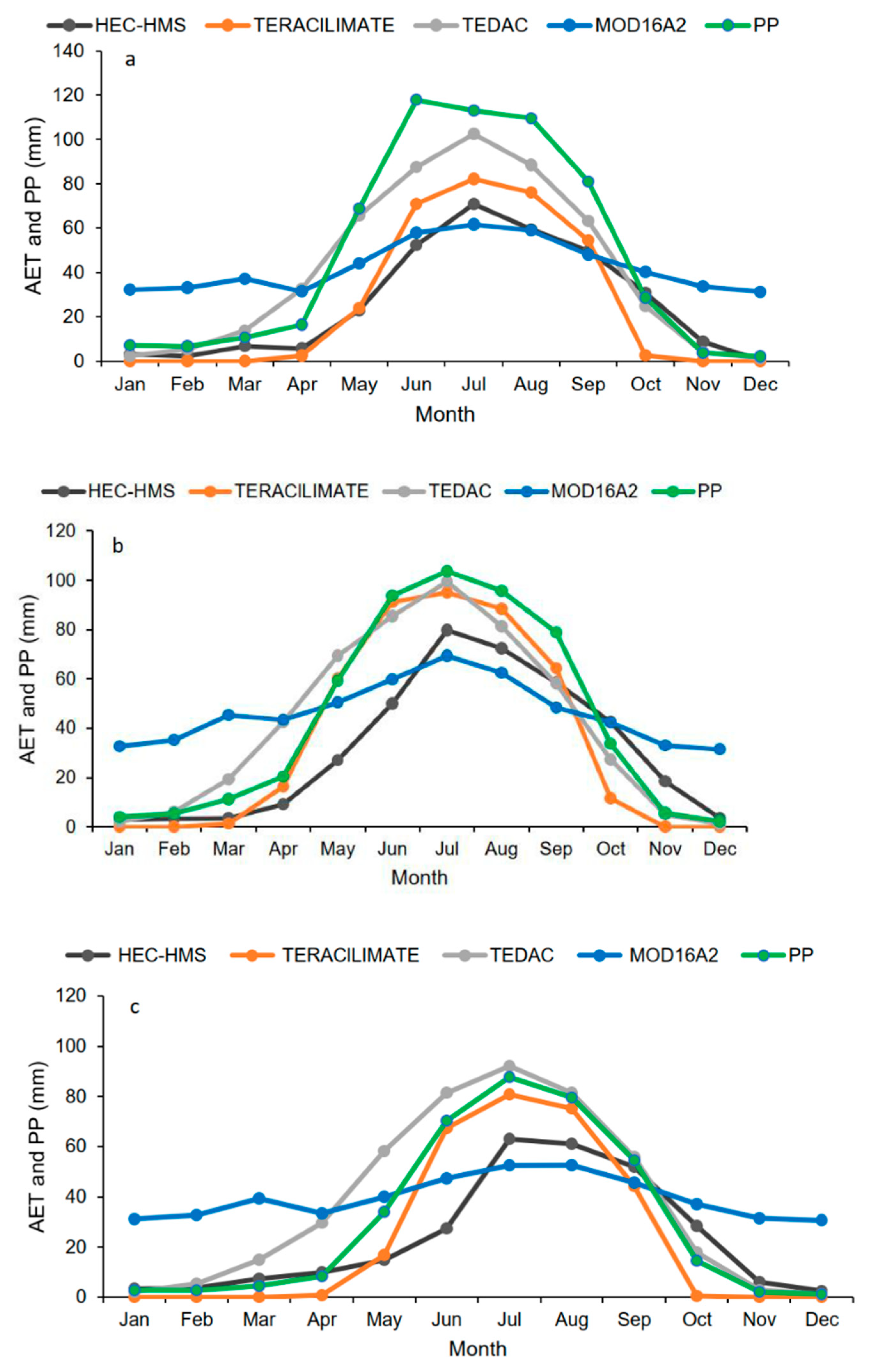
3.2.5. Actual Evapotranspiration
3.3. Uncertainties and Limitations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Edwards, P.J.; Williard, K.W.J.; Schoonover, J.E. Fundamentals of watershed hydrology. J. Contemp. Water Res. Educ. 2015, 154, 3–20. [Google Scholar] [CrossRef]
- Wu, P.; Christidis, N.; Stott, P. Anthropogenic impact on Earth’s hydrological cycle. Nat. Clim. Change 2013, 3, 807–810. [Google Scholar] [CrossRef]
- Jain, S.K.; Singh, V.P. Hydrological Cycles, Models and Applications to Forecasting. In Handbook of Hydrometeorological Ensemble Forecasting; Duan, Q., Pappenberger, F., Thielen, J., Wood, A., Cloke, H.L., Schaake, J.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 1–28. [Google Scholar]
- Pinto, D.B.; Silva, A.M.; Mello, C.R.; Beskow, S.; Coelho, G. Application of the Soil and Water Assessment Tool (SWAT) for sediment transport simulation at a headwater watershed in Minas Gerais State, Brazil. In Proceedings of the International Symposium on Erosion and Landscape Evolution (ISELE), Anchorage, AK, USA, 18–21 September 2011; p. 145. [Google Scholar]
- Singh, V.; Mishra, A.; Chowdhary, H.; Khedun, C.P. Climate Change and Its Impact on Water Resources. In Modern Water Resources Engineering; Wang, L.K., Yang, C.T., Eds.; Humana Press: Totowa, NJ, USA, 2014. [Google Scholar]
- Miller, M.P.; Susong, D.D.; Shope, C.L.; Heilweil, V.M.; Stolp, B.J. Continuous estimation of baseflow in snowmelt-dominated streams and rivers in the Upper Colorado River Basin: A chemical hydrograph separation approach. Water Resour. Res. 2014, 50, 6986–6999. [Google Scholar] [CrossRef]
- Xu, M. Study on water storage change and its consideration in water balance in the mountain regions over arid northwest China. Adv. Meteorol. 2017, 2017, 4291765. [Google Scholar] [CrossRef]
- Yan, C.-A.; Zhang, W.; Zhang, Z. Hydrological modeling of the Jiaoyi Watershed (China) using HSPF model. Sci. World J. 2014, 2014, 672360. [Google Scholar] [CrossRef]
- Kan, G.; He, X.; Li, J.; Ding, L.; Hong, Y.; Zhang, H.; Liang, K.; Zhang, M. Computer aided numerical methods for hydrological model calibration: An overview and recent development. Arch. Comput. Methods Eng. 2019, 26, 35–59. [Google Scholar] [CrossRef]
- Kumarasamy, K.; Belmont, P. Calibration parameter selection and watershed hydrology model evaluation in time and frequency domains. Water 2018, 10, 710. [Google Scholar] [CrossRef]
- Yin, Z.; Liao, W.; Lei, X.; Wang, H.; Wang, R. Comparing the Hydrological Responses of Conceptual and Process-Based Models with Varying Rain Gauge Density and Distribution. Sustainability 2018, 10, 3209. [Google Scholar] [CrossRef]
- Singh, V.P. Computer Models of Watershed Hydrology; Water Resources Publications: Littleton, CO, USA, 1995; p. 1144. [Google Scholar]
- Sorooshian, S.; Hsu, K.-L.; Coppola, E.; Tomassetti, B.; Verdecchia, M.; Visconti, G. Hydrological Modelling and the Water Cycle; Springer: Berlin, Heidelberg, 2008; p. 302. [Google Scholar]
- Dariane, A.B.; Javadianzadeh, M.M.; James, L.D. Developing an efficient auto-calibration algorithm for HEC-HMS program. Water Resour. Manag. 2016, 30, 1923–1937. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 265–284. [Google Scholar] [CrossRef]
- Boyle, D.P.; Gupta, H.V.; Sorooshian, S. Toward improved calibration of hydrologic models: Combining the strengths of manual and automatic methods. Water Resour. Res. 2000, 36, 3663–3674. [Google Scholar] [CrossRef]
- Ndiritu, J. A comparison of automatic and manual calibration using the Pitman model. Phys. Chem. Earth Parts A/B/C 2009, 34, 729–740. [Google Scholar] [CrossRef]
- Bhuiyan, A.K.M.H.; McNairn, H.; Powers, J.; Merzouki, A. Application of HEC-HMS in a cold region watershed and use of radarsat-2 soil moisture in initializing the model. Hydrology 2017, 4, 9. [Google Scholar] [CrossRef]
- Gebre, S. Application of the HEC-HMS model for runoff simulation of upper Blue Nile River basin. Hydrol. Curr. Res. 2015, 6, 1000199. [Google Scholar] [CrossRef]
- Koch, R.; Bene, K. Continuous hydrologic modeling with HMS in the Aggtelek Karst region. Hydrology 2014, 1, 1–7. [Google Scholar] [CrossRef]
- Ouédraogo, A.W.; Raude, M.J.; Gathenya, M.J. Continuous modeling of the Mkurumudzi River catchment in Kenya using the HEC-HMS conceptual model: Calibration, validation, model performance evaluation and sensitivity analysis. Hydrology 2018, 5, 44. [Google Scholar] [CrossRef]
- Bashar, K.; Zaki, A.F. SMA based continuous hydrologic simulation of the Blue Nile. In Proceedings of the International Conference of UNESCO Flanders FUST FRIEND/NILE Project “Towards a Better Cooperation”, Sharm El-Sheikh, Egypt, 12–15 November 2005; p. 10. [Google Scholar]
- Chea, S.; Oeurng, C. Flow simulation in an ungauged catchment of Tonle Sap Lake Basin in Cambodia: Application of the HEC-HMS model. Water Util. J. 2017, 17, 3–17. [Google Scholar]
- Fleming, M.; Neary, V. Continuous hydrologic modeling study with the Hydrologic Modeling System. J. Hydrol. Eng. 2004, 9, 175–183. [Google Scholar] [CrossRef]
- Gyawali, R.; David, W.W. Continuous hydrologic modeling of snow-affected watersheds in the Great Lakes Basin using HEC-HMS. J. Hydrol. Eng. 2013, 18, 29–39. [Google Scholar] [CrossRef]
- Neary, V.S.; Habib, E.; Fleming, M. Hydrologic modeling with NEXRAD precipitation in Middle Tennessee. J. Hydrol. Eng. 2004, 9, 339–349. [Google Scholar] [CrossRef]
- Mahmood, R.; Jia, S.; Lv, A.; Zhu, W. A preliminary assessment of environmental flow in the three rivers’ source region, Qinghai Tibetan Plateau, China and suggestions. Ecol. Eng. 2020, 144, 105709. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, L. Ecosystem change assessment in the Three-river Headwater Region, China: Patterns, causes, and implications. Ecol. Eng. 2016, 93, 24–36. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, L. Climate change and its impact on the eco-environment of the Three-Rivers Headwater Region on the Tibetan Plateau, China. Int. J. Environ. Res. Public Health 2015, 12, 12057. [Google Scholar] [CrossRef]
- Shen, X.; An, R.; Feng, L.; Ye, N.; Zhu, L.; Li, M. Vegetation changes in the Three-River Headwaters Region of the Tibetan Plateau of China. Ecol. Indic. 2018, 93, 804–812. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled Seamless SRTM data V4; International Centre for Tropical Agriculture: Cali, CO, USA, 2008. [Google Scholar]
- Loveland, T.R.; Reed, B.C.; Brown, J.F.; Ohlen, D.O.; Zhu, Z.; Yang, L.; Merchant, J.W. Development of a global land cover characteristics database and IGBP DISCover from 1 km AVHRR data. Int. J. Remote Sens. 2000, 21, 1303–1330. [Google Scholar] [CrossRef]
- Fischer, G.; Nachtergaele, F.; Prieler, S.; van Velthuizen, H.T.; Verelst, L.; Wiberg, D. Global Agro-ecological Zones Assessment for Agriculture (GAEZ 2008); FAO: Rome, Italy; IIASA: Laxenburg, Austria, 2008. [Google Scholar]
- Tedesco, M.; Kelly, R.; Foster, J.L.; Chang, A.T. AMSR-E/Aqua 5-Day L3 Global Snow Water Equivalent EASE-Grids, Version 2; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA; Available online: https://nsidc.org/data/ae_5dsno/versions/2 (accessed on 3 September 2019).
- Mudryk, L.R.; Derksen, C.; Kushner, P.J.; Brown, R. Characterization of Northern Hemisphere Snow Water Equivalent Datasets, 1981–2010. J. Clim. 2015, 28, 8037–8051. [Google Scholar] [CrossRef]
- Liyun, D.A.I.; Tao, C.H.E. Long-Term Series of Daily Snow Depth Dataset in China (1979–2019); National Tibetan Plateau Data Center: Beijing, China, 2015. [Google Scholar] [CrossRef]
- Yang, K. The Soil Moisture Dataset of China Based on Microwave Data Assimilation (2002–2011). In The Soil Moisture Dataset of China Based on Microwave Data Assimilation (2002–2011); National Tibetan Plateau Data Center: Beijing, China, 2018. [Google Scholar] [CrossRef]
- GMAO. Global Modeling and Assimilation Office (GMAO). MERRA-2 tavgU_2d_lnd_Nx: 2d, diurnal, Time-Averaged, Single-Level, Assimilation, Land Surface Diagnostics V5.12.4; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2015. [Google Scholar] [CrossRef]
- Swenson, S.C. GRACE Monthly Land Water Mass Grids NETCDF RELEASE 5.0. 2012. Available online: https://podaac.jpl.nasa.gov/dataset/TELLUS_LAND_NC_RL05 (accessed on 1 September 2022).
- Mao, J.; Yan, B. Global Monthly Mean Leaf Area Index Climatology, 1981–2015; ORNL DAAC: Oak Ridge, TN, USA, 2019. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Dobrowski, S.Z.; Parks, S.A.; Hegewisch, K.C. TerraClimate, a high-resolution global dataset of monthly climate and climatic water balance from 1958–2015. Sci. Data 2018, 5, 170191. [Google Scholar] [CrossRef] [Green Version]
- Jozsef, S.; Yinsheng, Z.; Ning, M.A.; Wenbin, L.I.U. Terrestrial Evapotranspiration Dataset Across China (1982–2017); National Tibetan Plateau Data Center: Beijing, China, 2019. [Google Scholar] [CrossRef]
- Running, S.; Mu, Q.; Zhao, M. MOD16A2 MODIS/Terra Net Evapotranspiration 8-Day L4 Global 500m SIN Grid V006; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2017. [Google Scholar] [CrossRef]
- William, A.S.; Fleming, M.J. Hydrologic Modeling System HEC-HMS: User’s Manual: Version 3.5; Hydrologic Engineering Center; Institute for Water Resources Davis: Davis, CA, USA, 2010; p. 318. [Google Scholar]
- Ramly, S.; Tahir, W. Application of HEC-GeoHMS and HEC-HMS as rainfall–runoff model for flood simulation. In ISFRAM 2015; Springer: Singapore, 2016; pp. 181–192. [Google Scholar]
- Munyaneza, O.; Mukubwa, A.; Maskey, S.; Uhlenbrook, S.; Wenninger, J. Assessment of surface water resources availability using catchment modelling and the results of tracer studies in the mesoscale Migina Catchment, Rwanda. Hydrol. Earth Syst. Sci. 2014, 18, 5289–5301. [Google Scholar] [CrossRef]
- Mahmood, R.; Jia, S. Assessment of impacts of climate change on the water resources of the transboundary Jhelum River basin of Pakistan and India. Water 2016, 8, 246. [Google Scholar] [CrossRef]
- Rangari, V.A.; Sridhar, V.; Umamahesh, N.V.; Patel, A.K. Rainfall runoff modelling of urban area using HEC-HMS: A case study of Hyderabad city. In Advances in Water Resources Engineering and Management; Springer: Singapore, 2020; pp. 113–125. [Google Scholar]
- Halwatura, D.; Najim, M.M.M. Application of the HEC-HMS model for runoff simulation in a tropical catchment. Environ. Model. Softw. 2013, 46, 155–162. [Google Scholar] [CrossRef]
- Meenu, R.; Rehana, S.; Mujumdar, P.P. Assessment of hydrologic impacts of climate change in Tunga-Bhadra River basin, India with HEC-HMS and SDSM. Hydrol. Processes 2013, 27, 1572–1589. [Google Scholar] [CrossRef]
- Hou, Z.-W.; Qin, C.-Z.; Zhu, A.X.; Liang, P.; Wang, Y.-J.; Zhu, Y.-Q. From manual to intelligent: A review of input data preparation methods for geographic modeling. Int. J. Geo-Inf. 2019, 8, 376. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, A.; Jin, Y. RM-MEDA: A regularity model-based multi-objective estimation of distribution algorithm. IEEE Trans. Evol. Comput. 2008, 12, 41–63. [Google Scholar] [CrossRef]
- Nasiri, S.; Ansari, H.; Ziaei, A.N. Simulation of water balance equation components using SWAT model in Samalqan Watershed (Iran). Arab. J. Geosci. 2020, 13, 421. [Google Scholar] [CrossRef]
- Ahbari, A.; Stour, L.; Agoumi, A.; Serhir, N. Estimation of initial values of the HMS model parameters: Application to the basin of Bin El Ouidane (Azilal, Morocco). J. Mater. Environ. Sci. 2018, 9, 305–317. [Google Scholar] [CrossRef]
- Cosby, B.J.; Hornberger, G.M.; Clapp, R.B.; Ginn, T.R. A statistical exploration of the relationships of soil moisture characteristics to the physical properties of soils. Water Resour. Res. 1984, 20, 682–690. [Google Scholar] [CrossRef]
- Clapp, R.B.; Hornberger, G.M. Empirical equations for some soil hydraulic properties. Water Resour. Res. 1978, 14, 601–604. [Google Scholar] [CrossRef]
- Rawls, W.J.; Brakensiek, D.L.; Saxtonn, K.E. Estimation of soil water properties. Trans. ASAE 1982, 25, 1316–1320. [Google Scholar] [CrossRef]
- Saxton, K.E.; Rawls, W.J. Soil water characteristic estimates by texture and organic matter for hydrologic solutions. Soil Sci. Soc. Am. J. 2006, 70, 1569–1578. [Google Scholar] [CrossRef]
- FAO. In Irrigation Water Management: Irrigation Methods; Training Manual No 5; The International Institute for Land Reclamation and Improvement: Wageningen, The Netherlands, 1988.
- Samady, M.K. Continuous Hydrologic Modeling for Analyzing the Effects of Drought on the Lower Colorado River in Texas. Ph.D. Thesis, Michigan Technological University, Houghton, MI, USA, 2017. [Google Scholar]
- Raghunath, H.M. Hydrology: Principles, Analysis and Design; New Age International (P) Limited: New Delhi, India, 2006; p. 476. [Google Scholar]
- Nathan, R.J.; McMahon, T.A. Evaluation of automated techniques for base flow and recession analyses. Water Resour. Res. 1990, 26, 1465–1473. [Google Scholar] [CrossRef]
- Berhail, S.; Ouerdachi, L.; Boutaghane, H. The use of the recession index as indicator for components of flow. Energy Procedia 2012, 18, 741–750. [Google Scholar] [CrossRef]
- Brown de Colstoun, E.C.; Huang, C.; Wang, P.; Tilton, J.C.; Tan, B.; Phillips, J.; Niemczura, S.; Ling, P.Y.; Wolfe, R.E. Global Man-made Impervious Surface (GMIS) Dataset from Landsat; NASA Socioeconomic Data and Applications Center (SEDAC): Palisades, NY, USA, 2017. [Google Scholar]
- Zhang, X.; Liu, L.; Wu, C.; Chen, X.; Gao, Y.; Xie, S.; Zhang, B. Development of a global 30 m impervious surface map using multisource and multitemporal remote sensing datasets with the Google Earth Engine platform. Earth Syst. Sci. Data 2020, 12, 1625–1648. [Google Scholar] [CrossRef]
- Verbeiren, B.; Ho, K.; Wirion, C.; Batelaan, O. An Earth observation based method to assess the influence of seasonal dynamics of canopy interception storage on the urban water balance. Belgeo 2016, 2, 17806. [Google Scholar] [CrossRef]
- Cronshey, R.G.; Roberts, R.T.; Miller, N. Urban Hydrology for Small Watersheds; United States Department of Agriculture: Washington, DC, USA, 1986; p. 164. [Google Scholar]
- Feldman, A.D. Techinical Reference Manual; Institute for Water Resources: Davis, CA, USA, 2000; p. 157. [Google Scholar]
- Clark, C.O. Storage and the unit yydrograph. Trans. Am. Soc. Civ. Eng. 1945, 110, 1419–1446. [Google Scholar] [CrossRef]
- USACE. Engineering and Design: Flood-Runoff Analysis (Engineer Manual 1110-2-1417); Military Bookshop; U.S. Army Corps of Engineers: Washington, DC, USA, 1994; p. 228. [Google Scholar]
- Devak, M.; Dhanya, C.T. Sensitivity analysis of hydrological models: Review and way forward. J. Water Clim. Change 2017, 8, 557–575. [Google Scholar] [CrossRef] [Green Version]
- Haan, C.T. Statistical Methods in Hydrology, 2nd ed.; Wiley-Blackwell; Iowa State Univ. Press: Ames, IA, USA, 2002. [Google Scholar]
- García, A.; Sainz, A.; Revilla, J.A.; Álvarez, C.; Juanes, J.A.; Puente, A. Surface water resources assessment in scarcely gauged basins in the north of Spain. J. Hydrol. 2008, 356, 312–326. [Google Scholar] [CrossRef]
- Mahmood, R.; Jia, S.; Babel, S.M. Potential Impacts of Climate Change on Water Resources in the Kunhar River Basin, Pakistan. Water 2016, 8, 23. [Google Scholar] [CrossRef]
- Verma, A.; Jha, M.; Mahana, R. Evaluation of HEC-HMS and WEPP for simulating watershed runoff using remote sensing and geographical information system. Paddy Water Env. 2010, 8, 131–144. [Google Scholar] [CrossRef]
- Murphy, R.; Graszkiewicz, Z.; Hill, P.; Neal, B.; Nathan, R.; Ladson, T. Australian Rainfall and Runoff Revision Project 7: Baseflow for Catchment Simulation; Engineering House: Barton, Australia, P7/S1/004; 2009; p. 121. [Google Scholar]
- Brodie, H.K.; Hostetler, S. A review of techniques for analysing baseflow from stream. In Proceedings of the NZHS-IAH-NZSSS 2005 Conference, Auckland, New Zealand, 2 December 2005; p. 2005. [Google Scholar]
- Chen, Z.; Jiang, W.; Wu, J.; Chen, K.; Deng, Y.; Jia, K.; Mo, X. Detection of the spatial patterns of water storage variation over China in recent 70 years. Sci. Rep. 2017, 7, 6423. [Google Scholar] [CrossRef]
- Ochoa-Sánchez, A.; Crespo, P.; Carrillo-Rojas, G.; Sucozhañay, A.; Célleri, R. Actual evapotranspiration in the high Andean grasslands: A comparison of measurement and estimation methods. Front. Earth Sci. 2019, 7, 55. [Google Scholar] [CrossRef]
- Jian, D.; Li, X.; Sun, H.; Tao, H.; Jiang, T.; Su, B.; Hartmann, H. Estimation of actual evapotranspiration by the complementary theory-based advection–aridity model in the Tarim River basin, China. J. Hydrometeorol. 2018, 19, 289–303. [Google Scholar] [CrossRef]
- Salama, M.A.; Yousef, K.M.; Mostafa, A.Z. Simple equation for estimating actual evapotranspiration using heat units for wheat in arid regions. J. Radiat. Res. Appl. Sci. 2015, 8, 418–427. [Google Scholar] [CrossRef]
- Zhu, W.; Jia, S.; Lall, U.; Cao, Q.; Mahmood, R. Relative contribution of climate variability and human activities on the water loss of the Chari/Logone River discharge into Lake Chad: A conceptual and statistical approach. J. Hydrol. 2019, 569, 519–531. [Google Scholar] [CrossRef]
- Van Liew, M.W.; Garbrecht, J. Hydrologic simulation of the little Washita River experimental watershed using SWAT. J. Am. Water Resour. As. 2003, 39, 413–426. [Google Scholar] [CrossRef]
- Meng, F.; Su, F.; Yang, D.; Tong, K.; Hao, Z. Impacts of recent climate change on the hydrology in the source region of the Yellow River basin. J. Hydrol. Reg. Stud. 2016, 6, 66–81. [Google Scholar] [CrossRef] [Green Version]
- Yang, T.; Wang, X.; Yu, Z.; Krysanova, V.; Chen, X.; Schwartz, F.W.; Sudicky, E.A. Climate change and probabilistic scenario of streamflow extremes in an alpine region. J. Geophys. Res. Atmos. 2014, 119, 8535–8551. [Google Scholar] [CrossRef]
- Zhang, Y.; Su, F.; Hao, Z.; Xu, C.; Yu, Z.; Wang, L.; Tong, K. Impact of projected climate change on the hydrology in the headwaters of the Yellow River basin. Hydrol. Processes 2015, 29, 4379–4397. [Google Scholar] [CrossRef]
- Guo, M.; Li, J.; Wang, Y.; Bai, P.; Wang, J. Distinguishing the relative contribution of environmental factors to runoff change in the headwaters of the Yangtze River. Water 2019, 11, 1432. [Google Scholar] [CrossRef]
- Wang, J.; Luo, S.; Li, Z.; Wang, S.; Li, Z. The freeze/thaw process and the surface energy budget of the seasonally frozen ground in the source region of the Yellow River. Theor. Appl. Climatol. 2019, 138, 1631–1646. [Google Scholar] [CrossRef]
- Zhang, L.; Su, F.; Yang, D.; Hao, Z.; Tong, K. Discharge regime and simulation for the upstream of major rivers over Tibetan Plateau. J. Geophys. Res. Atmos. 2013, 118, 8500–8518. [Google Scholar] [CrossRef]
- Lauri, H.; Räsänen, T.A.; Kummu, M. Using reanalysis and remotely sensed temperature and precipitation data for hydrological modeling in monsoon climate: Mekong River case study. J. Hydrometeorol. 2014, 15, 1532–1545. [Google Scholar] [CrossRef]
- Su, F.; Hong, Y.; Lettenmaier, D.P. Evaluation of TRMM Multisatellite Precipitation Analysis (TMPA) and its utility in hydrologic prediction in the La Plata basin. J. Hydrometeor. 2008, 9, 622–640. [Google Scholar] [CrossRef]
- Deng, M.; Meng, X.; Li, Z.; Lyv, Y.; Lei, H.; Zhao, L.; Zhao, S.; Ge, J.; Jing, H. Responses of soil moisture to regional climate change over the Three River Source Region on the Tibetan Plateau. Int. J. Climatol. 2019, 40, 6341. [Google Scholar] [CrossRef]
- Yuan, X.; Ji, P.; Wang, L.; Liang, X.Z.; Yang, K.; Ye, A.; Su, Z.; Wen, J. High-Resolution Land Surface Modeling of Hydrological Changes Over the Sanjiangyuan Region in the Eastern Tibetan Plateau: 1. Model Development and Evaluation. J. Adv. Modeling Earth Syst. 2018, 10, 2806–2828. [Google Scholar] [CrossRef]
- Zeng, J.; Li, Z.; Quan, C.; Bi, H.; Qiu, J.; Zou, P. Evaluation of remotely sensed and reanalysis soil moisture products over the Tibetan Plateau using in-situ observations. Remote Sens. Environ. 2015, 163, 91–110. [Google Scholar] [CrossRef]
- Zhang, Q.; Fan, K.; Singh, V.P.; Sun, P.; Shi, P. Evaluation of Remotely Sensed and Reanalysis Soil Moisture Against In Situ Observations on the Himalayan-Tibetan Plateau. J. Geophys. Res. 2018, 123, 7132–7148. [Google Scholar] [CrossRef]
- Chen, L.; Zheng, H.; Chen, Y.D.; Liu, C. Baseflow separation in the source region of the Yellow River. J. Hydrol. Eng. 2008, 13, 541–548. [Google Scholar] [CrossRef]
- Liu, Z.; Yao, Z.; Wang, R.; Yu, G. Estimation of the Qinghai-Tibetan Plateau runoff and its contribution to large Asian rivers. Sci. Total Environ. 2020, 749, 141570. [Google Scholar] [CrossRef]
- Lu, W.; Wang, W.; Shao, Q.; Yu, Z.; Hao, Z.; Xing, W.; Yong, B.; Li, J. Hydrological projections of future climate change over the source region of Yellow River and Yangtze River in the Tibetan Plateau: A comprehensive assessment by coupling RegCM4 and VIC model. Hydrol. Processes 2018, 32, 2096–2117. [Google Scholar] [CrossRef]
- Qian, K.; Wan, L.; Wang, X.-S.; Lv, J.; Liang, S. Periodical characteristics of baseflow in the source region of the Yangtze River. J. Arid. Land 2012, 4, 113–122. [Google Scholar] [CrossRef]
- Huang, Y.; Salama, M.; Krol, M.; Velde, R.; Hoekstra, A.; Zhou, Y.; Su, Z. Analysis of long-term terrestrial water storage variations in Yangtze River basin. Hydrol. Earth Syst. Sci. Discuss. 2012, 9, 11487–11520. [Google Scholar] [CrossRef]
- Jing, W.; Zhang, P.; Zhao, X. A comparison of different GRACE solutions in terrestrial water storage trend estimation over Tibetan Plateau. Sci. Rep. 2019, 9, 1765. [Google Scholar] [CrossRef]
- Xu, M.; Kang, S.; Chen, X.; Wu, H.; Wang, X.; Su, Z. Detection of hydrological variations and their impacts on vegetation from multiple satellite observations in the Three-River Source Region of the Tibetan Plateau. Sci. Total Environ. 2018, 639, 1220–1232. [Google Scholar] [CrossRef]
- Dai, L.; Che, T.; Ding, Y.; Hao, X. Evaluation of snow cover and snow depth on the Qinghai–Tibetan Plateau derived from passive microwave remote sensing. Cryosphere 2017, 11, 1933–1948. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, L.; Menard, C.; Luojus, K.; Lemmetyinen, J.; Pulliainen, J. Evaluation of snow products over the Tibetan Plateau. Hydrol. Processes 2015, 29, 10427. [Google Scholar] [CrossRef]
- Dawson, N.; Broxton, P.; Zeng, X. Evaluation of remotely-sensed snow water equivalent and snow cover extent over the contiguous United States. J. Hydrometeorol. 2018, 19, 1777–1791. [Google Scholar] [CrossRef]
- Li, X.; Long, D.; Han, Z.; Scanlon, B.R.; Sun, Z.; Han, P.; Hou, A. Evapotranspiration estimation for Tibetan Plateau headwaters using conjoint terrestrial and atmospheric water balances and multisource remote sensing. Water Resour. Res. 2019, 55, 8608–8630. [Google Scholar] [CrossRef]
- Sato, Y.; Ma, X.; Xu, J.; Matsuoka, M.; Zheng, H.; Liu, C.; Fukushima, Y. Analysis of long-term water balance in the source area of the Yellow River basin. Hydrol. Processes 2008, 22, 1618–1629. [Google Scholar] [CrossRef]
- Xue, B.-L.; Wang, L.; Li, X.; Yang, K.; Chen, D.; Sun, L. Evaluation of evapotranspiration estimates for two river basins on the Tibetan Plateau by a water balance method. J. Hydrol. 2013, 492, 290–297. [Google Scholar] [CrossRef]
- Bei, X.; Yao, Y.; Zhang, L.; Xu, T.; Jia, K.; Zhang, X.; Shang, K.; Xu, J.; Chen, X. Long-Term Spatiotemporal Dynamics of Terrestrial Biophysical Variables in the Three-River Headwaters Region of China from Satellite and Meteorological Datasets. Remote Sens. 2019, 11, 1633. [Google Scholar] [CrossRef]
- Renard, B.; Kavetski, D.; Kuczera, G.; Thyer, M.; Franks, S.W. Understanding predictive uncertainty in hydrologic modeling: The challenge of identifying input and structural errors. Water Resour. Res. 2010, 46, 1–22. [Google Scholar] [CrossRef]
- Liang, S.; Li, X.; Wang, J. Chapter 17-Precipitation. In Advanced Remote Sensing; Academic Press: Boston, MA, USA, 2012; pp. 533–556. [Google Scholar]
- Zhang, J.L.; Li, Y.P.; Huang, G.H.; Wang, C.X.; Cheng, G.H. Evaluation of uncertainties in input data and parameters of a hydrological model using a Bayesian framework: A case study of a snowmelt–precipitation-driven watershed. J. Hydrometeorol. 2016, 17, 2333–2350. [Google Scholar] [CrossRef]

| SR | Data Type | Spatial/Temporal Resolution | Source | Availability |
|---|---|---|---|---|
| 1 | Streamflow data | Daily | Hydrology and Water Resources Survey Bureau of Qinghai province | 1980–2015 |
| 2 | Climate data | Daily | Qinghai Meteorological Bureau (QMB) | 1980–2015 |
| 3 | DEM | 90 m | NASA’s Shuttle Radar Topography Mission (SRTM), Version 004 [31] (http://srtm.csi.cgiar.org) (accessed on 20 August 2019). | Updated 2008 |
| 4 | Land Use Land Cover | 1 km | Global Land Cover Characteristics [32] (https://earthexplorer.usgs.gov/) (accessed on 20 August 2019). | 1993 |
| 5 | Soil characteristics | 1 km | Harmonized World Soil Database Version 1.2 (http://www.fao.org/soils-portal/) (accessed on 20 August 2019) [33] | Update 2013 |
| 6 | Snow Water Equivalent (SWE)/snow depth | 25 km/daily, monthly | Advanced Microwave Scanning Radiometer-Earth Observing System (AMSR-E), Version 2 [34] | 2002/6–2011/10 |
| 1°/daily | Canadian Sea Ice and Snow Evolution (CanSISE) [35] | 1981–2010 | ||
| 0.25°/daily | Environmental and Ecological Science Data Center for West China (WESTDC) [36] | 1979–2019 | ||
| 7 | Soil Moisture Content | 0.25°/daily | European Space Agency (ESA) Climate Change Initiative Soil Moisture product (ESA-CCI-SM_v4.7), | 1978–2019 |
| 0.25°/daily | China Soil Moisture Dataset from Microwave Data Assimilation (ITP-LDAS) [37] | 2002–2011 | ||
| 0.5°′0.625°/diurnal | Modern-Era Retrospective analysis for Research and Applications (MERRA-2) [38] | 1980–2020 | ||
| 8 | GRACE data | 300 km/monthly | Geo-forschungs-Zentrum Potsdam (GFZP), University of Texas-Center for Space Research (UT-CSR), and UT-CSR Mascons [39], | 2002–2020 |
| 9 | Leaf Area Index | 0.25°/monthly | Global Monthly Mean Leaf Area Index Climatology, 1981–2015 [40] | 1981–2015 |
| 10 | Evapotranspiration | 4 km/monthly | TERRACLIMATE [41] | 1958–2019 |
| 0.1°/monthly | Terrestrial evapotranspiration dataset across China, version 1.5 [42] | 1982–2017 | ||
| 500 m/8-daily | MOD16A2 Version 6 [43] | 2000–2020 |
| Code | Description | % of the Total Area | Canopy Storage (mm) |
|---|---|---|---|
| 1 | Urban and Built-Up Land | 0.00 | 0.5 |
| 2 | Dryland Cropland and Pasture | 0.47 | 1.5 |
| 5 | Cropland/Grassland Mosaic | 0.01 | 2.0 |
| 6 | Cropland/Woodland Mosaic | 0.02 | 2.0 |
| 7 | Grassland | 88.61 | 2.0 |
| 8 | Shrubland | 1.99 | 2.5 |
| 9 | Mixed Shrubland/Grassland | 1.66 | 2.2 |
| 10 | Savanna | 1.05 | 2.0 |
| 11 | Deciduous Broadleaf Forest | 0.15 | 3.0 |
| 12 | Deciduous Needleleaf Forest | 0.13 | 2.0 |
| 14 | Evergreen Needleleaf Forest | 0.01 | 2.0 |
| 15 | Mixed Forest | 0.81 | 3.0 |
| 16 | Water Bodies | 1.51 | 0.0 |
| 17 | Herbaceous Wetland | 0.02 | 1.0 |
| 18 | Wooded Wetland | 0.00 | 1.0 |
| 19 | Glacier | 0.12 | 0.0 |
| 21 | Wooded Tundra | 3.43 | 2.0 |
| Surface | Slope (%) | Max Surface Storage (mm) |
|---|---|---|
| Paved impervious area | NA | 3.2–6.6 |
| Steep, smooth slopes | >30 | 1.0 |
| Moderate to gentle slopes | 5–30 | 12.7–6.4 |
| Flat, furrowed land | 0–5 | 50.8 |
| Jimai | Maqu | Tangnaihai | Zhimenda | Xiangda | |
|---|---|---|---|---|---|
| Calibration | |||||
| E | 0.66 | 0.85 | 0.83 | 0.74 | 0.69 |
| R2 | 0.73 | 0.88 | 0.89 | 0.83 | 0.73 |
| PVD (%) | 4.45 | 3.60 | 6.24 | 8.96 | −4.29 |
| NRMSE | 0.46 | 0.30 | 0.30 | 0.51 | 0.43 |
| Validation-1 | |||||
| E | 0.69 | 0.83 | 0.90 | 0.77 | 0.74 |
| R2 | 0.77 | 0.83 | 0.90 | 0.82 | 0.78 |
| PVD | 12.8 | 3.29 | −1.32 | 8.68 | 6.66 |
| NRMSE | 0.39 | 0.35 | 0.27 | 0.49 | 0.49 |
| Validation-2 | |||||
| E | 0.62 | 0.82 | 0.82 | 0.79 | 0.61 |
| R2 | 0.71 | 0.82 | 0.82 | 0.81 | 0.65 |
| PVD | 21.07 | −4.38 | −0.78 | 1.36 | −1.13 |
| NRMSE | 0.52 | 0.42 | 0.40 | 0.48 | 0.55 |
| Soil Moisture Content | Snow Water Equivalent | Baseflow | Terrestrial Water Storage Changes | Actual Evapotranspiration | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ESA-CCI-SM | MERRA-2 | ITP-LDAS | CanSISE | AMSR-E | WESTDC | DRF | GFZ | UT-CSR | UT-CSR_MASCON | TERRACLIMATE | MOD16A2 | TEDAC | |
| Analysis Period 2001–2010 | 2001–2010 | 1981–2015 | 2002–2015 | 2000–2010 | |||||||||
| The Source of the Lancang River (SLR) | |||||||||||||
| R | 0.72 | 0.60 | 0.44 | 0.51 | 0.75 | 0.72 | 0.95 | 0.72 | 0.70 | 0.76 | 0.89 | 0.79 | 0.87 |
| RMSE | 0.031 | 0.027 | 0.033 | 6.5 | 12.5 | 6.0 | 29.0 | 20.0 | 22.1 | 17.5 | 15.3 | 23.9 | 24.3 |
| PVD (%) | 4.5 | −6.6 | 9.0 | 64.1 | −51.7 | 111.8 | 18.1 | 11.0 | −5.3 | 34.3 | 0.1 | −38.6 | −36.3 |
| The Source of the Yellow River (SYER) | |||||||||||||
| R | 0.72 | 0.74 | 0.56 | 0.82 | 0.73 | 0.81 | 0.96 | 0.70 | 0.75 | 0.79 | 0.85 | 0.80 | 0.83 |
| RMSE | 0.029 | 0.020 | 0.022 | 3.6 | 6.3 | 2.5 | 100.8 | 21.7 | 20.4 | 17.7 | 21.9 | 24.5 | 22.2 |
| PVD (%) | 6.7 | 5.7 | −2.4 | −38.4 | −59.8 | 22.4 | 7.4 | 17.4 | 9.1 | 18.6 | −13.5 | −33.2 | −25.4 |
| The Source of the Yangtze River (SYAR) | |||||||||||||
| R | 0.80 | 0.84 | 0.49 | 0.24 | 0.33 | 0.32 | 0.96 | 0.64 | 0.66 | 0.55 | 0.86 | 0.73 | 0.81 |
| RMSE | 0.034 | 0.015 | 0.035 | 9.7 | 8.2 | 9.9 | 113.2 | 19.2 | 19.2 | 28.7 | 17.3 | 23.6 | 24.6 |
| PVD (%) | 11.5 | −0.9 | −10.2 | 318.4 | −11.3 | 410.4 | 20.1 | 16.3 | 5.1 | −23.8 | −3.5 | −42.2 | −37.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmood, R.; Jia, S. A Comprehensive Approach to Develop a Hydrological Model for the Simulation of All the Important Hydrological Components: The Case of the Three-River Headwater Region, China. Water 2022, 14, 2778. https://doi.org/10.3390/w14182778
Mahmood R, Jia S. A Comprehensive Approach to Develop a Hydrological Model for the Simulation of All the Important Hydrological Components: The Case of the Three-River Headwater Region, China. Water. 2022; 14(18):2778. https://doi.org/10.3390/w14182778
Chicago/Turabian StyleMahmood, Rashid, and Shaofeng Jia. 2022. "A Comprehensive Approach to Develop a Hydrological Model for the Simulation of All the Important Hydrological Components: The Case of the Three-River Headwater Region, China" Water 14, no. 18: 2778. https://doi.org/10.3390/w14182778







