Effects of Environmental Factors on Suspended Sediment Plumes in the Continental Shelf Out of Danshuei River Estuary
Abstract
:1. Introduction
2. Study Area and Data
3. Materials and Methods
3.1. Description of the 3D Hydrodynamic Model
3.2. Suspended Sediment Model
3.3. Model Setup
3.4. Model Performance Evaluation
4. Model Calibration and Validation
4.1. Calibration and Validation of the Hydrodynamic Model
4.2. Calibration and Validation of Suspended Sediment Model
4.3. Sensitivity Analysis of the Suspended Sediment Model
5. Model Applications and Discussion
5.1. Effect of Tidal Forcing
5.2. Effect of Salinity
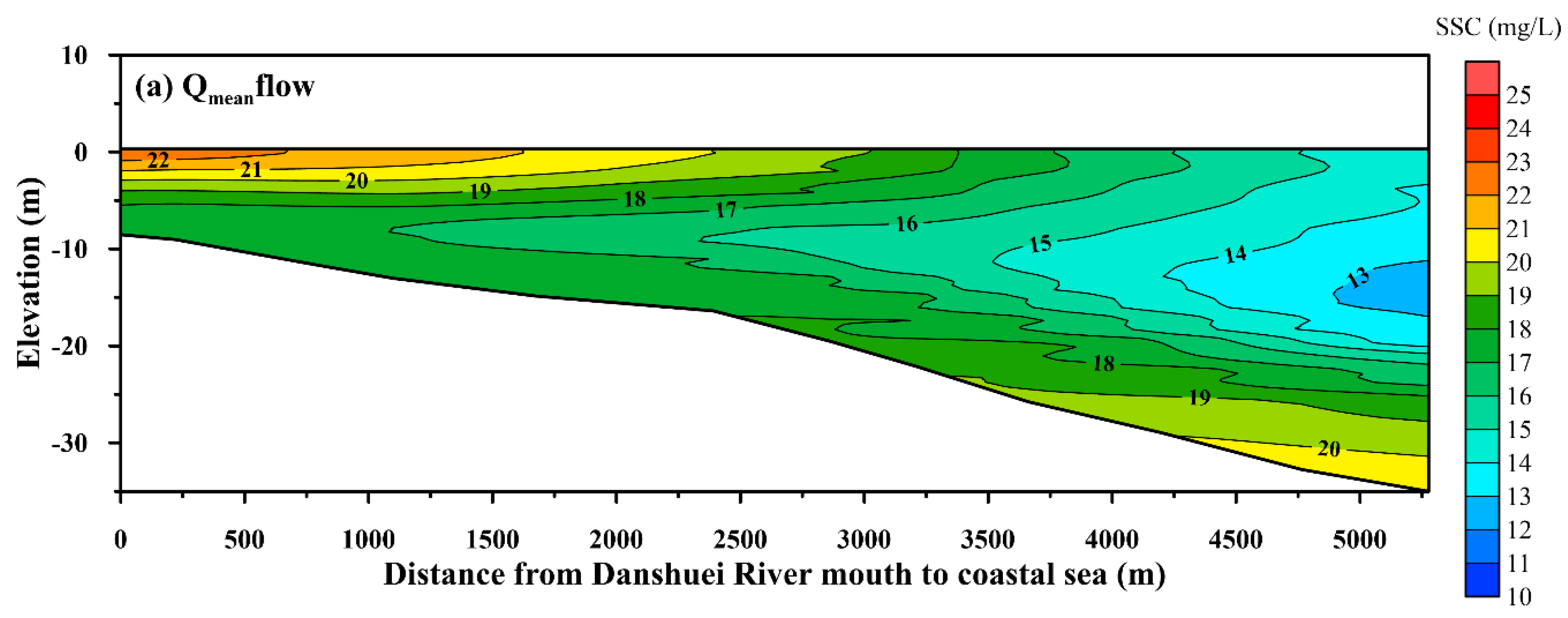
5.3. Effect of River Discharge
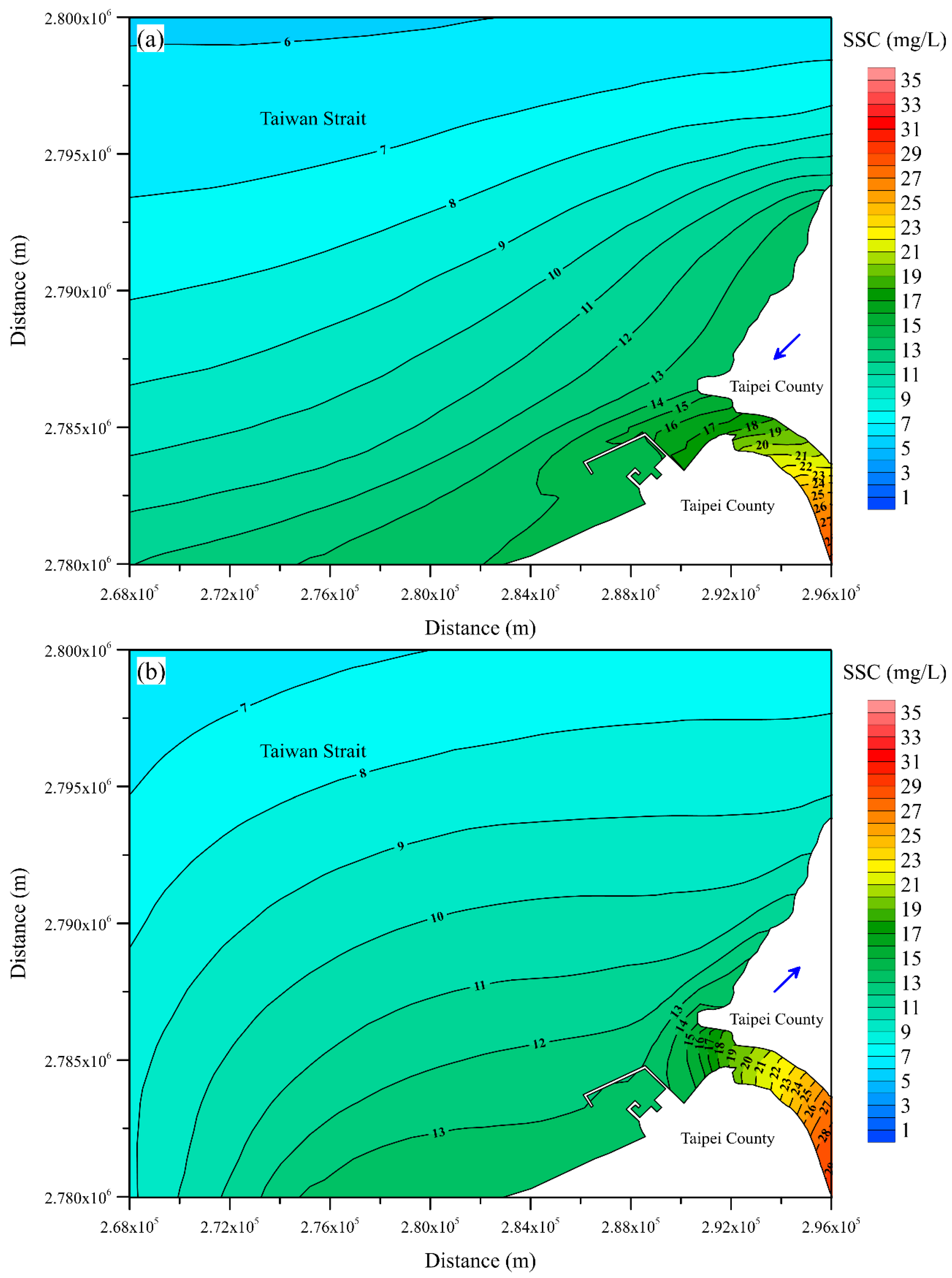
5.4. Effects of Wind Stress
5.5. Limitations and Future Directions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Perianez, R. Modelling the transport of suspended particulate matter by the Rhone River plume (France): Implications for pollutant dispersion. Environ. Pollut. 2005, 133, 351–364. [Google Scholar] [CrossRef]
- Liste, M.; Grifoll, M.; Monbaliu, J. River plume dispersion in response to flash flood events: Application to the Catalan shelf. Cont. Shelf Res. 2014, 87, 96–108. [Google Scholar] [CrossRef]
- Schiller, R.V.; Kourafalou, V.H.; Hogan, P.; Walker, N.D. The dynamics of the Mississippi River plume: Impact of topography, wind and offshore forcing on the fate of plume waters. J. Geophys. Res. 2011, 116, C06029. [Google Scholar] [CrossRef]
- MacCready, O.; Banas, N.S.; Hickey, B.M.; Dever, E.P.; Liu, Y. A model study of tide- and wind-induced mixing in the Columbia River Estuary and plume. Cont. Shelf Res. 2009, 29, 278–291. [Google Scholar] [CrossRef]
- Marques, W.C.; Fernandes, E.H.; Monteiro, I.O.; Moller, O.O. Numerical modeling of the Patos Lagoon coastal plume, Brazil. Cont. Shelf Res. 2009, 29, 556–571. [Google Scholar] [CrossRef]
- Sousa, M.C.; Vaz, N.; Alvarez, I.; Gomez-Gesteira, M.; Dias, J.M. Modeling the Minho River plume intrusion into the Rias Baixas (NW Iberian Peninsula). Cont. Shelf Res. 2014, 85, 30–41. [Google Scholar] [CrossRef]
- Androulidakis, Y.S.; Kourafalou, V.H.; Schiller, R.V. Process studies on the evolution of the Mississippi River plume: Impact of topography, wind and discharge conditions. Cont. Shelf Res. 2015, 107, 33–49. [Google Scholar] [CrossRef]
- Vallaeys, V.; Karna, T.; Delandmeter, P.; Lambrechts, J.; Baptista, A.M.; Deleersnijder, E.; Hanert, E. Discontinuous Galerkin modeling of the Columbia River’s coupled estuary-plume dynamics. Ocean Model. 2018, 124, 111–124. [Google Scholar] [CrossRef]
- Zhao, J.; Gong, W.; Shen, J. The effect of wind on the dispersal of a tropical small river plume. Front. Earth Sci. 2018, 12, 170–190. [Google Scholar] [CrossRef]
- Yu, X.; Guo, X.; Morimoto, A.; Buranapratheprat, A. Simulation of river plume behaviors in a tropical region: Case study of the Upper Gulf of Thailand. Cont. Shelf Res. 2018, 153, 16–29. [Google Scholar] [CrossRef]
- Osadchiev, A.; Sedakov, R.; Barymova, A. Response of a Small River Plume on Wind Forcing. Front. Mar. Sci. 2021, 8, 809566. [Google Scholar] [CrossRef]
- Zhi, H.; Wu, H.; Wu, J.; Zhang, W.; Wang, Y. River Plume Rooted on the Sea-Floor: Seasonal and Spring-Neap Variability of the Pearl River Plume Front. Front. Mar. Sci. 2022, 9, 791948. [Google Scholar] [CrossRef]
- Osadchiev, A.A.; Zavialov, P.O. Lagrangian model of a surface-advected river plume. Cont. Shelf Res. 2013, 58, 96–106. [Google Scholar] [CrossRef]
- Zheng, S.; Guan, W.; Cai, S.; Wei, X.; Huang, D. A model study of the effects of river discharges and interannual variation of winds on the plume front on winter in Pear River Estuary. Cont. Shelf Res. 2014, 73, 31–40. [Google Scholar] [CrossRef]
- Yao, H.Y.; Leonardi, N.; Li, J.F.; Fagherazzi, S. Sediment transport in a surface-advected estuarine plume. Cont. Shelf Res. 2016, 116, 122–135. [Google Scholar] [CrossRef]
- Kashyap, S.; Dibike, Y.; Shakibaeinia, A.; Prowse, T.; Droppo, I. Two-dimensional numerical modelling of sediment and chemical constituent transport within the lower reaches of the Athabasca River. Environ. Sci. Pollut. Res. 2017, 24, 2286–2303. [Google Scholar] [CrossRef]
- Cheng, P.; Li, M.; Li, Y. Generation of an estuarine sediment plume by a tropical storm. J. Geophys. Res. 2013, 118, 856–868. [Google Scholar] [CrossRef]
- Fissel, D.B.; Lin, Y.; Scoon, A.; Lim, J.; Brown, L.; Clouston, R. The variability of the sediment plumes and ocean circulation features of the Nass River Estuary, British Columbia. Satell. Oceanogr. Meteorol. 2017, 2, 1–15. [Google Scholar] [CrossRef]
- Luo, Z.; Zhu, J.; Wu, H.; Li, X. Dynamics of the sediment plume over the Yangtz Bank in the Yellow and East China Seas. J. Geophys. Res. 2017, 122, 10073–10090. [Google Scholar] [CrossRef]
- Whitney, M.M.; Garvine, R.W. Simulating the Delaware Bay buoyant outflow: Comparison with observations. J. Phys. Oceanogr. 2006, 36, 3–21. [Google Scholar] [CrossRef]
- Tarya, A.; Hoitink, A.J.F.; Van der Vegt, M. Tidal and subtidal flow patterns on a tropical continental shelf semi-insulated by coral reefs. J. Geophys. Res. 2010, 115, C09029. [Google Scholar] [CrossRef]
- Van, C.P.; Gourgue, O.; Sassi, M.; HoitinkTon, A.J.F.; Deleersnijder, E.; Soares-Frazao, S. Modelling fine-grained sediment transport in Mahakam land-sea continuum, Indonesia. J. Hydro-Environ. Res. 2016, 13, 103–120. [Google Scholar]
- Guo, K.; Zou, T.; Jiang, D.; Tang, C.; Zhang, H. Variability of Yellow River turbidity plume detected with satellite remote sensing during water sediment regulation. Cont. Shelf Res. 2017, 135, 74–86. [Google Scholar] [CrossRef]
- Talke, S.A.; de Swart, H.E.; Schuttelaars, H.M. Feedback between residual circulation and sediment distribution in highly turbid estuaries: An analytical model. Cont. Shelf Res. 2009, 29, 119–135. [Google Scholar] [CrossRef]
- Thanh, V.Q.; Reyns, J.; Wackerman, C.; Eidam, E.F.; Roelvink, D. Modelling suspended sediment dynamics on the subaqueous delta of the Mekong River. Cont. Shelf Res. 2017, 147, 213–230. [Google Scholar] [CrossRef]
- Tarya, A.; Ven der Vegt, M.; Hoitink, A.J.F. Wind forcing controls on river plume spreading on tropical continental shelf. J. Geophys. Res. 2015, 120, 16–35. [Google Scholar] [CrossRef]
- Xu, C.; Xu, Y.; Hu, J.; Li, S.; Wang, B. A numerical analysis of the summertime Pear River plume from 1999 to 2010: Dispersal patterns and intraseasonal variability. J. Mar. Syst. 2019, 192, 15–27. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.M.; Ruan, M.N.; Chen, J.W. The Jiulong River plume as cross-strait exporter and along-strait barrier for suspended sediment: Evidence from the endmember analysis of in-situ particle size. Estuar. Coast. Shelf Sci. 2015, 166, 146–152. [Google Scholar] [CrossRef]
- Horner-Devine, A.R.; Pietrzak, J.D.; Souza, A.J.; McKeon, M.A.; Meirelles, S.; Henriquez, M.; Flores, R.P.; Rijnburger, S. Cross-shore transport of nearshore sediment by river plume frontal pumping. Geophys. Res. Lett. 2017, 44, 6343–6351. [Google Scholar] [CrossRef]
- Zavialov, P.O.; Pelevin, V.V.; Belyaev, N.A.; Izhitskiy, A.S.; Konovalov, B.V.; Krementskiy, V.V.; Goncharenko, I.V.; Osadchiev, A.A.; Soloviev, D.M.; Garcia, C.A.E.; et al. High resolution LiDAR measurements reveal fine internal structure and variability of sediment-carrying coastal plume. Estuar. Coast. Shelf Sci. 2018, 205, 40–45. [Google Scholar] [CrossRef]
- Lee, J.; Liu, J.T.; Lee, I.H.; Fu, K.H.; Yang, R.J.; Gong, W.; Gan, J. Encountering shoaling internal waves on the dispersal pathway of the pearl river plume in summer. Sci. Rep. 2021, 11, 999. [Google Scholar]
- Shi, W.; Wang, M. Satellite observations of seasonal sediment plume in central East China Sea. J. Mar. Syst. 2010, 82, 280–285. [Google Scholar]
- Aurin, D.; Mannino, A.; Franz, B. Spatially resolving ocean color and sediment dispersion in river plumes, coastal systems, and continental shelf waters. Remote Sens. Environ. 2013, 137, 212–225. [Google Scholar]
- Kamel, A.M.Y.; El Serafy, G.Y.; Bhattacharya, B.; Van Kessel, T.; Solomatine, D.P. Using remote sensing to enhance modelling of fine sediment dynamic in the Dutch coastal zone. J. Hydroinform. 2014, 16, 458–476. [Google Scholar]
- Zhang, P.; Chen, X.; Lu, J.; Zhang, W. Assimilation of remote sensing observations into a sediment transport model of China’s largest freshwater lake: Spatial and temporal effects. Environ. Sci. Pollut. Res. 2015, 22, 18779–18792. [Google Scholar]
- Zheng, G.; DiGiacomo, P.M.; Kaushal, S.S.; Yuen-Murpgy, M.A.; Duan, S. Evolution of sediment plumes in the Chesapeake Bay and implications of climate variability. Environ. Sci. Technol. 2015, 49, 6494–6503. [Google Scholar] [PubMed]
- Reisinger, A.; Gibeaut, J.C.; Tissot, P.E. Estuarine Suspended Sediment Dynamics: Observations Derived from over a Decade of Satellite Data. Front. Mar. Sci. 2017, 4, 233. [Google Scholar]
- Sadeghian, A.; Hudson, J.; Wheater, H.; Lindenschmidt, K. Sediment plume model-a comparison between use of measured turbidity data and satellite images for model calibration. Environ. Sci. Pollut. Res. 2017, 24, 19583–19598. [Google Scholar]
- Pitarch, J.; Falcini, F.; Nardin, W.; Brando, V.E.; Di Cicco, A.; Marullo, S. Linking flow-stream variability grain size distribution of suspended sediment from a satellite-based analysis of the Tiber River plume (Tyrrhenian Sea). Sci. Rep. 2019, 9, 19729. [Google Scholar]
- Iles, I.V.R.L.; Walker, N.D.; White, J.R.; Rohli, R.V. Impacts of a major Mississippi River freshwater diversion on suspended sediment plume kinematics in Lake Pontchartrian, a semi-enclosed Gulf of Mexico Estuary. Estuaries Coasts 2021, 44, 704–721. [Google Scholar]
- Chang, Y.H.; Liou, J.Y. The morphological modelling of Tamsui River estuary. In Proceedings of the 37th Ocean Engineering Conference in Taiwan, Taipei, Taiwan, 18–19 November 2015; pp. 273–278. (In Chinese). [Google Scholar]
- Taiwan Water Resources Agency. Impacts on the Downstream River Ecology and Bed Evolution by the Operation of Flood Control and Sediment Desiltation of Shimen Reservoir (II); Final Report; Taiwan Water Resources Agency: Taichung City, Taiwan, 2017. (In Chinese)
- Wen, L.S.; Jiann, K.T.; Liu, K.K. Seasonal variation and flux of dissolved nutrients in the Danshuei Estuary, Taiwan: A hypoxic subtropical mountain river. Estuar. Coast. Shelf Sci. 2008, 78, 694–704. [Google Scholar]
- Wu, P.C.; Gong, G.C.; Cheng, J.S.; Liu, K.K.; Kao, S.J. Origins of particulate organic matter determined from nitrogen isotopic composition and C/N ratio in the highly eutrophic Danshuei Estuary, Northern Taiwan. Aquat. Geochem. 2016, 22, 291–311. [Google Scholar]
- Liu, W.C.; Liu, H.M.; Ken, P.J. Investigating the contaminant transport of heavy metals in estuarine waters. Environ. Monit. Assess. 2020, 192, 31. [Google Scholar]
- Liu, W.C.; Liu, H.M.; Young, C.C.; Huang, W.C. The Influence of Freshwater Discharge and Wind Forcing on the Dispersal of River Plumes Using a Three-Dimensional Circulation Model. Water 2022, 14, 429. [Google Scholar]
- Hsu, M.H.; Wu, C.R.; Liu, W.C.; Kuo, A.Y. Investigation of turbidity maximum in a mesotidal estuary, Taiwan. J. Am. Water Resour. Assoc. 2006, 42, 901–914. [Google Scholar]
- Hsu, M.H.; Kuo, A.Y.; Kuo, J.T.; Liu, W.C. Procedure to calibrate and verify numerical models of estuarine hydrodynamics. J. Hydraul. Eng. ASCE 1999, 125, 166–182. [Google Scholar]
- Liu, W.C.; Hsu, M.H.; Kuo, A.Y. Modeling of hydrodynamics and cohesive sediment transport in Tanshui River estuarine system. Mar. Pollut. Bull. 2002, 44, 1076–1088. [Google Scholar]
- Taiwan Environmental Protection Agency. Environmental Water Quality Monitoring Annual Report. 2020. Available online: https://wq.epa.gov.tw/EWQP/zh/ConService/DownLoad/AnnReport.aspx (accessed on 1 January 2022). (In Chinese)
- Zhang, Y.L.; Stanev, E.V.; Grashorn, S. Unstructured-grid model for the North Sea and Baltic Sea: Validation against observations. Ocean Model. 2016, 97, 91–108. [Google Scholar]
- Zhang, Y.L.; Ye, F.; Stanev, E.V.; Grasgorn, S. Seamless cross-scale modeling with SCHISM. Ocean Model. 2016, 102, 64–81. [Google Scholar]
- Ye, F.; Zhang, Y.J.; Friedrichs, M.A.M.; Wang, H.V.; Irby, I.D.; Shen, J.; Wang, Z. A 3D cross-scale, baroclinic model with implicit vertical transport for the Upper Chesapeake Bay and its tributaries. Ocean Model. 2016, 107, 82–96. [Google Scholar]
- Chao, Y.; Farrara, J.D.; Zhang, H.; Zhang, Y.J.; Ateljevich, E.; Chai, F.; Davis, C.O.; Dugdale, R.; Wilkerson, F. Development, implementation, and validation of a modeling system for the San Francisco Bay and Estuary. Estuar. Coast. Shelf Sci. 2017, 194, 40–56. [Google Scholar]
- Schleon, J.; Stanev, E.V.; Grashorn, S. Wave-current interactions in the southern North Sea: The impact on salinity. Ocean Model. 2017, 111, 19–37. [Google Scholar]
- Chiu, C.M.; Huang, C.J.; Wu, L.C.; Zhang, Y.J.; Chuang, L.Z.H.; Fan, Y.; Yu, H.C. Forecasting of oil-spill trajectories by using SCHISM and X-band radar. Mar. Pollut. Bull. 2018, 137, 566–581. [Google Scholar]
- Du, J.; Shen, J.; Zhang, Y.; Ye, F.; Liu, Z.; Wang, Z.; Wang, Y.P.; Yu, X.; Sisson, M.; Wang, H.V. Tidal response to sea-level rise in different types of estuaries: The importance of length, bathymetry, and geometry. Geophys. Res. Lett. 2018, 45, 227–235. [Google Scholar]
- Stanev, E.V.; Jacob, B.; Pein, J. German Bight estuaries: An inter-comparison on the basis of numerical modeling. Cont. Shelf Res. 2019, 174, 48–65. [Google Scholar]
- Ye, F.; Zhang, Y.J.; Yu, H.; Sun, W.; Moghimi, S.; Mayer, E.; Nunez, K.; Zhang, R.; Wang, H.V.; Roland, A.; et al. Simulating storm surge and compound flooding events with a creek-to-ocean model: Importance of baroclinic effects. Ocean Model. 2020, 145, 101526. [Google Scholar]
- Zhang, Y.J.; Ye, F.; Yu, H.; Sun, W.; Moghimi, S.; Mayers, E.; Nunez, K.; Zhang, R.; Wang, H.V.; Roland, A.; et al. Simulating compound flooding events in a hurricane. Ocean Dyn. 2020, 70, 621–640. [Google Scholar]
- Ye, F.; Zhang, Y.J.; Wang, H.V.; Friedrichs, M.A.M.; Irby, I.D.; Alteljevichm, E.; Valle-Levinson, A.; Wang, Z.; Huang, H.; Shen, J.; et al. A 3D unstructured-grid model for Chesapeake Bay: Importance of bathymetry. Ocean Model. 2018, 127, 16–30. [Google Scholar]
- Umlauf, L.; Burchard, H. A generic length-scale equation for geophysical turbulence models. J. Mar. Res. 2003, 61, 235–265. [Google Scholar]
- Partheniades, E. Erosion and deposition of cohesive soils. J. Hydraul. Div. 1965, 91, 105–139. [Google Scholar]
- Manning, A.J.; Langston, W.J.; Jonas, P.J.C. A review of sediment dynamics in the Severn Estuary: Influence of flocculation. Mar. Pollut. Bull. 2010, 61, 37–51. [Google Scholar] [PubMed]
- Winterwerp, J.C. The physical analysis of muddy sedimentation processes. Treatise Estuar. Coast. Sci. 2013, 2, 311–360. [Google Scholar]
- Lopez, J.E.; Baptista, A.M. Benchmarking an unstructured grid sediment model in an energetic estuary. Ocean Model. 2017, 110, 32–48. [Google Scholar]
- Hesse, R.F.; Zorndt, A.; Frohle, P. Modelling dynamics of the estuarine turbidity maximum and local net deposition. Ocean Dyn. 2019, 69, 489–507. [Google Scholar]
- Yan, Y.; Song, D.; Bao, X.; Wang, N. The response of turbidity maximum to peak river discharge in a macrotidal estuary. Water 2021, 13, 106. [Google Scholar]
- Einstein, H.A.; Krone, R.B. Experiments to determine models of cohesive sediment transport in salt water. J. Geophys. Res. 1962, 67, 1451–1461. [Google Scholar]
- Ariathuri, R.; Krone, R.B. Finite element model for cohesive sediment transport. J. Hydraul. Div. 1976, 102, 323–338. [Google Scholar]
- Chen, W.B.; Liu, W.C. Modeling investigation of asymmetric tidal mixing and residual circulation in a partially mixing estuary. Environ. Fluid Mech. 2016, 16, 167–191. [Google Scholar]
- Xia, M.; Xie, L.; Pietrafesa, L.J.; Whitney, W.M. The tidal response of a Gulf of Mexico estuary plume to wind forcing: Its connection with salt flux and a Lagrangian view. J. Geophys. Res. 2011, 116, C08035. [Google Scholar]
- Rong, Z.; Li, M. Tidal effects on bulge region of Changjiang River plume. Estuar. Coast. Shelf Sci. 2012, 97, 149–160. [Google Scholar]
- Wang, X.; Chao, Y.; Zhang, H.; Farrara, J.; Li, Z.; Jin, X.; Park, K.; Colas, F.; Williams, J.C.; Paternostro, C.; et al. Modeling tides and their influence on the circulation in Prince William Sound, Alaska. Cont. Shelf Res. 2013, 63, S126–S137. [Google Scholar]
- Bricheno, L.M.; Wolf, J.; Islam, S. Tidal intrusion within a mega delta: An unstructured grid modelling approach. Estuar. Coast. Shelf Sci. 2016, 182, 12–26. [Google Scholar]
- Chao, S.Y. Tidal modulation by estuarine plumes. J. Phys. Oceanogr. 1990, 20, 1115–1123. [Google Scholar]
- Li, L.; Wu, H.; Liu, J.T.; Zhu, J. Sediment transport induced by the advection of a moving salt wedge in the Changjiang Estuary. J. Coast. Res. 2015, 31, 671–679. [Google Scholar]
- Dzwonkowski, B.; Park, K.; Collini, R. The coupled estuarine-shelf response of a river-dominated system during the transition from low to high discharge. J. Geophys. Res. 2015, 120, 6145–6163. [Google Scholar]
- Chao, S.Y. Wind-driven motion of estuarine plumes. J. Phys. Oceanogr. 1988, 18, 1144–1166. [Google Scholar]
- Fong, D.A.; Geyer, W.R. Response of a river plume during an upwelling favorable wind event. J. Geophys. Res. 2001, 106, 1067–1084. [Google Scholar]
- Geyer, W.R.; Hill, P.S.; Kineke, G.C. The transport, transformation and dispersal of sediment by buoyant coastal flows. Cont. Shelf Res. 2004, 24, 927–949. [Google Scholar]
- Choi, B.J.; Wilkin, J.L. The effect of wind on the dispersal of the Hudson River plume. J. Phys. Oceanogr. 2007, 37, 1878–1897. [Google Scholar]
- Moffat, C.; Lentz, S. On the response of a buoyant plume to downwelling-favorable wind stress. J. Phys. Oceanogr. 2012, 42, 1083–1098. [Google Scholar]
- Nguyen, V.T.; Vu, M.T.; Zhang, C. Numerical investigation of hydrodynamics and cohesive sediment transport in Cua Lo and Cua Hoi Estuaries, Vietnam. J. Mar. Sci. Eng. 2021, 9, 1258. [Google Scholar]
- Rego, J.L.; Meselhe, E.; Stronach, J.; Habib, E. Numerical modeling of the Mississippi-Atchafalaya Rivers’ sediment transport and fate: Considerations for diversion scenarios. J. Coast. Res. 2010, 26, 212–220. [Google Scholar]
- Papanicolaou, A.N.; Elhakeem, M.; Krallis, G.; Prakash, S.; Edinger, J. Sediment transport modeling review-current and future developments. J. Hydraul. Eng. 2008, 134, 1–14. [Google Scholar]
- Yin, K.; Xu, S.; Huang, W. Modeling sediment concentration and transport induced by storm surge in Hengmen Eastern Access Channel. Nat. Hazards 2016, 82, 617–642. [Google Scholar]
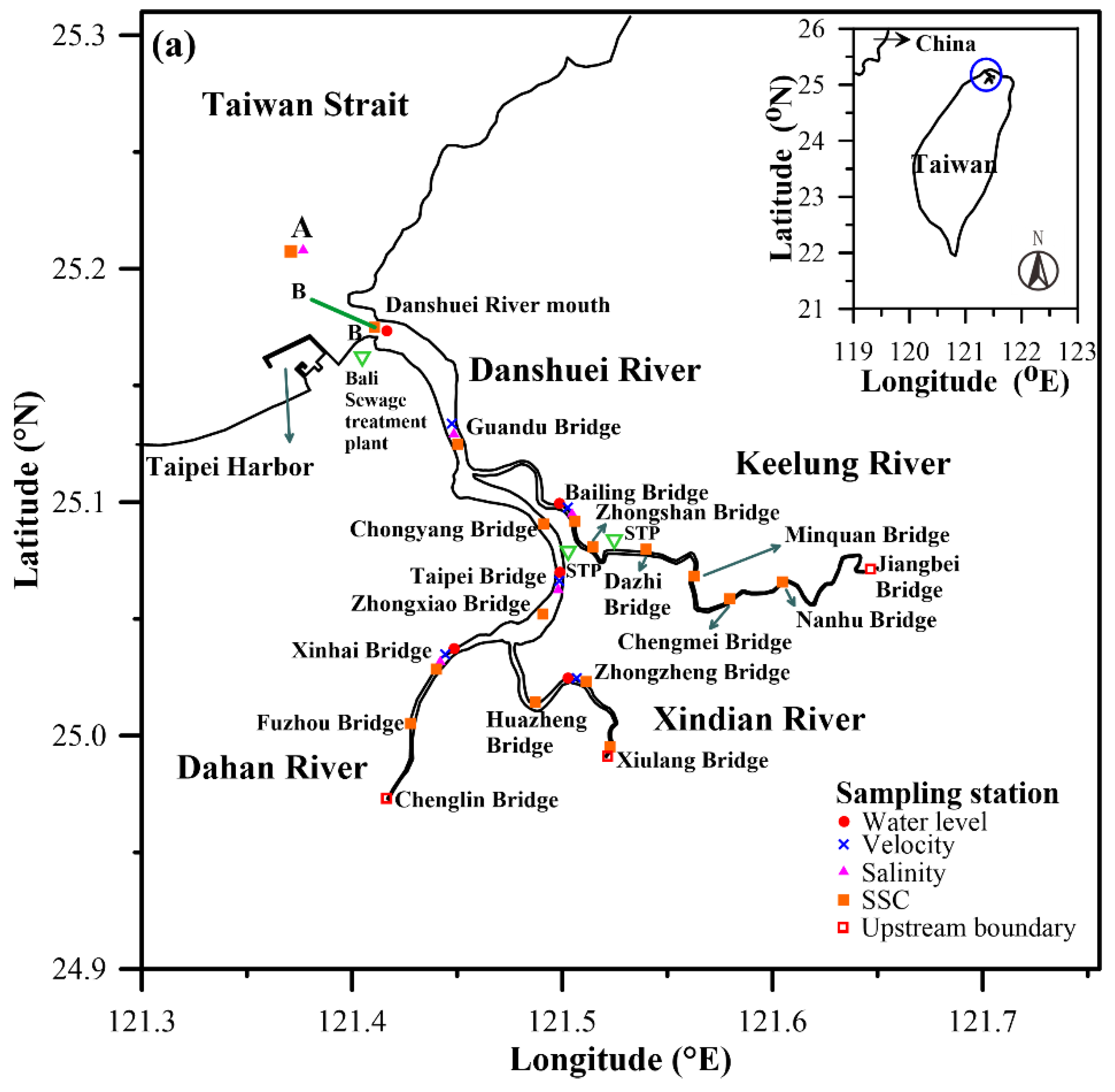
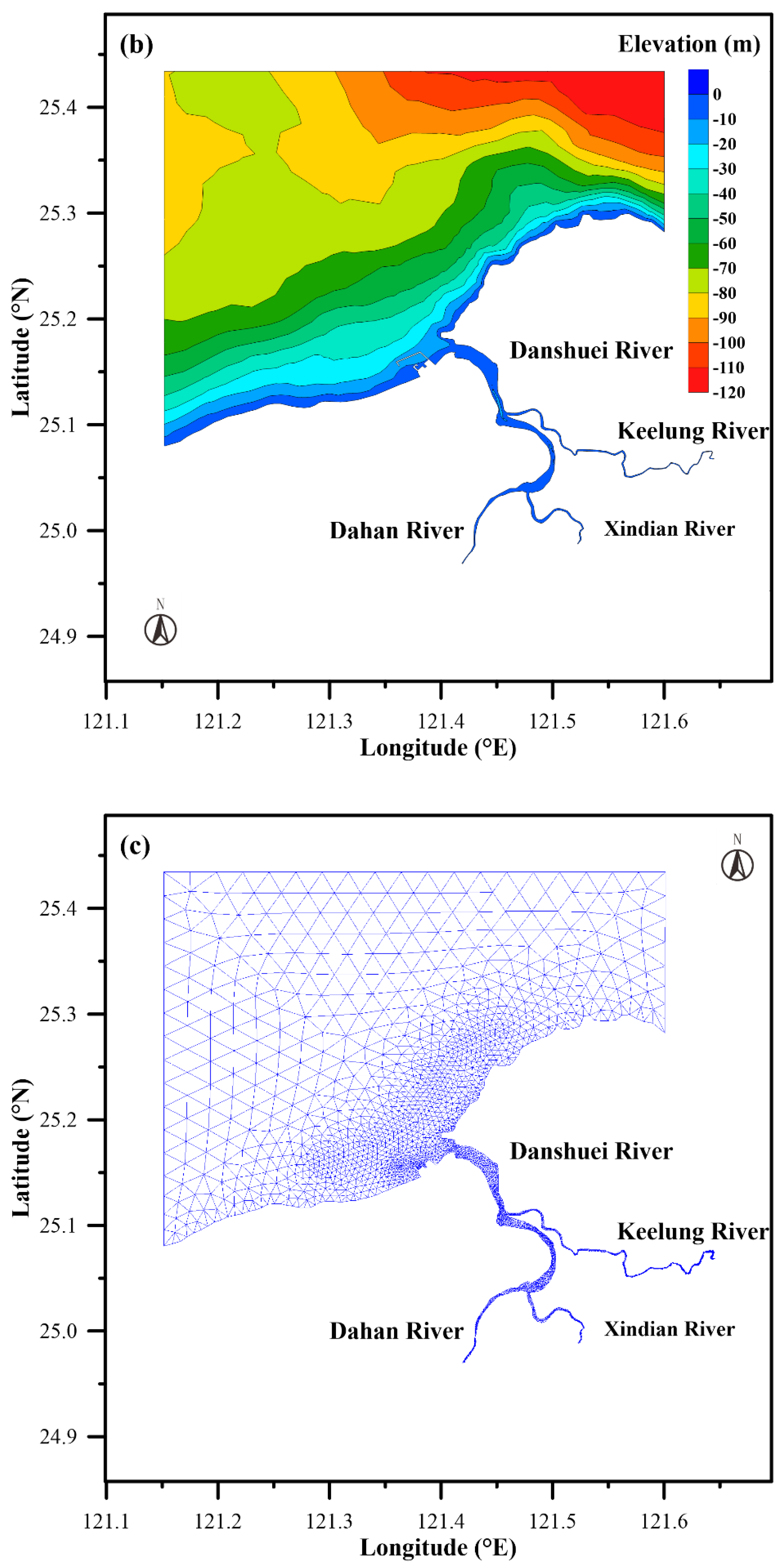
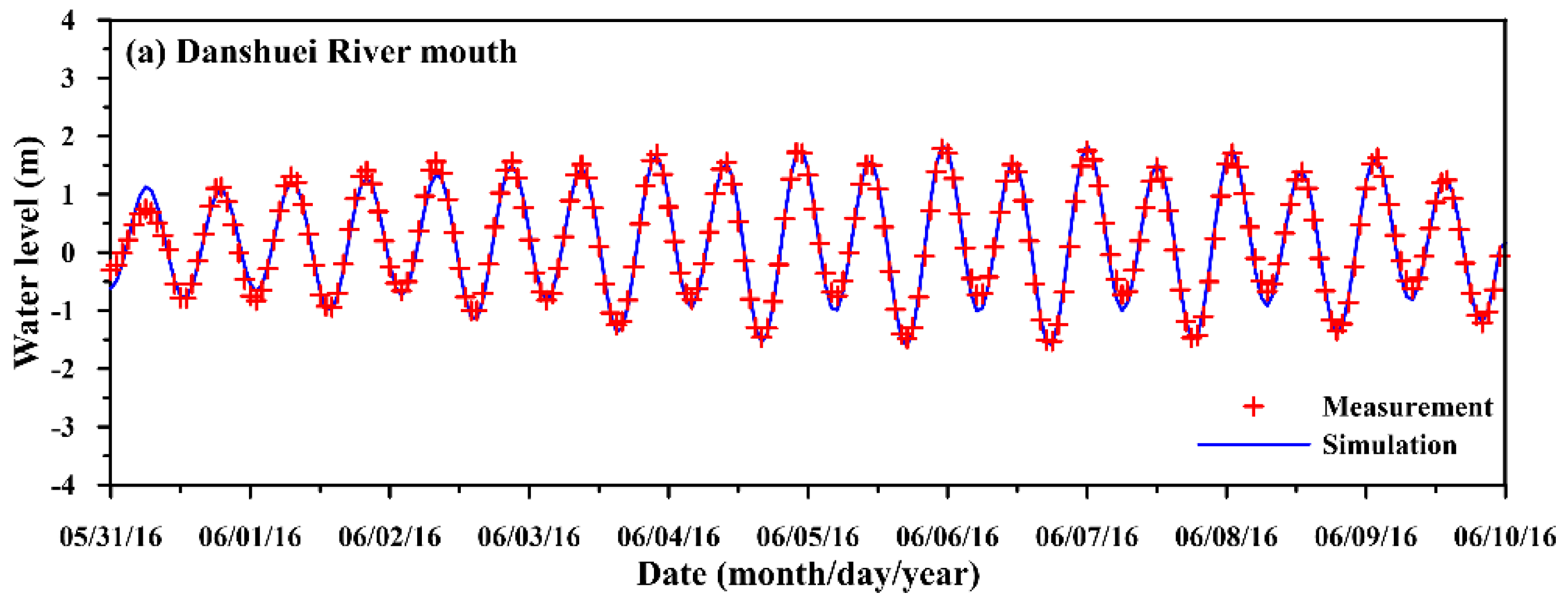
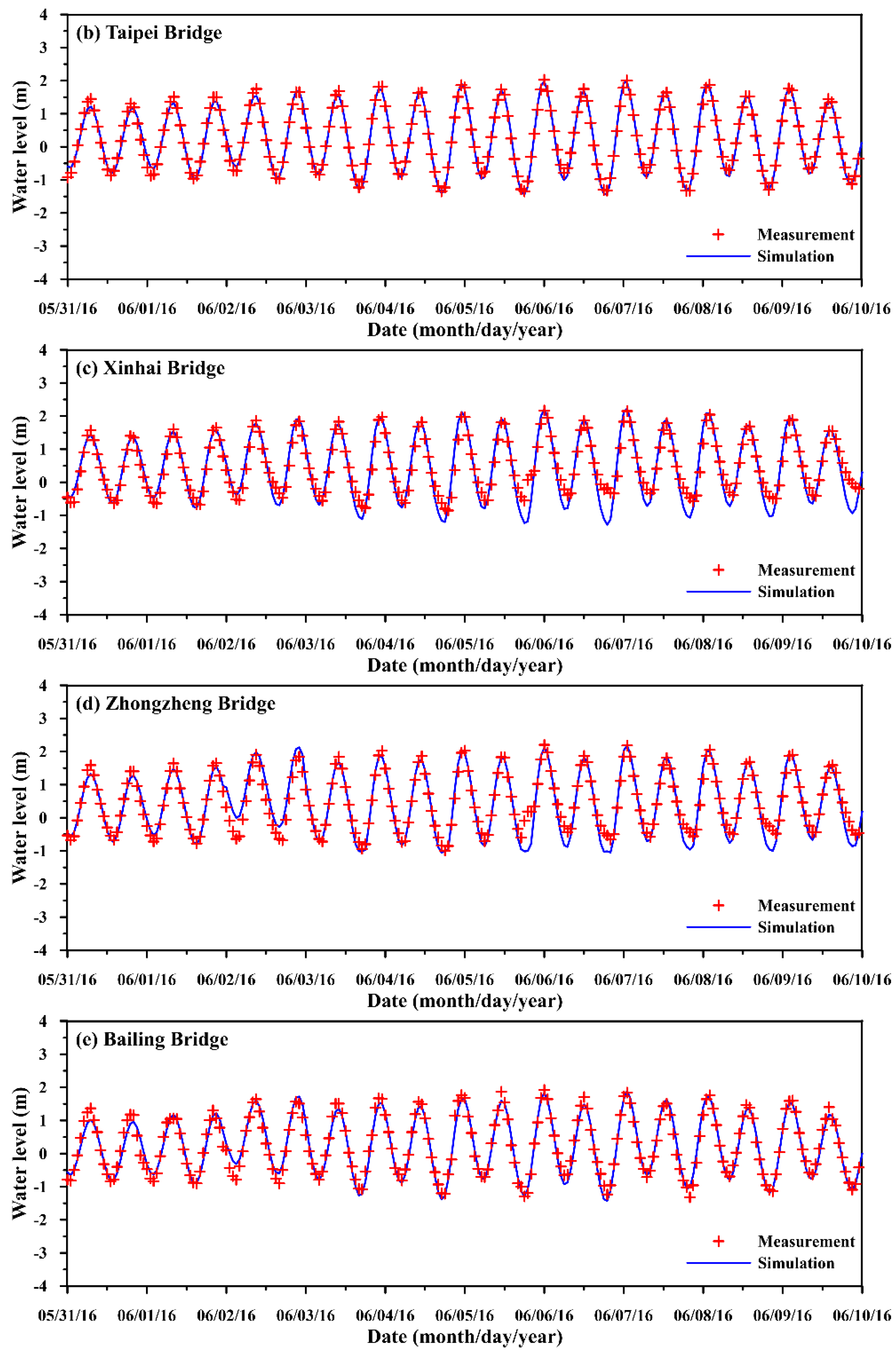
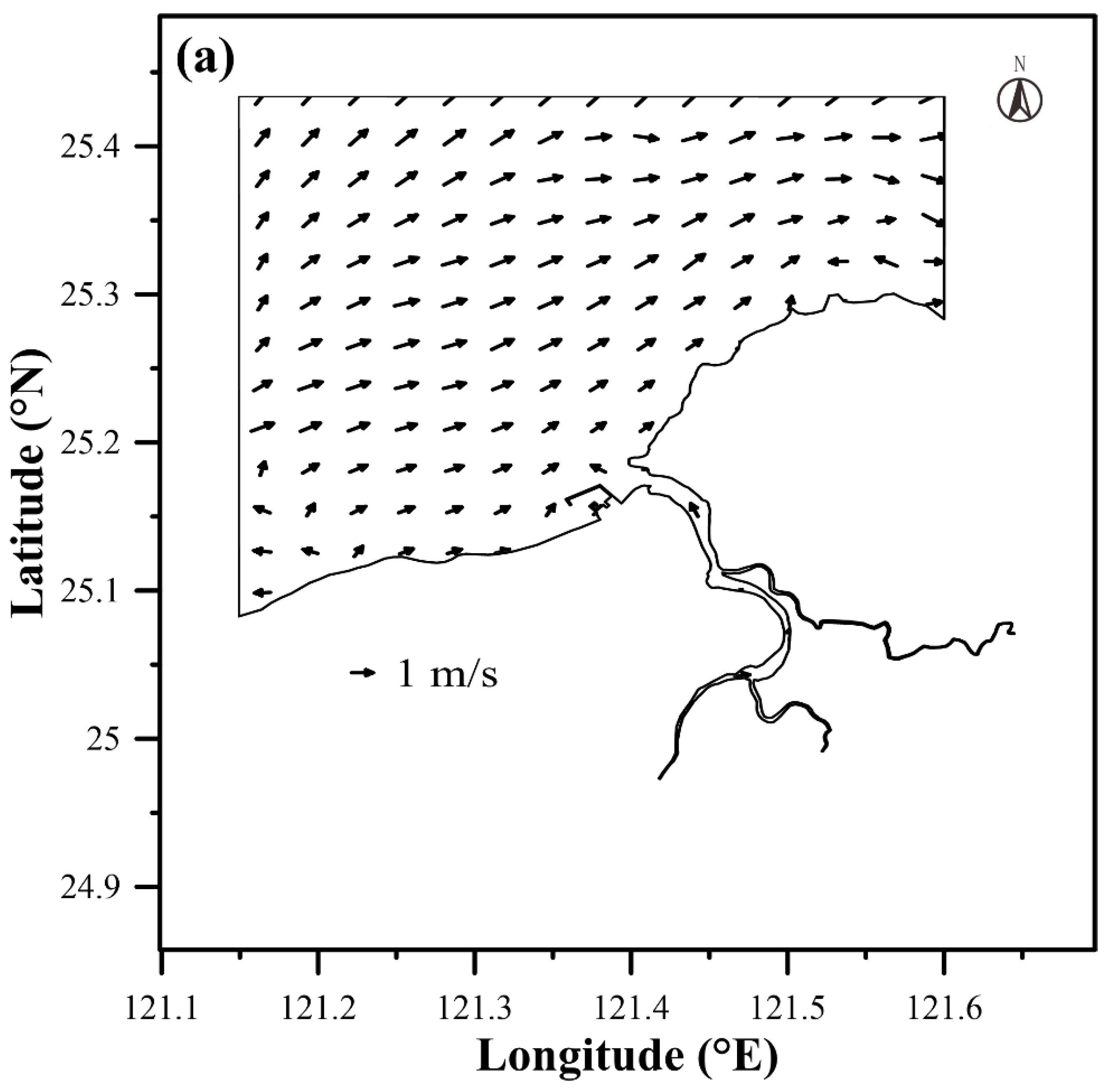
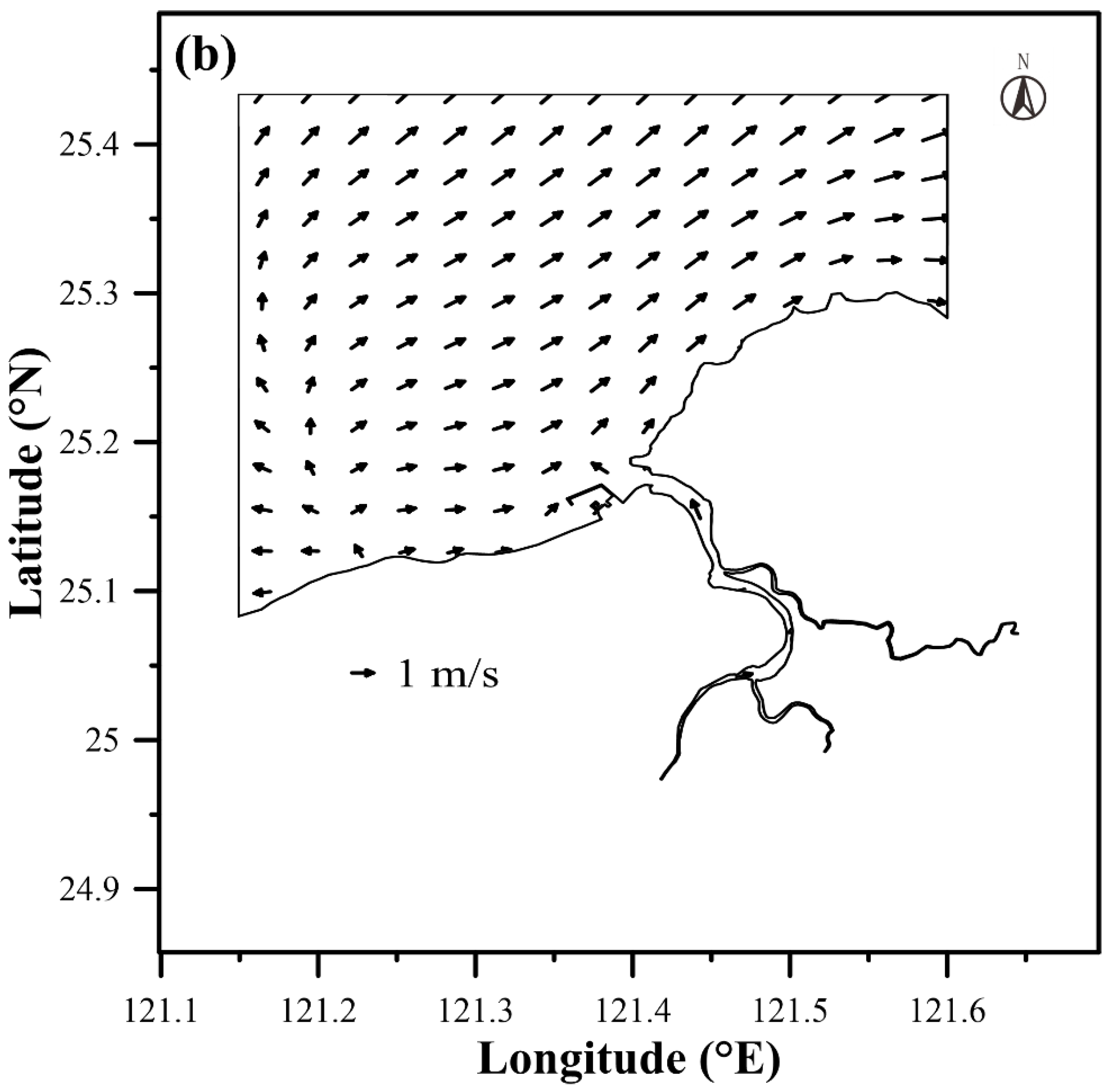
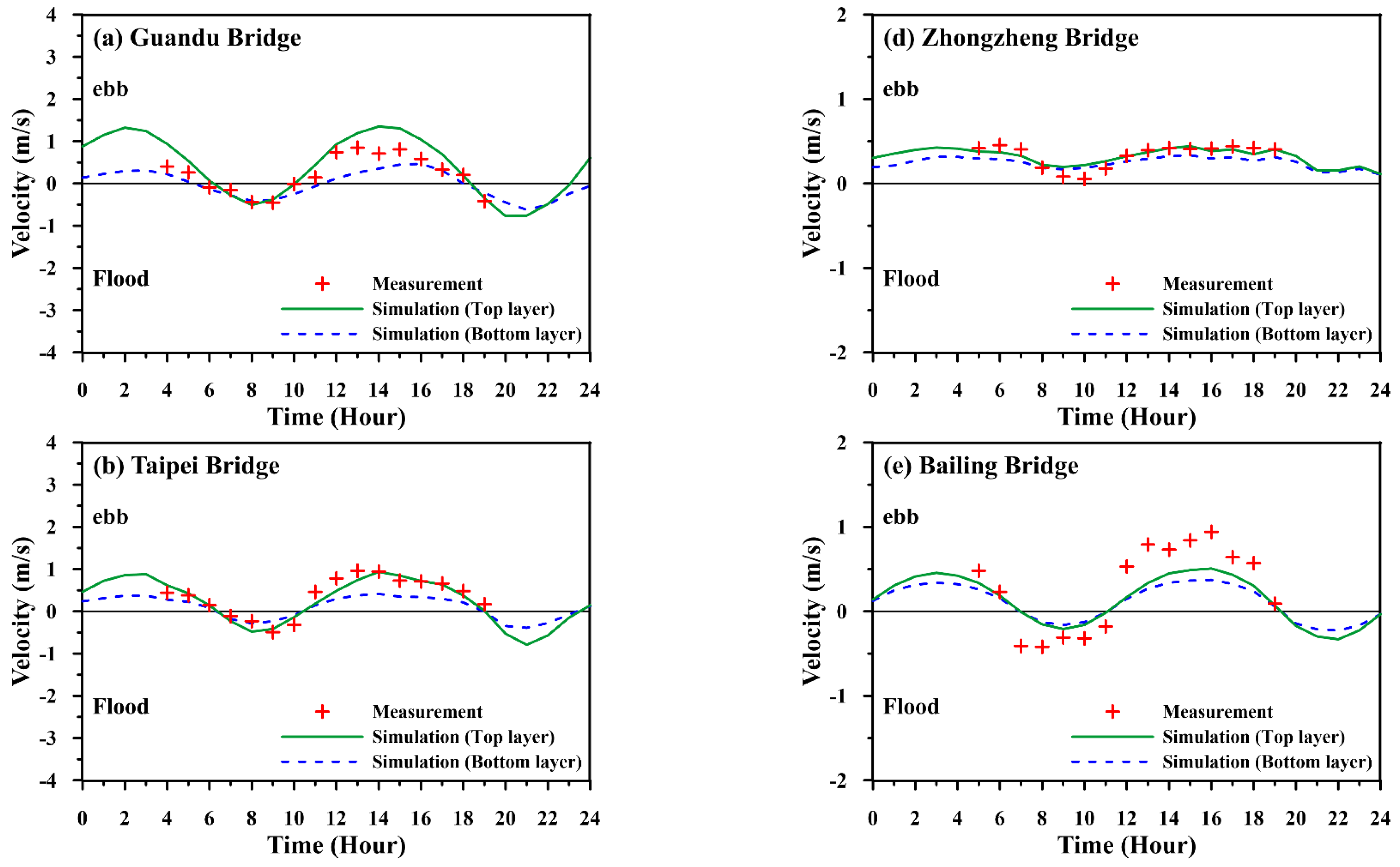
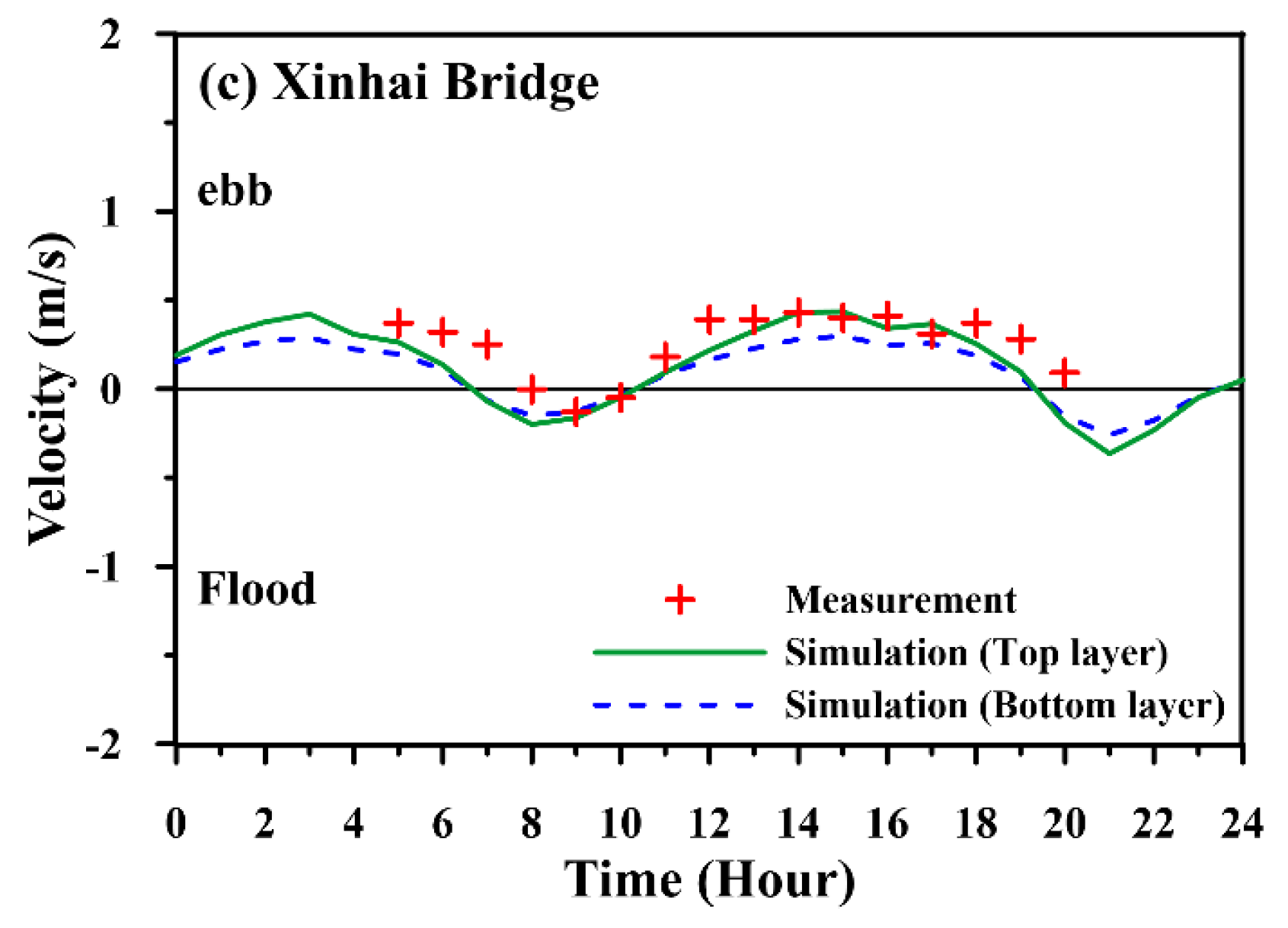
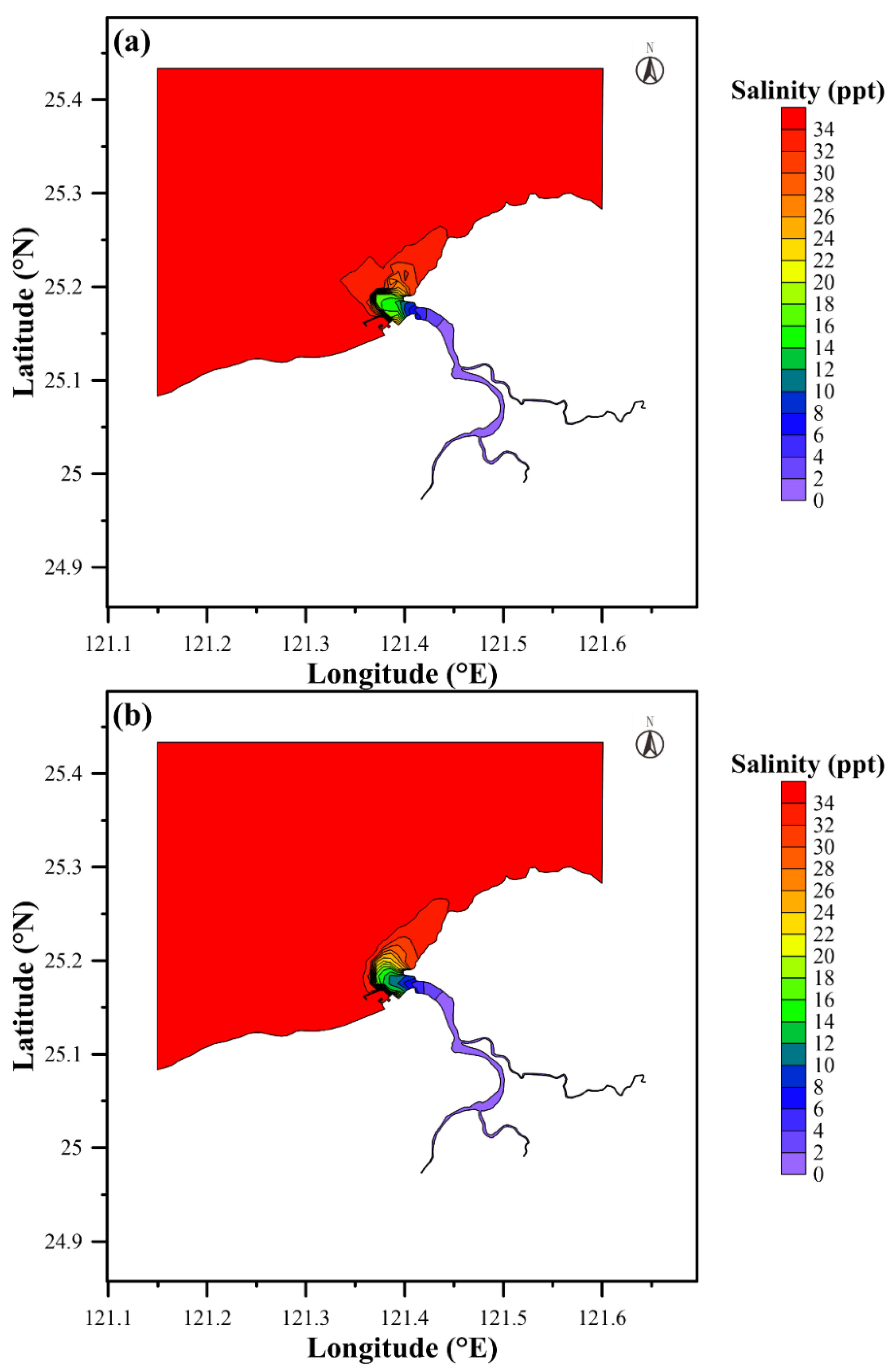
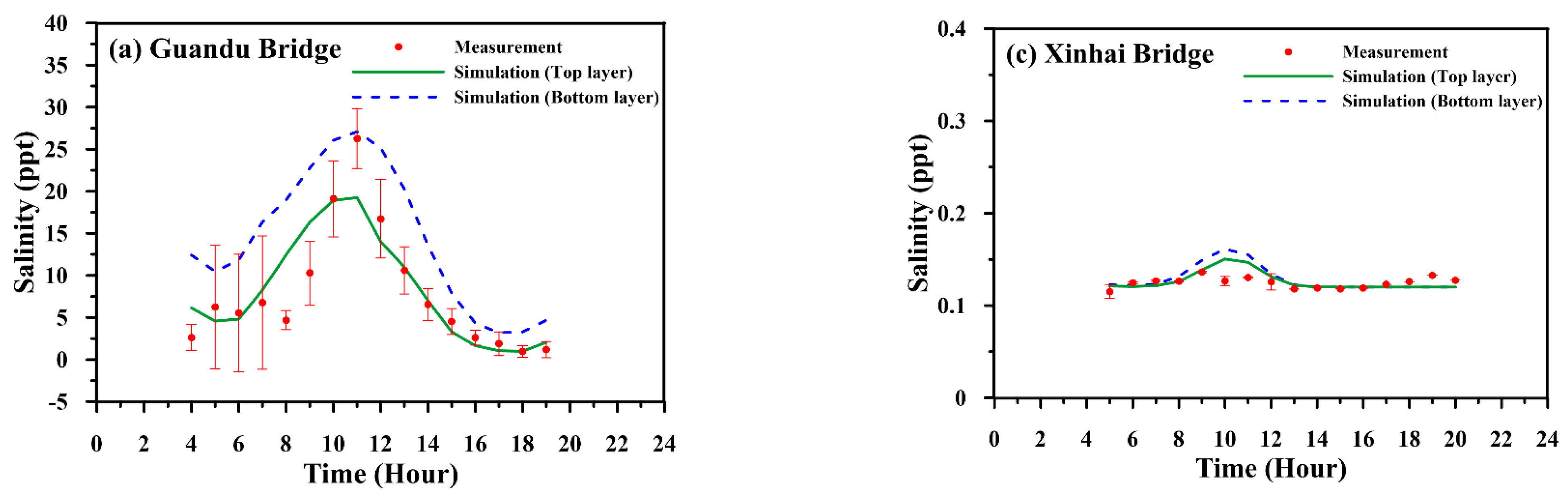
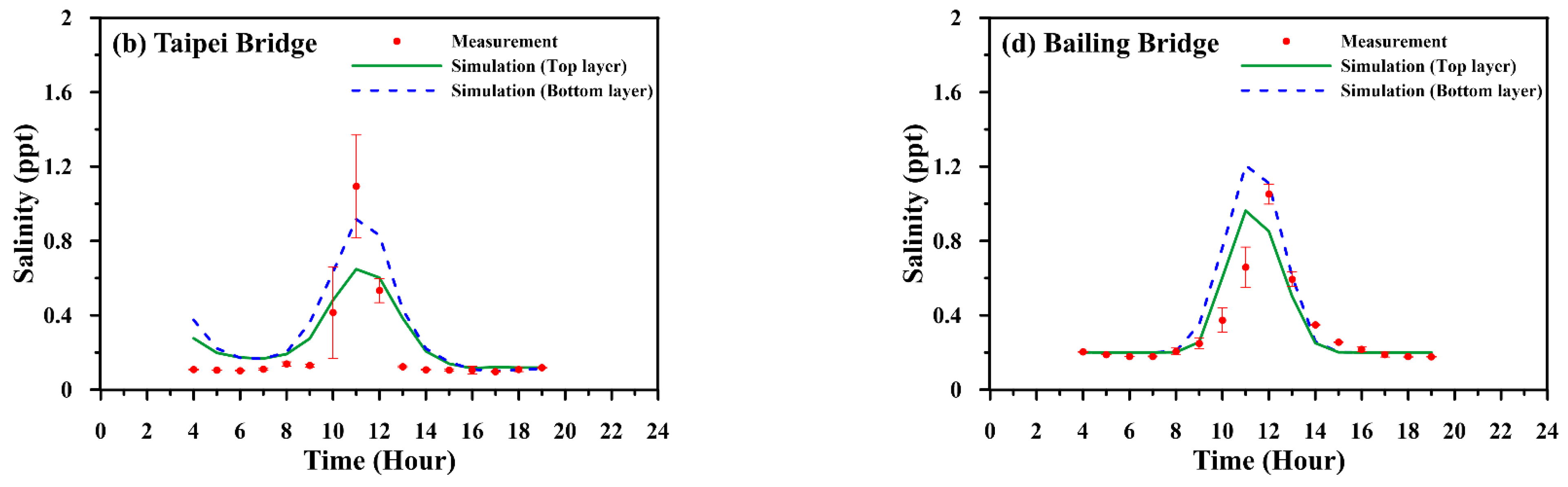
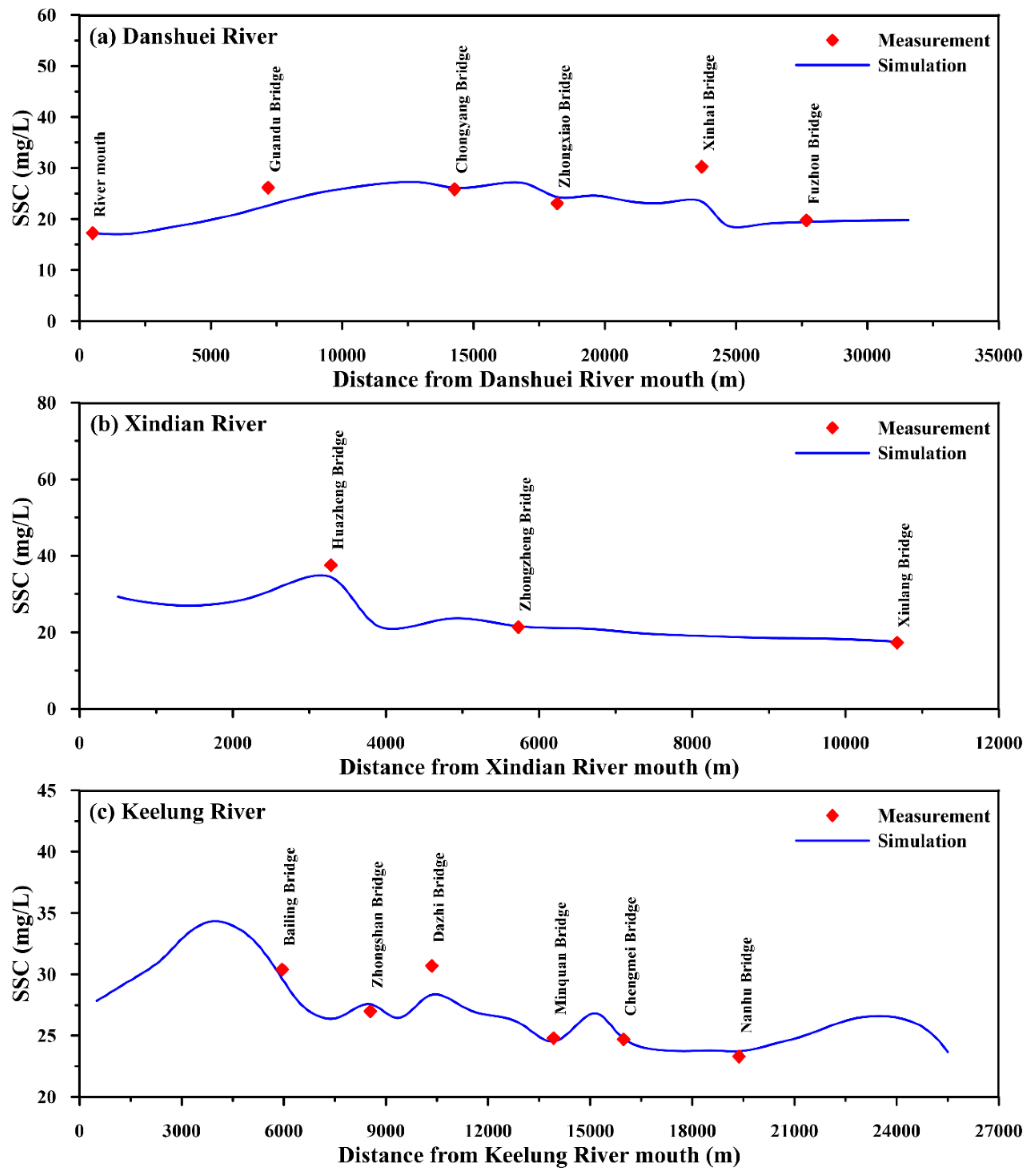
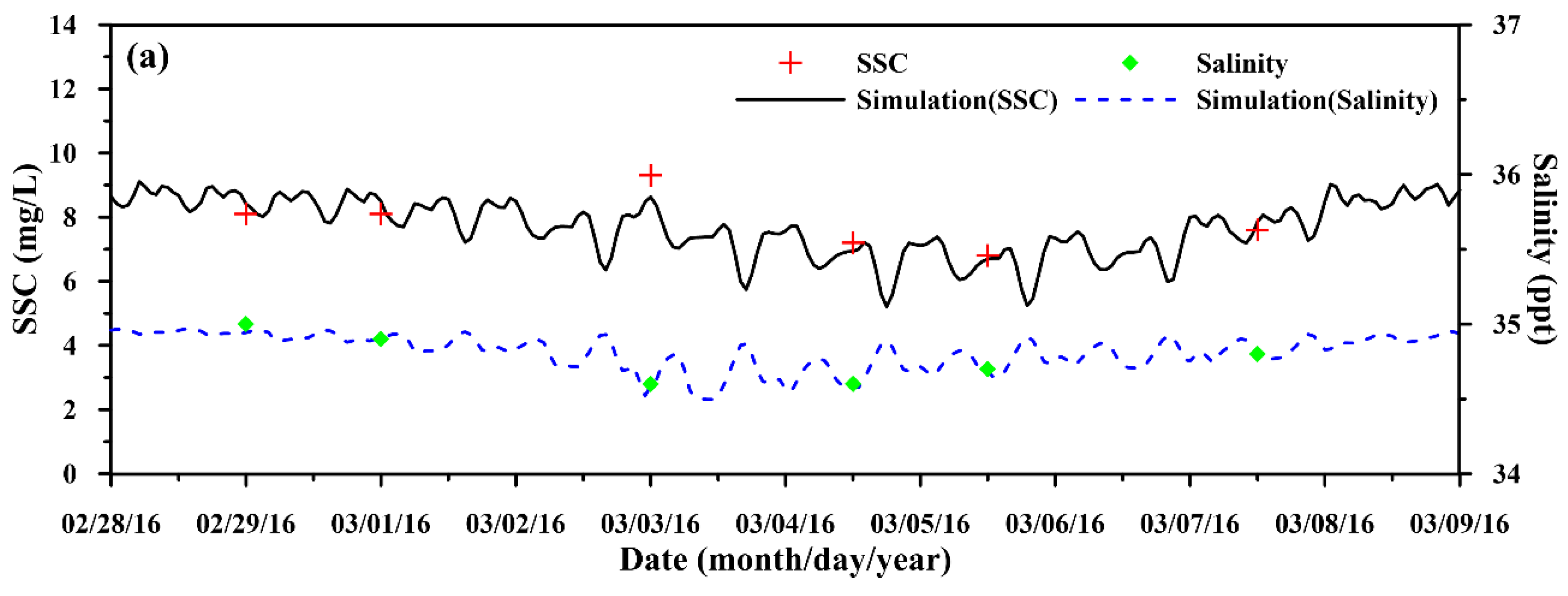
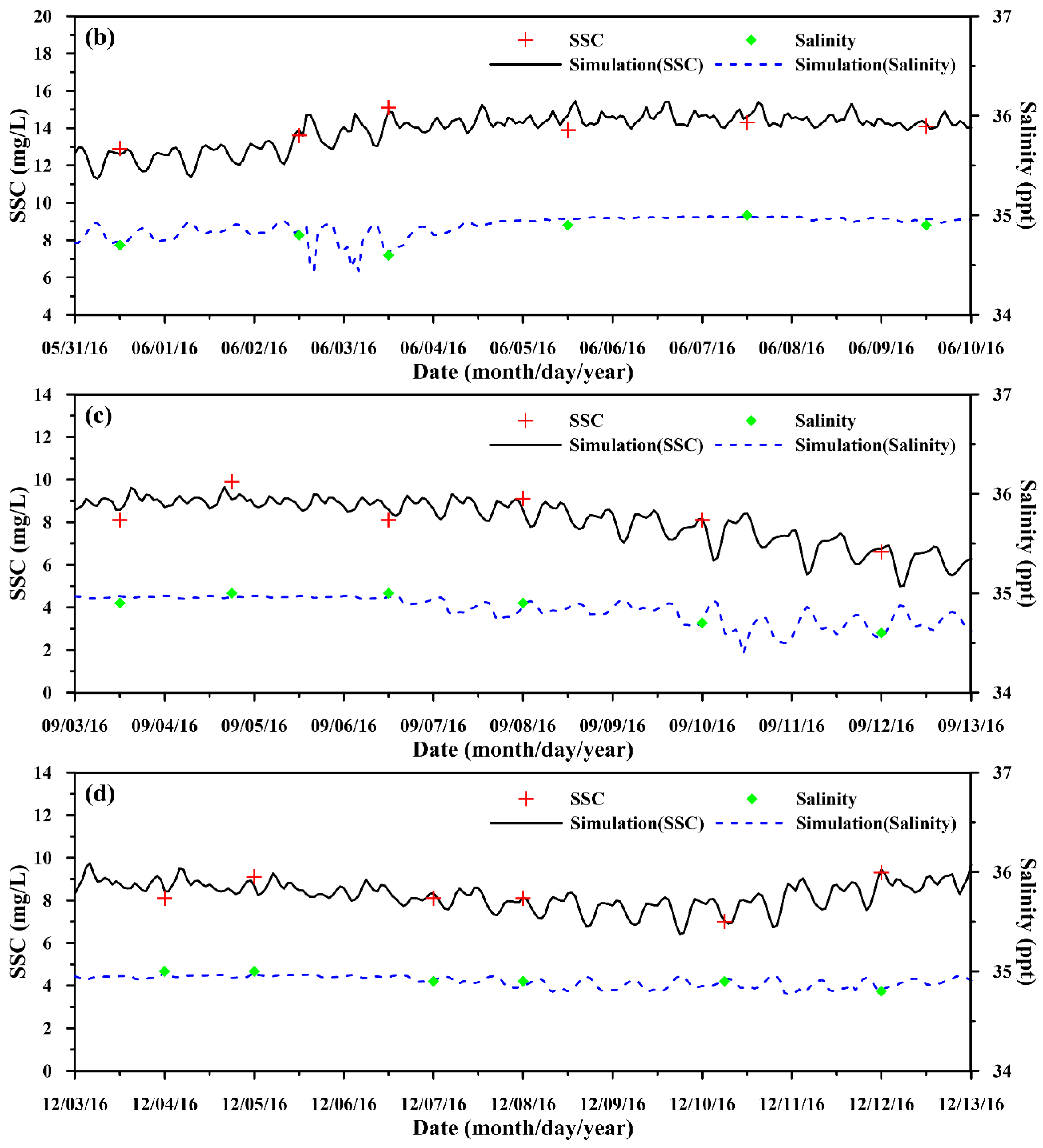
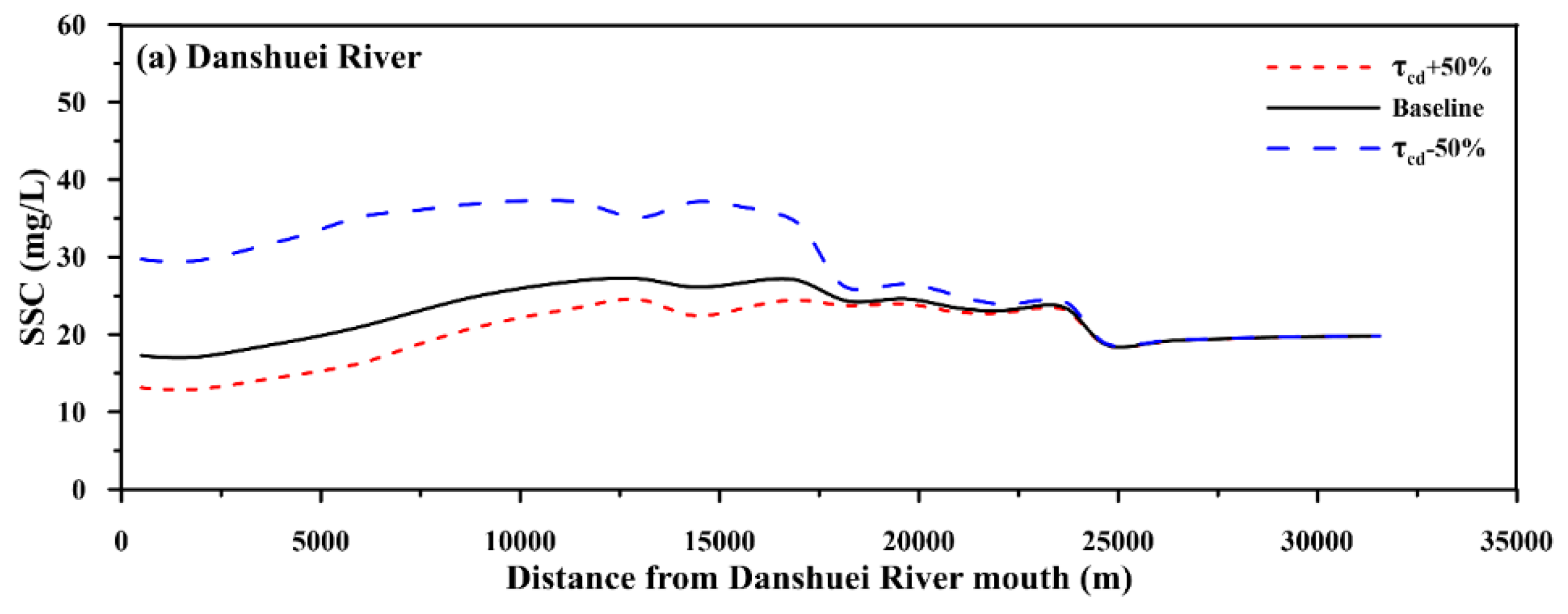

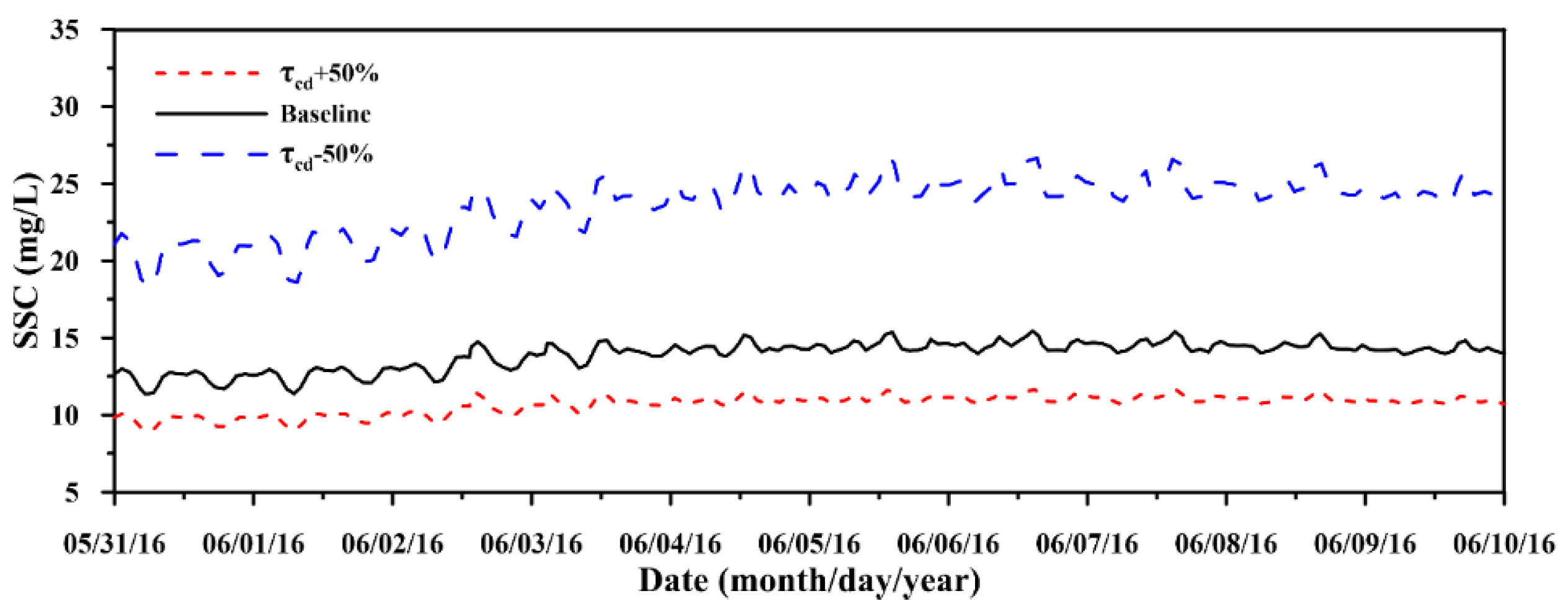
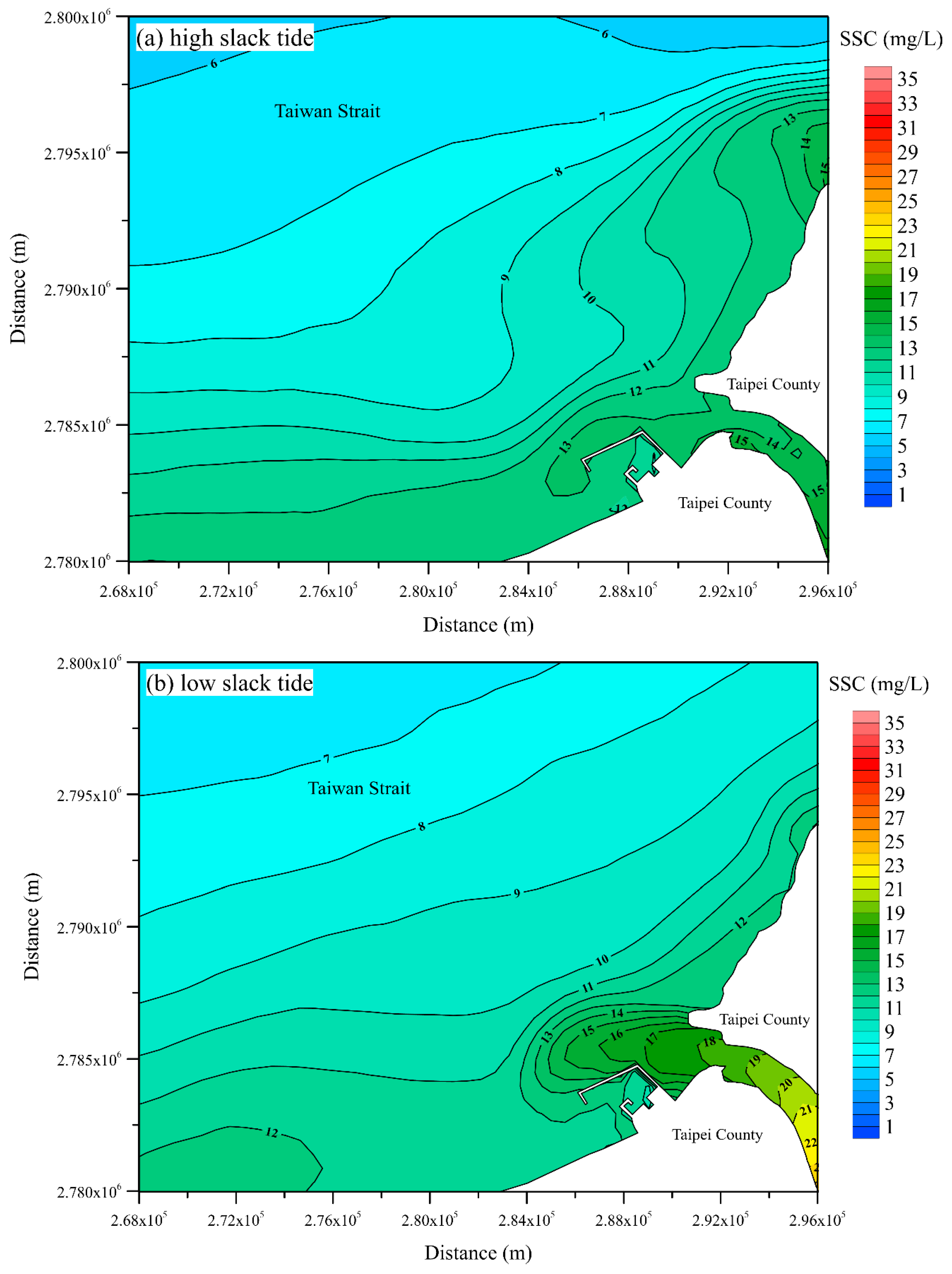
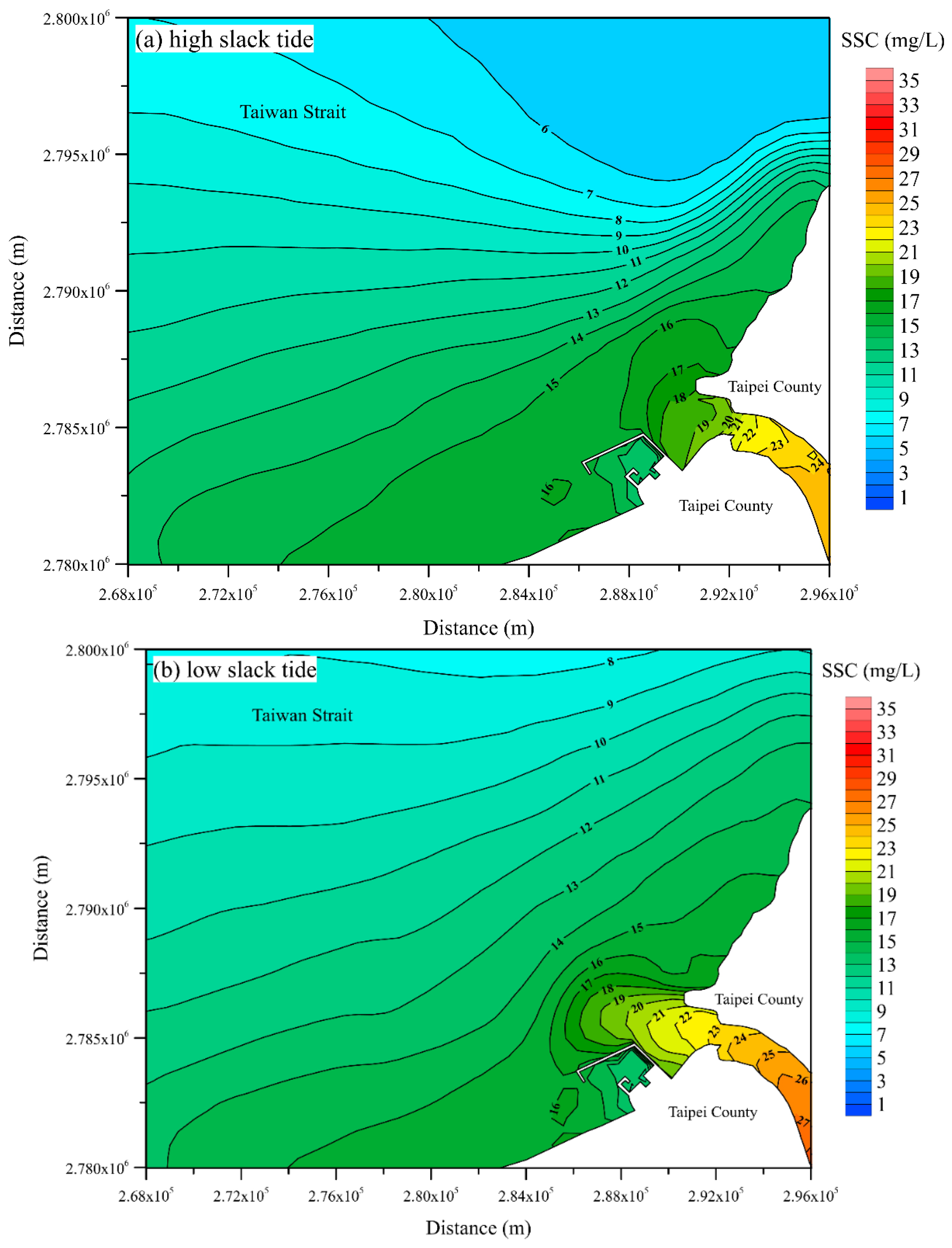
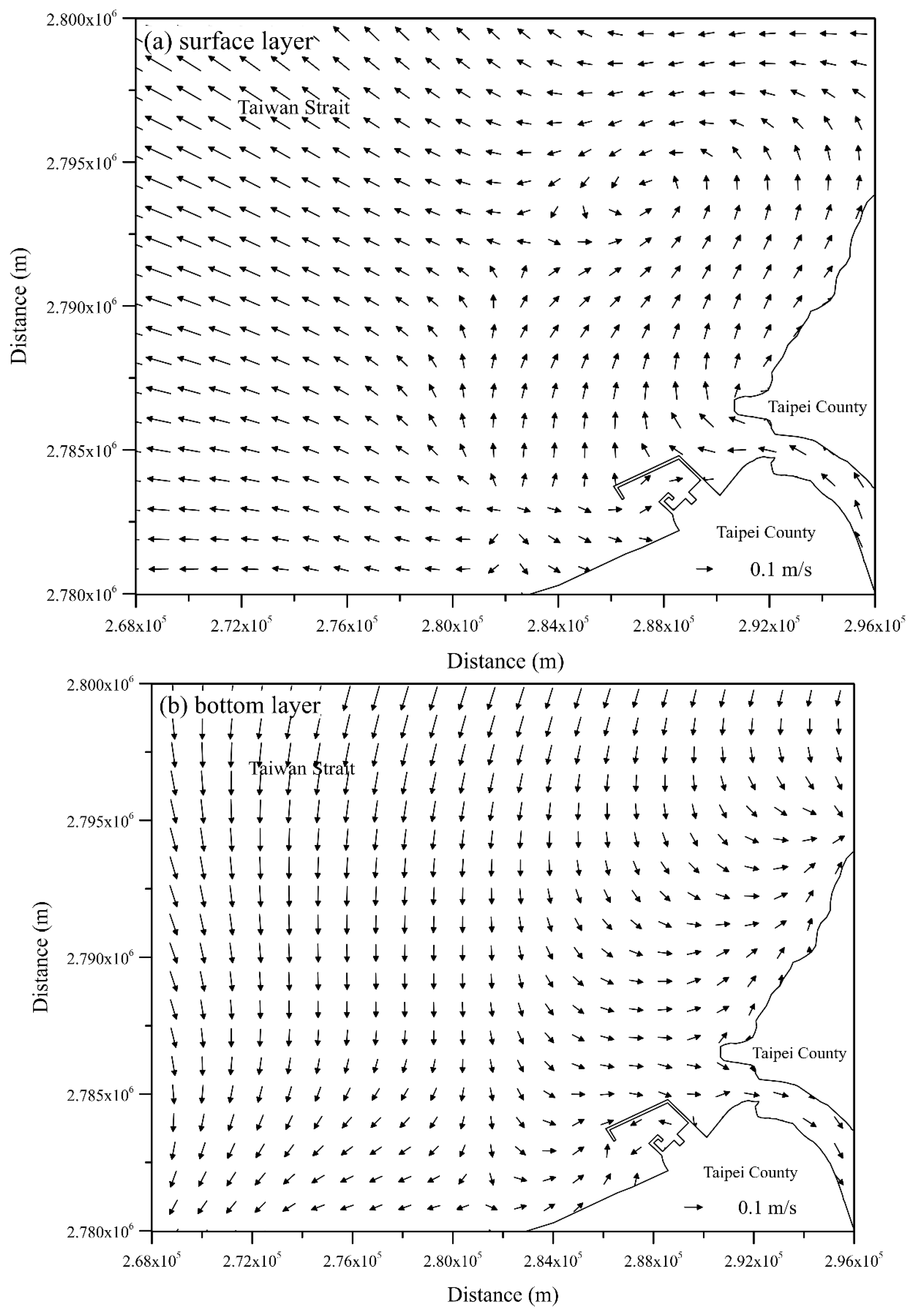
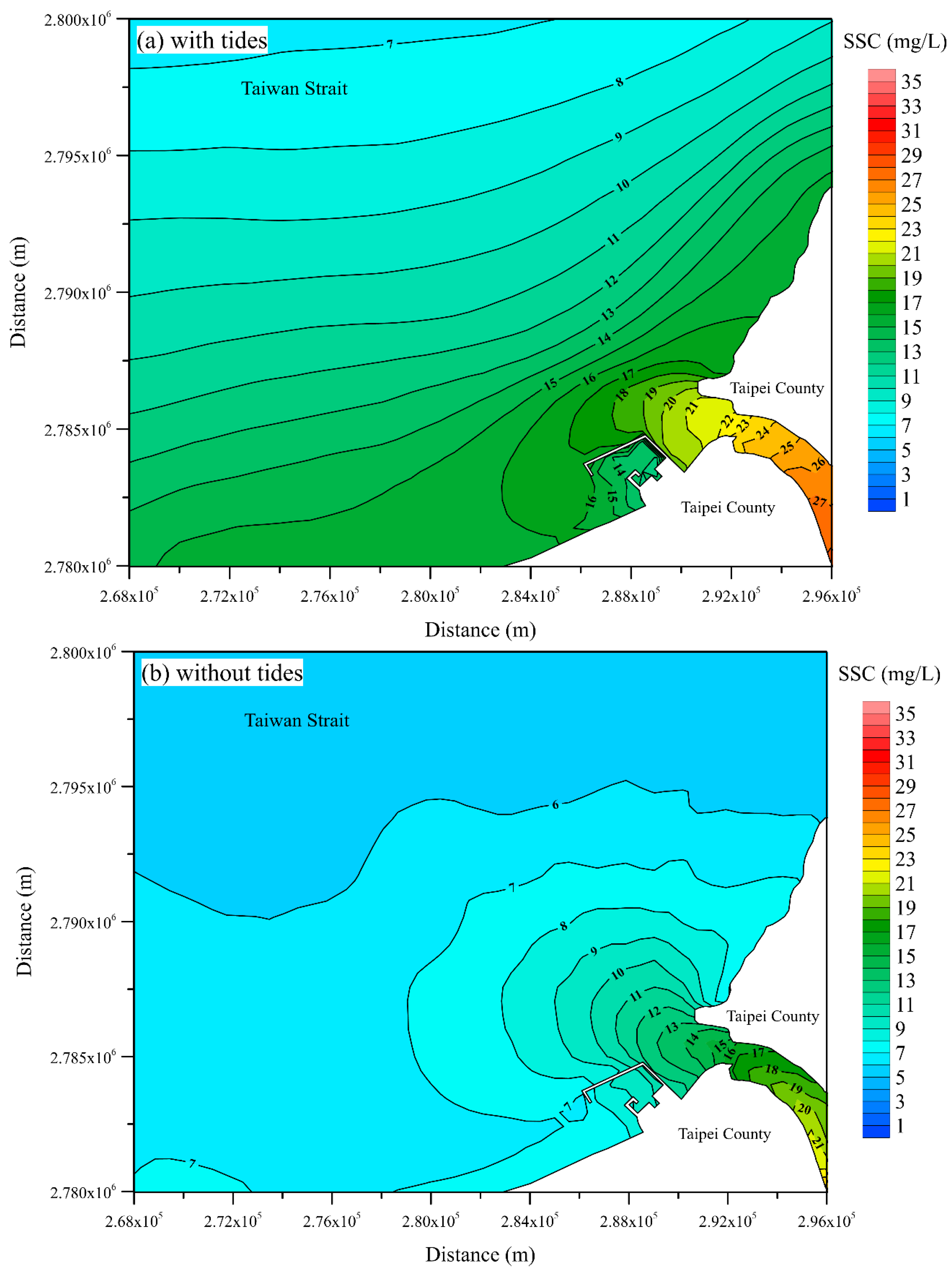
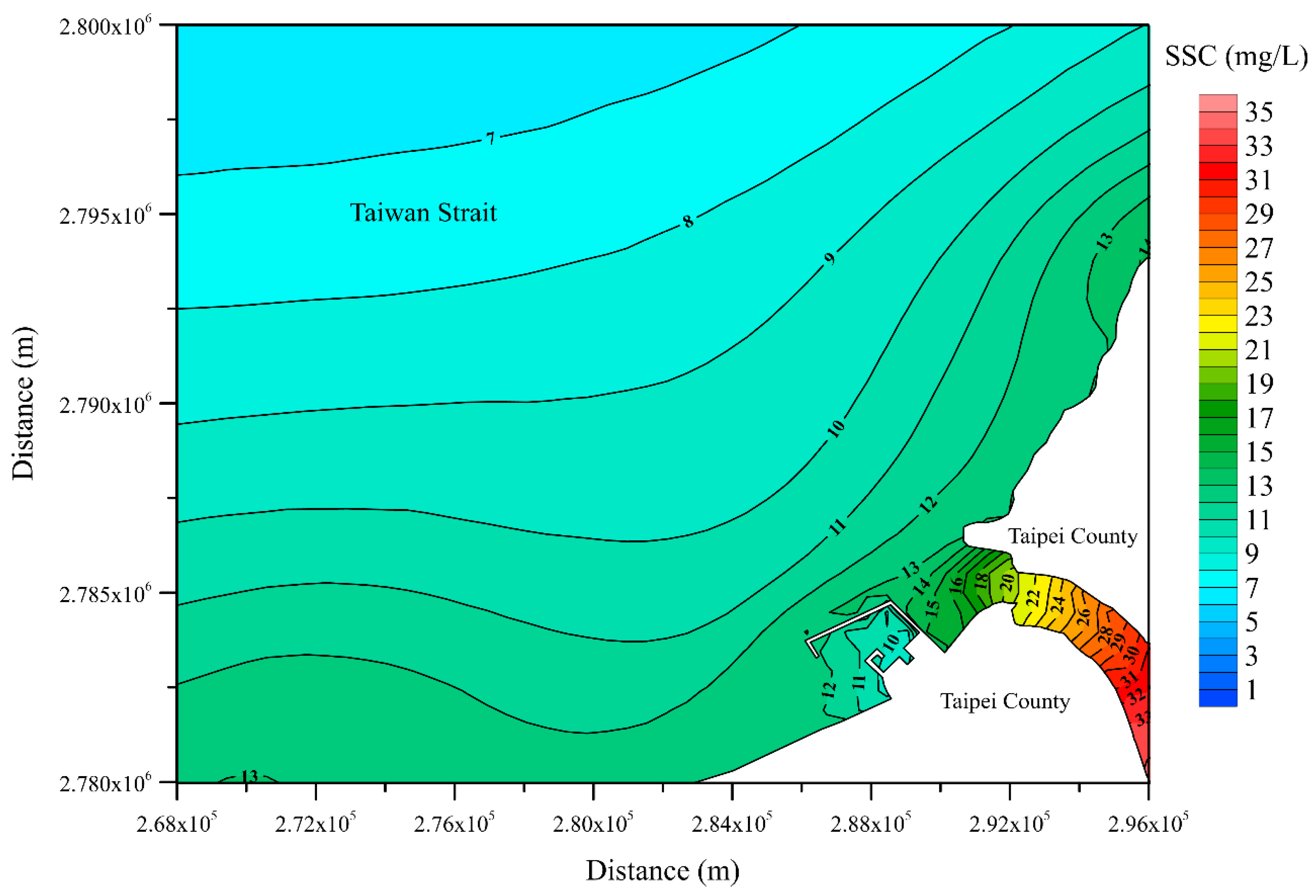
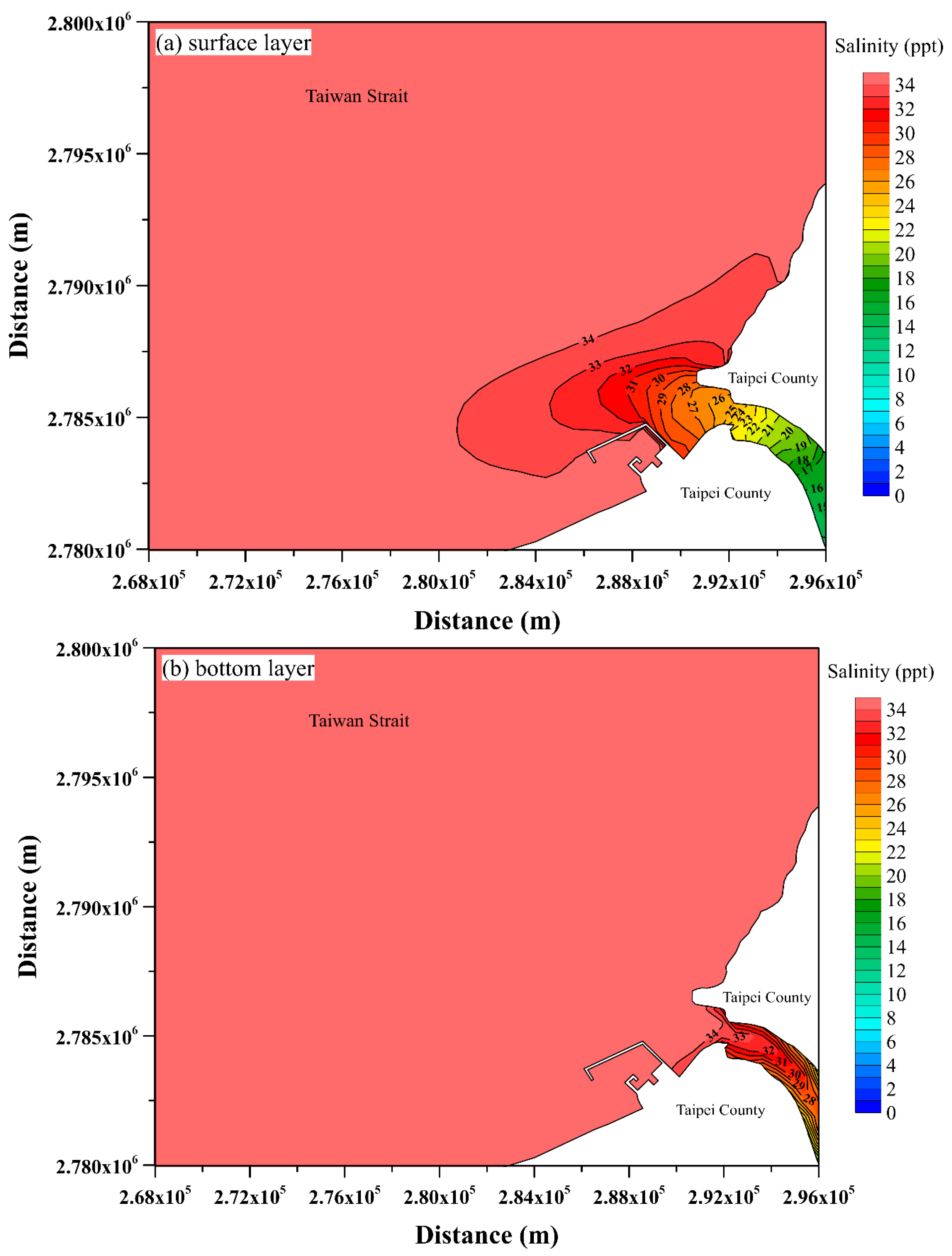
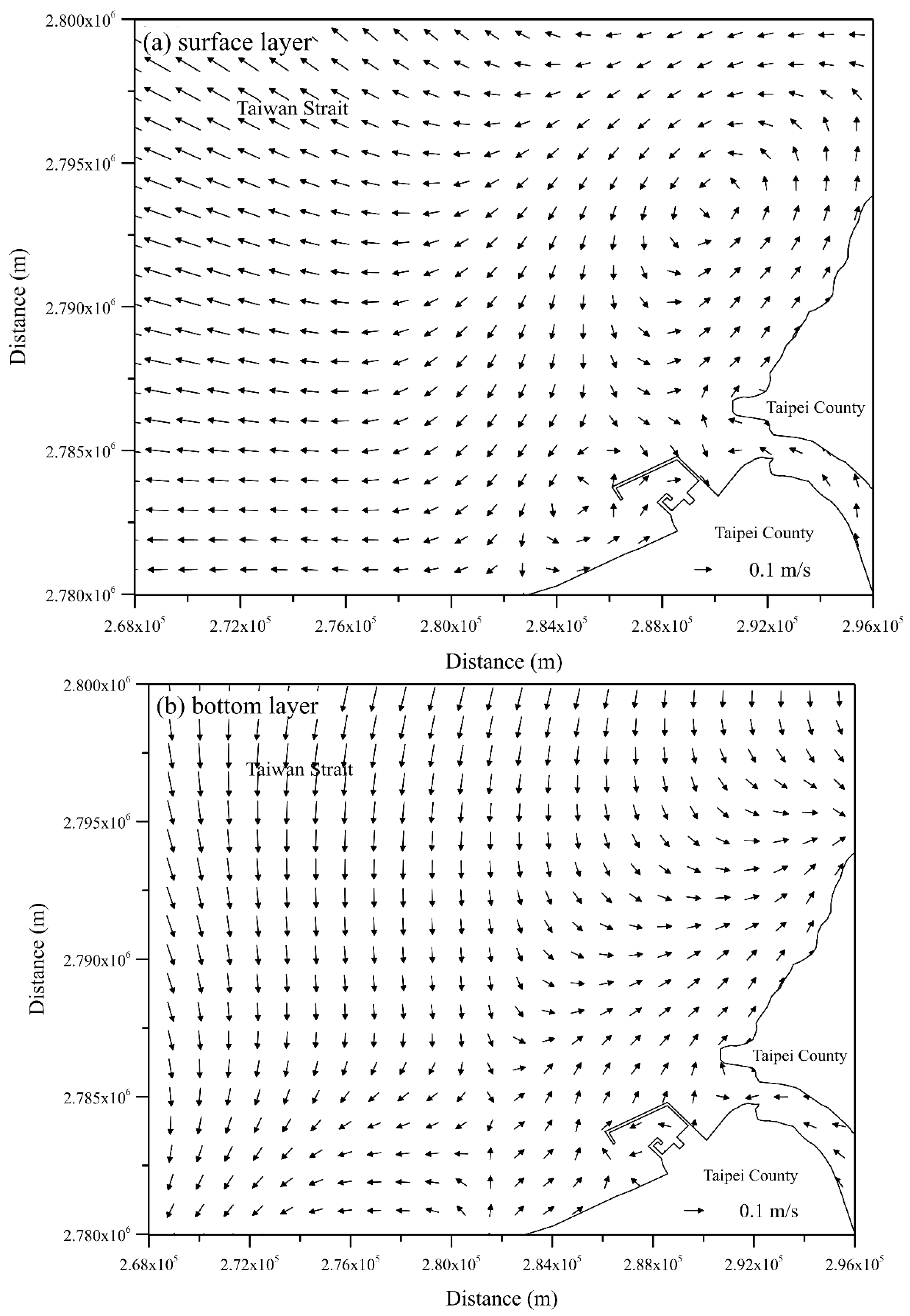
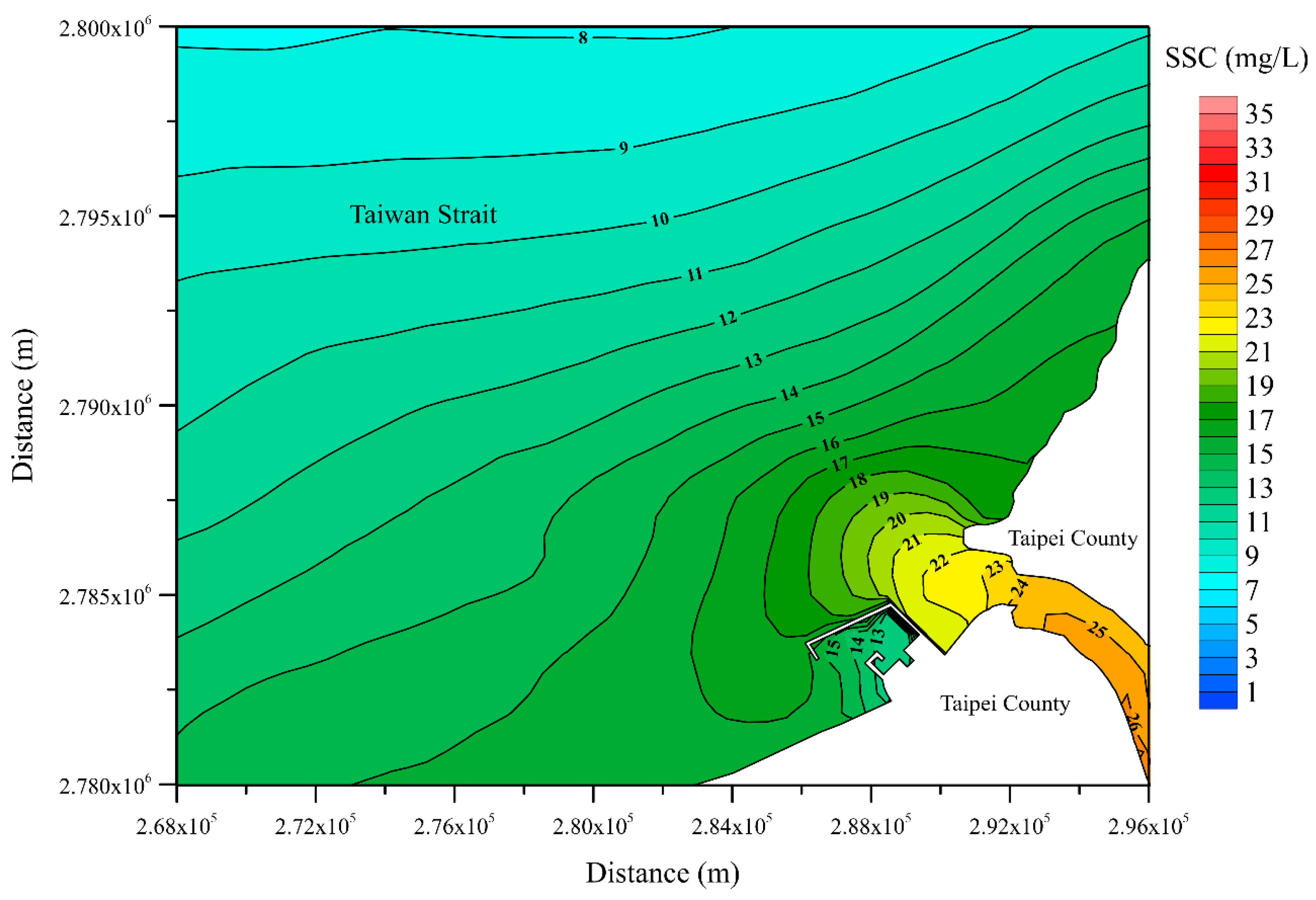

| Date (Period) | Station | MAE (m) | RMSE (m) | CC | SSE |
|---|---|---|---|---|---|
| 28 Feb. to 8 Mar. | Danshuei River mouth | 0.093 | 0.117 | 0.992 | 0.994 (Excellent) |
| Taipei Bridge | 0.124 | 0.157 | 0.990 | 0.990 (Excellent) | |
| Xinhai Bridge | 0.217 | 0.279 | 0.958 | 0.963 (Excellent) | |
| Zhongzheng Bridge | 0.149 | 0.184 | 0.983 | 0.986 (Excellent) | |
| Bailing Bridge | 0.159 | 0.200 | 0.982 | 0.982 (Excellent) | |
| 31 May to 9 Jun. | Danshuei River mouth | 0.093 | 0.118 | 0.991 | 0.995 (Excellent) |
| Taipei Bridge | 0.091 | 0.113 | 0.992 | 0.996 (Excellent) | |
| Xinhai Bridge | 0.270 | 0.354 | 0.950 | 0.966 (Excellent) | |
| Zhongzheng Bridge | 0.212 | 0.293 | 0.962 | 0.978 (Excellent) | |
| Bailing Bridge | 0.139 | 0.173 | 0.979 | 0.989 (Excellent) | |
| 3 Sep. to 12 Sep. | Danshuei River mouth | 0.057 | 0.072 | 0.996 | 0.998 (Excellent) |
| Taipei Bridge | 0.089 | 0.107 | 0.991 | 0.995 (Excellent) | |
| Xinhai Bridge | 0.113 | 0.148 | 0.971 | 0.985 (Excellent) | |
| Zhongzheng Bridge | 0.170 | 0.218 | 0.961 | 0.980 (Excellent) | |
| Bailing Bridge | 0.150 | 0.190 | 0.970 | 0.984 (Excellent) | |
| 3 Dec. to 12 Dec. | Danshuei River mouth | 0.090 | 0.113 | 0.990 | 0.995 (Excellent) |
| Taipei Bridge | 0.103 | 0.155 | 0.984 | 0.992 (Excellent) | |
| Xinhai Bridge | 0.207 | 0.260 | 0.943 | 0.968 (Excellent) | |
| Zhongzheng Bridge | 0.165 | 0.215 | 0.952 | 0.976 (Excellent) | |
| Bailing Bridge | 0.106 | 0.106 | 0.972 | 0.972 (Excellent) |
| Station | MAE (m/s) | RMSE (m/s) | CC | SSE |
|---|---|---|---|---|
| Guandu Bridge | 0.111 | 0.125 | 0.958 | 0.980 (Excellent) |
| Taipei Bridge | 0.183 | 0.213 | 0.937 | 0.925 (Excellent) |
| Xinhai Bridge | 0.134 | 0.160 | 0.872 | 0.822 (Excellent) |
| Zhongzheng Bridge | 0.078 | 0.087 | 0.853 | 0.814 (Excellent) |
| Bailing Bridge | 0.282 | 0.317 | 0.932 | 0.801 (Excellent) |
| Station | MAE (ppt) | RMSE (ppt) | CC | SSE |
|---|---|---|---|---|
| Guandu Bridge | 3.729 | 4.788 | 0.881 | 0.889 (Excellent) |
| Taipei Bridge | 0.112 | 0.148 | 0.866 | 0.900 (Excellent) |
| Xinhai Bridge | 0.008 | 0.011 | 0.495 | 0.566 (Very good) |
| Bailing Bridge | 0.074 | 0.137 | 0.892 | 0.928 (Excellent) |
| Date | River | Upstream Discharge (m3/s) | MAE (mg/L) | RMSE (mg/L) | CC | SSE |
|---|---|---|---|---|---|---|
| Mar. 2 | Danshuei River–Dahan River | 2.71 | 1.733 | 2.365 | 0.996 | 0.957 (Excellent) |
| Xindian River | 159.63 | 1.101 | 1.648 | 0.996 | 0.918 (Excellent) | |
| Keelung River | 250.20 | 0.392 | 0.589 | 0.750 | 0.770 (Excellent) | |
| Jun. 2 | Danshuei River–Dahan River | 29.61 | 2.040 | 3.199 | 0.763 | 0.807 (Excellent) |
| Xindian River | 622.77 | 1.212 | 1.850 | 0.999 | 0.987 (Excellent) | |
| Keelung River | 518.49 | 0.742 | 1.055 | 0.957 | 0.956 (Excellent) | |
| Sep. 6 | Danshuei River–Dahan River | 7.30 | 1.717 | 2.392 | 0.918 | 0.949 (Excellent) |
| Xindian River | 224.52 | 0.527 | 0.758 | 0.999 | 0.999 (Excellent) | |
| Keelung River | 329.10 | 1.949 | 2.280 | 0.878 | 0.867 (Excellent) | |
| Dec. 6 | Danshuei River–Dahan River | 4.82 | 3.818 | 5.425 | 0.983 | 0.949 (Excellent) |
| Xindian River | 69.56 | 0.792 | 0.973 | 0.995 | 0.993 (Excellent) | |
| Keelung River | 94.00 | 0.773 | 1.059 | 0.894 | 0.885 (Excellent) |
| Date | MAE | RMSE | CC | SSE | ||||
|---|---|---|---|---|---|---|---|---|
| Salinity (ppt) | SSC (mg/L) | Salinity (ppt) | SSC (mg/L) | Salinity (ppt) | SSC (mg/L) | Salinity (ppt) | SSC (mg/L) | |
| 28 Feb.–8 Mar. | 0.017 | 0.335 | 0.025 | 0.377 | 0.901 | 0.871 | 0.993 (Excellent) | 0.938 (Excellent) |
| 31 May–9 Jun. | 0.040 | 0.335 | 0.044 | 0.390 | 0.934 | 0.838 | 0.974 (Excellent) | 0.923 (Excellent) |
| 3 Sept.–12 Sep. | 0.044 | 0.420 | 0.045 | 0.495 | 0.955 | 0.862 | 0.977 (Excellent) | 0.918 (Excellent) |
| 3 Dec.–12 Dec. | 0.016 | 0.202 | 0.024 | 0.249 | 0.934 | 0.941 | 0.970 (Excellent) | 0.971 (Excellent) |
| River System or Coastal Region | Maximum Change Rate (MCR,%) | |||||||
|---|---|---|---|---|---|---|---|---|
+50% | −50% | +50% | −50% | +50% | −50% | +50% | +50% | |
| Danshuei River−Dahan River | −4.7% | 5.2% | −19.2% | 20.5% | −24.2% | 72.8% | 32.3% | −32.3% |
| Xindian River | −2.6% | 2.9% | −2.6% | 2.8% | −6.1% | 18.2% | 8.6% | −8.6% |
| Keelung River | −2.1% | 2.2% | −12.8% | 17.7% | −16.4% | 49.4% | 21.3% | −21.2% |
| Coastal region (station A) | −0.4% | 0.5% | −19.0% | 13.3% | −24.5% | 73.6% | 33.8% | −33.8% |
| Flow Condition | Wind Speed (Wind Direction) | |||
|---|---|---|---|---|
| 6.0 m/s (Northeast) | 6.0 m/s (Southwest) | 15.0 m/s (Northeast) | 15.0 m/s (Southwest) | |
| Qmean | 0.16 | 0.13 | 3.40 | 1.42 |
| 3Q10 | 0.15 | 0.12 | 1.17 | 1.03 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.-C.; Liu, H.-M.; Young, C.-C. Effects of Environmental Factors on Suspended Sediment Plumes in the Continental Shelf Out of Danshuei River Estuary. Water 2022, 14, 2755. https://doi.org/10.3390/w14172755
Liu W-C, Liu H-M, Young C-C. Effects of Environmental Factors on Suspended Sediment Plumes in the Continental Shelf Out of Danshuei River Estuary. Water. 2022; 14(17):2755. https://doi.org/10.3390/w14172755
Chicago/Turabian StyleLiu, Wen-Cheng, Hong-Ming Liu, and Chih-Chieh Young. 2022. "Effects of Environmental Factors on Suspended Sediment Plumes in the Continental Shelf Out of Danshuei River Estuary" Water 14, no. 17: 2755. https://doi.org/10.3390/w14172755








