Developing and Applying a QGIS-Based Model That Accounts for Nonpoint Source Pollution Due to Domestic Animals
Abstract
:1. Introduction
2. Materials and Methods
2.1. Addressing the Limitations of the STEPL
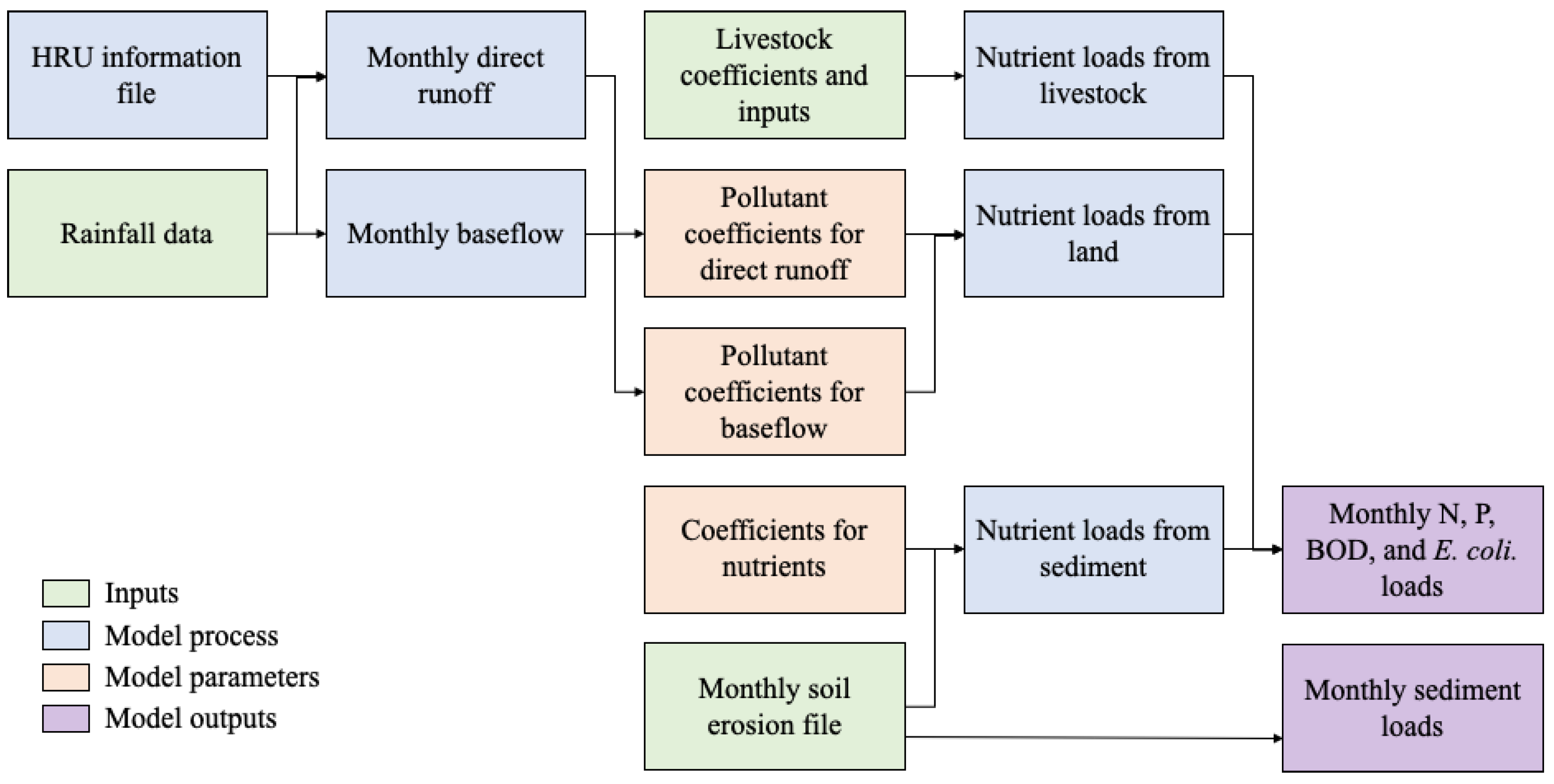
2.2. Predicting Direct Runoff and Baseflow
2.3. NPS Pollutant Prediction
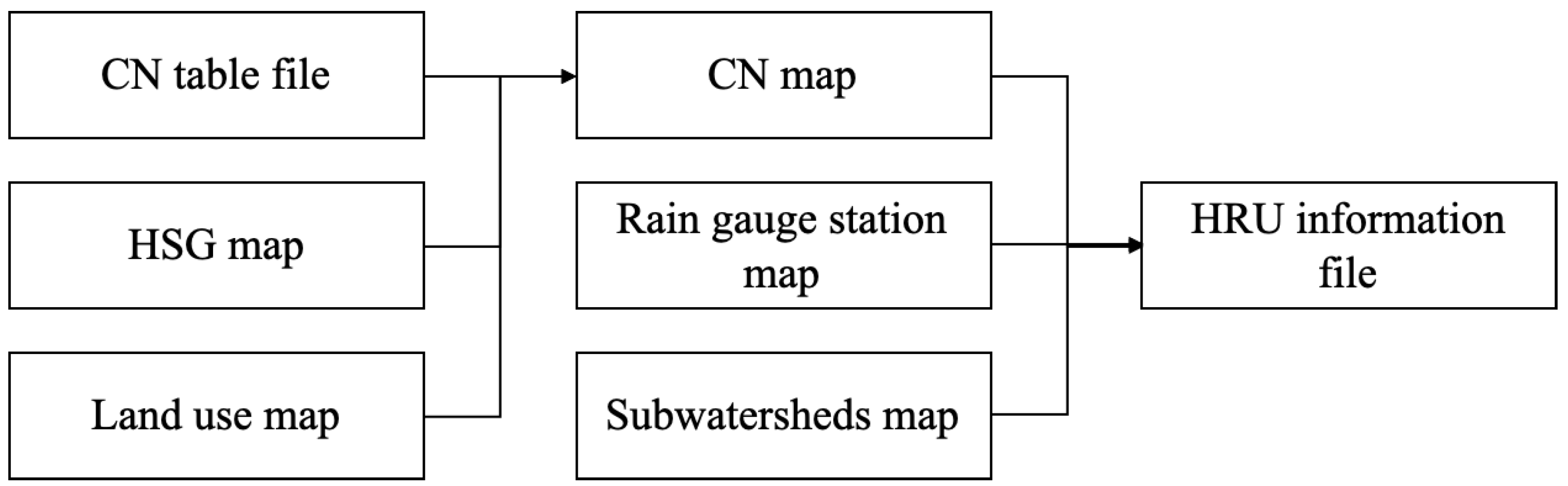
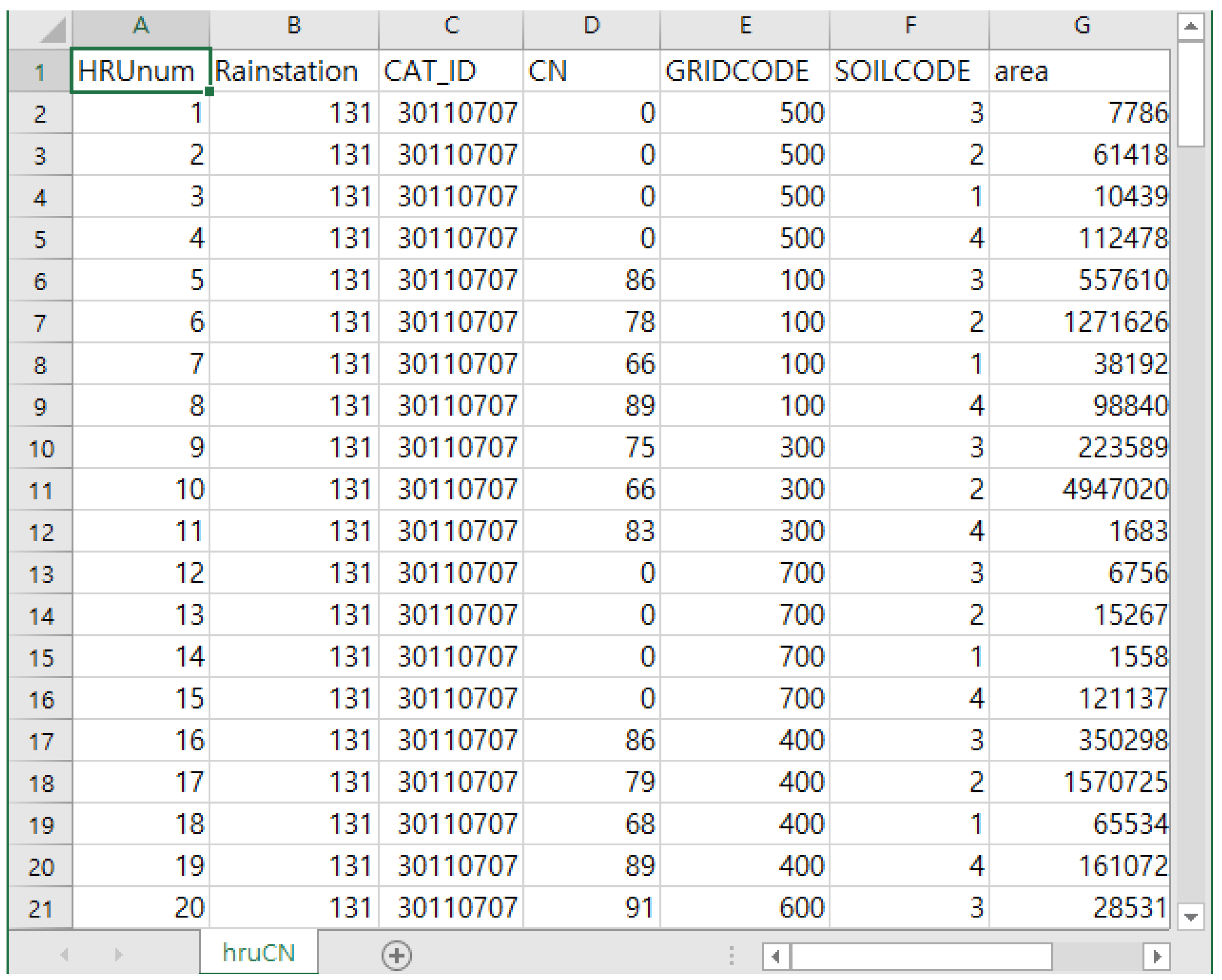
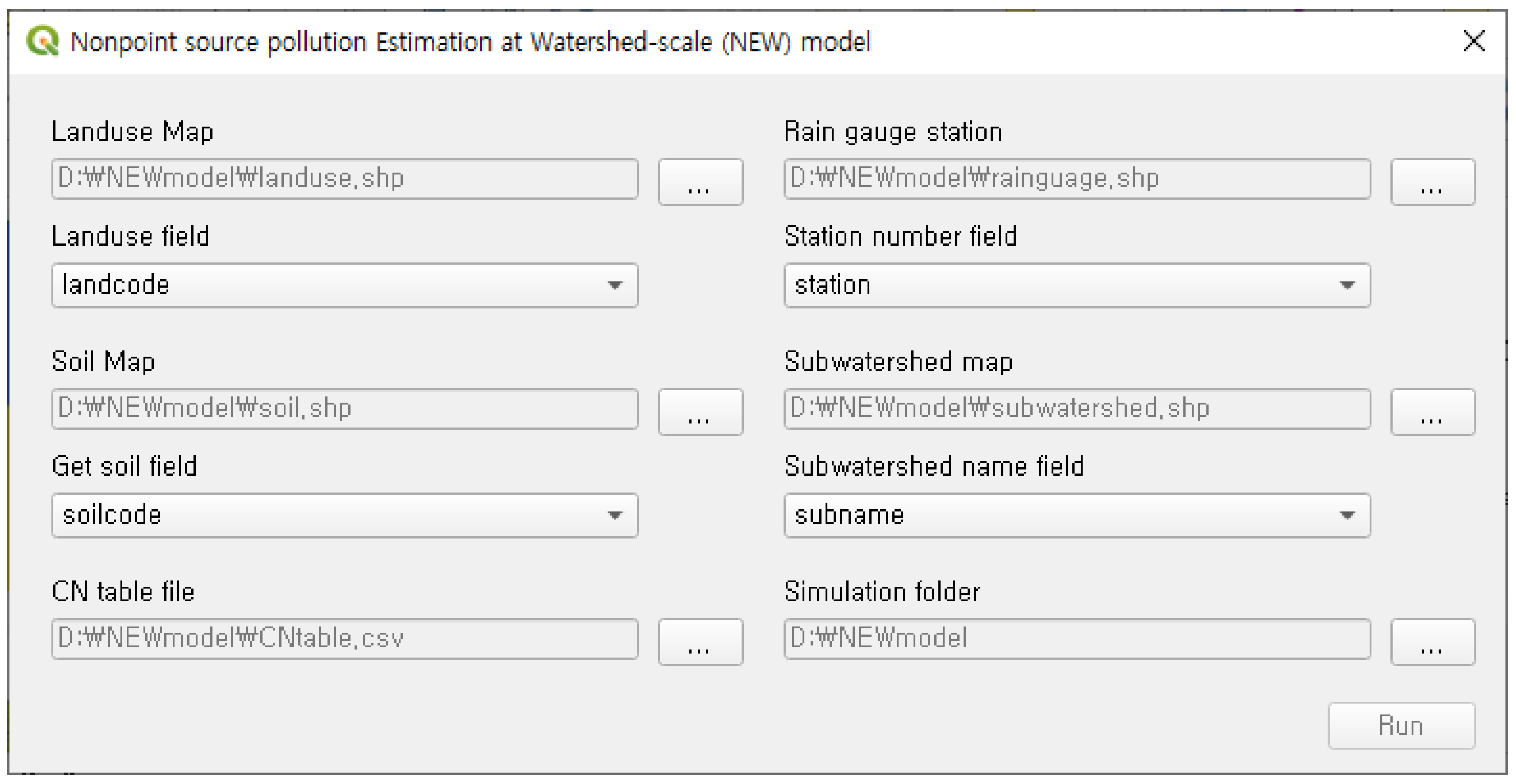
2.4. Developing Software to Predict Flow Rate and NPS Pollutant Load
2.5. Applying the Developed Model
3. Results
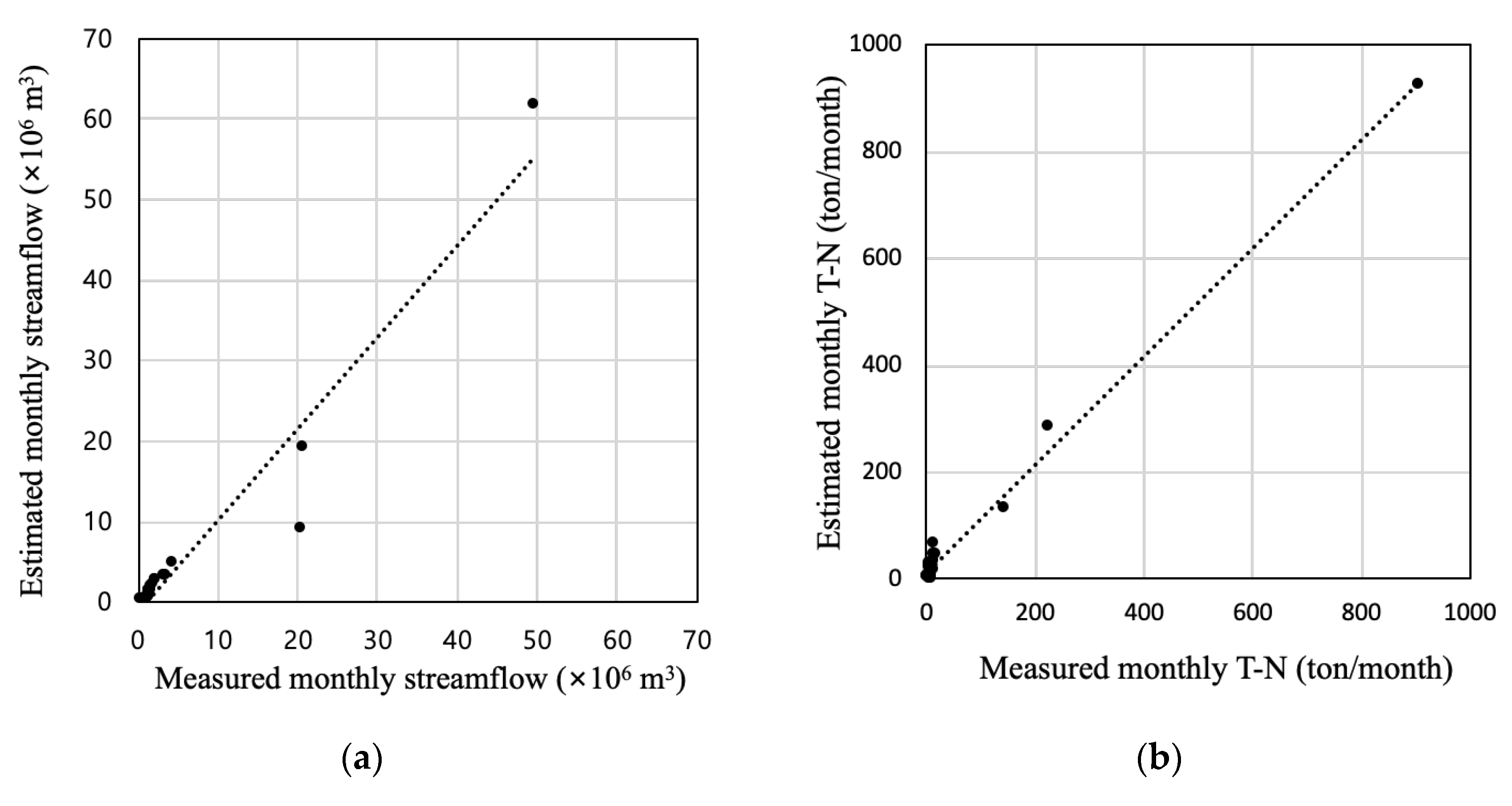
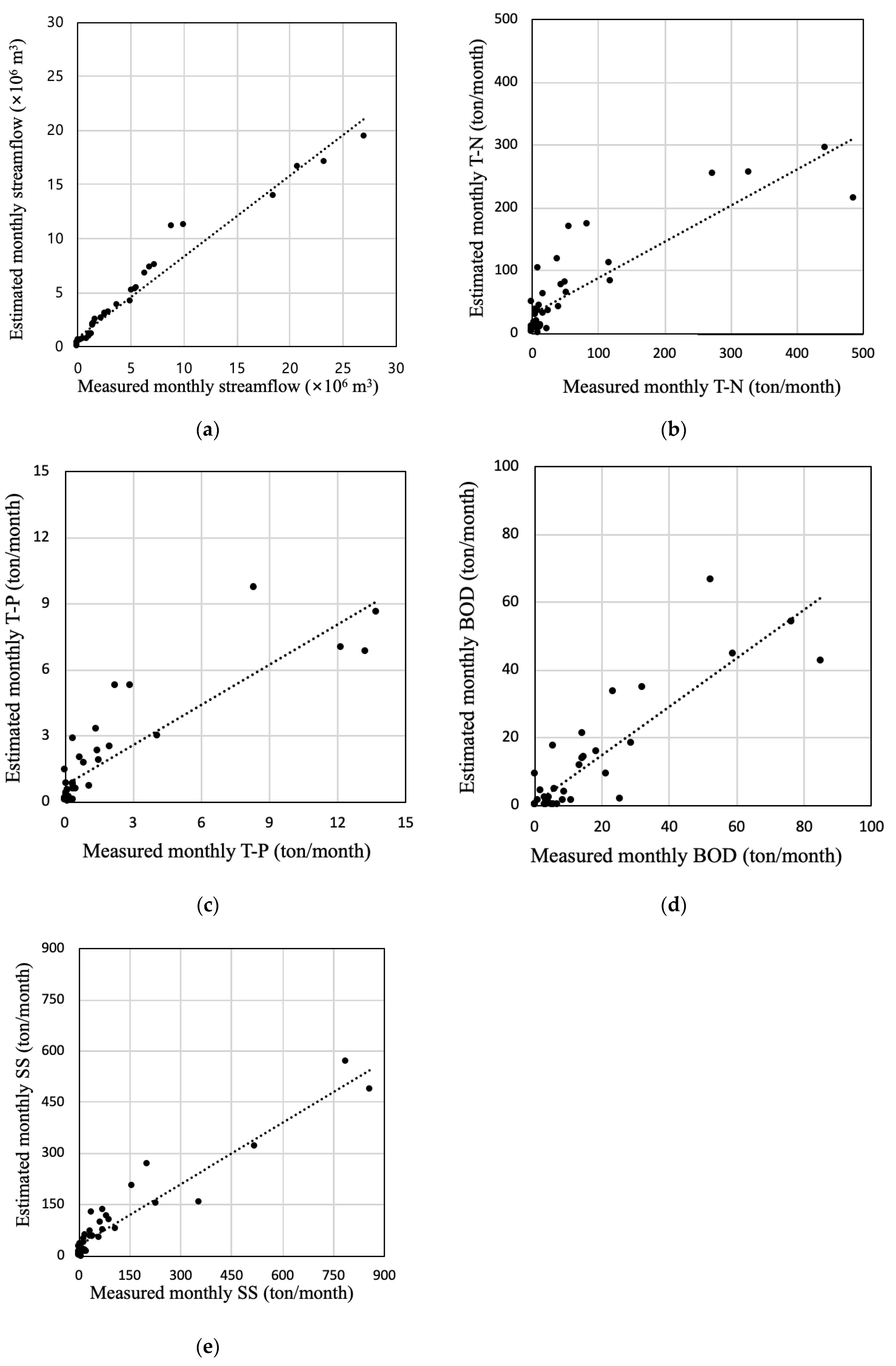
3.1. Model Calibration
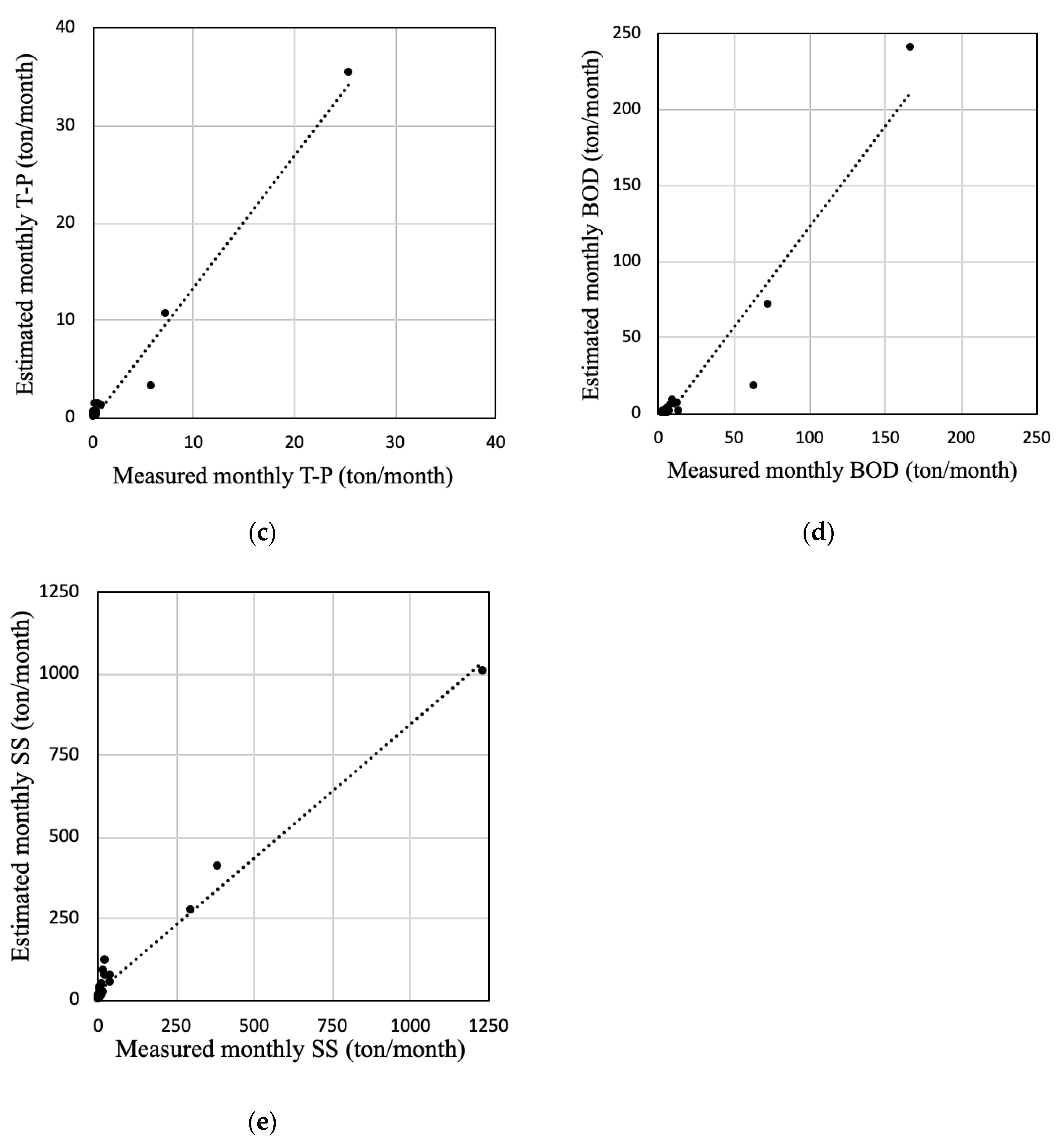
3.2. Model Validation
4. Discussion
5. Conclusions
- It provides user convenience by applying a graphical user interface.
- HRUs are determined by land use and HSG maps in the QGIS software.
- It facilitates the inclusion of livestock.
- Seasonal variances are provided in direct runoff, baseflow, and NPS load estimations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Atkins, J.T.; Wiley, J.B.; Paybins, K.S. Calibration Parameters Used to Simulate Streamflow from Application of the Hydrologic Simulation Program-FORTRAN Model (HSPF) to Mountainous Basins Containing Coal Mines in West Virginia; Scientific Investigations Report 2005-5099; US Geological Survey: McDowell County, WV, USA, 2005. [Google Scholar] [CrossRef]
- Caldwell, P.V.; Kennen, J.G.; Sun, G.; Kiang, J.E.; Butcher, J.B.; Eddy, M.C.; Hay, L.E.; LaFontaine, J.H.; Hain, E.F.; Nelson, S.A. A comparison of hydrologic models for ecological flows and water availability. Ecohydrology 2015, 8, 1525–1546. [Google Scholar] [CrossRef]
- Ryu, J.; Jang, W.S.; Kim, J.; Choi, J.D.; Engel, B.A.; Yang, J.E.; Lim, K.J. Development of a watershed-scale long-term hydrologic impact assessment model with the asymptotic curve number regression equation. Water 2016, 8, 153. [Google Scholar] [CrossRef]
- Cherkauer, D.S. Quantifying ground water recharge at multiple scales using PRMS and GIS. Groundwater 2004, 42, 97–110. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.S.; Engel, B.A.; Harbor, J. A web-based model to estimate the impact of best management practices. Water 2014, 6, 455–471. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.V.; Arnold, J.; Demissie, M. Hydrological modeling of the Iroquois River watershed using HSPF and SWAT1. J. Am. Water. Resour. Assoc. 2005, 41, 343–360. [Google Scholar] [CrossRef]
- Saleh, A.; Du, B. Evaluation of SWAT and HSPF within BASINS program for the upper North Bosque River watershed in central Texas. Trans. ASAE 2004, 47, 1039. [Google Scholar] [CrossRef]
- Sobel, R.; Rifai, H.; Petersen, T. Refinement and application of a coupled tidal prism model with HSPF for managing bacterial water quality impairment in a coastal watershed. WIT Trans. Ecol. Environ. 2015, 197, 201–209. [Google Scholar] [CrossRef]
- Bicknell, B.R.; Imhoff, J.C.; Kittle, J.L., Jr.; Jobes, T.H.; Donigian, A.S., Jr. Hydrological Simulation Program-Fortran, User’s Manual for Version 12. National Exposure Research Laboratory, U.S. Environmental Protection Agency: Athens, GA, USA, 2001. [Google Scholar]
- Arnold, J.G.; Allen, P.M. Automated methods for estimating baseflow and ground water recharge from streamflow records. J. Am. Water Resour. Assoc. 1999, 35, 411–424. [Google Scholar] [CrossRef]
- Neitsch, S.; Arnold, J.; Kiniry, J.; Srinivasan, R.; Williams, J. Soil and Water Assessment Tool. User’s Manual, Version 2009; Technical Report; Texas Water Resources Institute: College Station, TX, USA, 2010. [Google Scholar]
- Harbor, J. A practical method for estimating the impact of land-use change on surface runoff, groundwater recharge, and wetland hydrology. J. Am. Plan. Assoc. 1994, 60, 95–108. [Google Scholar] [CrossRef]
- Lee, H.; Chae, M.S.; Park, J.Y.; Lim, K.J.; Park, Y.S. Development and application of a QGIS-based model to estimate monthly streamflow. ISPRS Int. J. Geo-Inf. 2022, 11, 40. [Google Scholar] [CrossRef]
- Tetra Tech, Inc. User’s Guide. Spreadsheet Tool for the Estimation of Pollutant Load (STEPL) Version 4.1; Tetra Tech, Inc.: Fairfax, VA, USA, 2011. [Google Scholar]
- Bieger, K.; Hörmann, G.; Fohrer, N. The impact of land use change in the Xiangxi Catchment (China) on water balance and sediment transport. Reg. Environ. Chang. 2013, 15, 485–498. [Google Scholar] [CrossRef]
- Guse, B.; Pfannerstill, M.; Fohrer, N. Dynamic modelling of land use change impacts on nitrate loads in rivers. Environ. Process. 2015, 2, 575–592. [Google Scholar] [CrossRef]
- Martin, K.L.; Hwang, T.; Vose, J.M.; Coulston, J.W.; Wear, D.N.; Miles, B.; Band, L.E. Watershed impacts of climate and land use changes depend on magnitude and land use context. Ecohydrology 2017, 10, e1870. [Google Scholar] [CrossRef]
- Tague, C.L.; Band, L.E. RHESSys: Regional Hydro-Ecologic Simulation System-An object-oriented approach to spatially distributed modeling of carbon, water, and nutrient cycling. Earth Interact. 2004, 8, 1–42. [Google Scholar] [CrossRef]
- Kibii, J.; Kipkorir, E.C.; Kosgei, J.R. Application of Soil and Water Assessment Tool (SWAT) to evaluate the impact of land use and climate variability on the Kaptagat Catchment River discharge. Sustainability 2021, 13, 1802. [Google Scholar] [CrossRef]
- Hou, L.; Zhou, Z.; Wang, R.; Li, J.; Dong, F.; Kiu, J. Research on the non-point source pollution characteristics of important drinking water sources. Water 2022, 14, 211. [Google Scholar] [CrossRef]
- Cheng, H.; Ouyang, W.; Hao, F.; Ren, X.; Yang, S. The non-point source pollution in livestock-breeding areas of the Heihe River basin in Yellow River. Stoch. Environ. Res. Risk Assess. 2007, 21, 213–221. [Google Scholar] [CrossRef]
- Lee, H.; Woo, W.; Park, Y.S. A user-friendly software package to develop storm water management model (SWMM) inputs and suggest low impact development scenario. Water 2020, 12, 2344. [Google Scholar] [CrossRef]
- Kumar, S.; Mishra, A. Critical erosion area identification based on hydrological response unit level for effective sediment control in a river basin. Water Resour. Manag. 2015, 29, 1749–1765. [Google Scholar] [CrossRef]
- Savvidou, E.; Efstratiadis, A.; Koussis, A.D.; Koukouvinos, A.; Skarlatos, D. The curve number concept as a driver for delineating hydrological response units. Water 2018, 10, 194. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, B.; Liu, Y.; Xu, D. The application of a modified version of the SWAT model at the daily temporal scale and the hydrological response unit spatial scale: A case study covering an irrigation district in the Hei River Basin. Water 2018, 10, 1064. [Google Scholar] [CrossRef]
- Li, D.; Zheng, B.; Chu, Z.; Liu, Y.; Huang, M. Seasonal variations of performance and operation in field-scale storing multipond constructed wetlands for nonpoint source pollution mitigation in a plateau lake basin. Bioresour. Technol. 2019, 280, 295–302. [Google Scholar] [CrossRef]
- Lencha, S.M.; Ulsido, M.D.; Muluneh, A. Evaluation of seasonal and spatial variations in water quality and identification of potential sources of pollution using multivariate statistical techniques for Lake Hawassa watershed, Ethiopia. Appl. Sci. 2021, 11, 8991. [Google Scholar] [CrossRef]
- USDA. Urban Hydrology for Small Watersheds; National Resources Conservation Service, United States Department of Agriculture: Washington, DC, USA, 1986.
- Lee, H.; Choi, H.S.; Chae, M.S.; Park, Y.S. A study to suggest monthly baseflow estimation approach for the Long-Term Hydrologic Impact Analysis models: A case study in South Korea. Water 2021, 13, 2043. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses from Cropland East of the Rocky Mountains: A Guide for Selection of Practices for Soil and Water Conservation; Handbook No. 282; U.S. Department of Agriculture: Washington, DC, USA, 1965.
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; Handbook No. 537; U.S. Department of Agriculture: Washington, DC, USA, 1978.
- QGIS Development Team. QGIS Geographic Information System, Open Source Geospatial Foundation Project. 2009. Available online: http://qgis.osgeo.org (accessed on 1 July 2021).
- Environmental Geographic Information Service. Available online: https://egis.me.go.kr/main.do (accessed on 2 February 2021).
- Korea Meteorological Administration. Available online: https://www.weather.go.kr/w/index.do (accessed on 7 February 2021).
- Water Resources Management Information System. Available online: http://water.nier.go.kr/main/mainContent.do (accessed on 11 February 2021).
- Nonpoint Source Pollution Modeling Research Group. Available online: http://npslab.kongju.ac.kr (accessed on 11 February 2021).
- National Pollutant Survey System. Available online: https://wems.nier.go.kr/ (accessed on 7 February 2021).
- Runkel, R.L.; Crawford, C.G.; Cohn, T.A. Load Estimator (LOADEST): A Fortran Program for Estimating Constituent Loads in Streams and Rivers; U.S. Geological Survey Techniques and Methods: Reston, VA, USA, 2004. [Google Scholar]
- Duda, P.B.; Hummel, P.R.; Donigian, A.S.; Imhoff, J.C. BASINS/HSPF: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1523–1547. [Google Scholar] [CrossRef]
- Skaggs, R.W.; Youssef, M.A.; Chescheir, G.M. DRAINMOD: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1509–1522. [Google Scholar] [CrossRef]
- Wang, X.; Williams, J.; Gassman, P.; Baffaut, C.; Izaurralde, R.; Jeong, J.; Kiniry, J. EPIC and APEX: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1447–1462. [Google Scholar] [CrossRef]
- Engel, B.; Storm, D.; White, M.; Arnold, J.; Arabi, M. A hydrologic/water quality model application protocol. J. Am. Water Resour. Assoc. 2007, 43, 1223–1236. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar] [CrossRef] [Green Version]


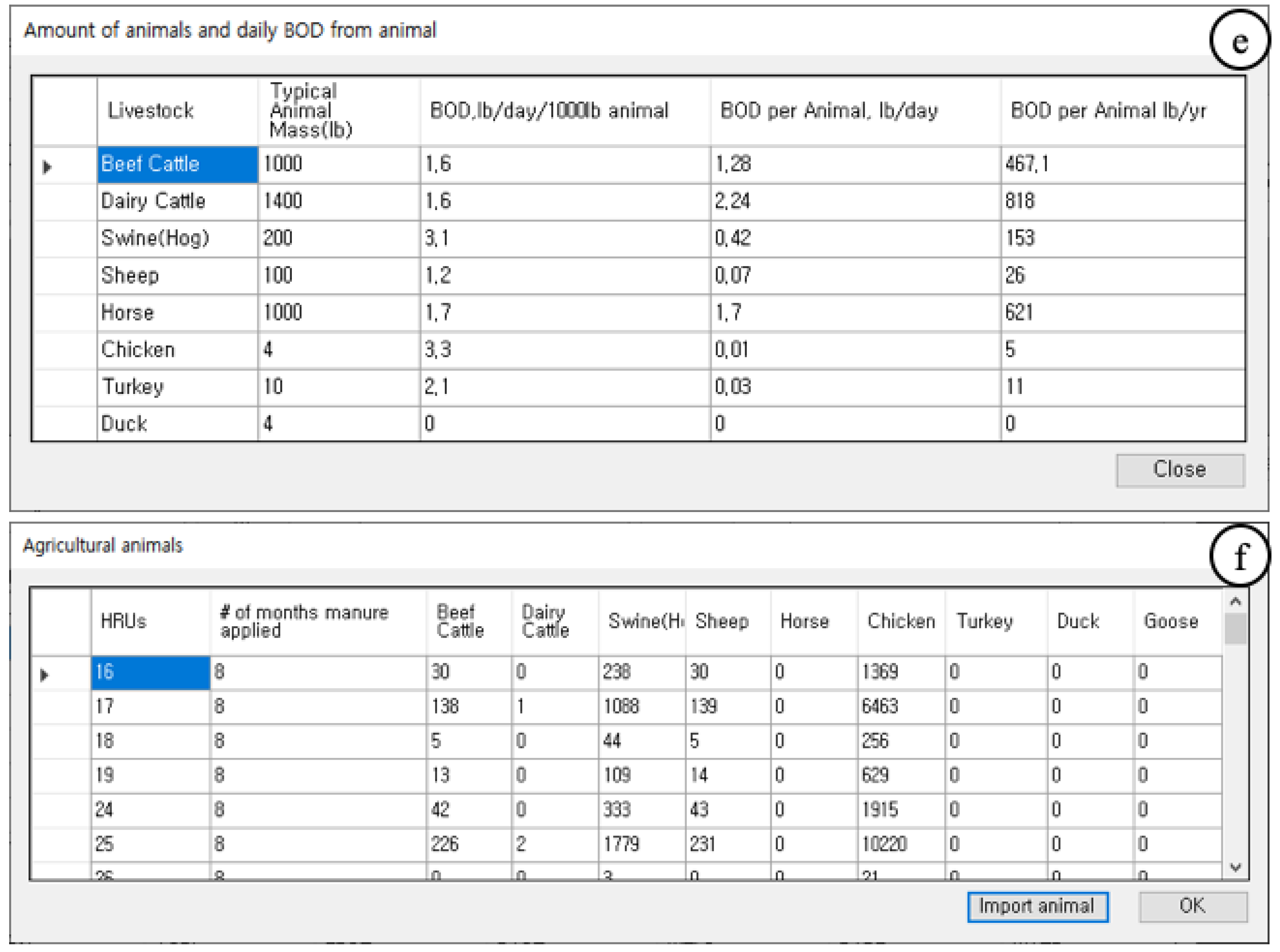
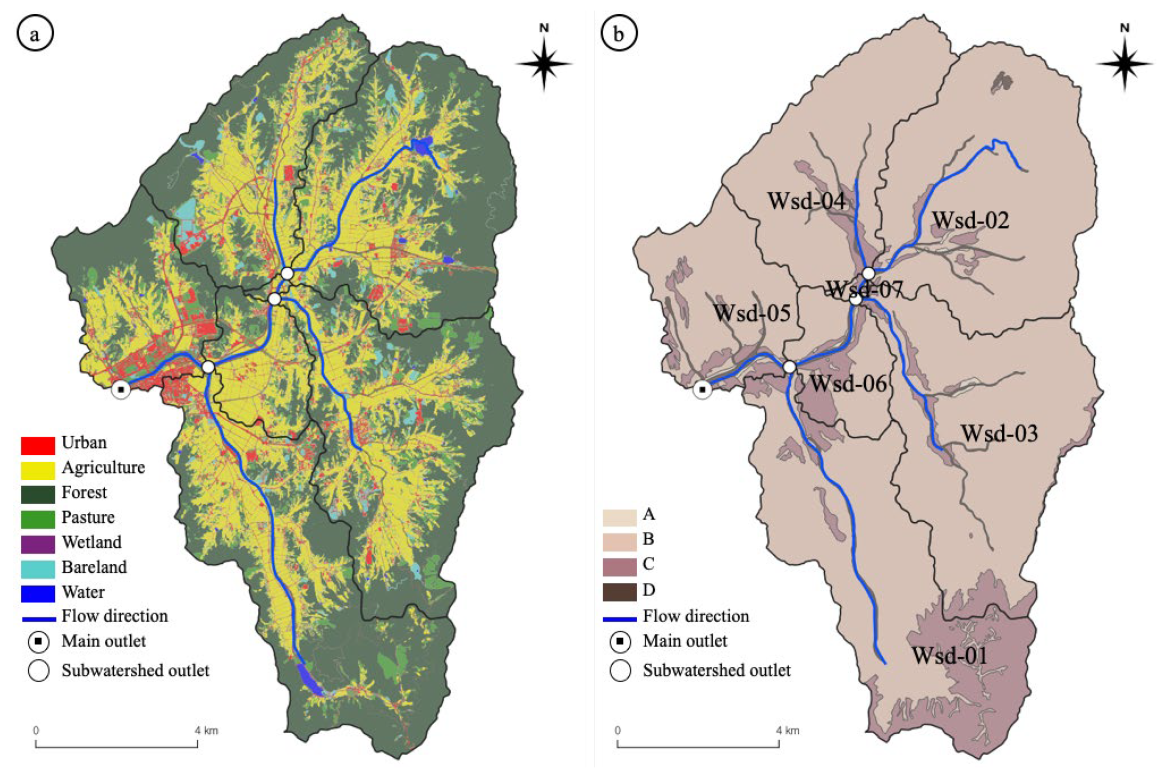
| Subwatershed | Area (ha) | |||||||
|---|---|---|---|---|---|---|---|---|
| Urban | Agriculture | Forest | Pasture | Wetland | Bare Land | Water | Total | |
| Wsd-01 | 213 | 774 | 1534 | 329 | 53 | 64 | 28 | 2995 |
| Wsd-02 | 170 | 761 | 1494 | 381 | 33 | 95 | 31 | 2964 |
| Wsd-03 | 167 | 817 | 1368 | 398 | 32 | 108 | 11 | 2901 |
| Wsd-04 | 147 | 562 | 849 | 259 | 19 | 99 | 6 | 1942 |
| Wsd-05 | 197 | 318 | 517 | 215 | 19 | 27 | 14 | 1307 |
| Wsd-06 | 69 | 346 | 161 | 112 | 17 | 14 | 6 | 723 |
| Wsd-07 | 5 | 12 | 10 | 6 | 3 | 3 | 1 | 39 |
| Subwatershed | Agricultural Animals | ||||
|---|---|---|---|---|---|
| Beef Cattle | Dairy Cattle | Swine (Hogs) | Sheep | Chickens | |
| Wsd-01 | 951 | 9 | 7521 | 971 | 43,031 |
| Wsd-02 | 2124 | 58 | 23,792 | 1131 | 318,575 |
| Wsd-03 | 1920 | 15 | 19,907 | 2086 | 30,929 |
| Wsd-04 | 1824 | 81 | 12,054 | 1185 | 155,363 |
| Wsd-05 | 460 | 3 | 3641 | 468 | 21,146 |
| Wsd-06 | 475 | 5 | 3779 | 453 | 24,533 |
| Wsd-07 | 50 | 1 | 350 | 31 | 4556 |
| NSE | R2 | |
|---|---|---|
| Streamflow | 0.8903 | 0.9327 |
| T-N | 0.9851 | 0.9906 |
| T-P | 0.8238 | 0.9793 |
| BOD | 0.7376 | 0.9187 |
| SS | 0.9527 | 0.9805 |
| NSE | R2 | |
|---|---|---|
| Streamflow | 0.8329 | 0.8633 |
| T-N | 0.7111 | 0.7546 |
| T-P | 0.7356 | 0.7869 |
| BOD | 0.7236 | 0.7596 |
| SS | 0.7981 | 0.9032 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Park, J.-Y.; Park, Y.S. Developing and Applying a QGIS-Based Model That Accounts for Nonpoint Source Pollution Due to Domestic Animals. Water 2022, 14, 2742. https://doi.org/10.3390/w14172742
Lee H, Park J-Y, Park YS. Developing and Applying a QGIS-Based Model That Accounts for Nonpoint Source Pollution Due to Domestic Animals. Water. 2022; 14(17):2742. https://doi.org/10.3390/w14172742
Chicago/Turabian StyleLee, Hanyong, Jong-Yoon Park, and Youn Shik Park. 2022. "Developing and Applying a QGIS-Based Model That Accounts for Nonpoint Source Pollution Due to Domestic Animals" Water 14, no. 17: 2742. https://doi.org/10.3390/w14172742









