The Northern Adriatic Forecasting System for Circulation and Biogeochemistry: Implementation and Preliminary Results
Abstract
:1. Introduction
2. Materials and Methods
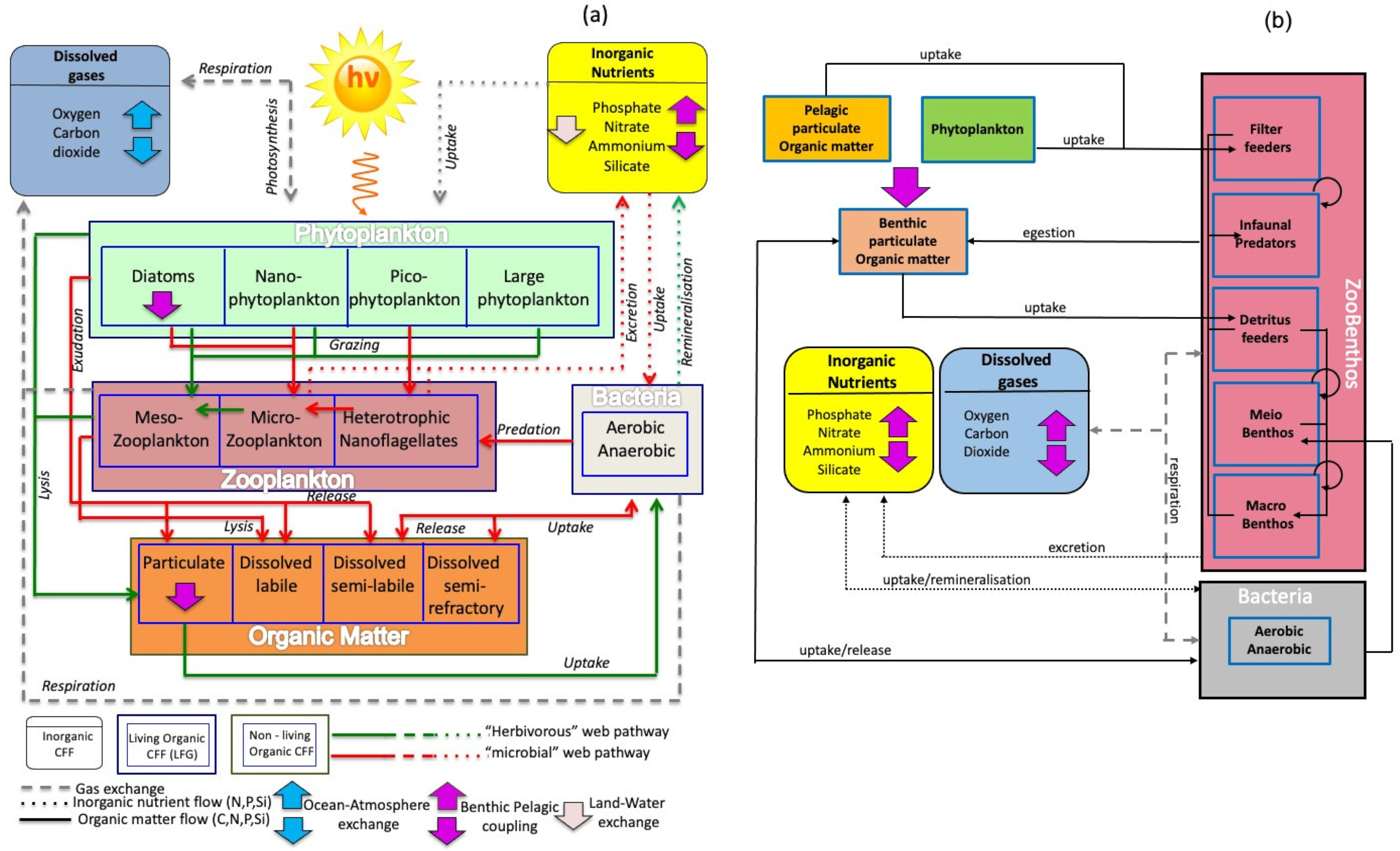
2.1. The Components of the NAD-FC
2.2. The Model Coupling
2.3. Model Implementation
2.3.1. Surface, Land-Based, and Open Boundary Conditions
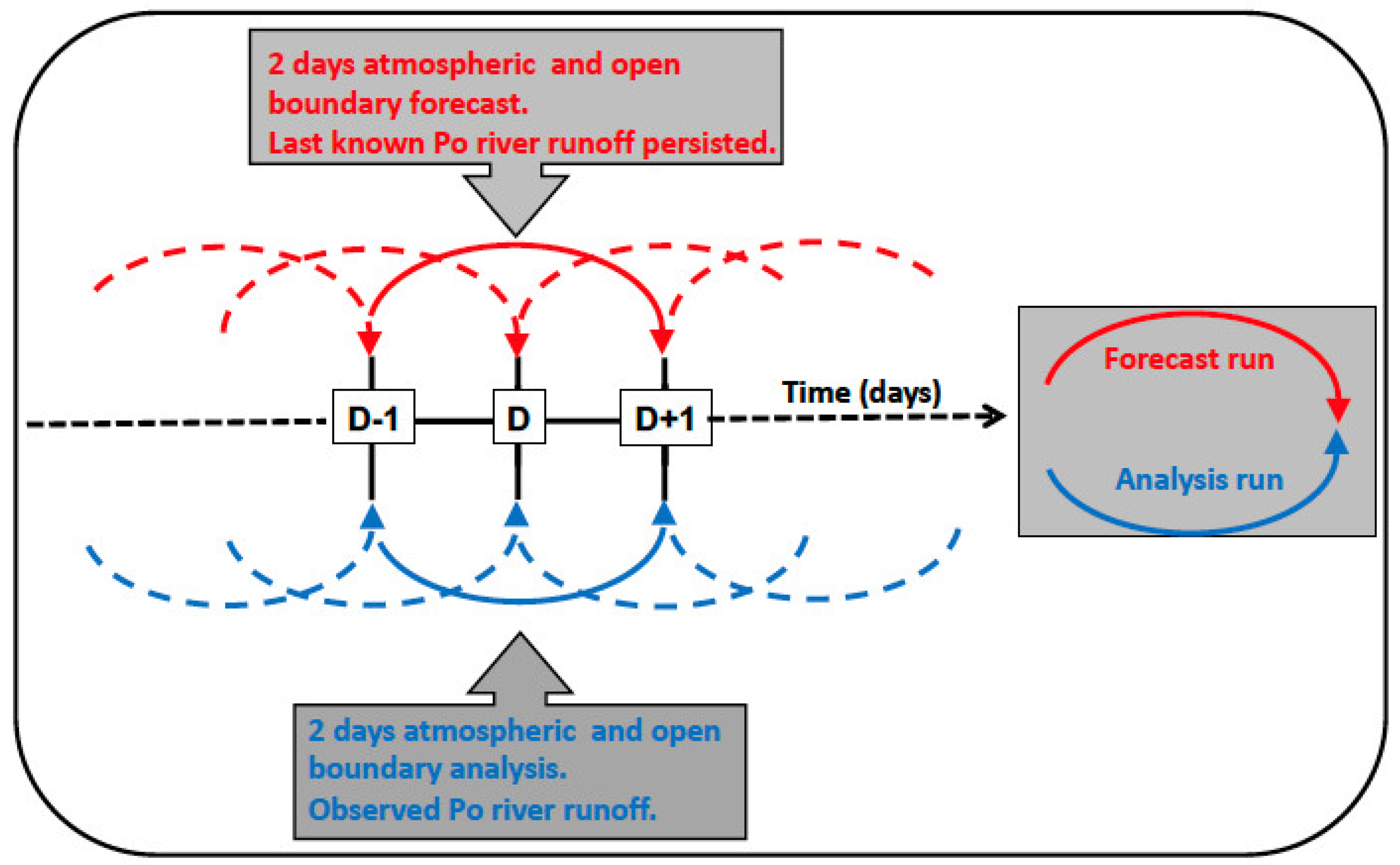
2.4. The Operational Chain
2.5. The Validation Datasets
2.5.1. Remote Observations
2.5.2. Observations from Fixed Stations
2.5.3. Observations from Coastal Observing System
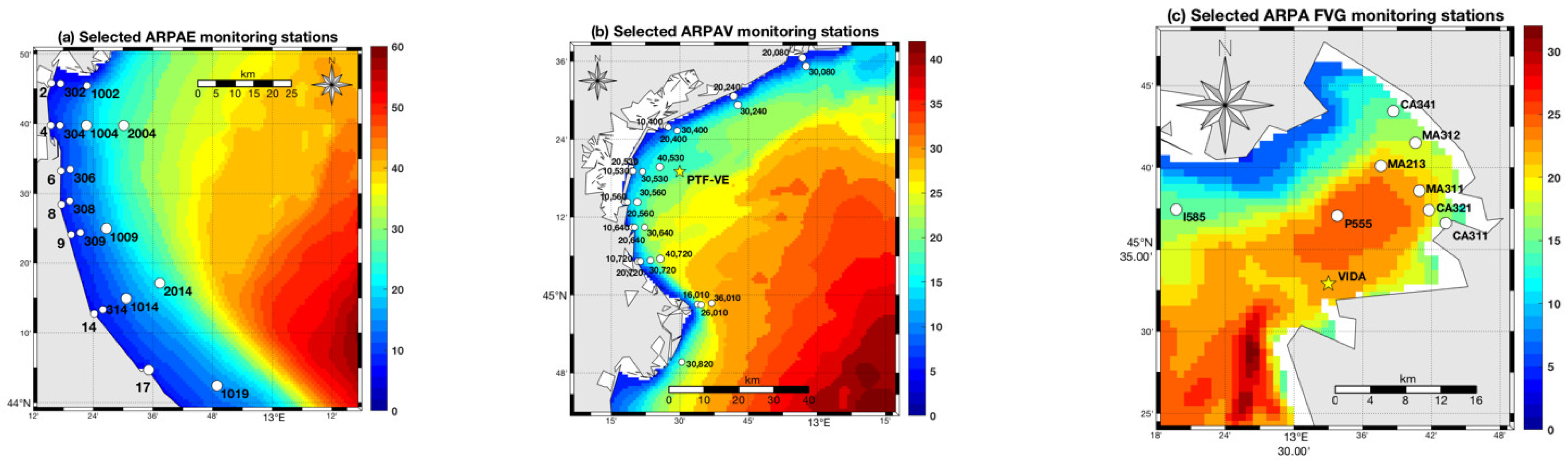
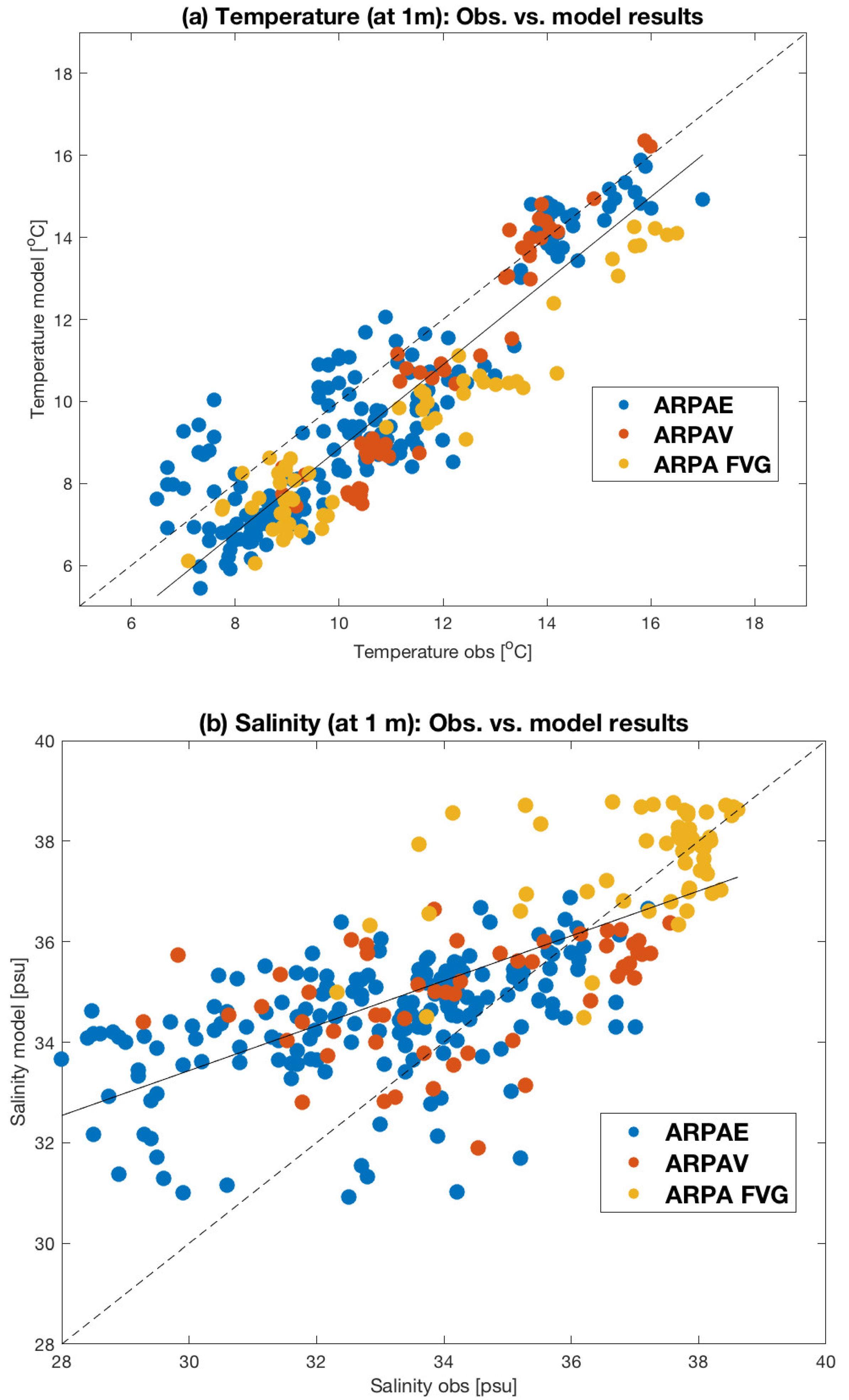
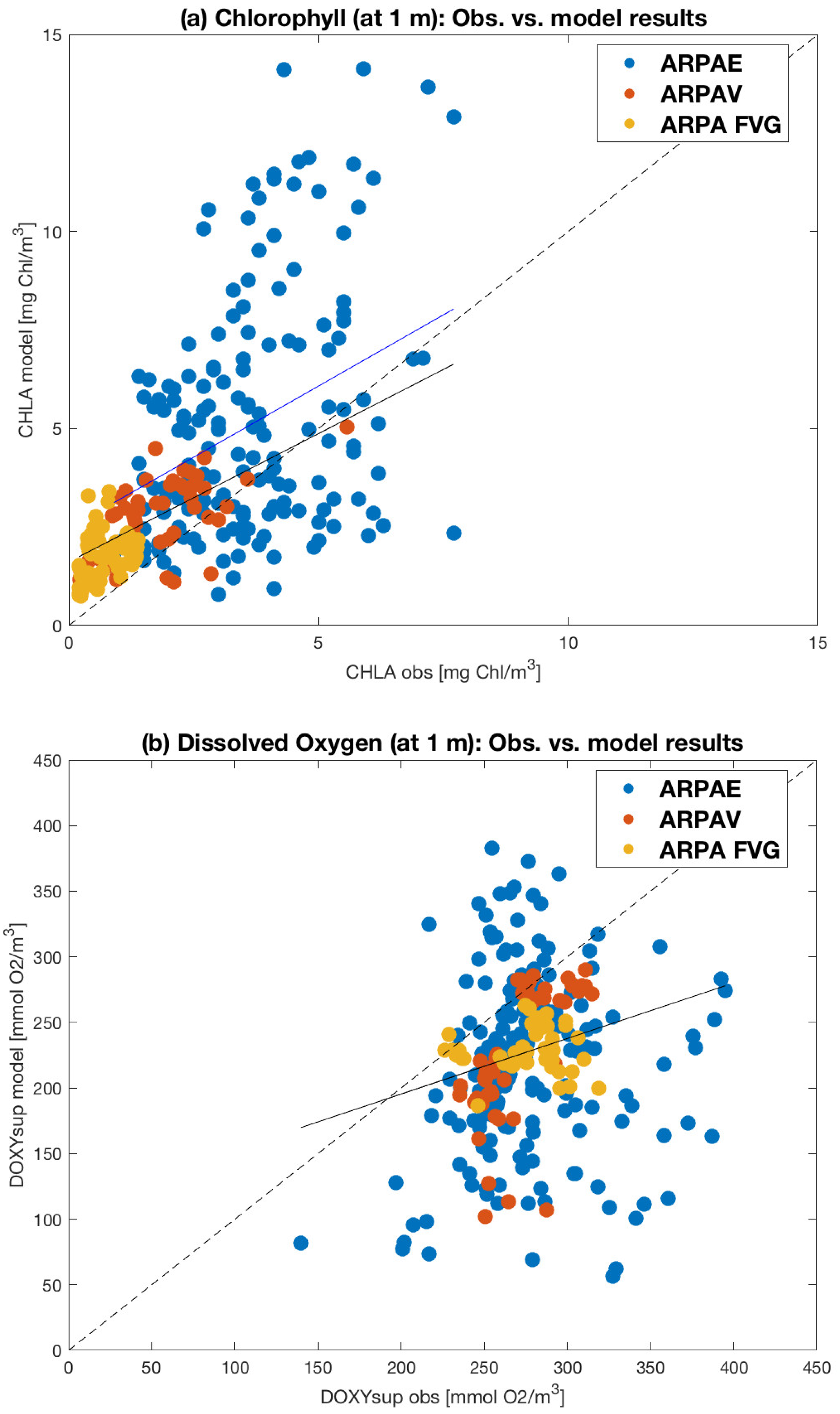
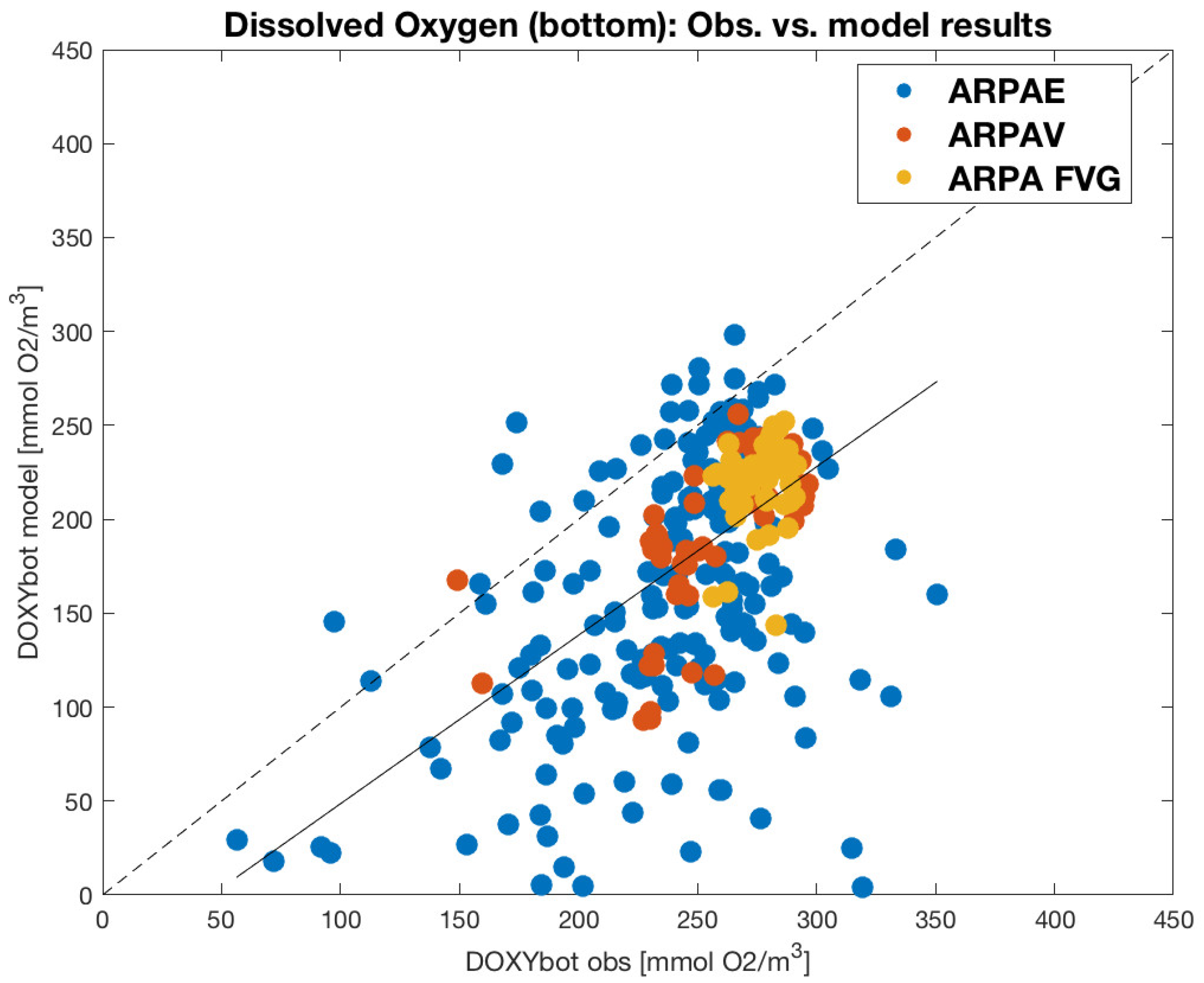
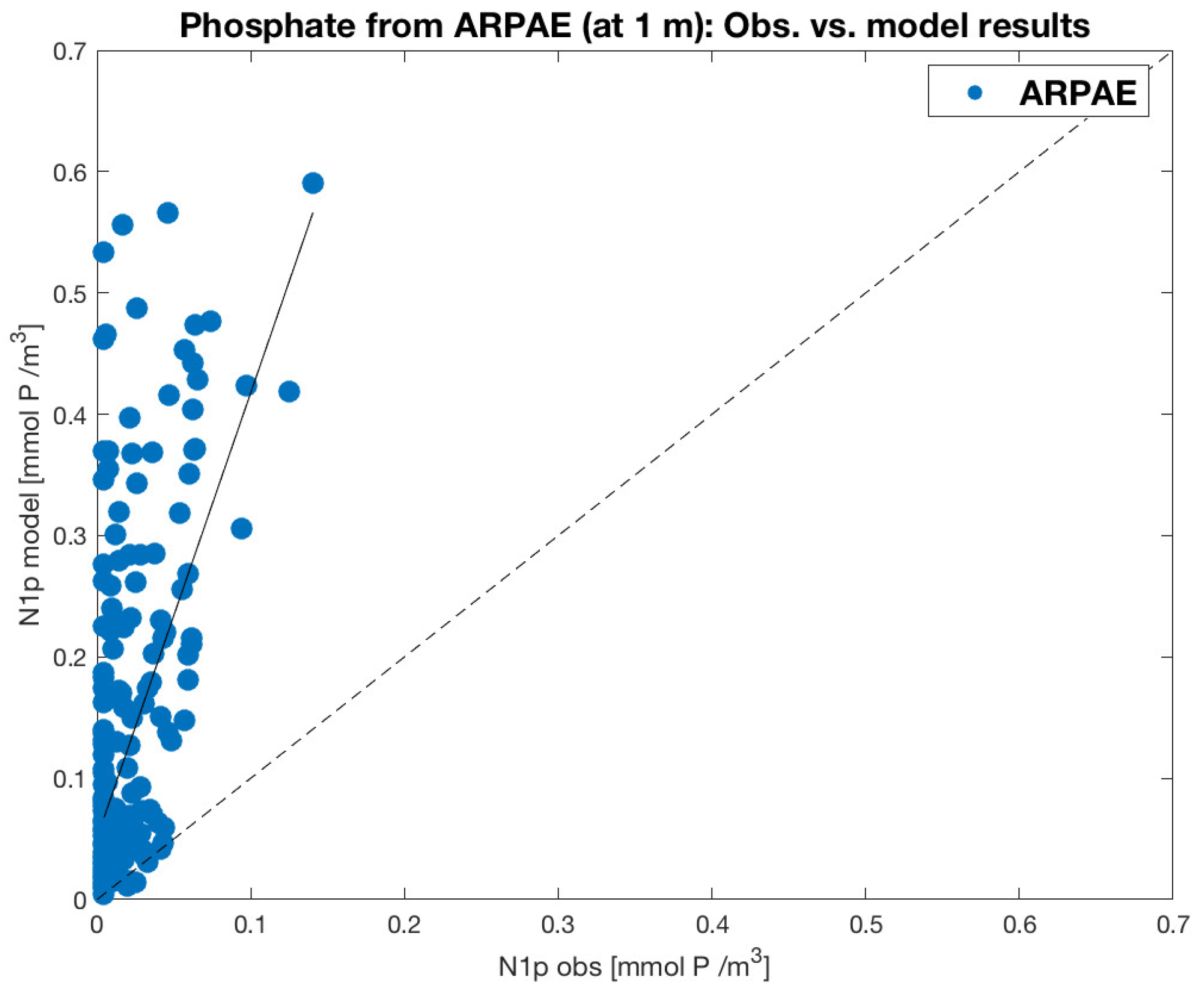
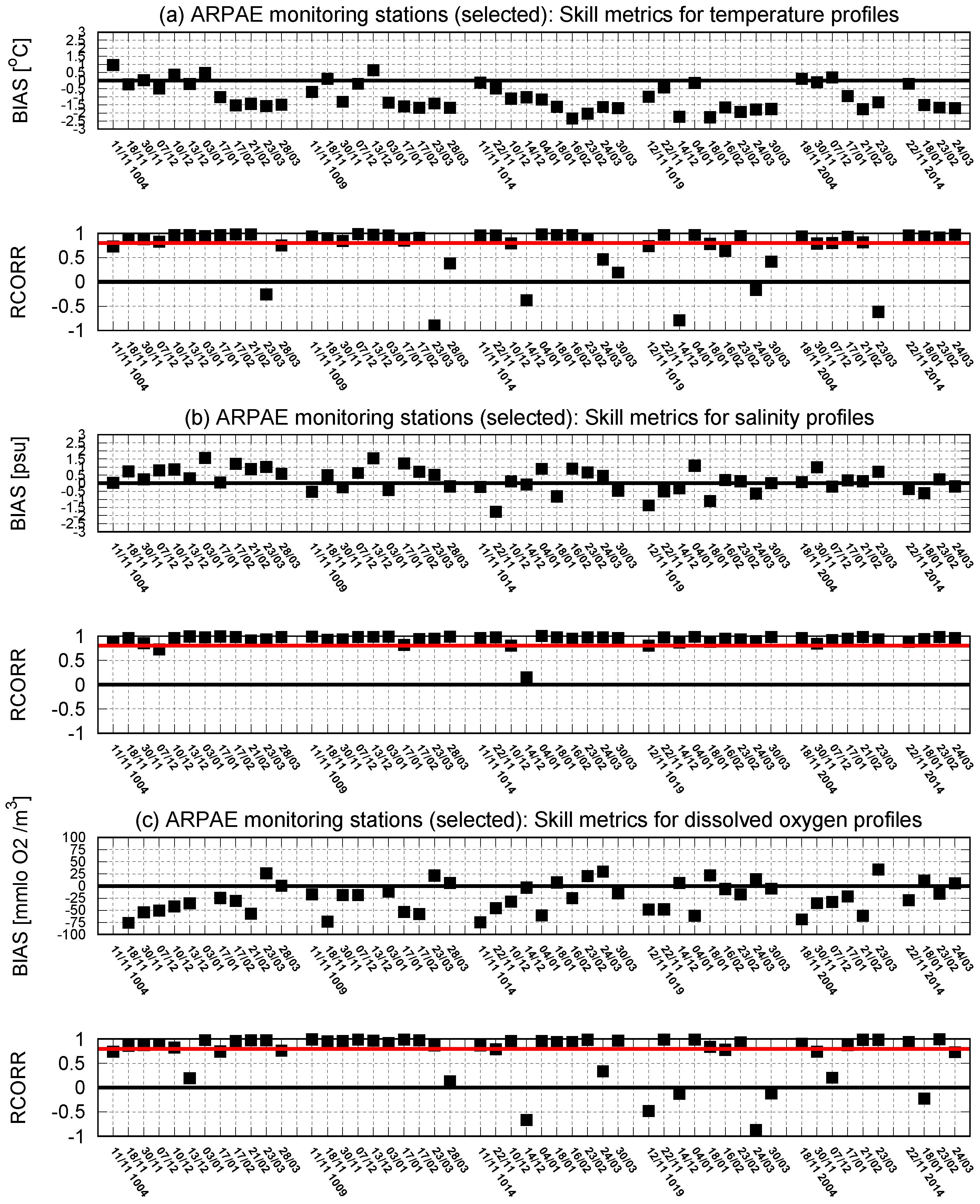
- Arpae (Regional Agency for Prevention, Environment, and Energy of the Emilia–Romagna Region, Figure 4a) observing system, composed of 29 monitoring stations located south of the Po river delta (Emilia–Romagna coastal region) and sampled with a 15 day periodicity.
- ARPAV (Environmental Protection Agency of the Veneto Region observing system, Figure 4b), composed of 28 monitoring stations, located in front and north of the Po River delta (along the Veneto coastal Region) and sampled during November 2021 and March 2022.
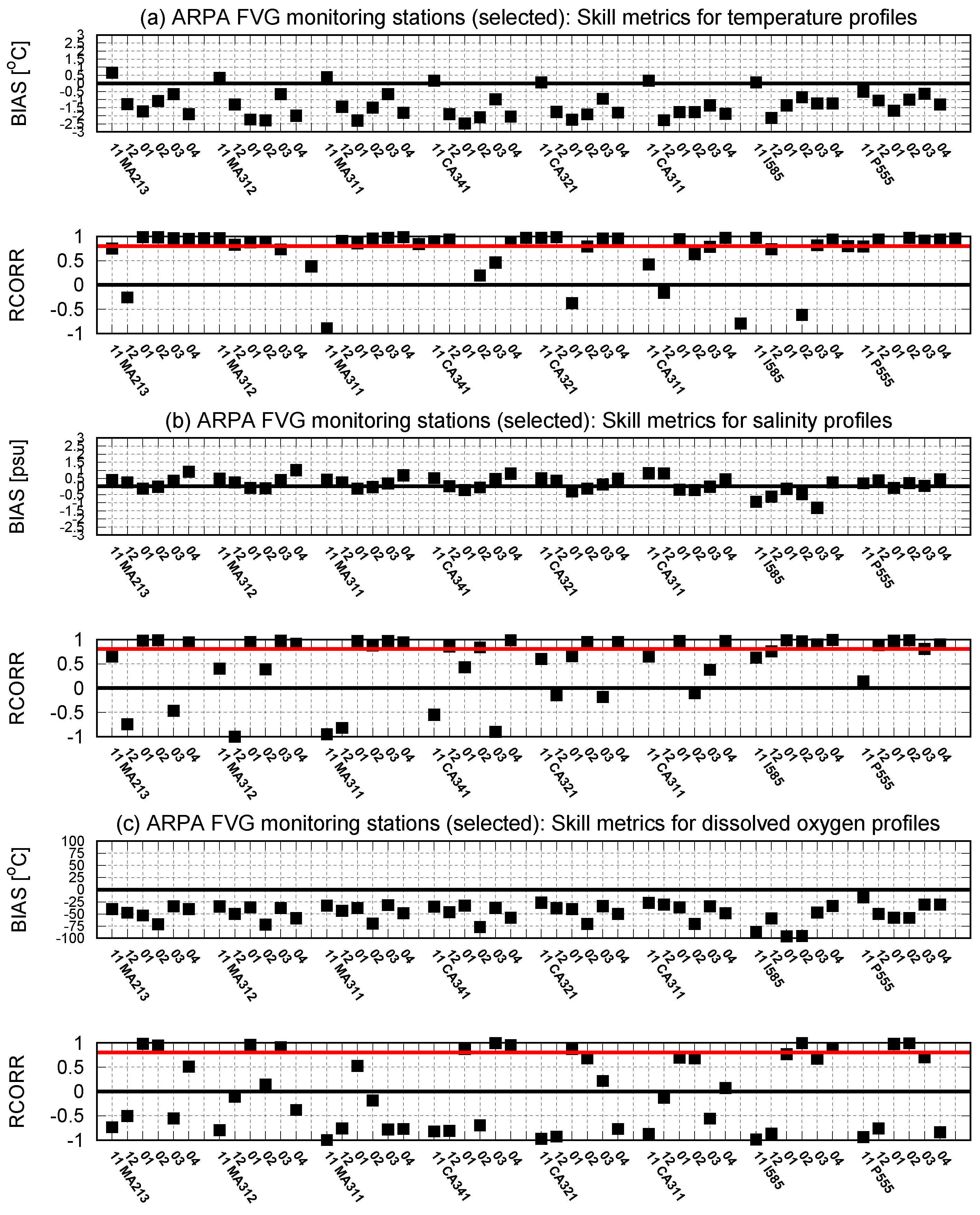
- ARPA FVG (Environmental Protection Agency of the Friuli Venezia Giulia Region, Figure 4c) observing system, composed of 21 monitoring stations, located within the Gulf of Trieste and sampled with a monthly periodicity.
3. Results
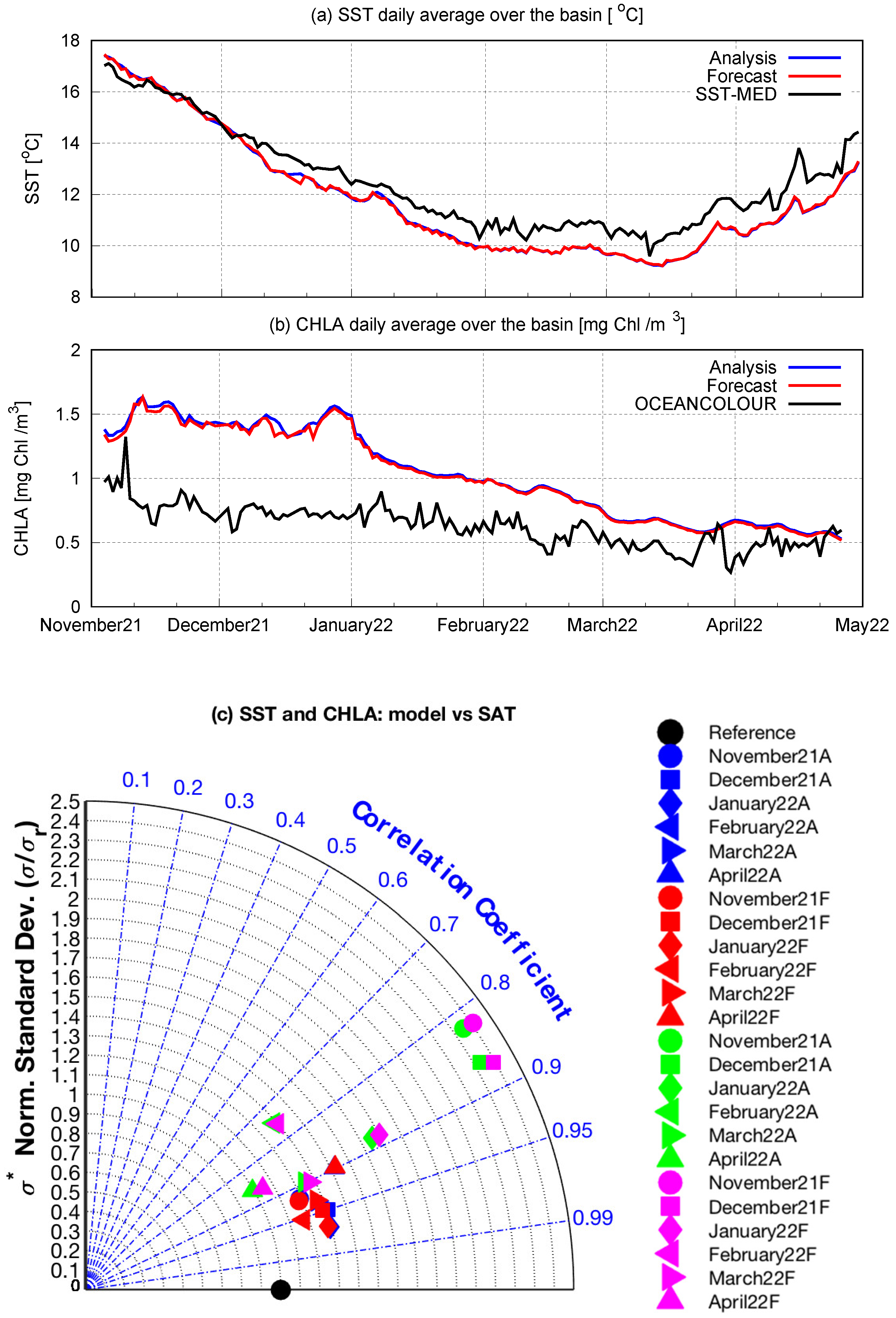
3.1. Comparison with Remote Observations
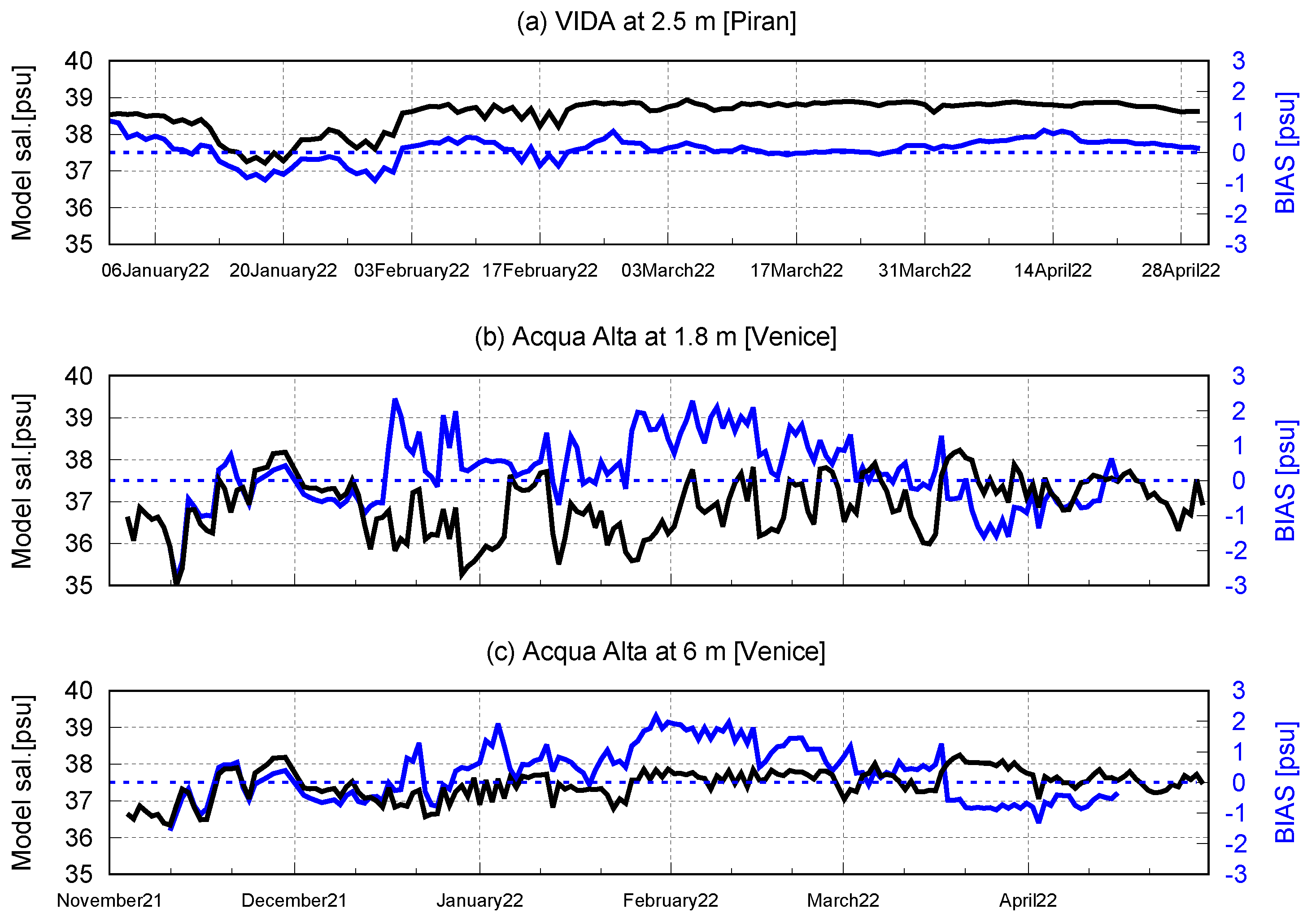
3.2. Comparison with Buoys Observations
3.3. Comparison with Data from Observing Systems
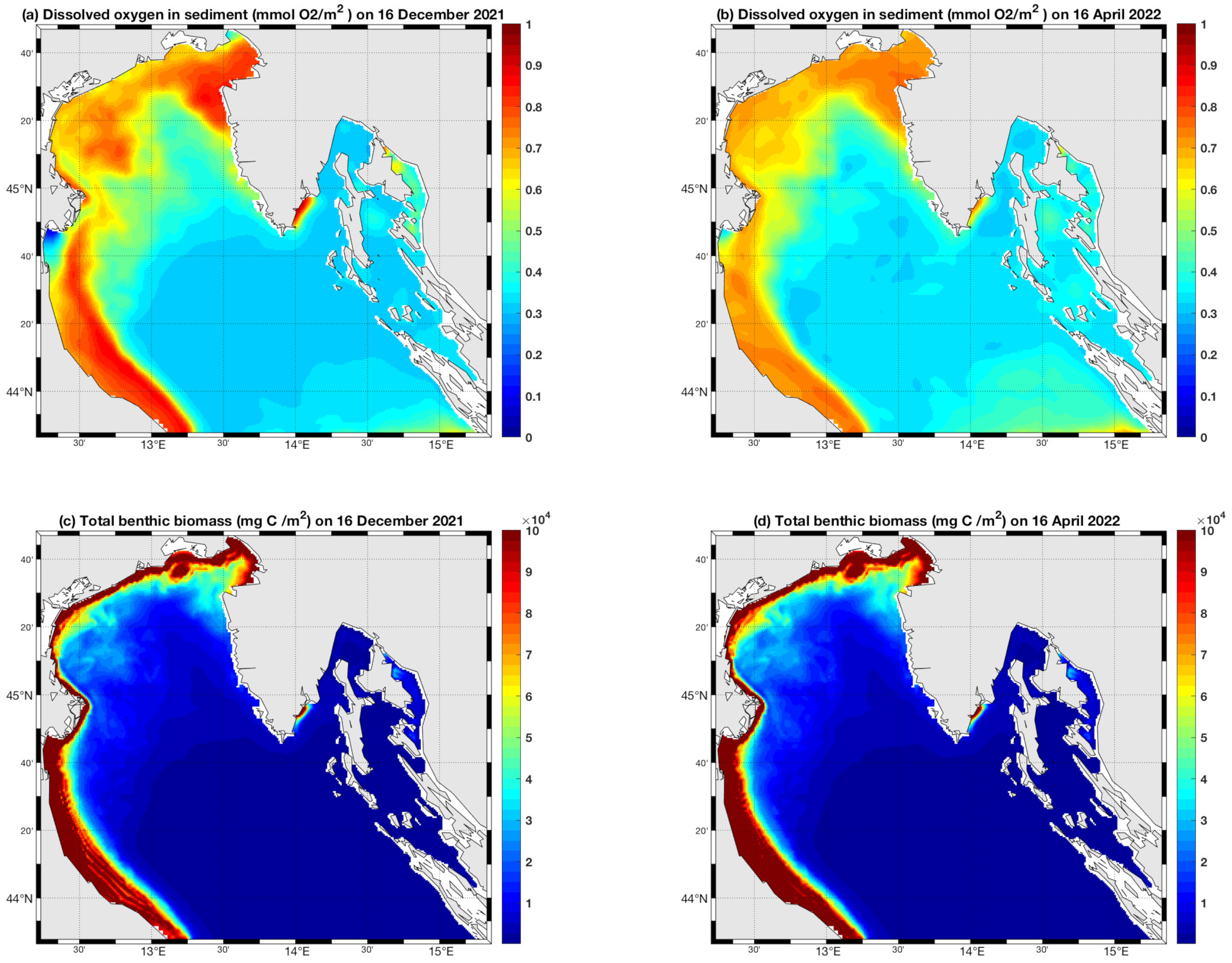
3.4. The Benthic Variables
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nihoul, J.C.J.; Djenidi, S. Coupled physical, chemical and biological models. In The Sea: The Global Coastal Ocean–Process and Method; Brink, K.H., Robinson, A.R., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 1998; Volume 10, pp. 483–506. [Google Scholar]
- Wollast, R. Evaluation and comparison of the global carbon cycle in the coastal zone and in the open ocean. In The Sea: The Global Coastal Ocean–Process and Method; Brink, K.H., Robinson, A.R., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 1998; Volume 10, pp. 213–252. [Google Scholar]
- Hofmann, E.E.; Powell, T.M. Environmental variability effects on marine fisheries: Four case histories. Ecol. Appl. 1998, 8, S23–S32. [Google Scholar] [CrossRef]
- Raicich, F. On the freshwater balance of the Adriatic Sea. J. Mar. Syst. 1996, 9, 305–319. [Google Scholar] [CrossRef]
- Simpson, J.H. Physical processes in the ROFI regime. J. Mar. Syst. 1997, 12, 3–15. [Google Scholar] [CrossRef]
- Artegiani, A.; Bregant, D.; Paschini, E.; Pinardi, N.; Russo, A. The Adriatic Sea general circulation. Part I: Air-Sea interactions and water mass structure. J. Phys. Oceanogr. 1997, 27, 1492–1514. [Google Scholar] [CrossRef]
- Artegiani, A.; Bregant, D.; Paschini, E.; Pinardi, N.; Russo, A. The Adriatic Sea general circulation. Part II: Baroclinic Circulation Structure. J. Phys. Oceanogr. 1997, 27, 1515–1532. [Google Scholar] [CrossRef]
- Artegiani, A.; Azzolini, R.; Salusti, E. On the dense water in the Adriatic Sea. Oceanol. Acta 1989, 12, 151–160. [Google Scholar]
- Mihanovic, H.; Vilibic, I.; Carniel, S.; Tudir, M.; Bergamasco, A.; Bubic, N.; Ljubesic, Z.; Vilicic, V.; Boldrin, A.; Malacic, V.; et al. Exceptional dense water formation on the Adriatic shelf in the winter of 2012. Ocean Sci. 2013, 9, 561–572. [Google Scholar] [CrossRef]
- Zavatarelli, M.; Pinardi, N. The Adriatic Sea modelling system: A nested approach. Ann. Geophys. 2003, 21, 345–364. [Google Scholar] [CrossRef]
- Degobbis, D.; Gilmartin, M. Nitrogen, Phosphorus and biogenic Silicon budgets for the northern Adriatic Sea. Oceanol. Acta 1990, 13, 31–45. [Google Scholar]
- Rinaldi, A.; Montanari, G.; Ghetti, A.; Ferrari, C.R. Anossie nelle acque costiere dell’Adriatico nord-occidentale. Loro Evoluzione e conseguenze sull’ecosistema bentonico. Biol. Mar. 1992, 1, 79–89. [Google Scholar]
- Solidoro, C.; Bastianini, M.; Bandelj, V.; Codermatz, R.; Cossarini, G.; Melaku Canu, D.; Ravagnan, E.; Salon, S.; Trevisani, S. Current state, scales of variability and trends of biogeochemical properties in the northern Adriatic Sea. J. Geophys. Res. 2009, 114, C07S91. [Google Scholar] [CrossRef]
- Giani, M.; Djakovac, T.; Degobbis, D.; Cozzi, S.; Solidoro, C.; Fonda Umani, S. Recent changes in the marine ecosystems of the northern Adriatic Sea. Estuar. Coast. Shelf Sci. 2012, 115, 1–13. [Google Scholar] [CrossRef]
- Griffiths, J.R.; Kadin, M.; Nascimento, F.J.A.; Tamelander, T.; Tornroos, A.; Bonaglia, S.; Bonsdorff, E.; Bruckert, V.; Gardmark, A.; Jarnstrom, M.; et al. The importance of benthic-Pelagic coupling for marine ecosystem functioning in a changing world. Glob. Chang. Biol. 2017, 23, 2179–2196. [Google Scholar] [CrossRef] [Green Version]
- Madec, G.; NEMO Team. NEMO Ocean Engine; Note du Pole de Modelisation de l’Institut Pierre-Simon Laplace No 27; Institut Pierre-Simon Laplace: Paris, France, 2016; 402p, Available online: https://www.nemo-ocean.eu/doc/ (accessed on 30 June 2022).
- Sun, F. A pseudo-non-time splitting method in air quality modeling. J. Comput. Phys. 2006, 127, 152–157. [Google Scholar] [CrossRef]
- Val Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1999, 32, 101–136. [Google Scholar] [CrossRef]
- Estubier, A.; Levy, M. Quel Schema Numerique pour le Transport D’organismes Biologiques par la Circulation Oceanique 2000; Note Techniques du Pole de Modelisation; Institut Pierre-Simon Laplace: Paris, France, 2016; 81p. [Google Scholar]
- Oddo, P.; Adani, M.; Pinardi, N.; Fratianni, C.; Tonani, M.; Pettenuzzo, D. A nested Atlantic-Mediterranean Sea general circulation model for operational forecasting. Ocean Sci. 2009, 5, 461–473. [Google Scholar] [CrossRef]
- Umlauf, L.; Burchard, H. A generic length-scale equation for geophysical turbulence models. J. Mar. Res. 2003, 61, 235–265. [Google Scholar] [CrossRef]
- Reffray, G.; Bourdalle-Badie, R.; Calone, C. Modelling turbulent vertical mixing sensitivity using a 1-D version of NEMO. Geosci. Model Dev. 2015, 8, 69–86. [Google Scholar] [CrossRef]
- Vichi, M.; Pinardi, N.; Masina, S. A generalized model of pelagic biogeochemistry for the global ocean ecosystem. Part 1: Theory. J. Mar. Syst. 2007, 64, 89–109. [Google Scholar] [CrossRef]
- Vichi, M.; Lovato, T.; Butenschön, M.; Tedesco, L.; Lazzari, P.; Cossarini, G.; Masina, S.; Pinardi, N.; Solidoro, C.; Zavatarelli, M. The Biogeochemical Flux Model (BFM): Equation Description and User Manual, BFM version 5.2; BFM Report Series N. 1; BFM Community: Bologna, Italy, 2020; p. 104. Available online: http://bfm-community.eu (accessed on 30 June 2022).
- Cushing, D.H. Grazing by herbivorous copepods in the sea. J. Cons. Int. Explor. Mer. 1968, 32, 70–82. [Google Scholar] [CrossRef]
- Cushing, D.H. A difference in structure between ecosystems in strongly stratified waters and in those that are only weakly stratified. J. Plankton Res. 1989, 11, 1–13. [Google Scholar] [CrossRef]
- Azam, F.; Fenchel, T.; Field, J.G.; Gray, J.S.; Meyer-Reyl, L.A.; Thingstad, F. The ecological role of water-column microbes in the sea. Mar. Ecol. Prog. Ser. 1983, 10, 57–99. [Google Scholar] [CrossRef]
- Thingstad, F.; Rassoulsadegan, F. Conceptual models for the biogeochemical role of the photic zone microbial food web with particular reference to the Mediterranean Sea. Progr. Oceanogr. 1997, 44, 271–286. [Google Scholar] [CrossRef]
- Legendre, L.; Rassoulsadegan, F. Plankton and nutrient dynamics in marine waters. Sarsia 1995, 41, 153–172. [Google Scholar] [CrossRef]
- Vichi, M.; Oddo, P.; Zavatarelli, M.; Coluccelli, A.; Coppini, G.; Celio, M.; Fonda Umani, S.; Pinardi, N. Calibration and validation of a one-dimensional complex marine biogeochemical flux model in different areas of the northern Adriatic shelf. Ann. Geophys. 2003, 21, 413–436. [Google Scholar] [CrossRef]
- Ebenhoh, W.; Kohlmeier, C.; Radford, P. The benthic biological submodel in the European Regional Seas Ecosystem Model. Neth. J. Sea Res. 1995, 33, 423–452. [Google Scholar] [CrossRef]
- Ruardij, P.; Raaphorst, W.V. Benthic nutrient regeneration in the ERSEM ecosystem model of the north sea. Neth. J. Sea Res. 1995, 33, 453–483. [Google Scholar] [CrossRef]
- Mussap, G.; Zavatarelli, M. A numerical study of the benthic pelagic coupling in a shallow shelf sea (Gulf of Trieste). Reg. Stud. Mar. Sci. 2017, 9, 24–34. [Google Scholar] [CrossRef]
- Butenschön, M.; Zavatarelli, M.; Vichi, M. Sensitivity of a marine coupled physical biogeochemical model to time resolution, integration scheme and time splitting method. Ocean Model. 2012, 52–53, 36–53. [Google Scholar] [CrossRef]
- GEBCO Bathymetric Compilation Group. The GEBCO_2021 Gri—A Continuous Terrain Model of the Global Oceans and Land; NERC EDS British Oceanographic Data Centre NOC: Liverpool, UK, 2021. [Google Scholar] [CrossRef]
- Castellari, S.; Pinardi, N.; Leaman, K. A model study of air-se interactions in the Mediterranean Sea. J. Mar. Syst. 1998, 18, 89–114. [Google Scholar] [CrossRef]
- Gastaldo, T.; Poli, V.; Marsigli, C.; Cesari, D.; Alberoni, P.P.; Paccagnella, T. Assimilation of radar reflectivity volumes in a pre-operational framework. Q. J. R. Meteorol. Soc. 2021, 147, 1–24. [Google Scholar] [CrossRef]
- Wanninkhof, R. Relationship between wind speed and gas exchange over the ocean. J. Geophys. Res. 1992, 97, 7373–7382. [Google Scholar] [CrossRef]
- Wanninkhof, R. Relationship between wind speed and gas exchange over the ocean revisited. Limnol. Oceanogr. Methods 2014, 12, 351–362. [Google Scholar] [CrossRef]
- Ludwig, W.; Bouwman, A.F.; Dumont, E.; Lespinas, F. Water and nutrient fluxes from major Mediterranean and Black Sea rivers: Past and future trends and their implications for the basin-scale budget. Glob. Biogeochem. Cycles 2010, 24, GB0A13. [Google Scholar] [CrossRef]
- Oddo, P.; Pinardi, N.; Zavatarelli, M. A numerical study of the interannual variability of the Adriatic Sea Circulation (1999–2002). Sci. Total Environ. 2005, 353, 39–56. [Google Scholar] [CrossRef]
- Clementi, E.; Aydoglu, A.; Goglio, A.C.; Pistoia, J.; Escudier, R.; Drudi, M.; Grandi, A.; Mariani, A.; Lyubartsev, V.; Lecci, R.; et al. Mediterranean Sea Physical Analysis and Forecast (CMEMS MED-Currents, EAS6 System) (Version 1) [Data Set]; Copernicus Monitoring Environment Marine Service (CMEMS): Toulouse, France, 2021. [Google Scholar] [CrossRef]
- Oddo, P.; Pinardi, N. Lateral open boundary conditions for nested limited area models: A scale selective approach. Ocean Model. 2008, 20, 134–156. [Google Scholar] [CrossRef]
- Orlansky, I. A simple boundary condition for unbounded hyperbolic flows. J. Comput. Phys. 1976, 21, 251–269. [Google Scholar] [CrossRef]
- Flather, R.A. A tidal model of the northwest European continental shelf. Mémoires de la Société Royale des Sciences de Liège 1976, 6, 141–164. [Google Scholar]
- Chust, G.; Allen, J.I.; Bopp, L.; Schrum, C.; Holt, J.; Tsiaras, K.; Zavatarelli, M.; Chifflet, M.; Cannaby, H.; Dadou, I.; et al. Biomass changes and trophic amplification of plankton in a warmer ocean. Glob. Chang. Biol. 2014, 20, 2124–2139. [Google Scholar] [CrossRef]
- Pisano, A.; Buongiorno Nardelli, B.; Tronconi, C.; Santoleri, R. The new Mediterranean optimally interpolated pathfinder AVHRR SST Dataset (1982–2012). Remote Sens. Environ. 2016, 176, 107–116. [Google Scholar] [CrossRef]
- Volpe, G.; Buongiorno Nardelli, B.; Colella, S.; Pisano, A.; Santoleri, R. An Operational Interpolated Ocean Colour Product in the Mediterranean Sea. 2018. Available online: https://diginole.lib.fsu.edu/islandora/object/fsu%3A602137 (accessed on 30 June 2022).
- Cavaleri, L. The oceanographic tower Acqua Alta—Activity and prediction of sea states at Venice. Coast. Eng. 2000, 39, 29–70. [Google Scholar] [CrossRef]
- Malacic, V. Wind Direction Measurements on Moored Coastal Buoys. J. Atmos. Ocean. Technol. 2019, 36, 1401–1418. [Google Scholar] [CrossRef]
- Stachowitsch, M. Coastal hypoxia and anoxia: A multi-tiered holistic approach. Biogeosciences 2014, 11, 2281–2285. [Google Scholar] [CrossRef]
- Djakovac, T.; Supic, N.; Bernardi Aubry, F.; Degobbis, D. Mechanisms of hypoxia frequency changes in the northern Adriatic Sea during the period 1972–2012. J. Mar. Syst. 2015, 141, 179–189. [Google Scholar] [CrossRef]
- Capet, A.; Meysman, F.J.; Akoumianaki, I.; Soetaert, K.; Gregoire, M. Integrating sediment biogeochemistry into 3D ocean models: A study of benthic pelagic coupling in the Black Sea. Ocean. Model. 2016, 101, 83–100. [Google Scholar] [CrossRef]
- Gili, J.M.; Coma, R. Benthic suspension feeders: Their paramount role in the littoral marine food webs. Trends Ecol. Evol. 1998, 13, 316–321. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scroccaro, I.; Zavatarelli, M.; Lovato, T.; Lanucara, P.; Valentini, A. The Northern Adriatic Forecasting System for Circulation and Biogeochemistry: Implementation and Preliminary Results. Water 2022, 14, 2729. https://doi.org/10.3390/w14172729
Scroccaro I, Zavatarelli M, Lovato T, Lanucara P, Valentini A. The Northern Adriatic Forecasting System for Circulation and Biogeochemistry: Implementation and Preliminary Results. Water. 2022; 14(17):2729. https://doi.org/10.3390/w14172729
Chicago/Turabian StyleScroccaro, Isabella, Marco Zavatarelli, Tomas Lovato, Piero Lanucara, and Andrea Valentini. 2022. "The Northern Adriatic Forecasting System for Circulation and Biogeochemistry: Implementation and Preliminary Results" Water 14, no. 17: 2729. https://doi.org/10.3390/w14172729





