Spatial Frequency Analysis by Adopting Regional Analysis with Radar Rainfall in Taiwan
Abstract
:1. Introduction
2. Materials and Methods
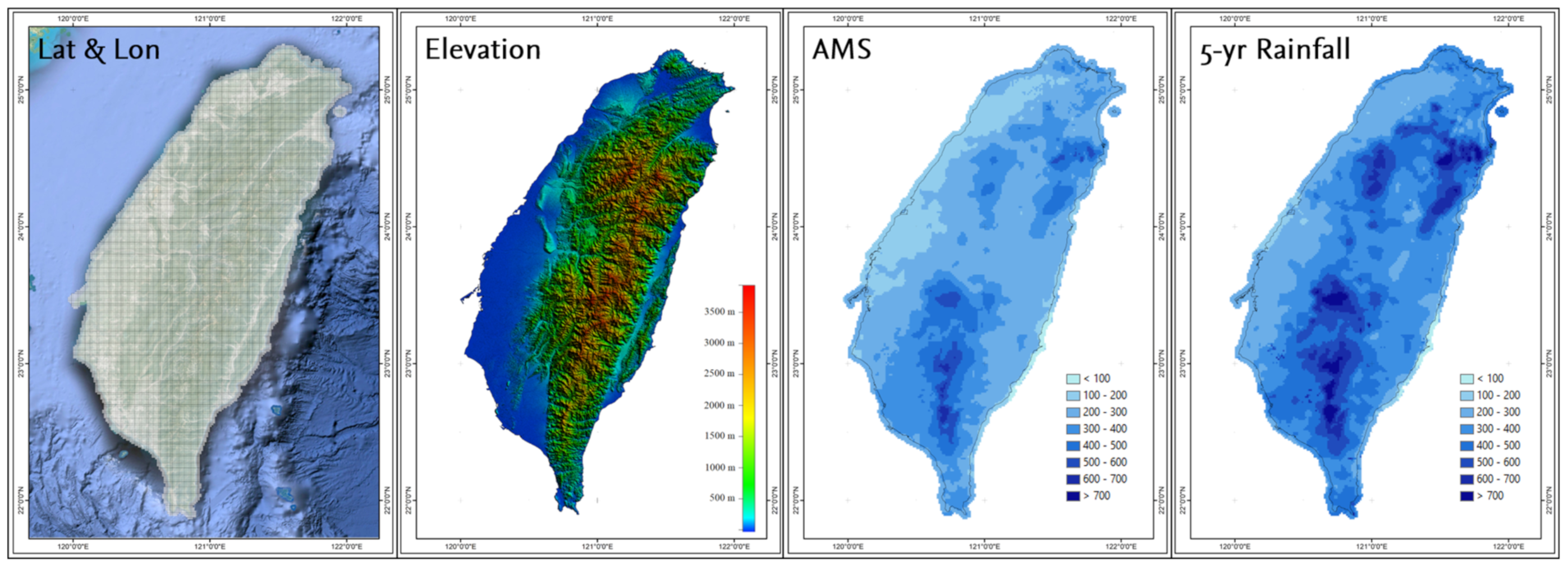
2.1. Study Area
2.2. Data
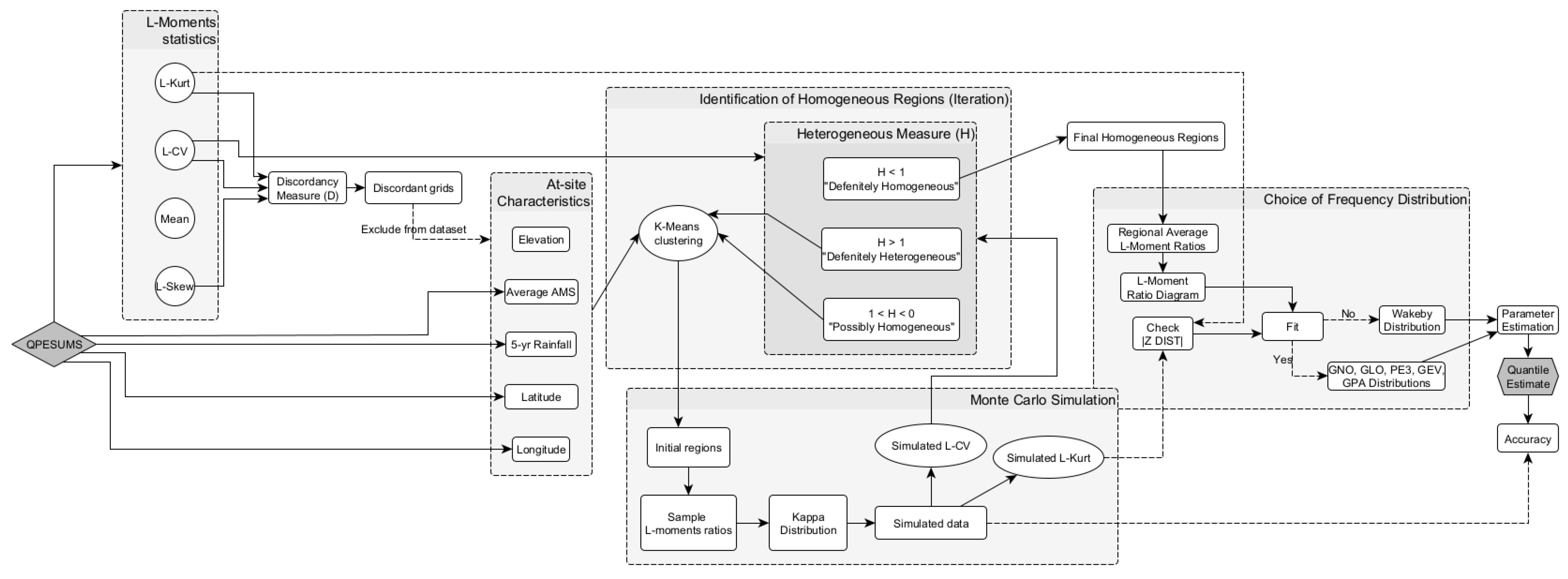
2.3. L-Moment approach
2.4. Discordancy Measure
2.5. K-Means Clustering
2.6. Heterogeneity Measure
2.7. Selection of Candidate Distributions
2.8. Estimation of Rainfall Quantiles
2.9. Accuracy Assessment
2.10. Regional and Grid-Based Estimates for Watershed Scale
3. Results & Discussion
3.1. Screening the Data
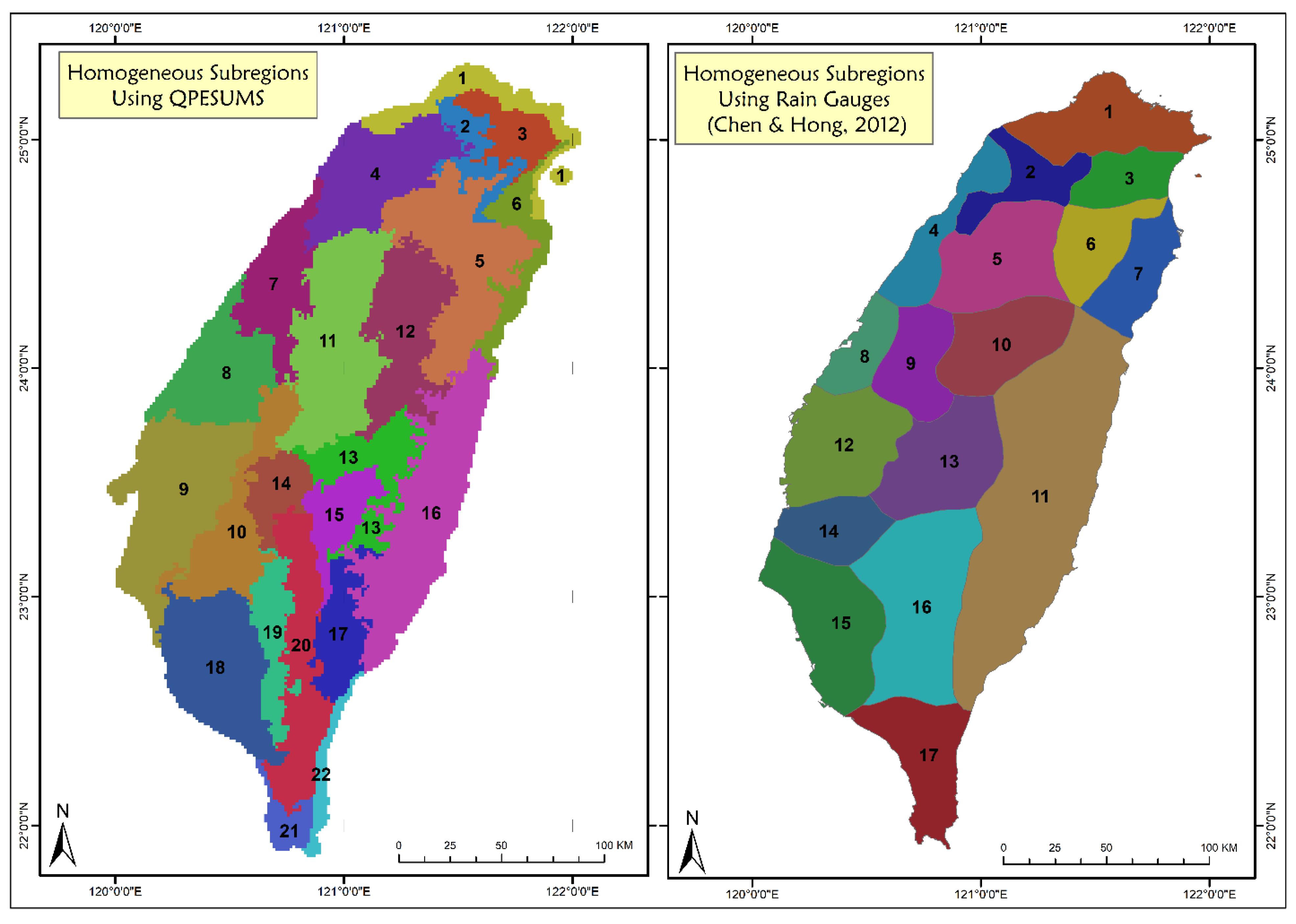
3.2. Identification of Homogeneous Regions
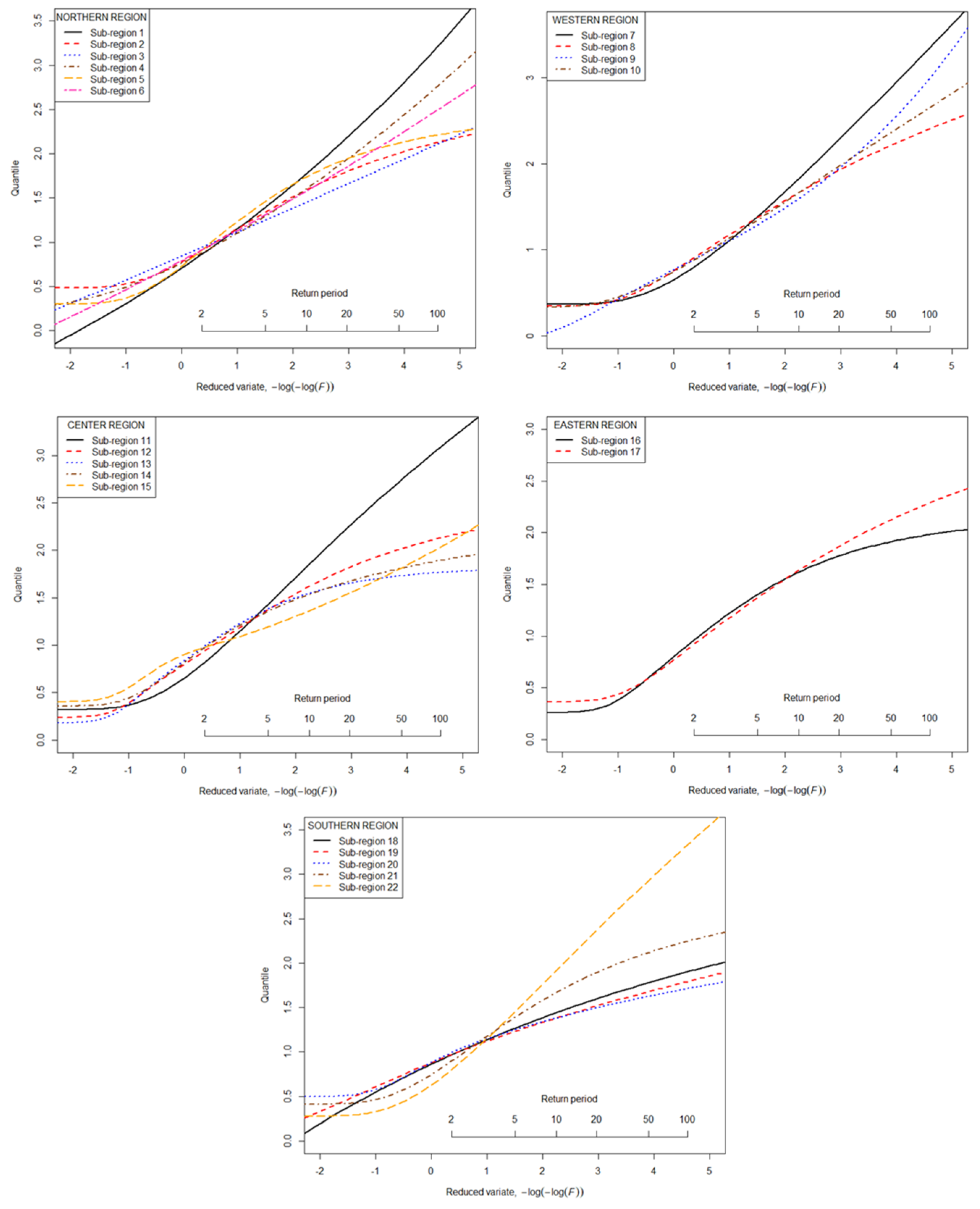
3.3. Selection of Distribution Models
3.4. Estimation of Regional Quantiles
3.5. Accuracy Result
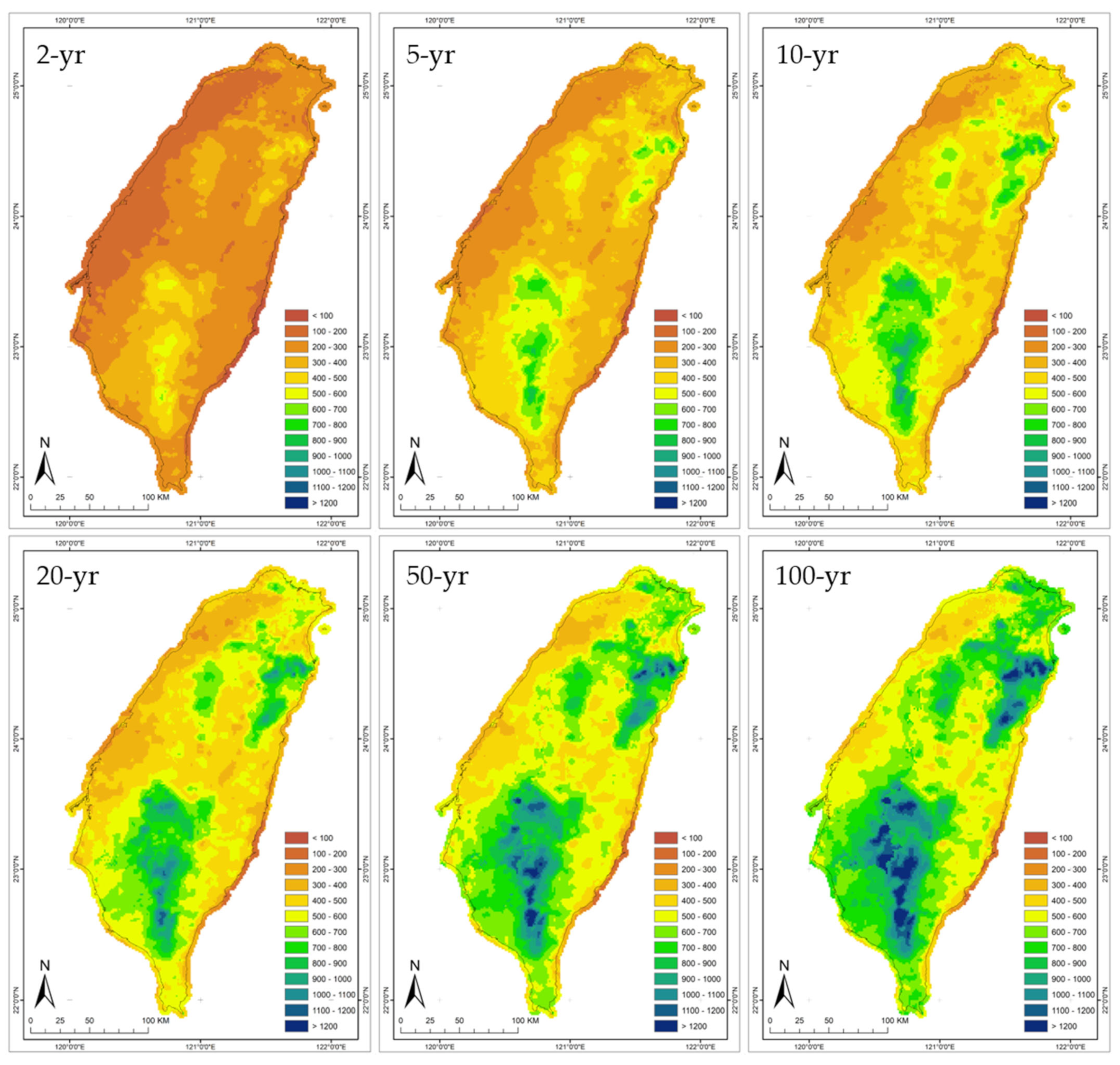
3.6. Spatial Mapping of Extreme Rainfall
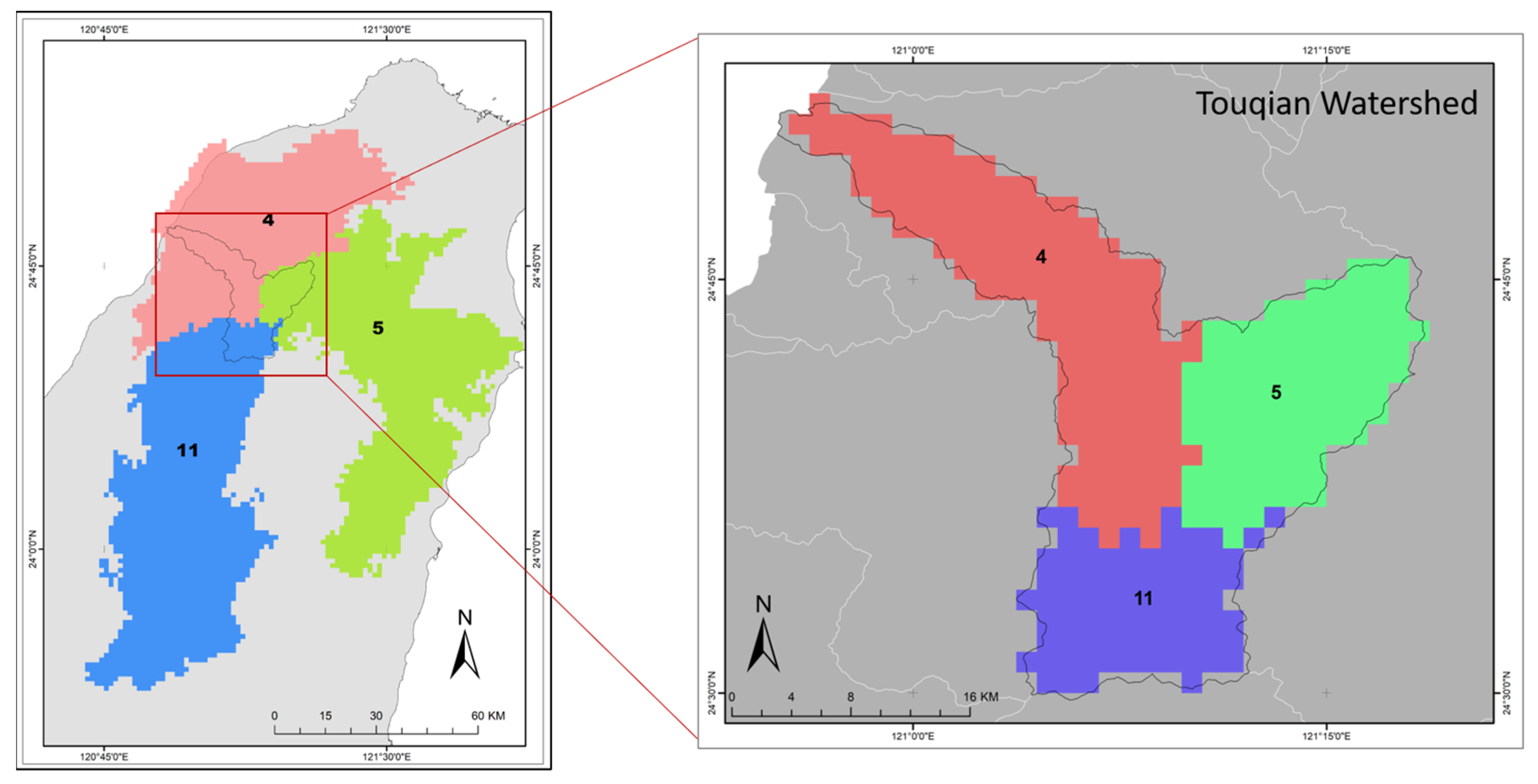
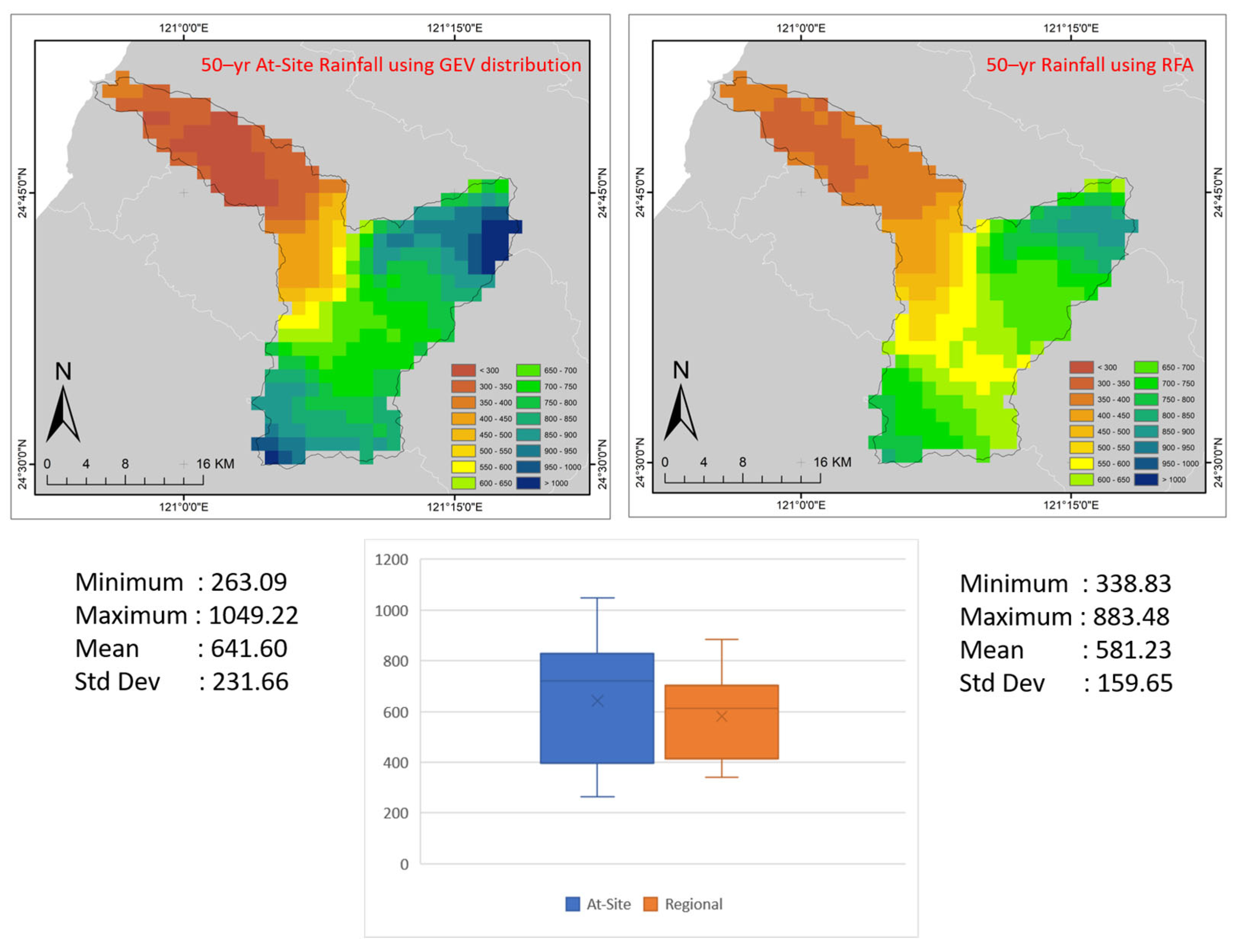
3.7. Regional and Grid-Based Estimates for Watershed Scale
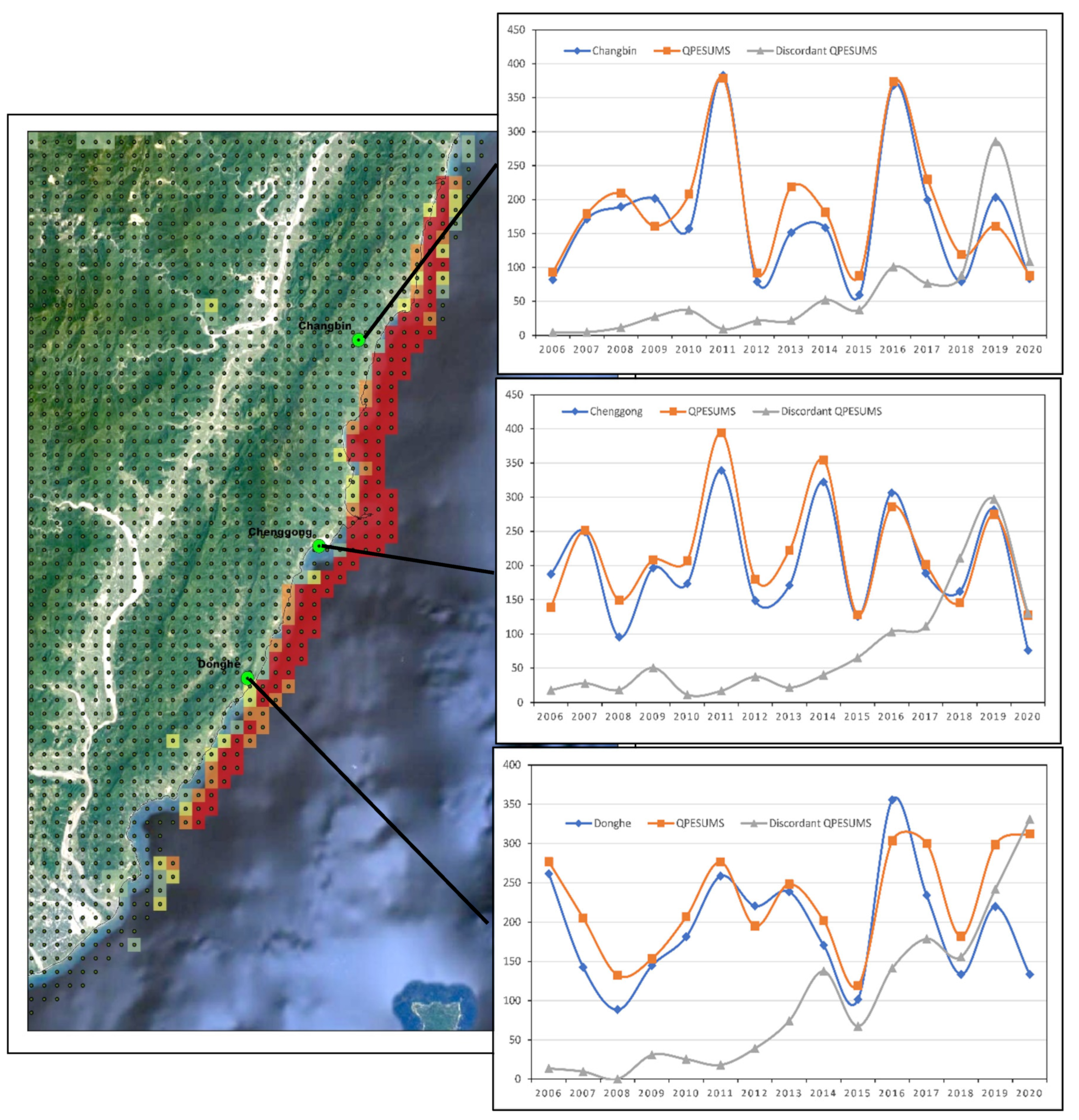
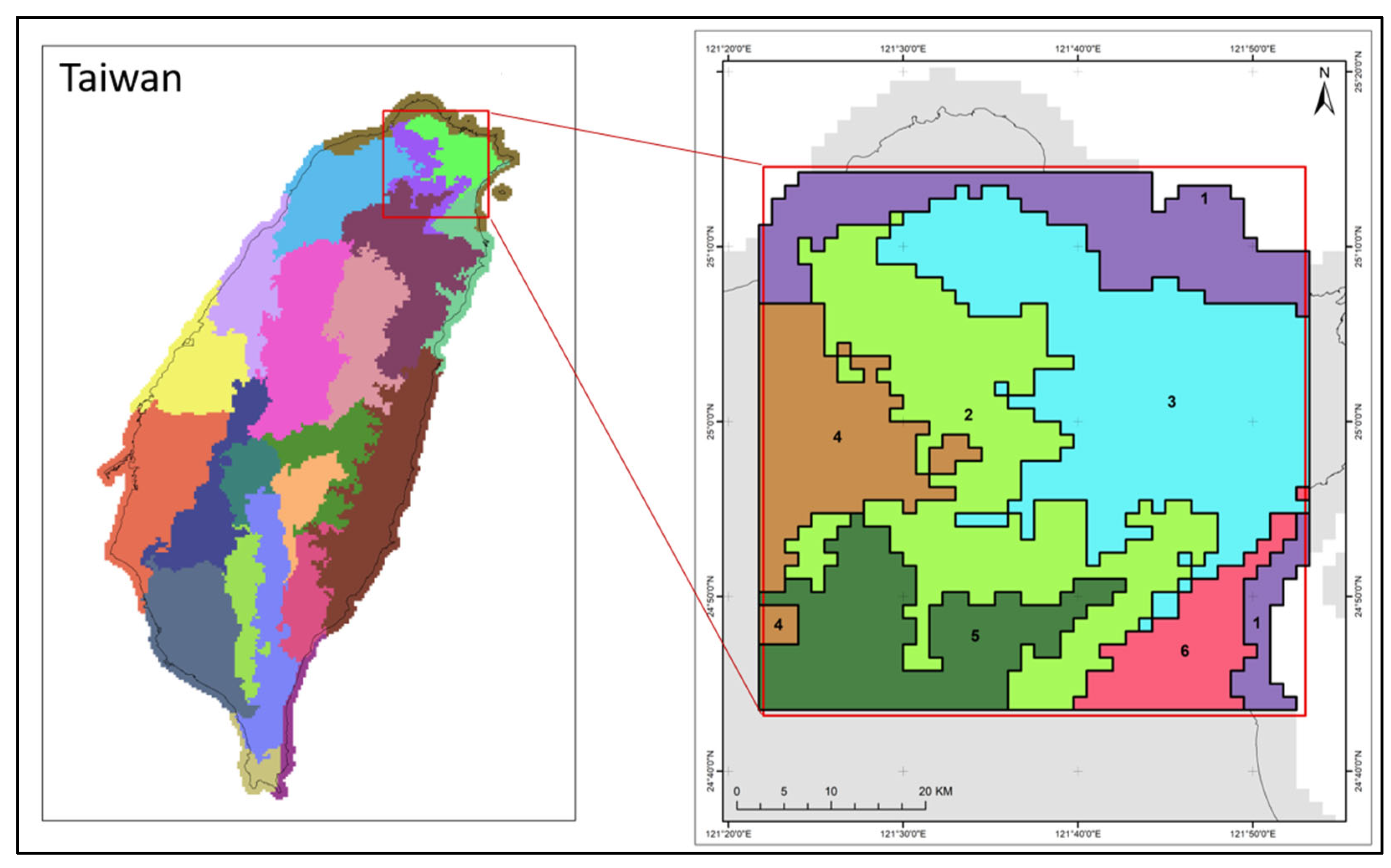
3.8. Small-Scale Spatial Investigation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Overeem, A. Climatology of Extreme Rainfall from Rain Gauges and Weather Radar; Wageningen University: Wageningen, The Netherlands, 2009. [Google Scholar]
- Chang’A, L.B.; Kijazi, A.L.; Mafuru, K.B.; Nying’Uro, P.A.; Ssemujju, M.; Deus, B.; Kondowe, A.L.; Yonah, I.B.; Ngwali, M.; Kisama, S.Y.; et al. Understanding the Evolution and Socio-Economic Impacts of the Extreme Rainfall Events in March-May 2017 to 2020 in East Africa. Atmos. Clim. Sci. 2020, 10, 553–572. [Google Scholar] [CrossRef]
- Rahman, H.T.; Mia, E.; Ford, J.D.; Robinson, B.E.; Hickey, G.M. Livelihood exposure to climatic stresses in the north-eastern floodplains of Bangladesh. Land Use Policy 2018, 79, 199–214. [Google Scholar] [CrossRef]
- Wei, L.; Hu, K.-H.; Hu, X.-D. Rainfall occurrence and its relation to flood damage in China from 2000 to 2015. J. Mt. Sci. 2018, 15, 2492–2504. [Google Scholar] [CrossRef]
- Alias, N.E.B. Improving Extreme Precipitation Estimates Considering Regional Frequency Analysis. Ph.D. Thesis, Kyoto University, Kyoto, Japan, 2014. [Google Scholar] [CrossRef]
- Liu, J.; Doan, C.D.; Liong, S.-Y.; Sanders, R.; Dao, A.T.; Fewtrell, T. Regional frequency analysis of extreme rainfall events in Jakarta. Nat. Hazards 2015, 75, 1075–1104. [Google Scholar] [CrossRef]
- Feng, Z.; Leung, L.R.; Hagos, S.; Houze, R.A.; Burleyson, C.D.; Balaguru, K. More frequent intense and long-lived storms dominate the springtime trend in central US rainfall. Nat. Commun. 2016, 7, 13429. [Google Scholar] [CrossRef]
- Fawad, M.; Yan, T.; Chen, L.; Huang, K.; Singh, V.P. Multiparameter probability distributions for at-site frequency analysis of annual maximum wind speed with L-Moments for parameter estimation. Energy 2019, 181, 724–737. [Google Scholar] [CrossRef]
- Harka, A.E.; Jilo, N.B.; Behulu, F. Spatial-temporal rainfall trend and variability assessment in the Upper Wabe Shebelle River Basin, Ethiopia: Application of innovative trend analysis method. J. Hydrol. Reg. Stud. 2021, 37, 100915. [Google Scholar] [CrossRef]
- Kim, D.-I.; Han, D.; Lee, T. Reanalysis Product-Based Nonstationary Frequency Analysis for Estimating Extreme Design Rainfall. Atmosphere 2021, 12, 191. [Google Scholar] [CrossRef]
- Tung, Y.-S.; Wang, C.-Y.; Weng, S.-P.; Yang, C.-D. Extreme index trends of daily gridded rainfall dataset (1960–2017) in Taiwan. Terr. Atmos. Ocean. Sci. 2022, 33, 8. [Google Scholar] [CrossRef]
- Mamoon, A.A.; Rahman, A. Uncertainty Analysis in Design Rainfall Estimation Due to Limited Data Length: A Case Study in Qatar. In Extreme Hydrology and Climate Variability; Elsevier Inc.: Amsterdam, The Netherlands, 2019. [Google Scholar] [CrossRef]
- Su, B.; Kundzewicz, Z.; Jiang, T. Simulation of extreme precipitation over the Yangtze River Basin using Wakeby distribution. Theor. Appl. Climatol. 2009, 96, 209–219. [Google Scholar] [CrossRef]
- Gaál, L.; Kyselý, J.; Szolgay, J. Region-of-influence approach to a frequency analysis of heavy precipitation in Slovakia. Hydrol. Earth Syst. Sci. 2008, 12, 825–839. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Landwehr, J.M.; Matalas, N.C.; Wallis, J.R. Probability weighted moments: Definition and relation to parameters of several distributions expressable in inverse form. Water Resour. Res. 1979, 15, 1049–1054. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-Moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics. J. R. Stat. Soc. Ser. B (Methodol.) 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Eldardiry, H.; Habib, E. Examining the Robustness of a Spatial Bootstrap Regional Approach for Radar-Based Hourly Precipitation Frequency Analysis. Remote Sens. 2020, 12, 3767. [Google Scholar] [CrossRef]
- Li, M.; Li, X.; Ao, T. Comparative Study of Regional Frequency Analysis and Traditional At-Site Hydrological Frequency Analysis. Water 2019, 11, 486. [Google Scholar] [CrossRef]
- Gaál, L.; Kyselý, J. Comparison of region-of-influence methods for estimating high quantiles of precipitation in a dense dataset in the Czech Republic. Hydrol. Earth Syst. Sci. 2009, 13, 2203–2219. [Google Scholar] [CrossRef]
- Malekinezhad, H.; Nachtnebel, H.; Klik, A. Comparing the index-flood and multiple-regression methods using L-moments. Phys. Chem. Earth Parts A/B/C 2011, 36, 54–60. [Google Scholar] [CrossRef]
- Gado, T.; Hsu, K.; Sorooshian, S. Rainfall frequency analysis for ungauged sites using satellite precipitation products. J. Hydrol. 2017, 554, 646–655. [Google Scholar] [CrossRef]
- Modarres, R.; Sarhadi, A. Statistically-based regionalization of rainfall climates of Iran. Glob. Planet. Chang. 2011, 75, 67–75. [Google Scholar] [CrossRef]
- Santos, M.; Fragoso, M.; Santos, J.A. Regionalization and susceptibility assessment to daily precipitation extremes in mainland Portugal. Appl. Geogr. 2017, 86, 128–138. [Google Scholar] [CrossRef]
- Yin, Y.; Chen, H.; Xu, C.-Y.; Xu, W.; Chen, C.; Sun, S. Spatio-temporal characteristics of the extreme precipitation by L-moment-based index-flood method in the Yangtze River Delta region, China. Theor. Appl. Climatol. 2016, 124, 1005–1022. [Google Scholar] [CrossRef]
- Mulaomerović-Šeta, A.; Blagojević, B.; Imširović, Š.; Nedić, B. Assessment of Regional Analyses Methods for Spatial Interpolation of Flood Quantiles in the Basins of Bosnia and Herzegovina and Serbia. In Lecture Notes in Networks and Systems; Springer: Berlin, Germany, 2022; Volume 316. [Google Scholar] [CrossRef]
- Overeem, A.; Buishand, T.A.; Holleman, I. Extreme rainfall analysis and estimation of depth-duration-frequency curves using weather radar. Water Resour. Res. 2009, 45, W10424. [Google Scholar] [CrossRef]
- Sarmadi, F.; Shokoohi, A. Regionalizing precipitation in Iran using GPCC gridded data via multivariate analysis and L-moment methods. Theor. Appl. Climatol. 2015, 122, 121–128. [Google Scholar] [CrossRef]
- Goudenhoofdt, E.; Delobbe, L.; Willems, P. Regional frequency analysis of extreme rainfall in Belgium based on radar estimates. Hydrol. Earth Syst. Sci. 2017, 21, 5385–5399. [Google Scholar] [CrossRef]
- Yeh, H.-F.; Chang, C.-F. Using Standardized Groundwater Index and Standardized Precipitation Index to Assess Drought Characteristics of the Kaoping River Basin, Taiwan. Water Resour. 2019, 46, 670–678. [Google Scholar] [CrossRef]
- Wu, C.-C.; Kuo, Y.-H. Typhoons Affecting Taiwan: Current Understanding and Future Challenges. Bull. Am. Meteorol. Soc. 1999, 80, 67–80. [Google Scholar] [CrossRef]
- Chen, H.-W.; Chen, C.-Y. Warning Models for Landslide and Channelized Debris Flow under Climate Change Conditions in Taiwan. Water 2022, 14, 695. [Google Scholar] [CrossRef]
- Chang, F.-J.; Chiang, Y.-M.; Tsai, M.-J.; Shieh, M.-C.; Hsu, K.-L.; Sorooshian, S. Watershed rainfall forecasting using neuro-fuzzy networks with the assimilation of multi-sensor information. J. Hydrol. 2014, 508, 374–384. [Google Scholar] [CrossRef]
- Chiou, P.T.; Chen, C.-R.; Chang, P.-L.; Jian, G.-J. Status and outlook of very short range forecasting system in Central Weather Bureau, Taiwan. In Applications with Weather Satellites II; SPIE: Washington, DC, USA, 2005; pp. 185–196. [Google Scholar] [CrossRef]
- Chang, R.-C.; Tsai, T.-S.; Yao, L. Intelligent Rainfall Monitoring System for Efficient Electric Power Transmission. In Information Technology Convergence; Springer: Dordrecht, The Netherlands, 2013; pp. 773–782. [Google Scholar] [CrossRef]
- Neykov, N.M.; Neytchev, P.N.; Van Gelder, P.H.A.J.M.; Todorov, V.K. Robust detection of discordant sites in regional frequency analysis. Water Resour. Res. 2007, 43, W06417. [Google Scholar] [CrossRef]
- Hosking, J.R.M. Regional Frequency Analysis Using L-Moments. 2019. Available online: https://cran.r-project.org/package=lmomRFA (accessed on 12 July 2021).
- Lin, G.-F.; Chen, L.-H. Identification of homogeneous regions for regional frequency analysis using the self-organizing map. J. Hydrol. 2006, 324, 1–9. [Google Scholar] [CrossRef]
- Alem, A.M.; Tilahun, S.A.; Moges, M.A.; Melesse, A.M. A regional hourly maximum rainfall extraction method for part of Upper Blue Nile Basin, Ethiopia. In Extreme Hydrology and Climate Variability; Elsevier: Amsterdam, The Netherlands, 2019; pp. 93–102. [Google Scholar] [CrossRef]
- Rao, A.R.; Srinivas, S.S. Regionalization of Watersheds: An Approach Based on Cluster Analysis; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar] [CrossRef]
- Abdi, A.; Hassanzadeh, Y.; Talatahari, S.; Fakheri-Fard, A.; Mirabbasi, R. Regional drought frequency analysis using L-moments and adjusted charged system search. J. Hydroinformatics 2017, 19, 426–442. [Google Scholar] [CrossRef]
- Wright, M.J.; Houck, M.H.; Ferreira, C.M. Discriminatory Power of Heterogeneity Statistics with Respect to Error of Precipitation Quantile Estimation. J. Hydrol. Eng. 2015, 20, 04015011. [Google Scholar] [CrossRef]
- Khan, S.A.; Hussain, I.; Hussain, T.; Faisal, M.; Muhammad, Y.S.; Shoukry, A.M. Regional Frequency Analysis of Extremes Precipitation Using L-Moments and Partial L-Moments. Adv. Meteorol. 2017, 2017, 6954902. [Google Scholar] [CrossRef]
- Busababodhin, P.; Seo, Y.A.; Park, J.-S.; Kumphon, B.-O. LH-moment estimation of Wakeby distribution with hydrological applications. Stoch. Environ. Res. Risk Assess. 2016, 30, 1757–1767. [Google Scholar] [CrossRef]
- Rahman, M.; Hassan, R.; Buyya, R. Jaccard Index based availability prediction in enterprise grids. Procedia Comput. Sci. 2010, 1, 2707–2716. [Google Scholar] [CrossRef]
- Chang, P.-L.; Zhang, J.; Tang, Y.-S.; Tang, L.; Lin, P.-F.; Langston, C.; Kaney, B.; Chen, C.-R.; Howard, K. An Operational Multi-Radar Multi-Sensor QPE System in Taiwan. Bull. Am. Meteorol. Soc. 2021, 102, E555–E577. [Google Scholar] [CrossRef]
- Hu, C.; Xia, J.; She, D.; Xu, C.; Zhang, L.; Song, Z.; Zhao, L. A modified regional L-moment method for regional extreme precipitation frequency analysis in the Songliao River Basin of China. Atmos. Res. 2019, 230, 104629. [Google Scholar] [CrossRef]
- Chen, L.-H.; Hong, Y.-T. Regional Taiwan rainfall frequency analysis using principal component analysis, self-organizing maps and L-moments. Hydrol. Res. 2012, 43, 275–285. [Google Scholar] [CrossRef]
- Szolgay, J.; Parajka, J.; Kohnová, S.; Hlavčová, K. Comparison of mapping approaches of design annual maximum daily precipitation. Atmos. Res. 2009, 92, 289–307. [Google Scholar] [CrossRef]
- Rossi, F.; Fiorentino, M.; Versace, P. Two-Component Extreme Value Distribution for Flood Frequency Analysis. Water Resour. Res. 1984, 20, 847–856. [Google Scholar] [CrossRef]
- Gabriele, S.; Arnell, N. A hierarchical approach to regional flood frequency analysis. Water Resour. Res. 1991, 27, 1281–1289. [Google Scholar] [CrossRef]
- De Luca, D.L.; Galasso, L. Stationary and Non-Stationary Frameworks for Extreme Rainfall Time Series in Southern Italy. Water 2018, 10, 1477. [Google Scholar] [CrossRef] [Green Version]
- Hao, W.; Hao, Z.; Yuan, F.; Ju, Q.; Hao, J. Regional Frequency Analysis of Precipitation Extremes and Its Spatio-Temporal Patterns in the Hanjiang River Basin, China. Atmosphere 2019, 10, 130. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente-Serrano, S.M. Mapping the Hazard of Extreme Rainfall by Peaks over Threshold Extreme Value Analysis and Spatial Regression Techniques. J. Appl. Meteorol. Clim. 2006, 45, 108–124. [Google Scholar] [CrossRef]
- Prudhomme, C.; Reed, D.W. Mapping Extreme Rainfall in a Mountainous Region Using Geostatistical Techniques: A Case Study in Scotland. Int. J. Climatol. 1999, 19, 1337–1356. [Google Scholar] [CrossRef]
- Su, S.-H.; Kuo, H.-C.; Hsu, L.-H.; Yang, Y.-T. Temporal and Spatial Characteristics of Typhoon Extreme Rainfall in Taiwan. J. Meteorol. Soc. Jpn. Ser. II 2012, 90, 721–736. [Google Scholar] [CrossRef]
- Malekinezhad, H.; Zare-Garizi, A. Regional frequency analysis of daily rainfall extremes using L-moments approach. Atmósfera 2014, 27, 411–427. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, Z.; Lai, C.; Lin, W.; Wu, X.; Chen, X. A regional frequency analysis of precipitation extremes in Mainland China with fuzzy c-means and L-moments approaches. Int. J. Clim. 2017, 37, 429–444. [Google Scholar] [CrossRef]



| Region/Sub-Region | Number of Grids | L-Moment Ratios | H1 | ||
|---|---|---|---|---|---|
| t | t_3 | t_4 | |||
| North | |||||
| 1 | 711 | 0.33 | 0.24 | 0.17 | −2.01 |
| 2 | 453 | 0.22 | 0.21 | 0.11 | −0.62 |
| 3 | 509 | 0.19 | 0.18 | 0.15 | −0.67 |
| 4 | 1359 | 0.25 | 0.28 | 0.17 | −0.14 |
| 5 | 1806 | 0.28 | 0.15 | 0.10 | −1.86 |
| 6 | 606 | 0.24 | 0.20 | 0.16 | −1.27 |
| West | |||||
| 7 | 980 | 0.32 | 0.34 | 0.17 | −5.83 |
| 8 | 1186 | 0.26 | 0.19 | 0.10 | −5.33 |
| 9 | 1961 | 0.27 | 0.26 | 0.20 | −7.71 |
| 10 | 1150 | 0.26 | 0.25 | 0.14 | 0.85 |
| Center | |||||
| 11 | 1938 | 0.32 | 0.29 | 0.08 | −4.97 |
| 12 | 1344 | 0.25 | 0.11 | 0.10 | −4.90 |
| 13 | 826 | 0.23 | 0.00 | 0.06 | −6.01 |
| 14 | 474 | 0.22 | 0.07 | 0.05 | −1.19 |
| 15 | 567 | 0.17 | 0.11 | 0.20 | −6.87 |
| East | |||||
| 16 | 2231 | 0.25 | 0.08 | 0.06 | −5.21 |
| 17 | 652 | 0.25 | 0.17 | 0.09 | 0.07 |
| South | |||||
| 18 | 1629 | 0.19 | 0.09 | 0.12 | −3.63 |
| 19 | 609 | 0.16 | 0.10 | 0.12 | −6.49 |
| 20 | 1283 | 0.16 | 0.05 | 0.08 | −3.25 |
| 21 | 265 | 0.25 | 0.20 | 0.07 | −2.55 |
| 22 | 248 | 0.35 | 0.30 | 0.14 | 0.92 |
| Reg | Goodness-of-Fit Measures | Best Fit Distribution | Parameter Estimates for Distributions Accepted at the 0.90 Level | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| GLO | GEV | GNO | PE3 | GPA | ξ/μ | α/σ | K/β | γ | δ | ||
| North | |||||||||||
| 1 | 7.44 | 0.61 | −2.28 | −7.59 | −16.25 | GEV | 0.71 | 0.42 | −0.11 | ||
| 2 | 18.58 | 11.54 | 9.70 | 5.99 | −4.92 | WAK | 0.48 | 0.68 | 0.32 | 0.00 | 0.00 |
| 3 | 7.45 | −0.08 | −1.17 | −3.90 | −16.92 | GEV | 0.84 | 0.27 | −0.01 | ||
| 4 | 13.00 | 5.05 | −0.08 | −9.14 | −15.97 | GNO | 0.88 | 0.38 | −0.58 | ||
| 5 | 34.65 | 17.03 | 16.09 | 11.85 | −20.90 | WAK | 0.30 | 1.04 | 0.49 | 0.00 | 0.00 |
| 6 | 5.87 | −1.60 | −3.35 | −7.00 | −18.90 | GEV | 0.79 | 0.33 | −0.05 | ||
| West | |||||||||||
| 7 | 19.51 | 14.45 | 8.66 | −1.41 | −0.68 | GPA | 0.37 | 0.62 | −0.02 | ||
| 8 | 31.21 | 18.77 | 16.39 | 11.10 | −9.58 | WAK | 0.35 | 0.58 | 2.62 | 0.58 | −0.17 |
| 9 | 1.52 | −7.88 | −13.01 | −22.24 | −33.28 | GLO | 0.89 | 0.24 | −0.26 | ||
| 10 | 19.89 | 11.13 | 7.17 | −0.05 | −10.72 | PE3 | 1.00 | 0.50 | 1.48 | ||
| Center | |||||||||||
| 11 | 63.27 | 53.04 | 45.54 | 32.36 | 25.38 | WAK | 0.32 | 0.74 | 0.10 | 0.00 | 0.00 |
| 12 | 30.61 | 13.51 | 14.22 | 11.95 | −21.70 | WAK | 0.24 | 2.03 | 7.43 | 0.70 | −0.34 |
| 13 | 35.70 | 16.95 | 21.79 | 21.79 | −16.88 | WAK | 0.18 | 2.61 | 8.57 | 0.92 | −0.69 |
| 14 | 29.02 | 16.95 | 18.71 | 18.19 | −6.53 | WAK | 0.36 | 0.92 | 1.90 | 0.42 | −0.30 |
| 15 | −11.39 | −20.36 | −19.99 | −21.20 | −38.83 | WAK | 0.40 | 2.43 | 5.54 | 0.20 | 0.11 |
| East | |||||||||||
| 16 | 56.21 | 32.30 | 34.29 | 32.08 | −15.90 | WAK | 0.26 | 1.17 | 5.37 | 0.83 | −0.50 |
| 17 | 24.58 | 14.92 | 13.61 | 10.26 | −6.62 | WAK | 0.36 | 0.56 | 2.58 | 0.58 | −0.21 |
| South | |||||||||||
| 18 | 23.65 | 1.61 | 5.38 | 3.62 | −36.65 | GEV | 0.86 | 0.30 | 0.12 | ||
| 19 | 12.97 | 1.83 | 2.73 | 1.61 | −20.65 | PE3 | 1.00 | 0.29 | 0.60 | ||
| 20 | 37.51 | 16.77 | 20.29 | 19.72 | −23.01 | WAK | 0.50 | 1.00 | 2.47 | 0.25 | −0.16 |
| 21 | 20.74 | 14.78 | 13.42 | 10.58 | 1.01 | GPA | 0.41 | 0.79 | 0.34 | ||
| 22 | 13.01 | 9.74 | 7.04 | 2.33 | 0.68 | GPA | 0.28 | 0.77 | 0.07 | ||
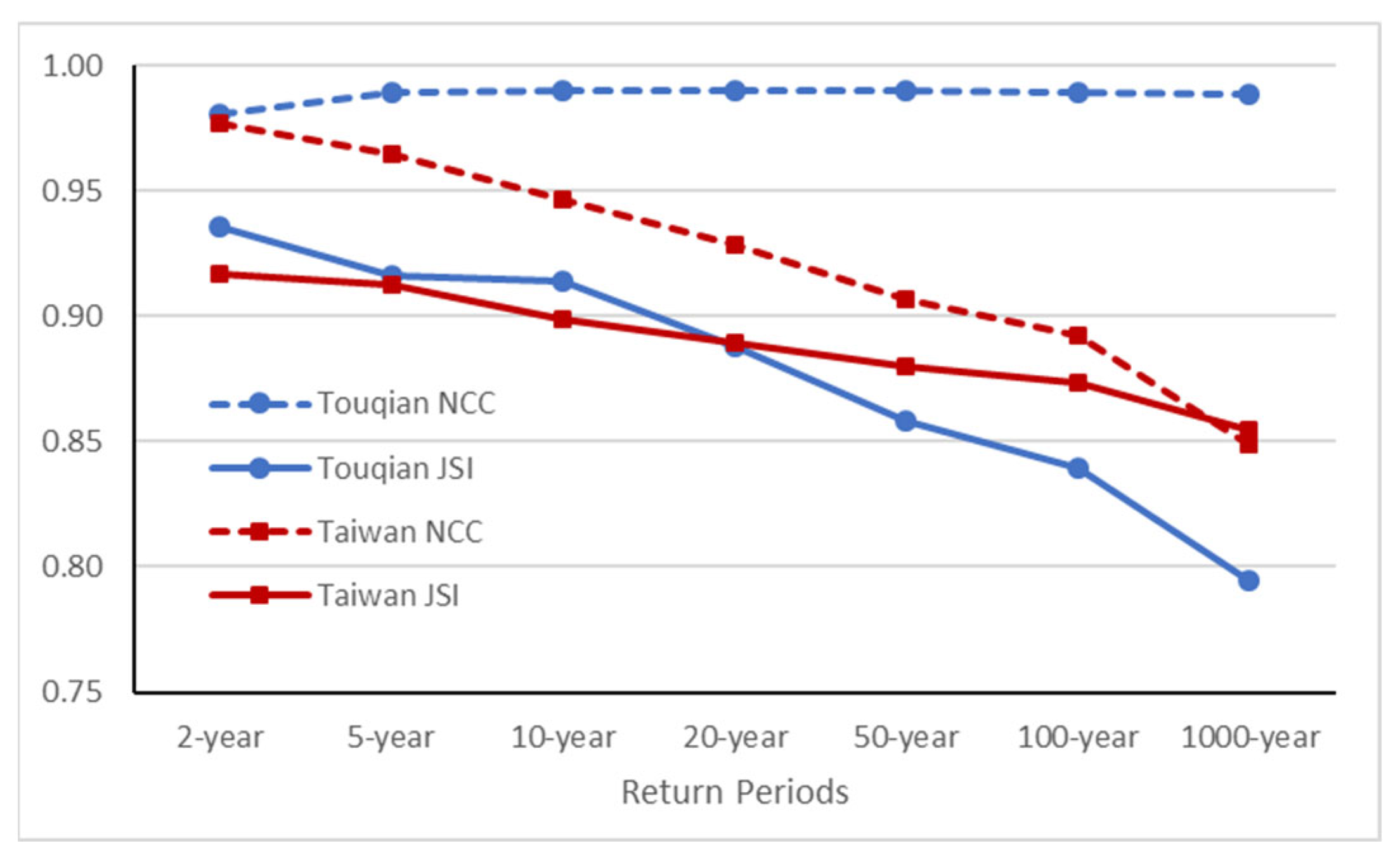
| Return Period | Touqian | Taiwan | ||
|---|---|---|---|---|
| NCC | JSI | NCC | JSI | |
| 2-year | 0.980 | 0.935 | 0.977 | 0.917 |
| 5-year | 0.989 | 0.916 | 0.965 | 0.912 |
| 10-year | 0.990 | 0.914 | 0.946 | 0.899 |
| 20-year | 0.990 | 0.888 | 0.929 | 0.890 |
| 50-year | 0.990 | 0.858 | 0.907 | 0.880 |
| 100-year | 0.989 | 0.839 | 0.892 | 0.874 |
| 1000-year | 0.988 | 0.795 | 0.849 | 0.855 |
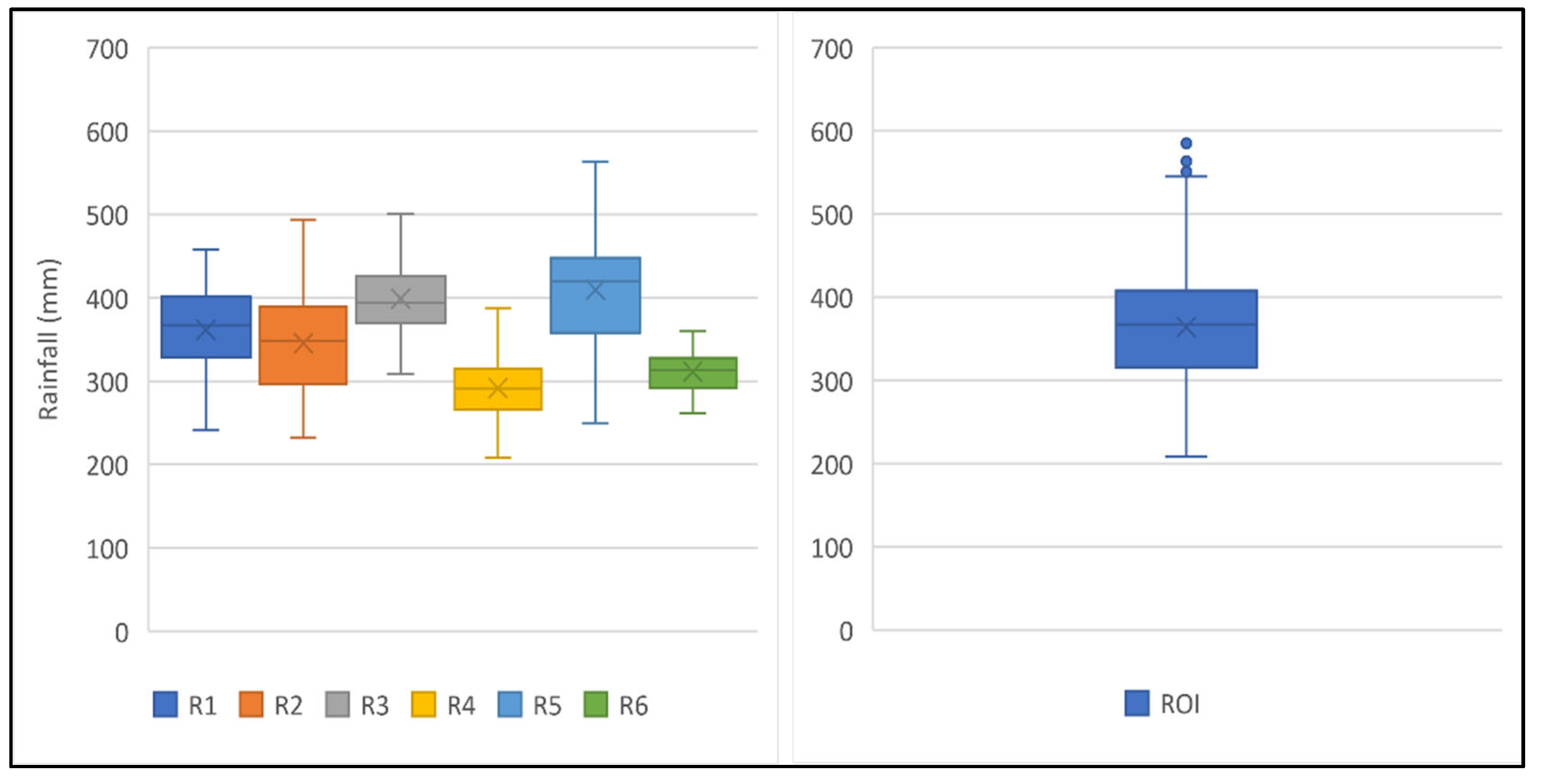
| Sub-Region | Region of Interest | Whole ROI | ||||
|---|---|---|---|---|---|---|
| Mean | Std Dev | CV | Mean | Std Dev | CV | |
| 1 | 361.51 | 49.78 | 13.77 | 363.95 | 67.23 | 18.47 |
| 2 | 345.39 | 59.00 | 17.08 | |||
| 3 | 399.03 | 38.45 | 9.64 | |||
| 4 | 291.57 | 35.03 | 12.01 | |||
| 5 | 409.32 | 63.94 | 15.62 | |||
| 6 | 311.17 | 23.14 | 7.44 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, C.-H.; Rahmad, R.; Wu, S.-J.; Hsu, C.-T. Spatial Frequency Analysis by Adopting Regional Analysis with Radar Rainfall in Taiwan. Water 2022, 14, 2710. https://doi.org/10.3390/w14172710
Chang C-H, Rahmad R, Wu S-J, Hsu C-T. Spatial Frequency Analysis by Adopting Regional Analysis with Radar Rainfall in Taiwan. Water. 2022; 14(17):2710. https://doi.org/10.3390/w14172710
Chicago/Turabian StyleChang, Che-Hao, Riki Rahmad, Shiang-Jen Wu, and Chih-Tsung Hsu. 2022. "Spatial Frequency Analysis by Adopting Regional Analysis with Radar Rainfall in Taiwan" Water 14, no. 17: 2710. https://doi.org/10.3390/w14172710






