Mapping of a Novel Zero-Liquid Discharge Desalination System Based on Humidification–Dehumidification onto the Field of Existing Desalination Technologies
Abstract
:1. Introduction
- A mathematical model for the proposed STEWARD system used to bound operational space through physical conservation laws and to estimate the thermodynamic states at each point of the desalination process;
- A sensitivity analysis highlighting the engineering tradeoffs associated with variations in product flow rate and feed salinity;
- An evaluation of the practical implications related to deploying the STEWARD system to potentially replace existing desalination plants or complement brine processing;
- Identification of deployment opportunities for STEWARD within the current operational space of existing desalination technologies.
2. Methodology
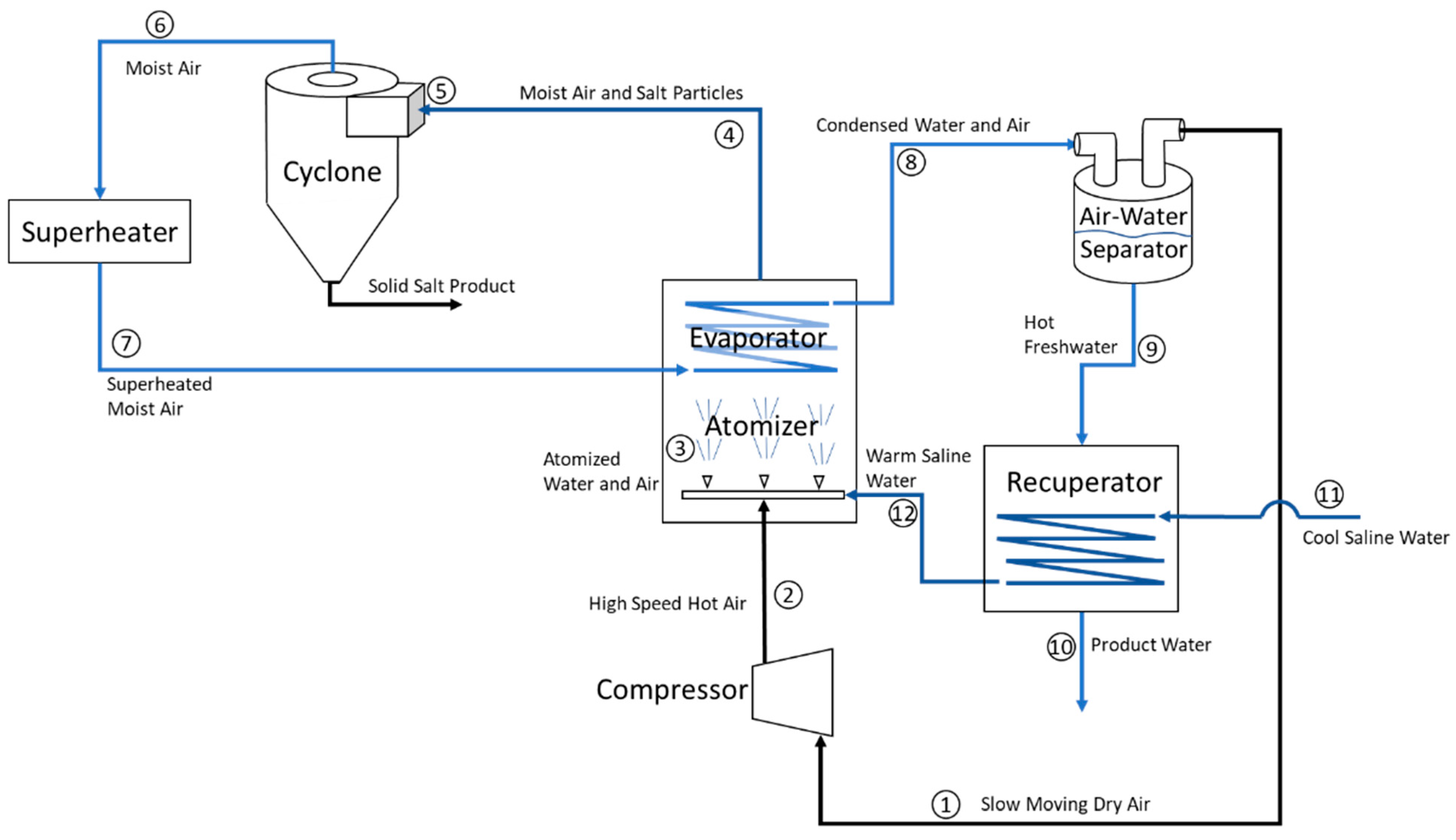
2.1. Overall System Description
2.2. Model Description
- The partial pressure of water ( is defined by and , which must be lower than to result in a positive humidity ratio:
- State 4 is calculated through an iterative algorithm that finds such that the resulting humidity ratio matches that of full evaporation of the warm saline water stream (. To guarantee heat transfer and full evaporation, must be slightly greater than , and thus, the checkpoint follows that:
- It has been determined that expansion cooling of the gas and cooling of the liquid through heat transfer are minimal during atomization processes, especially at fast discharges [27]. Therefore, the total enthalpy of the high-speed hot air and warm saline water streams before and after atomization mixing must remain equal or slightly lower due to losses in local evaporation and breaking of water droplets. The implemented checkpoint therefore ensures that is between 0 and 8% lower than the addition of the enthalpies in the streams preceding the atomizer such that:
- The superheated moist air temperature is an input to the model and must be larger than the calculated temperature at the evaporator outlet per the second law of thermodynamics. Furthermore, the temperature at the evaporator outlet must be lower than the temperature of the condensed water-and-air stream leaving the condenser. Therefore, the implemented checkpoint verifies that:
- The heat available on the condensing side of the evaporator must be greater than the heat required to complete evaporation . This condition checks that at minimum:
3. Results
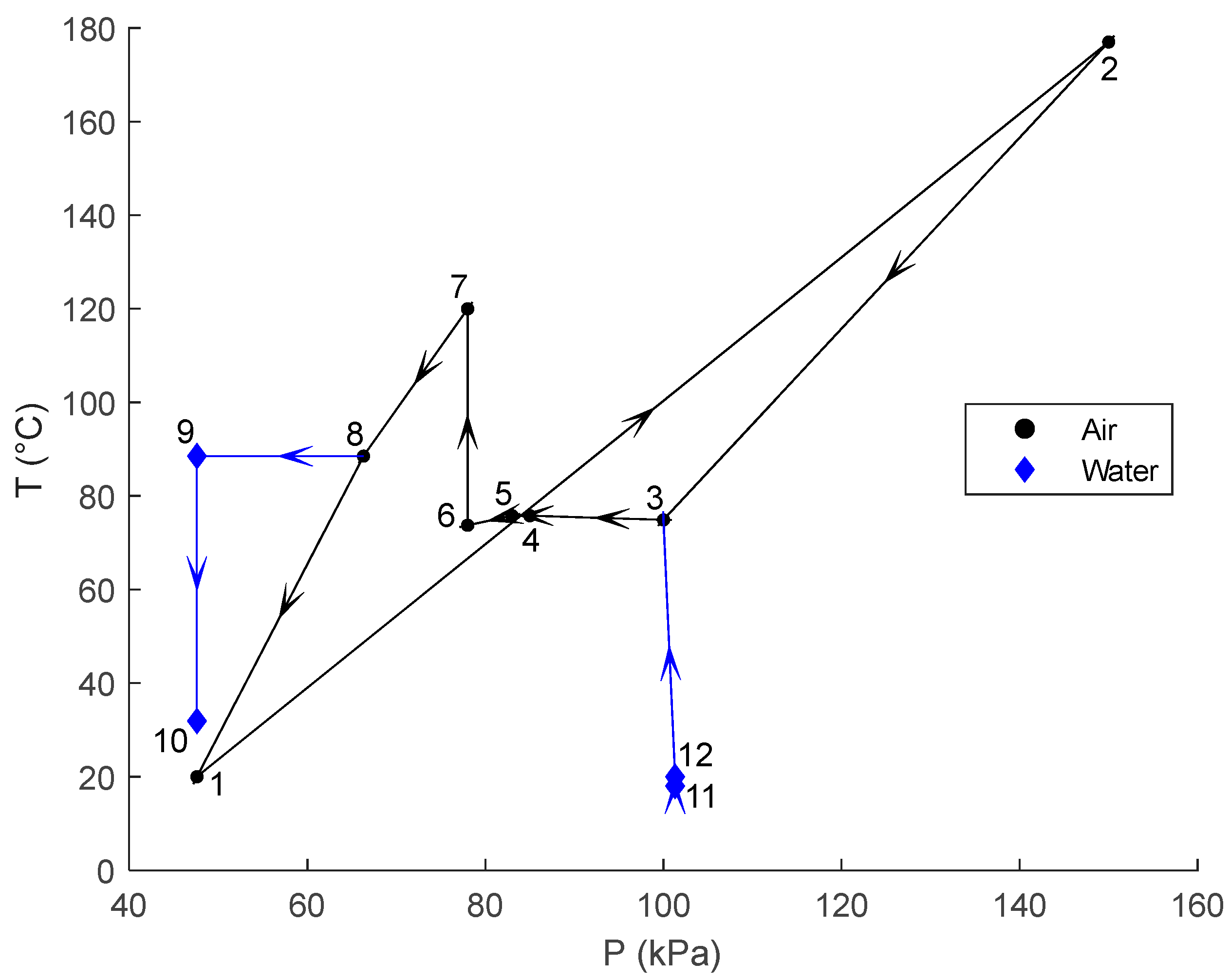
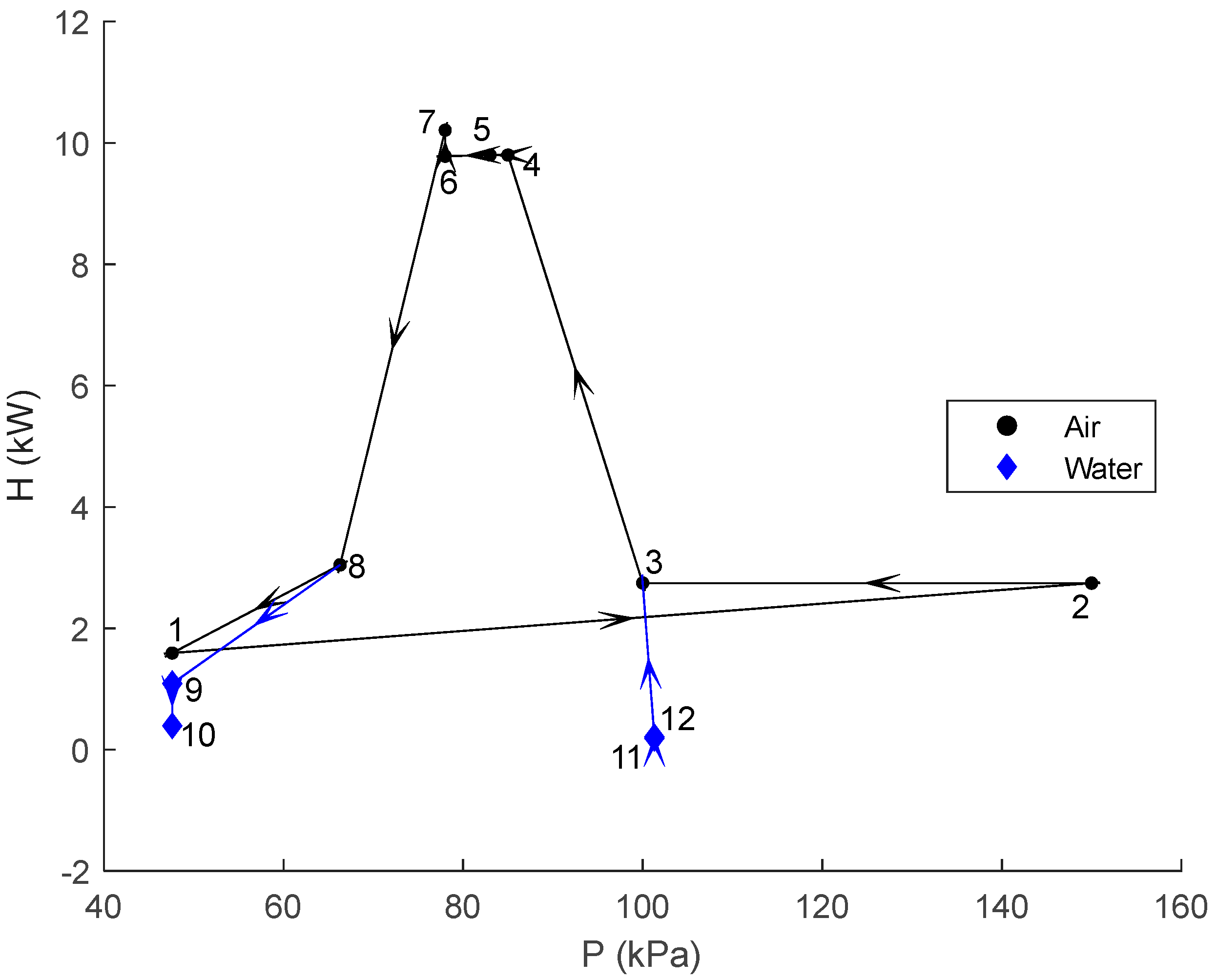
3.1. Baseline Operation
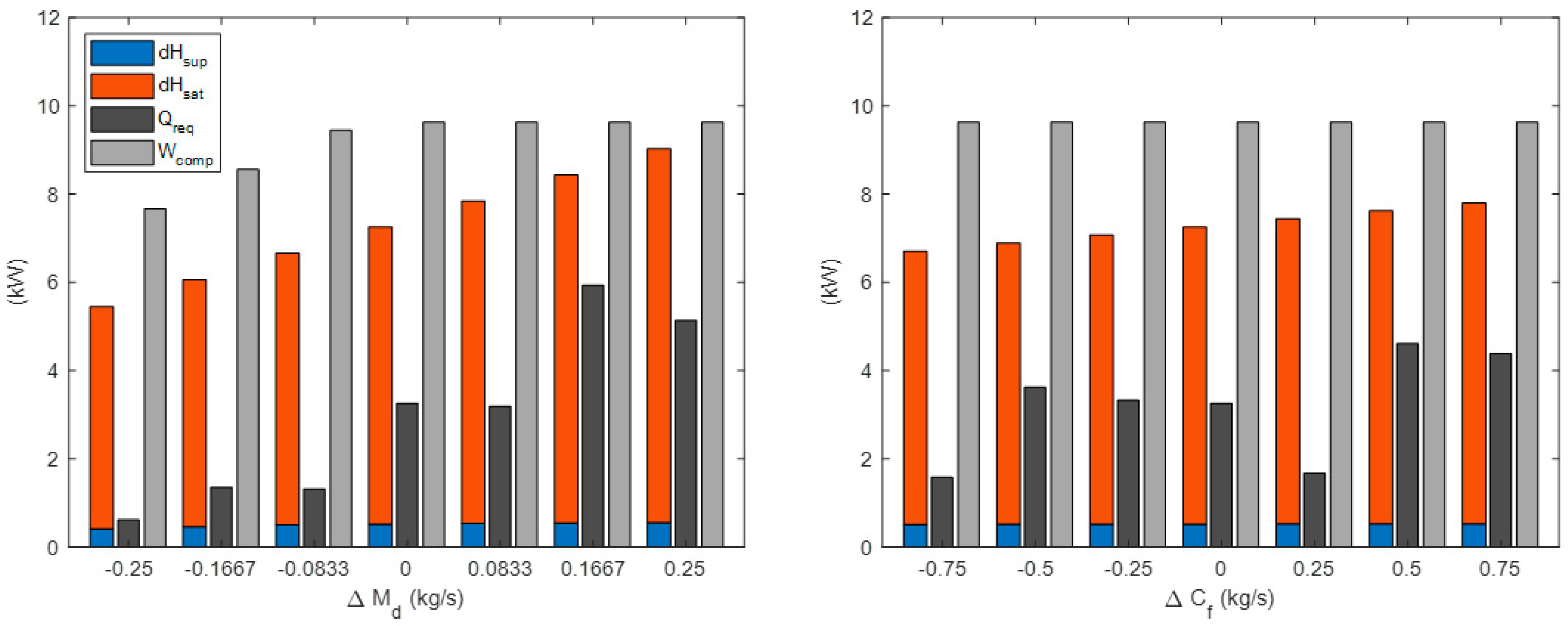
3.2. Sensitivity Analysis
4. Discussion
4.1. Practical Operation
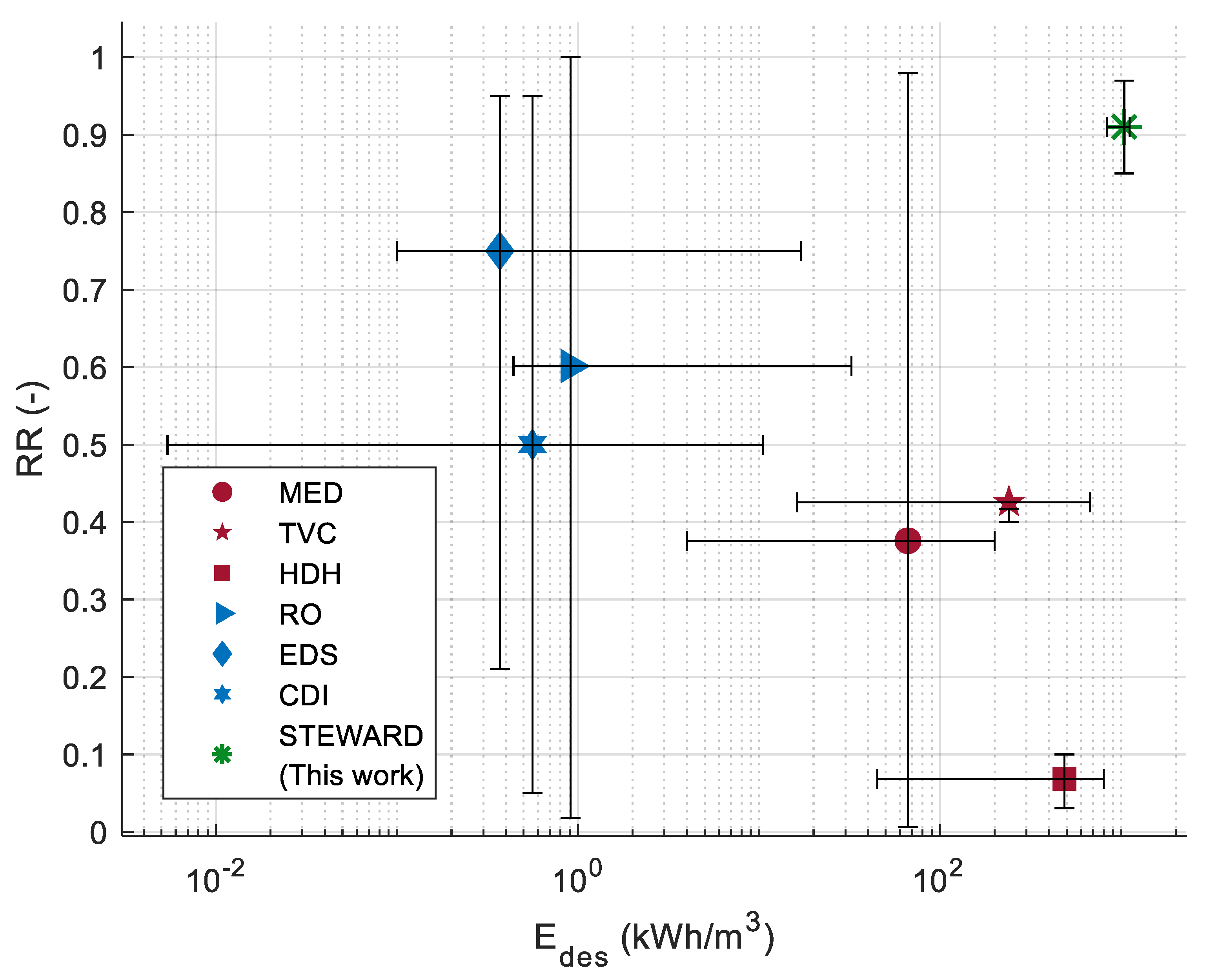
4.2. Operational Map
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahmed, F.E.; Khalil, A.; Hilal, N. Emerging Desalination Technologies: Current Status, Challenges and Future Trends. Desalination 2021, 517, 115183. [Google Scholar] [CrossRef]
- Lin, S.; Zhao, H.; Zhu, L.; He, T.; Chen, S.; Gao, C.; Zhang, L. Seawater Desalination Technology and Engineering in China: A Review. Desalination 2021, 498, 114728. [Google Scholar] [CrossRef]
- Al-Ahmad, M.; Aleem, F.A. Scale Formation and Fouling Problems and Their Predicted Reflection on the Performance of Desalination Plants in Saudi Arabia. Desalination 1994, 96, 409–419. [Google Scholar] [CrossRef]
- Mavukkandy, M.O.; Chabib, C.M.; Mustafa, I.; Al Ghaferi, A.; AlMarzooqi, F. Brine Management in Desalination Industry: From Waste to Resources Generation. Desalination 2019, 472, 114187. [Google Scholar] [CrossRef]
- Antony, A.; Low, J.H.; Gray, S.; Childress, A.E.; Le-Clech, P.; Leslie, G. Scale Formation and Control in High Pressure Membrane Water Treatment Systems: A Review. J. Memb. Sci. 2011, 383, 1–16. [Google Scholar] [CrossRef]
- Al-Karaghouli, A.; Kazmerski, L.L. Energy Consumption and Water Production Cost of Conventional and Renewable-Energy-Powered Desalination Processes. Renew. Sustain. Energy Rev. 2013, 24, 343–356. [Google Scholar] [CrossRef]
- Wenten, I.G.; Aryanti, P.T.P.; Hakim, A.N. Scale-up Strategies for Membrane-Based Desalination Processes: A Review. J. Membr. Sci. Res. 2016, 2, 42–58. [Google Scholar] [CrossRef]
- Sutzkover-Gutman, I.; Hasson, D. Feed Water Pretreatment for Desalination Plants. Desalination 2010, 264, 289–296. [Google Scholar] [CrossRef]
- Kavitha, J.; Rajalakshmi, M.; Phani, A.R.; Padaki, M. Pretreatment Processes for Seawater Reverse Osmosis Desalination Systems—A Review. J. Water Process Eng. 2019, 32, 100926. [Google Scholar] [CrossRef]
- Goh, P.S.; Lau, W.J.; Othman, M.H.D.; Ismail, A.F. Membrane Fouling in Desalination and Its Mitigation Strategies. Desalination 2018, 425, 130–155. [Google Scholar] [CrossRef]
- She, Q.; Wang, R.; Fane, A.G.; Tang, C.Y. Membrane Fouling in Osmotically Driven Membrane Processes: A Review. J. Memb. Sci. 2016, 499, 201–233. [Google Scholar] [CrossRef]
- Hoek, E.M.V.; Allred, J.; Knoell, T.; Jeong, B.-H. Modeling the Effects of Fouling on Full-Scale Reverse Osmosis Processes. J. Memb. Sci. 2008, 314, 33–49. [Google Scholar] [CrossRef]
- Jafari, M.; Vanoppen, M.; van Agtmaal, J.M.C.; Cornelissen, E.R.; Vrouwenvelder, J.S.; Verliefde, A.; van Loosdrecht, M.C.M.; Picioreanu, C. Cost of Fouling in Full-Scale Reverse Osmosis and Nanofiltration Installations in the Netherlands. Desalination 2021, 500, 114865. [Google Scholar] [CrossRef]
- Panagopoulos, A.; Haralambous, K.J.; Loizidou, M. Desalination Brine Disposal Methods and Treatment Technologies-A Review. Sci. Total Environ. 2019, 693, 133545. [Google Scholar] [CrossRef]
- Essa, F.A.; Abdullah, A.S.; Omara, Z.M.; Kabeel, A.E.; El-Maghlany, W.M. On the Different Packing Materials of Humidification-Dehumidification Thermal Desalination Techniques-A Review. J. Clean. Prod. 2020, 277, 123468. [Google Scholar] [CrossRef]
- Ahmadvand, S.; Abbasi, B.; Azarfar, B.; Elhashimi, M.; Zhang, X.; Abbasi, B. Looking Beyond Energy Efficiency: An Applied Review of Water Desalination Technologies and an Introduction to Capillary-Driven Desalination. Water 2019, 11, 696. [Google Scholar] [CrossRef]
- Heck, N.; Lykkebo Petersen, K.; Potts, D.C.; Haddad, B.; Paytan, A. Predictors of Coastal Stakeholders’ Knowledge about Seawater Desalination Impacts on Marine Ecosystems. Sci. Total Environ. 2018, 639, 785–792. [Google Scholar] [CrossRef]
- Ahmad, N.; Baddour, R.E. A Review of Sources, Effects, Disposal Methods, and Regulations of Brine into Marine Environments. Ocean Coast. Manag. 2014, 87, 1–7. [Google Scholar] [CrossRef]
- Yaqub, M.; Lee, W. Zero-Liquid Discharge (ZLD) Technology for Resource Recovery from Wastewater: A Review. Sci. Total Environ. 2019, 681, 551–563. [Google Scholar] [CrossRef]
- Cipolletta, G.; Lancioni, N.; Akyol, Ç.; Eusebi, A.L.; Fatone, F. Brine Treatment Technologies towards Minimum/Zero Liquid Discharge and Resource Recovery: State of the Art and Techno-Economic Assessment. J. Environ. Manage. 2021, 300, 113681. [Google Scholar] [CrossRef]
- Abbasi, B.; Khalifa, M.A.E.; Sharma, D.; Zhang, X. Method and Apparatus for Desalinating Water. US Patent 0039008A1, 11 February 2021. Available online: https://patents.google.com/patent/US20210039008A1/en (accessed on 27 July 2022).
- Alsehli, M. A New Approach to Solar Desalination Using a Humidification–Dehumidification Process for Remote Areas. Processes 2021, 9, 1120. [Google Scholar] [CrossRef]
- Santosh, R.; Kumaresan, G.; Selvaraj, S.; Arunkumar, T.; Velraj, R. Investigation of Humidification-Dehumidification Desalination System through Waste Heat Recovery from Household Air Conditioning Unit. Desalination 2019, 467, 1–11. [Google Scholar] [CrossRef]
- Elhashimi, M.A.; Zhang, X.; Abbasi, B. Empirical Prediction of Saline Water Atomization Pressure Loss and Spray Phase Change Using Local Flow Pressure Analysis. Desalination 2021, 514, 115156. [Google Scholar] [CrossRef]
- Sharma, D.; Ghosh, D.P.; Rote, J.N.; Dennis, S.J.; Messer, M.; Zhang, X.; Abbasi, B. Development of an Anti-Clogging Perforated Plate Atomizer for a Zero Liquid Discharge Humidification-Dehumidification Desalination System. Desalination 2021, 515, 115195. [Google Scholar] [CrossRef]
- Elhashimi, M.A.; Shorb, J.; Messer, M.; Abbasi, B. Assessment of Humid Air-Solids Cyclone Separators in A Novel Humidification-Dehumidification Desalination. In Proceedings of the IDA International Water Reuse and Recycling Conference, Rome, Italy, 11–13 October 2021. [Google Scholar]
- Jedelsky, J.; Jicha, M. Energy Conversion during Effervescent Atomization. Fuel 2013, 111, 836–844. [Google Scholar] [CrossRef]
- Hoffmann, A.C.; Stein, L.E. Gas Cyclones and Swirl Tubes; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 978-3-540-74694-2. [Google Scholar]
- de Nevers, N. Air Pollution Control Engineering, 2nd ed.; McGraw-Hill: Boston, MA, USA, 2000; ISBN 978-0070393677. [Google Scholar]
- Elhashimi, M.A.; Gee, M.; Abbasi, B. Unconventional Desalination: The Use of Cyclone Separators in HDH Desalination to Achieve Zero Liquid Discharge. Desalination 2022, 539, 115932. [Google Scholar] [CrossRef]
- Sharma, D.; Ghosh, D.P.; Dennis, S.J.; Abbasi, B. Fouling Mechanism in Airblast Atomizers and Its Suppression for Water Desalination. Water Res. 2022, 221, 118726. [Google Scholar] [CrossRef]
- Ochowiak, M.; Matuszak, M.; Włodarczak, S.; Krupińska, A.; Markowska, M.; Gościniak, A.; Szulc, T. The Concept Design and Study of Twin-Fluid Effervescent Atomizer with Air Stone Aerator. Chem. Eng. Process. Process Intensif. 2018, 124, 24–28. [Google Scholar] [CrossRef]
- Kourmatzis, A.; Lowe, A.; Masri, A.R. Combined Effervescent and Airblast Atomization of a Liquid Jet. Exp. Therm. Fluid Sci. 2016, 75, 66–76. [Google Scholar] [CrossRef]
- Tesař, V. New Concept: Low-Pressure, Wide-Angle Atomiser. Chem. Eng. Process. Process Intensif. 2014, 82, 19–29. [Google Scholar] [CrossRef]
- Abdelaziz, G.B.; Dahab, M.A.; Omara, M.A.; Sharshir, S.W.; Elsaid, A.M.; El-Said, E.M.S. Humidification Dehumidification Saline Water Desalination System Utilizing High Frequency Ultrasonic Humidifier and Solar Heated Air Stream. Therm. Sci. Eng. Prog. 2022, 27, 101144. [Google Scholar] [CrossRef]
- Tourab, E.A.; Blanco-Marigorta, A.M.; Elharidi, A.M.; Suárez-López, M.J. A Novel Humidification Technique Used in Water Desalination Systems Based on the Humidification–Dehumidification Process: Experimentally and Theoretically. Water 2020, 12, 2264. [Google Scholar] [CrossRef]
- Soomro, S.H.; Santosh, R.; Bak, C.U.; Kim, W.S.; Kim, Y.D. Humidification–Dehumidification Desalination System Powered by Simultaneous Air–Water Solar Heater. Sustainability 2021, 13, 13491. [Google Scholar] [CrossRef]
- Xiong, Z.; Lu, M.; Wang, M.; Gu, H.; Cheng, X. Study on Flow Pattern and Separation Performance of Air-Water Swirl-Vane Separator. Ann. Nucl. Energy 2014, 63, 138–145. [Google Scholar] [CrossRef]
- SFitz. AirProperties. Available online: https://github.com/sjfitz/AirProperties (accessed on 27 July 2022).
- Picard, A.; Davis, R.S.; Gläser, M.; Fujii, K. Revised Formula for the Density of Moist Air (CIPM-2007). Metrol 2008, 45, 149–155. [Google Scholar] [CrossRef]
- Tsilingiris, P.T. Thermophysical and Transport Properties of Humid Air at Temperature Range between 0 and 100 °C. Energy Convers. Manag. 2008, 49, 1098–1110. [Google Scholar] [CrossRef]
- Miller, J. Ideal Air Properties. Available online: https://www.mathworks.com/matlabcentral/fileexchange/25030-ideal-air-properties (accessed on 24 November 2020).
- Nayar, K.G.; Sharqawy, M.H.; Banchik, L.D.; Lienhard, J.H. Thermophysical Properties of Seawater: A Review and New Correlations That Include Pressure Dependence. Desalination 2016, 390, 1–24. [Google Scholar] [CrossRef]
- Sharqawy, M.H.; Lienhard, J.H.; Zubair, S.M. Thermophysical Properties of Seawater: A Review of Existing Correlations and Data. Desalin. Water Treat. 2010, 16, 354–380. [Google Scholar] [CrossRef]
- Holmgren, M. X Steam, Thermodynamic Properties of Water and Steam. Available online: https://www.mathworks.com/matlabcentral/fileexchange/9817-x-steam-thermodynamic-properties-of-water-and-steam (accessed on 27 July 2022).
- Romo, S.A.; Storch, M., Jr.; Srebric, J. Operation Modeling of Actual Desalination Plants. Desalination 2022. Under peer-review.. [Google Scholar]
- Romo, S.A.; Mattise, N.; Srebric, J. Desalination Metamodels and a Framework for Cross-Comparative Performance Simulations. Desalination 2022, 525, 115474. [Google Scholar] [CrossRef]
- Ettouney, H. Design and Analysis of Humidification Dehumidification Desalination Process. Desalination 2005, 183, 341–352. [Google Scholar] [CrossRef]
- Sharqawy, M.H.; Antar, M.A.; Zubair, S.M.; Elbashir, A.M. Optimum Thermal Design of Humidification Dehumidification Desalination Systems. Desalination 2014, 349, 10–21. [Google Scholar] [CrossRef]
- Farsad, S.; Behzadmehr, A.; Sarvari, S.M.H. Numerical Analysis of Solar Desalination Using Humidification—Dehumidification Cycle. Desalin. Water Treat. 2010, 19, 294–300. [Google Scholar] [CrossRef]
- Prihatiningtyas, I.; Al-Kebsi, A.H.A.H.; Hartanto, Y.; Zewdie, T.M.; Van der Bruggen, B. Techno-Economic Assessment of Pervaporation Desalination of Hypersaline Water. Desalination 2022, 527, 115538. [Google Scholar] [CrossRef]
- Jin, H.Q.; Shahane, S.; Zhang, Y.; Wang, S.; Nawaz, K. Modeling of Crystallization Fouling on a Horizontal-Tube Falling-Film Evaporator for Thermal Desalination. Int. J. Heat Mass Transf. 2021, 178, 121596. [Google Scholar] [CrossRef]
- El-Dessouky, H.T.; Ettouney, H.M.; Mandani, F. Performance of Parallel Feed Multiple Effect Evaporation System for Seawater Desalination. Appl. Therm. Eng. 2000, 20, 1679–1706. [Google Scholar] [CrossRef]
- Hodgkiess, T. Inter-Relationships between Corrosion and Mineral-Scale Deposition in Aqueous Systems. Water Sci. Technol. 2004, 49, 121–128. [Google Scholar] [CrossRef] [PubMed]
- Chaussemier, M.; Pourmohtasham, E.; Gelus, D.; Pécoul, N.; Perrot, H.; Lédion, J.; Cheap-Charpentier, H.; Horner, O. State of Art of Natural Inhibitors of Calcium Carbonate Scaling. A Review Article. Desalination 2015, 356, 47–55. [Google Scholar] [CrossRef]
- Fellows, C.M.; Al Hamzah, A.A.; East, C.P. Scale Control in Thermal Desalination. In Water-Formed Deposits: Fundamentals and Mitigation Strategies, 1st ed.; Amjad, Z., Demadis, K.D., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 457–476. [Google Scholar]
- Ziemkiewicz, P.; Hause, J.; Lovett, R.; Harry Johnson, D.L.; Patchen, D. Zero Discharge Water Management for Horizontal Shale Gas Well Development. Available online: http://www.osti.gov/servlets/purl/1054519/ (accessed on 27 July 2022).
- US Energy Information Administration Electric Sales, Revenue, and Average Price. Available online: https://www.eia.gov/electricity/sales_revenue_price/ (accessed on 6 January 2021).

| Component | Equation | Variables | ||
|---|---|---|---|---|
| Compressor | (7) | Compressor power, isentropic | ||
| Slow-moving dry-air mass flow rate | ||||
| Isentropic ratio | ||||
| Inlet pressure | ||||
| (8) | Outlet pressure | |||
| Actual compressor power | ||||
| Compressor isentropic efficiency | ||||
| Evaporator | (9) | Heat required for full evaporation | ||
| Saltwater flow rate | ||||
| Saltwater latent heat of vaporization | ||||
| Water-vapor flow rate | ||||
| Air flow rate | ||||
| Specific heat capacity of moist air | ||||
| Outlet temperature | ||||
| Inlet temperature | ||||
| Superheater | (10) | Superheat enthalpy difference | ||
| Water-vapor mass flow rate | ||||
| Water-vapor enthalpy at superheat temp. | ||||
| Water-vapor enthalpy at vapor saturation | ||||
| Dry-air mass flow rate | ||||
| Air enthalpy at superheat temp. | ||||
| Air enthalpy at saturation temp. | ||||
| Solid-salt mass flow rate | ||||
| Specific heat capacity of solid salt | ||||
| Superheat temp. | ||||
| Saturation temp. | ||||
| Condenser | (11) | Condensation enthalpy difference | ||
| Water-vapor enthalpy at liquid saturation | ||||
| Air enthalpy at saturation temp. | ||||
| (12) | Condensation heat | |||
| Cyclone | (13) | Outlet pressure | ||
| Inlet pressure | ||||
| Cyclone pressure drop | ||||
| (14) | System-salt flow rate | |||
| Inlet-salt flow rate | ||||
| Collection efficiency | ||||
| General Inputs | |
|---|---|
| Product flow rate, (kg/s) | 0.0027 |
| Intake salinity, (g/kg) | 100 |
| Intake temp., (°C) | 18 |
| Family Inputs | |
| Motive steam pressure, (kPa) | 200 |
| Specific Inputs | |
| Superheat temp., (°C) | 120 |
| Slow-moving dry-air pressure, (kPa) | 48 |
| Slow-moving dry-air temp., (°C) | 20 |
| Slow-moving dry-air rel. hum., (−) | 0.63 |
| Air flow rate, (kg/s) | 0.0054 |
| High-speed hot-air pressure, (kPa) | 150 |
| Warm saline-water temperature, (°C) | 20 |
| General Outputs | |
|---|---|
| Product flow rate, (kg/s) | 0.0027 |
| Feed-water flow rate, (kg/s) | 0.003 |
| Brine flow rate, (kg/s) | n/a |
| Product-water salinity, (g/kg) | 1 |
| Feed-water salinity, (g/kg) | 100 |
| Brine salinity, (g/kg) | n/a |
| Actual recovery ratio, | 0.91 |
| Family Outputs | |
| Specific energy, (kWh/m3) | Scenario 1: 986el, 53th Scenario 2: 1039el |
| Motive-steam flow rate, (kg/s) | 2.37 × 10−4/n/a |
| Gain ratio, | 11.4/n/a |
| Sp. cooling-water flow rate, (kg/kg) | n/a |
| Specific Outputs | |
| Atomized water-and-air temp., (°C) | 75 |
| Atomized water-and-air rel. hum., (−) | 0.69 |
| Solid salt-product flow rate., (kg/s) | 2.94 × 10−4 |
| Compressor power, (kW) | 9.6 |
| Evaporator heat required, (kW) | 3.3 |
| Condenser heat available, (kW) | 7.3 |
| Superheater heat, (kW) | 0.5 |
| System Type | MDT | MDT | ROX | ROX |
|---|---|---|---|---|
| Plant Location | Jeddah, KSA | Jamnagar, IN | Bimini, BS | Cát Bà, VT |
| (kg/s) | 55 | 284 | 12 | 17 |
| (g/kg) | 41.5 | 42 | 39 | 33 |
| (°C) | 30 | 26 | 29 | 32 |
| (kg/s) | 109 | 409 | 12 | 20 |
| (g/kg) | 62.5 | 70 | 78.9 | 62.9 |
| (°C) | 46 | 43 | 39 | 33 |
| (kWh/m3) | 132th | 76th | 2.7el | 2.4el |
| (kW) | 26,132 | 77,619 | n/a | n/a |
| (kW) | n/a | n/a | 110 | 149 |
| (-) | 0.34 | 0.41 | 0.50 | 0.47 |
| STEWARD Replacement | ||||
| Total (kg/s) | 55 | 284 | 12 | 17 |
| Units in Parallel | 20,385 | 105,170 | 4449 | 6306 |
| (kWh/m3) | 1036 | 1036 | 1036 | 1012 |
| (kW) | 9.6 | 9.6 | 9.6 | 9.6 |
| (kW) | 0.5 | 0.5 | 0.5 | 0.5 |
| (kW) | 3.0 | 2.9 | 1.6 | 2.1 |
| (-) | 0.96 | 0.96 | 0.96 | 0.97 |
| STEWARD Complement | ||||
| Total (kg/s) | 109 | 409 | 12 | 20 |
| Units in Parallel | 40,344 | 151,520 | 4442 | 7403 |
| (kWh/m3) | 1067 | 1069 | 1092 | 1072 |
| (kW) | 9.98 | 9.98 | 10.2 | 9.98 |
| (kW) | 0.5 | 0.5 | 0.5 | 0.5 |
| (kW) | 1.3 | 1.7 | 1.1 | 1.4 |
| (-) | 0.94 | 0.93 | 0.93 | 0.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romo, S.A.; Elhashimi, M.; Abbasi, B.; Srebric, J. Mapping of a Novel Zero-Liquid Discharge Desalination System Based on Humidification–Dehumidification onto the Field of Existing Desalination Technologies. Water 2022, 14, 2688. https://doi.org/10.3390/w14172688
Romo SA, Elhashimi M, Abbasi B, Srebric J. Mapping of a Novel Zero-Liquid Discharge Desalination System Based on Humidification–Dehumidification onto the Field of Existing Desalination Technologies. Water. 2022; 14(17):2688. https://doi.org/10.3390/w14172688
Chicago/Turabian StyleRomo, Sebastian A., Mohammed Elhashimi, Bahman Abbasi, and Jelena Srebric. 2022. "Mapping of a Novel Zero-Liquid Discharge Desalination System Based on Humidification–Dehumidification onto the Field of Existing Desalination Technologies" Water 14, no. 17: 2688. https://doi.org/10.3390/w14172688
APA StyleRomo, S. A., Elhashimi, M., Abbasi, B., & Srebric, J. (2022). Mapping of a Novel Zero-Liquid Discharge Desalination System Based on Humidification–Dehumidification onto the Field of Existing Desalination Technologies. Water, 14(17), 2688. https://doi.org/10.3390/w14172688






