Artificial Intelligence-Based Regional Flood Frequency Analysis Methods: A Scoping Review
Abstract
:1. Introduction
2. Methodology of the Scoping Review
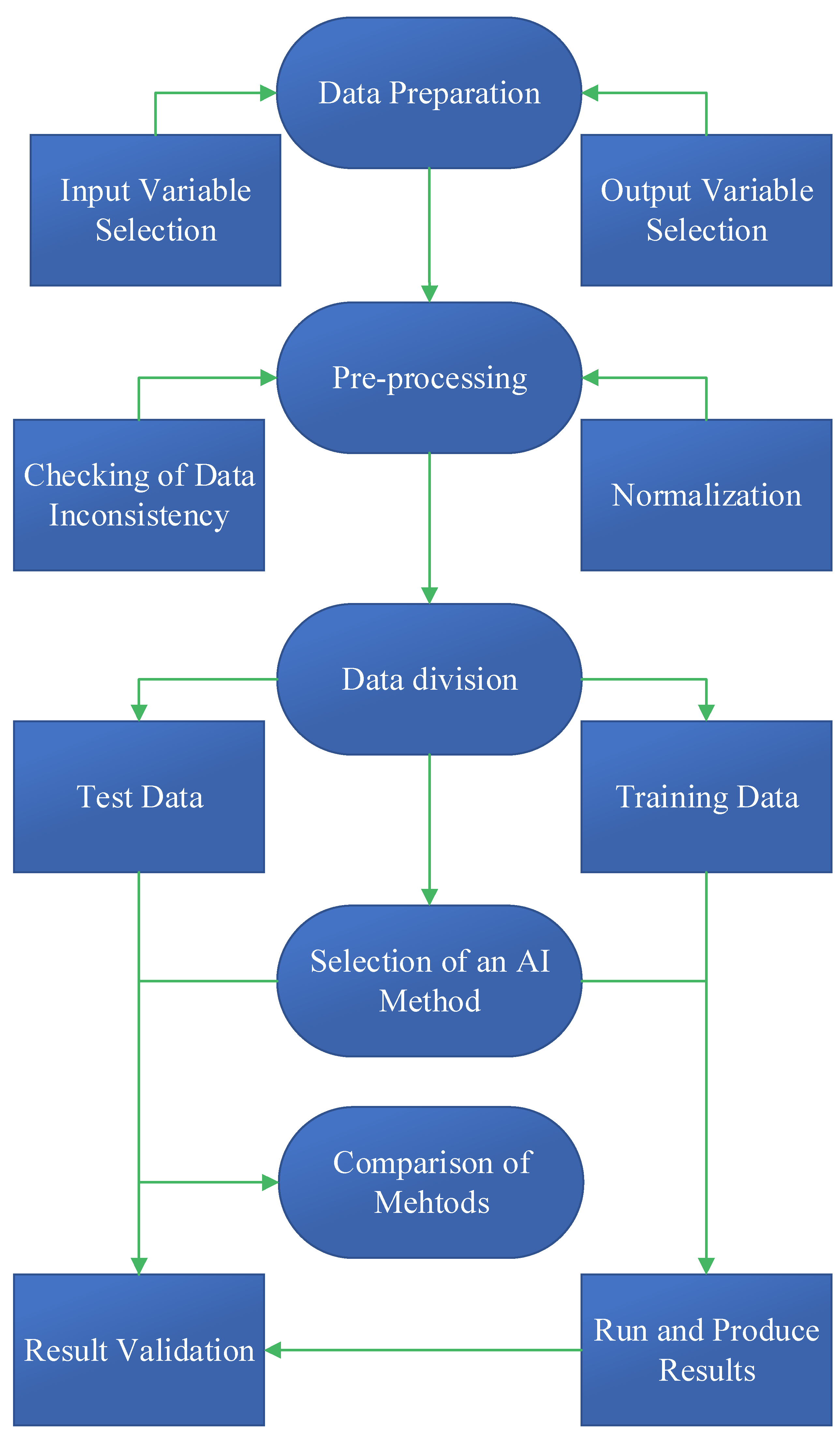
3. AI-Based RFFA Methods
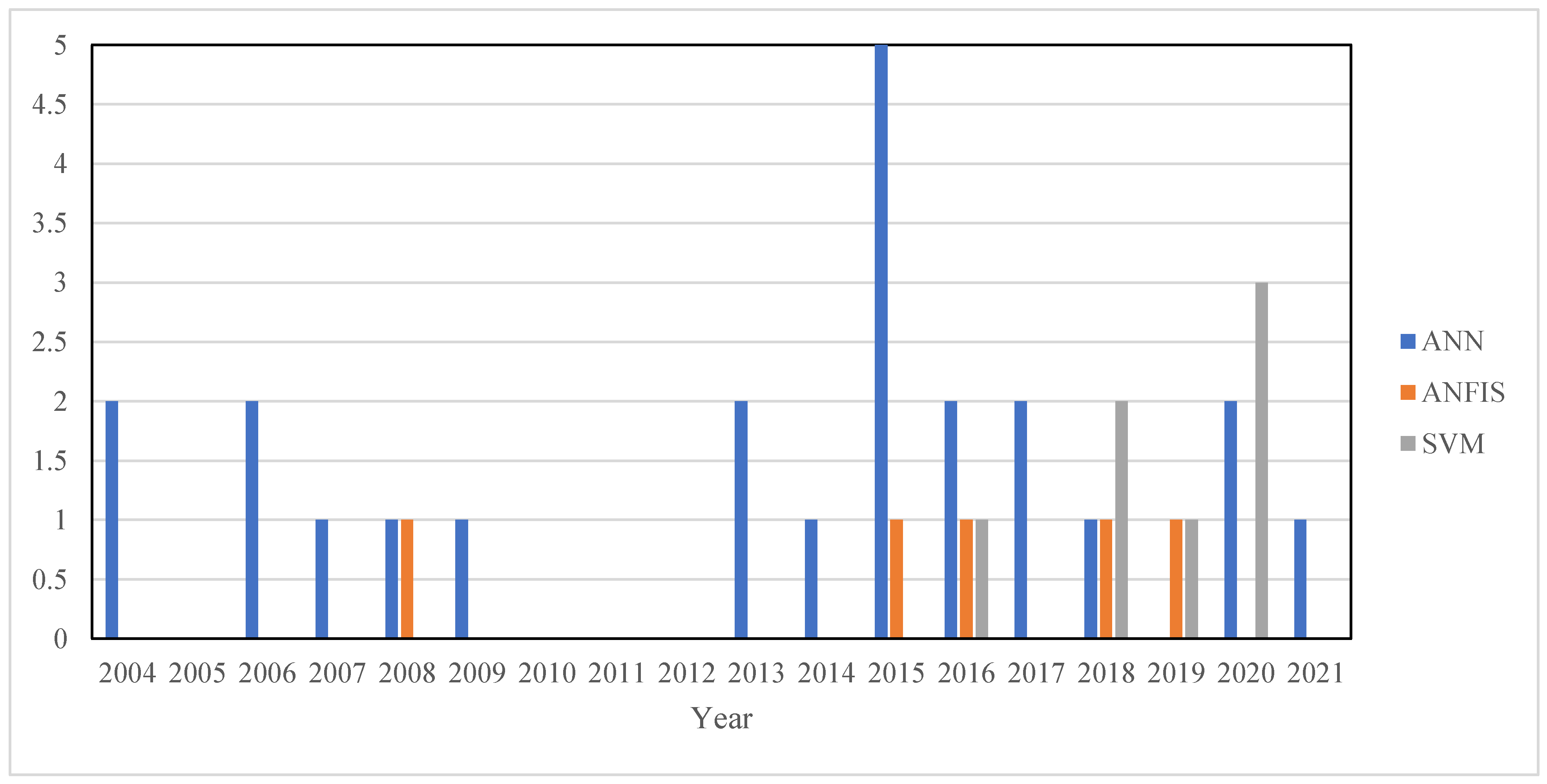
3.1. ANN-Based RFFA Models
3.2. ANFIS-Based RFFA Models
3.3. SVM-Based RFFA Models
3.4. GA and Hybrid Type of AI-Based RFFA Models
4. Comparative Assessment
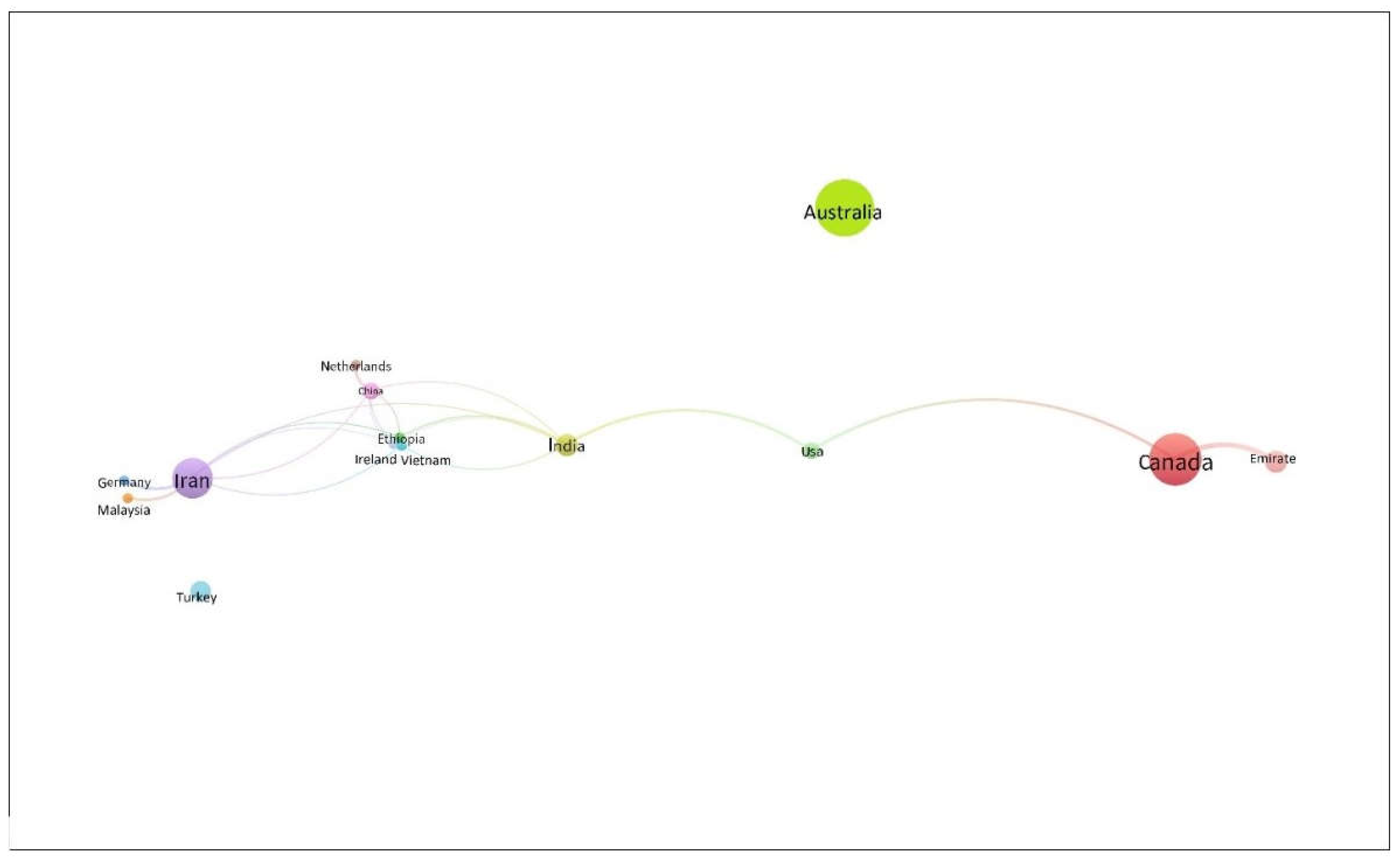
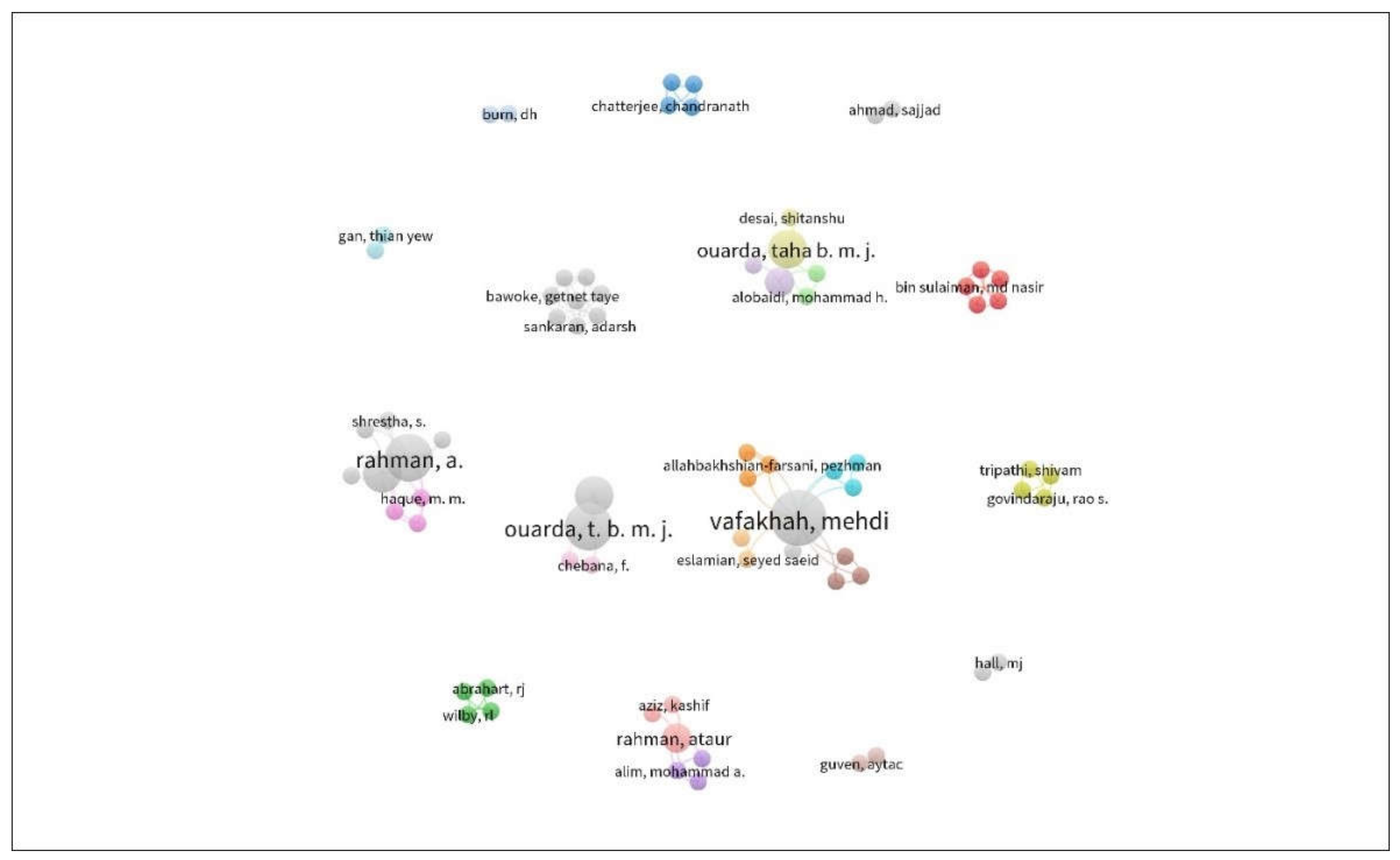
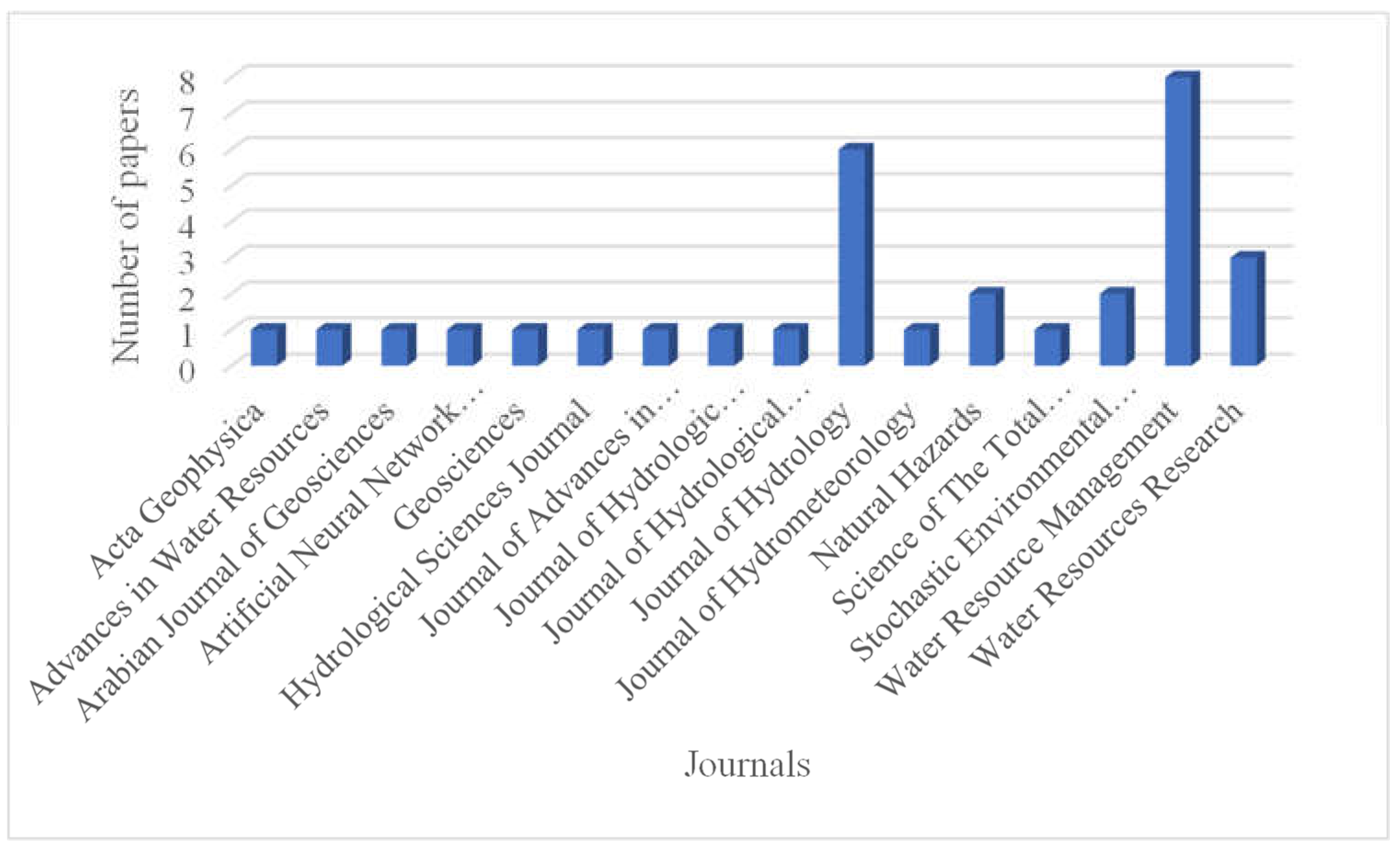
5. Bibliometric Analysis
6. Challenges and Future Research Directions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fernandez, A.; Black, J.; Jones, M.; Wilson, L.; Salvador-Carulla, L.; Astell-Burt, T.; Black, D. Flooding and mental health: A systematic mapping review. PLoS ONE 2015, 10, e0119929. [Google Scholar] [CrossRef] [PubMed]
- Longman, J.; Bennett-Levy, J.; Matthews, V.; Berry, H.; Passey, M.; Rolfe, M.; Morgan, G.; Braddon, M.; Bailie, R. Rationale and methods for a cross-sectional study of mental health and wellbeing following river flooding in rural Australia, using a community-academic partnership approach. BMC Public Health 2019, 19, 1255. [Google Scholar] [CrossRef] [PubMed]
- Mejia Manrique, S.A.; Harmsen, E.W.; Khanbilvardi, R.M.; González, J.E. Flood Impacts on Critical Infrastructure in a Coastal Floodplain in Western Puerto Rico during Hurricane María. Hydrology 2021, 8, 104. [Google Scholar] [CrossRef]
- Ogie, R.I.; Holderness, T.; Dunn, S.; Turpin, E. Assessing the vulnerability of hydrological infrastructure to flood damage in coastal cities of developing nations. Comput. Environ. Urban. Syst. 2018, 68, 97–109. [Google Scholar] [CrossRef]
- Ilinca, V. Using morphometrics to distinguish between debris flow, debris flood and flood (Southern Carpathians, Romania). Catena 2021, 197, 104982. [Google Scholar] [CrossRef]
- Marcato, G.; Bossi, G.; Rivelli, F.; Borgatti, L. Debris flood hazard documentation and mitigation on the Tilcara alluvial fan (Quebrada de Humahuaca, Jujuy province, North-West Argentina). Nat. Hazards Earth Syst. Sci. 2012, 12, 1873–1882. [Google Scholar] [CrossRef]
- Sung, C.-H.; Liaw, S.-C. A GIS-based approach for assessing social vulnerability to flood and debris flow hazards. Int. J. Disaster Risk Reduct. 2020, 46, 101531. [Google Scholar] [CrossRef]
- Kellermann, P.; Schöbel, A.; Kundela, G.; Thieken, A.H. Estimating flood damage to railway infrastructure–The case study of the March River flood in 2006 at the Austrian Northern Railway. Nat. Hazards Earth Syst. Sci. 2015, 15, 2485–2496. [Google Scholar] [CrossRef]
- Kellermann, P.; Schönberger, C.; Thieken, A.H. Large-scale application of the flood damage model RAilway Infrastructure Loss (RAIL). Nat. Hazards Earth Syst. Sci. 2016, 16, 2357–2371. [Google Scholar] [CrossRef]
- Jato-Espino, D.; Sillanpää, N.; Pathak, S. Flood modelling in sewer networks using dependence measures and learning classifier systems. J. Hydrol. 2019, 578, 124013. [Google Scholar] [CrossRef]
- Beg, M.N.A.; Rubinato, M.; Carvalho, R.F.; Shucksmith, J.D. CFD modelling of the transport of soluble pollutants from sewer networks to surface flows during urban flood events. Water 2020, 12, 2514. [Google Scholar] [CrossRef]
- Rajkhowa, S.; Sarma, J. 14—Climate change and flood risk, global climate change. In Global Climate Change; Singh, S., Singh, P., Rangabhashiyam, S., Srivastava, K.K., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 321–339. [Google Scholar]
- Lyu, H.-M.; Shen, S.-L.; Zhou, A.; Yang, J. Perspectives for flood risk assessment and management for mega-city metro system. Tunn. Undergr. Space Technol. 2019, 84, 31–44. [Google Scholar] [CrossRef]
- Kuhlicke, C.; Seebauer, S.; Hudson, P.; Begg, C.; Bubeck, P.; Dittmer, C.; Grothmann, T.; Heidenreich, A.; Kreibich, H.; Lorenz, D.F. The behavioral turn in flood risk management, its assumptions and potential implications. Wiley Interdiscip. Rev. Water 2020, 7, e1418. [Google Scholar] [CrossRef]
- Didier, D.; Baudry, J.; Bernatchez, P.; Dumont, D.; Sadegh, M.; Bismuth, E.; Bandet, M.; Dugas, S.; Sévigny, C. Multihazard simulation for coastal flood mapping: Bathtub versus numerical modelling in an open estuary, Eastern Canada. J. Flood Risk Manag. 2019, 12, e12505. [Google Scholar] [CrossRef]
- Vacondio, R.; Aureli, F.; Ferrari, A.; Mignosa, P.; Dal Palu, A. Simulation of the January 2014 flood on the Secchia River using a fast and high-resolution 2D parallel shallow-water numerical scheme. Nat. Hazards 2016, 80, 103–125. [Google Scholar] [CrossRef]
- Costabile, P.; Costanzo, C.; De Lorenzo, G.; Macchione, F. Is local flood hazard assessment in urban areas significantly influenced by the physical complexity of the hydrodynamic inundation model? J. Hydrol. 2020, 580, 124231. [Google Scholar] [CrossRef]
- Paprotny, D.; Morales-Nápoles, O.; Jonkman, S.N. Efficient pan-European river flood hazard modelling through a combination of statistical and physical models. Nat. Hazards Earth Syst. Sci. 2017, 17, 1267–1283. [Google Scholar] [CrossRef]
- Van den Honert, R.C.; McAneney, J. The 2011 Brisbane floods: Causes, impacts and implications. Water 2011, 3, 1149–1173. [Google Scholar] [CrossRef]
- Pappenberger, F.; Matgen, P.; Beven, K.J.; Henry, J.-B.; Pfister, L. Influence of uncertain boundary conditions and model structure on flood inundation predictions. Adv. Water Resour. 2006, 29, 1430–1449. [Google Scholar] [CrossRef]
- Wu, Y.; Ding, Y.; Zhu, Y.; Feng, J.; Wang, S. Complexity to forecast flood: Problem definition and spatiotemporal attention LSTM solution. Complexity 2020, 2020, 7670382. [Google Scholar] [CrossRef] [Green Version]
- Lavoie, B.; Mahdi, T.-F. Comparison of two-dimensional flood propagation models: SRH-2D and Hydro_AS-2D. Nat. Hazards 2017, 86, 1207–1222. [Google Scholar] [CrossRef]
- Tsakiris, G.; Bellos, V. A numerical model for two-dimensional flood routing in complex terrains. Water Resour. Manag. 2014, 28, 1277–1291. [Google Scholar] [CrossRef]
- Sahu, R.; Verma, M.; Ahmad, I. Regional Frequency Analysis Using L-Moment Methodology—A Review; Springer: Singapore, 2021; pp. 811–832. [Google Scholar] [CrossRef]
- Rahman, A.; Haddad, K.; Zaman, M.; Kuczera, G.; Weinmann, P.E. Design Flood Estimation in Ungauged Catchments: A Comparison Between the Probabilistic Rational Method and Quantile Regression Technique for NSW. Australas. J. Water Resour. 2011, 14, 127–139. [Google Scholar] [CrossRef]
- Darabi, H.; Haghighi, A.T.; Mohamadi, M.A.; Rashidpour, M.; Ziegler, A.D.; Hekmatzadeh, A.A.; Kløve, B. Urban flood risk mapping using data-driven geospatial techniques for a flood-prone case area in Iran. Hydrol. Res. 2020, 51, 127–142. [Google Scholar] [CrossRef]
- Ahmadalipour, A.; Moradkhani, H. A data-driven analysis of flash flood hazard, fatalities, and damages over the CONUS during 1996–2017. J. Hydrol. 2019, 578, 124106. [Google Scholar] [CrossRef]
- Villarini, G.; Smith, J.A.; Serinaldi, F.; Bales, J.; Bates, P.D.; Krajewski, W.F. Flood frequency analysis for nonstationary annual peak records in an urban drainage basin. Adv. Water Resour. 2009, 32, 1255–1266. [Google Scholar] [CrossRef]
- Saghafian, B.; Golian, S.; Ghasemi, A. Flood frequency analysis based on simulated peak discharges. Nat. Hazards 2014, 71, 403–417. [Google Scholar] [CrossRef]
- Yue, S. Applying Bivariate Normal Distribution to Flood Frequency Analysis. Water Int. 1999, 24, 248–254. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V. Bivariate flood frequency analysis using the copula method. J. Hydrol. Eng. 2006, 11, 150–164. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A. Selection of the best fit flood frequency distribution and parameter estimation procedure: A case study for Tasmania in Australia. Stoch. Environ. Res. Risk Assess. 2011, 25, 415–428. [Google Scholar] [CrossRef]
- Kousar, S.; Khan, A.R.; Ul Hassan, M.; Noreen, Z.; Bhatti, S.H. Some best-fit probability distributions for at-site flood frequency analysis of the Ume River. J. Flood Risk Manag. 2020, 13, e12640. [Google Scholar] [CrossRef]
- Ozga-Zielinski, B.; Ciupak, M.; Adamowski, J.; Khalil, B.; Malard, J. Snow-melt flood frequency analysis by means of copula based 2D probability distributions for the Narew River in Poland. J. Hydrol. Reg. Stud. 2016, 6, 26–51. [Google Scholar] [CrossRef]
- Ganamala, K.; Kumar, P.S. A case study on flood frequency analysis. Int. J. Civil. Eng. Technol. 2017, 8, 1762–1767. [Google Scholar]
- Bhat, M.S.; Alam, A.; Ahmad, B.; Kotlia, B.S.; Farooq, H.; Taloor, A.K.; Ahmad, S. Flood frequency analysis of river Jhelum in Kashmir basin. Quat. Int. 2019, 507, 288–294. [Google Scholar] [CrossRef]
- Drissia, T.K.; Jothiprakash, V.; Anitha, A.B. Flood Frequency Analysis Using L Moments: A Comparison between At-Site and Regional Approach. Water Resour. Manag. 2019, 33, 1013–1037. [Google Scholar] [CrossRef]
- Młyński, D.; Wałęga, A.; Stachura, T.; Kaczor, G. A new empirical approach to calculating flood frequency in ungauged catchments: A case study of the upper Vistula basin, Poland. Water 2019, 11, 601. [Google Scholar] [CrossRef]
- De Souza, G.R.; Merwade, V.; de Oliveira, L.F.C.; Viola, M.R.; de Sá Farias, M. Regional flood frequency analysis and uncertainties: Maximum streamflow estimates in ungauged basins in the region of Lavras, MG, Brazil. Catena 2021, 197, 104970. [Google Scholar] [CrossRef]
- Lee, D.-H.; Kim, N.W. Regional flood frequency analysis for a poorly gauged basin using the simulated flood data and L-moment method. Water 2019, 11, 1717. [Google Scholar] [CrossRef]
- Rahman, A.; Haddad, K.; Kuczera, G.; Weinmann, E. Regional flood methods. In The Australian Rainfall and Runoff: A Guide Flood Estimation. Book 3 Peak Flow Estim; Geoscience Australia: Canberra, Australia, 2019; pp. 105–146. [Google Scholar]
- Esha, R.I.; Imteaz, M.A. Assessing the predictability of MLR models for long-term streamflow using lagged climate indices as predictors: A case study of NSW (Australia). Hydrol. Res. 2018, 50, 262–281. [Google Scholar] [CrossRef]
- Tsakiri, K.; Marsellos, A.; Kapetanakis, S. Artificial neural network and multiple linear regression for flood prediction in Mohawk River, New York. Water 2018, 10, 1158. [Google Scholar] [CrossRef] [Green Version]
- Rahman, A.S.; Rahman, A. Application of principal component analysis and cluster analysis in regional flood frequency analysis: A case study in New South Wales, Australia. Water 2020, 12, 781. [Google Scholar] [CrossRef]
- Ahn, K.-H.; Palmer, R. Regional flood frequency analysis using spatial proximity and basin characteristics: Quantile regression vs. parameter regression technique. J. Hydrol. 2016, 540, 515–526. [Google Scholar] [CrossRef]
- Formetta, G.; Over, T.; Stewart, E. Assessment of peak flow scaling and its effect on flood quantile estimation in the United Kingdom. Water Resour. Res. 2021, 57, e2020WR028076. [Google Scholar] [CrossRef]
- Saf, B. Regional flood frequency analysis using L-moments for the West Mediterranean region of Turkey. Water Resour. Manag. 2009, 23, 531–551. [Google Scholar] [CrossRef]
- Kiran, K.G.; Srinivas, V.V. Fuzzy Ensemble Clustering Approach to Address Regionalization Uncertainties in Flood Frequency Analysis. Water Resour. Res. 2021, 57, e2020WR028412. [Google Scholar] [CrossRef]
- Srinivas, V.; Tripathi, S.; Rao, A.R.; Govindaraju, R.S. Regional flood frequency analysis by combining self-organizing feature map and fuzzy clustering. J. Hydrol. 2008, 348, 148–166. [Google Scholar] [CrossRef]
- Rahman, A.; Charron, C.; Ouarda, T.B.M.J.; Chebana, F. Development of regional flood frequency analysis techniques using generalized additive models for Australia. Stoch. Environ. Res. Risk Assess. 2018, 32, 123–139. [Google Scholar] [CrossRef]
- Shu, C.; Burn, D.H. Artificial neural network ensembles and their application in pooled flood frequency analysis. Water Resour. Res. 2004, 40, 1–10. [Google Scholar] [CrossRef]
- Cassalho, F.; Beskow, S.; de Mello, C.R.; de Moura, M.M.; de Oliveira, L.F.; de Aguiar, M.S. Artificial intelligence for identifying hydrologically homogeneous regions: A state-of-the-art regional flood frequency analysis. Hydrol. Process. 2019, 33, 1101–1116. [Google Scholar] [CrossRef]
- Kim, T.; Yang, T.; Gao, S.; Zhang, L.; Ding, Z.; Wen, X.; Gourley, J.J.; Hong, Y. Can artificial intelligence and data-driven machine learning models match or even replace process-driven hydrologic models for streamflow simulation?: A case study of four watersheds with different hydro-climatic regions across the CONUS. J. Hydrol. 2021, 598, 126423. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Xue, W.; Shahabi, H.; Li, S.; Hong, H.; Wang, X.; Bian, H.; Zhang, S.; Pradhan, B.; et al. Modeling flood susceptibility using data-driven approaches of naïve Bayes tree, alternating decision tree, and random forest methods. Sci. Total Environ. 2020, 701, 134979. [Google Scholar] [CrossRef]
- Shu, C.; Ouarda, T.B. Regional flood frequency analysis at ungauged sites using the adaptive neuro-fuzzy inference system. J. Hydrol. 2008, 349, 31–43. [Google Scholar] [CrossRef]
- Shu, C.; Ouarda, T.B. Flood frequency analysis at ungauged sites using artificial neural networks in canonical correlation analysis physiographic space. Water Resour. Res. 2007, 43, 1–12. [Google Scholar] [CrossRef]
- Ul Hassan, M.; Noreen, Z.; Ahmed, R. Regional frequency analysis of annual daily rainfall maxima in Skåne, Sweden. Int. J. Climatol. 2021, 41, 4307–4320. [Google Scholar] [CrossRef]
- Dhara, S.; Dang, T.; Parial, K.; Lu, X.X. Accounting for Uncertainty and Reconstruction of Flooding Patterns Based on Multi-Satellite Imagery and Support Vector Machine Technique: A Case Study of Can Tho City, Vietnam. Water 2020, 12, 1543. [Google Scholar] [CrossRef]
- Allahbakhshian-Farsani, P.; Vafakhah, M.; Khosravi-Farsani, H.; Hertig, E. Regional Flood Frequency Analysis Through Some Machine Learning Models in Semi-arid Regions. Water Resour. Manag. 2020, 34, 2887–2909. [Google Scholar] [CrossRef]
- Panahi, M.; Dodangeh, E.; Rezaie, F.; Khosravi, K.; Van Le, H.; Lee, M.-J.; Lee, S.; Thai Pham, B. Flood spatial prediction modeling using a hybrid of meta-optimization and support vector regression modeling. Catena 2021, 199, 105114. [Google Scholar] [CrossRef]
- Kumar, R.; Goel, N.K.; Chatterjee, C.; Nayak, P.C. Regional Flood Frequency Analysis using Soft Computing Techniques. Water Resour. Manag. 2015, 29, 1965–1978. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S.; Chang, F.-J. Explore an evolutionary recurrent ANFIS for modelling multi-step-ahead flood forecasts. J. Hydrol. 2019, 570, 343–355. [Google Scholar] [CrossRef]
- Kasiviswanathan, K.S.; He, J.; Tay, J.-H. Flood frequency analysis using multi-objective optimization based interval estimation approach. J. Hydrol. 2017, 545, 251–262. [Google Scholar] [CrossRef]
- Tayfur, G.; Singh, V.P.; Moramarco, T.; Barbetta, S. Flood Hydrograph Prediction Using Machine Learning Methods. Water 2018, 10, 968. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A. Regional flood frequency analysis: Evaluation of regions in cluster space using support vector regression. Nat. Hazards 2020, 102, 489–517. [Google Scholar] [CrossRef]
- Anaraki, M.V.; Farzin, S.; Mousavi, S.-F.; Karami, H. Uncertainty Analysis of Climate Change Impacts on Flood Frequency by Using Hybrid Machine Learning Methods. Water Resour. Manag. 2021, 35, 199–223. [Google Scholar] [CrossRef]
- Aziz, K.; Haque, M.; Rahman, A.; Shamseldin, A.Y.; Shoaib, M. Flood estimation in ungauged catchments: Application of artificial intelligence based methods for Eastern Australia. Stoch. Environ. Res. Risk Assess. 2017, 31, 1499–1514. [Google Scholar] [CrossRef]
- Khazaee Poul, A.; Shourian, M.; Ebrahimi, H. A Comparative Study of MLR, KNN, ANN and ANFIS Models with Wavelet Transform in Monthly Stream Flow Prediction. Water Resour. Manag. 2019, 33, 2907–2923. [Google Scholar] [CrossRef]
- Fleming, S.W.; Bourdin, D.R.; Campbell, D.; Stull, R.B.; Gardner, T. Development and Operational Testing of a Super-Ensemble Artificial Intelligence Flood-Forecast Model for a Pacific Northwest River. JAWRA J. Am. Water Resour. Assoc. 2015, 51, 502–512. [Google Scholar] [CrossRef]
- Bui, D.T.; Panahi, M.; Shahabi, H.; Singh, V.P.; Shirzadi, A.; Chapi, K.; Khosravi, K.; Chen, W.; Panahi, S.; Li, S.; et al. Novel Hybrid Evolutionary Algorithms for Spatial Prediction of Floods. Sci. Rep. 2018, 8, 15364. [Google Scholar] [CrossRef]
- Jung, K.; Ouarda, T.B.M.J.; Marpu, P.R. On the Value of River Network Information in Regional Frequency Analysis. J. Hydrometeorol. 2021, 22, 201–216. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A.; Zaman, M.; Shrestha, S. Applicability of Monte Carlo cross validation technique for model development and validation using generalised least squares regression. J. Hydrol. 2013, 482, 119–128. [Google Scholar] [CrossRef]
- Haddad, K.; Egodawatta, P.; Rahman, A.; Goonetilleke, A. Assessing uncertainty in pollutant wash-off modelling via model validation. Sci. Total Environ. 2014, 497–498, 578–584. [Google Scholar] [CrossRef] [Green Version]
- Dawdy, D.; Webster, V.; Gupta, V. Regional Flood-Frequency Analysis: How We Got Here and Where We Are Going. J. Hydrol. Eng. 2012, 17, 953–959. [Google Scholar] [CrossRef]
- Madsen, H.; Lawrence, D.; Lang, M.; Martinkova, M.; Kjeldsen, T. A Review of Applied Methods in Europe for Flood-Frequency Analysis in a Changing Environment; NERC: Atlanta, GA, USA, 2013. [Google Scholar]
- Khairudin, N.M.; Mustapha, N.; Aris, T.N.M.; Zolkepli, M. In-Depth review on machine learning models for long-term flood forecasting. J. Theor. Appl. Inf. Technol. 2022, 100, 1–19. [Google Scholar]
- Diaconu, D.C.; Costache, R.; Popa, M.C. An Overview of Flood Risk Analysis Methods. Water 2021, 13, 474. [Google Scholar] [CrossRef]
- Lohani, A.K.; Kumar, R.; Singh, R.D. Hydrological time series modeling: A comparison between adaptive neuro-fuzzy, neural network and autoregressive techniques. J. Hydrol. 2012, 442–443, 23–35. [Google Scholar] [CrossRef]
- Tanty, R.M.; Desmukh, T.S. Application of Artificial Neural Network in Hydrology—A Review. Int. J. Eng. Res. Technol. 2015, 4, 184–188. [Google Scholar]
- Jingyi, Z.; Hall, M. Regional flood frequency analysis for the Gan-Ming River basin in China. J. Hydrol. 2004, 296, 98–117. [Google Scholar] [CrossRef]
- Dawson, C.W.; Abrahart, R.J.; Shamseldin, A.Y.; Wilby, R.L. Flood estimation at ungauged sites using artificial neural networks. J. Hydrol. 2006, 319, 391–409. [Google Scholar] [CrossRef]
- Ouarda, T.B.; Shu, C. Regional low-flow frequency analysis using single and ensemble artificial neural networks. Water Resour. Res. 2009, 45, 1–16. [Google Scholar] [CrossRef]
- Singh, K.K.; Pal, M.; Singh, V. Estimation of mean annual flood in Indian catchments using backpropagation neural network and M5 model tree. Water Resour. Manag. 2010, 24, 2007–2019. [Google Scholar] [CrossRef]
- Seckin, N.; Cobaner, M.; Yurtal, R.; Haktanir, T. Comparison of artificial neural network methods with L-moments for estimating flood flow at ungauged sites: The case of East Mediterranean River Basin, Turkey. Water Resour. Manag. 2013, 27, 2103–2124. [Google Scholar] [CrossRef]
- Aziz, K.; Rahman, A.; Fang, G.; Shrestha, S. Application of artificial neural networks in regional flood frequency analysis: A case study for Australia. Stoch. Environ. Res. Risk Assess. 2014, 28, 541–554. [Google Scholar] [CrossRef]
- Alobaidi, M.H.; Marpu, P.R.; Ouarda, T.B.; Chebana, F. Regional frequency analysis at ungauged sites using a two-stage resampling generalized ensemble framework. Adv. Water Resour. 2015, 84, 103–111. [Google Scholar] [CrossRef]
- Durocher, M.; Chebana, F.; Ouarda, T.B. A nonlinear approach to regional flood frequency analysis using projection pursuit regression. J. Hydrometeorol. 2015, 16, 1561–1574. [Google Scholar] [CrossRef]
- Chokmani, K.; Ouarda, T.B. Physiographical space-based kriging for regional flood frequency estimation at ungauged sites. Water Resour. Res. 2004, 40, 1–13. [Google Scholar] [CrossRef]
- Wazneh, H.; Chebana, F.; Ouarda, T.B.M.J. Optimal depth-based regional frequency analysis. Hydrol. Earth Syst. Sci. 2013, 17, 2281–2296. [Google Scholar] [CrossRef]
- Chebana, F.; Charron, C.; Ouarda, T.B.; Martel, B. Regional frequency analysis at ungauged sites with the generalized additive model. J. Hydrometeorol. 2014, 15, 2418–2428. [Google Scholar] [CrossRef]
- Nezhad, M.K.; Chokmani, K.; Ouarda, T.B.; Barbet, M.; Bruneau, P. Regional flood frequency analysis using residual kriging in physiographical space. Hydrol. Process. 2010, 24, 2045–2055. [Google Scholar] [CrossRef]
- Ouali, D.; Chebana, F.; Ouarda, T.B. Fully nonlinear statistical and machine-learning approaches for hydrological frequency estimation at ungauged sites. J. Adv. Model. Earth Syst. 2017, 9, 1292–1306. [Google Scholar] [CrossRef]
- Ouarda, T.B.; Girard, C.; Cavadias, G.S.; Bobée, B. Regional flood frequency estimation with canonical correlation analysis. J. Hydrol. 2001, 254, 157–173. [Google Scholar] [CrossRef]
- Ouali, D.; Chebana, F.; Ouarda, T.B. Non-linear canonical correlation analysis in regional frequency analysis. Stoch. Environ. Res. Risk Assess. 2016, 30, 449–462. [Google Scholar] [CrossRef]
- Kordrostami, S.; Alim, M.A.; Karim, F.; Rahman, A. Regional flood frequency analysis using an artificial neural network model. Geosciences 2020, 10, 127. [Google Scholar] [CrossRef]
- Linh, N.T.T.; Ruigar, H.; Golian, S.; Bawoke, G.T.; Gupta, V.; Rahman, K.U.; Sankaran, A.; Pham, Q.B. Flood prediction based on climatic signals using wavelet neural network. Acta Geophys. 2021, 69, 1413–1426. [Google Scholar] [CrossRef]
- Desai, S.; Ouarda, T.B. Regional hydrological frequency analysis at ungauged sites with random forest regression. J. Hydrol. 2021, 594, 125861. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. In Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers by Lotfi A Zadeh; World Scientific: Singapore, 1996; pp. 394–432. [Google Scholar]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man. Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Jang, J.S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Zalnezhad, A.; Rahman, A.; Vafakhah, M.; Samali, B.; Ahamed, F. Regional Flood Frequency Analysis Using the FCM-ANFIS Algorithm: A Case Study in South-Eastern Australia. Water 2022, 14, 1608. [Google Scholar] [CrossRef]
- Aziz, K.; Rahman, A.; Shamseldin, A.; Shoaib, M. Co-active neuro fuzzy inference system for regional flood estimation in Australia. J. Hydrol. Environ. Res. 2013, 1, 11–20. [Google Scholar]
- Haddad, K.; Rahman, A. Regional flood frequency analysis in eastern Australia: Bayesian GLS regression-based methods within fixed region and ROI framework–Quantile Regression vs. Parameter Regression Technique. J. Hydrol. 2012, 430, 142–161. [Google Scholar] [CrossRef]
- Bozchaloei, S.K.; Vafakhah, M. Regional analysis of flow duration curves using adaptive neuro-fuzzy inference system. J. Hydrol. Eng. 2015, 20, 06015008. [Google Scholar] [CrossRef]
- Aziz, K.; Rahman, A.; Shamseldin, A. Development of artificial intelligence based regional flood estimation techniques for Eastern Australia. In Artificial Neural Network Modelling; Springer: Berlin/Heidelberg, Germany, 2016; pp. 307–323. [Google Scholar]
- Wu, J.; Liu, H.; Wei, G.; Song, T.; Zhang, C.; Zhou, H. Flash flood forecasting using support vector regression model in a small mountainous catchment. Water 2019, 11, 1327. [Google Scholar] [CrossRef]
- Dodangeh, E.; Panahi, M.; Rezaie, F.; Lee, S.; Tien Bui, D.; Lee, C.-W.; Pradhan, B. Novel hybrid intelligence models for flood-susceptibility prediction: Meta optimization of the GMDH and SVR models with the genetic algorithm and harmony search. J. Hydrol. 2020, 590, 125423. [Google Scholar] [CrossRef]
- Gizaw, M.S.; Gan, T.Y. Regional flood frequency analysis using support vector regression under historical and future climate. J. Hydrol. 2016, 538, 387–398. [Google Scholar] [CrossRef]
- Sharifi Garmdareh, E.; Vafakhah, M.; Eslamian, S.S. Regional flood frequency analysis using support vector regression in arid and semi-arid regions of Iran. Hydrol. Sci. J. 2018, 63, 426–440. [Google Scholar] [CrossRef]
- Ghaderi, K.; Motamedvaziri, B.; Vafakhah, M.; Dehghani, A.A. Regional flood frequency modeling: A comparative study among several data-driven models. Arab. J. Geosci. 2019, 12, 588. [Google Scholar] [CrossRef]
- Vafakhah, M.; Khosrobeigi Bozchaloei, S. Regional analysis of flow duration curves through support vector regression. Water Resour. Manag. 2020, 34, 283–294. [Google Scholar] [CrossRef]
- Seckin, N.; Guven, A. Estimation of peak flood discharges at ungauged sites across Turkey. Water Resour. Manag. 2012, 26, 2569–2581. [Google Scholar] [CrossRef]
- Aziz, K.; Rai, S.; Rahman, A. Design flood estimation in ungauged catchments using genetic algorithm-based artificial neural network (GAANN) technique for Australia. Nat. Hazards 2015, 77, 805–821. [Google Scholar] [CrossRef]


| Reference | Author, Year | Model | Predictor Variables (Inputs) | Model Output | Catchment, Year | Journal | Country (Catchment) | RMSE * | RRMSE/NASH * | R2 * |
|---|---|---|---|---|---|---|---|---|---|---|
| [102] | Zalnezhad et al., 2022 | ANFIS(FCM) * ANFIS(SC) ANFIS(GP) QRT | A, I, MAR, SF, MAE, SDEN, S1085, FOR | Q2–100 | 181 Stations 40–89 Year | Water | Australia | 50.88 | RRMSE = 0.78 | NA |
| [97] | Desai and Ouarda, 2021 | CCA-RFR * PFR CCA-GAM EANN ANN CCA-MLR CCA-Kriging CCA-EANN CCA-ANN | A, MBS, FAL, AMP, AMD | Q10–100 | 151 stations, ≥15 year | Journal of Hydrology | Canada (Quebec) | 0.05 | NASH = 0.57 RRMSE = 29.44 | NA |
| [96] | Linh et al., 2021 | WNN * ANN | SLP, SST | Max monthly discharge (MAD) | 3 stations, 37 years | Acta Geophysica | Iran (Golestan Dam, Madarsoo) | 0.68 | NASH = 0.99 | 0.99 |
| [59] | Allahbakhshian-Farsani et al., 2020 | SVR * MARS BRT PPR NLR | A, AA, AMP, MXP, NDP, CC, CR, TC, P, SL, DD, SS, MBS, PF, SDT, RA, BL, FLA, FOR, RLA, DA, WA, EL, MXEL, MNEL | Q2–200 | 54 stations, 19 years | Water Resources Management | Iran (Karun and Karkhe River) | 50.70 | NASH = 0.94 RRMSE = 63.93 | 0.96 |
| [95] | Kordrostami et al., 2020 | ANN | A, AEV, AMP, FOR, I, SS, SF and DD | Q5–100 | 88 stations, 25–82 years | Geosciences | Australia (New South Wales) | NA | RRMSE = 0.48 | 0.74 |
| [65] | Haddad and Rahman, 2020 | MDS-SVR * MDS-BGLSR | A, AEV, SF, DD, SS, FOR, I and AMP | Q2–100 | 202 stations, 25–82 years | Natural Hazards | Australia (New South Wales and Victoria) | NA | RRMSE = 56 | 0.78 |
| [112] | Vafakhah and Khosrobeigi Bozchaloei, 2020 | SVR * ANN NLR | A, AA, AEV, P, MBS, MXEL, MNEL, EL, SL, DD, SS, AMP, T, PF, RLA, BL, GA, RA | Q2–90 | 33 Stations, 20 years | Water Resources Management | Iran (Namak Lake) | 0.11 | NASH = 0.91 RRMSE = 1.45 | 0.96 |
| [111] | Ghaderi et al., 2019 | SVM * ANFIS GEP | A, P, MBS, EL, L, SL, SS, DD, MXSO, FF, L, CR, CC, AMP, MXP, BL, FOR | Q50 | 47 stations, 21 years | Arabian Journal of Geosciences | Iran (South-west) | 239.94 | NASH = 0.75 | 0.76 |
| [110] | Sharifi Garmdareh et al., 2018 | ANFIS * SVR ANN NLR | A, AEV, P, DD, MXEL, MNEL, MBS, EL, SL, SS, T, AMP, | Q2–100 | 55 stations, 20 years | Hydrological Sciences Journal | Iran (Namak Lake) | 8.40 | NASH = 0.90 | 0.95 |
| [67] | Aziz et al., 2017 | ANN * GEP * QRT | A, AEV, AMP, SS, I | Q2–100 | 452 stations, 25–75 years | Stochastic Environmental Research and Risk Assessment | Australia (New South Wales, Victoria, Queensland and Tasmania) | Na | NASH for ANN for smaller ARIs = 0.78 NASH for GEP for larger ARIs = 0.73 | NA |
| [92] | Ouali et al., 2017 | NLCCA-GAM * NLCCA-EANN CCA-ANN CCA-EANN NLCCA-ANN NLCCA-GAM/ STPW | A, MBS, FAL, AMP, AMD | Q10–100 | 151, 204 and 69 stations, ≥15 years | Journal of Advances in Modeling Earth Systems | Canada and United states (Quebec, Arkansas, Texas) | NA | RRMSE = 0.28 NASH > 0.8 | NA |
| [109] | Gizaw and Gan, 2016 | SVR * ANN | A, SS, SL, TC, I, AMP | Q10–100 | 26 and 23 stations, ≥15 years | Journal of Hydrology | Canada (British Columbia, Ontario) | 46.2 | NA | 0.7 |
| [106] | Aziz et al., 2016 | ANN * GAANN CANFIS GEP | A, AEV, I, AMP, SS, | Q2–100 | 452 Stations, 25–75 years | Artificial Neural Network Modelling (Book) | Australia (New South Wales, Victoria, Queensland and Tasmania) | NA | NASH = 0.69 | NA |
| [61] | Kumar et al., 2015 | FIS * ANN L-moments (PE3) | A, AMP, SDT, EL | Q2–1000 | 17 stations, 15–29 years | Water Resources Management | India (Godavari river) | 2.32 | Na | NA |
| [114] | Aziz et al., 2015 | GAANN BPANN | A, I | Q2–100 | 452 stations, 25–75 years | Natural Hazards | Australia (New South Wales, Victoria, Queensland, and Tasmania) | NA | NA | NA |
| [105] | Bozchaloei and Vafakhah, 2015 | ANFIS * ANN NLR | A, AA, AEV, P, MBS, MXEL, MNEL, EL, SL, DD, SS, AMP, T, PF, RLA, BL, GA, RA | Q2–92 | 33 stations, 20 years | Journal of Hydrologic Engineering | Iran (Namak Lake) | 0.008 | NASH = 0.92 | 0.99 |
| [87] | Durocher et al., 2015 | PPR * | A, SL, SS, MBS, FOR, FAL, AMP, AMPS, AMPL, MLS, AMD | Q10–100 | 151 stations, ≥15 years | Journal of Hydrometeorology | Canada (Quebec) | NA | RRMSE = 0.40 | NA |
| [86] | Alobaidi et al., 2015 | G-EANN * EANN | A, MBS, FAL, AMD, AMP | Q10–100 | 151 stations, ≥15 years | Advances in Water Resources | Canada (Quebec) | NA | RRMSE = 0.34 | NA |
| [85] | Aziz et al., 2014 | ANN * QRT | A, AEV, AMP, SS, I | Q2–100 | 452 stations, 25–75 years | Stochastic Environmental Research and Risk Assessment | Australia (New South Wales, Victoria, Queensland, Tasmania) | NA | NA | NA |
| [103] | Aziz et al., 2013 | BGLS-QRT-ROI * CANFIS | A and I | Q2–100 | 452 stations, 25–75 years | Journal of Hydrological Environment Resources | Australia (New South Wales, Victoria, Queensland, and Tasmania) | NA | NA | NA |
| [84] | Seckin et al., 2013 | MLP * L-moment RBNN GRNN MLR MNLR | A, EL, LAT, LON, and RP | Q1.111–1000 | 13 stations, 10-39 years | Water Resources Management | Turkey (East Mediterranean River) | 0.173 | NA | 0.84 |
| [113] | Seckin and Guven, 2012 | GEP * LGP LR | A, EL, LAT, LON, and RP | Q25.7–174.3 | 543 stations, ≥15 years | Water Resource Management | Turkey (Rivers across the country) | NA | NA | 0.57 |
| [83] | Singh et al., 2010 | BNN * M5 | A, MRD, AMP, RP, MBS and FOR | Q2.33 | 93 stations, 10–83 years | Water Resources Management | India (Catchments across the country) | NA | NA | NA |
| [82] | Ouarda and Shu, 2009 | ANN * Multiple regression model | A, FAL, FOR, AMD, AMPL, NT27, CN | Q2–10 | 134 stations, ≥10 years | Water Resources Research | Canada (Quebec) | 27.33 | NASH = 0.96, RRMSE = 36.17 | NA |
| [55] | Shu and Ouarda, 2008 | ANFIS * ANN NLR NLR-R | A, MBS, FAL, AMP, AMD, HDB, TOPO | Q10–100 | 151 stations- ≥15 years | Journal of Hydrology | Canada (Quebec) | 316 | NASH = 0.85 RRMSE = 57 | NA |
| [49] | Srinivas et al., 2008 | SOFM * CCA Regional regression | A, SS, SRC, SSC, AMP, SL, EL, FOR, R24h | Q2–100 | 11 stations, 6–42 years | Journal of Hydrology | United states (Indiana) | NA | RRMSE = 0.276 | NA |
| [56] | Shu and Ouarda, 2007 | ANN * ANN-CCA | A, AMD, AMP, FAL, MBS | Q10–50 | 151 stations, ≥15 year | Water Resources Research | Canada (Quebec) | 0.053 | NASH = 0.82 RRMSE = 38 | NA |
| [81] | Dawson et al., 2006 | ANN * MLR | A, AMP, L, DA, IF | Q10, 20, 30 | 850 stations, 20 years | Journal of Hydrology | United kingdom (Catchment across the UK) | NA | NA | NA |
| [80] | Jingyi and Hall, 2004 | ANN * Cluster analysis | A, AMP, MXP, SL, SS, EL, GFI and PLN | Q50 | 86 stations 15–36 years | Journal of Hydrology | China (Jiangxi and Fujian, Gan and Ming rivers) | 47 | NA | NA |
| [51] | (Shu and Burn, 2004) | ANN * Ordinary least squares regression (REG_OLS) Non-linear regression (REG_NONLINEAR) | A, AMP, SDT, FARL | Q10 | 404 stations 29 years | Water Resources Management | United Kingdom (England, Scotland, and Wales) | NA | NA | NA |
| Symbol/Abbreviation | Unit | Name of Variable |
|---|---|---|
| A | km2 | Catchment area |
| AA | km2 | Agricultural area of catchment |
| AEV | mm | Annual evaporation (mean) |
| AMD | degree-day | Annual mean degree-day above 0 °C |
| AMP | mm | Annual mean total precipitation |
| AMPL | mm | Mean liquid precipitation during Jul–Dec, Summer mean liquid precipitation, Spring Precipitation—the total basin precipitation from the start of active snowmelt to the start of the spring crest |
| AMPS | mm | Mean solid annual precipitation, Winter precipitation—the total basin precipitation from November 1st of previous year to the start of active snowmelt during the flood year, measured in inches; |
| BL | % | Percentage of barren land |
| CC | NA | Watershed compactness coefficient |
| CN | NA | Curve number |
| CR | NA | Watershed circulatory ratio |
| DA | km2 | Developed area |
| DD | NA | Drainage density |
| EL | m | Elevation |
| EP | mm | Equivalent precipitation at the time of flood event |
| FAL | % | Fraction of catchment area occupied by lake |
| FARL | NA | Reservoir/lake effects |
| FF | NA | Form factor |
| FLA | km2 | Fallow land area |
| FOR | % | Percentage of catchment covered by forest |
| GA | km2 | Garden area |
| GFI | NA | Geological feature index |
| HDB | NA | Hydrological database |
| I | mm/s | Design rainfall intensity |
| IF | NA | Index flood |
| L | km | Catchment length |
| LAT | NA | Latitude |
| LON | NA | Longitude |
| MAR | mm | Mean Annual Rainfall |
| MAE | mm | Mean annual evapo-transpiration |
| MBS | NA | Mean basin slope |
| MLS | mm | Mean level of snow on the 30th of March |
| MNEL | m | Minimum watershed elevation |
| MRD | day | Average annual rainfall duration |
| MXEL | m | Maximum watershed elevation |
| MXP | mm | Maximum 24 h rainfall |
| MXSO | NA | Maximum stream order |
| NDP | Number (NA) | Number of days of precipitation |
| NT27 | Number (NA) | The average number of days with a temperature above 27 °C |
| P | km | Watershed perimeter |
| PF | km2 | Permeable formation area |
| PLN | NA | Plantation cover index |
| R24h | mm | 24-h rainfall having a recurrence interval of 2 years |
| RA | km2 | Rock area |
| RLA | km2 | Rangeland area |
| RP | Year | Return period |
| S1085 | m/km | Slope of central 75% of the mainstream |
| SDEN | km−1 | Stream density |
| SDT | NA | Soil drainage type |
| SF | NA | Shape factor |
| SL | km | Mainstream length |
| SLP | Mbar | Sea-level pressure |
| SRC | NA | Soil runoff coefficient |
| SS | NA | Slope of the main channel in the drainage basin |
| SSC | NA | Soil storage coefficient |
| SST | °C | Sea surface temperature |
| T | °C | Mean annual temperature |
| TC | Hour | Time of concentration |
| TOPO | NA | Topographic digital maps |
| WA | % | Water area |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zalnezhad, A.; Rahman, A.; Nasiri, N.; Haddad, K.; Rahman, M.M.; Vafakhah, M.; Samali, B.; Ahamed, F. Artificial Intelligence-Based Regional Flood Frequency Analysis Methods: A Scoping Review. Water 2022, 14, 2677. https://doi.org/10.3390/w14172677
Zalnezhad A, Rahman A, Nasiri N, Haddad K, Rahman MM, Vafakhah M, Samali B, Ahamed F. Artificial Intelligence-Based Regional Flood Frequency Analysis Methods: A Scoping Review. Water. 2022; 14(17):2677. https://doi.org/10.3390/w14172677
Chicago/Turabian StyleZalnezhad, Amir, Ataur Rahman, Nastaran Nasiri, Khaled Haddad, Muhammad Muhitur Rahman, Mehdi Vafakhah, Bijan Samali, and Farhad Ahamed. 2022. "Artificial Intelligence-Based Regional Flood Frequency Analysis Methods: A Scoping Review" Water 14, no. 17: 2677. https://doi.org/10.3390/w14172677








