Evaluating Monthly Flow Prediction Based on SWAT and Support Vector Regression Coupled with Discrete Wavelet Transform
Abstract
:1. Introduction
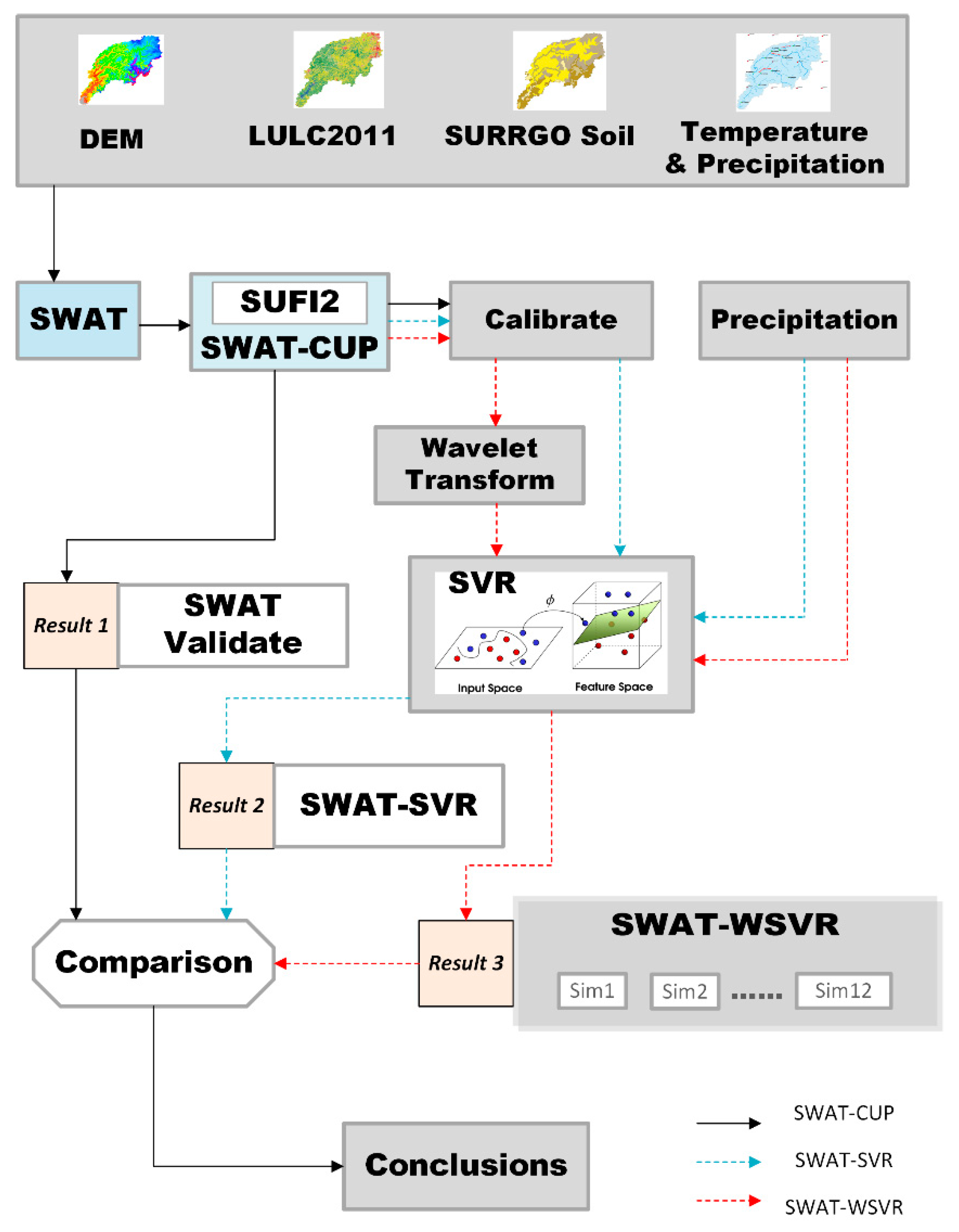
2. Methodology
2.1. Watershed Description and Data Source
2.2. Hydrological Model
2.3. Support Vector Machine
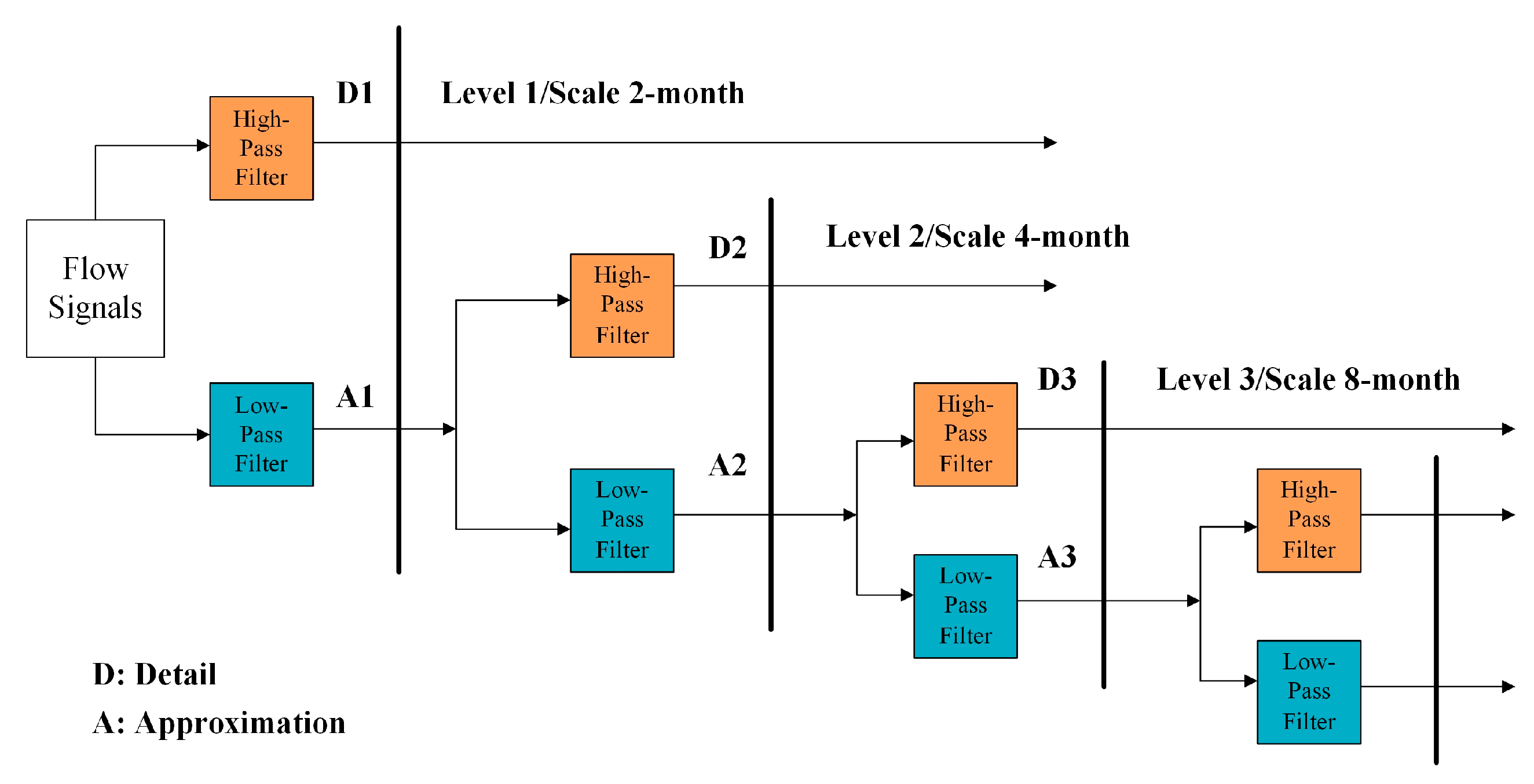
2.4. Wavelet Transforms
2.5. Model Performance Evaluation
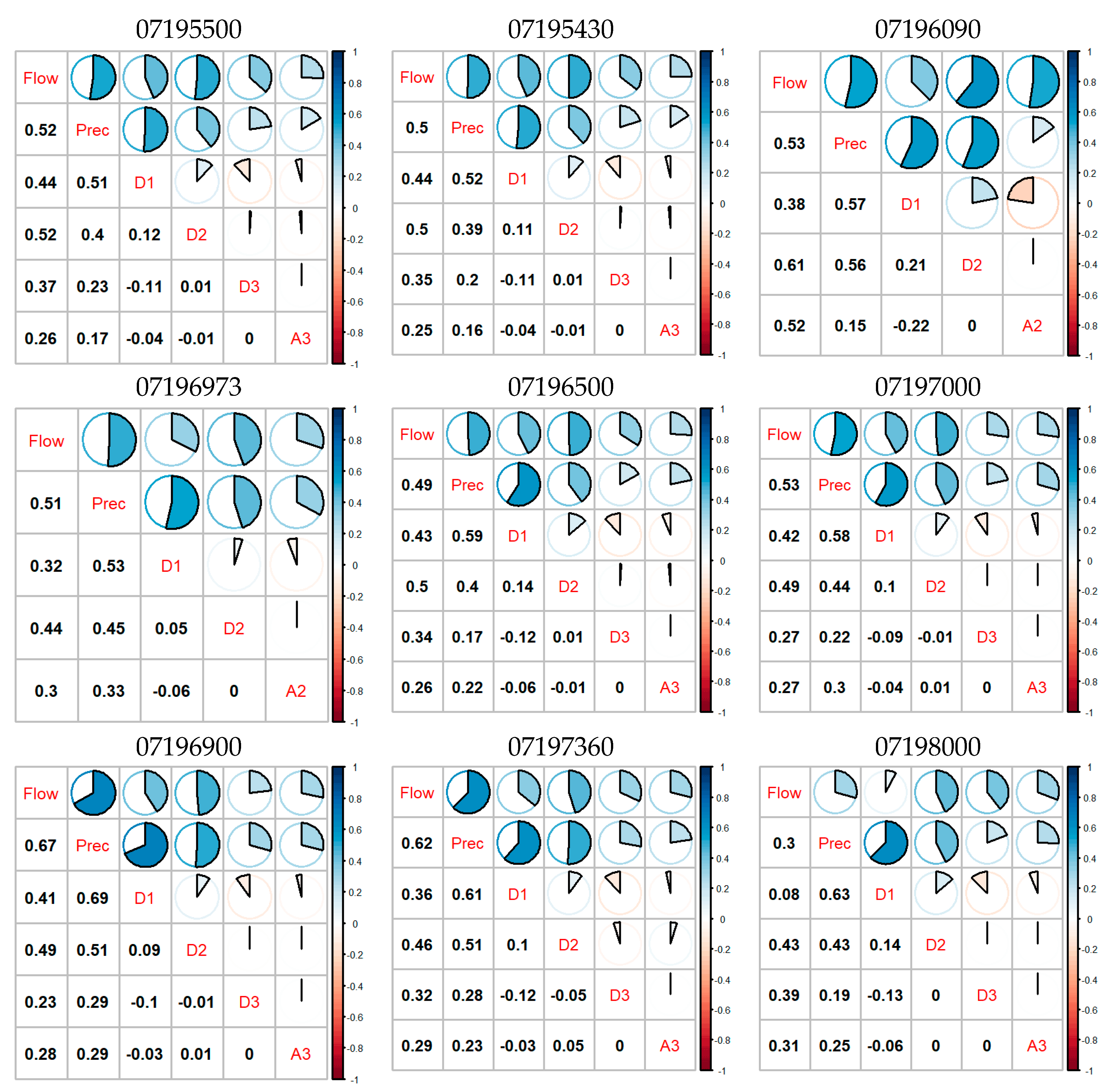
3. Results and Discussion
3.1. Flow Prediction by SWAT-CUP
3.2. Flow Prediction by SWAT-SVR
3.3. SWAT-WSVR Development and Evaluation
3.3.1. Development of SWAT-WSVR
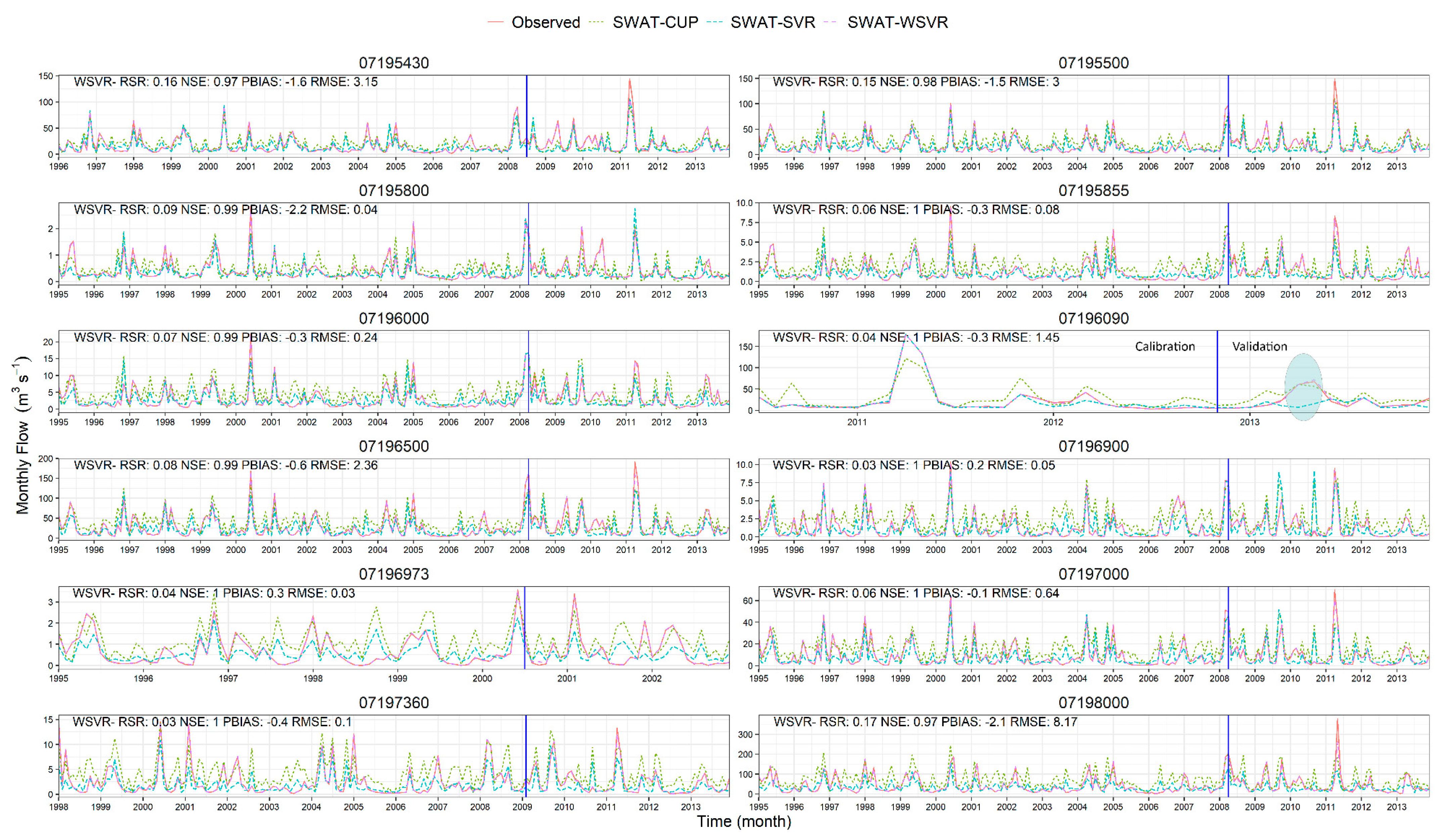
3.3.2. Statistical Evaluation of SWAT-WSVR
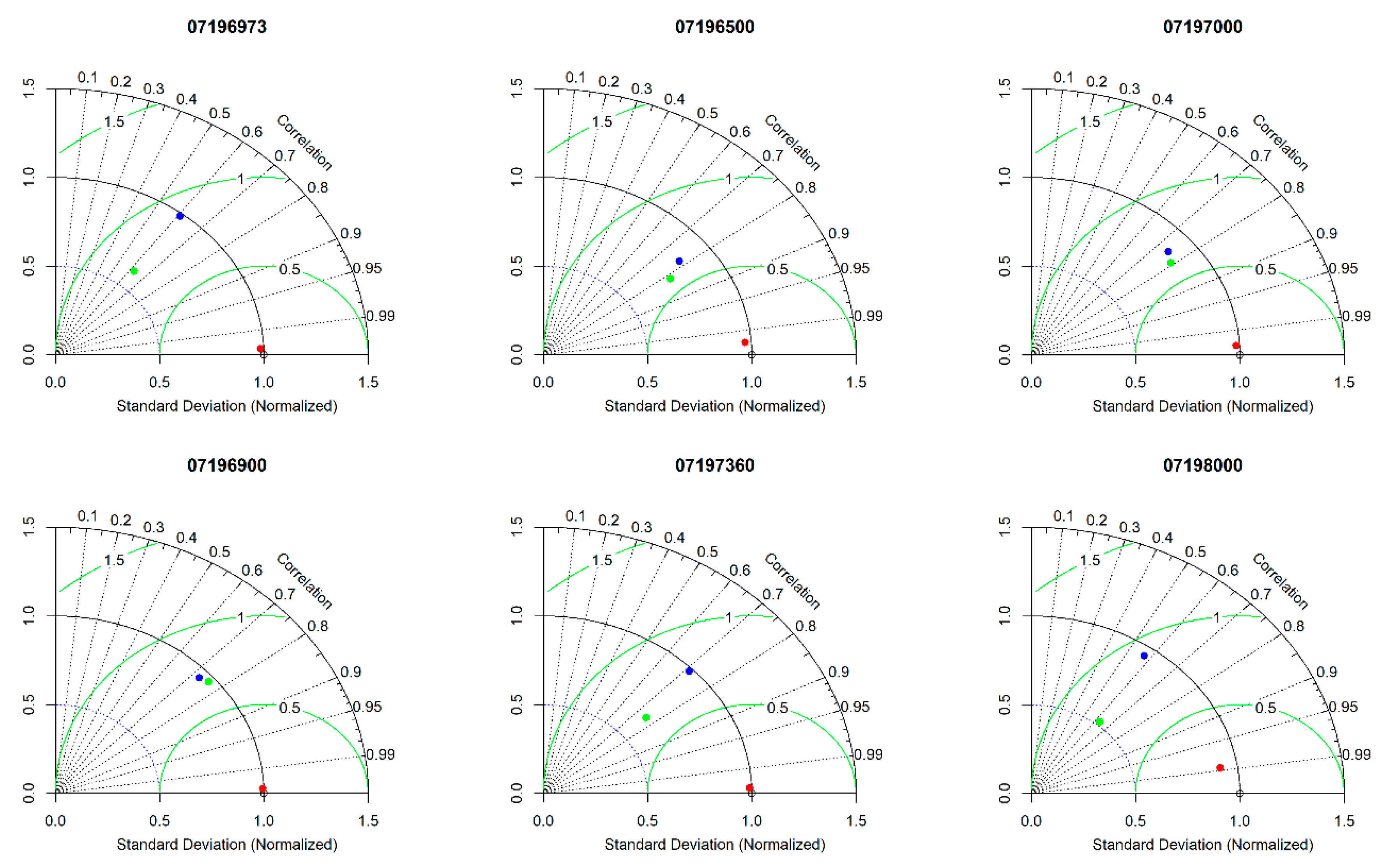
3.4. Taylor Diagram and Hydrographic Comparison between Different Models
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alizadeh, M.J.; Kavianpour, M.R.; Kisi, O.; Nourani, V. A new approach for simulating and forecasting the rainfall-runoff process within the next two months. J. Hydrol. 2017, 548, 588–597. [Google Scholar] [CrossRef]
- Huo, Z.; Feng, S.; Kang, S.; Huang, G.; Wang, F.; Guo, P. Integrated neural networks for monthly river flow estimation in arid inland basin of Northwest China. J. Hydrol. 2012, 420–421, 159–170. [Google Scholar] [CrossRef]
- U.S. EPA. A Review of Watershed and Water Quality Tools for Nutrient Fate and Transport; EPA/600/R-19/232; Center for Environmental Solutions & Emergency Response|Groundwater Characterization & Remediation Division, Office of Research and Development (EPA): Ada, OK, USA, 2019.
- Kalteh, A.M. Monthly River Flow Forecasting Using Artificial Neural Network and Support Vector Regression Models Coupled with Wavelet Transform. Comput. Geosci. 2013, 54, 1–8. [Google Scholar] [CrossRef]
- Yuan, L.; Zhou, Q. Complexity of soil erosion and sediment yield system in a watershed. J. Chongqing Inst. Technol. (Nat. Sci.) 2008, 22, 112–116. [Google Scholar]
- Zhang, Z.; Chen, X.; Xu, C.; Yuan, L.; Yong, B.; Yan, S. Evaluating the non-stationary relationship between precipitation and streamflow in nine major basins of China during the past 50 years. J. Hydrol. 2011, 409, 81–93. [Google Scholar] [CrossRef]
- Nourani, V.; Hosseini Baghanam, A.; Adamowski, J.; Kisi, O. Applications of hybrid wavelet–Artificial Intelligence models in hydrology: A review. J. Hydrol. 2014, 514, 358–377. [Google Scholar] [CrossRef]
- Yuan, L.; Yang, G.; Li, H.; Zhang, Z. Spatio-Temporal Variation Analysis of Precipitation during 1960–2008 in the Poyang Lake Basin, China. Open J. Mod. Hydrol. 2016, 6, 115–127. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Herrnegger, M.; Sampson, A.K.; Hochreiter, S.; Nearing, G.S. Toward improved predictions in ungauged basins: Exploiting the power of machine learning. Water Resour. Res. 2019, 55, 11344–11354. [Google Scholar] [CrossRef]
- Hsu, K.l.; Gupta, H.V.; Sorooshian, S. Artificial neural network modeling of the rainfall-runoff process. Water Resour. Res. 1995, 31, 2517–2530. [Google Scholar] [CrossRef]
- Yuan, L.; Forshay, K. Enhanced streamflow prediction with SWAT using support vector regression for spatial calibration: A case study in the Illinois River watershed, U.S. PLoS ONE 2021, 16, e0248489. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Noraini, I.; Norhaiza, A. Comparative performance of support vector regressions for accurate streamflow predictions. Malays. J. Fundam. Appl. Sci. 2017, 325–330. [Google Scholar]
- Misra, D.; Oommen, T.; Agarwal, A.; Mishra, S.K.; Thompson, A.M. Application and Analysis of Support Vector Machine Based Simulation for Runoff and Sediment Yield. Biosyst. Eng. 2009, 103, 527–535. [Google Scholar] [CrossRef]
- Zhang, X.; Srinivasan, R.; Van Liew, M. Approximating SWAT model using artificial neural network and support vector machine. J. Am. Water Resour. Assoc. 2009, 45, 460–474. [Google Scholar] [CrossRef]
- Yuan, L.; Li, W.; Zhang, Q.; Zou, L. Debris flow hazard assessment based on support vector machine. In Proceedings of the IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 4221–4224. [Google Scholar]
- Raghavendra, N.S.; Deka, P.C. Support vector machine applications in the field of hydrology: A review. Appl. Soft Comput. 2014, 19, 372–386. [Google Scholar] [CrossRef]
- Shabri, A.; Suhartono. Streamflow forecasting using least-squares support vector machines. Hydrol. Sci. J. 2012, 57, 1275–1293. [Google Scholar] [CrossRef]
- Chiogna, G.; Marcolini, G.; Liu, W.; Perez Ciria, T.; Tuo, Y. Coupling hydrological modeling and support vector regression to model hydropeaking in alpine catchments. Sci. Total Environ. 2018, 633, 220–229. [Google Scholar] [CrossRef]
- Nourani, V.; Alizadeh, F.; Roushangar, K. Evaluation of a two-stage SVM and spatial statistics methods for modeling monthly river suspended sediment load. Water Resour. Manag. 2015, 30, 393–407. [Google Scholar] [CrossRef]
- USGS Water Data for the Nation. Available online: https://nwis.waterdata.usgs.gov (accessed on 18 January 2018).
- Hrachowitz, M.; Savenije, H.H.G.; Blöschl, G.; McDonnell, J.J.; Sivapalan, M.; Pomeroy, J.W.; Arheimer, B.; Blume, T.; Clark, M.P.; Ehret, U.; et al. A decade of Predictions in Ungauged Basins (PUB)—A review. Hydrol. Sci. J. 2013, 58, 1198–1255. [Google Scholar] [CrossRef]
- Devia, G.K.; Ganasri, B.P.; Dwarakish, G.S. A Review on Hydrological Models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, P.; Chen, G.; Guo, L. Evaluating a coupled discrete wavelet transform and support vector regression for daily and monthly streamflow forecasting. J. Hydrol. 2014, 519, 2822–2831. [Google Scholar] [CrossRef]
- Zhu, S.; Zhou, J.; Ye, L.; Meng, C. Streamflow estimation by support vector machine coupled with different methods of time series decomposition in the upper reaches of Yangtze River, China. Environ. Earth Sci. 2016, 75, 531. [Google Scholar] [CrossRef]
- Sun, Y.; Niu, J.; Sivakumar, B. A comparative study of models for short-term streamflow forecasting with emphasis on wavelet-based approach. Stoch. Environ. Res. Risk Assess. 2019, 33, 1875–1891. [Google Scholar] [CrossRef]
- Nalley, D.; Adamowski, J.; Khalil, B.; Biswas, A. A comparison of conventional and wavelet transform based methods for streamflow record extension. J. Hydrol. 2020, 582, 124503. [Google Scholar] [CrossRef]
- Quilty, J.; Adamowski, J. Addressing the incorrect usage of wavelet-based hydrological and water resources forecasting models for real-world applications with best practices and a new forecasting framework. J. Hydrol. 2018, 563, 336–353. [Google Scholar] [CrossRef]
- Yuan, L.; Sinshaw, T.; Forshay, K.J. Review of watershed-scale water quality and nonpoint source pollution models. Geosciences 2020, 10, 25. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.; Van Griensven, A.; Van Liew, M.W. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Abbaspour, K.C. SWAT-CUP: SWAT Calibration and Uncertainty Programs—A User Manual; Eawag: Swiss Federal Institute of Aquatic Science and Technology: Zurich, Switzerland, 2015. [Google Scholar]
- Yuan, L.; Forshay, K.J. Using SWAT to evaluate streamflow and lake sediment loading in the Xinjiang River basin with limited data. Water 2019, 12, 39. [Google Scholar] [CrossRef]
- Jajarmizadeh, M.; Kakaei Lafdani, E.; Harun, S.; Ahmadi, A. Application of SVM and SWAT models for monthly streamflow prediction, a case study in South of Iran. KSCE J. Civ. Eng. 2014, 19, 345–357. [Google Scholar] [CrossRef]
- Jimeno-Sáez, P.; Senent-Aparicio, J.; Pérez-Sánchez, J.; Pulido-Velazquez, D. A comparison of SWAT and ANN models for daily runoff simulation in different climatic zones of peninsular Spain. Water 2018, 10, 192. [Google Scholar] [CrossRef]
- Noori, N.; Kalin, L. Coupling SWAT and ANN models for enhanced daily streamflow prediction. J. Hydrol. 2016, 533, 141–151. [Google Scholar] [CrossRef]
- Gassman, P.W.; Balmer, C.; Siemers, M.; Srinivasan, R. The SWAT literature database: Overview of database structure and key SWAT literature trends. In Proceedings of the SWAT 2014 Conference, Pernambuco, Brazil, 28 July–1 August 2014; Available online: http://swat.tamu.edu/conferences/2014/ (accessed on 27 June 2018).
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; TR-406; Texas Water Resources Institute: College Station, TX, USA, 2009. [Google Scholar]
- Soil Conservation Service. National Engineering Handbook; United States Department of Agriculture: Washington, DC, USA, 1972; Section 4 Hydrology.
- Storm, D.E.; Busteed, P.R.; Mittelstet, A.R.; White, M.J. Hydrologic Modeling of the Oklahoma/Arkansas Illinois River Basin Using SWAT 2005; Oklahoma Department of Environmental Quality: Stillwater, OK, USA, 2010. [Google Scholar]
- Mittelstet, A.R.; Storm, D.E.; White, M.J. Using SWAT to enhance watershed-based plans to meet numeric water quality standards. Sustain. Water Qual. Ecol. 2016, 7, 5–21. [Google Scholar] [CrossRef] [Green Version]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Danandeh Mehr, A.; Nourani, V.; Karimi Khosrowshahi, V.; Ghorbani, M.A. A hybrid support vector regression–firefly model for monthly rainfall forecasting. Int. J. Environ. Sci. Technol. 2018, 16, 335–346. [Google Scholar] [CrossRef]
- Hsu, C.-W.; Chang, C.-C.; Lin, C.-J. A Practical Guide to Support Vector Classification; Department of Computer Science, National Taiwan University: Taipei, Taiwan, 2003. [Google Scholar]
- Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F. e1071: Misc Functions of the Department of Statistics, Probability Theory Group (Formerly: E1071); Rstudio: Boston, MA, USA, 2019. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; Rstudio: Boston, MA, USA, 2022. [Google Scholar]
- Liu, Z.; Menzel, L. Identifying long-term variations in vegetation and climatic variables and their scale-dependent relationships: A case study in Southwest Germany. Glob. Planet. Chang. 2016, 147, 54–66. [Google Scholar] [CrossRef]
- Makwana, J.J.; Tiwari, M.K. Intermittent Streamflow Forecasting and Extreme Event Modelling using Wavelet based Artificial Neural Networks. Water Resour. Manag. 2014, 28, 4857–4873. [Google Scholar] [CrossRef]
- Labat, D. Recent advances in wavelet analyses: Part 1. A review of concepts. J. Hydrol. 2005, 314, 275–288. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Nourani, V.; Komasi, M.; Mano, A. A multivariate ANN-Wavelet approach for rainfall–runoff modeling. Water Resour. Manag. 2009, 23, 2877–2894. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M. hydroGOF: Goodness-of-Fit Functions for Comparison of Simulated and Observed Hydrological Time Series; Rstudio: Boston, MA, USA, 2017. [Google Scholar]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Kisi, O.; Cimen, M. A wavelet-support vector machine conjunction model for monthly streamflow forecasting. J. Hydrol. 2011, 399, 132–140. [Google Scholar] [CrossRef]
- De Macedo Machado Freire, P.K.; Santos, C.A.G.; da Silva, G.B.L. Analysis of the use of discrete wavelet transforms coupled with ANN for short-term streamflow forecasting. Appl. Soft Comput. 2019, 80, 494–505. [Google Scholar] [CrossRef]
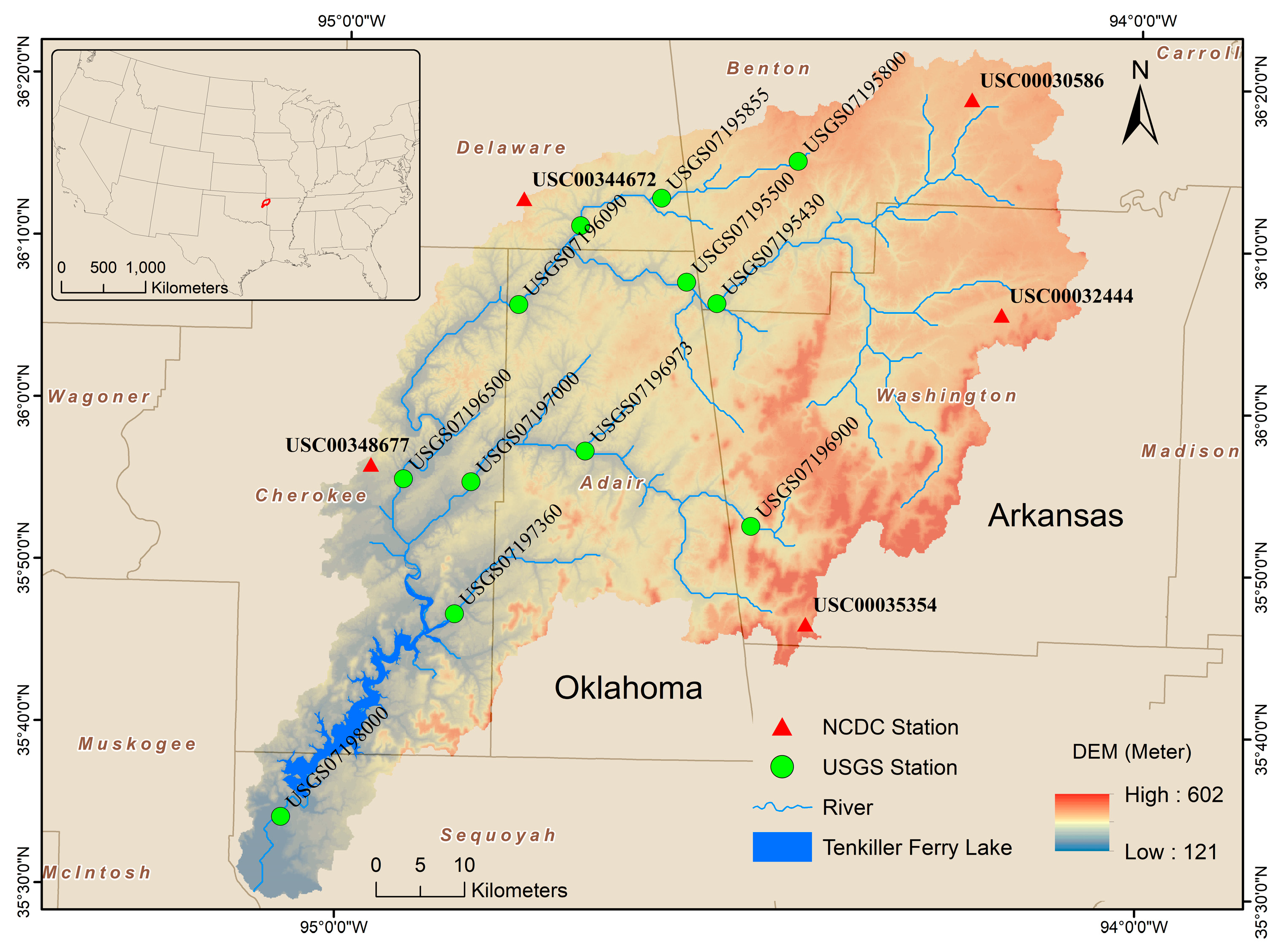



| No. | USGS Station | Upstream Area (km2) | Data Period (month.year) | Number of Data | Average Monthly Streamflow (m3 s−1) | Flow Descriptive Statistics (m3 s−1) | |||
|---|---|---|---|---|---|---|---|---|---|
| Max | Min | Median | Standard Deviation | ||||||
| 1 | 07195800 | 36.8 | 1.1995–12.2013 | 228 | 0.41 | 2.90 | 0.05 | 0.25 | 0.44 |
| 2 | 07195855 | 155.0 | 1.1995–12.2013 | 228 | 1.27 | 9.53 | 0.11 | 0.74 | 1.43 |
| 3 | 07196000 | 300.7 | 1.1995–12.2013 | 228 | 3.01 | 22.26 | 0.42 | 1.78 | 3.25 |
| 4 | 07195500 | 1633.0 | 1.1995–12.2013 | 228 | 18.71 | 149.42 | 2.73 | 10.75 | 20.02 |
| 5 | 07195430 | 1490.5 | 1.1996–12.2013 | 216 | 17.68 | 144.61 | 1.89 | 10.58 | 19.29 |
| 6 | 07196090 | 2138.5 | 7.2010–12.2013 | 42 | 23.19 | 178.54 | 2.95 | 11.77 | 33.59 |
| 7 | 07196973 | 64.8 | 1.1995–12.2002 | 96 | 0.66 | 3.57 | 0.00 | 0.38 | 0.75 |
| 8 | 07196500 | 2462.5 | 1.1995–12.2013 | 228 | 27.76 | 190.80 | 2.99 | 17.09 | 30.17 |
| 9 | 07197000 | 808.7 | 1.1995–12.2013 | 228 | 9.27 | 69.73 | 0.33 | 4.93 | 11.44 |
| 10 | 07196900 | 105.2 | 1.1995–12.2013 | 228 | 1.31 | 10.35 | 0.00 | 0.59 | 1.76 |
| 11 | 07197360 | 233.8 | 1.1998–12.2013 | 192 | 2.41 | 15.18 | 0.10 | 1.46 | 2.88 |
| 12 | 07198000 | 4186.2 | 1.1995–12.2013 | 228 | 44.03 | 378.65 | 0.98 | 25.59 | 46.81 |
| No. | Parameter Name † | Parameter Description | Range | Fitted Value |
|---|---|---|---|---|
| 1 | R__CN2.mgt | SCS runoff curve number II | −0.25–0.25 | −0.179 |
| 2 | V__GWQMN.gw | Threshold depth of water in the shallow aquifer required for return flow to occur (mm H2O) | 0–2000 | 1764 |
| 3 | V__GW_REVAP.gw | Groundwater “revap” coefficient | 0.02–0.2 | 0.135 |
| 4 | V__REVAPMN.gw | Threshold depth of water in the shallow aquifer for ‘revap’ to occur (mm) | 0–500 | 121 |
| 5 | V__EPCO.hru | Plant uptake compensation factor | 0–1 | 0.154 |
| 6 | V_ESCO.hru | Soil evaporation compensation factor | 0–1 | 0.354 |
| 7 | R__SOL_AWC (1).sol | Available water capacity of the 1st soil layer (mm H2O mm soil−1) | 0.08–0.2 | 0.177 |
| 8 | A__OV_N.hru | Manning’s “n” value for overland flow | 0.01–30 | 26.941 |
| 9 | R__HRU_SLP.hru | Average slope steepness (m m−1) | 0–1 | 0.034 |
| Indicator Name | Calculation Equation † | Description |
|---|---|---|
| Pearson’s Correlation Coefficient (r) | Range [−1, 1] | |
| Nash–Sutcliffe efficiency (NSE) | Range (−∞, 1], and 1 is the optimal value | |
| Percent Bias (PBIAS) | Range (−∞, +∞), and 0 is the optimal value | |
| RMSE-observations standard deviation ratio (RSR) | Range [0, +∞), and 0 is the optimal value | |
| Root Mean Square Error (RMSE) | Range [0, +∞), and 0 is the optimal value |
| Station | SWAT-CUP | SWAT-SVR | SWAT-WSVR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RSR | NSE | PBIAS | RMSE (m3 s−1) | RSR | NSE | PBIAS | RMSE (m3 s−1) | RSR | NSE | PBIAS | RMSE (m3 s−1) | ||
| Calibration | 07195800 | 0.76 | 0.41 | 24.00 | 0.33 | 0.58 | 0.68 | −10.80 | 0.25 | 0.08 | 0.99 | −1.90 | 0.04 |
| 07195855 | 0.95 | 0.09 | 66.50 | 1.32 | 0.63 | 0.60 | −10.00 | 0.88 | 0.01 | 1.00 | 0.10 | 0.01 | |
| 07196000 | 0.96 | 0.07 | 67.90 | 3.18 | 0.57 | 0.68 | 0.50 | 1.88 | 0.01 | 1.00 | 0.10 | 0.02 | |
| 07195500 | 0.74 | 0.46 | 44.60 | 13.68 | 0.55 | 0.70 | −5.50 | 10.23 | 0.01 | 1.00 | 0.10 | 0.23 | |
| 07195430 | 0.67 | 0.54 | 29.30 | 11.40 | 0.55 | 0.70 | −5.30 | 9.30 | 0.01 | 1.00 | 0.20 | 0.22 | |
| 07196090 | 0.52 | 0.72 | 31.40 | 19.81 | 0.14 | 0.98 | −3.30 | 5.18 | 0.02 | 1.00 | −0.60 | 0.70 | |
| 07196973 | 10.70 | −0.15 | 69.90 | 0.78 | 0.73 | 0.46 | −6.50 | 0.53 | 0.02 | 1.00 | 0.20 | 0.01 | |
| 07196500 | 0.78 | 0.39 | 52.30 | 22.62 | 0.58 | 0.67 | −10.20 | 16.71 | 0.02 | 1.00 | 0.10 | 0.48 | |
| 07197000 | 0.87 | 0.24 | 69.50 | 10.04 | 0.57 | 0.67 | −11.80 | 6.64 | 0.01 | 1.00 | 0.10 | 0.09 | |
| 07196900 | 0.93 | 0.14 | 86.00 | 1.69 | 0.57 | 0.68 | −13.60 | 1.04 | 0.01 | 1.00 | 0.00 | 0.02 | |
| 07197360 | 0.97 | 0.06 | 74.90 | 2.89 | 0.70 | 0.51 | −21.30 | 2.07 | 0.00 | 1.00 | 0.00 | 0.01 | |
| 07198000 | 1.17 | −0.39 | 74.50 | 50.21 | 0.78 | 0.39 | −15.90 | 33.42 | 0.03 | 1.00 | −0.20 | 1.41 | |
| Mean | 1.67 | 0.22 | 57.57 | 11.50 | 0.58 | 0.64 | −9.48 | 7.34 | 0.02 | 1.00 | −0.15 | 0.27 | |
| Validation | 07195800 | 0.85 | 0.26 | 8.70 | 0.35 | 0.89 | 0.20 | −20.40 | 0.36 | 0.11 | 0.99 | −2.90 | 0.04 |
| 07195855 | 0.89 | 0.19 | 22.80 | 1.35 | 0.81 | 0.33 | −27.00 | 1.23 | 0.09 | 0.99 | −1.10 | 0.14 | |
| 07196000 | 0.98 | 0.03 | 29.60 | 3.03 | 0.86 | 0.24 | −16.00 | 2.68 | 0.14 | 0.98 | −1.00 | 0.43 | |
| 07195500 | 0.59 | 0.65 | 15.40 | 13.59 | 0.58 | 0.65 | −20.50 | 13.48 | 0.24 | 0.94 | −4.60 | 5.49 | |
| 07195430 | 0.58 | 0.66 | −6.70 | 13.88 | 0.58 | 0.68 | −23.80 | 13.74 | 0.24 | 0.94 | −4.80 | 5.77 | |
| 07196090 | 0.71 | 0.45 | 38.30 | 14.32 | 1.15 | −0.43 | −41.70 | 23.16 | 0.12 | 0.98 | 0.70 | 2.47 | |
| 07196973 | 1.03 | −0.10 | 62.30 | 0.83 | 0.87 | 0.22 | −15.70 | 0.69 | 0.06 | 1.00 | 0.70 | 0.05 | |
| 07196500 | 0.66 | 0.56 | 19.70 | 21.55 | 0.63 | 0.60 | −25.50 | 20.62 | 0.13 | 0.98 | −2.20 | 4.28 | |
| 07197000 | 0.88 | 0.22 | 64.80 | 9.84 | 0.72 | 0.47 | −6.30 | 8.07 | 0.10 | 0.99 | −0.40 | 1.17 | |
| 07196900 | 1.07 | −0.17 | 87.90 | 1.72 | 0.96 | 0.06 | 3.60 | 1.54 | 0.05 | 0.99 | 0.60 | 0.08 | |
| 07197360 | 0.88 | 0.21 | 55.80 | 2.34 | 0.66 | 0.58 | −25.10 | 1.76 | 0.07 | 0.99 | −1.40 | 0.18 | |
| 07198000 | 0.90 | 0.18 | 33.20 | 49.62 | 0.84 | 0.29 | −29.80 | 48.22 | 0.27 | 0.93 | −6.10 | 14.81 | |
| Mean | 0.84 | 0.26 | 35.98 | 11.04 | 0.80 | 0.32 | −20.68 | 11.30 | 0.14 | 0.98 | −1.88 | 2.91 | |
| The whole series data † | 07195800 | 0.79 | 0.37 | 19.50 | 0.33 | 0.68 | 0.53 | −13.60 | 0.29 | 0.09 | 0.99 | −2.20 | 0.04 |
| 07195855 | 0.93 | 0.13 | 52.30 | 1.33 | 0.70 | 0.51 | −15.50 | 1.00 | 0.06 | 1.00 | −0.30 | 0.08 | |
| 07196000 | 0.97 | 0.06 | 55.90 | 3.13 | 0.66 | 0.56 | −4.60 | 2.15 | 0.07 | 0.99 | −0.30 | 0.24 | |
| 07195500 | 0.68 | 0.53 | 35.00 | 13.65 | 0.56 | 0.68 | −10.40 | 11.30 | 0.15 | 0.98 | −1.50 | 3.00 | |
| 07195430 | 0.63 | 0.60 | 16.80 | 12.19 | 0.56 | 0.68 | −11.70 | 10.81 | 0.16 | 0.97 | −1.60 | 3.15 | |
| 07196090 | 0.55 | 0.69 | 33.50 | 18.41 | 0.39 | 0.84 | −14.70 | 13.13 | 0.04 | 1.00 | −0.30 | 1.45 | |
| 07196973 | 1.06 | −0.14 | 67.80 | 0.79 | 0.78 | 0.38 | −9.10 | 0.58 | 0.04 | 1.00 | 0.30 | 0.03 | |
| 07196500 | 0.74 | 0.45 | 41.80 | 22.31 | 0.60 | 0.64 | −15.10 | 17.97 | 0.08 | 0.99 | −0.60 | 2.36 | |
| 07197000 | 0.87 | 0.24 | 68.20 | 9.98 | 0.62 | 0.61 | −10.30 | 7.90 | 0.06 | 1.00 | −0.10 | 0.64 | |
| 07196900 | 0.97 | 0.06 | 86.50 | 1.70 | 0.69 | 0.53 | −8.70 | 1.21 | 0.03 | 1.00 | 0.20 | 0.05 | |
| 07197360 | 0.95 | 0.10 | 69.50 | 2.73 | 0.69 | 0.52 | −22.40 | 1.98 | 0.03 | 1.00 | −0.40 | 0.10 | |
| 07198000 | 1.07 | −1.50 | 61.20 | 50.03 | 0.81 | 0.35 | −20.30 | 37.70 | 0.17 | 0.97 | −2.10 | 8.17 | |
| Mean | 0.85 | 0.13 | 50.67 | 11.38 | 0.65 | 0.57 | −13.03 | 8.84 | 0.08 | 0.99 | −0.74 | 1.61 | |
| Station | SWAT-SVR | SWAT-WSVR | |||||
|---|---|---|---|---|---|---|---|
| Model Input † | C | γ | Model Input | Decomposition Levels | C | γ | |
| 07195800 | Flow + Prec | 36.015625 | 3 | Prec + D1 + D2 + D3 + A3 | 3 | 5.015625 | 1 |
| 07195855 | Flow + Prec | 22.015625 | 1 | Prec + D1 + D2 + D3 + A3 | 3 | 2.015625 | 3 |
| 07196000 | Flow + Prec | 255.015625 | 1 | Prec + D1 + D2 + D3 + A3 | 3 | 255.015625 | 1 |
| 07195500 | Flow + Prec | 103.015625 | 1 | Prec + D1 + D2 + D3 + A3 | 3 | 96.015625 | 1 |
| 07195430 | Flow + Prec | 255.015625 | 1 | Prec + D1 + D2 + D3 + A3 | 3 | 87.015625 | 1 |
| 07196090 | Flow + Prec | 255.015625 | 5 | Prec + D1 + D2 + A2 | 2 | 255.015625 | 1 |
| 07196973 | Flow + Prec | 2.015625 | 1 | Prec + D1 + D2 + A2 | 2 | 5.015625 | 1 |
| 07196500 | Flow + Prec | 130.015625 | 1 | Prec + D1 + D2 + D3 + A3 | 3 | 125.015625 | 1 |
| 07197000 | Flow + Prec | 57.015625 | 1 | Prec + D1 + D2 + D3 + A3 | 3 | 242.015625 | 1 |
| 07196900 | Flow + Prec | 4.015625 | 14 | Prec + D1 + D2 + D3 + A3 | 3 | 15.015625 | 1 |
| 07197360 | Flow + Prec | 13.015625 | 1 | Prec + D1 + D2 + D3 + A3 | 3 | 35.015625 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, L.; Forshay, K.J. Evaluating Monthly Flow Prediction Based on SWAT and Support Vector Regression Coupled with Discrete Wavelet Transform. Water 2022, 14, 2649. https://doi.org/10.3390/w14172649
Yuan L, Forshay KJ. Evaluating Monthly Flow Prediction Based on SWAT and Support Vector Regression Coupled with Discrete Wavelet Transform. Water. 2022; 14(17):2649. https://doi.org/10.3390/w14172649
Chicago/Turabian StyleYuan, Lifeng, and Kenneth J. Forshay. 2022. "Evaluating Monthly Flow Prediction Based on SWAT and Support Vector Regression Coupled with Discrete Wavelet Transform" Water 14, no. 17: 2649. https://doi.org/10.3390/w14172649
APA StyleYuan, L., & Forshay, K. J. (2022). Evaluating Monthly Flow Prediction Based on SWAT and Support Vector Regression Coupled with Discrete Wavelet Transform. Water, 14(17), 2649. https://doi.org/10.3390/w14172649









