Analysis of Irrigation Performance of a Solid-Set Sprinkler Irrigation System at Different Experimental Conditions
Abstract
:1. Introduction
2. Materials and Methods
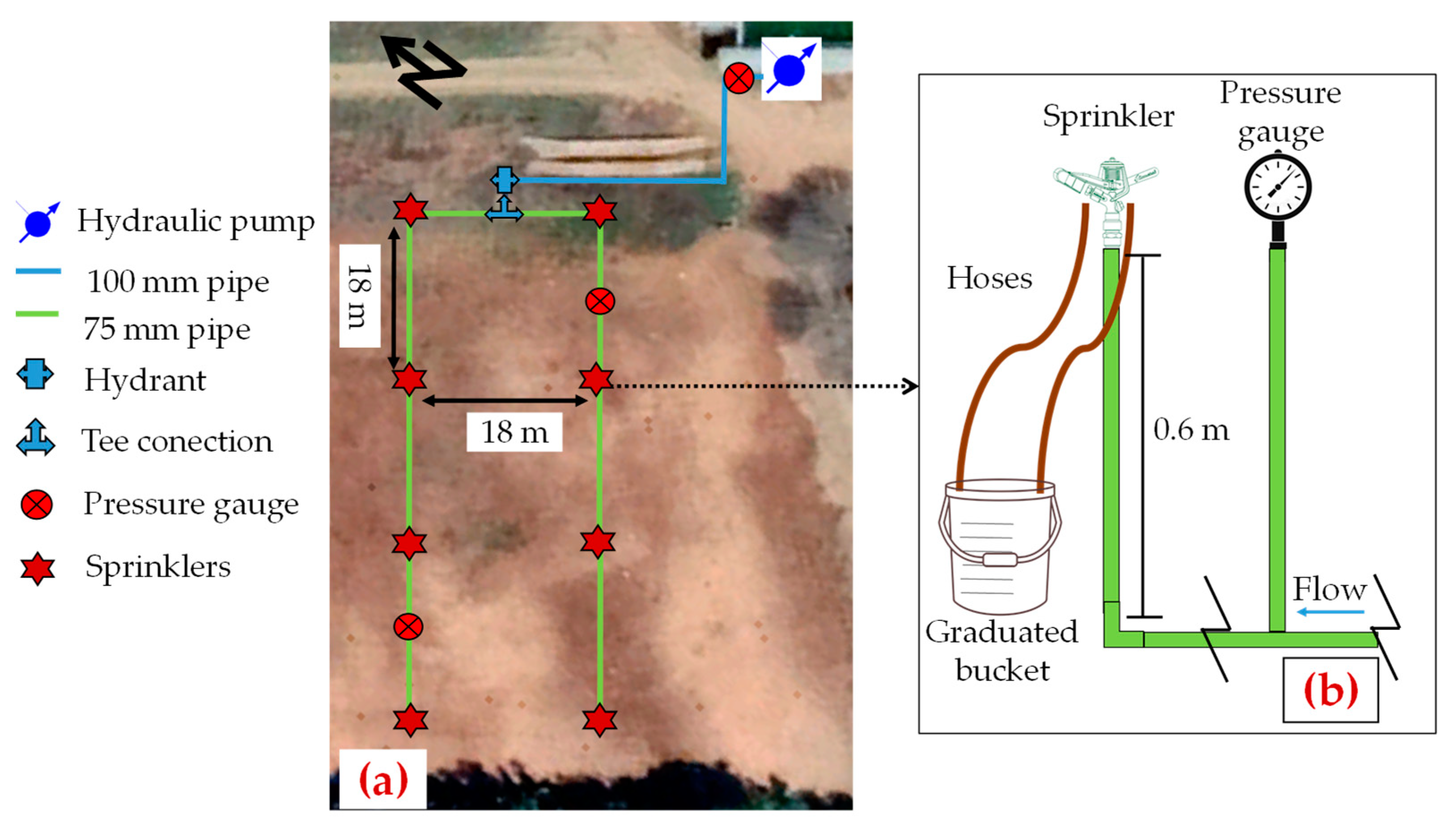
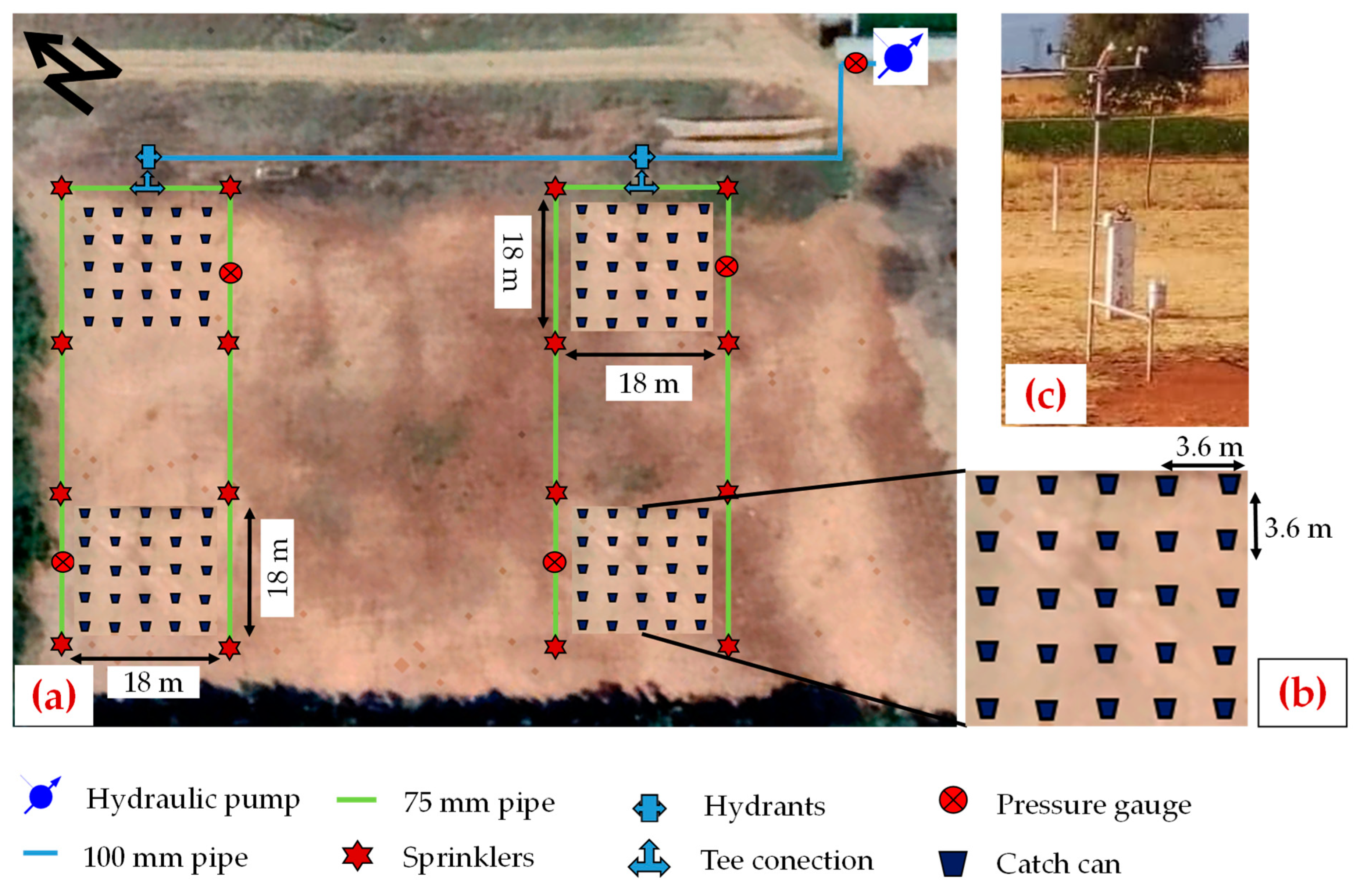
2.1. Field Solid-Set Experiments
2.2. Isolated Sprinkler Flow Measurements
2.3. Irrigation Performance Measurements
2.4. Data Analysis
3. Results and Discussion
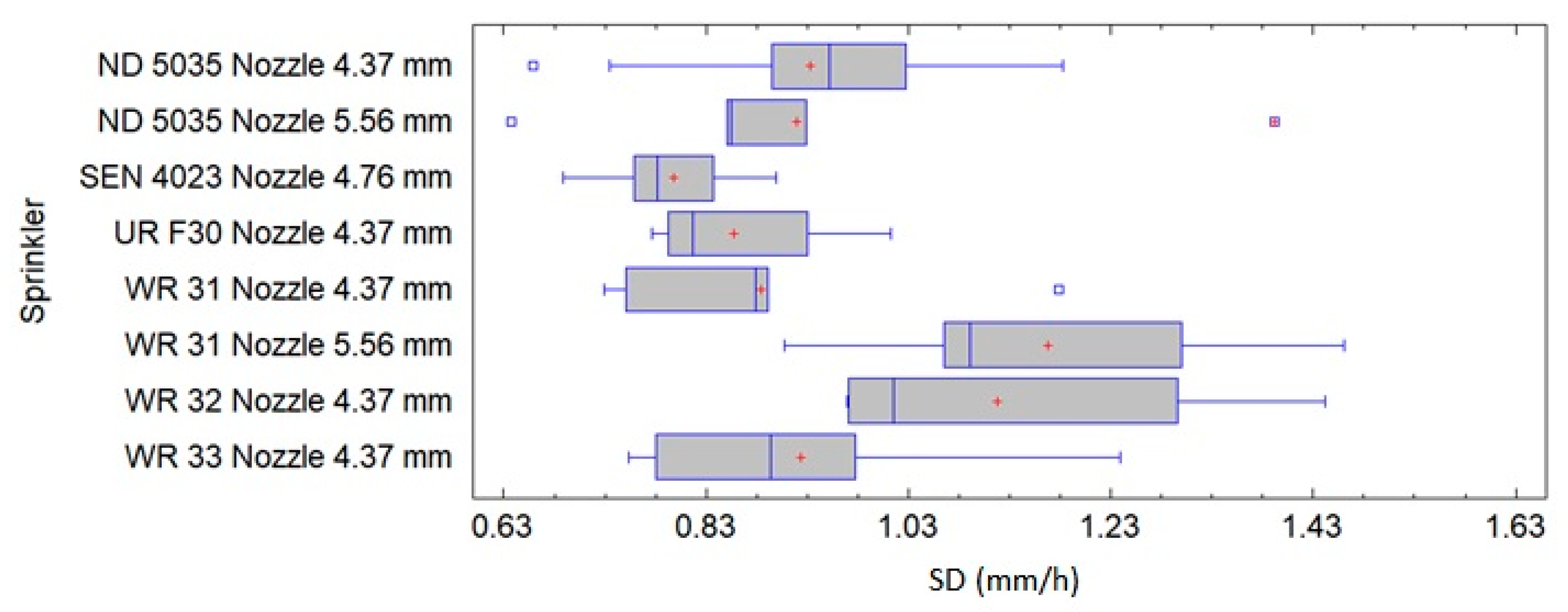
3.1. Sprinklers Flow
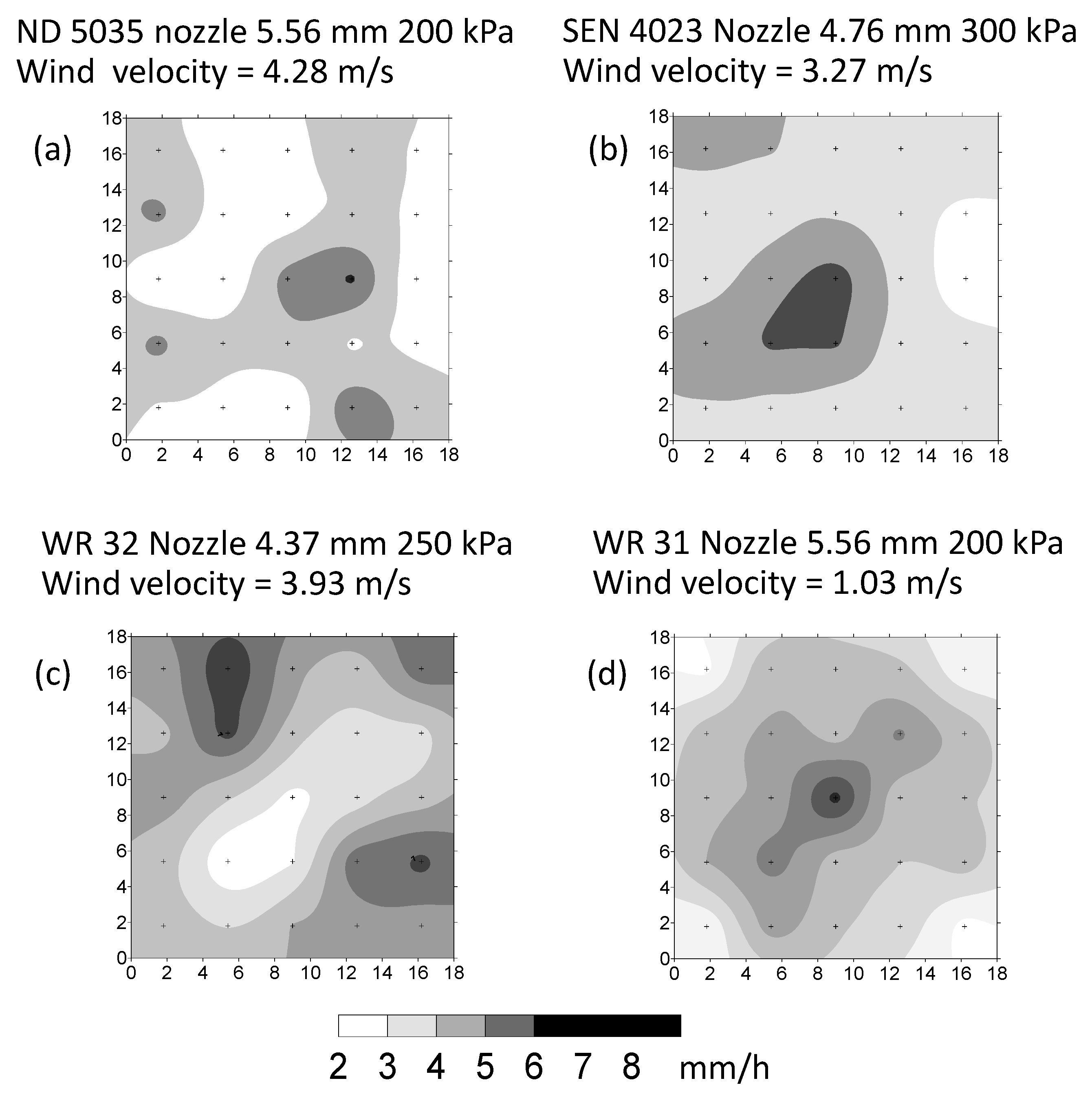
3.2. Sprinklers’ Water Distribution Patterns
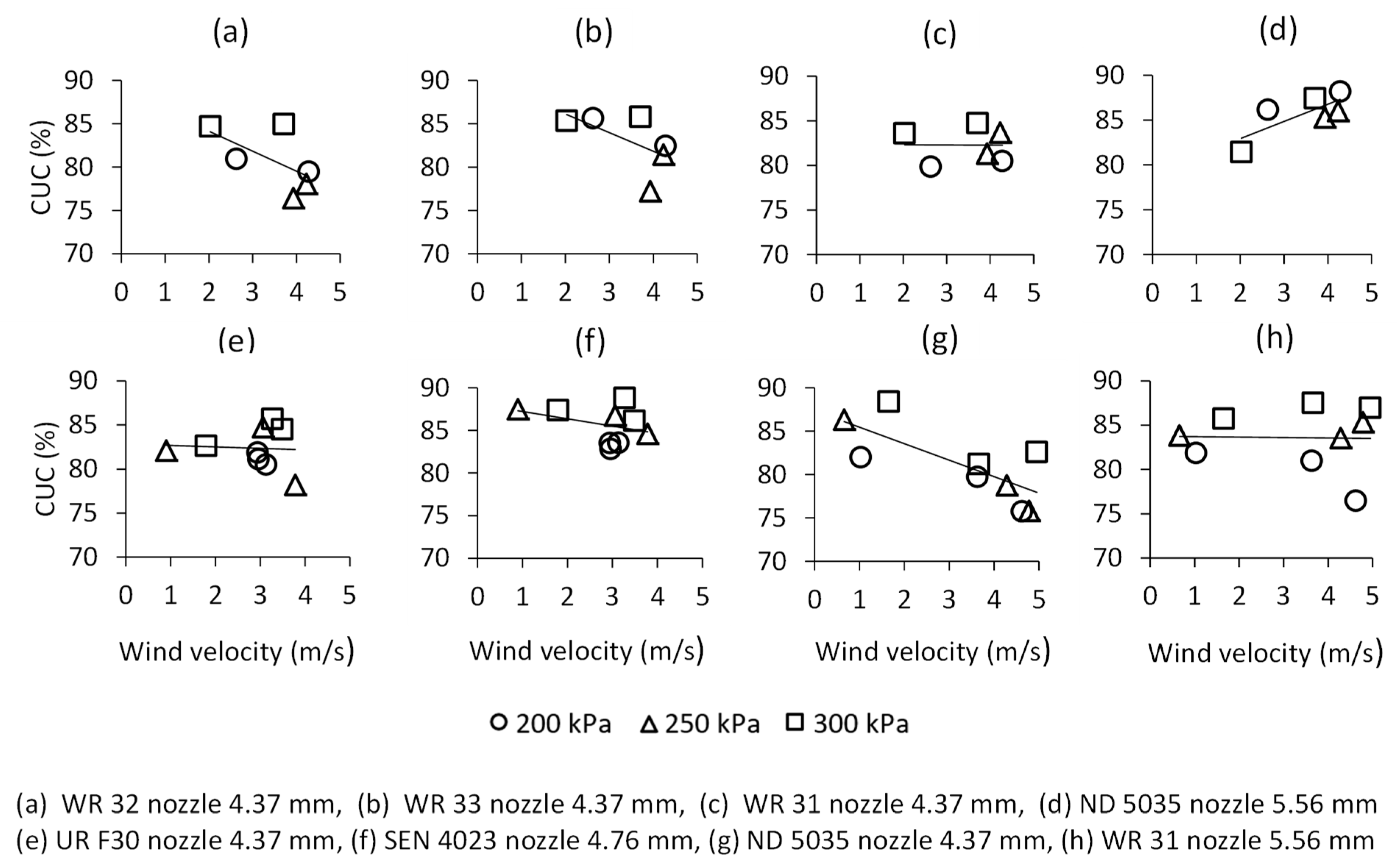
3.3. Irrigation Performance Based on CUC
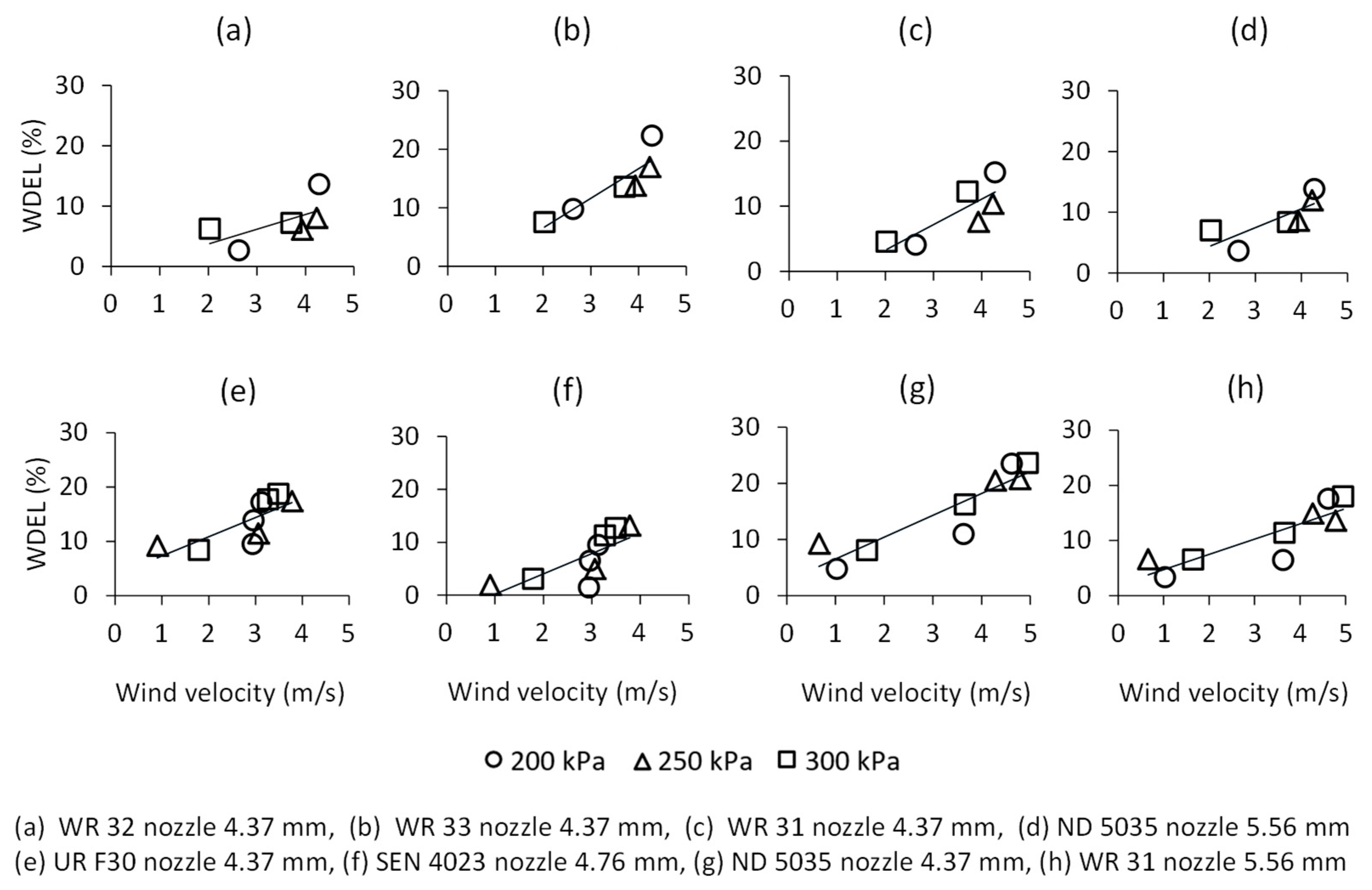
3.4. Wind Drift and Evaporation Losses
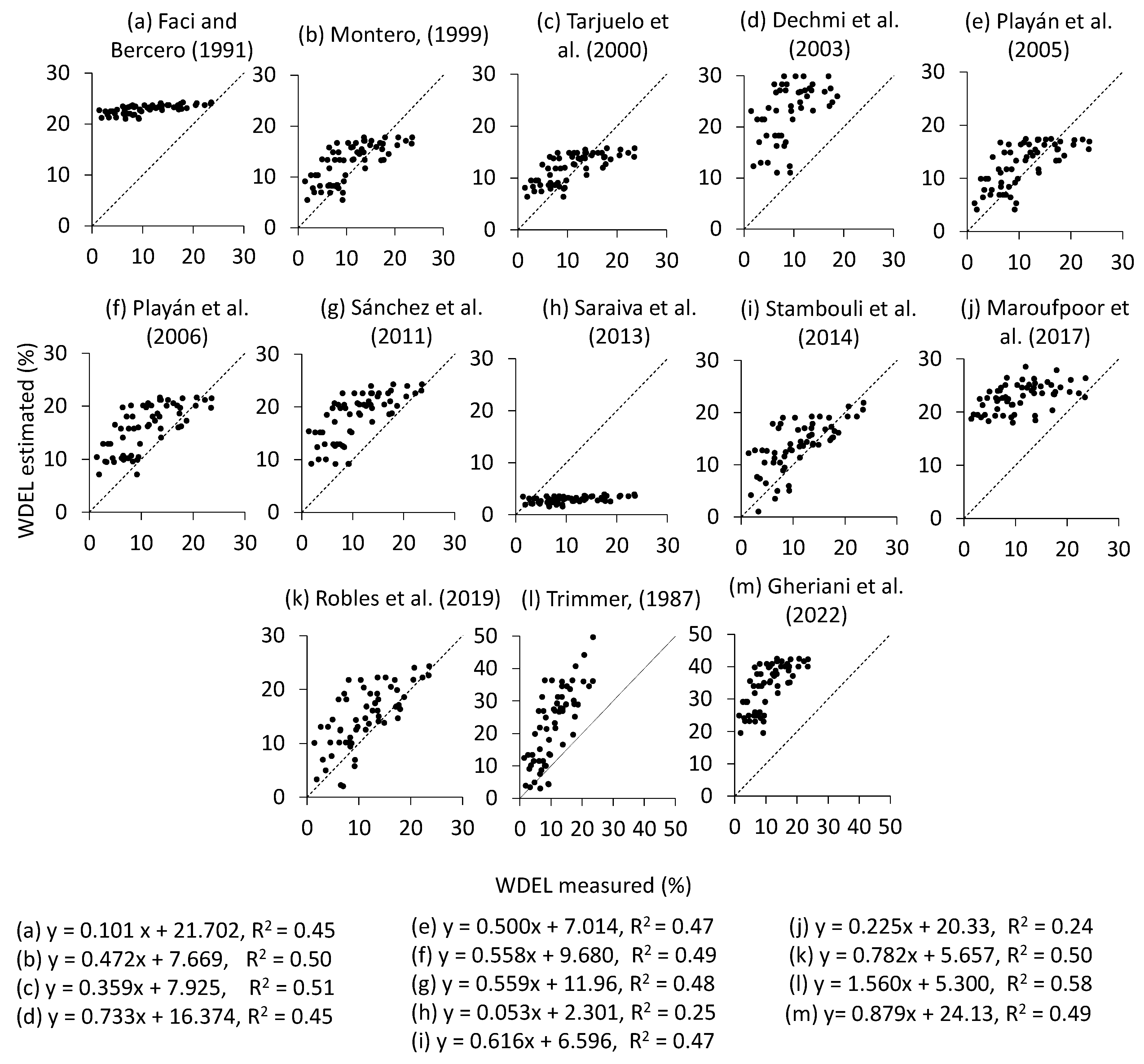
3.5. Comparison between CUC Models
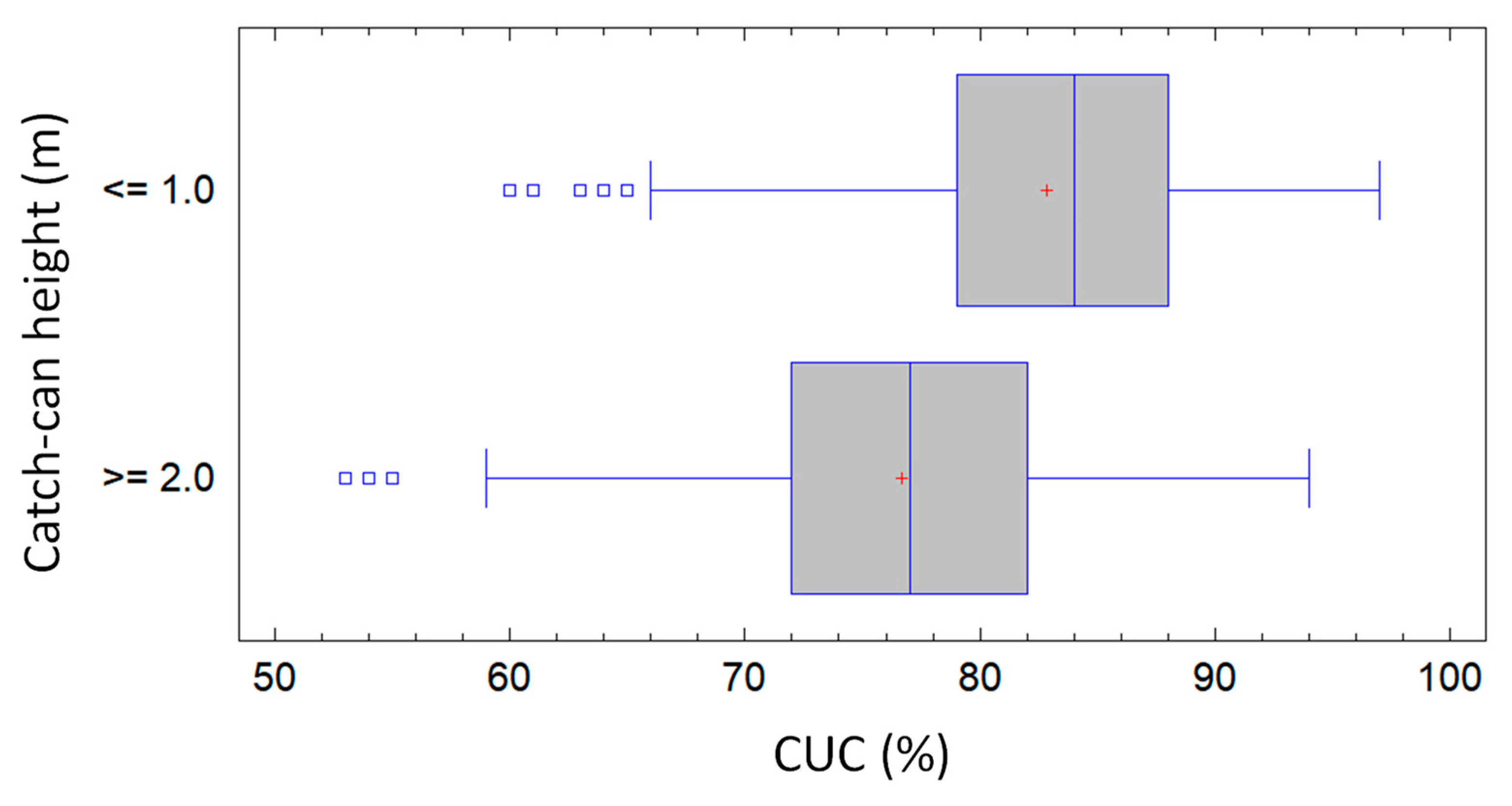
3.6. Influence of the Catch-Can Height on Irrigation Performance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Sprinkler | Nozzle (mm) | Pressure | Wind Velocity | T | RH | CUC | DU | WDEL | |
|---|---|---|---|---|---|---|---|---|---|
| Main | Auxiliary | (kPa) | (m/s) | (°C) | (%) | (%) | (%) | (%) | |
| WR 32 | 4.37 | 3.18 | 200 | 2.63 | 17.70 | 69.29 | 80.95 | 71.94 | 2.66 |
| 200 | 4.28 | 24.09 | 41.55 | 79.48 | 72.15 | 13.62 | |||
| 250 | 3.93 | 19.86 | 64.44 | 76.41 | 65.81 | 6.10 | |||
| 250 | 4.23 | 24.39 | 46.14 | 78.07 | 67.99 | 8.05 | |||
| 300 | 2.03 | 16.41 | 77.86 | 84.69 | 79.48 | 6.25 | |||
| 300 | 3.71 | 22.79 | 52.34 | 84.95 | 76.87 | 7.21 | |||
| WR 33 | 4.37 | 3.18 | 200 | 2.63 | 17.70 | 69.29 | 85.64 | 77.73 | 9.79 |
| 200 | 4.28 | 24.09 | 41.55 | 82.47 | 74.22 | 22.31 | |||
| 250 | 3.93 | 19.86 | 64.44 | 77.23 | 63.97 | 13.80 | |||
| 250 | 4.23 | 24.39 | 46.14 | 81.46 | 71.74 | 16.96 | |||
| 300 | 2.03 | 16.41 | 77.86 | 85.36 | 79.00 | 7.52 | |||
| 300 | 3.71 | 22.79 | 52.34 | 85.80 | 77.47 | 13.57 | |||
| WR 31 | 4.37 | 3.18 | 200 | 2.63 | 17.70 | 69.29 | 79.85 | 66.63 | 4.09 |
| 200 | 4.28 | 24.09 | 41.55 | 80.49 | 73.92 | 15.18 | |||
| 250 | 3.93 | 19.86 | 64.44 | 81.33 | 76.60 | 7.62 | |||
| 250 | 4.23 | 24.39 | 46.14 | 83.67 | 77.97 | 10.37 | |||
| 300 | 2.03 | 16.41 | 77.86 | 83.6 | 73.55 | 4.53 | |||
| 300 | 3.71 | 22.79 | 52.34 | 84.73 | 75.15 | 12.25 | |||
| ND 5035 | 5.56 | 2.50 | 200 | 2.63 | 17.70 | 69.29 | 86.15 | 82.92 | 3.64 |
| 200 | 4.28 | 24.09 | 41.55 | 88.18 | 84.41 | 13.81 | |||
| 250 | 3.93 | 19.86 | 64.44 | 85.30 | 79.39 | 8.61 | |||
| 250 | 4.23 | 24.39 | 46.14 | 86.01 | 80.92 | 11.99 | |||
| 300 | 2.03 | 16.41 | 77.86 | 81.45 | 71.89 | 7.00 | |||
| 300 | 3.71 | 22.79 | 52.34 | 87.44 | 82.09 | 8.36 | |||
| UR F30 | 4.37 | 3.18 | 200 | 2.94 | 16.20 | 82.73 | 81.88 | 75.37 | 9.49 |
| 200 | 2.96 | 20.11 | 65.84 | 81.12 | 74.98 | 13.87 | |||
| 200 | 3.13 | 22.41 | 58.06 | 80.50 | 73.80 | 17.18 | |||
| 250 | 0.90 | 15.28 | 84.63 | 82.10 | 71.97 | 9.21 | |||
| 250 | 3.06 | 22.59 | 55.29 | 84.76 | 77.86 | 11.49 | |||
| 250 | 3.78 | 23.85 | 50.21 | 78.20 | 69.46 | 17.40 | |||
| 300 | 1.79 | 16.80 | 79.04 | 82.63 | 75.23 | 8.39 | |||
| 300 | 3.27 | 21.86 | 58.01 | 85.68 | 78.31 | 17.73 | |||
| 300 | 3.49 | 23.69 | 54.71 | 84.50 | 78.75 | 18.75 | |||
| SEN 4023 | 4.76 | 2.38 | 200 | 2.94 | 16.20 | 82.73 | 83.53 | 75.76 | 1.44 |
| 200 | 2.96 | 20.11 | 65.84 | 82.84 | 75.22 | 6.49 | |||
| 200 | 3.13 | 22.41 | 58.06 | 83.54 | 75.57 | 9.46 | |||
| 250 | 0.90 | 15.28 | 84.63 | 87.48 | 79.75 | 1.91 | |||
| 250 | 3.06 | 22.59 | 55.29 | 86.74 | 81.82 | 4.96 | |||
| 250 | 3.78 | 23.85 | 50.21 | 84.61 | 76.13 | 13.16 | |||
| 300 | 1.79 | 16.80 | 79.04 | 87.37 | 81.16 | 3.07 | |||
| 300 | 3.27 | 21.86 | 58.01 | 88.81 | 86.47 | 11.27 | |||
| 300 | 3.49 | 23.69 | 54.71 | 86.14 | 81.50 | 12.67 | |||
| ND 5035 | 4.37 | 2.50 | 200 | 1.03 | 16.40 | 74.64 | 82.01 | 72.74 | 4.78 |
| 200 | 4.62 | 23.03 | 50.59 | 75.75 | 68.02 | 23.50 | |||
| 200 | 3.63 | 23.96 | 43.79 | 79.73 | 73.89 | 10.97 | |||
| 250 | 0.66 | 16.76 | 70.26 | 86.34 | 78.38 | 9.28 | |||
| 250 | 4.28 | 22.63 | 46.59 | 78.75 | 73.40 | 20.53 | |||
| 250 | 4.78 | 24.00 | 42.71 | 75.81 | 70.88 | 20.74 | |||
| 300 | 1.65 | 18.18 | 73.26 | 88.40 | 81.43 | 8.08 | |||
| 300 | 4.95 | 23.59 | 44.44 | 82.60 | 78.61 | 23.60 | |||
| 300 | 3.66 | 23.16 | 40.43 | 81.21 | 77.73 | 16.21 | |||
| WR 31 | 5.56 | 3.18 | 200 | 1.03 | 16.40 | 74.64 | 81.87 | 69.25 | 3.35 |
| 200 | 4.62 | 23.03 | 50.59 | 76.48 | 66.45 | 17.55 | |||
| 200 | 3.63 | 23.96 | 43.79 | 80.99 | 69.67 | 6.45 | |||
| 250 | 0.66 | 16.76 | 70.26 | 83.85 | 71.86 | 6.63 | |||
| 250 | 4.28 | 22.63 | 46.59 | 83.54 | 74.66 | 14.92 | |||
| 250 | 4.78 | 24.00 | 42.71 | 85.35 | 75.88 | 13.62 | |||
| 300 | 1.65 | 18.18 | 73.26 | 85.75 | 80.33 | 6.56 | |||
| 300 | 4.95 | 23.59 | 44.44 | 86.96 | 79.41 | 17.99 | |||
| 300 | 3.66 | 23.16 | 40.43 | 87.54 | 80.06 | 11.36 | |||
References
- ONU. Population. Available online: https://www.un.org/es/sections/issues-depth/population/index.html (accessed on 20 March 2020).
- Alexandratos, N.; Bruinsma, J. World Agricultural towards 2030–2050: The 2012 Revision; ESA Working Paper No. 12–03; FAO: Rome, Italy, 2012. [Google Scholar]
- AQUASAT. Water Use by Sector. Available online: https://www.fao.org/aquastat/statistics/query/index.html?lang=en (accessed on 27 May 2022).
- FAO. Strategy on Climate Change. July 2017. Available online: https://www.fao.org/3/i7175e/i7175e.pdf (accessed on 5 June 2022).
- Meehl, G.A.; Stocker, T.F.; Collins, W.D.; Friedlingstein, P.; Gaye, A.T.; Gregory, J.M.; Kitoh, A.; Knutti, R.; Murphy, J.M.; Noda, A.; et al. Global climate projections. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, 2nd ed.; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; pp. 748–845. Available online: https://www.ipcc.ch/site/assets/uploads/2018/02/ar4-wg1-chapter10-1.pdf (accessed on 8 June 2022).
- FAO. World Agriculture: Towards 2015/2030: An FAO Perspective. 2003. Available online: https://www.fao.org/3/y4252e/y4252e.pdf (accessed on 8 June 2022).
- FAO. Modernization of irrigation system operations. In Proceedings of the 5th ITIS Network International Meeting, Introduction: Modernization of Irrigation Systems: A Continuing Process, Aurangabad, India, 28–30 October 1998; Available online: https://www.fao.org/3/X6626E/x6626e04.htm#P9_135 (accessed on 10 June 2022).
- OECD. Water Use in Agriculture. Available online: https://www.oecd.org/environment/water-use-in-agriculture.htm (accessed on 11 June 2022).
- Hatfield, J.L.; Dold, C. Water-use efficiency: Advances and challenges in a changing climate. Front. Plant Sci. 2019, 10, 103. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, A. Water-use efficiency under changing climatic conditions. In Changing Climate and Resource Use Efficiency in Plants, 1st ed.; Bhattacharya, A., Ed.; Indian Institute of Pulses Research: Kanpur, India, 2019; pp. 111–180. [Google Scholar] [CrossRef]
- Arroyo, M.M. El Riego Inteligente en la Agricultura de Regadío. Serie Agua y Riego. Núm. 22. Artículos Técnicos de INTAGRI. México. 2018. Available online: https://www.intagri.com/articulos/agua-riego/el-riego-inteligente-en-la-agricultura-de-regadio (accessed on 11 June 2022).
- Keller, J.; Bliesner, R.D. Sprinkle and Trickle Irrigation; Van Nostrand Reinhold: New York, NY, USA, 1990. [Google Scholar]
- ISO Standard-15886-3; Agricultural Irrigation Equipment, Sprinklers. Part 3: Characterization of Distribution and Test Methods. ISO: Geneva, Switzerland, 2012.
- Merriam, J.L.; Keller, J. Farm Irrigation System Evaluation: A Guide for Management, Dept. of Agricultural and Irrigation Engineering; Utah State University: Logan, UT, USA, 1978. [Google Scholar]
- Burt, C.M.; Clemmens, A.J.; Strelkoff, T.S.; Solomon, K.H.; Bliesner, R.D.; Hardy, L.A.; Howell, T.A.; Eisenhauer, D.E. Irrigation performance measures: Efficiency and uniformity. J. Irrig. Drain. Eng. 1997, 123, 423–442. [Google Scholar] [CrossRef]
- Christiansen, J.E. Irrigation by Sprinkling; Bulletin 670; University of California, College of Agriculture, Agricultural Experiment Station: Berkeley, CA, USA, 1942; p. 124. [Google Scholar]
- ASCE. Describing irrigation efficiency and uniformity. On-farm irrigation committee of the irrigation and drainage division. J. Irrig. Drain. Div. 1978, 104, 35–41. [Google Scholar] [CrossRef]
- ASAE S398.1 (40th ed.); Procedure for Sprinkler Testing and Performance Reporting. ASAE: St. Joseph, MI, USA, 1993.
- Martín-Benito, J.M.T.; Gómez, M.V.; Pardo, J.L. Working conditions of sprinkler to optimize application of water. J. Irrig. Drain. Eng. 1992, 118, 895–913. [Google Scholar] [CrossRef]
- Dechmi, F.; Playán, E.; Cavero, J.; Martínez-Cob, A.; Faci, J.M. A coupled crop and solid-set sprinkler simulation model: I. Model development. J. Irrig. Drain. Eng. ASCE 2004, 130, 499–510. [Google Scholar] [CrossRef]
- Pair, H.P.; Larsen, D.C.; Kohl, R.A. Solid Set Sprinkler Systems; College of Agriculture, Series No. 272; University of Idaho, Cooperative Extension Service Agricultural Experiment Station: Boise, ID, USA, 1975. Available online: https://eprints.nwisrl.ars.usda.gov/id/eprint/1157/1/316.pdf (accessed on 12 June 2022).
- Tarjuelo, J.; Montero, J.; Honrubia, F.; Ortiz, J.; Ortega, J. Analysis of uniformity of sprinkle irrigation in a semi-arid area. Agric. Water Manag. 1999, 40, 315–331. [Google Scholar] [CrossRef]
- Playán, E.; Salvador, R.; Faci, J.; Zapata, N.; Martínez-Cob, A.; Sánchez, I. Day and night wind drift and evaporation losses in sprinkler solid-sets and moving laterals. Agric. Water Manag. 2005, 76, 139–159. [Google Scholar] [CrossRef]
- Robles, O.; Latorre, B.; Zapata, N.; Burguete, J. Self-calibrated ballistic model for sprinkler irrigation with a field experiments data base. Agric. Water Manag. 2019, 223, 105711. [Google Scholar] [CrossRef]
- Ascough, G.; Kiker, G. The effect of irrigation uniformity on irrigation water requirements. Water SA 2002, 28, 235–242. [Google Scholar] [CrossRef] [Green Version]
- INIFAP. National Institute for Forestry, Agricultural and Livestock Research, Zacatecas Mexico. Available online: http://zacatecas.inifap.gob.mx/ (accessed on 13 June 2022).
- Kincaid, D.C. Impact sprinkler pattern modification. Trans. ASAE 1991, 34, 2397–2403. [Google Scholar] [CrossRef]
- Playán, E.; Zapata, N.; Faci, J.M.; Tolosa, D.; Lacueva, J.L.; Pelegrín, J.; Salvador, R.; Sánchez, I.; Lafita, A. Assessing sprinkler irrigation uniformity using a ballistic simulation model. Agric. Water Manag. 2006, 84, 89–100. [Google Scholar] [CrossRef]
- Robles, O.; Playán, E.; Cavero, J.; Zapata, N. Assessing low-pressure solid-set sprinkler irrigation in maize. Agric. Water Manag. 2017, 191, 37–49. [Google Scholar] [CrossRef]
- Trimmer, W.L. Sprinkler evaporation loss equation. J. Irrig. Drain. Eng. ASCE 1987, 113, 616–620. [Google Scholar] [CrossRef]
- Montero, J. Análisis De La Distribución De Agua En Sistemas De Riego Por Aspersión Estacionario. Desarrollo Del Modelo De Sim-ulación De Riego Por Aspersión (SIRIAS). Ph.D. Thesis, University of Castilla-la Mancha, Albacete, Spain, June 1999. [Google Scholar]
- Tarjuelo, J.M.; Ortega, J.F.; Montero, J.; De Juar, J.A. Modeling evaporation and drift losses in irrigation with medium size impact sprinklers under semi-arid conditions. Agric. Water Manag. 2000, 43, 263–284. [Google Scholar] [CrossRef]
- Nin, R. Tecnología del Riego por aspersión estacionario. Calibración y validación de un modelo de simulación. Ph.D. Thesis, University of Castilla-La Mancha, Albacete, Spain, November 2008. [Google Scholar]
- Saraiva, G.S.; Bonomo, R.; De Souza, J.M. Perdas de água por evaporação e arraste pelo vento, em sistemas de aspersão fixa, norte do Espírito Santo. Rev. Bras. Agric. Irrig. 2013, 7, 235–247. [Google Scholar] [CrossRef]
- Faci, J.M.; Bercero, A. Efecto del viento en la uniformidad y en las pérdidas por evaporación y arrastre en el riego por aspersión. Inv. Agric. Prod. Prot. Veg. 1991, 6, 171–182. [Google Scholar]
- Dechmi, F.; Playán, E.; Cavero, J.; Faci, J.M.; Martínez-Cob, A. Wind effects on solid set sprinkler irrigation depth and yield of maize (Zea mays). Irrig. Sci. 2003, 22, 67–77. [Google Scholar] [CrossRef]
- Sanchez, I.; Faci, J.; Zapata, N. The effects of pressure, nozzle diameter and meteorological conditions on the performance of agricultural impact sprinklers. Agric. Water Manag. 2011, 102, 13–24. [Google Scholar] [CrossRef]
- Stambouli, T.; Zapata, N.; Faci, J.M. Performance of new agricultural impact sprinkler fitted with plastic nozzles. Biosyst. Eng. 2014, 118, 39–51. [Google Scholar] [CrossRef]
- Ouazaa, S.; Burguete, J.; Zapata, N. Solid-set sprinklers irrigation of field boundaries: Experiments and modeling. Irrig. Sci. 2016, 34, 85–103. [Google Scholar] [CrossRef] [Green Version]
- Maroufpoor, E.; Sanikhani, H.; Emamgholizadeh, S.; Kişi, Ö. Estimation of wind drift and evaporation losses from sprinkler irrigation systems by different data-driven methods. Irrig. Drain. 2017, 67, 222–232. [Google Scholar] [CrossRef]
- Gheriani, S.; Noureddine, M.E.Z.A.; Boutoutaou, D. Modeling wind drift and evaporation losses during sprinkler irrigation in arid areas (case of Touggourt-Algeria). Res. Sq. 2022; in press. [Google Scholar] [CrossRef]
- Yazar, A. Evaporation and drift losses from sprinkler irrigation systems under various operating conditions. Agric. Water Manag. 1984, 8, 439–449. [Google Scholar] [CrossRef]
- Zapata, N.; Robles, O.; Playán, E.; Paniagua, P.; Romano, C.; Salvador, R.; Gil Montoya, F. Low-pressure sprinkler irrigation in maize: Differences in water distribution above and below the crop canopy. Agric. Water Manag. 2018, 203, 353–365. [Google Scholar] [CrossRef]
- Paniagua, M.P. Mejora Del Riego Por Aspersion En Parcela. Ph.D. Thesis, Universidad de Zaragoza, Zaragoza, Spain, November 2015. [Google Scholar]
- Tarjuelo, J.M. El Riego por Aspersión y su Tecnología, 3rd ed.; Ediciones Mundi-Prensa: Madrid, España, 2005. [Google Scholar]
- Salvatierra, B.B. Evaluación De La Distribución Del Agua En Sistemas De Riego Por Aspersión Estacionarios Con Viento. Ph.D. Thesis, Universidad de Sevilla, Sevilla, Spain, November 2019. Available online: https://idus.us.es/bitstream/handle/11441/94149/TESIS%20BENITO%20SALVATIERRA.pdf?sequence=1&isAllowed=y (accessed on 20 March 2020).



| Sprinkler */Abbreviation | Main Nozzle (mm) | Auxiliary Nozzle (mm) | Pressure (kPa) | Wetted Diameter (m) | Theoretical Flow (L/h) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Pressure (kPa) | |||||||||
| 200 | 250 | 300 | 200 | 250 | 300 | ||||
| Naandanjain 5035SD/ND 5035 | 4.37 | 2.50 | 200, 250, 300 | − ** | − | − | − | − | − |
| 5.56 | 2.50 | 200, 250, 300 | − | − | 32.0 | − | − | 2390 | |
| Senninger 4023-2/SEN 4023 | 4.76 | 2.38 | 200, 250, 300 | 28.0 | 29.0 | 30.2 | 1560 | 1720 | 1940 |
| Unirain F30/UR F30 | 4.37 | 3.18 | 200, 250, 300 | 26.5 | − | 28.6 | 1370 | − | 1690 |
| Wade Rain 33/WR 33 | 4.37 | 3.18 | 200, 250, 300 | 25.0 | − | 25.6 | 1548 | − | 1944 |
| Wade Rain 32/WR 32 | 4.37 | 3.18 | 200, 250, 300 | 22.8 | 26.0 | 28.0 | 1548 | 1728 | 1944 |
| Wade Rain 31/WR 31 | 4.37 | 3.18 | 200, 250, 300 | 26.8 | − | 29.8 | 1332 | − | 1548 |
| 5.56 | 3.18 | 200, 250, 300 | − | − | − | − | − | − | |
| Author (s) | WDEL Model | CUC Model |
|---|---|---|
| Trimmer (1987) [30] | - | |
| Faci and Bercero (1991) [35] | - | |
| Montero (1999) [31] | - | |
| Tarjuelo et al. (2000) [32] | - | |
| Dechmi et al. (2003) [36] | - | |
| Playán et al. (2005) [23] | - | |
| Playán et al. (2006) [28] | ||
| Nin (2008) [33] | - | |
| Sánchez et al. (2011) [37] | ||
| Saraiva et al. (2013) [34] | ||
| Stambouli et al. (2014) [38] | ||
| Ouazaa et al. (2016) [39] | - | |
| Maroufpoor et al. (2017) [40] | - | |
| Robles et al. (2019) [24] | ||
| Gheriani et al. (2022) [41] | - |
| Research Work. | Reference | Pressure (kPa) | Sprinkler Height (Sh, m) | Catch-Can Height (Cc, m) | Effective Height (Sh-Cc, m) |
|---|---|---|---|---|---|
| Playán et al. (2006) | [28] | 200, 300, 400 | 2.0 | 0.35 | 1.65 |
| Nin, (2008) | [33] | 220, 320, 450 | 2.0 | 0.0 | 2.0 |
| Sánchez et al. (2011) | [37] | 240, 320, 420 | 2.0 | 0.25 | 1.75 |
| Stambouli et al. (2014) | [38] | 200, 300, 400 | 2.0 | 0.4 | 1.6 |
| Paniagua (2015) | [44] | 200, 300 | 2.45 | 0.85 | 1.6 |
| Robles et al. (2017) | [29] | 200, 300 | 2.5 | 1.0 | 1.5 |
| 200, 300 | 2.5 | 2.0 | 0.5 | ||
| 200, 300 | 2.5 | 2.3 | 0.2 | ||
| Robles et al. (2019) | [24] | 200, 300 | 2.0 | 0.35 | 1.65 |
| CUC measured | – | 200, 250, 300 | 0.6 | 0.0 | 0.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García Bandala, M.; Robles Rovelo, C.O.; Bautista-Capetillo, C.; González-Trinidad, J.; Júnez-Ferreira, H.E.; Servín Palestina, M.; Pineda Martínez, H.; Morales de Avila, H.; Rivas Recendez, M.I. Analysis of Irrigation Performance of a Solid-Set Sprinkler Irrigation System at Different Experimental Conditions. Water 2022, 14, 2641. https://doi.org/10.3390/w14172641
García Bandala M, Robles Rovelo CO, Bautista-Capetillo C, González-Trinidad J, Júnez-Ferreira HE, Servín Palestina M, Pineda Martínez H, Morales de Avila H, Rivas Recendez MI. Analysis of Irrigation Performance of a Solid-Set Sprinkler Irrigation System at Different Experimental Conditions. Water. 2022; 14(17):2641. https://doi.org/10.3390/w14172641
Chicago/Turabian StyleGarcía Bandala, Martín, Cruz Octavio Robles Rovelo, Carlos Bautista-Capetillo, Julián González-Trinidad, Hugo Enrique Júnez-Ferreira, Miguel Servín Palestina, Hugo Pineda Martínez, Heriberto Morales de Avila, and Maria Ines Rivas Recendez. 2022. "Analysis of Irrigation Performance of a Solid-Set Sprinkler Irrigation System at Different Experimental Conditions" Water 14, no. 17: 2641. https://doi.org/10.3390/w14172641









