Flushing Capacity of a Stored Volume of Water: An Experimental Study
Abstract
:1. Introduction
- To analyze the capacity of flushing sediments in a reservoir using only that water previously stored in it.
- To characterize the effects of the initial water head, the initial volume of water, the bed slope, and the sediment grain size on the efficacy of flushing. This efficacy is herein defined as the volume of sediments removed to the volume of water released.
2. Methodology
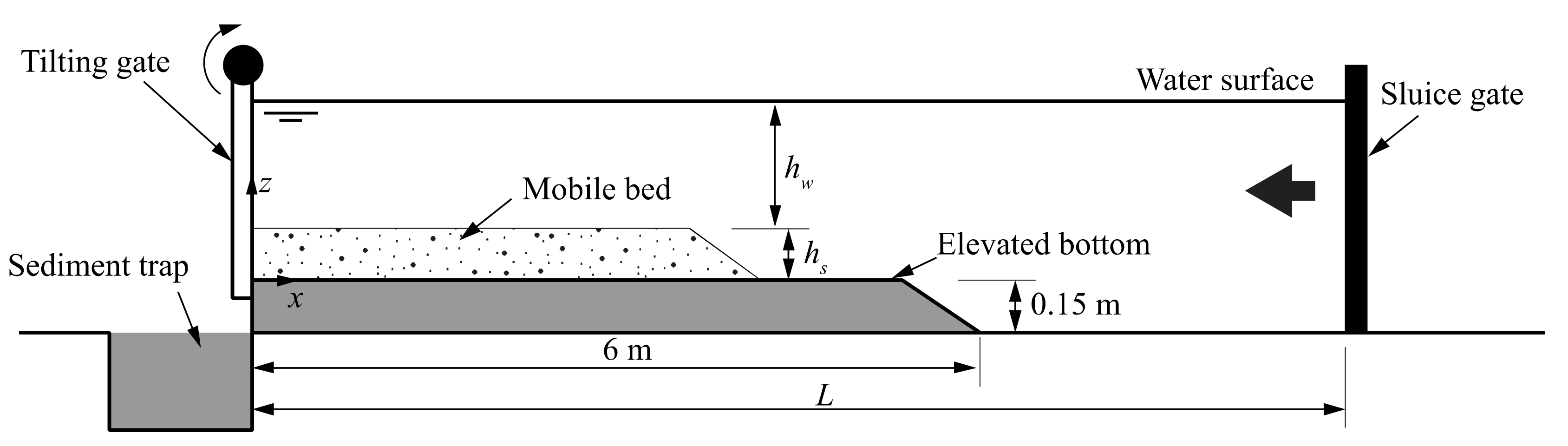
2.1. Experimental Facility and Procedure
- For hs = 0.05 m, hw = 0.05 m, 0.10 m, 0.15 m, and 0.20 m.
- For hs = 0.10 m, hw = 0.05 m, 0.10 m, and 0.15 m.
- For hs = 0.15 m, hw = 0.05 m, and 0.10 m.
- For hs = 0.20 m, hw = 0.05 m.
- Thirty experiments in which ten pairs hs—hw were tested for an initial bed slope S0 = 0.0%, for the medium sand, and for three different reservoir lengths: L = 5.997 m, 9.287 m, and 12.043 m with ΔL = ±0.001 m accuracy.
- Twenty experiments in which ten pairs hs—hw were tested for S0 = 0.5%, and 1.0%, for the medium sand, and for L = 12.043 m.
- Forty experiments in which ten pairs hs—hw were tested for S0 = 0.0%, for the fine and coarse sands, and for L = 5.997 m, and 12.043 m.
2.2. Dimensional Analysis
2.3. Studies for Comparison
3. Results
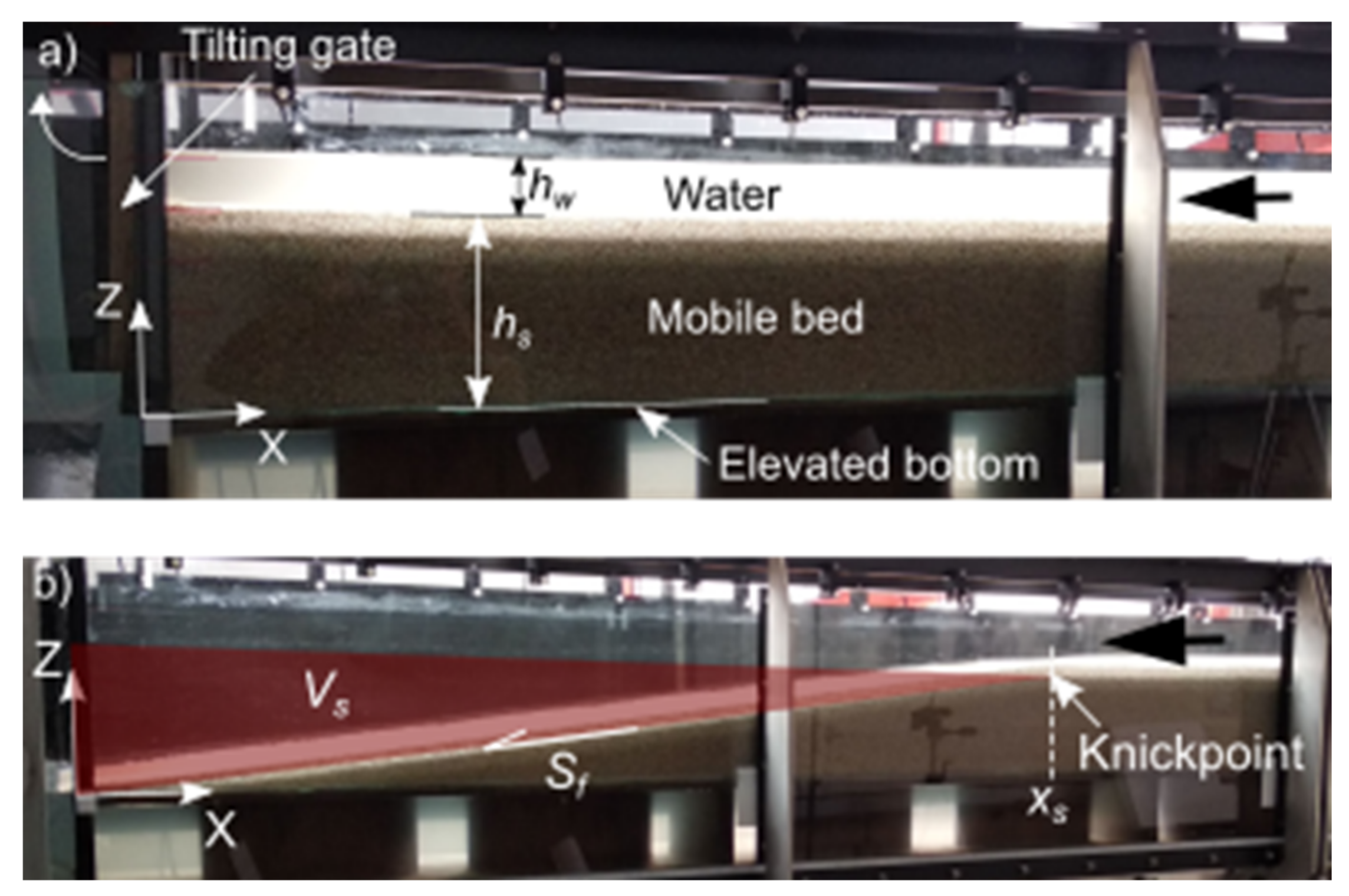
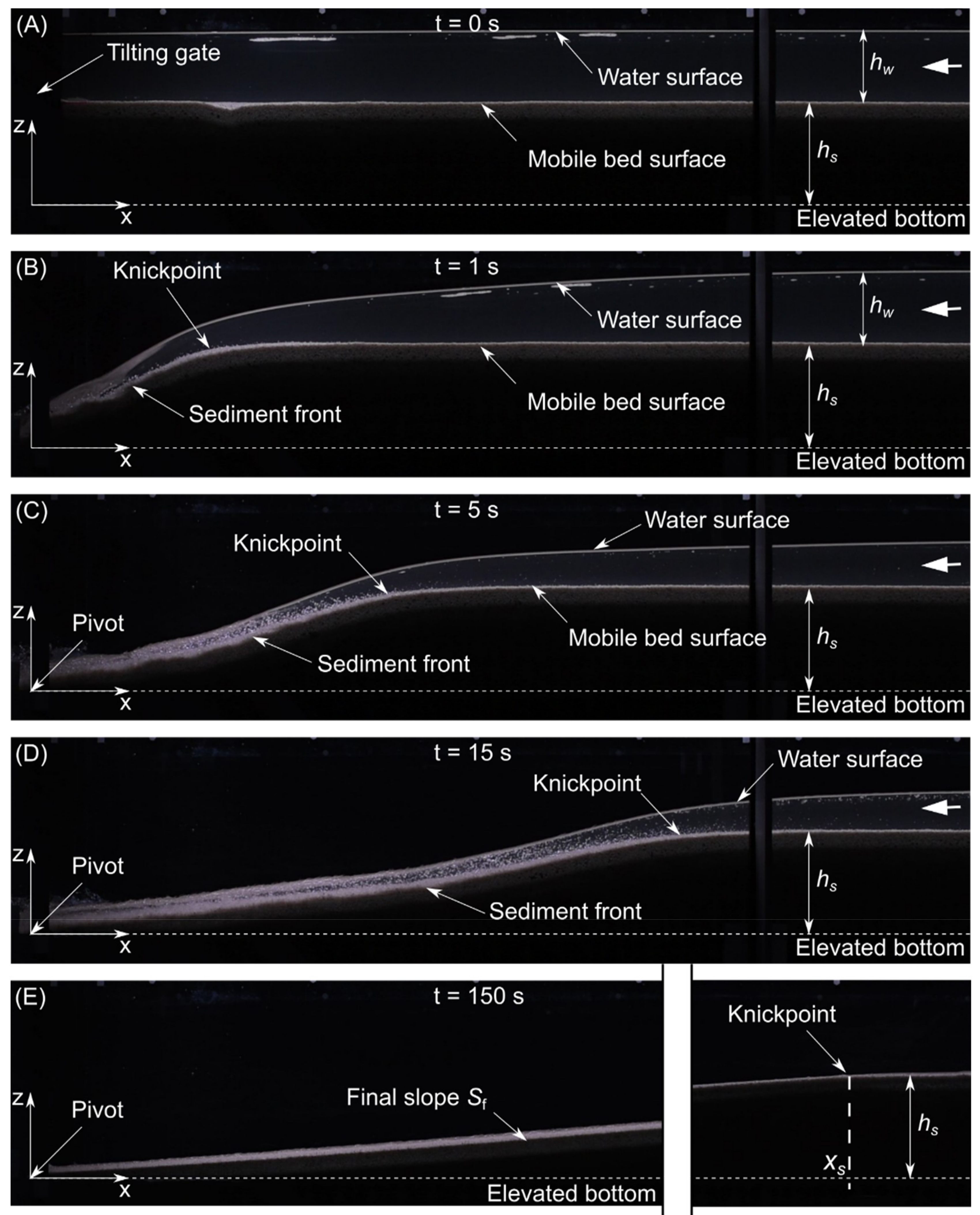
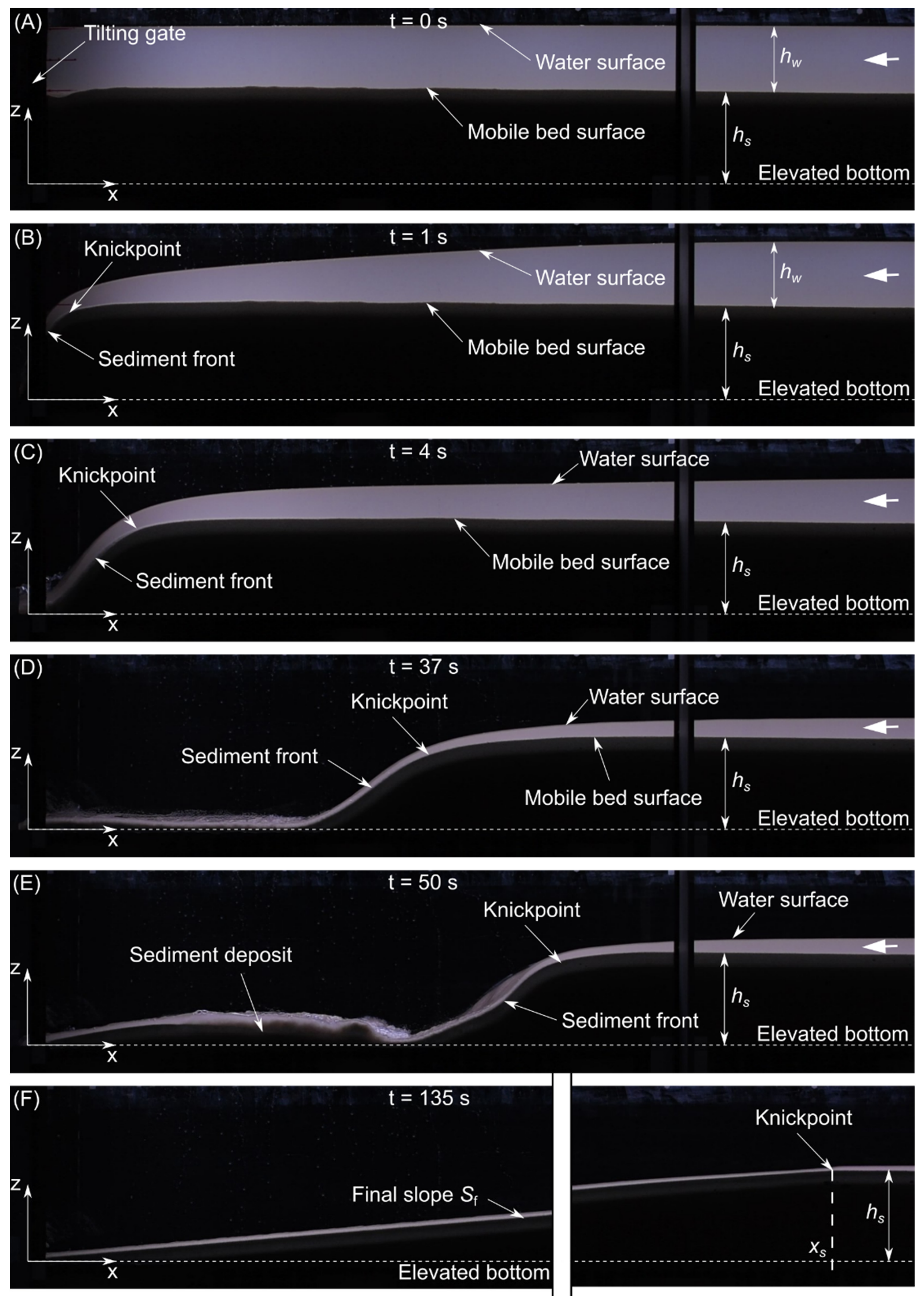
3.1. Morphodynamics of the Experiments
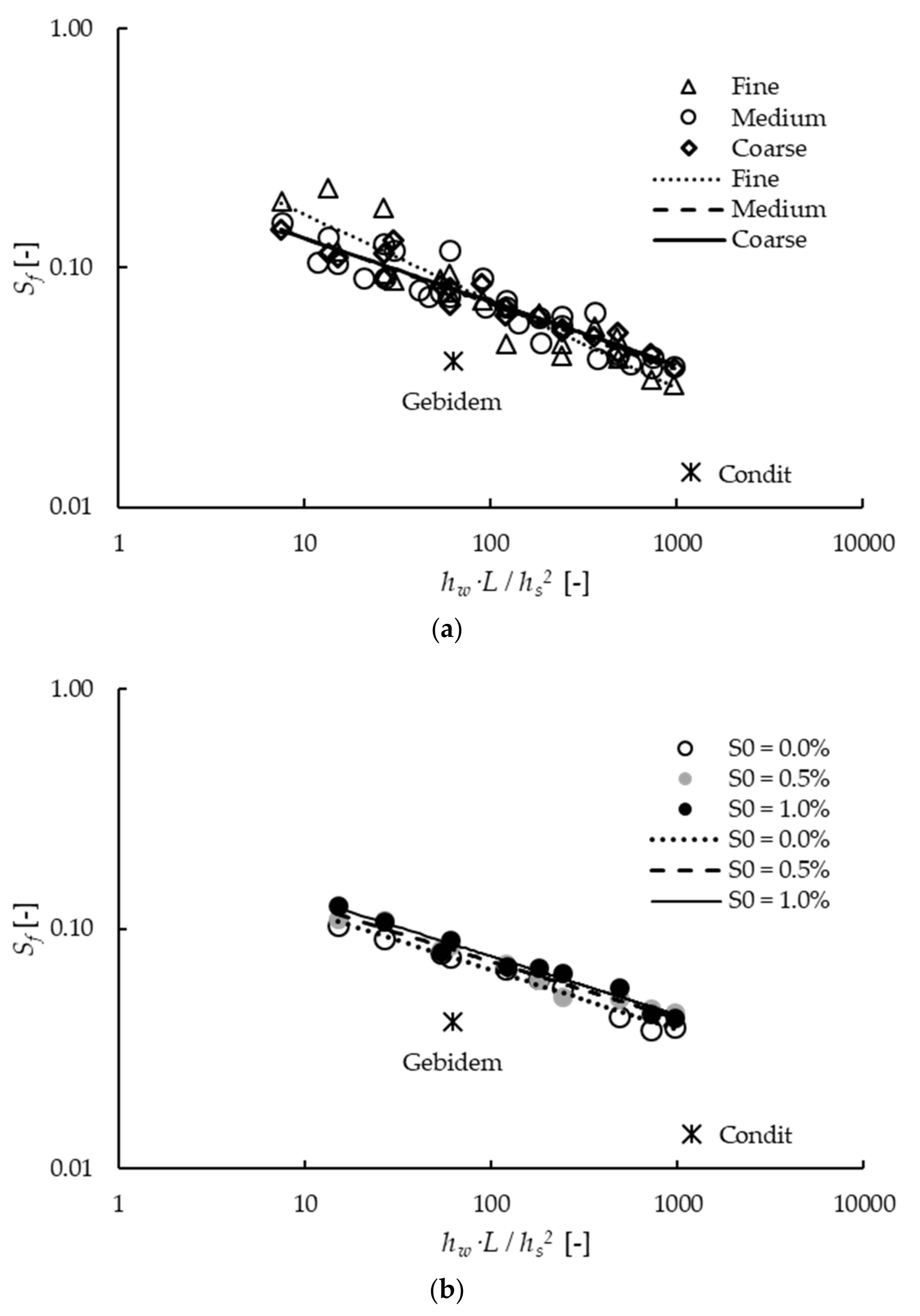
3.2. Sf for Varying Values of hw·L/hs2, D*, and S0
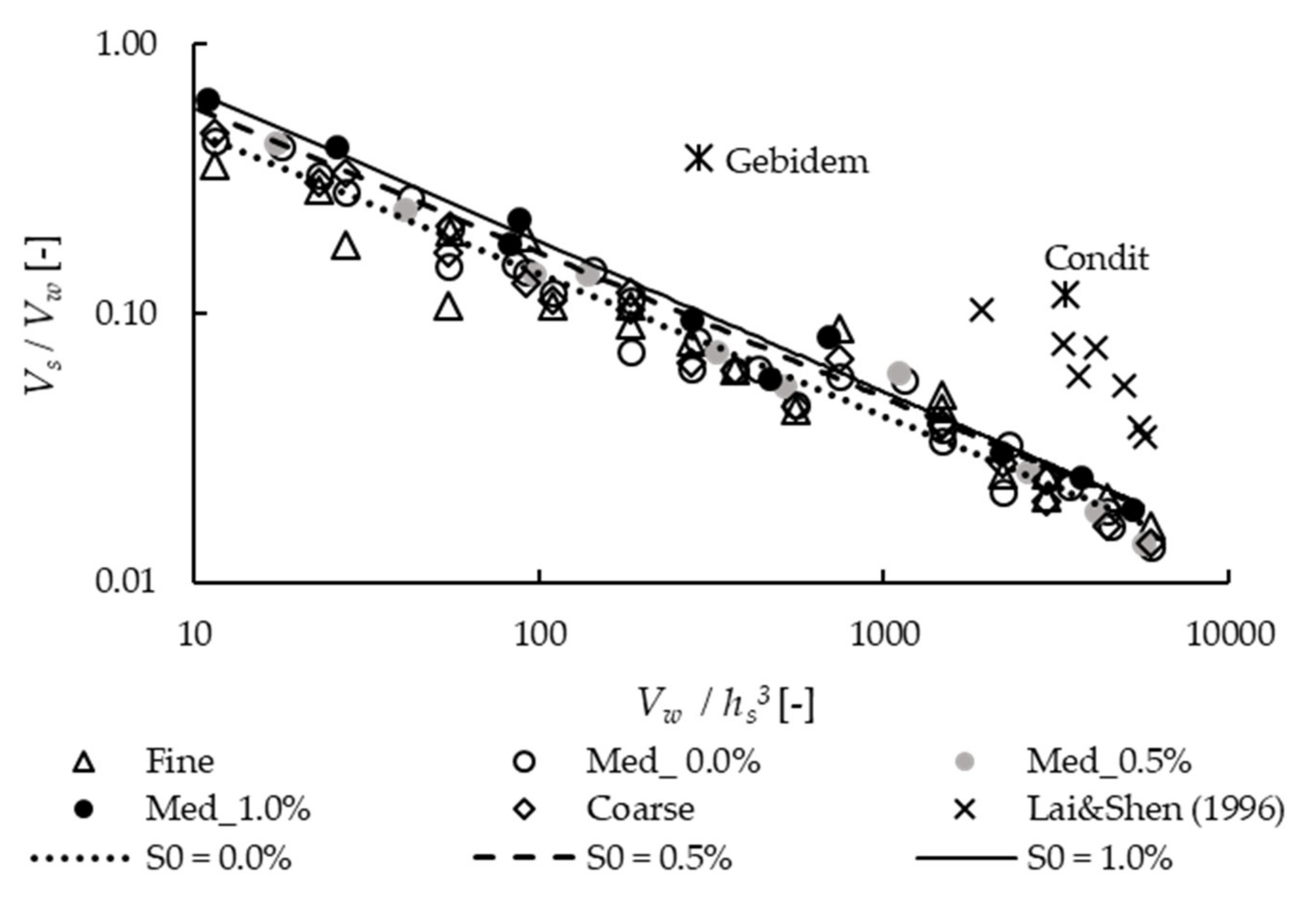
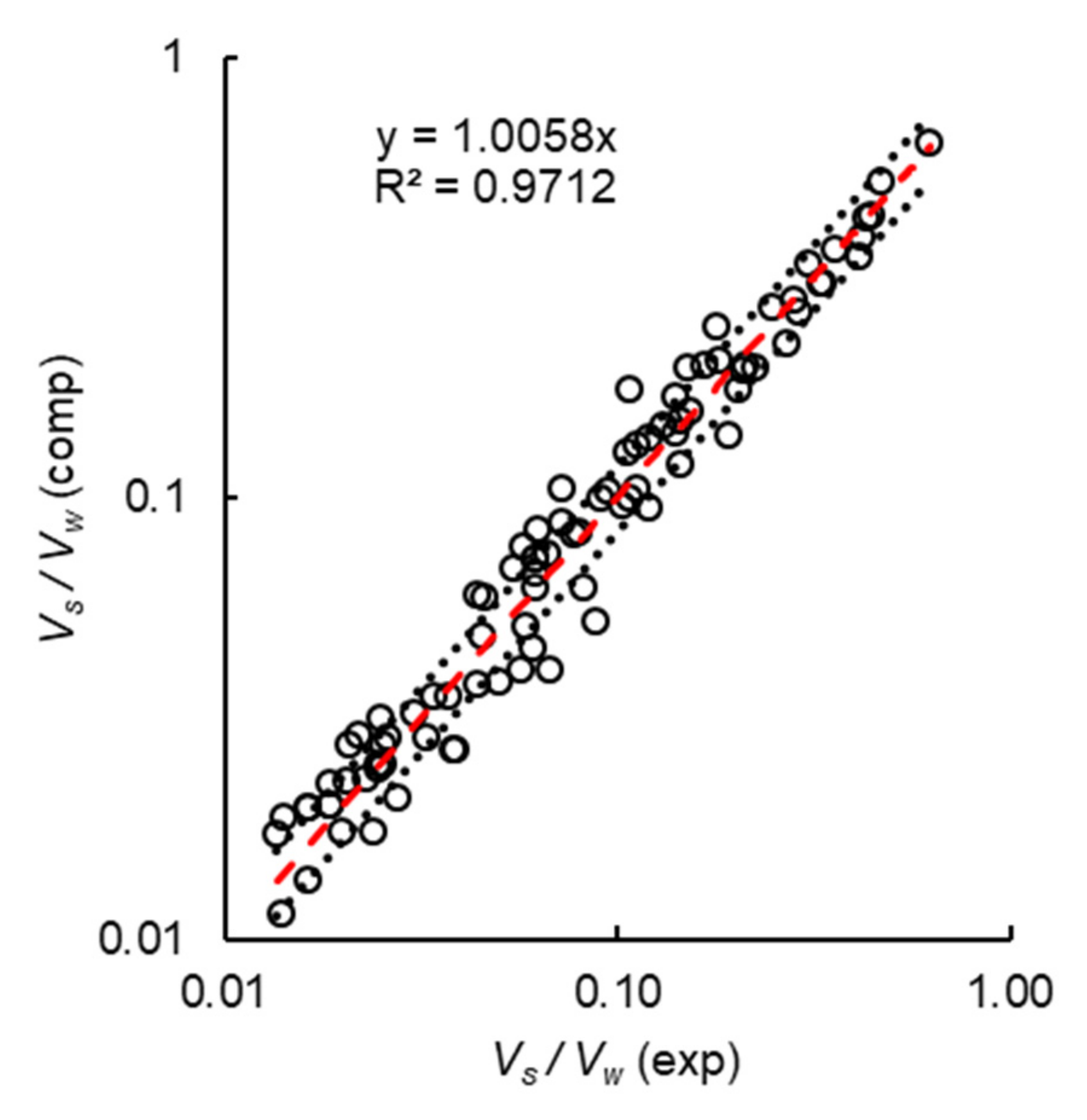
3.3. Flushing Efficacy for Varying Values of Vw/hs3, S0 and D*
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Annandale, G.W.; Morris, G.L.; Karki, P. Extending the Life of Reservoirs: Sustainable Sediment Management for Dams and Run-of-River Hydropower; The World Bank: Washington, DC, USA, 2016. [Google Scholar] [CrossRef]
- Morris, G.L.; Fan, J. Reservoir Sedimentation Handbook: Design and Management of Dams, Reservoirs, and Watersheds for Sustainable Use, 1.04; McGraw-Hill Book Co.: New York, NY, USA, 1998. [Google Scholar]
- Kondolf, G.M.; Rubin, Z.K.; Minear, J.T. Dams on the Mekong: Cumulative sediment starvation. Water Resour. Res. 2014, 50, 5158–5169. [Google Scholar] [CrossRef]
- Franssen, N.R.; Tobler, M. Upstream effects of a reservoir on fish assemblages 45 years following impoundment. J. Fish Biol. 2013, 82, 1659–1670. [Google Scholar] [CrossRef] [PubMed]
- Bellmore, R.J.; Duda, J.J.; Craig, L.S.; Greene, S.L.; Torgersen, C.E.; Collins, M.J.; Vittum, K. Status and trends of dam removal research in the United States. Wiley Interdiscip. Rev. Water 2017, 4, e1164. [Google Scholar] [CrossRef]
- Schleiss, A.J.; Franca, M.J.; Juez, C.; De Cesare, G. Reservoir sedimentation. J. Hydraul. Res. 2016, 54, 595–614. [Google Scholar] [CrossRef]
- Mahmood, K. Reservoir Sedimentation: Impact, Extent, and Mitigation; Technical Paper WTP71; The World Bank: Washington, DC, USA, 1987. [Google Scholar]
- Sumi, T.; Okano, M.; Yasufumi, T. Reservoir sedimentation management with bypass tunnels in Japan. In Proceedings of the Ninth International Symposium on River Sedimentation, Yichang, China, 18–21 October 2004; pp. 1036–1043. [Google Scholar]
- Minear, J.T.; Kondolf, G.M. Estimating reservoir sedimentation rates at large spatial and temporal scales: A case study of California. Water Resour. Res. 2009, 45, 1–8. [Google Scholar] [CrossRef]
- Shrestha, B.; Babel, M.S.; Maskey, S.; van Griensven, A.; Uhlenbrook, S.; Green, A.; Akkharath, I. Impact of climate change on sediment yield in the Mekong River basin: A case study of the Nam Ou basin, Lao PDR. Hydrol. Earth Syst. Sci. 2013, 17, 1–20. [Google Scholar] [CrossRef]
- Guillén-Ludeña, S.; Manso, P.; Schleiss, A. Multidecadal Sediment Balance Modelling of a Cascade of Alpine Reservoirs and Perspectives Based on Climate Warming. Water 2018, 10, 1759. [Google Scholar] [CrossRef]
- Kondolf, G.M.; Gao, Y.; Annandale, G.W.; Morris, G.L.; Jiang, E.; Zhang, J.; Cao, Y.; Carling, P.; Fu, K.; Guo, Q.; et al. Sustainable sediment management in reservoirs and regulated rivers: Experiences from five continents. Earth’s Future 2014, 2, 256–280. [Google Scholar] [CrossRef]
- White, R. Evacuation of Sediments from Reservoirs; Thomas Telford Publishing: London, UK, 2001. [Google Scholar] [CrossRef]
- Cantelli, A.; Paola, C.; Parker, G. Experiments on upstream-migrating erosional narrowing and widening of an incisional channel caused by dam removal. Water Resour. Res. 2004, 40, 1–12. [Google Scholar] [CrossRef]
- Wilcox, A.C.; O’Connor, J.E.; Major, J.J. Rapid reservoir erosion, hyperconcentrated flow, and downstream deposition triggered by breaching of 38 m tall Condit Dam, White Salmon River, Washington. J. Geophys. Res. Earth Surf. 2014, 119, 1376–1394. [Google Scholar] [CrossRef]
- Major, J.J.; O’Connor, J.E.; Podolak, C.J.; Keith, M.K.; Grant, G.E.; Spicer, K.R.; Pittman, S.; Bragg, H.M.; Wallick, J.R.; Tanner, D.Q.; et al. Geomorphic Response of the Sandy River, Oregon, to Removal of Marmot Dam; U.S. Geological Survey: Reston, VA, USA, 2012. [CrossRef]
- Atkinson, E. The Feasibility of Flushing Sediment from Reservoirs; Report OD 137; HR Wallingford: Wallingford, UK, 1996. [Google Scholar]
- Batuca, D.G.; Jordaan, J.M. Silting and Desilting of Reservoirs; Taylor & Francis: Oxfordshire, UK, 2000. [Google Scholar]
- Di Silvio, G. Modeling Desiltation of Reservoirs by Bottom-Outlet Flushing. In Movable Bed Physical Models; Shen, H.W., Ed.; Springer: Dordrecht, The Netherlands, 1990; pp. 159–171. [Google Scholar] [CrossRef]
- Castillo, L.G.; Carrillo, J.M.; Álvarez, M.A. Complementary Methods for Determining the Sedimentation and Flushing in a Reservoir. J. Hydraul. Eng. 2015, 141, 05015004. [Google Scholar] [CrossRef]
- Dahal, S.; Crosato, A.; Omer, A.Y.A.; Lee, A.A. Validation of Model-Based Optimization of Reservoir Sediment Releases by Dam Removal. J. Water Resour. Plan. Manag. 2021, 147, 04021033. [Google Scholar] [CrossRef]
- Esmaeili, T.; Sumi, T.; Kantoush, S.; Kubota, Y.; Haun, S.; Rüther, N. Three-Dimensional Numerical Study of Free-Flow Sediment Flushing to Increase the Flushing Efficiency: A Case-Study Reservoir in Japan. Water 2017, 9, 900. [Google Scholar] [CrossRef]
- Esmaeili, T.; Sumi, T.; Kantoush, S.A.; Kubota, Y. Free-Flow Sediment Flushing: Insights from Prototype-Scale Studies. J. Disaster Res. 2018, 13, 677–690. [Google Scholar] [CrossRef]
- Lai, J.-S.; Shen, H.W. Flushing sediment through reservoirs. J. Hydraul. Res. 1996, 34, 237–255. [Google Scholar] [CrossRef]
- Shields, A. Application of similarity principles and turbulence research to bed-load movement. In Hydrodynamics Laboratory Publ. No. 167; Ott, W.P., van Uchelen, J.C., Eds.; U.S. Department of Agriculture, Soil Conservation Service Cooperative Laboratory, California Institute of Technology: Pasadena, CA, USA, 1936. [Google Scholar]
- van Rijn, L.C. Sediment Transport, Part I: Bed Load Transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef] [Green Version]
- Lai, J.-S. Hydraulic Flushing for Reservoir Desiltation; University of California, Berkeley: Berkeley, CA, USA, 1994. [Google Scholar]
- Tullos, D.; Wang, H.-W. Morphological responses and sediment processes following a typhoon-induced dam failure, Dahan River, Taiwan. Earth Surf. Process. Landf. 2014, 39, 245–258. [Google Scholar] [CrossRef]
- Begin, Z.B.; Schumm, S.A.; Meyer, D.F. Knickpoint Migration due to Baselevel Lowering. J. Waterw. Port Coast. Ocean Div. 1980, 106, 369–388. [Google Scholar] [CrossRef]
- Brush, L.M.J.; Wolman, M.G. Knicpoint behavior in noncohesive material: A laboratory study. GSA Bull. 1960, 71, 59–74. [Google Scholar] [CrossRef]
- Schumm, S.A.; Mosley, M.P.; Weaver, W.E. Incised Channels. In Experimental Fluvial Geomorphology; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1987; pp. 192–225. [Google Scholar]
- Loget, N.; Van Den Driessche, J. Wave train model for knickpoint migration. Geomorphology 2009, 106, 376–382. [Google Scholar] [CrossRef]
- Shepherd, R.G.; Schumm, S.A. Experimental study of river incision: Discussion and reply. Geol. Soc. Am. Bull. 1976, 87, 320. [Google Scholar] [CrossRef]
- Doyle, M.W.; Stanley, E.H.; Harbor, J.M. Geomorphic analogies for assessing probable channel response to dam removal. J. Am. Water Resour. Assoc. 2002, 38, 1567–1579. [Google Scholar] [CrossRef]
- Pizzuto, J. Effects of dam removal on river form and process. Bioscience 2002, 52, 683–691. [Google Scholar] [CrossRef]
- Doyle, M.W.; Stanley, E.H.; Harbor, J.M. Channel adjustments following two dam removals in Wisconsin. Water Resour. Res. 2003, 39, 1–15. [Google Scholar] [CrossRef]
- MacBroom, J.G. Evolution of Channels Upstream of Dam Removal Sites. In Proceedings of the Managing Watersheds for Human and Natural Impacts, Williamsburg, VA, USA, 19–22 July 2005; pp. 1–12. [Google Scholar] [CrossRef]
- Bento, A.M.; Amaral, S.; Viseu, T.; Cardoso, R.; Ferreira, R.M.L. Direct Estimate of the Breach Hydrograph of an Overtopped Earth Dam. J. Hydraul. Eng. 2017, 143, 06017004. [Google Scholar] [CrossRef]
- Pickert, G.; Weitbrecht, V.; Bieberstein, A. Breaching of overtopped river embankments controlled by apparent cohesion. J. Hydraul. Res. 2011, 49, 143–156. [Google Scholar] [CrossRef]
| hw·L/hs2 | Vw/hs3 | S0 | D* |
|---|---|---|---|
| [-] | [-] | [%] | [-] |
| Min = 7.5 Max = 963.4 | Min = 11.5 Max = 5934.8 | 0.0 0.5% 1.0% | 10 (Fine) 20 (Medium) 39 (Coarse) |
| Dam/Experiment | Data Source | L | hw | hs | Vw | Vs | Sf | hw·L/hs2 | Vw/hs3 | Vs/Vw |
|---|---|---|---|---|---|---|---|---|---|---|
| [m] | [m] | [m] | [m3] | [m3] | [-] | [-] | [-] | [%] | ||
| Condit (USA) | [15] | 2900 | 25 | 8 | 1.6 × 106 | 1.8 × 105 | 1.4% | 1192 | 3354 | 12% |
| Gebidem (CH) | [2] | 450 | 13 | 10 | 0.3 × 106 | 1.0 × 105 | 4.1% | 62 | 292 | 38% |
| Lai and Shen Run 1 | [27] | 33 | 0.07 | 0.1 | 5.53 | 0.21 | - | 230 | 5530 | 4% |
| Lai and Shen Run 2 | 22 | 0.07 | 0.1 | 3.69 | 0.22 | - | 154 | 3691 | 6% | |
| Lai and Shen Run 3 | 42 | 0.03 | 0.1 | 3.31 | 0.26 | - | 138 | 3313 | 8% | |
| Lai and Shen Run 4 | 24 | 0.07 | 0.1 | 4.13 | 0.31 | - | 172 | 4134 | 7% | |
| Lai and Shen Run 6 | 35 | 0.07 | 0.1 | 5.75 | 0.20 | - | 239 | 5747 | 3% | |
| Lai and Shen Run 7 | 30 | 0.07 | 0.1 | 4.98 | 0.27 | - | 208 | 4982 | 5% | |
| Lai and Shen Run 8 | 36 | 0.02 | 0.1 | 1.93 | 0.20 | - | 80 | 1930 | 10% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guillén-Ludeña, S.; Toapaxi, J.A.; Castillo, L.G. Flushing Capacity of a Stored Volume of Water: An Experimental Study. Water 2022, 14, 2607. https://doi.org/10.3390/w14172607
Guillén-Ludeña S, Toapaxi JA, Castillo LG. Flushing Capacity of a Stored Volume of Water: An Experimental Study. Water. 2022; 14(17):2607. https://doi.org/10.3390/w14172607
Chicago/Turabian StyleGuillén-Ludeña, Sebastián, Jorge A. Toapaxi, and Luis G. Castillo. 2022. "Flushing Capacity of a Stored Volume of Water: An Experimental Study" Water 14, no. 17: 2607. https://doi.org/10.3390/w14172607






