Comparison of the Calibrated Objective Functions for Low Flow Simulation in a Semi-Arid Catchment
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
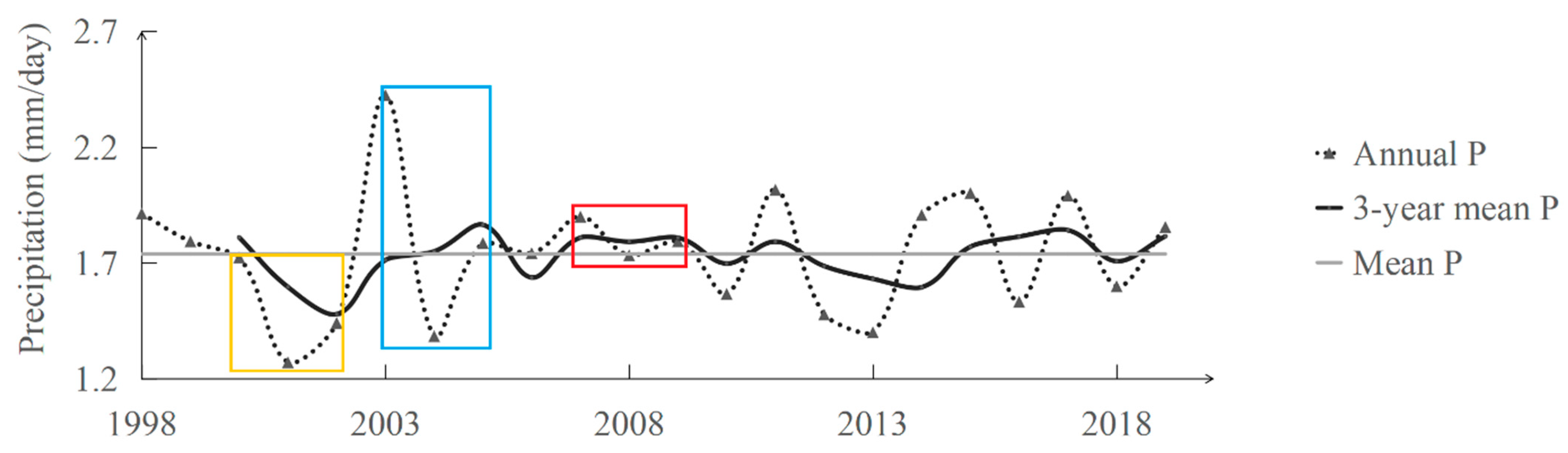
2.2. Data
3. Methods
3.1. Hydrological Model and Model Optimization
3.2. Calibration Objective Functions
| Classes | Criteria | Name | Description | Reference |
|---|---|---|---|---|
| Single objective | KGE(log(Q)) | OBJ1 | KGE calculated on logarithmic transformed discharges | Oudin et al. [33] |
| KGE(1/Q) | OBJ2 | KGE calculated on inverse transformed discharges | Pushpalatha et al. [34] | |
| Muti objective | KGE(Q)+KGE(log(Q)) | OBJ3 | Sum of KGE calculated on discharges and logarithmic transformed discharges | Proposed in this study |
| KGE(Q)+KGE(1/Q) | OBJ4 | Sum of KGE calculated on discharges and inverse transformed discharges | Garcia et al. [3] | |
| KGE(Qsort)+KGE(log(Qsort)) | OBJ5 | Sum of KGE calculated on the FDC and logarithmic transformed of the FDC | Proposed in this study | |
| KGE(Qsort)+KGE(1/Qsort) | OBJ6 | Sum of KGE calculated on the FDC and logarithmic transformed of the FDC | Garcia et al. [3] | |
| Split objective | split KGE(Q) | OBJ7 | Averaged KGE calculated on discharges in each year | Fowler et al. [35] |
| split (KGE(Q)+KGE(1/Q)) | OBJ8 | Averaged sum of KGE calculated on discharges and inverse transformed discharges in each year | Proposed in this study |
3.3. Model Performance Assessment
Climatic Robustness Assessment
3.4. Assessment Criteria
4. Results
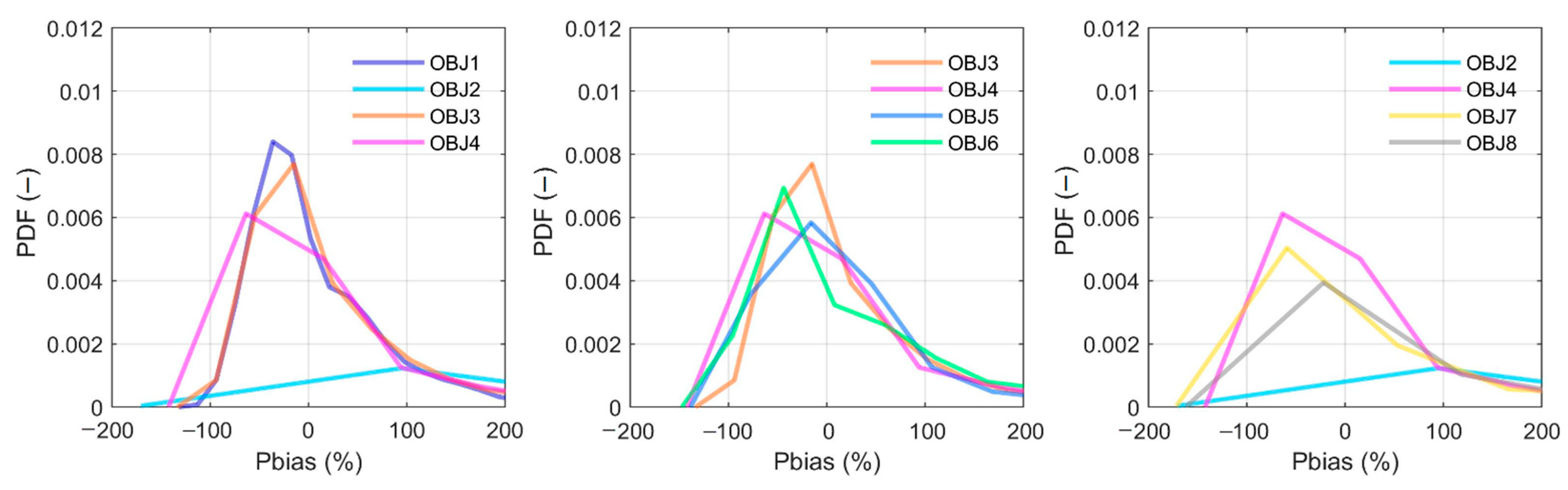
4.1. Objective Functions Evaluation
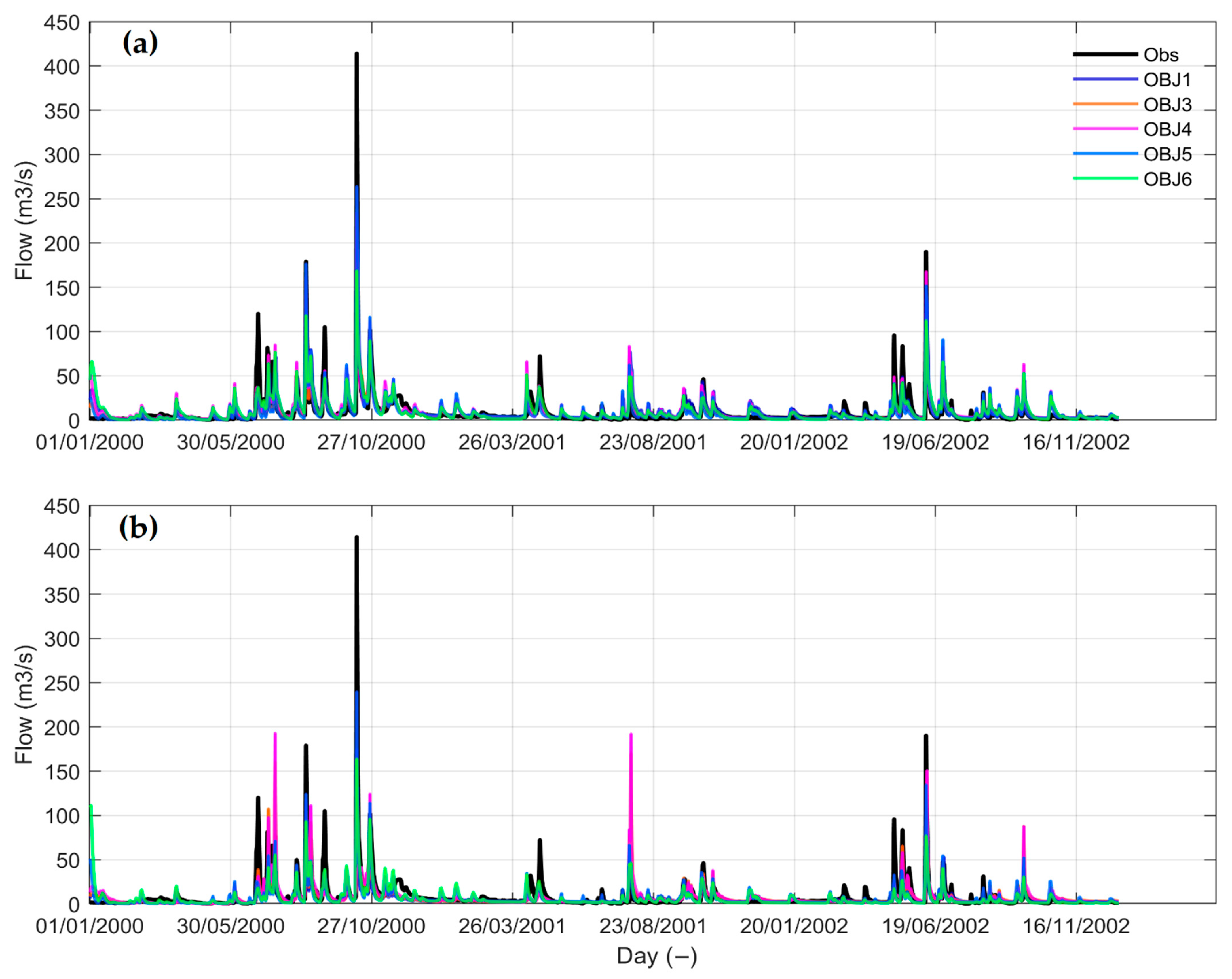
4.1.1. Hydrograph Simulation
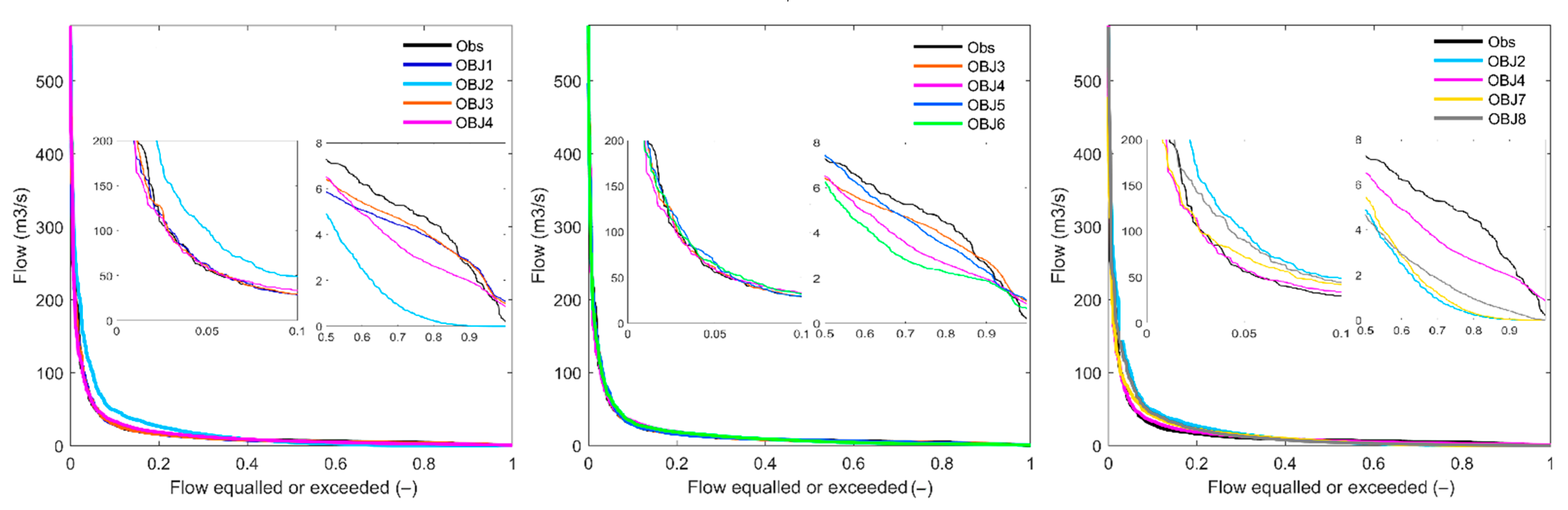
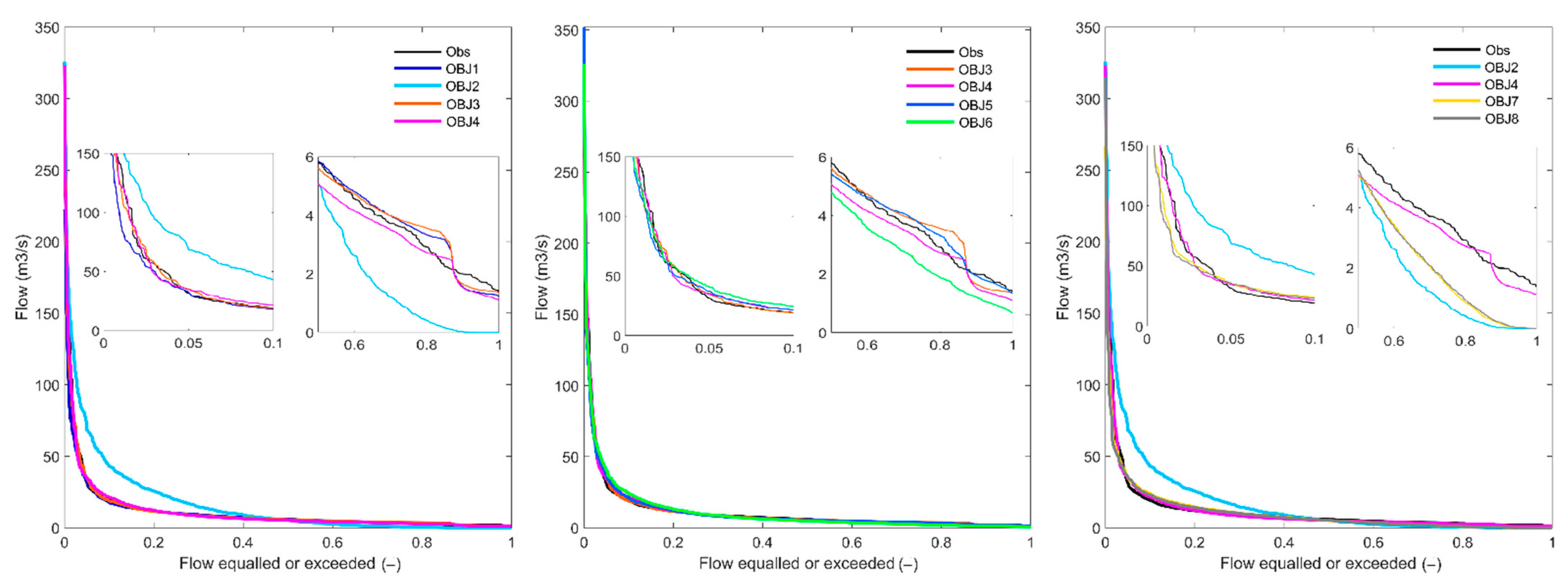
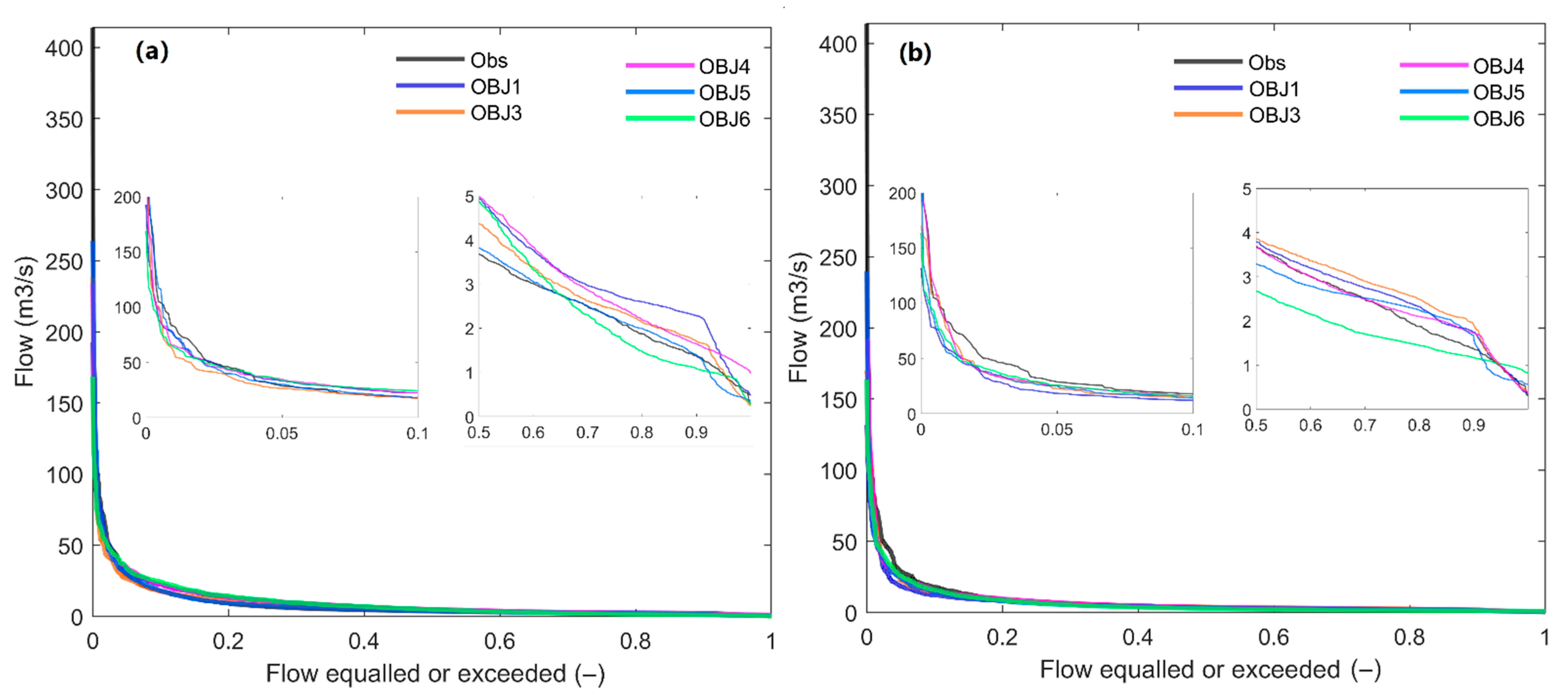
4.1.2. Flow Duration Curves
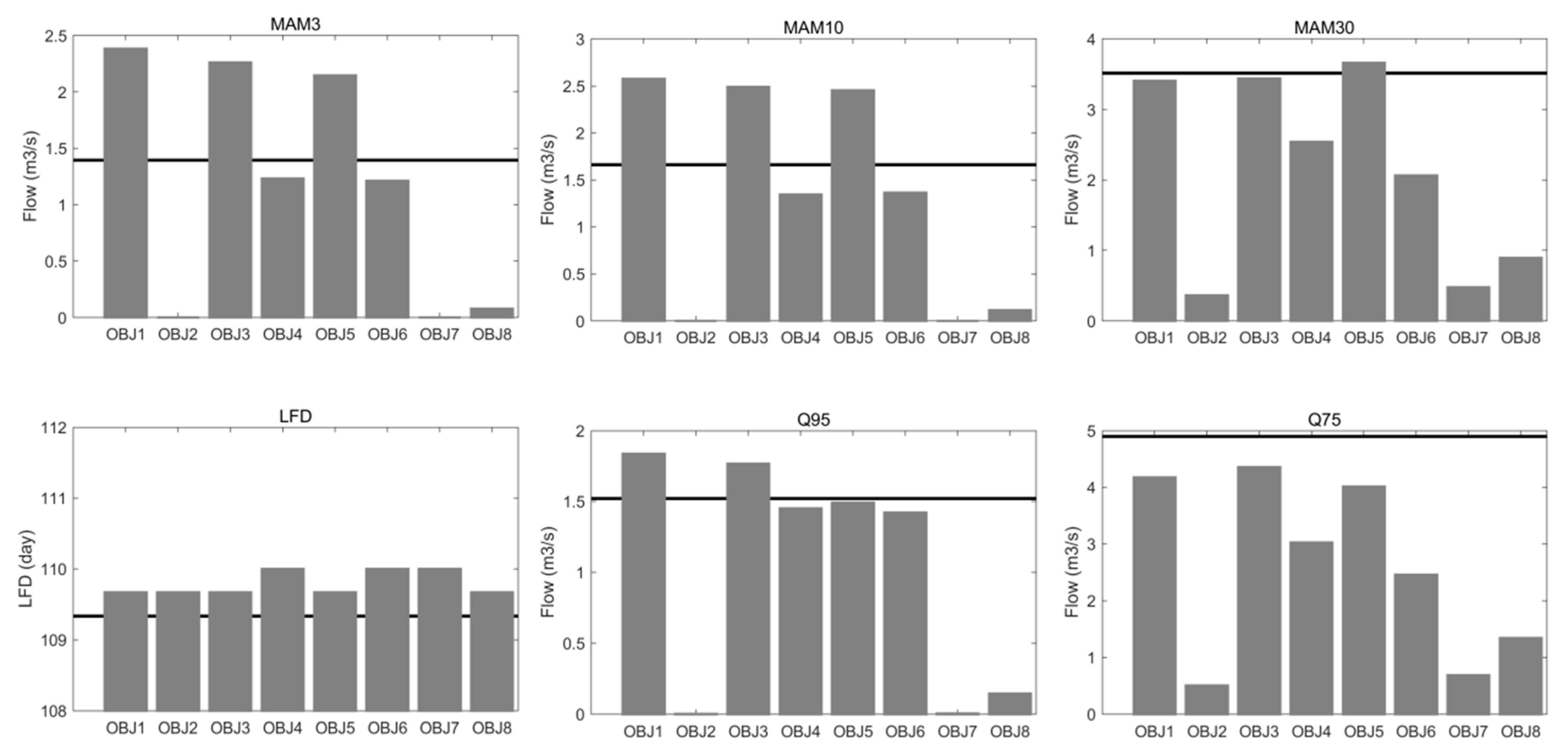
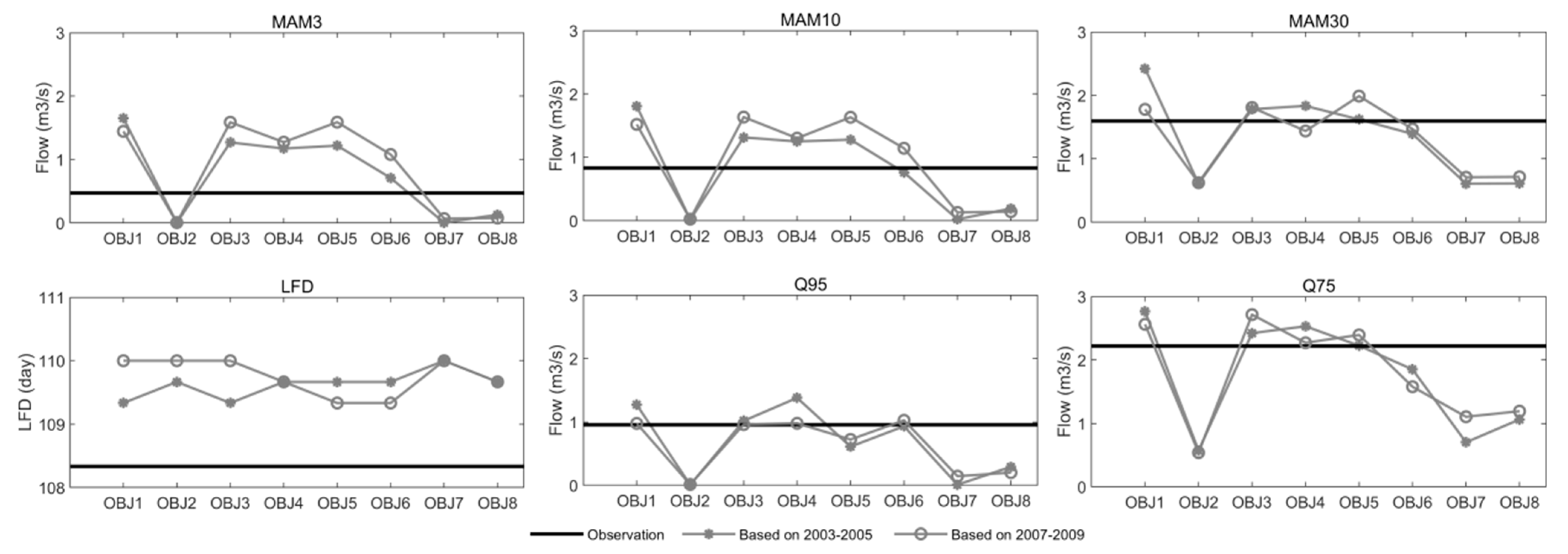
4.1.3. Low Flow Indices
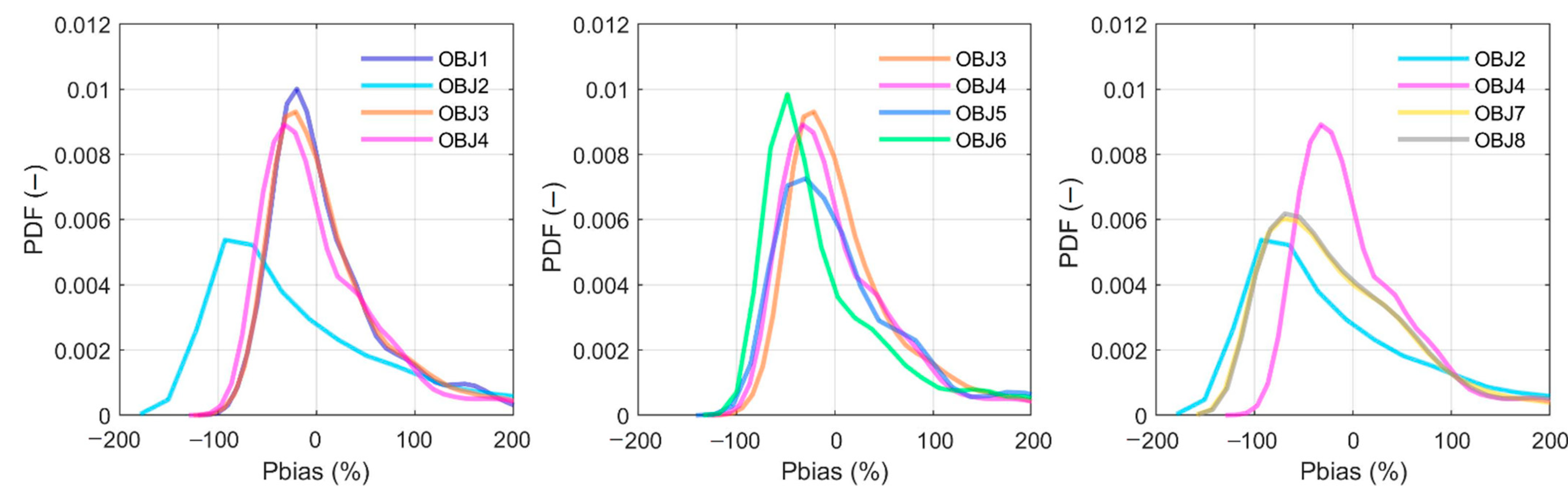
4.2. Climatic Robustness Assessment
4.2.1. Hydrograph Simulation
4.2.2. Flow Duration Curves
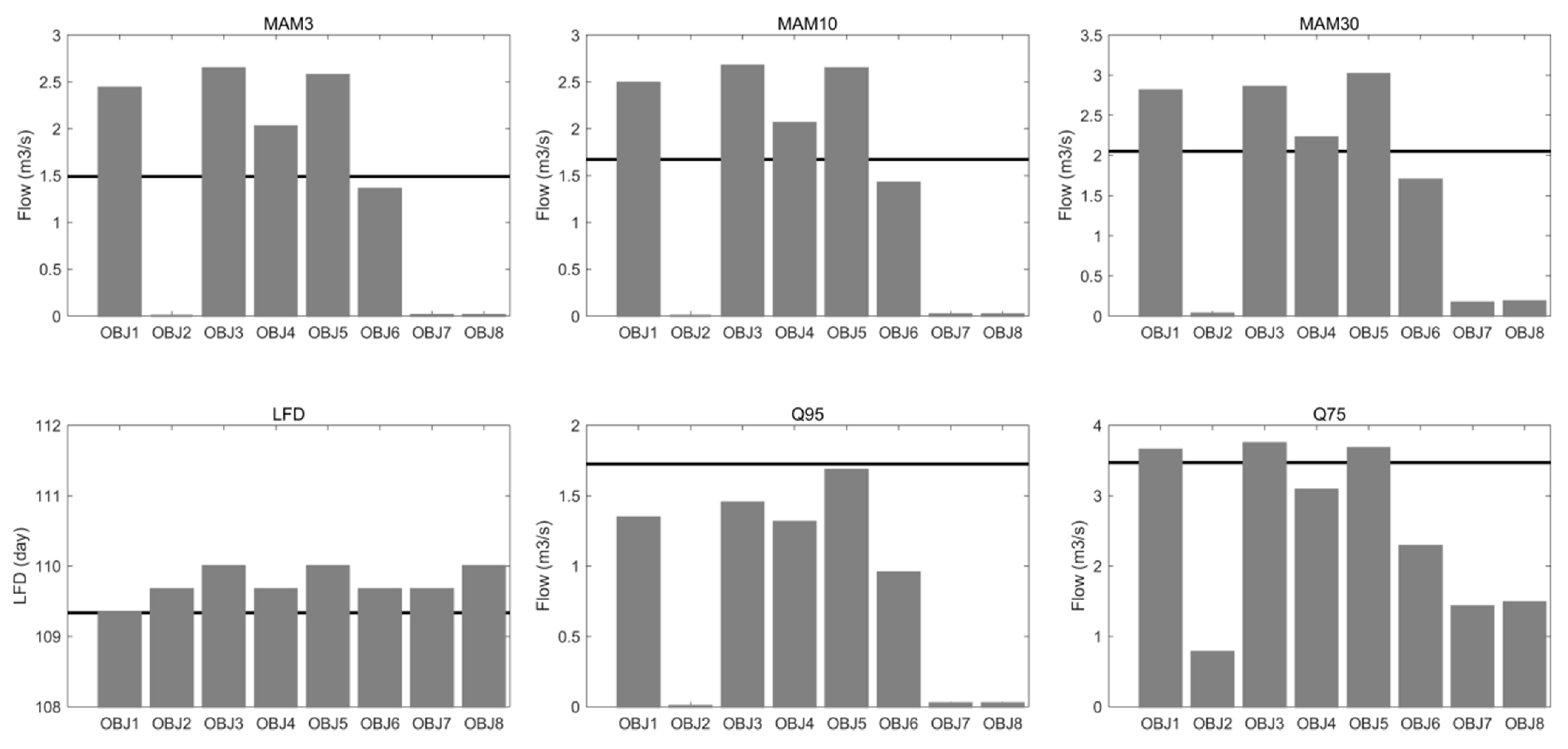
4.2.3. Low Flow Indices
5. Discussion
5.1. Objective Functions Evaluation
5.2. Climatic Robustness Assessment
6. Conclusions
- -
- The influence of the included transformation formats in objective functions on low flow simulation is pronounced, and logarithmic transformation is recommended.
- -
- Among the three classes of objective functions, the combined multi-class is highly recommended, and the mean of KGE(Q) and KGE(log(Q)) remains a first choice. In contrast, the class of split objectives is regarded as the last choice as it demonstrated the worst performance.
- -
- Replacing the objective function from the time series based on the FDC could not improve the simulation performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Engeland, K.; Hisdal, H. A comparison of low flow estimates in ungauged catchments using regional regression and the HBV-model. Water Resour. Manag. 2009, 23, 2567–2586. [Google Scholar] [CrossRef]
- Lang Delus, C. Les étiages: Définitions hydrologique, statistique et seuils réglementaires. Cybergeo Eur. J. Geogr. 2011. [Google Scholar] [CrossRef]
- Garcia, F.; Folton, N.; Oudin, L. Which objective function to calibrate rainfall-runoff models for low-flow index simulations? Hydrol. Sci. J. 2017, 62, 1149–1166. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, J.; Gao, H.; Mao, G. Can multi-objective calibration of streamflow guarantee better hydrological model accuracy? J. Hydroinform. 2018, 20, 687–698. [Google Scholar] [CrossRef]
- Kim, H.S.; Lee, S. Assessment of the adequacy of the regional relationships between catchment attributes and catchment response dynamics, calibrated by a multi-objective approach. Hydrol. Process. 2014, 28, 4023–4041. [Google Scholar] [CrossRef]
- Peel, M.C.; Blöschl, G. Hydrologic modelling in a changing world. Prog. Phys. Geogr. 2011, 35, 249–261. [Google Scholar] [CrossRef]
- Misgana, M.K. Model Performance Sensitivity to Objective Function during Automated Calibrations. J. Hydrol. Eng. 2012, 17, 756–767. [Google Scholar]
- Reed, P.M.; Hadka, D.; Herman, J.D.; Kasprzyk, J.R.; Kollat, J.B. Evolutionary multiobjective optimization in water resources: The past, present, and future. Adv. Water Resour. 2013, 51, 438–456. [Google Scholar] [CrossRef]
- Efstratiadis, A.; Koutsoyiannis, D. One decade of multi-objective calibration approaches in hydrological modelling: A review. Hydrol. Sci. J. J. Sci. Hydrol. 2010, 55, 58–78. [Google Scholar] [CrossRef]
- Pfannerstill, M.; Guse, B.; Fohrer, N. Smart low flow signature metrics for an improved overall performance evaluation of hydrological models. J. Hydrol. 2014, 510, 447–458. [Google Scholar] [CrossRef]
- Asadzadeh, M.; Leon, L.; McCrimmon, C.; Yang, W.; Liu, Y.; Wong, I.; Fong, P.; Bowen, G. Watershed derived nutrients for Lake Ontario inflows: Model calibration considering typical land operations in Southern Ontario. J. Gt. Lakes Res. 2015, 41, 1037–1051. [Google Scholar] [CrossRef]
- Coello, C.A.; Aguirre, A.H.; Zitzler, E. Evolutionary multi-objective optimization. Eur. J. Oper. Res. 2007, 181, 1617–1619. [Google Scholar] [CrossRef]
- Tian, F.; Hu, H.; Sun, Y.; Li, H.; Lu, H. Searching for an Optimized Single-objective Function Matching Multiple Objectives with Automatic Calibration of Hydrological Models. Chin. Geogr. Sci. 2019, 29, 934–948. [Google Scholar] [CrossRef]
- Chilkoti, V.; Bolisetti, T.; Balachandar, R. Multi-objective autocalibration of SWAT model for improved low flow performance for a small snowfed catchment. Hydrol. Sci. J. 2018, 63, 1482–1501. [Google Scholar] [CrossRef]
- Shafii, M.; De Smedt, F. Multi-objective calibration of a distributed hydrological model (WetSpa) using a genetic algorithm. Hydrol. Earth Syst. Sci. 2009, 13, 2137–2149. [Google Scholar] [CrossRef]
- Kim, H.S. Adequacy of a Multi-objective Regional Calibration Method Incorporating a Sequential Regionalisation. Water Resour. Manag. 2014, 28, 5507–5526. [Google Scholar] [CrossRef]
- Lombardi, L.; Toth, E.; Castellarin, A.; Montanari, A.; Bratha, A. Calibration of a rainfall-runoff model at regional scale by optimising river discharge statistics: Performance analysis for the average/low flow regime. Phys. Chem. Earth 2012, 42, 77–84. [Google Scholar] [CrossRef]
- He, Y.; Qiu, H.; Song, J.; Zhao, Y.; Zhang, L.; Hu, S.; Hu, Y. Quantitative contribution of climate change and human activities to runoff changes in the Bahe River watershed of the Qinling Mountains, China. Sustain. Cities Soc. 2019, 51, 101729. [Google Scholar] [CrossRef]
- Zhao, R.J.; Zhang, Y.L.; Fang, L.R.; Liu, X.R.; Zhang, Q.S. The Xinanjiang Model. In Hydrological Forecasting; IAHS Press: Wallingford, UK, 1980; pp. 351–356. [Google Scholar]
- Zhao, R.J. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar]
- Yang, X.; Magnusson, J.; Huang, S.; Beldring, S.; Xu, C.Y. Dependence of regionalization methods on the complexity of hydrological models in multiple climatic regions. J. Hydrol. 2020, 582, 124357. [Google Scholar] [CrossRef]
- An, D.; Li, Z.J.; Kan, G.Y.; Li, Q.L. Comparison between the Application of Data-driven Model and Conceptual Model. Water Power 2013, 39, 9–12. [Google Scholar]
- Lin, K.; Liu, P.; He, Y.; Guo, S. Multi-site evaluation to reduce parameter uncertainty in a conceptual hydrological modeling within the GLUE framework. J. Hydroinform. 2014, 16, 60–73. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 265–284. [Google Scholar] [CrossRef]
- Jeon, J.H.; Park, C.G.; Engel, B. Comparison of performance between genetic algorithm and SCE-UA for calibration of SCS-CN surface runoff simulation. Water 2014, 6, 3433–3456. [Google Scholar] [CrossRef]
- Zeng, Q.; Chen, H.; Xu, C.Y.; Jie, M.X.; Chen, J.; Guo, S.L.; Liu, J. The effect of rain gauge density and distribution on runoff simulation using a lumped hydrological modelling approach. J. Hydrol. 2018, 563, 106–122. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Lobligeois, F.; Andréassian, V.; Perrin, C.; Tabary, P.; Loumagne, C. When does higher spatial resolution rainfall information improve streamflow simulation? An evaluation using 3620 flood events. Hydrol. Earth Syst. Sci. 2014, 18, 575–594. [Google Scholar] [CrossRef]
- Magand, C. Influence de la Représentation des Processus Nivaux sur L’hydrologie de la Durance et sa Réponse Auchangement Climatique. Ph.D. Thesis, Université Pierre et Marie Curie, Paris, France, 2014. [Google Scholar]
- Osuch, M.; Romanowicz, R.J.; Booij, M.J. The influence of parametric uncertainty on the relationships between HBV model parameters and climatic characteristics. Hydrol. Sci. J. 2015, 60, 1299–1316. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the Use of “Goodness-of-Fit” Measures in Hydrologic and Hydroclimatic Model Validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Oudin, L.; Andréassian, V.; Mathevet, T.; Perrin, C.; Michel, C. Dynamic averaging of rainfall-runoff model simulations from comple-mentary model parameterizations. Water Resour. Res. 2006, 42, W07410.1–W07410.10. [Google Scholar] [CrossRef]
- Pushpalatha, R.; Perrin, C.; Moine, N.L.; Andréassian, V. A review of efficiency criteria suitable for evaluating low-flow simulations. J. Hydrol. 2012, 420, 171–182. [Google Scholar] [CrossRef]
- Fowler, K.; Peel, M.; Western, A.; Zhang, L. Improved Rainfall-Runoff Calibration for Drying Climate: Choice of Objective Function. Water Resour. Res. 2018, 54, 3392–3408. [Google Scholar] [CrossRef]
- Klemeš, V. Operational testing of hydrological simulation models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Laaha, G.; Blöschl, G. Seasonality indices for regionalizing low flows. Hydrol. Process. 2006, 20, 3851–3878. [Google Scholar] [CrossRef]
- Price, K.; Purucker, S.T.; Kraemer, S.R.; Babendreier, J.E. Tradeoffs among watershed model calibration targets for parameter estimation. Water Resour. Res. 2012, 48, W10542.1–W10542.16. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmer, R.D.; Veith, T.L. Model Evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Matrosov, E.S.; Huskova, I.; Kasprzyk, J.R.; Harou, J.J.; Lambert, C.; Reed, P.M. Many-objective optimization and visual analytics reveal key trade-offs for London’s water supply. J. Hydrol. 2015, 531, 1040–1053. [Google Scholar] [CrossRef]
- Jie, M.X.; Chen, H.; Xu, C.Y.; Zeng, Q.; Tao, X. A comparative study of different objective functions to improve the flood forecasting accuracy. Hydrol. Res. 2016, 47, 718–735. [Google Scholar] [CrossRef]
- Kamali, B.; Mousavi, S.J.; Abbaspour, K.C. Automatic calibration of HEC-HMS using single-objective and multiobjective PSO algorithms. Hydrol. Process. 2013, 27, 4028–4042. [Google Scholar] [CrossRef]
- Her, Y.; Seong, C. Responses of hydrological model equifinality, uncertainty, and performance to multi-objective parameter calibration. J. Hydroinform. 2018, 20, 864–885. [Google Scholar] [CrossRef]

| Criteria | Description |
|---|---|
| KGE | Kling-Gupta Efficiency (see Equation (1)) |
| KGElog | KGE calculated on logarithmic transformed flow |
| MAM3 | Mean Annual Minimum 3-day mean flow at 3-year return period |
| MAM10 | Mean Annual Minimum 10-day mean flow at 3-year return period |
| MAM30 | Mean Annual Minimum 30-day mean flow at 3-year return period |
| LFD | The duration of low flow smaller than 30% of the time |
| Q95 | Flow exceeded 95% of the time |
| Q75 | Flow exceeded 75% of the time |
| Evaluation Criteria | KGE | KGElog | ||
|---|---|---|---|---|
| Calibration Period | 2003–2005 | 2007–2009 | 2003–2005 | 2007–2009 |
| OBJ1 | 0.85 | 0.63 | 0.78 | 0.84 |
| OBJ2 | 0.60 | 0.25 | / | / |
| OBJ3 | 0.90 | 0.78 | 0.77 | 0.83 |
| OBJ4 | 0.92 | 0.78 | 0.70 | 0.79 |
| OBJ5 | 0.89 | 0.62 | 0.74 | 0.69 |
| OBJ6 | 0.90 | 0.55 | 0.68 | 0.61 |
| OBJ7 | 0.85 | 0.68 | / | / |
| OBJ8 | 0.74 | 0.69 | / | / |
| Calibration Period | 2003–2005 | 2007–2009 | ||
|---|---|---|---|---|
| Evaluation Criteria | KGE | KGElog | KGE | KGElog |
| OBJ1 | 0.61 | 0.67 | 0.42 | 0.69 |
| OBJ3 | 0.68 | 0.70 | 0.58 | 0.68 |
| OBJ4 | 0.68 | 0.62 | 0.61 | 0.71 |
| OBJ5 | 0.79 | 0.67 | 0.58 | 0.63 |
| OBJ6 | 0.61 | 0.64 | 0.49 | 0.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Yu, C.; Li, X.; Luo, J.; Xie, J.; Zhou, B. Comparison of the Calibrated Objective Functions for Low Flow Simulation in a Semi-Arid Catchment. Water 2022, 14, 2591. https://doi.org/10.3390/w14172591
Yang X, Yu C, Li X, Luo J, Xie J, Zhou B. Comparison of the Calibrated Objective Functions for Low Flow Simulation in a Semi-Arid Catchment. Water. 2022; 14(17):2591. https://doi.org/10.3390/w14172591
Chicago/Turabian StyleYang, Xue, Chengxi Yu, Xiaoli Li, Jungang Luo, Jiancang Xie, and Bin Zhou. 2022. "Comparison of the Calibrated Objective Functions for Low Flow Simulation in a Semi-Arid Catchment" Water 14, no. 17: 2591. https://doi.org/10.3390/w14172591
APA StyleYang, X., Yu, C., Li, X., Luo, J., Xie, J., & Zhou, B. (2022). Comparison of the Calibrated Objective Functions for Low Flow Simulation in a Semi-Arid Catchment. Water, 14(17), 2591. https://doi.org/10.3390/w14172591





