A Data-Driven Dam Deformation Forecasting and Interpretation Method Using the Measured Prototypical Temperature Data
Abstract
:1. Introduction
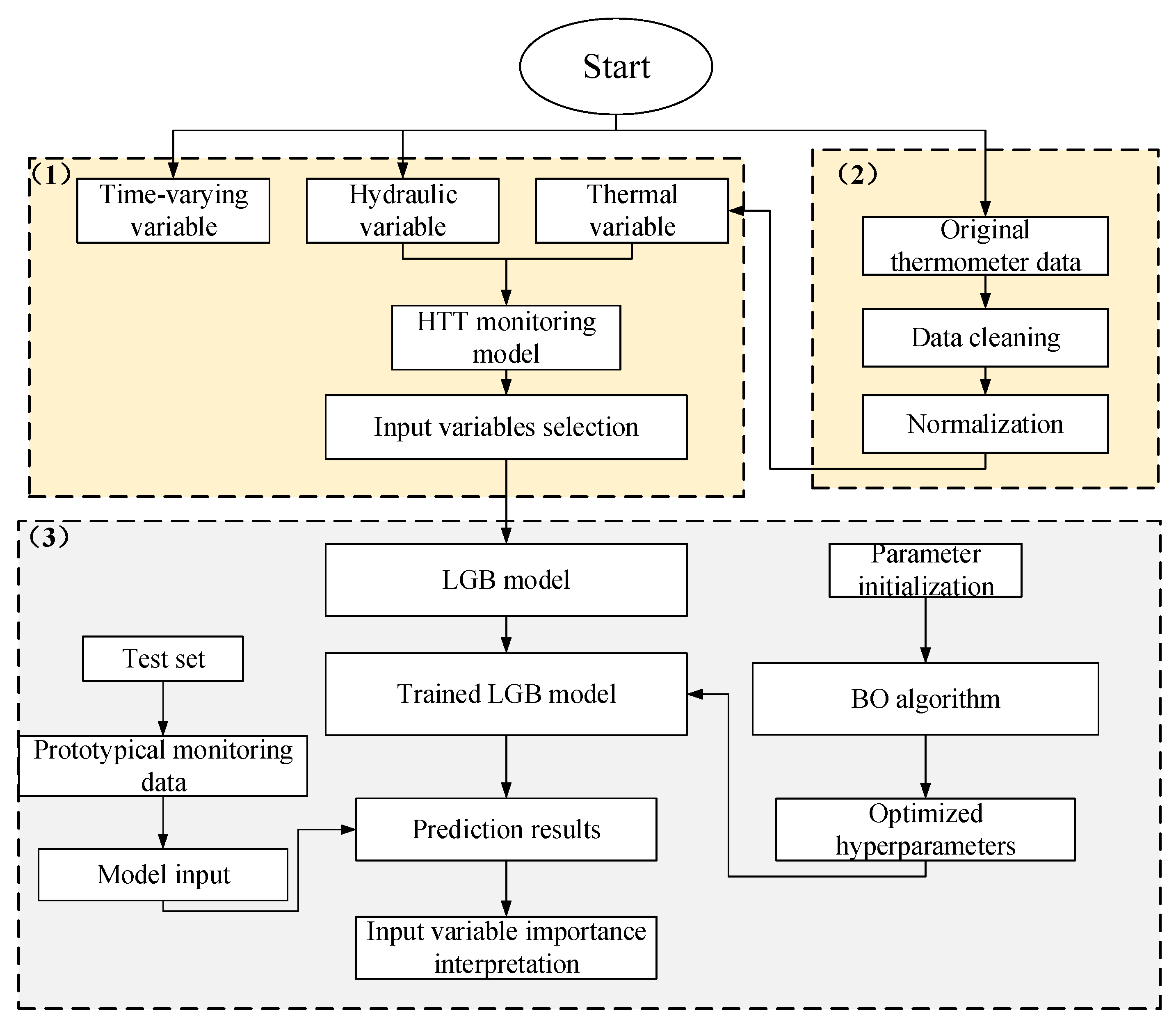
2. Methodology
2.1. Dam Deformation Statistical Monitoring Model
2.2. LGB
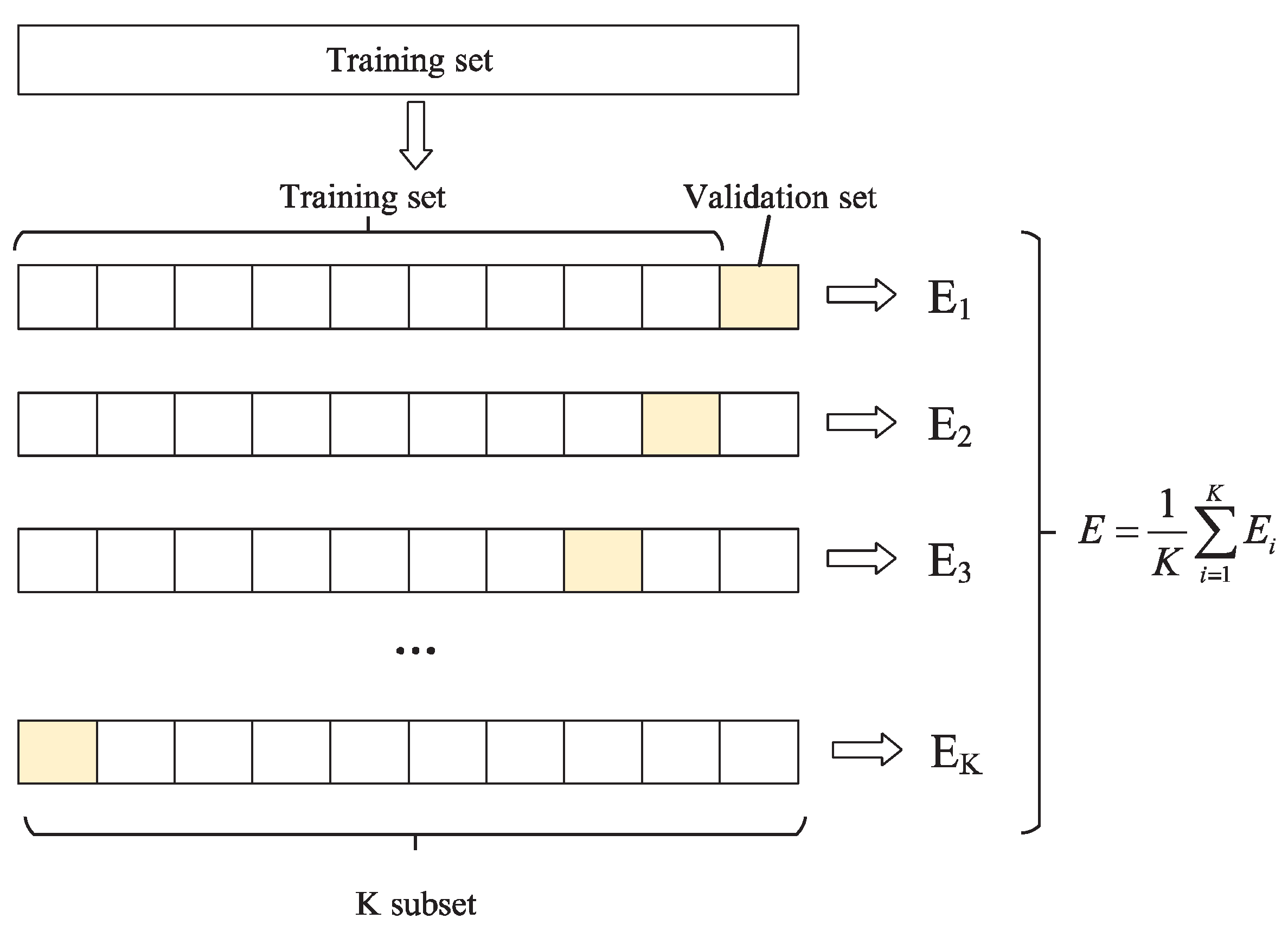
2.3. Bayesian Optimization and Cross-Validation
- Step 1:
- The training set is randomly divided into K disjoint subsets;
- Step 2:
- The 1st and K-1th subsets are used as the training set, and the Kth subset is used as the verification set. Then, the prediction accuracy of the K group subset is calculated;
- Step 3:
- The second to Kth group subsets are used as the training set, and the first group subset is used as the verification set to obtain the prediction accuracy of the Kth group subset test;
- Step 4:
- The average prediction accuracy of the above K model is taken as the performance index of the model under K-fold cross-validation.
3. Case Study
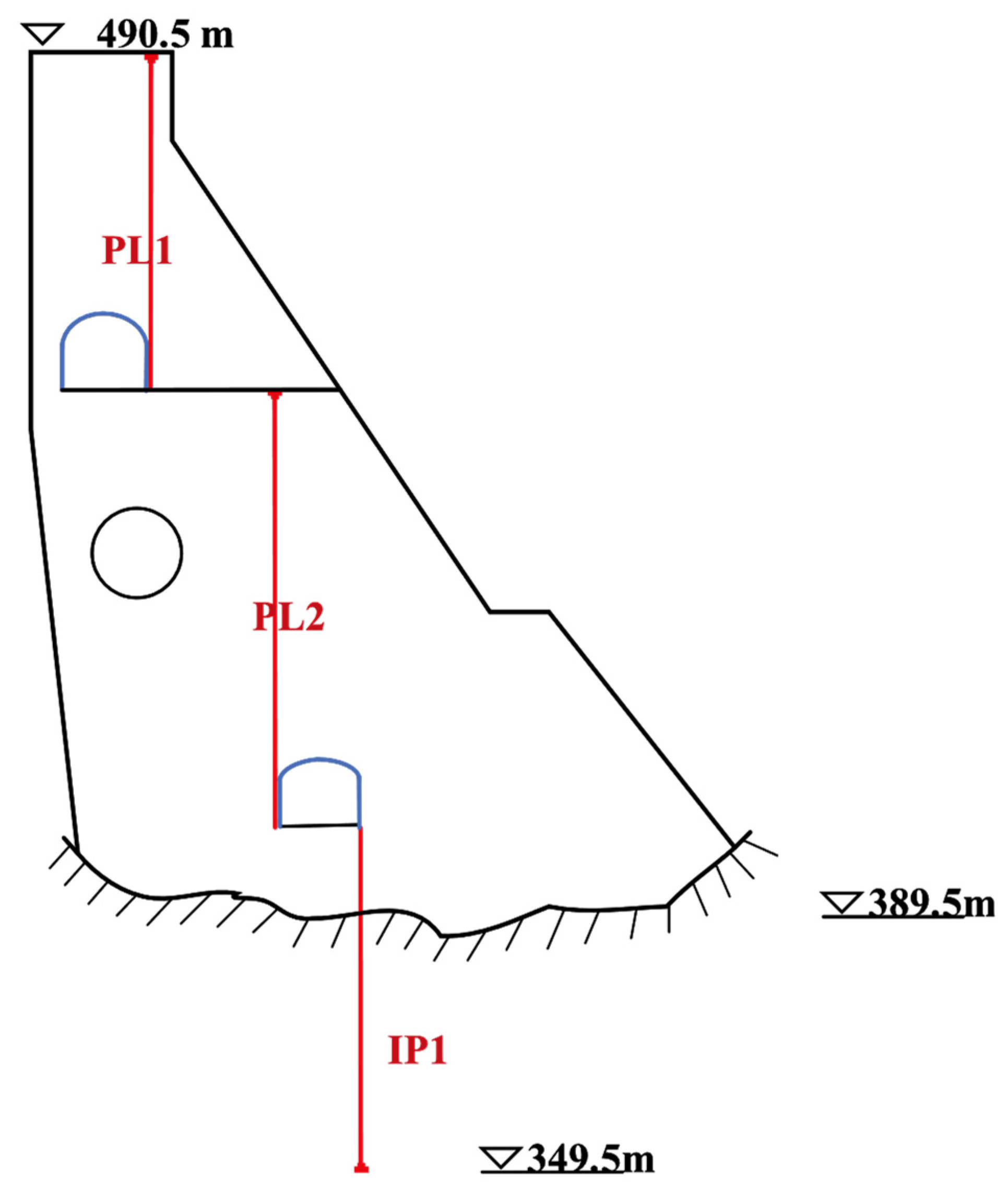
3.1. Project Description
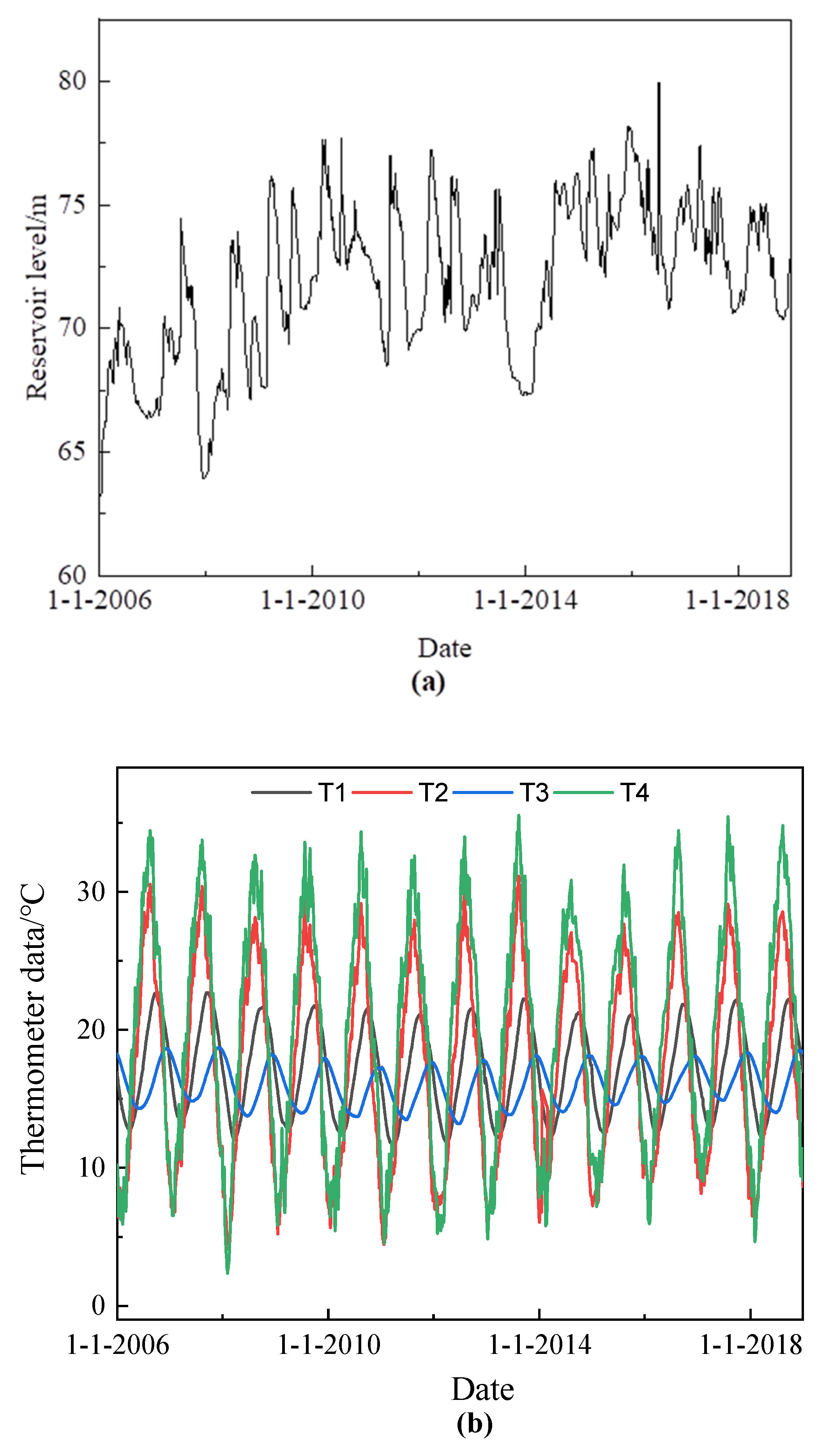
3.2. Data Collection and Preprocessing
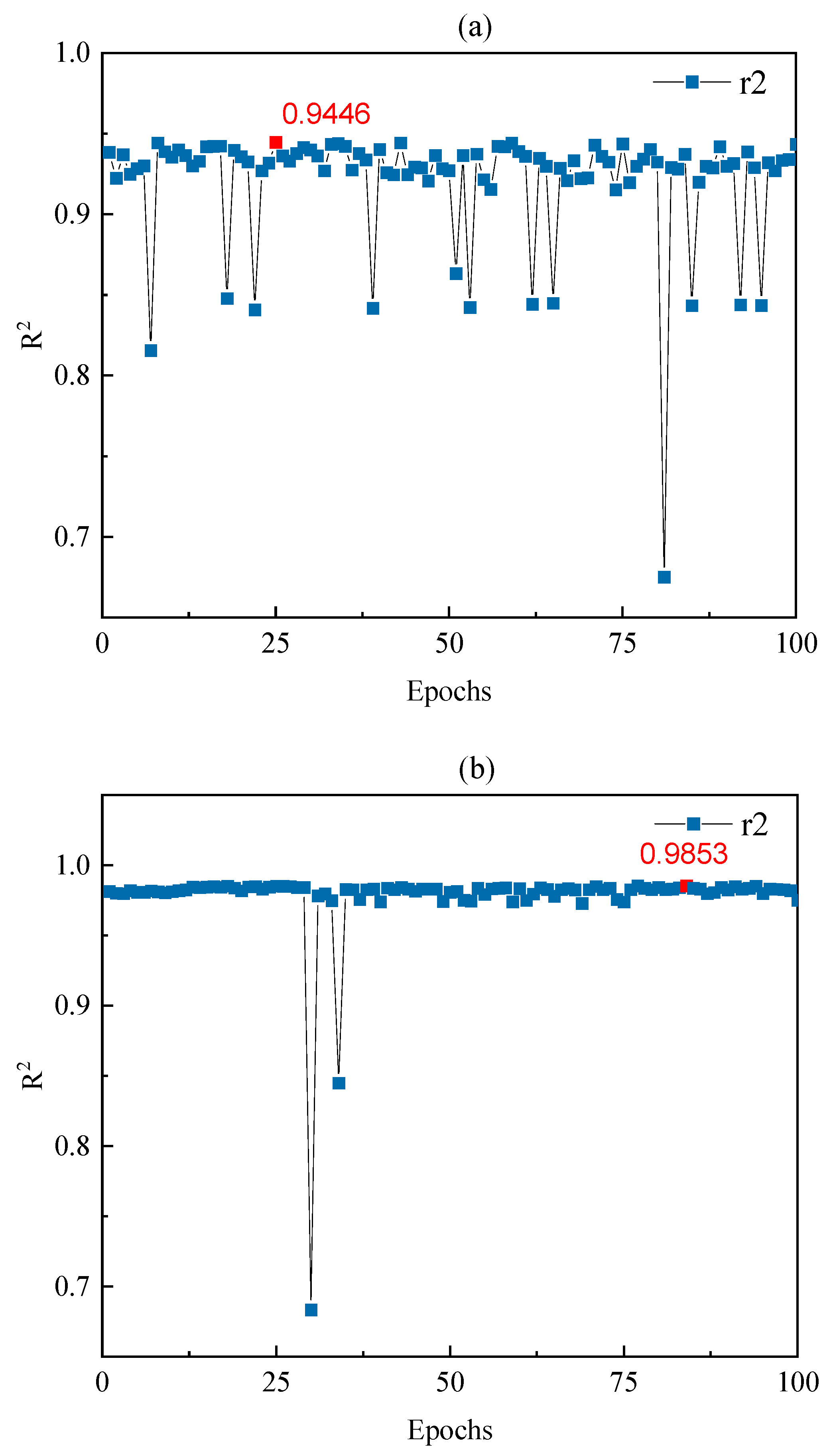
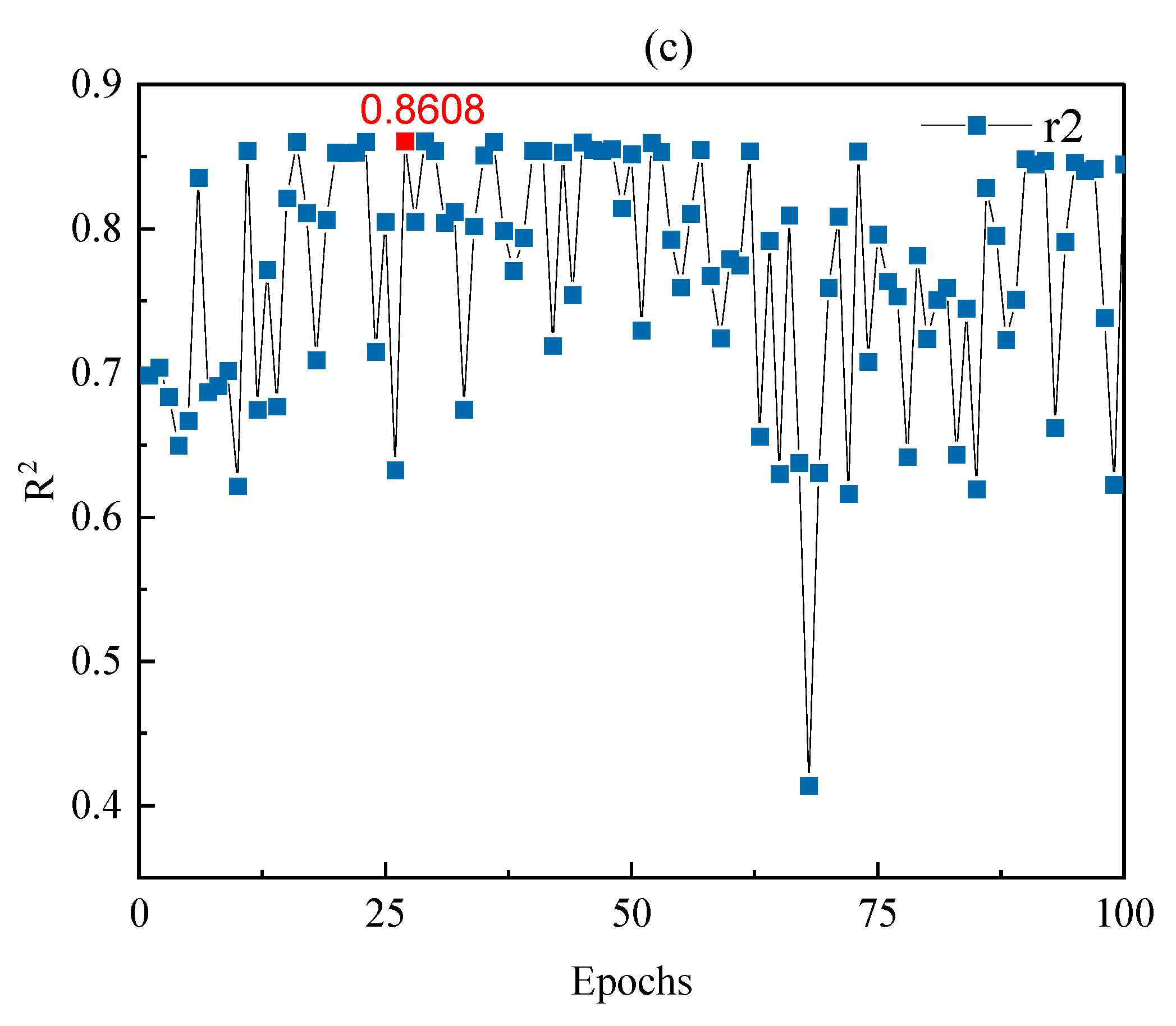
3.3. Experiment Environment Setting and Parameter Tuning
4. Results Discussion
4.1. Project Description
4.2. Model Generalization Capability Evaluation
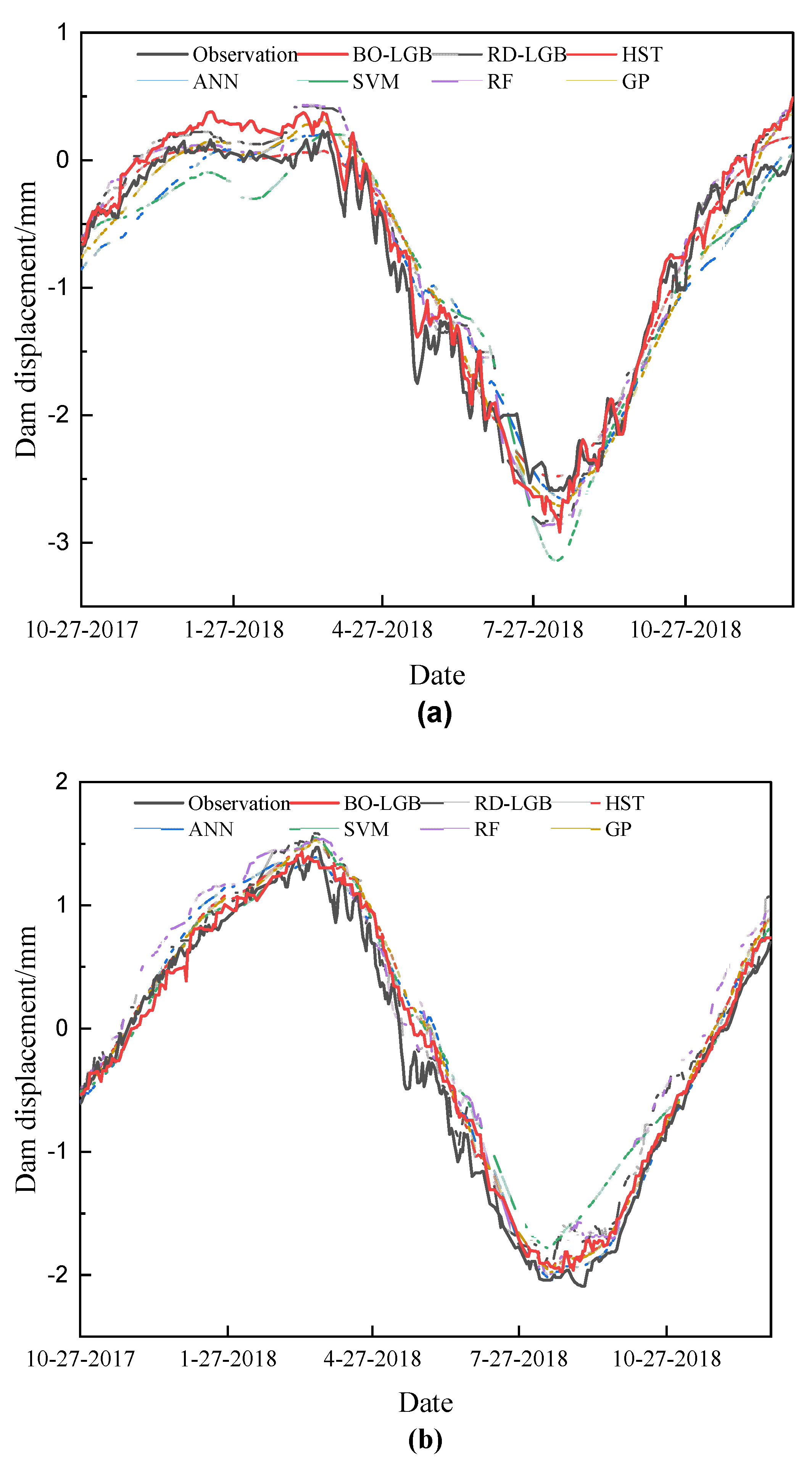
4.2.1. Short-Term Prediction Performance Evaluation
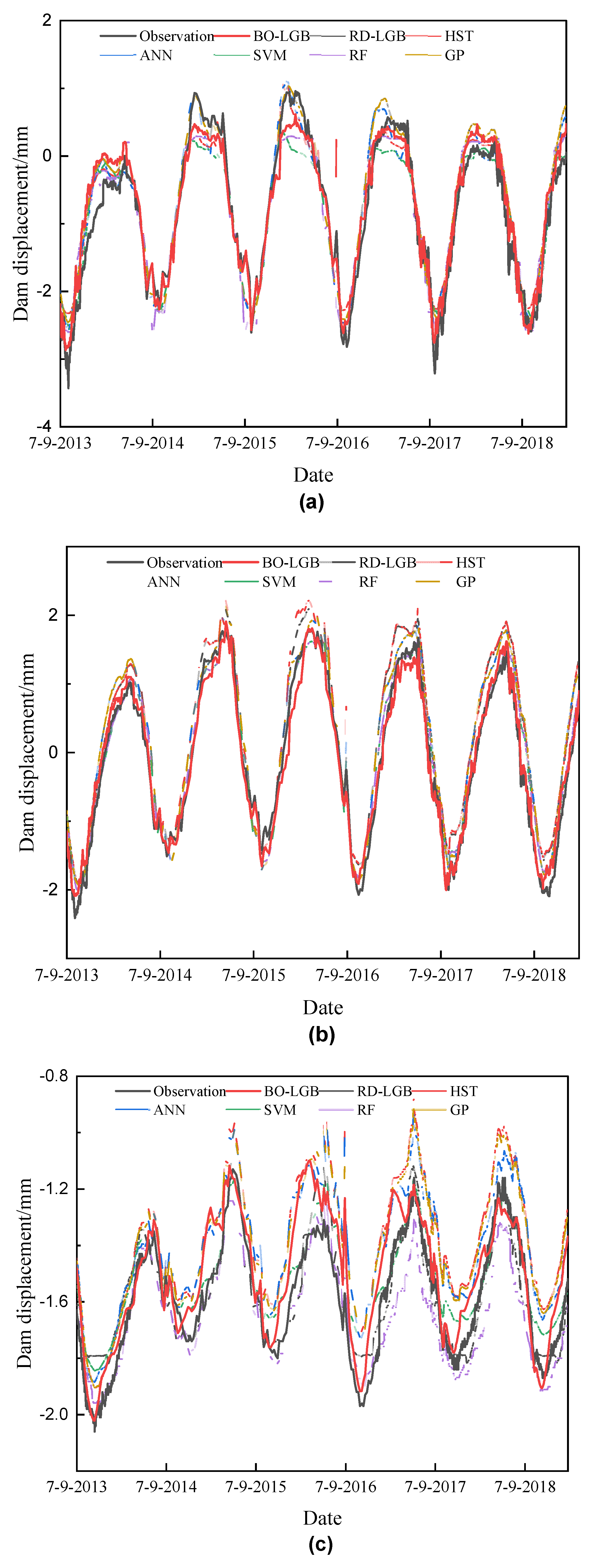
4.2.2. Long-Term Prediction Performance Evaluation
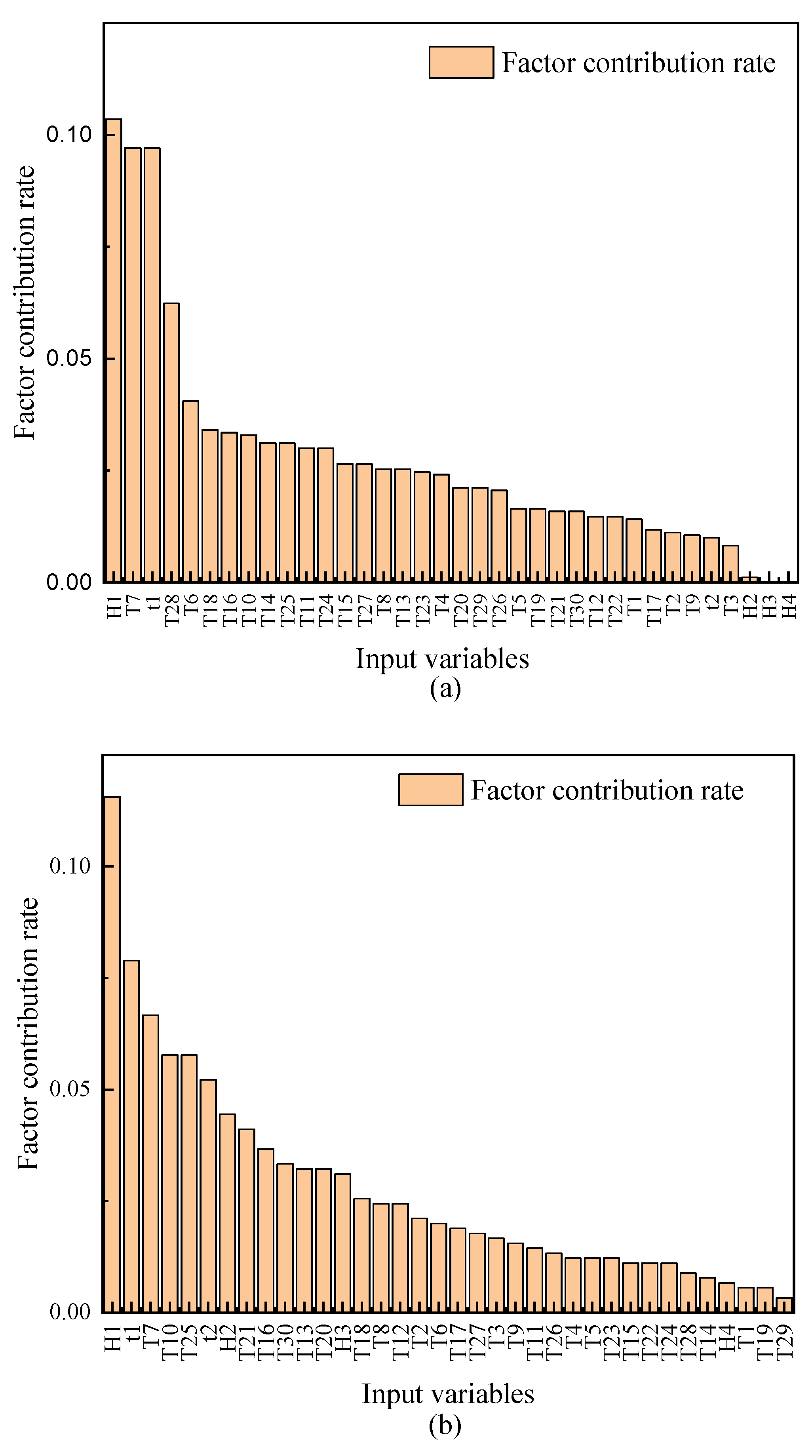
4.3. Model Interpretability Assessment
5. Conclusions
- The proposed BO–LGB model shows strong capability when dealing with the long-term dam monitoring data both in modeling accuracy and efficiency;
- The proposed method achieves remarkable performance in a variety of dam displacement prediction scenarios (both in short-term prediction and long-term prediction);
- The proposed method can analyze the main factors affecting dam displacement changes based on prototypical monitoring data.
Author Contributions
Funding
Conflicts of Interest
References
- Kang, F.; Li, J.; Zhao, S.; Wang, Y. Structural health monitoring of concrete dams using long-term air temperature for thermal effect simulation. Eng. Struct. 2019, 180, 642–653. [Google Scholar] [CrossRef]
- Kang, F.; Li, J. Displacement Model for Concrete Dam Safety Monitoring via Gaussian Process Regression Considering Extreme Air Temperature. J. Struct. Eng. 2020, 146, 05019001. [Google Scholar] [CrossRef]
- Tatin, M.; Briffaut, M.; Dufour, F.; Simon, A.; Fabre, J.-P. Thermal displacements of concrete dams: Accounting for water temperature in statistical models. Eng. Struct. 2015, 91, 26–39. [Google Scholar] [CrossRef]
- Kang, F.; Liu, X.; Li, J. Concrete Dam Behavior Prediction Using Multivariate Adaptive Regression Splines with Meas-ured Air Temperature. Arab. J. Sci. Eng. 2019, 44, 8661–8673. [Google Scholar] [CrossRef]
- Li, Y.; Bao, T.; Shu, X.; Chen, Z.; Gao, Z.; Zhang, K. A Hybrid Model Integrating Principal Component Analysis, Fuzzy C-Means, and Gaussian Process Regression for Dam Deformation Prediction. Arab. J. Sci. Eng. 2020, 46, 4293–4306. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, X.C.; Chen, W.; Hong, X. Breach Discharge Estimates and Surface Velocity Measurements for an Earth Dam Failure Process Due to Overtopping Based on the LS-PIV Method. Arab. J. Sci. Eng. 2019, 44, 329–339. [Google Scholar] [CrossRef]
- Ma, C.; Gao, Z.; Yang, J.; Cheng, L.; Chen, L. Operation Performance and Seepage Flow of Impervious Body in Blast-Fill Dams Using Discrete Element Method and Measured Data. Water 2022, 14, 1443. [Google Scholar] [CrossRef]
- Tong, F.; Yang, J.; Ma, C.; Cheng, L.; Li, G. The Prediction of Concrete Dam Displacement Using Copula-PSO-ANFIS Hybrid Model. Arab. J. Sci. Eng. 2022, 47, 4335–4350. [Google Scholar] [CrossRef]
- Salazar, F.; Toledo, M.; Oñate, E.; Morán, R. An empirical comparison of machine learning techniques for dam behaviour modelling. Struct. Saf. 2015, 56, 9–17. [Google Scholar] [CrossRef]
- Xi, R.; Zhou, X.; Jiang, W.; Chen, Q. Simultaneous estimation of dam displacements and reservoir level variation from GPS measurements. Measurement 2018, 122, 247–256. [Google Scholar] [CrossRef]
- Liu, H.Z.; Wang, S.L.; Liu, J.Y. LS-SVM Prediction Model Based on Phase Space Reconstruction for Dam Deformation. Adv. Mater. Res. 2013, 663, 55–59. [Google Scholar] [CrossRef]
- Shao, C.; Gu, C.; Yang, M.; Xu, Y.; Su, H. A novel model of dam displacement based on panel data. Struct. Control Health Monit. 2018, 25, e2037. [Google Scholar] [CrossRef]
- Yang, L.; Su, H.; Wen, Z. Improved PLS and PSO methods-based back analysis for elastic modulus of dam. Adv. Eng. Softw. 2019, 131, 205–216. [Google Scholar] [CrossRef]
- Li, B.; Yang, J.; Hu, D. Dam monitoring data analysis methods: A literature review. Struct. Control Health Monit. 2020, 27, e2501. [Google Scholar] [CrossRef]
- Thangam, Y.Y.; Kalanithi, M.; Anbarasi, C.M.; Rajendran, S. Inhibition of Corrosion of Carbon Steel in a Dam Water by Sodium Molybdate–Zn2+ System. Arab. J. Sci. Eng. 2009, 34, 49–60. [Google Scholar]
- Lin, C.; Li, T.; Chen, S.; Liu, X.; Lin, C.; Liang, S. Gaussian process regression-based forecasting model of dam deformation. Neural Comput. Appl. 2019, 31, 8503–8518. [Google Scholar] [CrossRef]
- Qu, X.; Yang, J.; Chang, M. A Deep Learning Model for Concrete Dam Deformation Prediction Based on RS-LSTM. J. Sens. 2019, 2019, 4581672. [Google Scholar] [CrossRef]
- Mata, J.; de Castro, A.T.; da Costa, J.S. Constructing Statistical Models for Arch Dam Deformation. Struct. Control Health Monit. 2014, 21, 423–437. [Google Scholar] [CrossRef]
- Su, H.; Li, X.; Yang, B.; Wen, Z. Wavelet support vector machine-based prediction model of dam deformation. Mech. Syst. Signal Process. 2018, 110, 412–427. [Google Scholar] [CrossRef]
- Beaujoint, N.J. Discussion of “Dead Load Stress in Model Dams by Method of Integration”. J. Struct. Div. 1962, 88, 317–318. [Google Scholar] [CrossRef]
- Belmokre, A.; Mihoubi, M.K.; Santillán, D. Analysis of Dam Behavior by Statistical Models: Application of the Random Forest Approach. KSCE J. Civ. Eng. 2019, 23, 4800–4811. [Google Scholar] [CrossRef]
- Salazar, F.; Morán, R.; Toledo, M.; Oñate, E. Data-Based Models for the Prediction of Dam Behaviour: A Review and Some Methodological Considerations. Arch. Comput. Methods Eng. 2017, 24, 1–21. [Google Scholar] [CrossRef]
- Hu, J.; Wu, S. Statistical modeling for deformation analysis of concrete arch dams with influential horizontal cracks. Struct. Health Monit. 2019, 18, 546–562. [Google Scholar] [CrossRef]
- Wieland, M.; Kirchen, G.F. Long-term dam safety monitoring of Punt dal Gall arch dam in Switzerland. Front. Struct. Civ. Eng. 2012, 6, 76–83. [Google Scholar] [CrossRef]
- Li, M.; Shen, Y.; Ren, Q.; Li, H. A new distributed time series evolution prediction model for dam deformation based on constituent elements. Adv. Eng. Inform. 2019, 39, 41–52. [Google Scholar] [CrossRef]
- Ren, Q.; Li, M.; Song, L.; Liu, H. An optimized combination prediction model for concrete dam deformation considering quantitative evaluation and hysteresis correction. Adv. Eng. Inform. 2020, 46, 101154. [Google Scholar] [CrossRef]
- Li, Y.; Bao, T.; Gong, J.; Shu, X.; Zhang, K. The Prediction of Dam Displacement Time Series Using STL, Extra-Trees, and Stacked LSTM Neural Network. IEEE Access 2020, 8, 94440–94452. [Google Scholar] [CrossRef]
- Bui, K.-T.T.; Tien Bui, D.; Zou, J.; Van Doan, C.; Revhaug, I. A novel hybrid artificial intelligent approach based on neural fuzzy inference model and particle swarm optimization for horizontal displacement modeling of hydropower dam. Neural Comput. Appl. 2018, 29, 1495–1506. [Google Scholar] [CrossRef]
- Li, X.; Wen, Z.; Su, H. An approach using random forest intelligent algorithm to construct a monitoring model for dam safety. Eng. Comput. 2021, 37, 39–56. [Google Scholar] [CrossRef]
- Milillo, P.; Perissin, D.; Salzer, J.T.; Lundgren, P.; Lacava, G.; Milillo, G.; Serio, C. Monitoring dam structural health from space: Insights from novel InSAR techniques and multi-parametric modeling applied to the Pertusillo dam Basilicata, Italy. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 221–229. [Google Scholar] [CrossRef]
- Ribeiro, L.S.; Wilhelm, V.E.; Faria, F.; Correa, J.M.; dos Santos, A.C.P. A comparative analysis of long-term concrete deformation models of a buttress dam. Eng. Struct. 2019, 193, 301–307. [Google Scholar] [CrossRef]
- Gui, G.; Pan, H.; Lin, Z.; Li, Y.; Yuan, Z. Data-driven support vector machine with optimization techniques for structural health monitoring and damage detection. KSCE J. Civ. Eng. 2017, 21, 523–534. [Google Scholar] [CrossRef]
- Ma, J.; Cheng, J.C.; Jiang, F.; Chen, W.; Wang, M.; Zhai, C. A bi-directional missing data imputation scheme based on LSTM and transfer learning for building energy data. Energy Build. 2020, 216, 109941. [Google Scholar] [CrossRef]
- Malekloo, A.; Ozer, E.; AlHamaydeh, M.; Girolami, M. Machine Learning and Structural Health Monitoring Overview with Emerging Technology and High-Dimensional Data Source Highlights. Struct. Health Monit. 2022, 21, 1906–1955. [Google Scholar] [CrossRef]
- Chen, S.; Gu, C.; Lin, C.; Zhao, E.; Song, J. Safety Monitoring Model of a Super-High Concrete Dam by Using RBF Neural Network Coupled with Kernel Principal Component Analysis. Math. Probl. Eng. 2018, 2018, 1712653. [Google Scholar] [CrossRef]
- Su, Y.; Weng, K.; Lin, C.; Zheng, Z. An Improved Random Forest Model for the Prediction of Dam Displacement. IEEE Access 2021, 9, 9142–9153. [Google Scholar] [CrossRef]
- Ren, Q.; Li, M.; Li, H.; Song, L.; Si, W.; Liu, H. A robust prediction model for displacement of concrete dams subjected to irregular water-level fluctuations. Comput. -Aided Civ. Infrastruct. Eng. 2021, 36, 577–601. [Google Scholar] [CrossRef]
- Li, M.; Li, M.; Ren, Q.; Li, H.; Song, L. DRLSTM: A dual-stage deep learning approach driven by raw monitoring data for dam dis-placement prediction. Adv. Eng. Inform. 2022, 51, 101510. [Google Scholar] [CrossRef]
- Ren, Q.; Li, M.; Kong, T.; Ma, J. Multi-sensor real-time monitoring of dam behavior using self-adaptive online sequential learning. Autom. Constr. 2022, 140, 104365. [Google Scholar] [CrossRef]




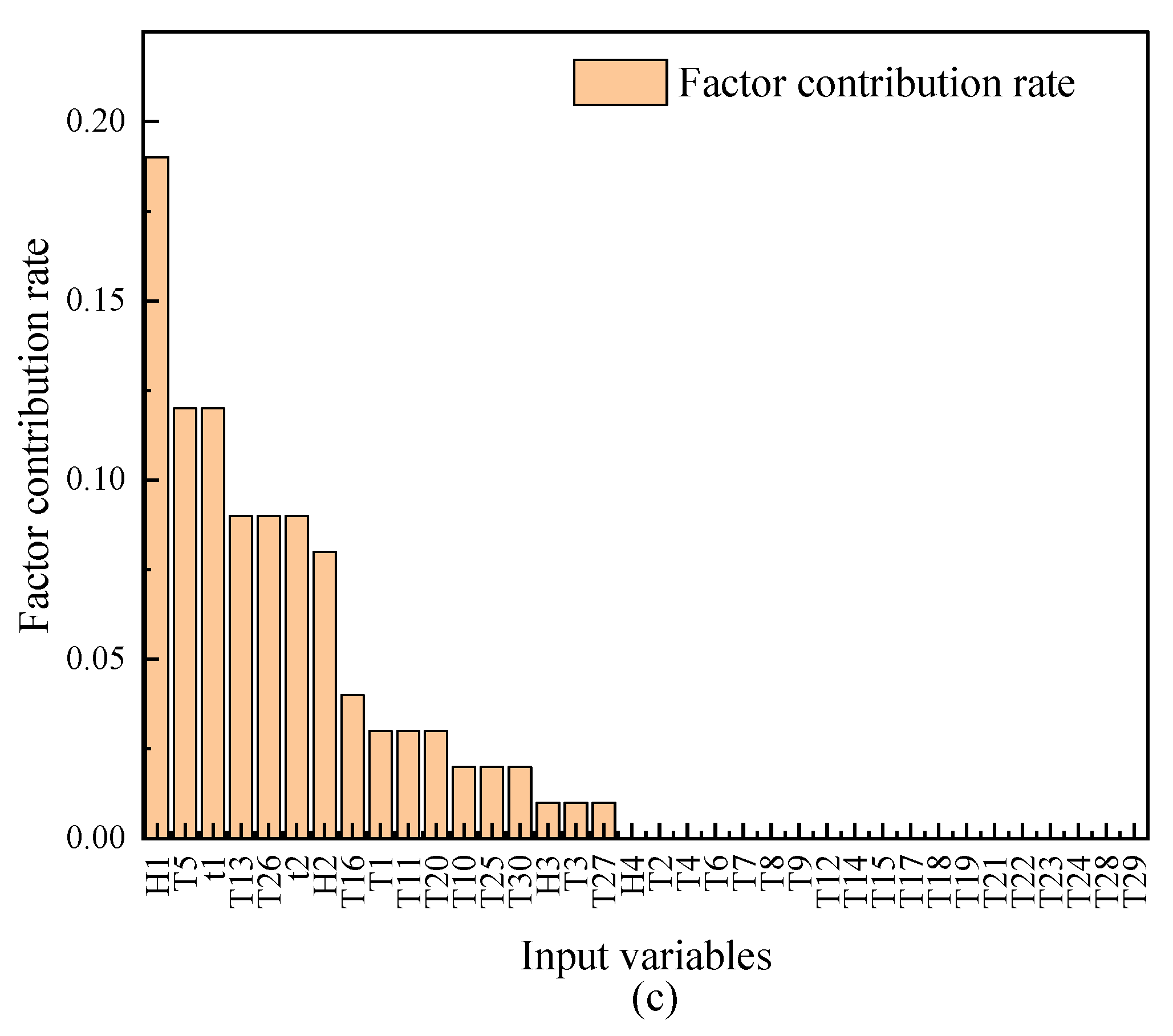
| Parameters | Parameter Optimization Range |
|---|---|
| n_Estimators | num_Leaves | min_Child_Samples | Max_Depth | Feature_Fraction | Bagging_Fraction | |
|---|---|---|---|---|---|---|
| PL01 | 474 | 19 | 9 | 50 | 0.96 | 0.67 |
| PL02 | 500 | 10 | 20 | 73 | 0.5 | 0.5 |
| IP01 | 424 | 48 | 17 | 2 | 0.73 | 0.89 |
| Proposed | RD_LGB | HST | ANN | SVM | RF | GP | ||
|---|---|---|---|---|---|---|---|---|
| PL01 | R2 | 0.9600 | 0.9238 | 0.9490 | 0.9103 | 0.8739 | 0.9243 | 0.9323 |
| MSE | 0.1920 | 0.2689 | 0.1950 | 0.2532 | 0.3171 | 0.2666 | 0.2440 | |
| MAE | 0.1622 | 0.2226 | 0.1378 | 0.2057 | 0.2598 | 0.2106 | 0.1882 | |
| PL02 | R2 | 0.9703 | 0.9638 | 0.9621 | 0.9607 | 0.3334 | 0.9289 | 0.9608 |
| MSE | 0.1751 | 0.1928 | 0.2072 | 0.1981 | 0.7291 | 0.2806 | 0.2104 | |
| MAE | 0.1327 | 0.1641 | 0.1591 | 0.1423 | 0.6231 | 0.2474 | 0.1589 | |
| IP01 | R2 | 0.9855 | 0.9836 | 0.8879 | 0.8796 | 0.5692 | 0.8499 | 0.9354 |
| MSE | 0.0269 | 0.0284 | 0.0688 | 0.0678 | 0.1198 | 0.0764 | 0.0528 | |
| MAE | 0.0217 | 0.0227 | 0.0633 | 0.0573 | 0.1120 | 0.0663 | 0.0480 |
| Proposed | RD_LGB | HST | ANN | SVM | RF | GP | ||
|---|---|---|---|---|---|---|---|---|
| PL01 | R2 | 0.9067 | 0.8703 | 0.8669 | 0.8833 | 0.8656 | 0.8746 | 0.8703 |
| MSE | 0.3044 | 0.3708 | 0.3354 | 0.3354 | 0.3306 | 0.3440 | 0.3708 | |
| MAE | 0.2472 | 0.3158 | 0.2801 | 0.2758 | 0.2578 | 0.2793 | 0.3158 | |
| PL02 | R2 | 0.9724 | 0.8505 | 0.8390 | 0.8737 | 0.9454 | 0.9454 | 0.8737 |
| MSE | 0.1804 | 0.4542 | 0.4753 | 0.4179 | 0.2559 | 0.2559 | 0.4179 | |
| MAE | 0.1490 | 0.4151 | 0.4348 | 0.3723 | 0.1942 | 0.1942 | 0.3723 | |
| IP01 | R2 | 0.7792 | 0.7734 | 0.2823 | 0.3622 | 0.6911 | 0.6186 | 0.3518 |
| MSE | 0.1064 | 0.0932 | 0.2139 | 0.1853 | 0.0968 | 0.1114 | 0.1976 | |
| MAE | 0.0825 | 0.0770 | 0.2028 | 0.1736 | 0.0793 | 0.0925 | 0.1884 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, P.; Li, Y. A Data-Driven Dam Deformation Forecasting and Interpretation Method Using the Measured Prototypical Temperature Data. Water 2022, 14, 2538. https://doi.org/10.3390/w14162538
He P, Li Y. A Data-Driven Dam Deformation Forecasting and Interpretation Method Using the Measured Prototypical Temperature Data. Water. 2022; 14(16):2538. https://doi.org/10.3390/w14162538
Chicago/Turabian StyleHe, Peng, and Yueyang Li. 2022. "A Data-Driven Dam Deformation Forecasting and Interpretation Method Using the Measured Prototypical Temperature Data" Water 14, no. 16: 2538. https://doi.org/10.3390/w14162538
APA StyleHe, P., & Li, Y. (2022). A Data-Driven Dam Deformation Forecasting and Interpretation Method Using the Measured Prototypical Temperature Data. Water, 14(16), 2538. https://doi.org/10.3390/w14162538





