Estimation of Boundary Shear Stress Distribution in a Trapezoidal Cross-Section Channel with Composite Roughness
Abstract
:1. Introduction
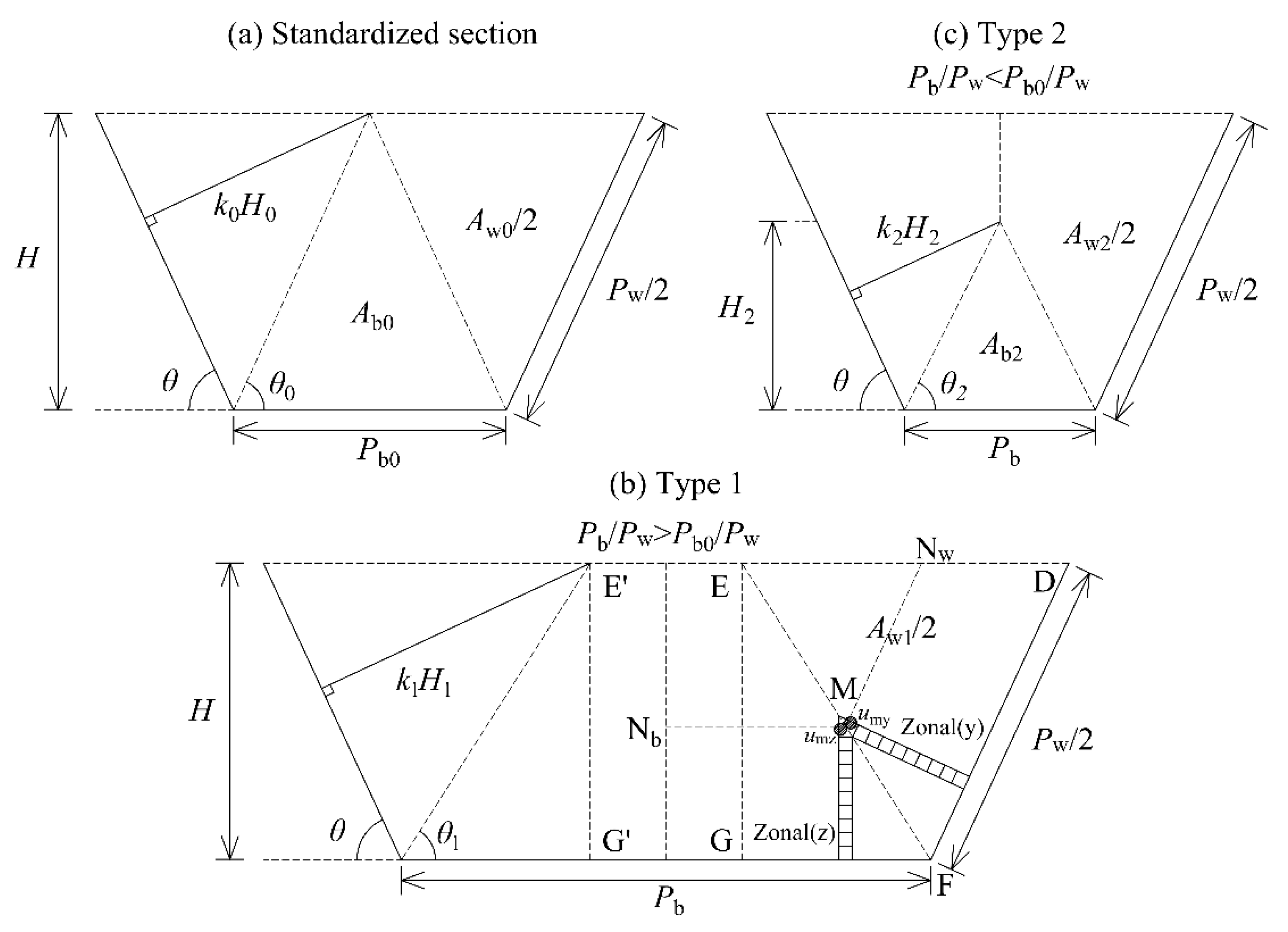
2. A New Partition Model of a Cross-Section
3. “Equal Local-Region Velocity” Assumption and Empirical Treatments
3.1. “Equal Local-Region Velocity” Assumption
3.2. Empirical Treatments
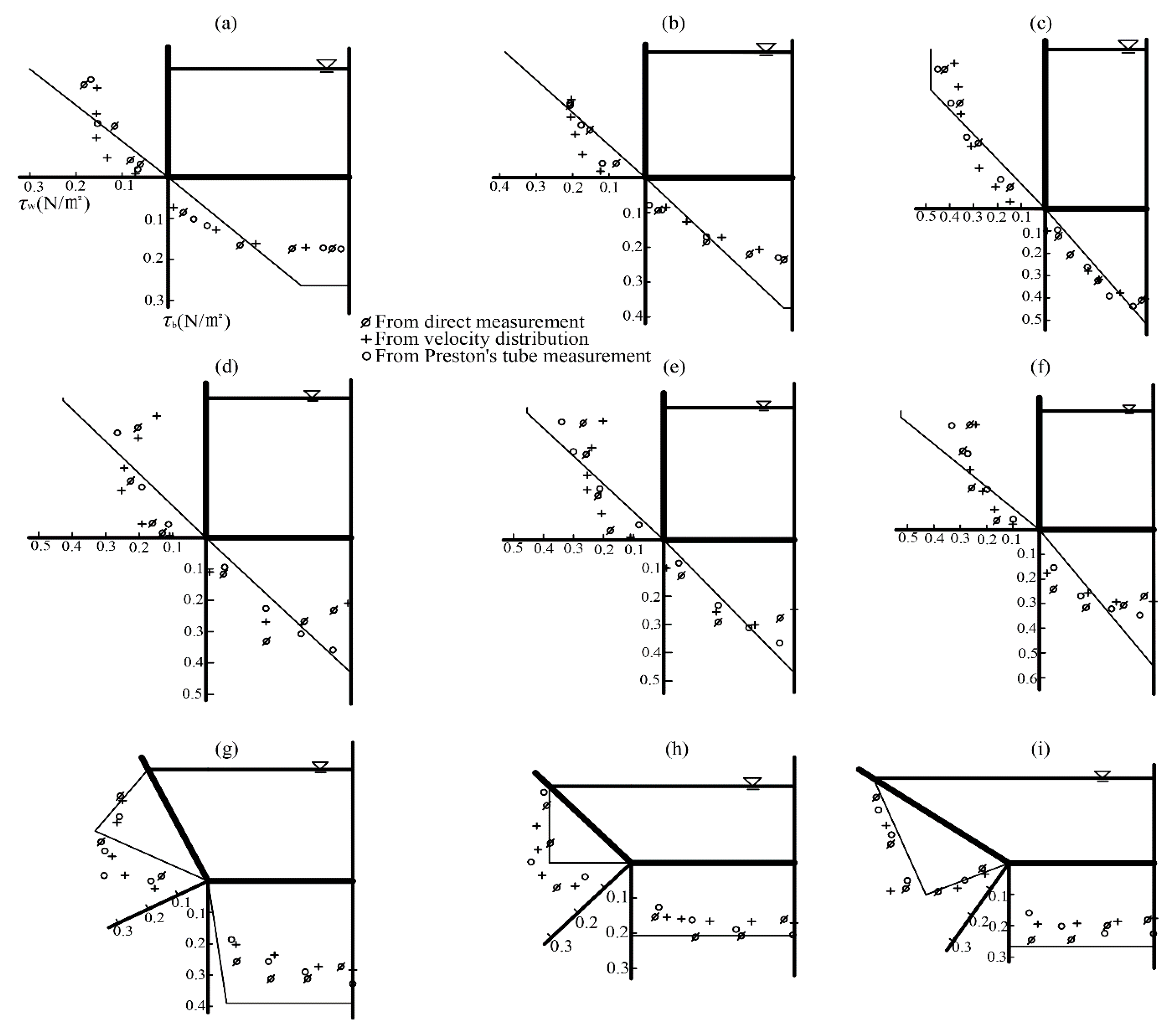
4. New Methods and Comparisons
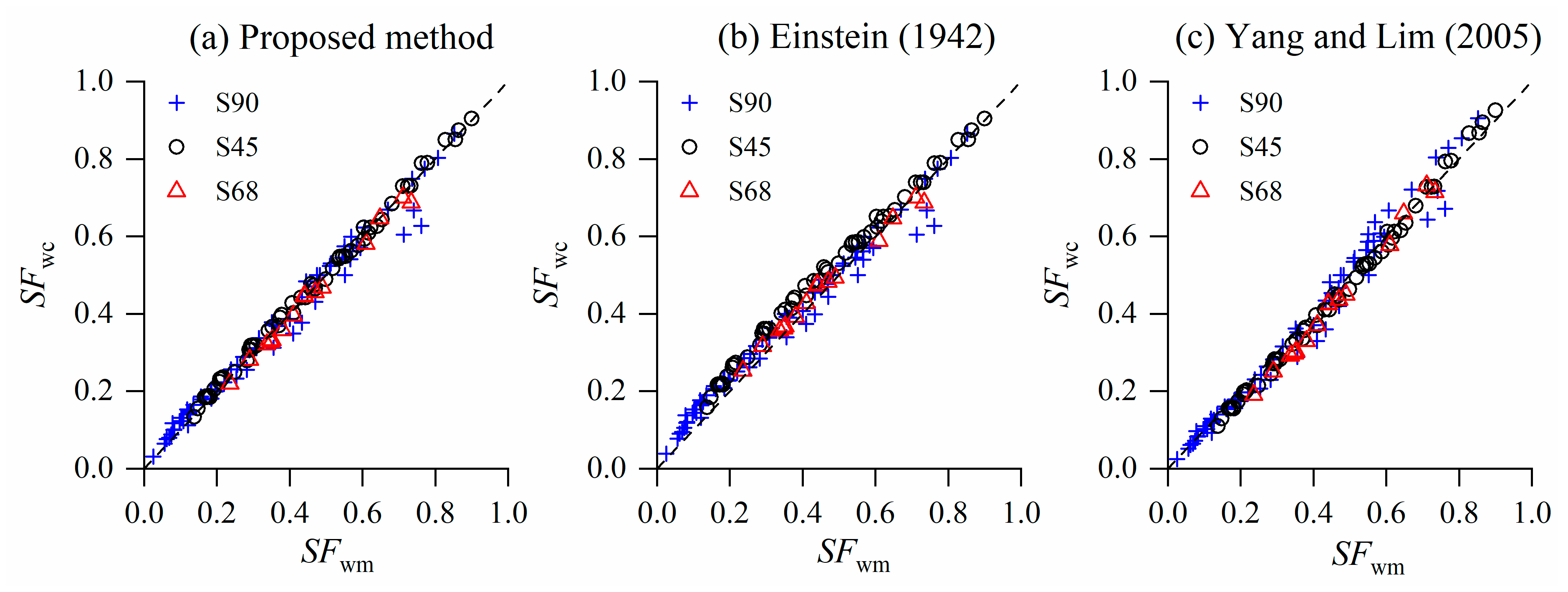
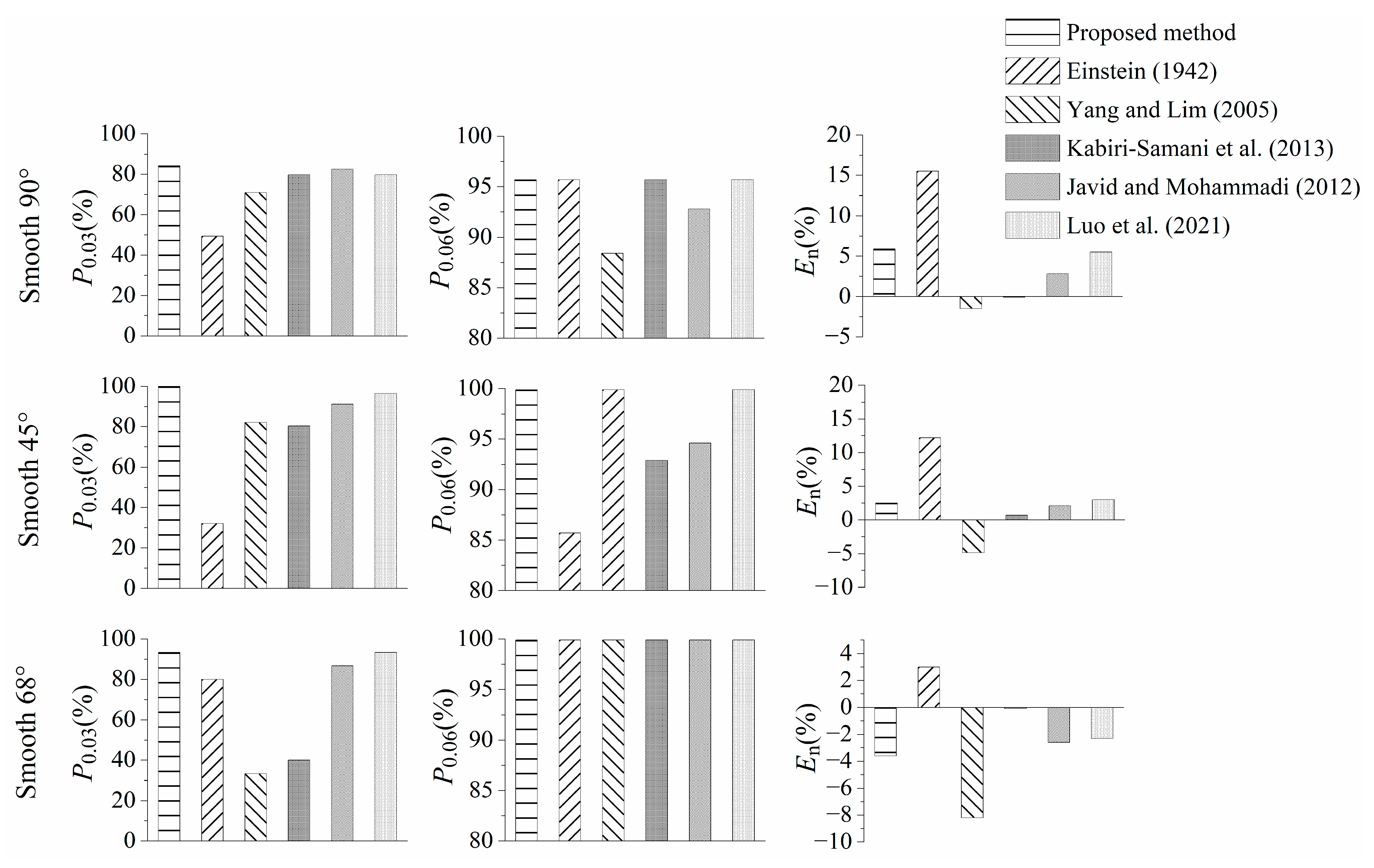
4.1. Smooth Boundary Cases
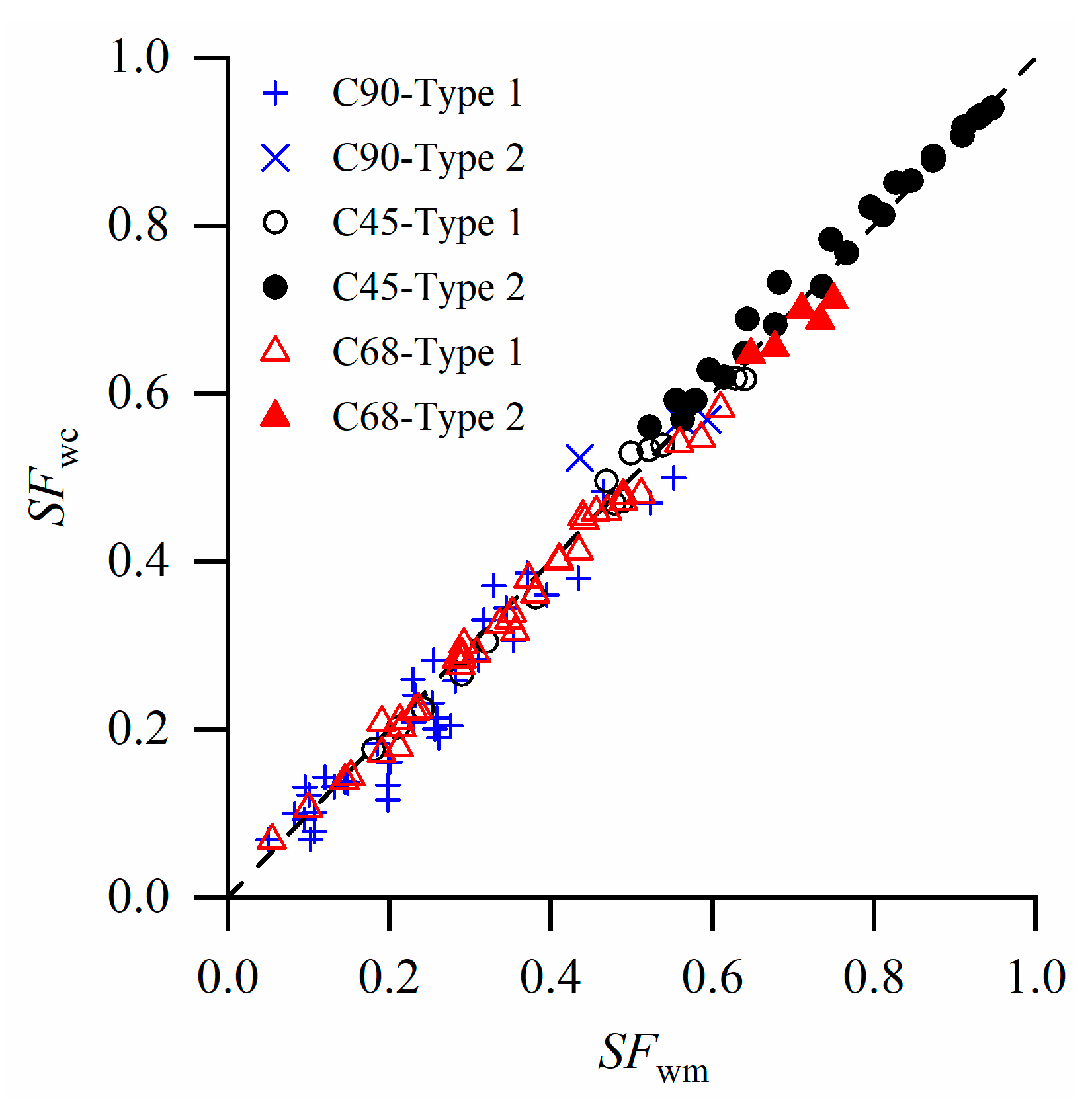
4.2. Composite Roughness Cases
5. Discussion
5.1. The Effect of Secondary Currents and Empirical Treatments
5.2. The Improvement of the Proposed Method
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Calculation of Resistance Coefficient f
Appendix A.2. Calculation of k1 and k2
References
- Rajaratnam, N.; Muralidhar, D. Boundary shear stress distribution in rectangular open channels. Houille Blanche 1969, 1, 603–610. [Google Scholar] [CrossRef]
- Yuen, K.W.H. A Study of Boundary Shear Stress, Flow Resistance and Momentum Transfer in Open Channels with Simple and Compound Trapezoidal Cross Sections. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 1989. [Google Scholar]
- Khodashenas, S.R.; Paquier, A. A geometrical method for computing the distribution of boundary shear stress across irregular straight open channels. J. Hydraul. Res. 1999, 37, 381–388. [Google Scholar] [CrossRef]
- Knight, D.W.; Demetriou, J.D.; Hamed, M.E. Boundary shear in smooth rectangular channels. J. Hydraul. Eng. 1984, 110, 405–422. [Google Scholar] [CrossRef]
- Cacqueray, N.D.; Hargreaves, D.M.; Morvan, H.P. A computational study of shear stress in smooth rectangular channels. J. Hydraul. Res. 2009, 47, 50–57. [Google Scholar] [CrossRef]
- Yang, S.Q.; Lim, S.Y. Mechanism of energy transportation and turbulent flow in a 3D channel. J. Hydraul. Eng. 1997, 123, 684–692. [Google Scholar] [CrossRef]
- Ansari, K.; Morvan, H.P.; Hargreaves, D.M. Numerical investigation into secondary currents and wall shear in trapezoidal channels. J. Hydraul. Eng. 2011, 137, 432–440. [Google Scholar] [CrossRef]
- Khodashenas, S.R.; El kadi Abderrezzak, K.; Paquier, A. Boundary shear stress in open channel flow: A comparison among six methods. J. Hydraul. Res. 2008, 46, 598–609. [Google Scholar] [CrossRef]
- Flintham, T.P.; Carling, P.A. Prediction of mean bed and wall boundary shear in uniform and compositely rough channels. In International Conference on River Regime; Hydraulics Research Limited: Wallingford, UK, 1988; pp. 267–287. [Google Scholar]
- Khozani, Z.S.; Bonakdari, H.; Zaji, A.H. Using two soft computing methods to predict wall and bed shear stress in smooth rectangular channels. Appl. Water Sci. 2017, 7, 3973–3983. [Google Scholar] [CrossRef]
- Vazquez, P.M.; Sharifi, S. Modelling boundary shear stress distribution in open channels using a face recognition technique. J. Hydroinform. 2017, 19, 157–172. [Google Scholar] [CrossRef]
- Wormleaton, P.R.; Merrett, D.J. An improved method of calculation for steady uniform flow in prismatic main channel/flood plain sections. J. Hydraul. Res. 1990, 28, 157–174. [Google Scholar] [CrossRef]
- Prinos, P.; Townsend, R.D. Comparison of methods for predicting discharge in compound open channels. Adv. Water Resour. 1984, 7, 180–187. [Google Scholar] [CrossRef]
- Moreta, P.J.; Martin-Vide, J.P. Apparent friction coefficient in straight compound channels. J. Hydraul. Res. 2010, 48, 169–177. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, Q.; Jiang, L. Determination of apparent shear stress and its application in compound channels. Procedia Eng. 2016, 154, 459–466. [Google Scholar] [CrossRef]
- Leighly, J.B. Toward a theory of the morphologic significance of turbulence in the flow of water in streams. Prog. Phys. Geogr. 1932, 6, 1–22. [Google Scholar]
- Nezu, I.; Nakagawa, H.E.D. Turbulence in Open-Channel Fows; Balkema: Rotterdam, The Netherlands, 1993. [Google Scholar]
- Keulegan, G.H. Laws of turbulent flow in open channels. J. Res. Natl. Bur. Stand. 1938, 21, 708–741. [Google Scholar] [CrossRef]
- Einstein, H.A. Formulas for the transportation of bed load. Trans. ASCE 1942, 107, 561–597. [Google Scholar] [CrossRef]
- Chien, N.; Wang, Z. Mechanics of Sediment Transport; Science Press: Beijing, China, 1986. (In Chinese) [Google Scholar]
- Yang, S.Q.; Lim, S.Y. Boundary shear stresses distributions in smooth rectangular open channel flows. Proc. Inst. Civ. Eng.-Water Marit. Energy 1998, 130, 163–173. [Google Scholar]
- Yang, S.Q.; Lim, S.Y. Boundary shear stress distributions in trapezoidal channels. J. Hydraul. Res. 2005, 43, 98–102. [Google Scholar] [CrossRef]
- Yang, S.Q.; Yu, J.X.; Wang, Y.Z. Estimation of diffusion coefficients, lateral shear stress, and velocity in open channels with complex geometry. Water Resour. Res. 2004, 40, W05202. [Google Scholar] [CrossRef]
- Shiono, K.; Knight, D.W. Turbulent open-channel flows with variable depth across the channel. J. Fluid Mech. 1991, 222, 617–646. [Google Scholar] [CrossRef]
- Guo, J.; Julien, P.Y. Shear stress in smooth rectangular open-channel flows. J. Hydraul. Eng. 2005, 131, 30–37. [Google Scholar] [CrossRef]
- Kabiri-Samani, A.; Farshi, F.; Chamani, M.R. Boundary Shear Stress in Smooth Trapezoidal Open Channel Flows. J. Hydraul. Eng. 2013, 139, 205–212. [Google Scholar] [CrossRef]
- Javid, S.; Mohammadi, M. Boundary shear stress in a trapezoidal channel. Int. J. Eng. 2012, 25, 323–332. [Google Scholar] [CrossRef]
- Luo, Y.; Zhu, S.; Cao, B.; Jiang, C.J. A “Standard Cross-section” Method for the calculation of Riverbed and Bank shear stress. Appl. Math. Mech. 2021, 42, 915–923. (In Chinese) [Google Scholar]
- Han, Y.; Yang, S.Q.; Sivakumar, M.; Qiu, L.C.; Chen, J. Flow Partitioning in Rectangular Open Channel Flow. Math. Probl. Eng. 2018, 2018, 11. [Google Scholar] [CrossRef]
- Yang, S.Q.; Han, Y.; Lin, P.; Jiang, C.; Walker, R. Experimental study on the validity of flow region division. J. Hydro-Environ. Res. 2014, 8, 421–427. [Google Scholar] [CrossRef]
- Han, Y.; Yang, S.Q.; Dharmasiri, N.; Sivakumar, M. Experimental study of smooth channel flow division based on velocity distribution. J. Hydraul. Eng. 2015, 141, 06014025. [Google Scholar] [CrossRef]
- Johnson, J.W. The importance of considering sidewall friction in bed-load investigations. Civil Eng. 1942, 12, 329–332. [Google Scholar]
- Vanoni, V.A.; Brooks, N.H. Laboratory Studies of the Roughness and Suspended Load of Alluvial Streams; Sedimentation Laboratory Report No. E68; California Institute of Technology: Pasadena, CA, USA, 1957. [Google Scholar]
- Nezu, I.; Nakagawa, H.E.D.; Tominaga, H. Secondary currents in a straight channel flow and the relation to its aspect ratio. Turbul. Shear. Flows 1985, 4, 246–260. [Google Scholar]
- State Key Laboratory of Hydraulics and Mountain River Engineering (SKLHMRE). Hydraulics; Higher Education Press: Beijing, China, 2015; p. 131. (In Chinese) [Google Scholar]
- Cruff, R.W. Cross-Channel Transfer of Linear Momentum in Smooth Rectangular Channels; Water-Supply Paper 1592-B, United States Geological Survey: Reston, VA, USA, 1965. [Google Scholar]
- Ghosh, S.N.; Roy, N. Boundary shear distribution in open channel flow. J. Hydraul. Div. 1970, 96, 967–994. [Google Scholar] [CrossRef]
- Kartha, V.C.; Leutheusser, H.J. Distribution of tractive force in open channels. J. Hydraul. Div. 1970, 96, 1469–1483. [Google Scholar] [CrossRef]
- Knight, D.W.; Macdonald, J.A. Hydraulic resistance of artificial strip roughness. J. Hydraul. Div. 1979, 105, 675–690. [Google Scholar] [CrossRef]
- Knight, D.W.; Macdonald, J.A. Open channel flow with varying bed roughness. J. Hydraul. Div. 1979, 105, 1167–1183. [Google Scholar] [CrossRef]
- Myers, W.R.C. Flow resistance in wide rectangular channels. J. Hydraul. Div. 1982, 108, 471–482. [Google Scholar] [CrossRef]
- Noutsopoulos, G.C.; Hadjipanos, P. Discussion: Boundary Shear in Smooth and Rough Channels. J. Hydraul. Div. 1982, 108, 809–812. [Google Scholar] [CrossRef]
- Seckin, G.; Seckin, N.; Yurtal, R. Boundary shear stress analysis in smooth rectangular channels. Can. J. Civ. Eng. 2006, 33, 336–342. [Google Scholar] [CrossRef]
- Knight, D.W. Boundary shear in smooth and rough channels. J. Hydraul. Div. 1981, 107, 839–851. [Google Scholar] [CrossRef]
- Alhamid, A.I. Boundary Shear Stress and Velocity Distribution in Differentially Roughened Trapezoidal Open Channels. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 1991. [Google Scholar]
- Blasius, H. Das Ähnlichkeitsgesetz bei Reibungsvorgängen in Flüssigkeiten; Forschungs-Arbeit des Ingenieur-Wesens 131; Springer: Berlin/Heidelberg, Germany, 1913. (In German) [Google Scholar]
- Einstein, H.A. The Bed-Load Function for Sediment Transportation in Open Channel Flows; Technical Bulletin No. 1026, U.S. Department of Agriculture, Soil Conservation Service: Washington, DC, USA, 1950. [Google Scholar]
- Da Silva, A.M.F.; Bolisetti, T. A method for the formulation of Reynolds number functions. Can. J. Civil Eng. 2000, 27, 829–833. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Zhu, S.; Yang, F.; Gao, W.; Yan, C.; Yan, R. Estimation of Boundary Shear Stress Distribution in a Trapezoidal Cross-Section Channel with Composite Roughness. Water 2022, 14, 2530. https://doi.org/10.3390/w14162530
Luo Y, Zhu S, Yang F, Gao W, Yan C, Yan R. Estimation of Boundary Shear Stress Distribution in a Trapezoidal Cross-Section Channel with Composite Roughness. Water. 2022; 14(16):2530. https://doi.org/10.3390/w14162530
Chicago/Turabian StyleLuo, You, Senlin Zhu, Fan Yang, Wenxiang Gao, Caiming Yan, and Rencong Yan. 2022. "Estimation of Boundary Shear Stress Distribution in a Trapezoidal Cross-Section Channel with Composite Roughness" Water 14, no. 16: 2530. https://doi.org/10.3390/w14162530
APA StyleLuo, Y., Zhu, S., Yang, F., Gao, W., Yan, C., & Yan, R. (2022). Estimation of Boundary Shear Stress Distribution in a Trapezoidal Cross-Section Channel with Composite Roughness. Water, 14(16), 2530. https://doi.org/10.3390/w14162530