Identification of Suitable Locations in a Small Water Supply Network for the Placement of Water Quality Sensors Based on Different Criteria under Demand-Driven Conditions
Abstract
:1. Introduction
2. Materials and Methods
3. Case Study
3.1. Description of the Case Study
3.2. The Methodology Applied—Assumptions
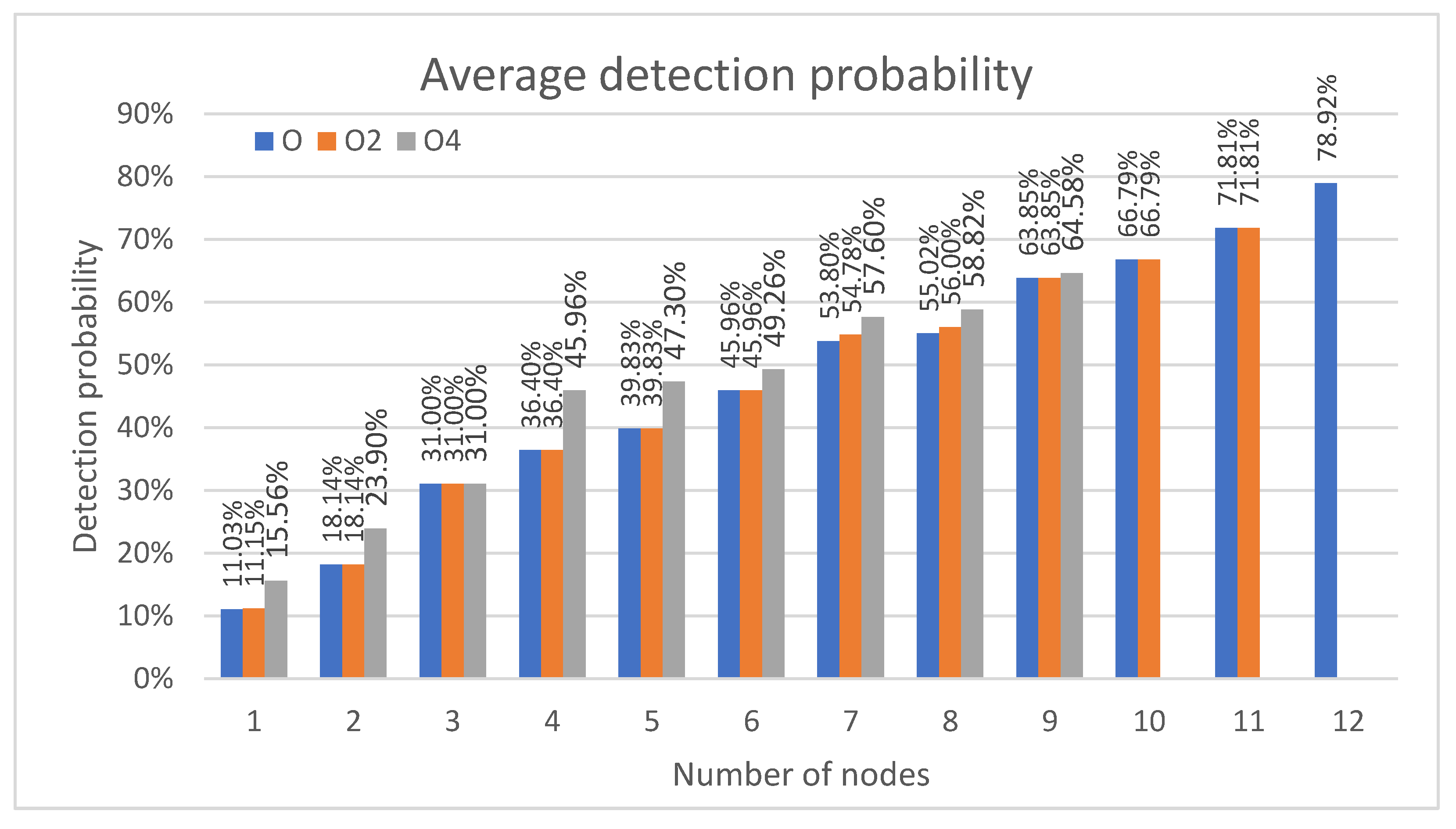
4. Results and Discussion
4.1. Contaminant Injected at Time t = 0
4.2. Contaminant Injected at Every One Hour for 24 h
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Oliker, N.; Ohar, Z.; Ostfeld, A. Spatial event classification using simulated water quality data. Environ. Model. Softw. 2016, 77, 71–80. [Google Scholar] [CrossRef]
- Hart, W.E.; Murray, R. Review of Sensor Placement Strategies for Contamination Warning Systems in Drinking Water Distribution Systems. J. Water Resour. Plan. Manag. 2010, 136, 611–619. [Google Scholar] [CrossRef]
- Berry, J.W.; Fleischer, L.; Hart, W.E.; Phillips, C.A.; Watson, J.-P. Sensor Placement in Municipal Water Networks. J. Water Resour. Plan. Manag. 2005, 131, 237–243. [Google Scholar] [CrossRef]
- Trachtman, G.B. A “Strawman” Common Sense Approach for Water Quality Sensor Site Selection. In Proceedings of the Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar] [CrossRef]
- Bahadur, R.; Samuels, W.B.; Grayman, W.; Amstutz, D.; Pickus, J. PipelineNet: A model for monitoring introduced contami-nants in a distribution system. In Proceedings of the World Water & Environmental Resources Congress, Philadelphia, PA, USA, 23–26 June 2003. [Google Scholar]
- Ghimire, S.R.; Barkdoll, B.D. A heuristic method for water quality sensor location in a municipal water distribution system: Mass-released based approach. In Proceedings of the Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar] [CrossRef]
- Xu, J.; Fischbeck, P.S.; Small, M.J.; VanBriesen, J.M.; Casman, E. Identifying Sets of Key Nodes for Placing Sensors in Dynamic Water Distribution Networks. J. Water Resour. Plan. Manag. 2008, 134, 378–385. [Google Scholar] [CrossRef]
- Rathi, S.; Gupta, R. Sensor Placement Methods for Contamination Detection in Water Distribution Networks: A Review. Procedia Eng. 2014, 89, 181–188. [Google Scholar] [CrossRef]
- Lee, B.H.; Deininger, R.A. Optimal Locations of Monitoring Stations in Water Distribution System. J. Environ. Eng. 1992, 118, 4–16. [Google Scholar] [CrossRef]
- Berry, J.; Hart, W.E.; Phillips, C.A.; Uber, J. A general integer-programming-based framework for sensor placement in mu-nicipal water networks. In Proceedings of the Critical Transitions in Water and Environmental Resources Management, Salt Lake City, UT, USA, 27 June–1 July 2004. [Google Scholar]
- Ostfeld, A.; Salomons, E. Optimal Layout of Early Warning Detection Stations for Water Distribution Systems Security. J. Water Resour. Plan. Manag. 2004, 130, 377–385. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E. Securing Water Distribution Systems Using Online Contamination Monitoring. J. Water Resour. Plan. Manag. 2005, 131, 402–405. [Google Scholar] [CrossRef]
- Kessler, A.; Ostfeld, A.; Sinai, G. Detecting Accidental Contaminations in Municipal Water Networks. J. Water Resour. Plan. Manag. 1998, 124, 192–198. [Google Scholar] [CrossRef]
- Propato, M. Contamination Warning in Water Networks: General Mixed-Integer Linear Models for Sensor Location Design. J. Water Resour. Plan. Manag. 2006, 132, 225–233. [Google Scholar] [CrossRef]
- Kumar, A.; Kansal, M.L.; Arora, G.; Ostfeld, A.; Kessler, A. Detecting accidental contaminations in municipal water networks. J. Water Resour. Plan. Manag. 1999, 125, 308–310. [Google Scholar] [CrossRef]
- Kumar, A.; Kansal, M.L.; Arora, G. Identification of Monitoring Stations in Water Distribution System. J. Environ. Eng. 1997, 123, 746–752. [Google Scholar] [CrossRef]
- Watson, J.-P.; Greenberg, H.J.; Hart, W.E. A Multiple-Objective Analysis of Sensor Placement Optimization in Water Networks. In Proceedings of the Critical Transitions in Water and Environmental Resources Management, Salt Lake City, UT, USA, 27 June–1 July 2004. [Google Scholar]
- Ostfeld, A.; Uber, J.G.; Salomons, E.; Berry, J.W.; Hart, W.E.; Phillips, C.A.; Watson, J.-P.; Dorini, G.; Jonkergouw, P.; Kapelan, Z.; et al. The Battle of the Water Sensor Networks (BWSN): A Design Challenge for Engineers and Algorithms. J. Water Resour. Plan. Manag. 2008, 134, 556–568. [Google Scholar] [CrossRef]
- Dorini, G.; Jonkergouw, P.; Kapelan, Z.; di Pierro, F.; Khu, S.T.; Savic, D. An Efficient Algorithm for Sensor Placement in Water Distribution Systems. In Proceedings of the Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar] [CrossRef]
- Eliades, D.; Polycarpou, M. Iterative Deepening of Pareto Solutions in Water Sensor Networks. In Proceedings of the Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar] [CrossRef]
- Huang, J.J.; McBean, E.A.; James, W. Multi-objective optimization for monitoring sensor placement in water distribution sys-tems. In Proceedings of the Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar] [CrossRef]
- Gueli, R. Predator—Prey Model for Discrete Sensor Placement. In Proceedings of the Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E. Sensor Network Design Proposal for the Battle of the Water Sensor Networks (BWSN). In Proceedings of the 8th Annual Water Distribution System Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar] [CrossRef]
- Preis, A.; Ostfeld, A. Multiobjective Sensor Design for Water Distribution Systems Security. In Proceedings of the Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar] [CrossRef]
- Shen, H.; McBean, E. Pareto Optimality for Sensor Placements in a Water Distribution System. J. Water Resour. Plan. Manag. 2011, 137, 243–248. [Google Scholar] [CrossRef]
- Giudicianni, C.; Herrera, M.; Di Nardo, A.; Greco, R.; Creaco, E.; Scala, A. Topological placement of quality sensors in water-distribution networks without the recourse to hydraulic modeling. J.Water Resour. Plan. Manag. 2020, 146, 04020030. [Google Scholar] [CrossRef]
- Cardoso, S.M.; Barros, D.B.; Oliveira, E.; Brentan, B.; Ribeiro, L. Optimal sensor placement for contamination detection: A multi-objective and probabilistic approach. Environ. Model. Softw. 2020, 135, 104896. [Google Scholar] [CrossRef]
- Berry, J.W.; Hart, W.E.; Phillips, C.A.; Watson, J.-P. A Facility Location Approach to Sensor Placement Optimization. In Proceedings of the Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar] [CrossRef]
- Guan, J.; Aral, M.; Maslia, M.L.; Grayman, W.M. Optimization Model and Algorithms for Design of Water Sensor Placement in Water Distribution Systems. In Proceedings of the Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar] [CrossRef]
- Krause, A.; Leskovec, J.; Isovitsch, S.; Xu, J.; Guestrin, C.; VanBriesen, J.; Small, M.; Fischbeck, P. Optimizing Sensor Placements in Water Distribution Systems Using Submodular Function Maximization. In Proceedings of the Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar] [CrossRef]
- Propato, M.; Piller, O. Battle of the water sensor networks. In Proceedings of the Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Walski, T. Multi-Objective Optimization of Sensor Placement in Water Distribution Systems. In Proceedings of the Water Distribution Systems Analysis Symposium, ASCE, Cincinnati, OH, USA, 27–30 August 2006; pp. 1–110. [Google Scholar] [CrossRef]
- Guidorzi, M.; Franchini, M.; Alvisi, S. A multi-objective approach for detecting and responding to accidental and intentional contamination events in water distribution systems. Urban Water J. 2009, 6, 115–135. [Google Scholar] [CrossRef]
- Hu, C.; Dai, L.; Yan, X.; Gong, W.; Liu, X.; Wang, L. Modified NSGA-III for sensor placement in water distribution system. Inf. Sci. 2020, 509, 488–500. [Google Scholar] [CrossRef]
- Adedoja, O.S.; Hamam, Y.; Khalaf, B.; Sadiku, R. A state-of-the-art review of an optimal sensor placement for contaminant warning system in a water distribution network. Urban Water J. 2018, 15, 985–1000. [Google Scholar] [CrossRef]
- Poulin, A.; Mailhot, A.; Grondin, P.; Delorme, L.; Villeneuve, J.-P. Optimization of Operational Response to Contamination in Water Networks. In Proceedings of the 8th Annual Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar] [CrossRef]
- Cozzolino, L.; Mucherino, C.; Pianese, D.; Pirozzi, F. Optimal allocation of monitoring stations aiming at an early detection of intentional contamination of water supply systems. In Proceedings of the CCWI 2005 Conference, Exeter, UK, 5–7 September 2005; Savic, D., Walters, G., King, R., Khu, S.-T., Eds.; University of Exeter: Exeter, UK. [Google Scholar]
- Palumbo, A.; Cozzolino, L.; Pianese, D. Optimal positioning of quality monitoring stations in water dis-tribution systems: A stochastic approach. In Proceedings of the Water Management Challenges in Global Change: Supplement to the Proceedings of the CCWI2007 and SUWM2007 Conference, Leicester, UK, 3–5 September 2007; pp. 32–41. [Google Scholar]
- Blokker, E.J.M.; Vreeburg, J.H.G.; Buchberger, S.G.; van Dijk, J.C. Importance of demand modelling in network water quality models: A review. Drink. Water Eng. Sci. 2008, 1, 27–38. [Google Scholar] [CrossRef]
- Rathi, S.; Gupta, R.; Ormsbee, L. A review of sensor placement objective metrics for contamination detection in water distri-bution networks. Water Sci. Technol. Water Supply 2015, 15, 898–917. [Google Scholar] [CrossRef]
- Cozzolino, L.; Della Morte, R.; Palumbo, A.; Pianese, D. Stochastic approaches for sensors placement against intentional contaminations in water distribution systems. Civ. Eng. Environ. Syst. 2011, 28, 75–98. [Google Scholar] [CrossRef]
- Rathi, S.; Gupta, R. Locations of Sampling Stations for Water Quality Monitoring in Water Distribution Networks. J. Environ. Sci. Eng. 2014, 56, 169–178. [Google Scholar] [PubMed]
- Preis, A.; Ostfeld, A. Multiobjective Contaminant Sensor Network Design for Water Distribution Systems. J. Water Resour. Plan. Manag. 2008, 134, 366–377. [Google Scholar] [CrossRef]
- Austin, R.G.; Choi, C.Y.; Preis, A.; Ostfeld, A.; Lansey, K. Multi-Objective Sensor Placements with Improved Water Quality Models in a Network with Multiple Junctions. In Proceedings of the World Environmental and Water Resources Congress 2009: Great Rivers, Kansas City, MO, USA, 17–21 May 2009. [Google Scholar]
- Dorini, G.; Jonkergouw, P.; Kapelan, Z.; Savic, D. SLOTS: Effective algorithm for sensor placement in water distribution sys-tems. J. Water Resour. Plan. Manag. 2010, 136, 620–628. [Google Scholar] [CrossRef]
- Xu, J.; Johnson, M.P.; Fischbeck, P.S.; Small, M.J.; VanBriesen, J.M. Robust placement of sensors in dynamic water distribution systems. Eur. J. Oper. Res. 2010, 202, 707–716. [Google Scholar] [CrossRef]
- Brentan, B.; Carpitella, S.; Barros, D.; Meirelles, G.; Certa, A.; Izquierdo, J. Water Quality Sensor Placement: A Multi-Objective and Multi-Criteria Approach. Water Resour. Manag. 2021, 35, 225–241. [Google Scholar] [CrossRef]
- Ohar, Z.; Lahav, O.; Ostfeld, A. Optimal sensor placement for detecting organophosphate intrusions into water distribution systems. Water Res. 2015, 73, 193–203. [Google Scholar] [CrossRef]
- Zhang, Q.; Zheng, F.; Kapelan, Z.; Savic, D.; He, G.; Ma, Y. Assessing the global resilience of water quality sensor placement strategies within water distribution systems. Water Res. 2020, 172, 115527. [Google Scholar] [CrossRef]
- Berry, J.; Carr, R.D.; Hart, W.E.; Leung, V.J.; Phillips, C.A.; Watson, J.-P. Designing Contamination Warning Systems for Municipal Water Networks Using Imperfect Sensors. J. Water Resour. Plan. Manag. 2009, 135, 253–263. [Google Scholar] [CrossRef]
- Xu, J.; Small, M.; Fischbeck, P.; VanBriesen, J. Integrating Location Models with Bayesian Analysis to Inform Decision Making. J. Water Resour. Plan. Manag. 2010, 136, 209–216. [Google Scholar] [CrossRef]
- Comboul, M.; Ghanem, R. Value of Information in the Design of Resilient Water Distribution Sensor Networks. J. Water Resour. Plan. Manag. 2013, 139, 449–455. [Google Scholar] [CrossRef]
- de Winter, C.; Palleti, V.R.; Worm, D.; Kooij, R. Optimal placement of imperfect water quality sensors in water distribution networks. Comput. Chem. Eng. 2018, 121, 200–211. [Google Scholar] [CrossRef]
- Ciaponi, C.; Creaco, E.; Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Musmarra, D.; Santonastaso, G.F. Reducing Impacts of Contamination in Water Distribution Networks: A Combined Strategy Based on Network Partitioning and Installation of Water Quality Sensors. Water 2019, 11, 1315. [Google Scholar] [CrossRef]
- Aral, M.M.; Guan, J.; Maslia, M.L. Optimal Design of Sensor Placement in Water Distribution Networks. J. Water Resour. Plan. Manag. 2010, 136, 5–18. [Google Scholar] [CrossRef]
- Alvisi, S.; Franchini, M.; Gavanelli, M.; Nonato, M. Near-optimal scheduling of device activation in water distribution systems to reduce the impact of a contamination event. J. Hydroinformat. 2011, 14, 345–365. [Google Scholar] [CrossRef]
- Studziński, A.; Pietrucha-Urbanik, K. Failure risk analysis of water distributions systems using hydraulic models on real field data. Ekon. Śr. 2019, 1, 152–165. [Google Scholar] [CrossRef]
- Hart, W.E.; Berry, J.W.; Boman, E.G.; Murray, R.; Phillips, C.A.; Riesen, L.A.; Watson, J.-P. The TEVA-SPOT Toolkit for Drinking Water Contaminant Warning System Design. In Proceedings of the World Environmental and Water Resources Congress, Honolulu, HI, USA, 12–16 May 2008; ASCE: Reston, VA, USA, 2008; pp. 1–12. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Tolikas, D. Managing water resources and supply systems: Fail-safe vs. safe-fail. In Proceedings of the 5th EWRA International Conference Water Resources Management in the Era of Transition, Athens, Greece, 4–8 September 2002; Tsakiris, G., Ed.; EWRA: Athens, Greece, 2002; pp. 194–204. [Google Scholar]
- Kanakoudis, V.K. Vulnerability based management of water resources systems. J. Hydroinform. 2004, 6, 133–156. [Google Scholar] [CrossRef]
- Sarker, S. Pipe Network Design and Analysis: An Example with WaterCAD. EngrXiv Arch. 2021. [Google Scholar] [CrossRef]
- Giudicianni, C.; Herrera, M.; Di Nardo, A.; Creaco, E.; Greco, R. Multi-criteria method for the realistic placement of water quality sensors on pipes of water distribution systems. Environ. Model. Softw. 2022, 152, 105405. [Google Scholar] [CrossRef]
- Hu, Z.; Chen, W.; Shen, D.; Chen, B.; Ye, S.; Tan, D. Optimal sensor placement for contamination identification in water dis-tribution system considering contamination probability variations. Comput. Chem. Eng. 2021, 153, 107404. [Google Scholar] [CrossRef]
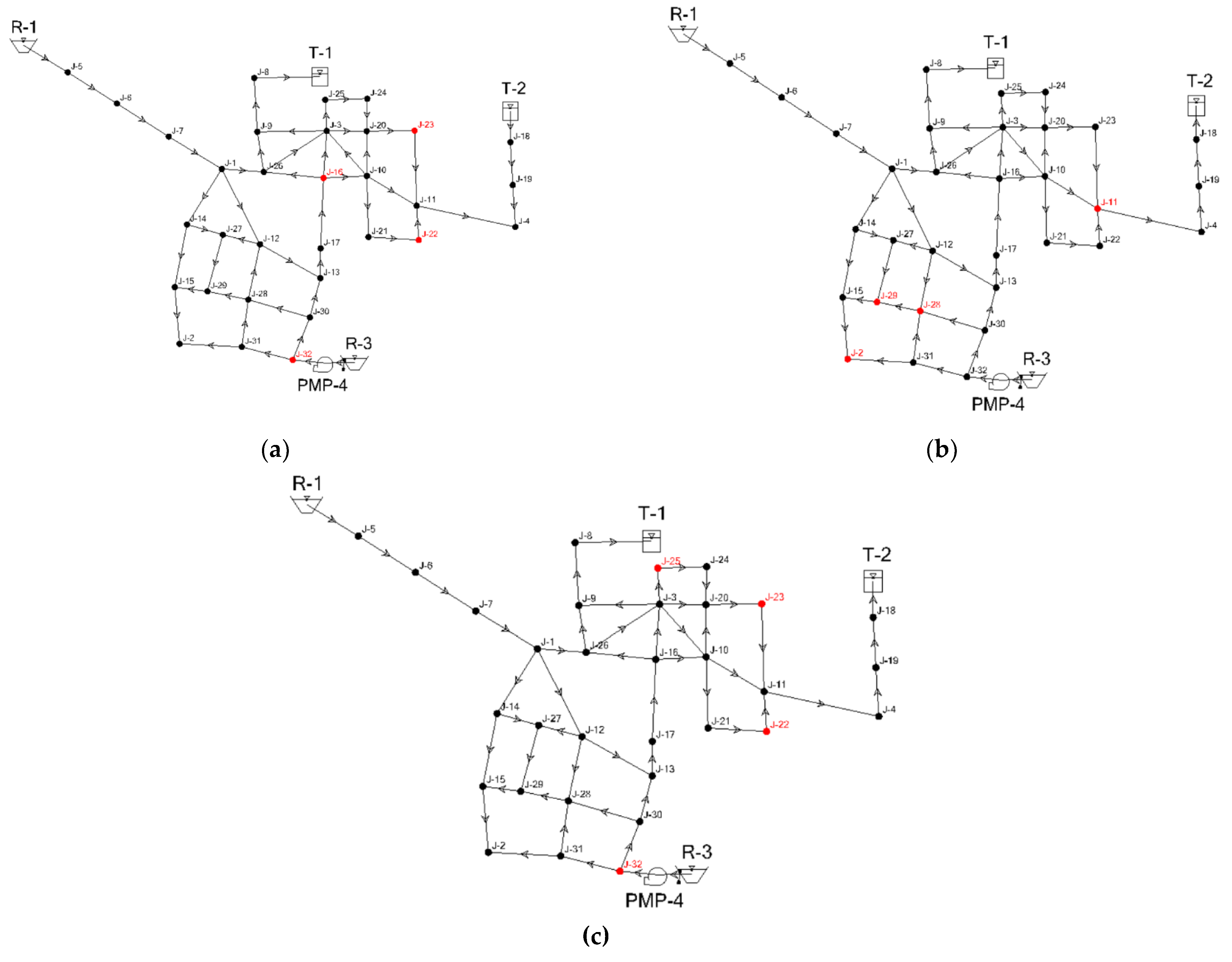

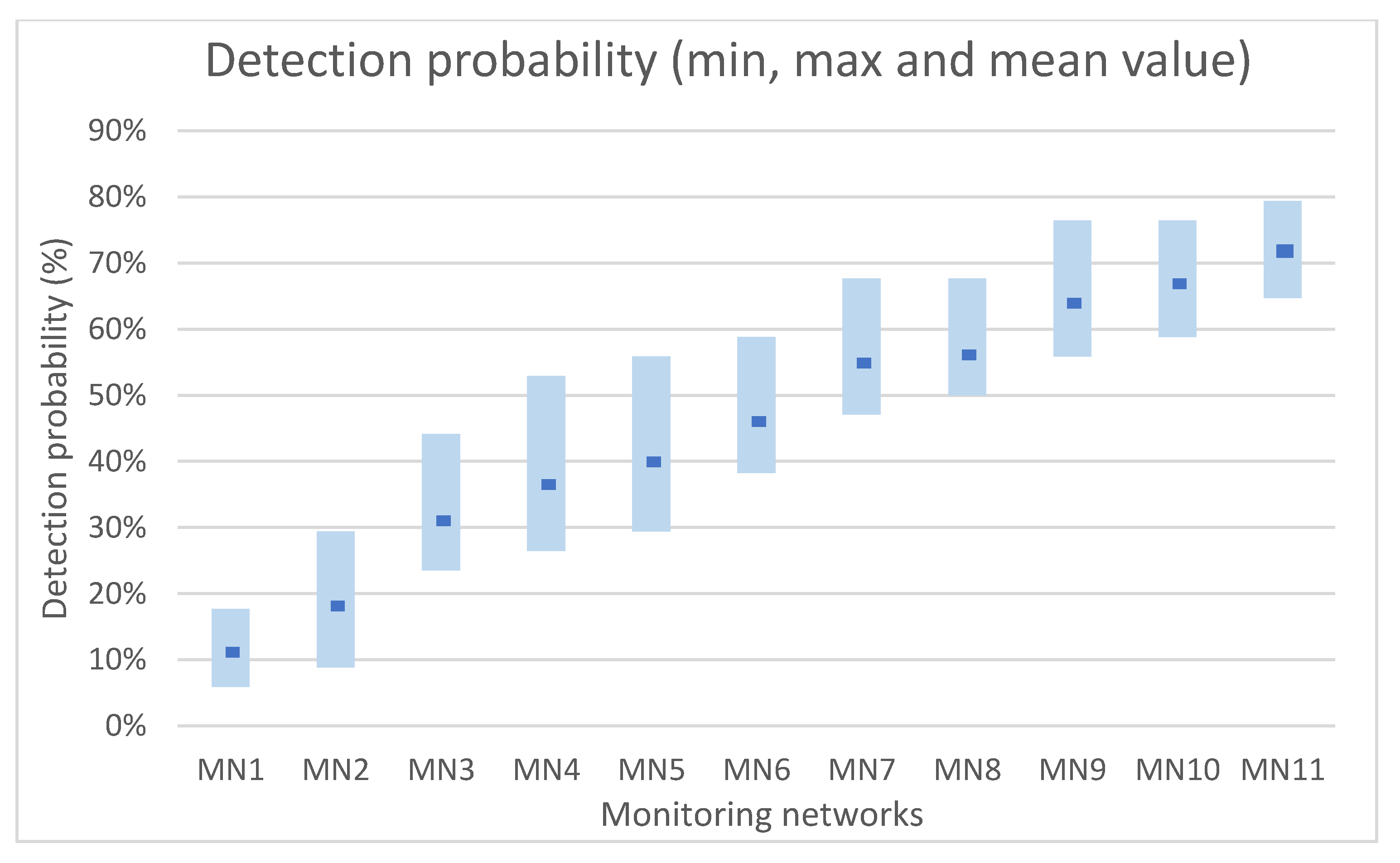
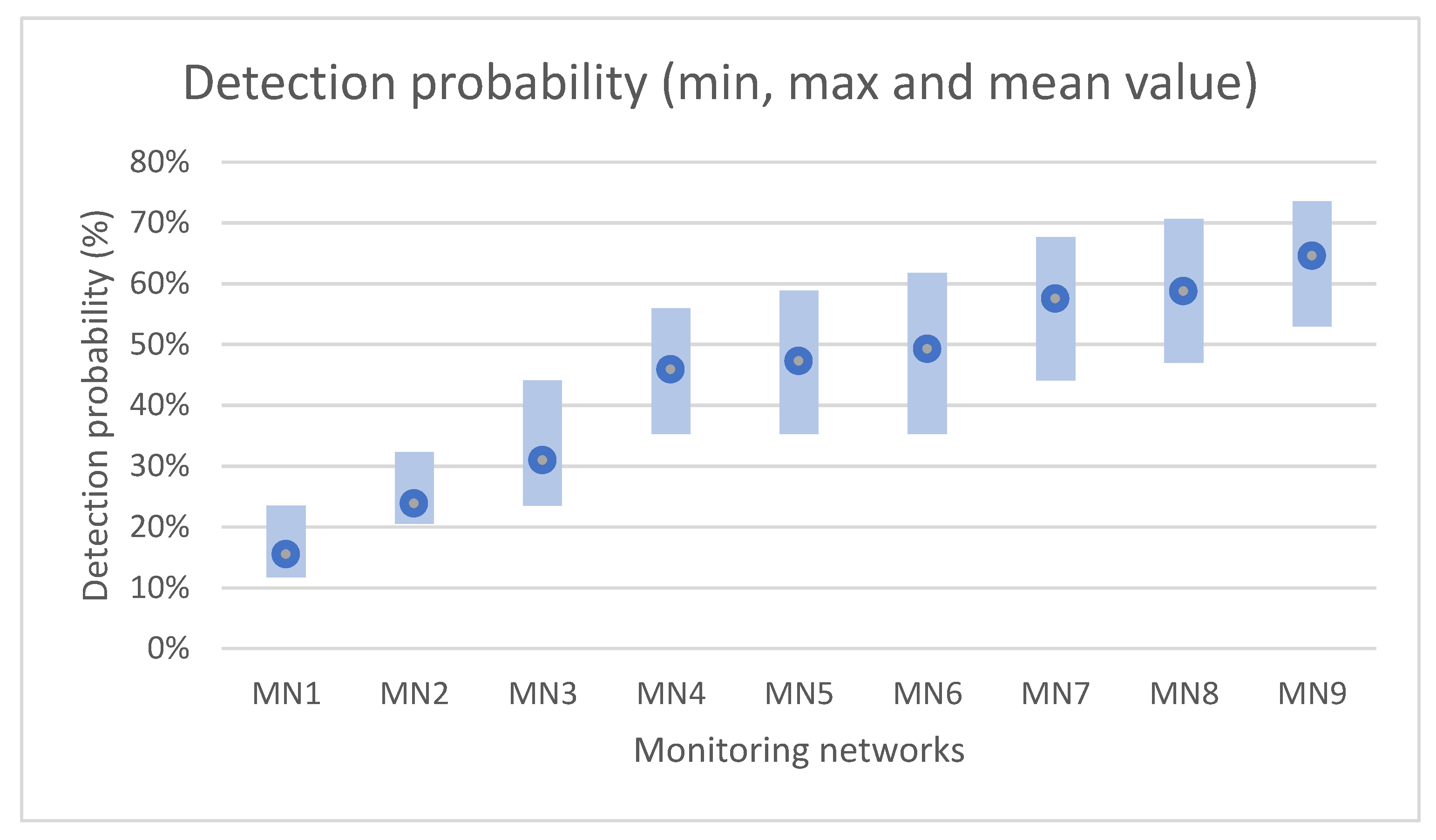
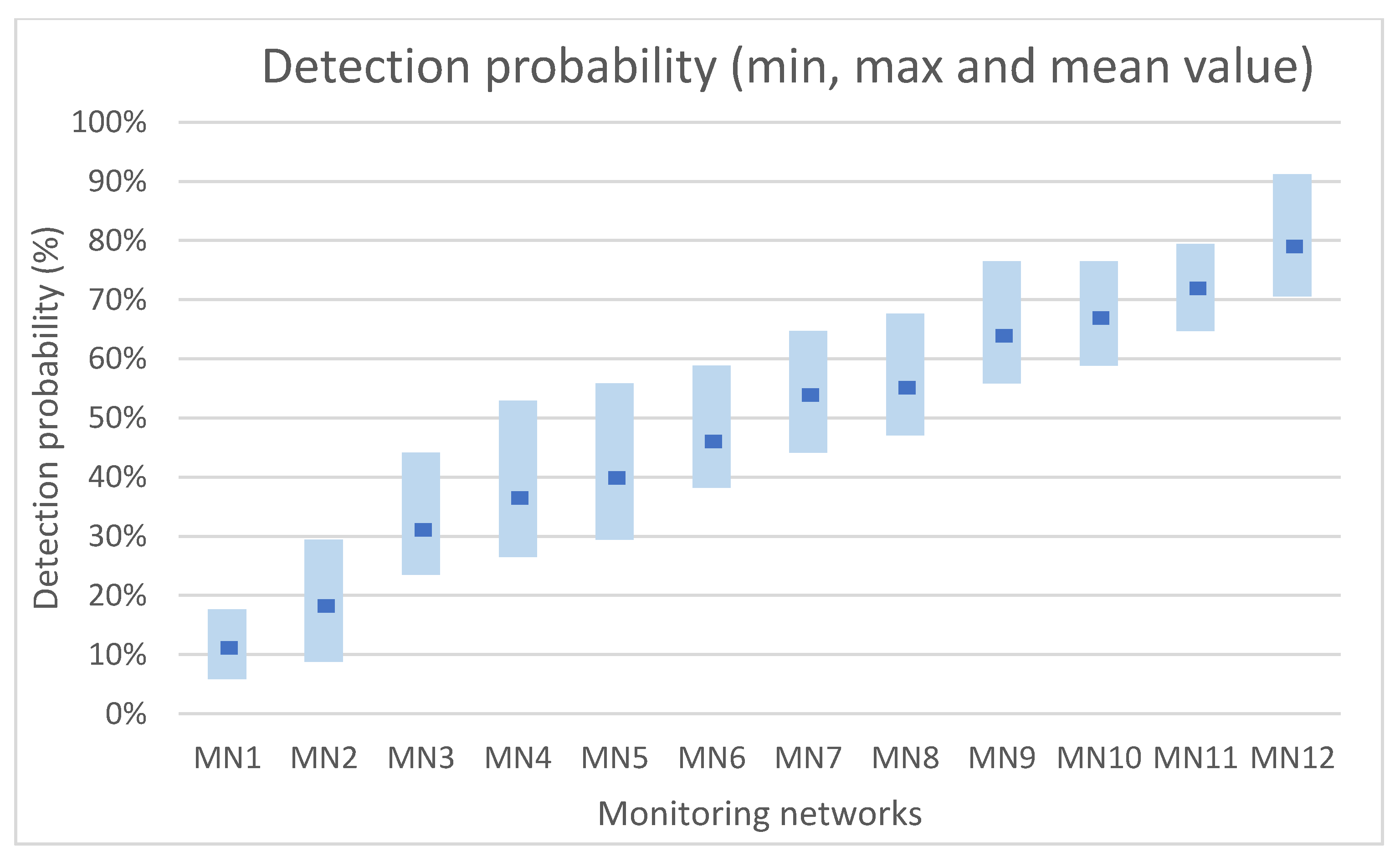
| Contamination Scenarios | ||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | |
| Nodes | J-1 | J-2 | J-3 | J-4 | J-5 | J-6 | J-7 | J-8 | J-9 | J-10 | J-11 | J-12 | J-13 | J-14 | J-15 | J-16 | J-17 | J-18 | J-19 | J-20 | J-21 | J-22 | J-23 | J-24 | J-25 | J-26 | J-27 | J-28 | J-29 | J-30 | J-31 | J-32 | R-1 | R-3 |
| J-1 | 10 | 0 | 0 | 0 | 0 | 10 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-2 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.1 | 2.1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.7 | 0 | 7.9 | 7.9 | 0 | 0 |
| J-3 | 2.4 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7.6 | 7.1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2.9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-4 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 4.3 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2.4 | 3.3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-5 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 |
| J-6 | 0 | 0 | 0 | 0 | 10 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 |
| J-7 | 0 | 0 | 0 | 0 | 10 | 10 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-8 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 10 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-9 | 4.9 | 0 | 4.1 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 3.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6.9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-10 | 0 | 0 | 2.3 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 9.2 | 7.6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-11 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 4.2 | 10 | 0 | 0 | 0 | 0 | 3.2 | 0 | 0 | 0 | 3.3 | 2.4 | 2.4 | 3.3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-12 | 10 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-13 | 5.6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5.6 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4.4 | 0 | 4.4 | 0 | 0 |
| J-14 | 10 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-15 | 0.7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.7 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2.2 | 6 | 8.3 | 0 | 0 | 0 | 0 | 0 |
| J-16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 10 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5.6 | 10 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4.4 | 0 | 0 | 0 | 0 |
| J-18 | 0 | 0 | 0 | 8.6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-19 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-20 | 0 | 0 | 6.8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4.8 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 3.2 | 3.2 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-21 | 0 | 0 | 2.4 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 7.5 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-23 | 0 | 0 | 6.9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 10 | 3.1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-24 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-25 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7.1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 2.9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-26 | 8 | 0 | 0 | 0 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2.0 | 2.0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-27 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7.4 | 0 | 2.6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J-28 | 1.2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 6.7 | 2.1 | 8 | 0 | 0 |
| J-29 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2.9 | 0 | 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2.2 | 7.8 | 10 | 5.2 | 0.4 | 0 | 0 | 0 |
| J-30 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 10 | 0 | 0 |
| J-31 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 10 | 0 | 0 |
| J-32 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 |
| R-1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 |
| R-3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 |
| T-1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.7 | 0.4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T-2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.3 | 0.2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Objective | Node ID | Value | Node ID | Value | Node ID | Value | Node ID | Value |
|---|---|---|---|---|---|---|---|---|
| O1 (people) | J-32 | 17 | J-22 | 20 | J-23 | 22 | J-16 | 29 |
| O2 (m3) | J-32 | 3.3 | J-22 | 3.9 | J-23 | 4.4 | J-16 | 5.7 |
| O3 (%) | J-11 | 23.53 | J-29 | 20.59 | J-2 | 17.65 | J-28 | 17.65 |
| O4 (g) | J-22 | 22.2 | J-32 | 28.6 | J-23 | 31.1 | J-25 | 46.3 |
| O | J-32 | 0.014 | J-22 | 0.016 | J-23 | 0.017 | J-16 | 0.023 |
| Criterion | Injection Time (Hours) | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | |
| O1 | J-32 | J-32 | R-3 | J-32 | J-22 | J-22 | J-22 | J-22 | J-32 | J-32 | J-32 | J-32 | J-32 | J-32 | J-1 | J-22 | J-22 | J-22 | J-22 | J-22 | J-32 | R-3 | J-32 | J-32 |
| J-22 | J-30 | J-32 | J-22 | J-23 | J-23 | J-23 | J-16 | J-22 | J-22 | J-22 | J-22 | J-30 | J-22 | J-22 | J-23 | J-23 | J-23 | J-23 | J-23 | J-30 | J-32 | R3 | J-30 | |
| J-23 | J-31 | J-31 | J-1 | J-17 | J-17 | J-17 | J-23 | J-30 | J-30 | J-30 | J-30 | J-31 | J-23 | J-23 | J-17 | J-32 | J-32 | J-17 | J-17 | J-31 | J-30 | J-30 | J-31 | |
| J-16 | R-3 | J-1 | J-23 | J-29 | J-29 | J-29 | J-17 | J-31 | J-23 | J-31 | J-23 | J-22 | J-1 | J-9 | J-1 | J-17 | J-30 | J-29 | J-29 | J-1 | J-31 | J-31 | R-3 | |
| O2 | J-32 | J-32 | R-3 | J-32 | J-22 | J-22 | J-22 | J-22 | J-32 | J-32 | J-32 | J-32 | J-32 | J-32 | J-1 | J-22 | J-22 | J-22 | J-22 | J-22 | J-32 | R-3 | J-32 | J-32 |
| J-22 | J-30 | J-32 | J-22 | J-23 | J-23 | J-23 | J-16 | J-22 | J-22 | J-22 | J-22 | J-30 | J-22 | J-22 | J-23 | J-23 | J-23 | J-23 | J-23 | J-30 | J-32 | R3 | J-30 | |
| J-23 | J-31 | J-31 | J-1 | J-17 | J-17 | J-17 | J-23 | J-30 | J-30 | J-30 | J-30 | J-31 | J-23 | J-23 | J-17 | J-32 | J-32 | J-17 | J-17 | J-31 | J-30 | J-30 | J-31 | |
| J-16 | R-3 | J-1 | J-23 | J-29 | J-29 | J-29 | J-17 | J-31 | J-23 | J-31 | J-23 | J-22 | J-1 | J-9 | J-1 | J-17 | J-30 | J-29 | J-29 | J-1 | J-31 | J-31 | R-3 | |
| O4 | J-22 | J-32 | J-32 | J-23 | J-22 | J-22 | J-22 | J-22 | J-22 | J-22 | J-22 | J-22 | J-32 | J-32 | J-23 | J-22 | J-22 | J-22 | J-22 | J-22 | J-22 | J-32 | J-32 | J-32 |
| J-32 | J-30 | R-3 | J-22 | J-23 | J-23 | J-23 | J-32 | J-32 | J-32 | J-32 | J-32 | J-30 | J-23 | J-22 | J-23 | J-23 | J-23 | J-23 | J-23 | J-23 | R-3 | J-23 | J-22 | |
| J-23 | J-31 | J-23 | J-32 | J-29 | J-29 | J-29 | J-23 | J-31 | J-23 | J-23 | J-23 | J-31 | J-22 | J-9 | J-25 | J-29 | J-29 | J-29 | J-29 | J-29 | J-22 | R-3 | J-30 | |
| J-25 | J-23 | J-31 | J-9 | J-25 | J-25 | J-25 | J-30 | J-30 | J-31 | J-30 | J-30 | J-29 | J-31 | J-32 | J-29 | J-25 | J-32 | J-32 | J-32 | J-32 | J-23 | J-30 | J-31 | |
| O3 | J-11 | J-11 | J-11 | J-11 | J-10 | J-10 | J-10 | J-11 | J-11 | J-11 | J-11 | J-11 | J-11 | J-11 | J-11 | J-10 | J-10 | J-10 | J-10 | J-10 | J-11 | J-11 | J-11 | J-11 |
| J-29 | J-4 | J-10 | J-10 | J-11 | J-11 | J-11 | J-29 | J-29 | J-29 | J-29 | J-13 | J-4 | J-10 | J-10 | J-11 | J-11 | J-11 | J-11 | J-11 | J-10 | J-4 | J-4 | J-29 | |
| J-2 | J-2 | J-4 | J-4 | J-2 | J-2 | J-2 | J-28 | J-2 | J-2 | J-2 | J-12 | J-27 | J-4 | J-4 | J-20 | J-2 | J-2 | J-2 | J-2 | J-2 | J-2 | J-10 | J-4 | |
| J-28 | J-23 | J-28 | J-2 | J-3 | J-3 | J-3 | J-23 | J-28 | J-20 | J-12 | J-2 | J-3 | J-3 | J-3 | J-3 | J-3 | J-3 | J-3 | J-3 | J-3 | J-23 | J-2 | J-2 | |
| O | J-32 | J-32 | R-3 | J-32 | J-22 | J-22 | J-22 | J-22 | J-32 | J-32 | J-32 | J-32 | J-32 | J-32 | J-23 | J-22 | J-22 | J-22 | J-22 | J-22 | J-32 | R-3 | J-32 | J-32 |
| J-22 | J-30 | J-32 | J-23 | J-23 | J-23 | J-23 | J-16 | J-22 | J-22 | J-22 | J-22 | J-30 | J-23 | J-22 | J-23 | J-23 | J-23 | J-23 | J-23 | J-30 | J-32 | R-3 | J-30 | |
| J-23 | J-31 | J-31 | J-22 | J-17 | J-17 | J-17 | J-23 | J-30 | J-23 | J-30 | J-23 | J-31 | J-22 | J-1 | J-17 | J-32 | J-32 | J-17 | J-17 | J-31 | J-31 | J-30 | J-31 | |
| J-16 | J-23 | J-23 | J-1 | J-29 | J-29 | J-29 | J-17 | J-31 | J-30 | J-23 | J-30 | J-22 | J-4 | J-9 | J-1 | J-17 | J-30 | J-29 | J-29 | J-1 | J-30 | J-31 | R-3 | |
| Monitoring Network (MN) | Selected Nodes for Sensor Placement | ||
|---|---|---|---|
| Analysis Based on O2 | Analysis Based on O4 | Analysis Based on O | |
| MN1 | J-22 | J-23 | J-22 |
| MN2 | J-22, J-32 | J-23, J-22 | J-22, J-32 |
| MN3 | J-22, J-32, J-23 | J-23, J-22, J-32 | J-22, J-32, J-23 |
| MN4 | J-22, J-32, J-23, J-30 | J-23, J-22, J-32, J-29 | J-22, J-32, J-23, J-30 |
| MN5 | J-22, J-32, J-23, J-30, J-31 | J-23, J-22, J-32, J-29, J-30 | J-22, J-32, J-23, J-30, J-31 |
| MN6 | J-22, J-32, J-23, J-30, J-31, J-17 | J-23, J-22, J-32, J-29, J-30, J-31 | J-22, J-32, J-23, J-30, J-31, J-17 |
| MN7 | J-22, J-32, J-23, J-30, J-31, J-17, J-1 | J-23, J-22, J-32, J-29, J-30, J-31, J-25 | J-22, J-32, J-23, J-30, J-31, J-17, J-29 |
| MN8 | J-22, J-32, J-23, J-30, J-31, J-17, J-1, R-3 | J-23, J-22, J-32, J-29, J-30, J-31, J-25, R-3 | J-22, J-32, J-23, J-30, J-31, J-17, J-29, R-3 |
| MN9 | J-22, J-32, J-23, J-30, J-31, J-17, J-1, R-3, J-29 | J-23, J-22, J-32, J-29, J-30, J-31, J-25, R-3, J-9 | J-22, J-32, J-23, J-30, J-31, J-17, J-29, R-3, J-1 |
| MN10 | J-22, J-32, J-23, J-30, J-31, J-17, J-1, R-3, J-29, J-16 | J-22, J-32, J-23, J-30, J-31, J-17, J-29, R-3, J-1, J-16 | |
| MN11 | J-22, J-32, J-23, J-30, J-31, J-17, J-1, R-3, J-29, J-16, J-9 | J-22, J-32, J-23, J-30, J-31, J-17, J-29, R-3, J-1, J-16, J-9 | |
| MN12 | J-22, J-32, J-23, J-30, J-31, J-17, J-29, R-3, J-1, J-16, J-9, J-4 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsitsifli, S.; Kanakoudis, V. Identification of Suitable Locations in a Small Water Supply Network for the Placement of Water Quality Sensors Based on Different Criteria under Demand-Driven Conditions. Water 2022, 14, 2504. https://doi.org/10.3390/w14162504
Tsitsifli S, Kanakoudis V. Identification of Suitable Locations in a Small Water Supply Network for the Placement of Water Quality Sensors Based on Different Criteria under Demand-Driven Conditions. Water. 2022; 14(16):2504. https://doi.org/10.3390/w14162504
Chicago/Turabian StyleTsitsifli, Stavroula, and Vasilis Kanakoudis. 2022. "Identification of Suitable Locations in a Small Water Supply Network for the Placement of Water Quality Sensors Based on Different Criteria under Demand-Driven Conditions" Water 14, no. 16: 2504. https://doi.org/10.3390/w14162504
APA StyleTsitsifli, S., & Kanakoudis, V. (2022). Identification of Suitable Locations in a Small Water Supply Network for the Placement of Water Quality Sensors Based on Different Criteria under Demand-Driven Conditions. Water, 14(16), 2504. https://doi.org/10.3390/w14162504







