A Comparative Analysis of Statistical Models and Mathematics in Reverse Osmosis Evaluation Processes as a Search Path to Achieve Better Efficiency
Abstract
:1. Introduction
1.1. Model Concentration Polarization
1.1.1. Mathematical Modeling
1.1.2. Membrane Modeling Approaches
1.1.3. Mathematical Modeling in Reverse Osmosis
1.2. RO Optimization Modeling
1.3. Statistical Modeling
2. Goals
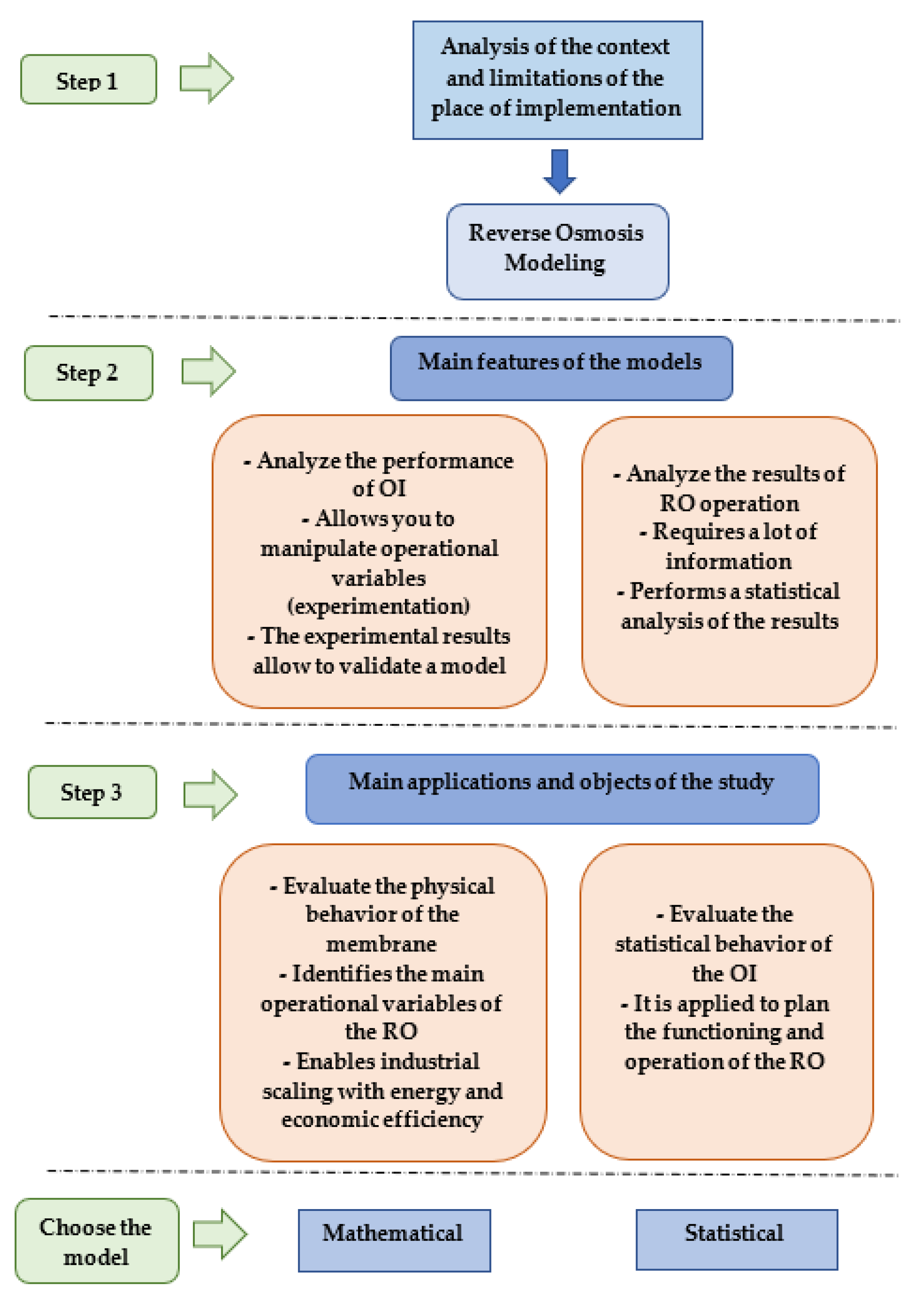
3. Review and Analysis Process
- -
- The type of model applied
- -
- Reverse osmosis system efficiency considerations
- -
- Ease of operation
- -
- Economic criteria
- -
- Energy efficiency
- -
- The efficiency and effectiveness in the results of contaminant rejection and flux production
- -
- Keywords: reverse osmosis, mathematical model, statistical model, heavy metals;
- -
- Databases: Scopus, Google Scholar;
- -
- Main conclusions: physical analysis of the membrane, energy efficiency in the process, main operating variables of the process.
4. Results
Mechanism for the Identification and Application of the Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Intaraburt, W.; Sangsanont, J.; Limpiyakorn, T.; Ruangrassamee, P.; Suttinon, P.; Suwannasilp, B.B. Feasibility Study of Water Reclamation Projects in Industrial Parks Incorporating Environmental Benefits: A Case Study in Chonburi, Thailand. Water 2022, 14, 1172. [Google Scholar] [CrossRef]
- Atab, M.; Smallbone, A.; Roskilly, A. A hybrid reverse osmosis/adsorption desalination plant for irrigation and drinking water. Desalination 2018, 444, 44–52. [Google Scholar] [CrossRef]
- Shigidi, I.; Anqi, A.E.; Elkhaleefa, A.; Mohamed, A.; Ali, I.H.; Brima, E.I. Temperature Impact on Reverse Osmosis Permeate Flux in the Remediation of Hexavalent Chromium. Water 2022, 14, 44. [Google Scholar] [CrossRef]
- Ray, S.; Chen, S.; Sangeetha, D.; Chang, H.; Thanh, C.; Le, Q.; Ku, H. Developments in forward osmosis and membrane distillation for desalination of waters. Environ. Chem. Lett. 2018, 16, 1247–1265. [Google Scholar] [CrossRef]
- Chenghan, C.; Han, Q. A Mathematical Modeling of the Reverse Osmosis Concentration Process of a Glucose Solution. Processes 2019, 7, 271. [Google Scholar] [CrossRef]
- Chung, T.; Zhang, S.; Wang, K.; Su, J.; Ling, M. Forward osmosis processes: Yesterday, today and tomorrow. Desalination 2012, 287, 78–81. [Google Scholar] [CrossRef]
- Khulbe, K.C.; Matsuura, T. Removal of heavy metals and pollutants by membrane adsorption techniques. Appl. Water Sci. 2018, 8, e19. [Google Scholar] [CrossRef]
- Ray, S.; Chen, S.; Nguyen, N.; Nguyen, H.; Dan, N.; Thanh, B. Exploration of polyelectrolyte incorporated with Triton-X 114 surfactant based osmotic agent for forward osmosis desalination. J. Environ. Manag. 2018, 209, 346–353. [Google Scholar] [CrossRef]
- Feria-Díaz, J.J.; Correa-Mahecha, F.; López-Méndez, M.C.; Rodríguez-Miranda, J.P.; Barrera-Rojas, J. Recent Desalination Technologies by Hybridization and Integration with Reverse Osmosis: A Review. Water 2021, 13, 1369. [Google Scholar] [CrossRef]
- Saravanan, A.; Senthil Kumar, P.; Jeevanantham, S.; Karishma, S.; Tajsabreen, B.; Yaashikaa, P.R.; Reshma, B. Effective water/wastewater treatment methodologies for toxic pollutants removal: Processes and applications towards sustainable development. Chemosphere 2021, 280, e130595. [Google Scholar] [CrossRef]
- Sablani, S.S.; Goosen, M.F.A.; Al-Belushi, R.; Wilf, M. Concentration polarization in ultrafiltration and reverse osmosis: A critical review. Desalination 2001, 141, 269–289. [Google Scholar] [CrossRef]
- Soltanieh, M.; Gill, W. Review of reverse osmosis membranes and transport models. Chem. Eng. Commun. 1981, 12, 279–363. [Google Scholar] [CrossRef]
- Sherwood, T.K.; Brian, P.L.T.; Fisher, R.E. Desalination by reverse osmosis. Ind. Eng. Chem. Fundam. 1967, 6, 2–12. [Google Scholar]
- Kedem, O.; Katchalsky, A. Thermodynamic analysis of the permeability of biological membranes to non-electrolytes. Biochim. Biophys. Acta 1958, 27, 229–246. [Google Scholar]
- Abbas, A. Model predictive control of a reverse osmosis desalination unit. Desalination 2016, 194, 268–280. [Google Scholar] [CrossRef]
- Subramani, S.; Panda, R. Statistical regression and modeliing analysis for reverse osmosis desalination process. Desalination 2014, 351, 120–127. [Google Scholar] [CrossRef]
- Garrido, A.E.; Strosnider, W.H.; Wilson, R.T.; Condori, J.; Nairn, R.W. Metal-contaminated potato crops and potential human health risk in Bolivian mining highlands. Environ. Geochem. Health 2017, 39, 681–700. [Google Scholar] [CrossRef]
- Quaghebeur, W.; Mulhern, R.E.; Ronsse, S.; Heylen, S.; Blommaert, H.; Potemans, S.; Valdivia Mendizábal, C.; Terrazas García, J. Arsenic contamination in rainwater harvesting tanks around Lake Poopó in Oruro, Bolivia: An unrecognized health risk. Sci. Total Environ. 2019, 688, 224–230. [Google Scholar] [CrossRef]
- AlSawaftah, N.; Abuwatfa, W.; Darwish, N.; Husseini, G. A Comprehensive Review on Membrane Fouling: Mathematical Modelling, Prediction, Diagnosis, and Mitigation. Water 2021, 13, 1327. [Google Scholar] [CrossRef]
- Wei, W.; Zou, X.; Ji, X.; Zhou, R.; Zhao, K.; Wang, Y. Analysis of Concentration Polarisation in Full-Size Spiral Wound Reverse Osmosis Membranes Using Computational Fluid Dynamics. Membranes 2021, 11, 353. [Google Scholar] [CrossRef]
- Qasim, M.; Badrelzaman, M.; Darwish, N.N.; Darwish, N.A.; Hilal, N. Reverse osmosis desalination: A state-of-the-art review. Desalination 2019, 459, 59–104. [Google Scholar] [CrossRef]
- Fariñas, M. Osmosis Inversa. Fundamentos Tecnología y Aplicaciones; Mc GrawHill, Ente Vasco de la Ingeniería, EVE, e IBERDROLA, España: Madrid, Spain, 1999; pp. 163–168. [Google Scholar]
- García, C. Aplicación de Ósmosis Inversa y Nanofiltración en Acondicionamiento de Agua para Calderas. Ph.D. Thesis, Universidad de Oviedo, Asturias, Spain, 2002. Available online: https://www.tesisenred.net/handle/10803/11146 (accessed on 27 June 2021).
- Spiegler, K.; Kedem, O. Thermodynamics of hyperfiltration (reverse osmosis): Criteria for efficient membranes. Desalination 1966, 1, 311–326. [Google Scholar] [CrossRef]
- Otero-Fernández, A.; Otero, J.A.; Maroto, A.; Carmona, J.; Palacio, L.; Prádanos, P.; Hernández, A. Concentration-polarization in nanofiltration of low concentration Cr(VI) aqueous solutions. Effect of operative conditions on retention. J. Clean. Prod. 2017, 150, 243–252. [Google Scholar] [CrossRef]
- Al-Obaidi, M.A.; Kara-Zaïtri, C.; Mujtaba, I.M. Wastewater treatment by spiral wound reverse osmosis: Development and validation of a two dimensional process model. J. Clean. Prod. 2017, 140, 1429–1443. [Google Scholar] [CrossRef]
- Lora, J.; López, M.; Cardona, S.; Fombuena, V.; Carbonell, A. Análisis del consumo Energético como factor clave en proyectos de desalación de agua de mar. In Proceedings of the 24th International Congress on Project Management and Engineering, Alcoi, Spain, 7–9 July 2020; pp. 991–1003. Available online: http://dspace.aeipro.com/xmlui/handle/123456789/2486 (accessed on 22 June 2022).
- Mulder, M. Basic Principles of Membrane Technology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996; pp. 246–248. Available online: https://ebookcentral.proquest.com/lib/bibliotecaupves-ebooks/reader.action?docID=3102158&ppg=1 (accessed on 22 June 2022).
- Alanood, A.; Al-Obajdib, M.A.; Al-Hroubc, A.M.; Patela, R.; Mujtaba, I.M. Evaluation and minimisation of energy consumption in a mediumscale reverse osmosis brackish water desalination plant. J. Clean. Prod. 2020, 248, 119220. [Google Scholar] [CrossRef]
- Ahmed, F.; Hashaikeh, R.; Diabat, A.; Hilal, N. Mathematical and optimization modelling in desalination: State-of-the-art and future direction. Desalination 2019, 469, 114092. [Google Scholar] [CrossRef]
- Lin, S.; Elimelec, M. Operación de ósmosis inversa por etapas: Configuraciones, eficiencia energética y potencial de aplicación. Desalination 2015, 366, 9–14. [Google Scholar]
- Gu, B.; Adjiman, C.S.; Xu, X.Y. Correlations for Concentration Polarization and Pressure Drop in Spacer-Filled RO Membrane Modules Based on CFD Simulations. Membranes 2021, 11, 338. [Google Scholar] [CrossRef]
- Salcedo, R.; García-Algado, P.; García-Rodríguez, M.; Fernández-Sempere, J.; Ruiz-Beviá, F. Visualization and modeling of the polarization layer in crossflow reverse osmosis in a slit-type channel. J. Membr. Sci. 2014, 456, 21–30. [Google Scholar] [CrossRef]
- Ersoy, Y.; Moscardini, A.O. Mathematical Modeling Courses for Engineering Education; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Sarker, R.A.; Newton, C.S. Optimization Modeling: A Practical Approach; CRC Press: EEUU, Florida, 2007. [Google Scholar]
- Walker, D.; Leonard, M.; Metcalfe, A.; Lambert, M. Engineering Modelling and Analysis; Taylor & Francis: Abingdon, UK, 2009. [Google Scholar]
- Yang, X.-S.; Koziel, S. Computational Optimization and Applications in Engineering and Industry; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2019; Volume 359. [Google Scholar]
- Sundaramoorthy, S.; Srinivasan, G.; Murthy, D. An analytical model for spiral wound reverse osmosis membrane modules: Part I—Model development and parameter estimation. Desalination 2011, 280, 403–411. [Google Scholar] [CrossRef]
- Van der Bruggen, B. Chapter 2—Microfiltration, ultrafiltration, nanofiltration, reverse osmosis and direct osmosis. In Fundamental Modeling of Membrane Systems, Membrane and Process Performance; Luis, P., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 25–70. [Google Scholar]
- Ismail, A.F.; Khulbe, K.C.; Matsuura, T. Chapter 1—Introduction—Do RO membranes have pores? In Reverse Osmosis; Elsiever: Amsterdam, The Netherlands, 2018; pp. 1–24. [Google Scholar]
- Pontié, M.; Dach, H.; Leparc, J.; Hafsi, M.; Lhassani, A. Novel approach combining physico-chemical characterizations and mass transfer modelling of nanofiltration and low pressure reverse osmosis membranes for brackish water desalination intensification. Desalination 2008, 221, 174–191. [Google Scholar] [CrossRef]
- Villena, E.; Alvizuri, P.; Torregrza-López, J.-I.; Lora, J.; Lo-Iacono, V. Reverse Osmosis Pilot Plant to Removal Heavy Metals Pb, Fe, As, Zn and Mn in Consumption Waters in Bolivia. In Proceedings of the 24th International Congress on Project Management and Engineering, Alcoi, Spain, 7–9 July 2020; pp. 1252–1264. [Google Scholar]
- Salcedo, R. Aplicación de la interferometría holográfica al estudio de la capa de polarización en ósmosis inversa. Efecto de la convección natural. Ph.D. Thesis; Universidad de Alicante: Asturias, Spain, 2006. Available online: https://dialnet.unirioja.es/servlet/tesis?codigo=68704 (accessed on 27 June 2021).
- Hidalgo, A.M.; Gómez, M.; Murcia, M.D.; Serrano, J.; Otón, J. Caracterización de la membrana NF-97 mediante disoluciones salinas. Aplicación del modelo de Spiegler-Kedem-Kachalsky. Afinidad 2013, 70, 48–53. Available online: https://raco.cat/index.php/afinidad/article/view/268539 (accessed on 22 June 2022).
- Zarzo, D.; Prats, D. Desalination and energy consumption. What can we expect in the near future? Desalination 2018, 427, 1–9. [Google Scholar] [CrossRef]
- Geise, G.; Park, H.; Sagle, A.; Freeman, B.; McGrath, J. Water permeability and water/salt selectivity tradeoff in polymers for desalination. J. Membr. Sci. 2011, 369, 130–138. [Google Scholar] [CrossRef]
- Lin, S.; Elimelech, M. Kinetics and energetics trade-off in reverse osmosis desalination with different configurations. Desalination 2017, 401, 42–52. [Google Scholar] [CrossRef]
- Chong, T.H.; Krantz, W.B. Process economics and operating strategy for the energy-efficient reverse osmosis (EERO) process. Desalination 2018, 443, 70–84. [Google Scholar] [CrossRef]
- Kim, J.; Hong, S. A novel single-pass reverse osmosis configuration for high-purity water production and low energy consumption in seawater desalination. Desalination 2018, 429, 142–154. [Google Scholar]
- Voutchkov, N. Energy use for membrane seawater desalination—Current status and trends. Desalination 2018, 431, 2–14. [Google Scholar] [CrossRef]
- Han, D.; Hwang, M.; Kim, I.S. Effect of boron rejection and recovery rate on a single-pass design of SWRO using hybrid membrane inter-stage design (HID) concept. Desalination 2017, 404, 215–223. [Google Scholar]
- Peñate, B.; García-Rodríguez, L. Reverse osmosis hybrid membrane inter-stage design: A comparative performance assessment. Desalination 2011, 281, 354–363. [Google Scholar]
- Molina, V.G.; Busch, M.; Sehn, P. Cost savings by novel seawater reverse osmosis elements and design concepts. Desalination Water Treat. 2009, 7, 160–177. [Google Scholar]
- Jeong, K.; Park, M.; JinKi, S.; HaKim, J. A systematic optimization of Internally Staged Design (ISD) for a full-scale reverse osmosis process. J. Membr. Sci. 2017, 540, 285–296. [Google Scholar] [CrossRef]
- Kotb, H.; Ame, E.H.; Ibrahim, K.A. On the optimization of RO (Reverse Osmosis) system arrangements and their operating conditions. Energy 2016, 103, 127–150. [Google Scholar]
- Miyamoto, J.; Nakamura, K.; Nakamura, T. Searching for an Efficient Fouling Index for Reverse Osmosis Desalination: A Statistical Approach. In Proceedings of the 2010 International Conference on Industrial Engineering and Operations Management, Dhaka, Bangladesh, 9–10 January 2010; pp. 9–10. [Google Scholar]
- Khajet, M.; Cojocaru, C. Air gap membrane distillation desalination modelling and optimization. Desalination 2012, 287, 138–145. [Google Scholar] [CrossRef]
- Khajet, M.; Essalh, M.; Tmenta-Deu, A. Optimization of solar powered reverse osmosis desalination pilot plant using response surface methodology. Desalination 2010, 261, 284–292. [Google Scholar] [CrossRef]
- Tort-Martorell, J. Diseños Factoriales Fraccionales—Aplicación al Control de Calidad Mediante el Diseño de Productos y Procesos. Ph.D. Thesis, Universidad Politecnica de Catalunia, Barcelona, Spain, 1985. [Google Scholar]
- Taguchi, G.; Chowdhury, S.; Wu, Y. Taguchi’s Quality Engineering Handbook; John Wiley and Sons: Hoboken, NJ, USA, 2005; ISBN 047-141-334-8. [Google Scholar]
- Mohsen, M.; Salem, G. Performance evaluation of reverse osmosis desalination plant. A case study of Wadi Ma’in, Zara and Mujib plant. Desalin. Water Treat. 2010, 14, 265–272. [Google Scholar] [CrossRef]
- De-wei, L.; Yang, N.; Qui, H.; Xi, Y. FPGA based QDMC control for reverse-osmosis water desalination system. Desalination 2012, 285, 83–90. [Google Scholar]
- Feo, J.; Jaime, J.; Alvarez, L. Cost analysis in RO desalination plants production lines. Mathematical model and simulation. Desalin. Water Treat. 2013, 51, 4800–4805. [Google Scholar]
- Box, G.E.; Wilson, K.B. On the experimental attainment of optimum conditions. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992; pp. 270–310. [Google Scholar]
- Gil, E. Fotocatálisis: Una alternativa viable para la eliminación de compuestos orgánicos. Rev. Universidad EAFIT 2002, 127, 59–64. Available online: https://repository.eafit.edu.co/handle/10784/17256 (accessed on 27 June 2021).
- Guerra, C.; Ruíz, A.; Herrera, M.; Fernández, L. La Modelación Matemático-Estadística en la Metodología de Superficie de Respuesta. Apl. Agrícolas. Ing. Agrícola 2018, 8, 67–73. Available online: https://scholar.google.com.bo/scholar?hl=es&as_sdt=0%2C5&as_vis=1&q=Guerra+C.%2C+Ru%C3%Adz+A.%2C+Herrera+M.+y+Fern%C3%A1ndez+L.+2018.+La+Modelaci%C3%B3n+Matem%C3%A1tico-Estad%C3%Adstica+en+la+Metodolog%C3%Ada+de+Superficie+de+Respuesta.+Aplicaciones+agr%C3%Adcolas.+Ingenier%C3%Ada+Agr%C3%Adcola.+8%2C+67-73.&btnG= (accessed on 19 June 2022).
- Hernández, A.; Guillón, M.; García, L. La metodología de Taguchi en el control estadístico de la calidad. Investig. Operativa. 2015, 37, 65–83. Available online: https://revistas.unc.edu.ar/index.php/revahttp:/revistas.unc.edu.ar/index.php/epio/article/view/11986.ine (accessed on 19 June 2022).
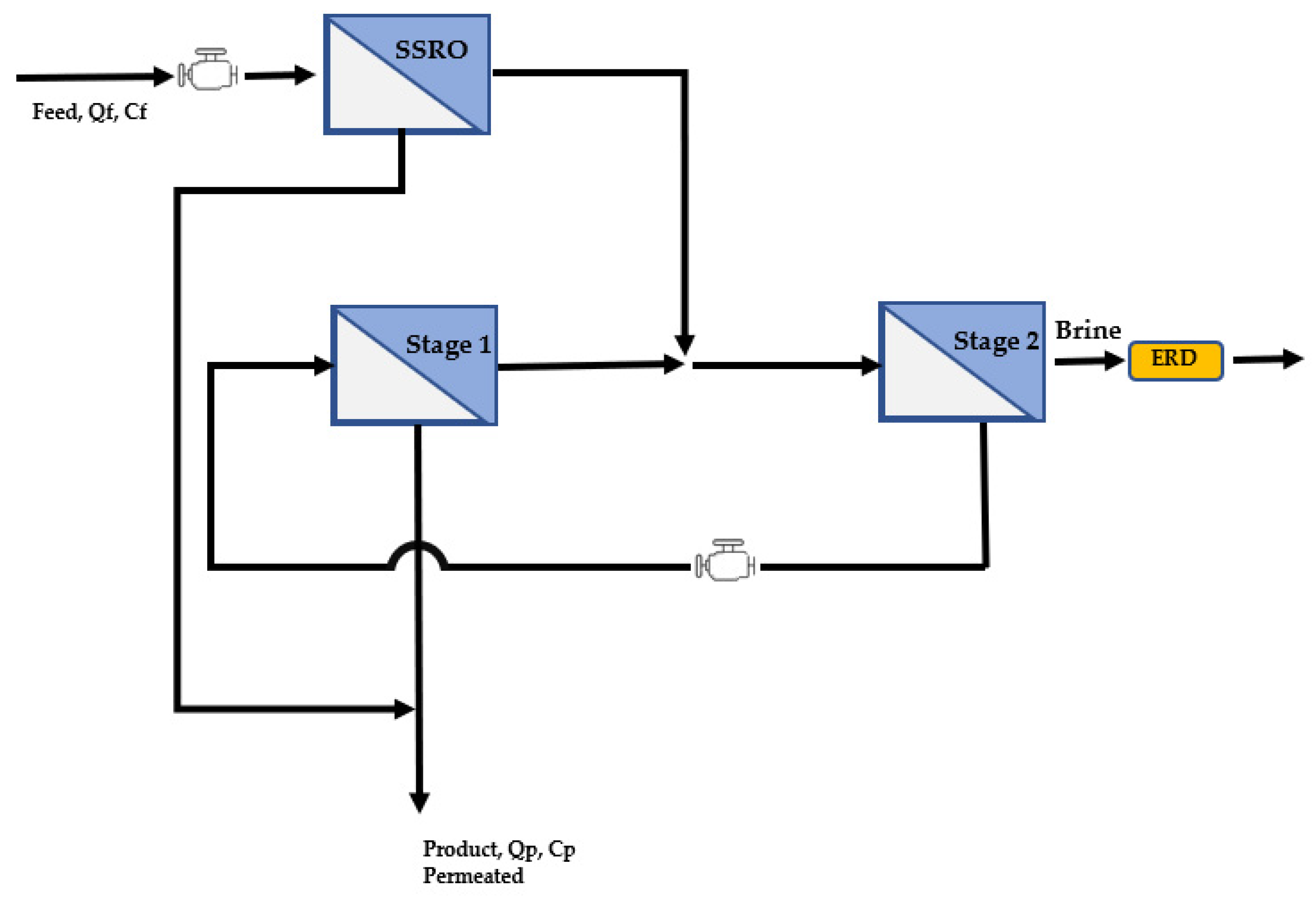
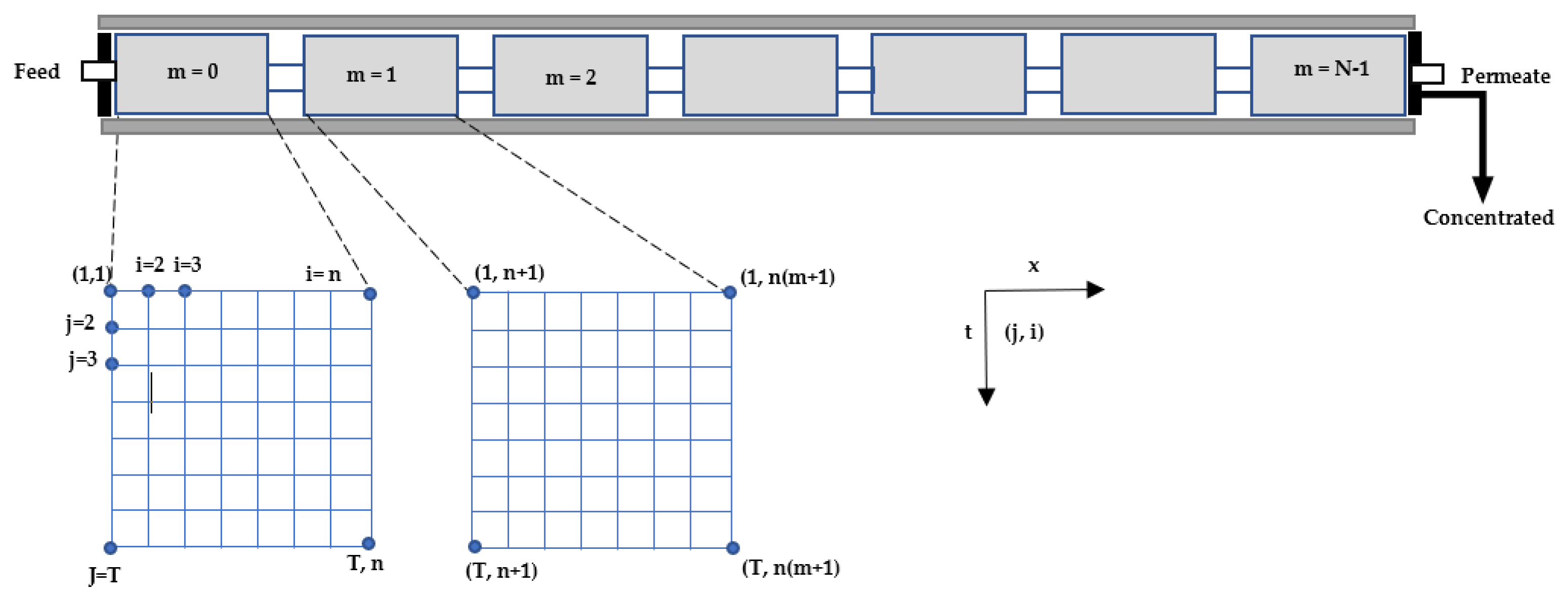
| Model | Typology | Characteristic | Efficiency and Effectiveness in the Results of Contaminant Rejection and Flux Production | ||||
|---|---|---|---|---|---|---|---|
| Type of Model Applied | Reverse Osmosis System Efficiency Considerations | Ease of Operation | Economic Criteria | Energy Efficiency | |||
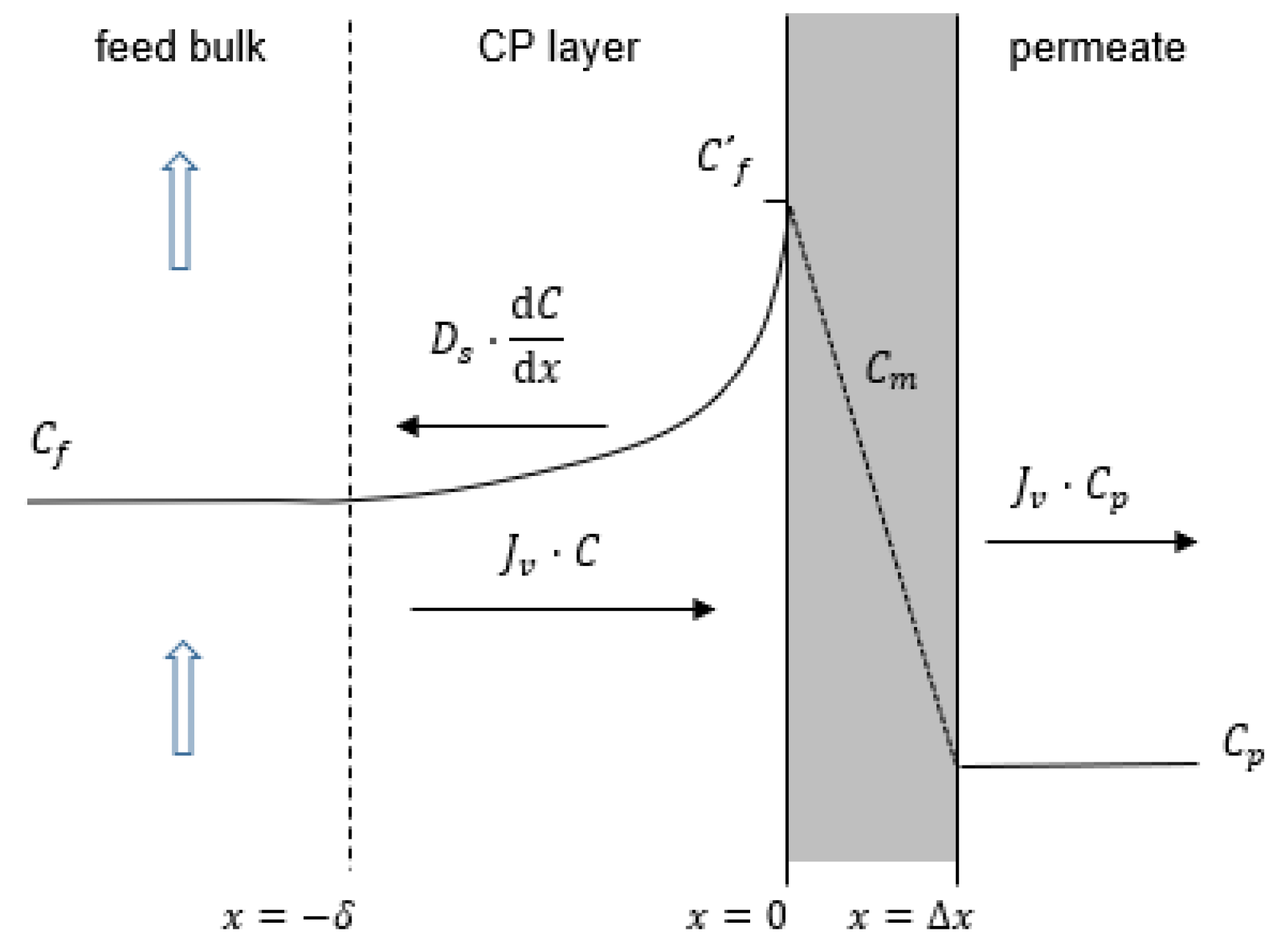
| Concentration Polarization | Matemática—Kedem model [5,14,19,34,35,41] | Physical behavior of the membrane | Evidence physical/chemical phenomena that govern the process | Determine key operating variables—Shows the behavior of the system interrelating result—widely used in experimental processes [5]. | Energy consumption is the most important factor of the total cost—Electricity price variability generates changes in process conditions such as pressures, concentrations in permeate flows [8,9,20,21]. | The model allows the process to be analyzed at low pressures, identifying the most sensitive operating variables that allow industrial scaling with energy efficiency [10,38]. | Rejection of contaminants greater than 99% |
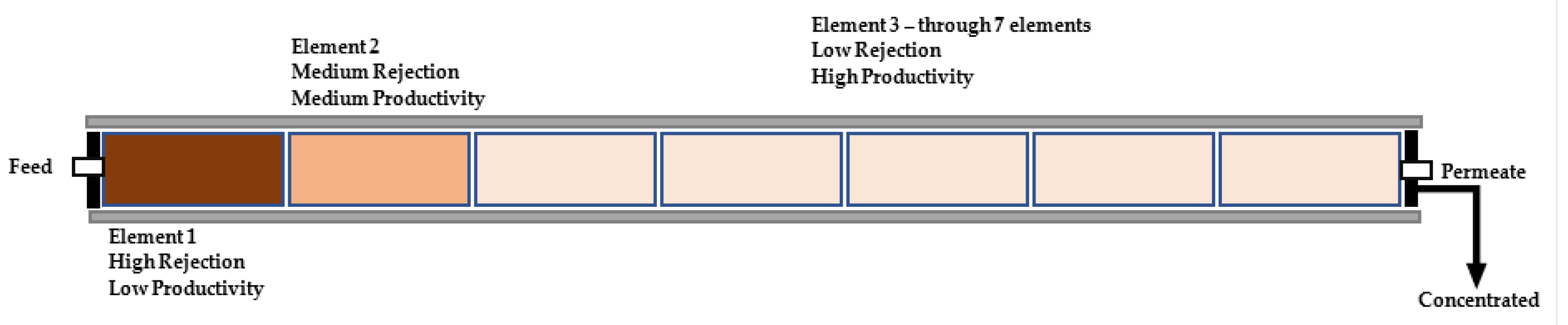
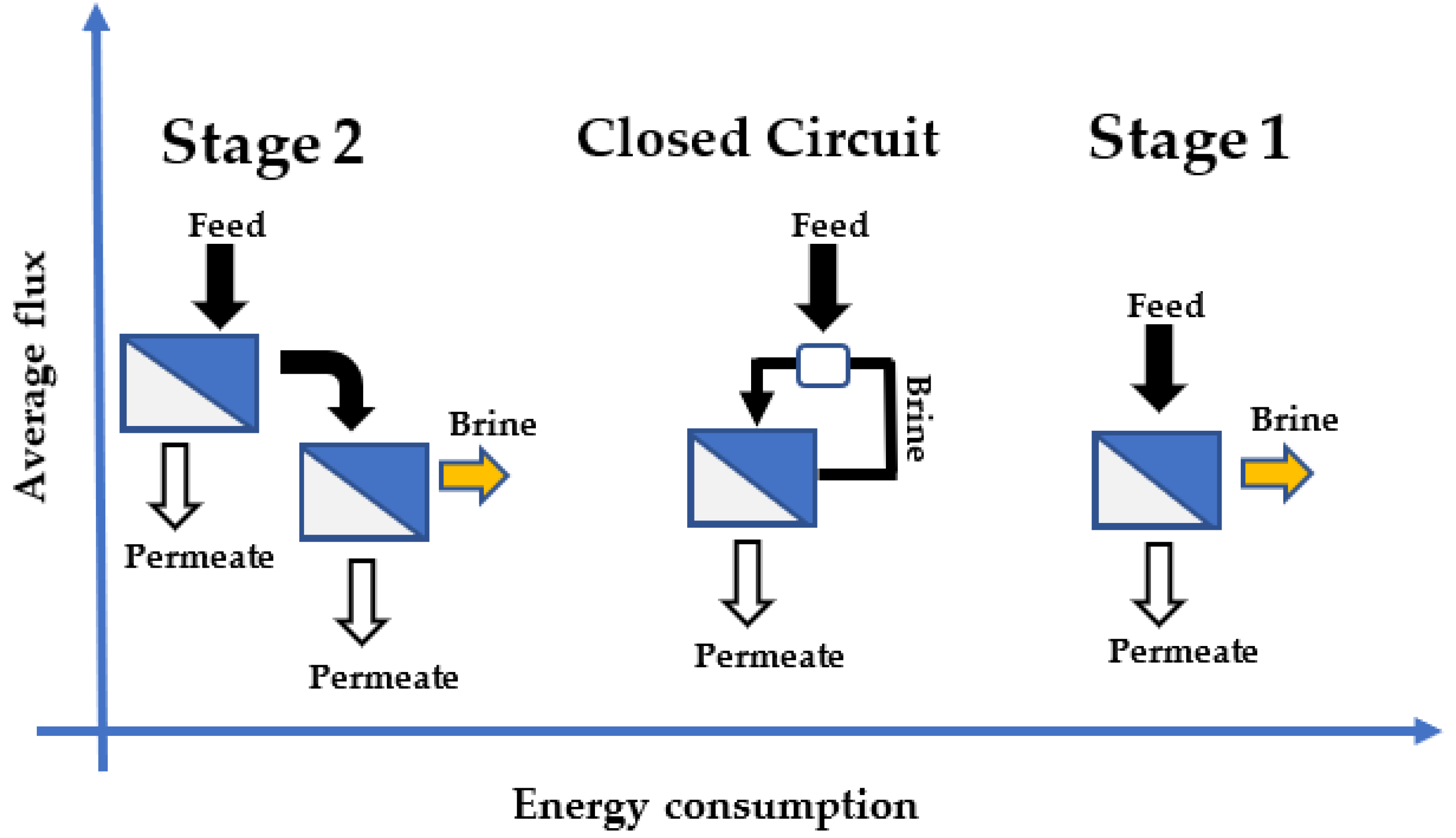
| Physical configuration | Specific energy consumption (SEC) | 1 Stage, 2 Step and CCRO [31,47] | The compensation quantifies the relationship between mean water flow and SEC at module scale with 1-stage, 2-stage, and closed-loop—Operation based on the kinetics [47] | Quantify compensation using the relationship between average water flow and SEC in module-scale reverse osmosis processes with 1-stage, 2-stage, and closed-loop configurations [47] | The reduction of the normalized SEC will have a significantly stronger impact In absolute energy savings, system configuration and operating conditions also have significant impacts on energy or economic costs of pretreatment processes and energy recovery [45]. | A 1-stage RO process usually yields the highest average water flux but also consumes the most energy a 2-stage RO process typically consumes the least energy and yields a moderate average water flux and a CC-RO process yields the lowest average water flux and consumes more energy than a 2-stage RO process but less energy than a 1-stage RO process [31,47] | The optimization of RO operation based on the kinetics-energetics tradeoff should be conducted in the range of operation conditions that would not drastically undermine other aspects of RO performance |
| Energy-Efficient Reverse Osmosis (EERO) | The energy-efficient reverse osmosis (EERO) desalination process was developed to achieve a highfull water recovery [48] | Feeds retentate from one or more stages of Single Stage Reverse Osmosis (SSRO) in series to a countercurrent membrane cascade with recycle (CMCR) consisting of a reverse osmosis (RO) terminal stage and one or more low salt rejection stages | The process, it develops with an operational strategy that involves increasing the pressure to the low salt rejection stage of the CMCR to compensate for the use of membranes with a higher salt rejection than required | An achieve 75% total water recovery at a lower total cost of water production than conventional SSRO operated with only 50% water recovery [48] | The EERO process can reduce the osmotic pressure differential by 50% relative to conventional SSRO for the same total water recovery | The EERO process significantly reduces the infrastructure costs—The 1-2 and 2-2 configurations of the EERO process can achieve reductions of 3.7% and 6.2%, respectively, in the total cost of water production for operation at 75% total water recovery relative to conventional SSRO operating at only 50% total water recover associated with pre-treatment [48] | |
| Hybrid membrane configuration combining SWRO | Combining SWRO elements of different productivity and rejection within the same vessel [50,51] | The hybrid membrane interstage design (HID) is evaluated to improve the SEC efficiency of the reverse osmosis process | The system allows estimating the energy efficiency of the HID under three feeding conditions: high concentration and high temperature (Case 1); low concentration and high temperature (Case 2); and low concentration and low temperature (Case 3) | HID application can save up to 0.41 kWh/m3 of SEC. | Configuration of seven elements per vessel, each element of the membrane would produce one seventh (14.3%) of the total flow of permeate [50] | Temperature is a more important design factor than recovery rate for HID application. | |
| Internally Staged Design (ISD) | Numerically optimized, based on a finite difference method [54] | It is a method of systematic optimization to find better sequences of membrane elements in a pressure vessel. | A large-scale RO process was numerically modeled to assess the impact of the membrane element configuration on the long-term operation in the presence of colloidal contaminants [54] | The proposed method for optimizing ISD is useful for more economical and efficient design and is a good reference for manufacturers to further improve their RO membranes [54] | The ISD system improves water recovery rate and energy efficiency of SWRO processes during a long-term operation | The optimization ISD shows higher water flow and higher energy efficiency in long-term operation (90 days) compared to conventional designs [30]. | |
| Statistics | Reverse Osmosis (RO) Steady State Statistical Models | Constructions of correlations between inputs/outputs [16] | Understanding of the mechanism/behavior of the interaction between input and output variables of the desalination plant by formulating regression models. | Show interaction between input and output variables—They are used to plan and shows the sensitivity of variables against the operation of the system—Characteristic data of the current are used (flow rate, concentration, and pH) over a period | The model developed here is useful for planning, monitoring, and analysis of the current separation system | The model is obtained after multivariate resulting analysis that the P values are smaller than α < 0.052, indicating independently distributed residuals with mean residual values for a confidence level of 95% and 99% that are insignificant | The proposal requires more field as well as experiments to confirm findings based on physical or chemical viewpoints [16] |
| New fouling index, β called the “permeation coefficient” | Development of a new fouling index that is more reliable and feasible than the SDI [56] | Definition of a new fouling index β called “permeation coefficient” under natural environmental conditions from a statistical point of view | Regression models allow predicting the rate of return and the specific performance index that takes into account energy consumption based on different variables | The analysis of the performance of the membranes based on their fouling, allows better criteria of its preservation to improve its performance, allowing better energy and economic savings. | It provides new insights into the performance and shortcomings of SDI from a statistical point of view. | adoption of a new fouling index would require further field testing, as well as experiments or theory to confirm the findings based on physical or chemical points of view [56] | |
| Response surface methodology (RS) | Applied for modeling and optimization of the air gap membrane distillation process used in desalination [58,59,60,65] | Regression models are used to predict the rate of return and the specific performance index that takes into account energy consumption based on different variables | The developed models have been statistically validated by analysis of variance | Two optimal operating conditions were found by solving two different problems. optimization cases: (i) maximization of the performance index and (ii) maximization of the specific performance index. This allows design with greater energy and economic savings in the systems. | From the RS models, the optimal AGMD conditions were determined using the multi-stage Monte Carlo simulation technique. | For the performance index, the optimal solution was a cooling inlet temperature of 13.9 °C, a feed inlet temperature of 71 °C and a feed flow rate of 183 L/h [58,59] | |
| Model Predictive Control (MPC) | It is an advanced control algorithm widely used in the process industries, as reverse osmosis plant [62] | In this paper, the QDMC controller is used to control a simulated reverse-osmosis (RO) water desalination system with spiral wound element (SWM). A cascaded control system was designed with the QDMC controller and a PID controller for the desalination process, where the QDMC controller optimizes the set point of the PID controller and directly controls one output. | Support software is available to help engineers adjust QDMC controller parameters. Since the QDMC controller is implemented in an embedded system, the system cost is reduced, which is helpful for RO desalination system application | Dado que todo el controlador QDMC está implementado a través de un chip FPGA, el costo es muy bajo, lo que es útil para una amplia aplicación en plantas prácticas | QDMC control system can also handle the system constraints and is very effective in controlling the complex coupled process of a RO plant. | The model compared the results of the proposed QDMC cascade control system with the traditional two-PID control strategy used in the industry. The model considers three different scenarios, with set point control and disturbance rejections. Based on the simulation results [62] | |
| Statistical data processing, applied to research studies related to costs | Report of a mathematical model based on statistical processing related to production costs. The analysis of the cost of one m3 of desalinated water by reverse osmosis (RO) is carried out [63] | A mathematical model is proposed based on expressions related to costs based on production capacity. | All cost data are plotted on bar charts and box-and-whisker plots. The study of atypical values was carried out as well as that of Kolmogorov–Smirnov and Shapiro–Wilk tests were performed based on Hubera’s M, Tukey’s biweight, Hampel’s M and Andrew’s wave estimators. Subsequently, factorial analysis was performed using the Bartlett and Kaiser-Meyer-Olkin tests; Possible mathematical models were analyzed | the model shows that desalination costs can be up to 1.5%, more efficient in the production line compared to the rest of the observed lines | The model provides an innovative aspect in cost analysis because the study focused exclusively in the search for technologically more efficient and lower cost production lines impact on the plant. | The proposed equation corresponds to the mathematical model based on the statistical data adjusted to 98% of the real cost for small desalination plants [63] | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villena-Martínez, E.M.; Alvizuri-Tintaya, P.A.; Lora-Garcia, J.; Torregrosa-López, J.I.; Lo-Iacono-Ferreira, V.G. A Comparative Analysis of Statistical Models and Mathematics in Reverse Osmosis Evaluation Processes as a Search Path to Achieve Better Efficiency. Water 2022, 14, 2485. https://doi.org/10.3390/w14162485
Villena-Martínez EM, Alvizuri-Tintaya PA, Lora-Garcia J, Torregrosa-López JI, Lo-Iacono-Ferreira VG. A Comparative Analysis of Statistical Models and Mathematics in Reverse Osmosis Evaluation Processes as a Search Path to Achieve Better Efficiency. Water. 2022; 14(16):2485. https://doi.org/10.3390/w14162485
Chicago/Turabian StyleVillena-Martínez, Esteban Manuel, Paola Andrea Alvizuri-Tintaya, Jaime Lora-Garcia, Juan Ignacio Torregrosa-López, and Vanesa Gladys Lo-Iacono-Ferreira. 2022. "A Comparative Analysis of Statistical Models and Mathematics in Reverse Osmosis Evaluation Processes as a Search Path to Achieve Better Efficiency" Water 14, no. 16: 2485. https://doi.org/10.3390/w14162485
APA StyleVillena-Martínez, E. M., Alvizuri-Tintaya, P. A., Lora-Garcia, J., Torregrosa-López, J. I., & Lo-Iacono-Ferreira, V. G. (2022). A Comparative Analysis of Statistical Models and Mathematics in Reverse Osmosis Evaluation Processes as a Search Path to Achieve Better Efficiency. Water, 14(16), 2485. https://doi.org/10.3390/w14162485