A Decision Support System to Enhance Electricity Grid Resilience against Flooding Disasters
Abstract
:Highlights
- A decision support system framework based on network cost minimization is proposed to divert flood waters from flood-susceptible utility poles, thereby enhancing electricity grid resilience.
- This optimization framework is evaluated in three different watersheds in the United States using state-of-the-art mathematical optimization platforms, i.e., JuMP/Julia interface and the Gurobi solver.
- The results of this proposed optimization framework could provide adequate flood diversion capacity to prevent failure of utility poles.
Abstract
1. Introduction
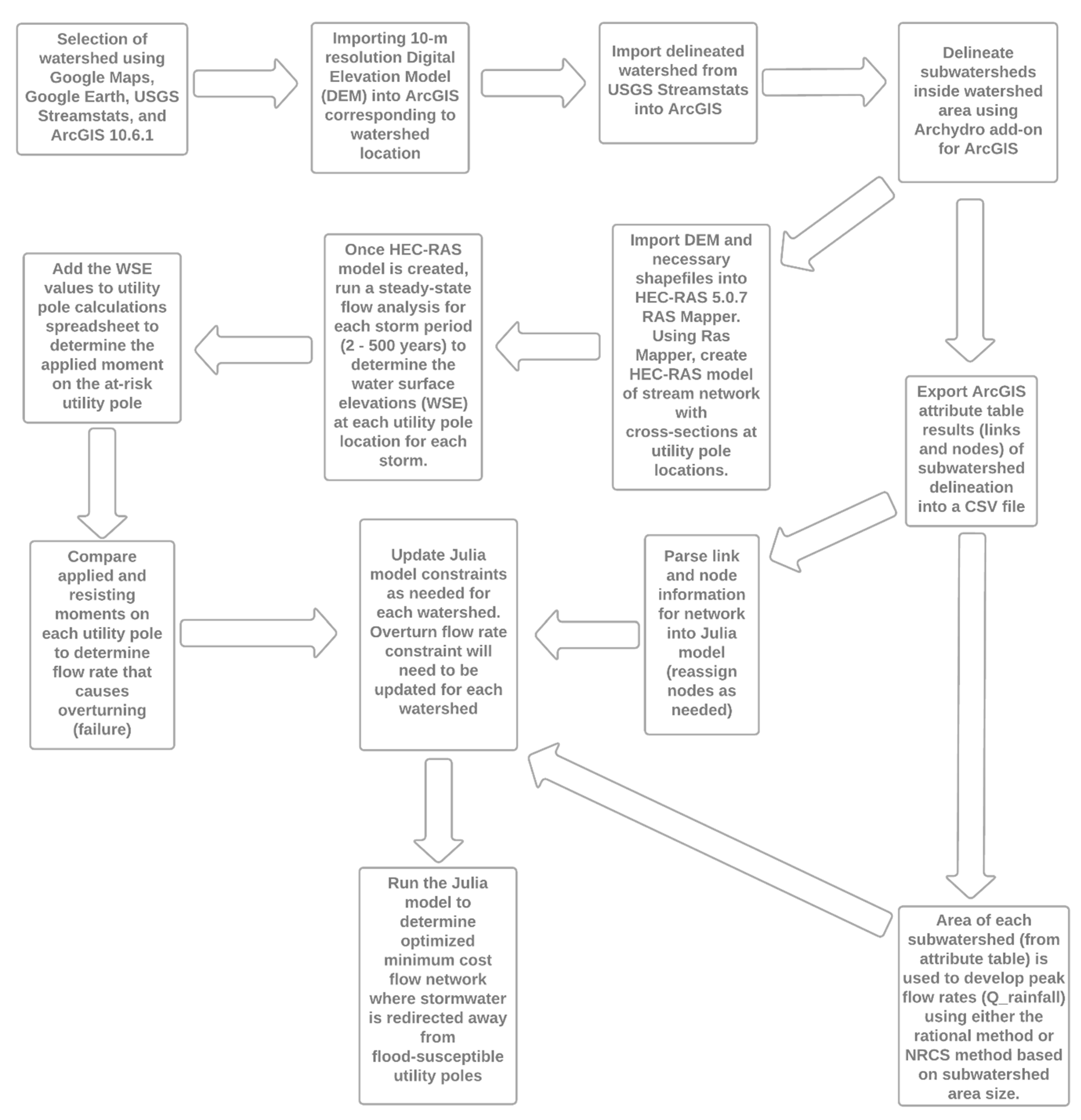
2. Methodology
2.1. Study Areas and Hydrologic Analyses
2.2. Pole Failure Model
- (1)
- Utility pole–soil interactions can be modeled as a small retaining wall subjected to a passive pressure earth force (Equation (2)), which contributes to the total resisting moment. This total resisting moment opposes the moment created by the force applied by stormwater Equation (1) and the WSE.
- (2)
- The governing drag force formula,was considered to be used to calculate the applied (horizontal) force from stormwater, where V is the velocity of water flow colliding with a utility pole, Cd is the drag coefficient, A is the cross-sectional area, and ρ is the density of water. We also considered the momentum equation for the flow in motion: assuming the velocity is dissipated after hitting the pole (as a conservative assumption), which resulted in more conservative values compared to drag forces, and thus selected in this paper.
- (3)
- (4)
- Full setting depth is determined by the commonly accepted rule, 10% of the utility pole length plus two feet [35].
- (5)
- All utility poles are directly buried in the soil with no embedment foundation, based on observations made in Google Street View.
- (6)
- The version of the Rankine passive earth pressure force of the soil (Equation (11)) was used based on the assumption that the soils in each watershed are predominantly granular [36].
- (7)
- In Rankine theory, it is assumed that the structure being modeled as a retaining wall is completely vertical and has a smooth surface. Therefore, factors such as wall–soil friction and retaining wall sloping are negligible.
- (8)
- Equation (3) assumes that there is no angle of incline and only takes into consideration the angle of friction. Kp is the Rankine passive pressure coefficient, which can be calculated from the following equation.
- (9)
- Based on [36], it is assumed the resisting force is applied at approximately 2/3 of the utility pole (retaining wall) burial depth (measured from the ground line downward), or a distance 1/3 from the bottom of the utility pole (measured upward).
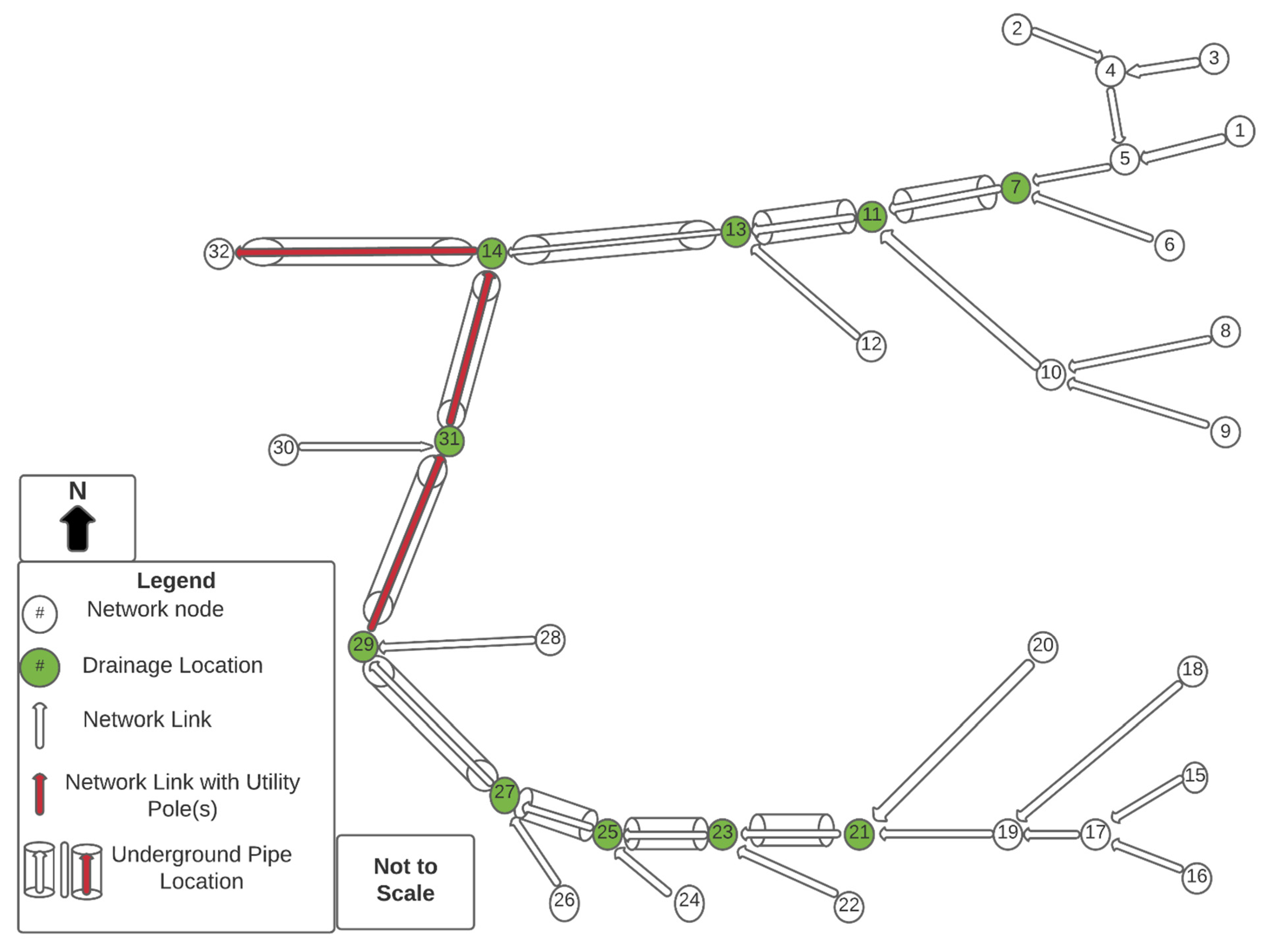
2.3. Minimum Cost Network Flow Optimization Problem
- (1)
- pipe extending vertically downward from surface nodes to connect to horizontal pipe and
- (2)
- horizontal pipe conveying stormwater to the network outfall, or discharge point.
3. Results
4. Discussions and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pant, R.; Thacker, S.; Hall, J.W.; Alderson, D.; Barr, S. Critical infrastructure impact assessment due to flood exposure. J. Flood Risk Manag. 2018, 11, 22–33. [Google Scholar] [CrossRef]
- Anderson, G.B.; Bell, M.L. Lights Out: Impact of the August 2003 Power Outage on Mortality in New York, NY. Epidemiology 2012, 23, 189–193. [Google Scholar] [CrossRef] [PubMed]
- Klinger, C.; Owen Landeg, V.M. Power outages, extreme events and health: A systematic review of the literature from 2011–2012. PLoS Curr. 2014, 6, 14–27. [Google Scholar] [CrossRef]
- Marx, M.A.; Rodriguez, C.V.; Greenko, J.; Das, D.; Heffernan, R.; Karpati, A.M.; Mostashari, F.; Balter, S.; Layton, M.; Weiss, D. Diarrheal illness detected through syndromic surveillance after a massive power outage: New York City, August 2003. Am. J. Public Health 2006, 96, 547–553. [Google Scholar] [CrossRef] [PubMed]
- Campbell, R.J.; Lowry, S. Weather-Related Power Outages and Electric System Resiliency; CRS Report for Congress: Washington, DC, USA, 2012. [Google Scholar]
- Hines, P.; Apt, J.; Talukdar, S. Trends in the history of large blackouts in the United States. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–8. [Google Scholar]
- Hemme, K. Critical infrastructure protection: Maintenance is national security. J. Strateg. Secur. 2015, 8, 25–39. [Google Scholar] [CrossRef]
- Manshadi, S.; Khodayar, M. Resilient Operation of Multiple Energy Carrier Microgrids. IEEE Trans. Smart Grid 2015, 6, 2283–2292. [Google Scholar] [CrossRef]
- Manshadi, S.; Khodayar, M. Preventive reinforcement under uncertainty for islanded microgrids with electricity and natural gas networks. J. Mod. Power Syst. Clean Energy 2018, 6, 1223–1233. [Google Scholar] [CrossRef]
- Li, Z.; Guo, J. Wisdom about age [aging electricity infrastructure]. IEEE Power Energy Mag. 2006, 4, 44–51. [Google Scholar]
- McLaughlin, K. Photos and Videos Show the Destruction after 2 Dams Collapsed in Michigan, Threatening a Town with 9 Feet of Flooding. Insider. Available online: https://www.insider.com/photos-videos-show-michigan-dam-collapse-destruction-2020-5 (accessed on 20 May 2020).
- Turnquist, M.; Vugrin, E. Design for resilience in infrastructure distribution networks. Environ. Syst. Decis. 2013, 33, 104–120. [Google Scholar] [CrossRef]
- Crucitti, P.; Latora, V.; Marchiori, M. Model for cascading failures in complex networks. Phys. Rev. E 2004, 69, 045104. [Google Scholar] [CrossRef]
- Maringanti, C.; Chaubey, I.; Arabi, M.; Engel, B. Application of a Multi-Objective Optimization Method to Provide Least Cost Alternatives for NPS Pollution Control. Environ. Manag. 2011, 48, 448–461. [Google Scholar] [CrossRef] [PubMed]
- Muleta, M.K.; Nicklow, J.W. Evolutionary algorithms for multiobjective evaluation of watershed management decisions. J. Hydroinformatics 2002, 4, 83–97. [Google Scholar] [CrossRef]
- Evenson, D.E.; Moseley, J.C. Simulation/Optimization Techniques for Multi-Basin Water Resource Planning1. J. Am. Water Resour. Assoc. 1970, 6, 725–736. [Google Scholar] [CrossRef]
- Sigvaldson, O.T. A simulation model for operating a multipurpose multireservoir system. Water Resour. Res. 1976, 12, 263–278. [Google Scholar] [CrossRef]
- Ilich, N. Limitations of Network Flow Algorithms in River Basin Modeling. J. Water Resour. Plan. Manag. 2009, 135, 48–55. [Google Scholar] [CrossRef]
- Labadie, J.W.; Bode, D.A.; Pineda, A.M. Network Model for Decision Support in Municipal Raw Water Supply. J. Am. Water Resour. Assoc. 1986, 22, 927–940. [Google Scholar] [CrossRef]
- Andrews, E.S.; Chung, F.I.; Lund, J.R. Multilayered, Priority—Based Simulation of Conjunctive Facilities. J. Water Resour. Plan. Manag. 1992, 118, 32–53. [Google Scholar] [CrossRef]
- Bixby, R. A Brief History of Linear and Mixed-Integer Programming Computation. Doc. Math. 2012, 2012, 107–121. [Google Scholar]
- Liu, S.; Konstantopoulou, F.; Gikas, P.; Papageorgiou, L.G. A mixed integer optimisation approach for integrated water resources management. Comput. Chem. Eng. 2011, 35, 858–875. [Google Scholar] [CrossRef]
- Veintimilla-Reyes, J.; Cattrysse, D.; De Meyer, A.; Van Orshoven, J. Mixed integer linear programming (MILP) approach to deal with spatio-temporal water allocation. Procedia Eng. 2016, 162, 221–229. [Google Scholar] [CrossRef]
- Watson, J.-P.; Greenberg, H.J.; Hart, W.E. A Multiple-Objective Analysis of Sensor Placement Optimization in Water Networks. Crit. Transit. Water Environ. Resour. Manag. 2004, 5, 1–10. [Google Scholar]
- Mani, A.; Tsai, F.T.-C.; Paudel, K.P. Mixed Integer Linear Fractional Programming for Conjunctive Use of Surface Water and Groundwater. J. Water Resour. Plan. Manag. 2016, 142, 04016045. [Google Scholar] [CrossRef]
- Carini, M.; Maiolo, M.; Pantusa, D.; Chiaravalloti, F.; Capano, G. Modelling and optimization of least-cost water distribution networks with multiple supply sources and users. Ric. Mat. 2018, 67, 465–479. [Google Scholar] [CrossRef]
- Bieupoude, P.; Azoumah, Y.; Neveu, P. Optimization of drinking water distribution networks: Computer-based methods and constructal design. Comput. Environ. Urban Syst. 2012, 36, 434–444. [Google Scholar] [CrossRef]
- Ghelichi, Z.; Tajik, J.; Pishvaee, M.S. A novel robust optimization approach for an integrated municipal water distribution system design under uncertainty: A case study of Mashhad. Comput. Chem. Eng. 2018, 110, 13–34. [Google Scholar] [CrossRef]
- Alqattan, N.A. A Multi-Period Mixed Integer Linear Programming Model for Desalination and Electricity Co-generation in Kuwait. Graduate Thesis, USF Tampa, Tampa, FL, USA, 2014. [Google Scholar]
- Lubchenco, J.; Hayes, J. A better eye on the storm. Sci. Am. 2012, 306, 68–73. [Google Scholar] [CrossRef]
- Teegavarapu, R.S. Climate variability and changes in precipitation extremes and characteristics. In Sustainable Water Resources Planning and Management Under Climate Change; Springer: Berlin/Heidelberg, Germany, 2017; pp. 3–37. [Google Scholar]
- Trenberth, K.E. Changes in precipitation with climate change. Clim. Res. 2011, 47, 123–138. [Google Scholar] [CrossRef]
- Groisman, P.Y.; Knight, R.W.; Karl, T.R. Changes in intense precipitation over the central United States. J. Hydrometeorol. 2012, 13, 47–66. [Google Scholar] [CrossRef]
- Davisson, M.; Prakash, S. A Review of Soil-Pole Behavior; Highway Research Record (39); Highway Research Board: Washington, DC, USA, 1963. [Google Scholar]
- Keshavarzian, M. Self-supported Wood Pole Fixity at ANSI Groundline. Pract. Period. Struct. Des. Constr. 2002, 7, 147–155. [Google Scholar] [CrossRef]
- Das, B.M. Principles of Foundation Engineering, 8th ed.; Cengage Learning: Boston, MA, USA, 2016; pp. 593–645. [Google Scholar]
- Al-Shammary, A.A.G.; Kouzani, A.Z.; Kaynak, A.; Khoo, S.Y.; Norton, M.; Gates, W. Soil Bulk Density Estimation Methods: A Review. Pedosphere 2018, 28, 581–596. [Google Scholar] [CrossRef]
- USDA NRCS. (n.d.). Soil Bulk Density/Moisture/Aeration. USDA-NRCS. Available online: https://www.nrcs.usda.gov/Internet/FSE_DOCUMENTS/nrcs142p2_053260.pdf (accessed on 20 January 2021).
- USDA Forest Service Engineering Staff. Slope Stability Reference Guide for National Forests in the United States. USDA. 1994. Available online: https://www.fs.fed.us/rm/pubs_other/wo_em7170_13/wo_em7170_13_vol2.pdf (accessed on 20 January 2021).
- Bareither, C.A.; Edil, T.B.; Benson, C.H.; Mickelson, D.M. Geological and Physical Factors Affecting the Friction Angle of Compacted Sands. J. Geotech. Geoenvironmental Eng. 2008, 134, 1476–1489. [Google Scholar] [CrossRef]
- Koloski, J.W.; Schwarz, S.D.; Tubbs, D.W. Geotechnical Properties of Geologic Materials. 1989. Available online: http://www.tubbs.com/geotech/geotech.htm (accessed on 20 January 2021).
- Wolfe, R.W.; Moody, R.C. ANSI Pole Standards: Development and Maintenance. In Proceedings of the First Southeastern Pole Conference, Madison, WI, USA, 8–11 November 1992; pp. 143–149. [Google Scholar]
- Durbin, M.; Hoffman, K. OR PRACTICE—The Dance of the Thirty-Ton Trucks: Dispatching and Scheduling in a Dynamic Environment. Oper. Res. 2008, 56, 3–19. [Google Scholar] [CrossRef]
- Su, L.-H.; Cheng, T.C.E.; Chou, F.-D. A minimum-cost network flow approach to preemptive parallel-machine scheduling. Comput. Ind. Eng. 2013, 64, 453–458. [Google Scholar] [CrossRef]
- Dunning, I.; Huchette, J.; Lubin, M. JuMP: A Modeling Language for Mathematical Optimization. SIAM Rev. 2017, 59, 295–320. [Google Scholar] [CrossRef]
- Alam, M.M.; Zhu, Z.; Eren Tokgoz, B.; Zhang, J.; Hwang, S. Automatic Assessment and Prediction of the Resilience of Utility Poles Using Unmanned Aerial Vehicles and Computer Vision Techniques. Int. J. Disaster Risk Sci. 2020, 11, 119–132. [Google Scholar] [CrossRef]
- Charlotte-Mecklenburg Stormwater Services. Charlotte-Mecklenburg Storm Water Design Manual Chapter 2. Charlotte Chamber Design Manual Task Force. 2014. Available online: https://charlottenc.gov/StormWater/Regulations/Documents/SWDMC/SWDMChap2Final12312013.pdf (accessed on 27 January 2021).
- U.S. Geological Survey; City of Charlotte and Mecklenburg County; Weaver, J. Frequency of Annual Maximum Precipitation in the City of Charlotte and Mecklenburg County, North Carolina, through 2004. 2006. Available online: https://pubs.usgs.gov/sir/2006/5017/pdf/report.pdf (accessed on 20 January 2021).
- City of Colorado Springs. Drainage Criteria Manual Vol I. 2014. Available online: https://coloradosprings.gov/sites/default/files/images/dcm_volume_1.pdf (accessed on 27 January 2021).
- Merwade, V. Creating SCS Curve Number Grid using HEC-GeoHMS; Purdue University: West Lafayette, IN, USA, 2010. [Google Scholar]
- City of Fayetteville Engineering Division. Fayetteville Arkansas Drainage Criteria Manual. 2014. Available online: https://www.fayetteville-ar.gov/DocumentCenter/View/2248/Drainage-Criteria-Manual-2014-PDF (accessed on 27 January 2021).
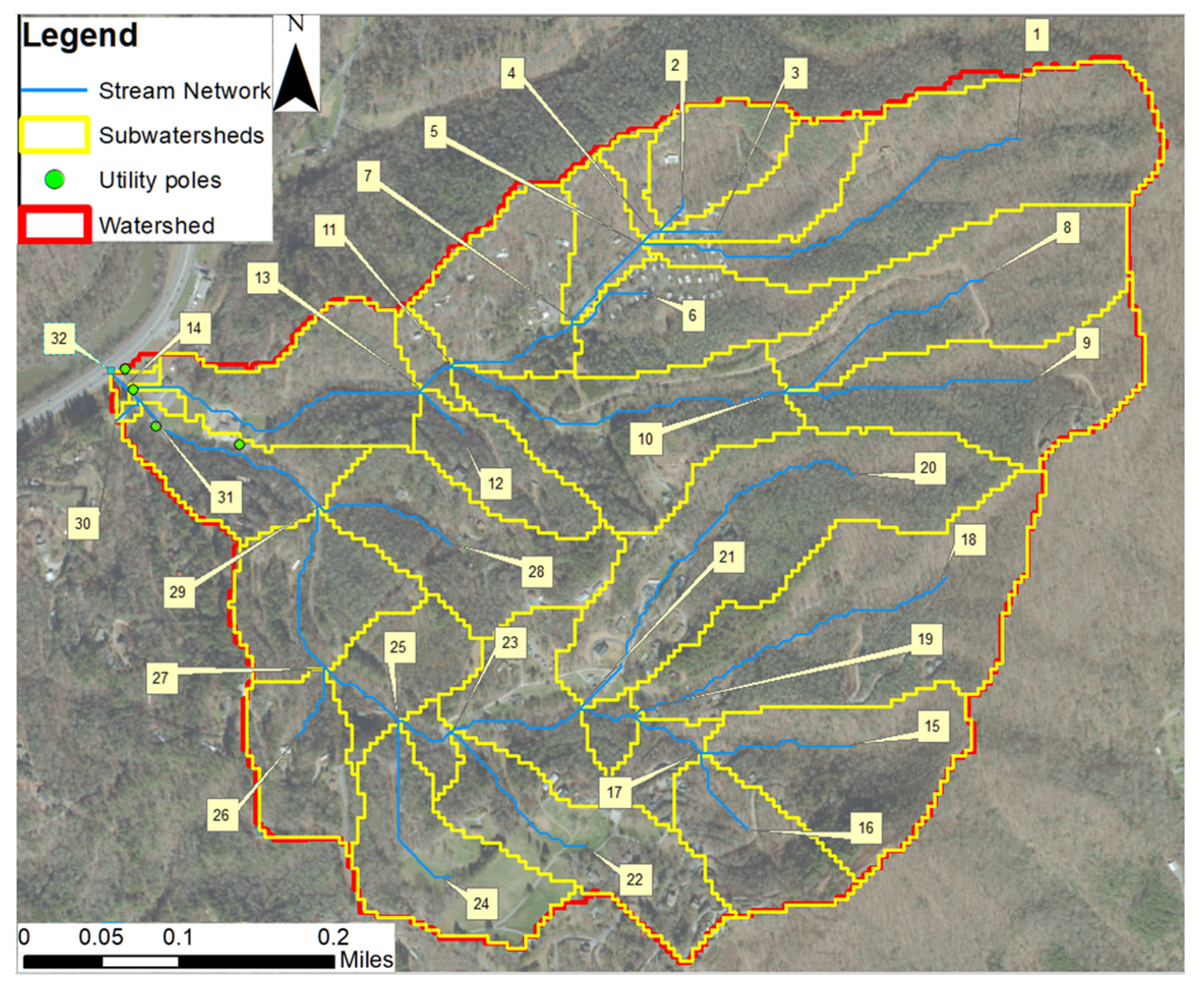


| Watershed | Dominant Soil Texture | Amount of Vegetation | 1 Bulk Density (g/cm3) |
|---|---|---|---|
| Whittier, NC | Sandy loam | plentiful | 1.40 |
| Leadville, CO | Gravely, sandy loam | sparse | 1.63 |
| London, AR | Sandy loam | plentiful | 1.40 |
| Watershed | Pole Class | 1 Length Range (ft) | 1 Assumed Length (ft) | 2 Top Circ. (in) | 2 Circ. 6 ft from Pole Bottom (in) | 3 Fiber Stress (lb/in2) | 1 Setting Depth (ft) |
|---|---|---|---|---|---|---|---|
| Whittier, NC | 7 | 20–45 | 30 | 15 | 21.00 | 8000 | 5 |
| Leadville, CO | 7 | 20–45 | 35,45 | 15 | 22.25, 24.75 | 8000 | 5.5, 6.5 |
| London, AR | 7 | 20–45 | 45 | 15 | 24.75 | 8000 | 6.5 |
| Utility Pole * | Storm Return Period (year) | 1 Flow Rate Colliding with Pole (ft3/s) | 2 WSE (ft) | 3 Applied Moment (ft-lb) | 3 Resisting Moment (ft-lb) | Pass/Fail? | 1 Overturn Flow Rate (ft3/s) |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 233.97 | 0.13 | 2109.61 | 26,686.93 | Pass | 2959.91 |
| 1 | 5 | 297.41 | 0.18 | 4719.74 | 26,686.93 | Pass | 1681.73 |
| 1 | 10 | 328.01 | 0.2 | 6378.83 | 26,686.93 | Pass | 1372.35 |
| 1 | 25 | 387.83 | 0.39 | 17389.02 | 26,686.93 | Pass | 595.22 |
| 1 | 50 | 425.5 | 0.46 | 24688.61 | 26,686.93 | Pass | 459.96 |
| 1 | 100 | 468.72 | 0.54 | 35167.58 | 26,686.93 | Fail | 355.70 |
| 1 | 500 | 569.1 | 0.61 | 58565.07 | 26,686.93 | Fail | 259.34 |
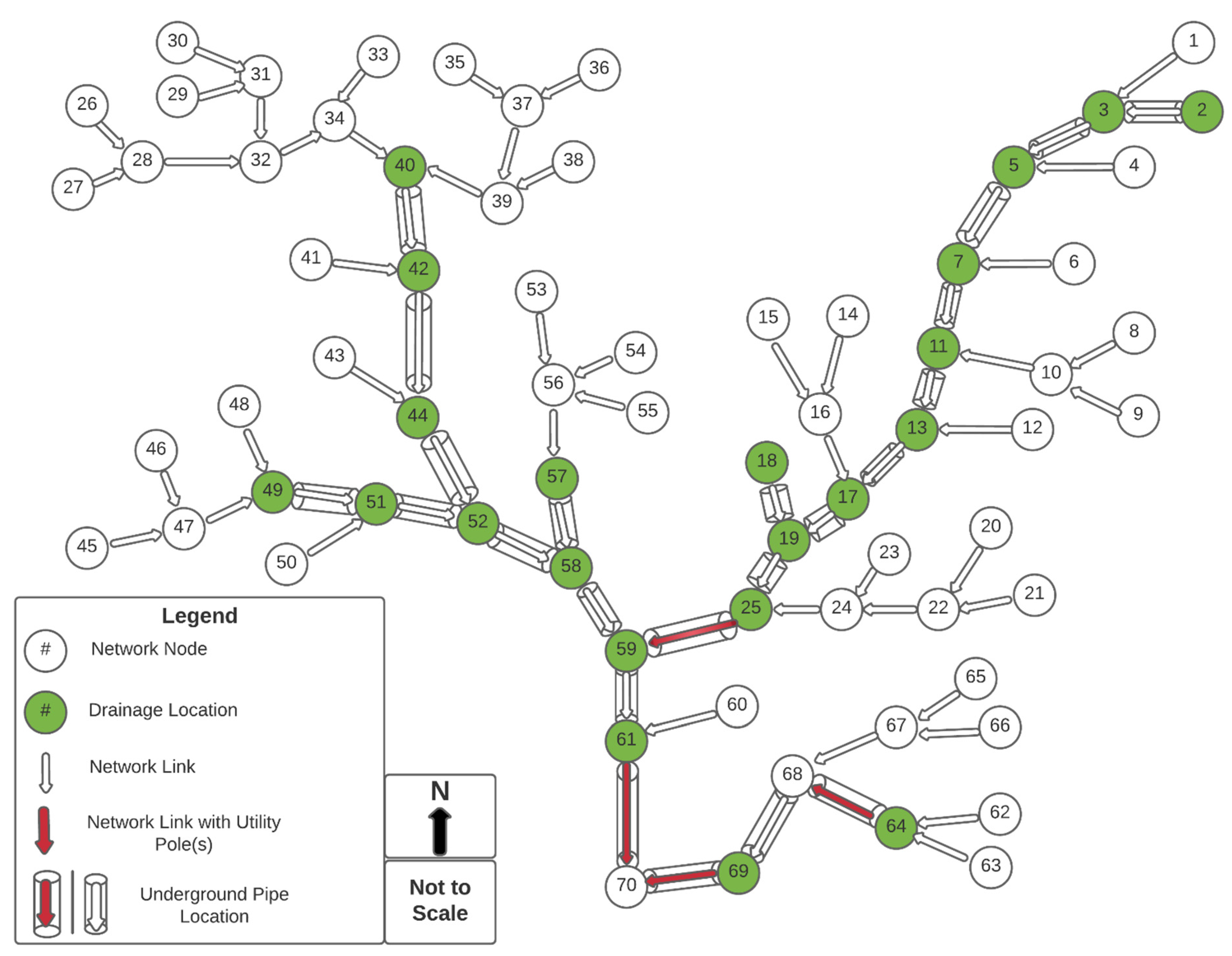
| Node | 1 Drainage Capacity Recommended (ft3/s) | Links | 2 Underground Pipe Flow (ft3/s) |
|---|---|---|---|
| 1 | 1.5 | ||
| 2 | 2.4 | ||
| 3 | 3.4 | ||
| 4 | 4.5 | ||
| 5 | 5.7 | ||
| 6 | 6.7 | ||
| 7 | 75.00 | 7.11 | 75.00 |
| 8 | 8.10 | ||
| 9 | 9.10 | ||
| 10 | 10.11 | ||
| 11 | 75.00 | 11.13 | 150.00 |
| 12 | 12.13 | ||
| 13 | 75.00 | 13.14 | 225.00 |
| 14 | 75.00 | 15.17 | |
| 15 | 16.17 | ||
| 16 | 17.19 | ||
| 17 | 18.19 | ||
| 18 | 19.21 | ||
| 19 | 20.21 | ||
| 20 | 21.23 | 75.00 | |
| 21 | 75.00 | 22.23 | |
| 22 | 23.25 | 127.04 | |
| 23 | 52.04 | 24.25 | |
| 24 | 25.27 | 202.04 | |
| 25 | 75.00 | 26.27 | |
| 26 | 27.29 | 277.04 | |
| 27 | 75.00 | 28.29 | |
| 28 | 29.31 | 352.04 | |
| 29 | 75.00 | 30.31 | |
| 30 | 31.14 | 427.04 | |
| 31 | 75.00 | 14.32 | 727.04 |
| 32 |
| Nodes | 1 Drainage Capacity Recommended (ft3/s) | Links | 2 Underground Pipe Flow (ft3/s) |
|---|---|---|---|
| 1 | 1.3 | ||
| 2 | 2375 | 2.3 | 2375 |
| 3 | 2375 | 3.5 | 4750 |
| 4 | 4.5 | ||
| 5 | 2375 | 5.7 | 7125 |
| 6 | 6.7 | ||
| 7 | 2375 | 7.11 | 9500 |
| 8 | 8.10 | ||
| 9 | 9.10 | ||
| 10 | 10.11 | ||
| 11 | 2375 | 11.13 | 11,875 |
| 12 | 12.13 | ||
| 13 | 2375 | 13.17 | 14,250 |
| 14 | 14.16 | ||
| 15 | 15.16 | ||
| 16 | 16.17 | ||
| 17 | 2375 | 17.19 | 16,625 |
| 18 | 112.10 | 18.19 | 112.10 |
| 19 | 2375 | 19.25 | 19,112.10 |
| 20 | 20.22 | ||
| 21 | 21.22 | ||
| 22 | 22.24 | ||
| 23 | 23.24 | ||
| 24 | 24.25 | ||
| 25 | 2375 | 26.28 | |
| 26 | 27.28 | ||
| 27 | 28.32 | ||
| 28 | 30.31 | ||
| 29 | 29.31 | ||
| 30 | 31.32 | ||
| 31 | 32.34 | ||
| 32 | 33.34 | ||
| 33 | 35.37 | ||
| 34 | 36.37 | ||
| 35 | 37.39 | ||
| 36 | 38.39 | ||
| 37 | 39.40 | ||
| 38 | 34.40 | ||
| 39 | 40.42 | 2375 | |
| 40 | 2375 | 41.42 | |
| 41 | 42.44 | 4750 | |
| 42 | 2375 | 43.44 | |
| 43 | 44.52 | 7125 | |
| 44 | 2375 | 45.47 | |
| 45 | 46.47 | ||
| 46 | 47.49 | ||
| 47 | 48.49 | ||
| 48 | 49.51 | 178.75 | |
| 49 | 178.75 | 50.51 | |
| 50 | 51.52 | 2553.75 | |
| 51 | 2375 | 53.57 | |
| 52 | 2375 | 54.56 | |
| 53 | 55.56 | ||
| 54 | 56.57 | ||
| 55 | 57.58 | 952.81 | |
| 56 | 52.58 | 12,053.75 | |
| 57 | 952.81 | 58.59 | 15,381.57 |
| 58 | 2375 | 25.59 | 21,487.10 |
| 59 | 2336.96 | 59.61 | 39,205.63 |
| 60 | 60.61 | ||
| 61 | 2375 | 62.64 | |
| 62 | 63.64 | ||
| 63 | 64.68 | 484.43 | |
| 64 | 484.43 | 65.67 | |
| 65 | 66.67 | ||
| 66 | 67.68 | ||
| 67 | 68.69 | 484.43 | |
| 68 | 69.70 | 2195.88 | |
| 69 | 1711.44 | 61.70 | 41,580.63 |
| 70 |
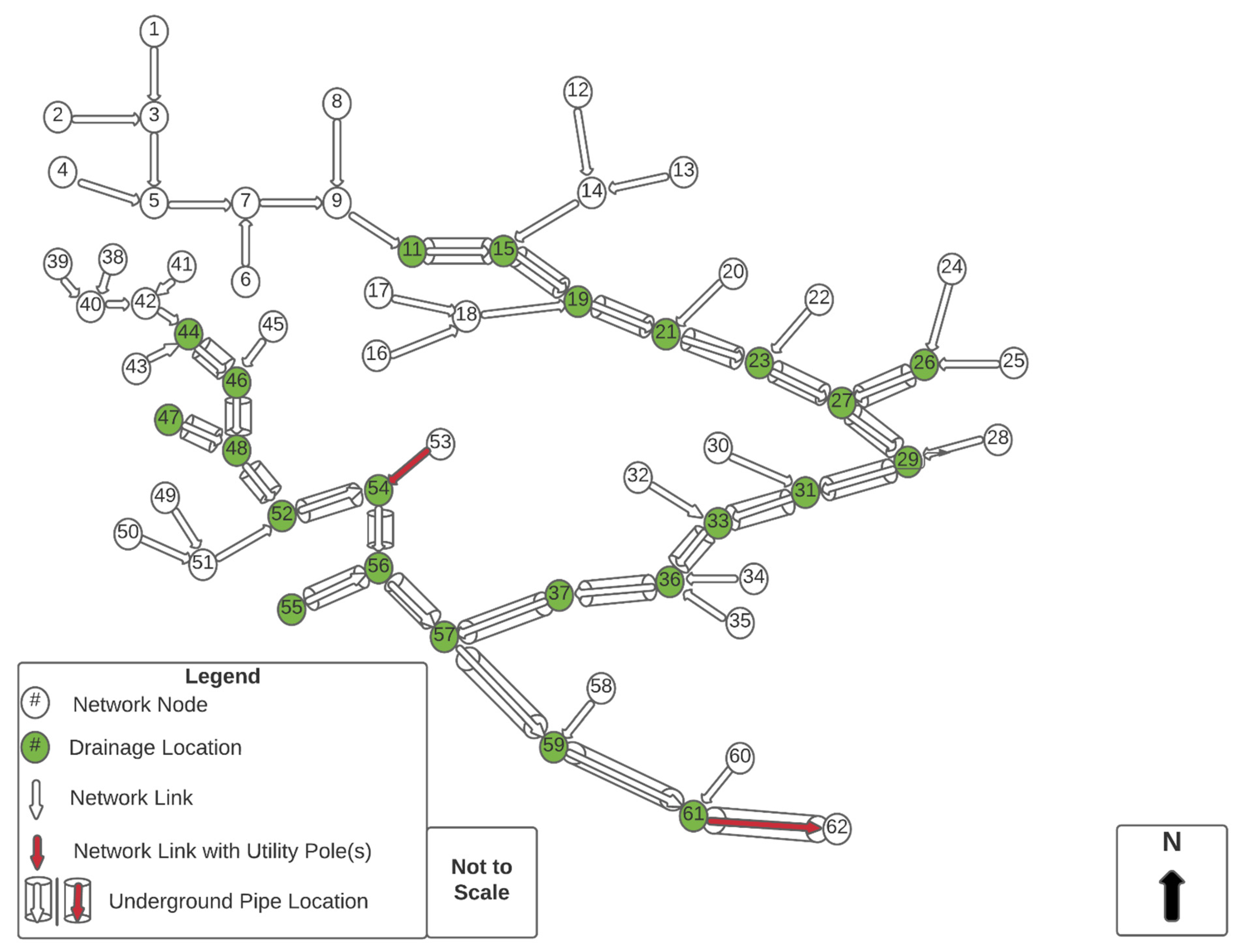
| Nodes | 1 Drainage Capacity Recommended (ft3/s) | Links | 2 Underground Pipe Flow (ft3/s) |
|---|---|---|---|
| 1 | 1.3 | ||
| 2 | 2.3 | ||
| 3 | 3.5 | ||
| 4 | 4.5 | ||
| 5 | 5.7 | ||
| 6 | 6.7 | ||
| 7 | 7.9 | ||
| 8 | 8.9 | ||
| 9 | 9.11 | ||
| 10 | 10.11 | ||
| 11 | 1490 | 11.15 | 1490 |
| 12 | 12.14 | ||
| 13 | 13.14 | ||
| 14 | 14.15 | ||
| 15 | 1490 | 15.19 | 2980 |
| 16 | 16.18 | ||
| 17 | 17.18 | ||
| 18 | 18.19 | ||
| 19 | 1490 | 19.21 | 4470 |
| 20 | 20.21 | ||
| 21 | 1490 | 21.23 | 5960 |
| 22 | 22.23 | ||
| 23 | 1490 | 23.27 | 7450 |
| 24 | 24.26 | ||
| 25 | 25.26 | ||
| 26 | 1490 | 26.27 | 1490 |
| 27 | 1490 | 27.29 | 10,430 |
| 28 | 28.29 | ||
| 29 | 1490 | 29.31 | 11,920 |
| 30 | 30.31 | ||
| 31 | 1490 | 31.33 | 13,410 |
| 32 | 32.33 | ||
| 33 | 1490 | 33.36 | 14,900 |
| 34 | 34.36 | ||
| 35 | 35.36 | ||
| 36 | 1349.02 | 36.37 | 16,249.02 |
| 37 | 1490 | 38.40 | |
| 38 | 39.40 | ||
| 39 | 40.42 | ||
| 40 | 41.42 | ||
| 41 | 42.44 | ||
| 42 | 43.44 | ||
| 43 | 44.46 | 1490 | |
| 44 | 1490 | 45.46 | |
| 45 | 46.48 | 2891.27 | |
| 46 | 1401.27 | 47.48 | 843.03 |
| 47 | 843.03 | 48.52 | 5222.30 |
| 48 | 1490 | 49.51 | |
| 49 | 50.51 | ||
| 50 | 51.52 | ||
| 51 | 52.54 | 6714.30 | |
| 52 | 1490 | 53.54 | |
| 53 | 54.56 | 8202.30 | |
| 54 | 1490 | 55.56 | 1490 |
| 55 | 1490 | 56.57 | 11,184.30 |
| 56 | 1490 | 37.57 | 17,739.02 |
| 57 | 1490 | 57.59 | 30,413.33 |
| 58 | 58.59 | ||
| 59 | 1490 | 59.61 | 31,903.33 |
| 60 | 60.61 | ||
| 61 | 1490 | 61.62 | 33,393.33 |
| 62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Violante, M.; Davani, H.; Manshadi, S.D. A Decision Support System to Enhance Electricity Grid Resilience against Flooding Disasters. Water 2022, 14, 2483. https://doi.org/10.3390/w14162483
Violante M, Davani H, Manshadi SD. A Decision Support System to Enhance Electricity Grid Resilience against Flooding Disasters. Water. 2022; 14(16):2483. https://doi.org/10.3390/w14162483
Chicago/Turabian StyleViolante, Michael, Hassan Davani, and Saeed D. Manshadi. 2022. "A Decision Support System to Enhance Electricity Grid Resilience against Flooding Disasters" Water 14, no. 16: 2483. https://doi.org/10.3390/w14162483
APA StyleViolante, M., Davani, H., & Manshadi, S. D. (2022). A Decision Support System to Enhance Electricity Grid Resilience against Flooding Disasters. Water, 14(16), 2483. https://doi.org/10.3390/w14162483






