Network Subsystems for Robust Design Optimization of Water Distribution Systems
Abstract
:1. Introduction
2. Material and Methods
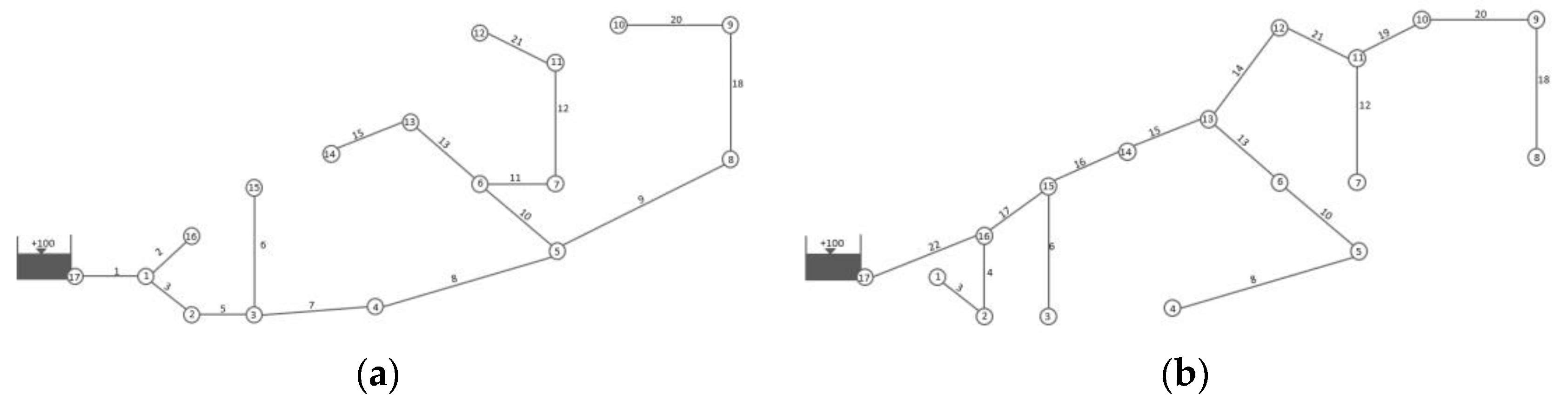
2.1. Subsystem Enumeration
Subsystem Pair Optimization
2.2. Robust Counterpart Optimization
2.3. Least Cost Design of WDS Matrix Formulation
2.3.1. Uncorrelated Model of Data Uncertainty
2.3.2. Correlated Robust Counterpart
Linearization of the Operating Domain [Q1,Q2]
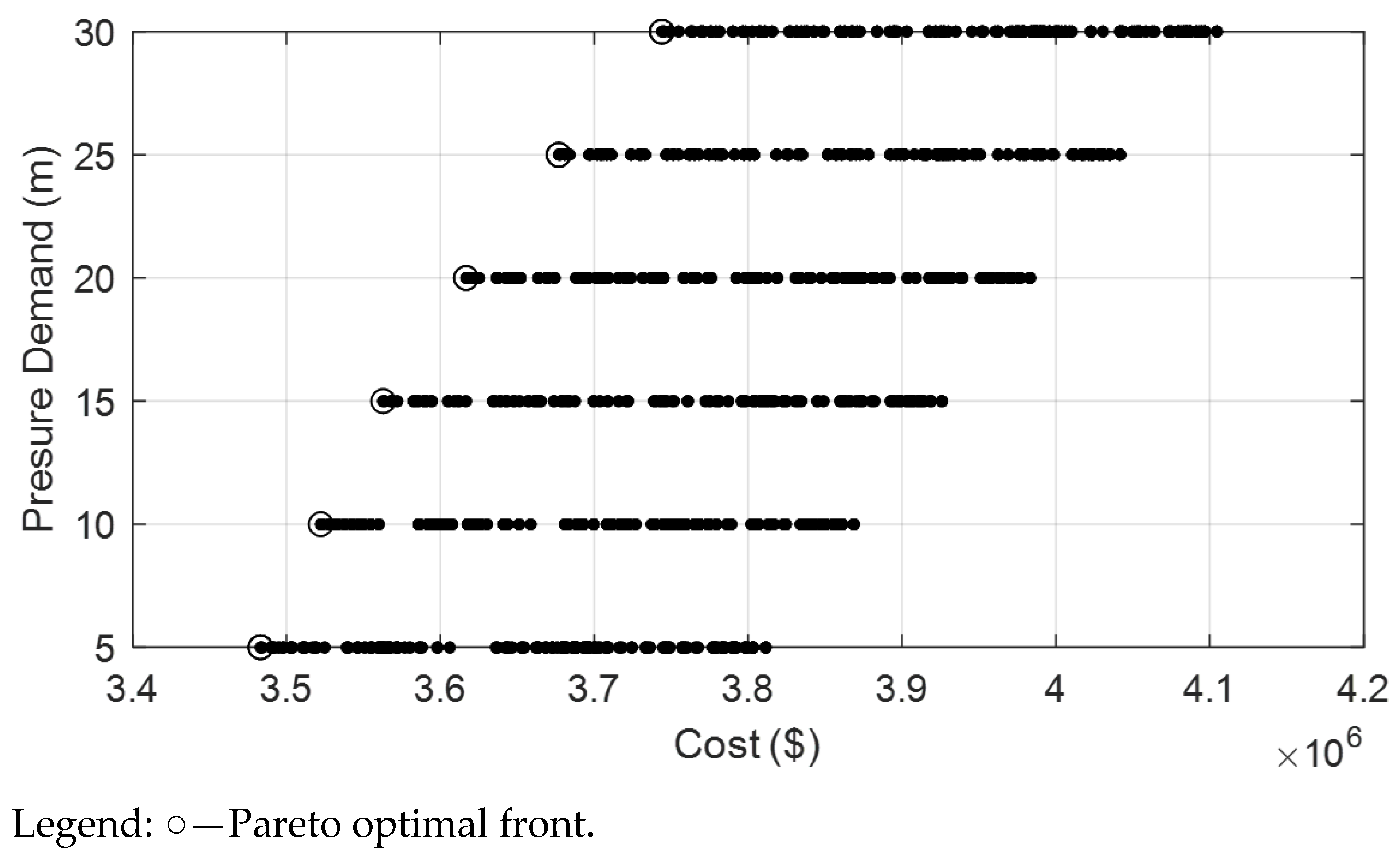
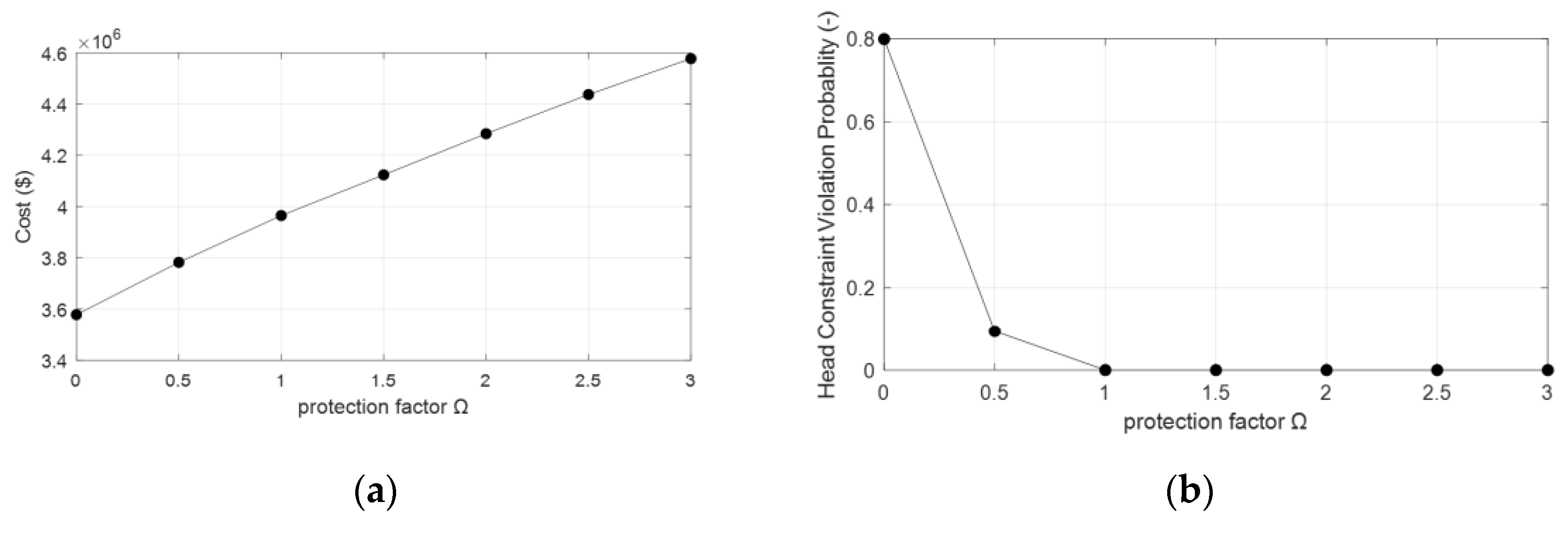
3. Results
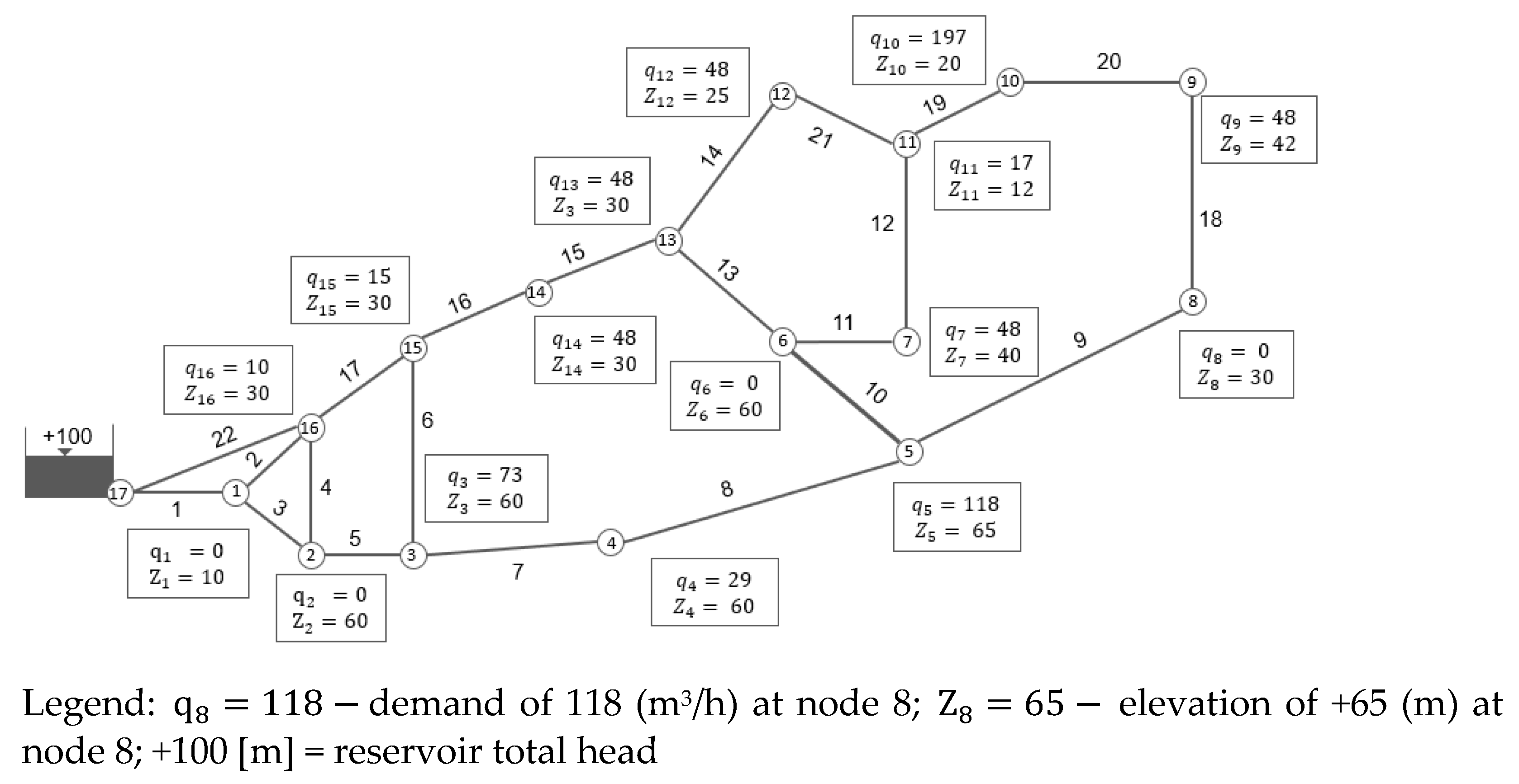
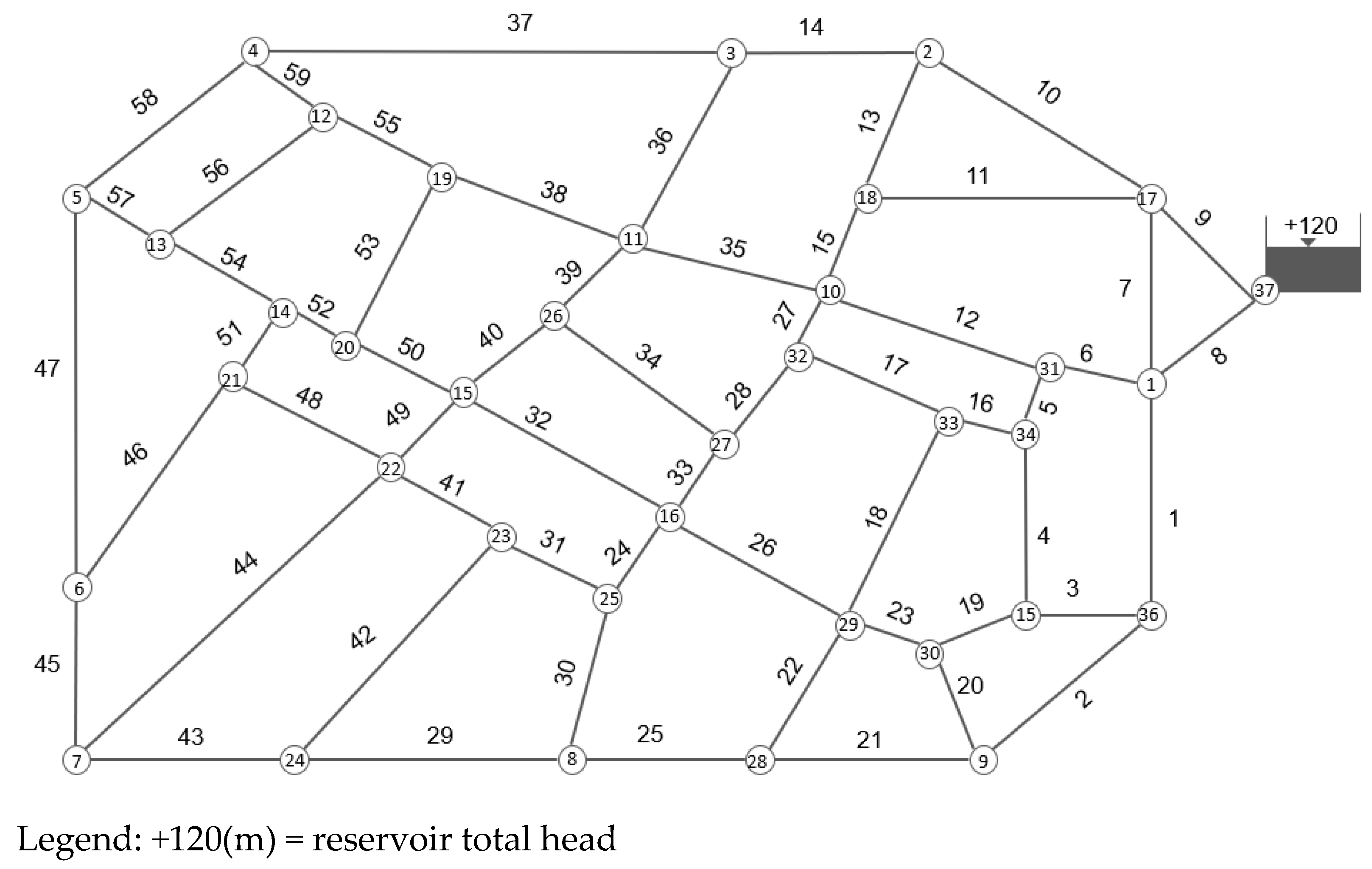
3.1. FOWM Distribution Network
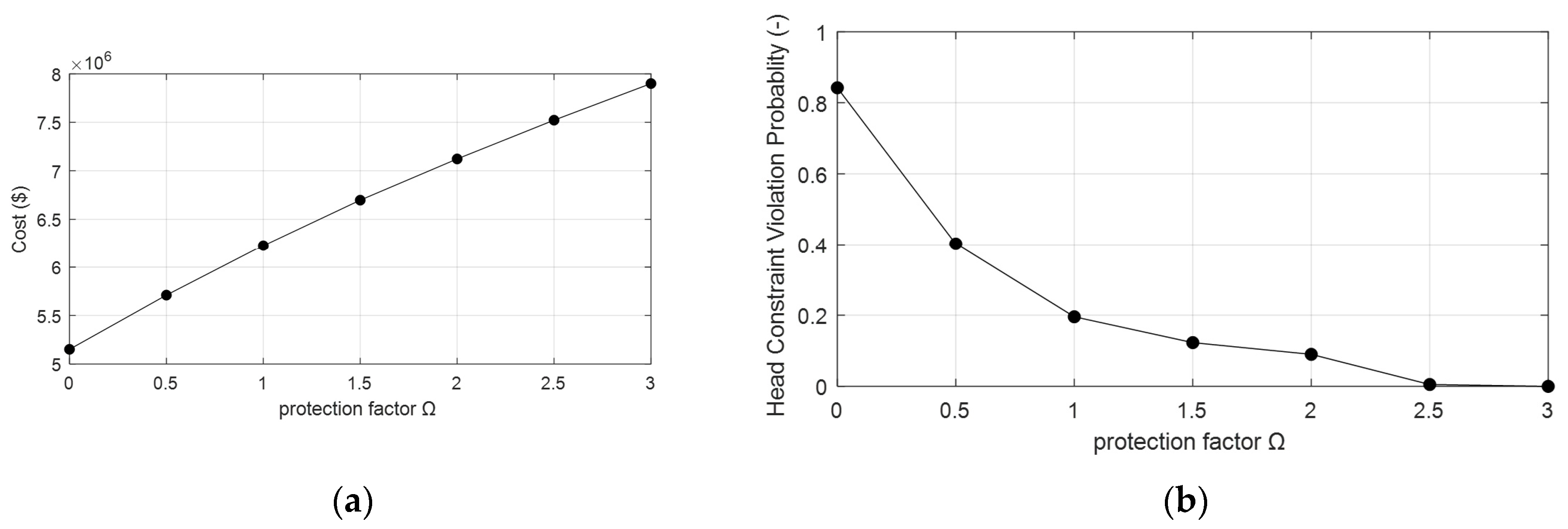
3.1.1. Uncorrelated Data Uncertainty
3.1.2. Correlated Data Uncertainty
3.2. Fossolo Distribution Network
3.2.1. Uncorrelated Data Model
3.2.2. Correlated Data Uncertainty
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Solution to a Subproblem
References
- Ormsbee, L.; Kessler, A. Optimal upgrading of hydraulic-network reliability. J. Water Resour. Plan. Manag. 1991, 116, 784–802. [Google Scholar] [CrossRef]
- Agrawal, M.L.; Gupta, R.; Bhave, P.R. Optimal Design of Level 1 Redundant Water Distribution Networks Considering Nodal Storage. J. Environ. Eng. 2007, 133, 319–330. [Google Scholar] [CrossRef]
- Rathi, S.; Gupta, R. Genetic Algorithm for Minimization of Variance of Pipe Flow-Series for Looped Water Distribution Networks. In Hydrological Modeling; Springer: Cham, Switzerland, 2022; pp. 205–219. [Google Scholar] [CrossRef]
- Yazdani, A.; Jeffrey, P. Applying Network Theory to Quantify the Redundancy and Structural Robustness of Water Distribution Systems. J. Water Resour. Plan Manag. 2012, 138, 153–161. [Google Scholar] [CrossRef]
- Rathi, S.; Gupta, R.; Palod, N.; Ormsbee, L. Minimizing the variance of flow series using a genetic algorithm for reliability-based design of looped water distribution networks. Eng. Optim. 2020, 52, 637–651. [Google Scholar] [CrossRef]
- Gupta, R.; Kakwani, N.; Ormsbee, L. Optimal Upgrading of Water Distribution Network Redundancy. J. Water Resour. Plan Manag. 2015, 141, 04014043. [Google Scholar] [CrossRef]
- Jung, D.; Kim, J.H. Water distribution system design to minimize costs and maximize topological and hydraulic reliability. J. Water Resour. Plan Manag. 2018, 144, 06018005. [Google Scholar] [CrossRef]
- Ostfeld, A.; Shamir, U. Design of optimal reliable multiquality water-supply systems. J. Water Resour. Plan. Manag. 1996, 122, 322–333. [Google Scholar] [CrossRef]
- Filion, Y.R.; Adams, B.J.; Karney, B.W. Stochastic design of water distribution systems with expected annual damages. J. Water Resour. Plan Manag. 2007, 133, 244–252. [Google Scholar] [CrossRef] [Green Version]
- Kapelan, Z.; Babayan, A.V.; Savic, D.A.; Walters, G.A.; Khu, S.T. Two new approaches for the stochastic least cost design of water distribution systems. Water Sci. Technol. Water Supply 2004, 4, 355–363. [Google Scholar] [CrossRef]
- Guistolisi, O.; Laucelli, D.; Colombo, A.F. Deterministic versus stochastic design of water distribution networks. J. Water Resour. Plan Manag. 2009, 135, 117–127. [Google Scholar] [CrossRef]
- Ben-Tal, A.; El Ghaoui, L.; Nemirovski, A. Robust Optimization; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Perelman, L.; Housh, M.; Ostfeld, A. Robust optimization for water distribution systems least cost design. Water Resour. Res. 2013, 49, 6795–6809. [Google Scholar] [CrossRef]
- Perelman, L.; Housh, M.; Ostfeld, A. Explicit demand uncertainty formulation for robust design of water distribution systems. In Proceedings of the World Environmental and Water Resources Congress 2013: Showcasing the Future, Cincinnati, OH, USA, 19–23 May 2013; pp. 684–695. [Google Scholar] [CrossRef]
- Itai, A.; Rodeh, M. Multi-Tree Approach To Reliability in Distributed Networks. Annu. Symp. Comput. Sci. 1984, 79, 43–59. [Google Scholar]
- Takeaki, U.N.O. An algorithm for enumerating all directed spanning trees in a directed graph. In International Symposium on Algorithms and Computation; Lect Notes Comput Sci (Including Subser Lect Notes Artif Intell Lect Notes Bioinformatics); Springer: Berlin/Heidelberg, Germany, 1996; Volume 1178, pp. 167–173. [Google Scholar] [CrossRef]
- Geen, Z.W. Multiobjective Optimization of Water Distribution Networks Using Fuzzy Theory and Harmony Search. Water 2015, 7, 3613–3625. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayelom, A.; Ostfeld, A. Network Subsystems for Robust Design Optimization of Water Distribution Systems. Water 2022, 14, 2443. https://doi.org/10.3390/w14152443
Hayelom A, Ostfeld A. Network Subsystems for Robust Design Optimization of Water Distribution Systems. Water. 2022; 14(15):2443. https://doi.org/10.3390/w14152443
Chicago/Turabian StyleHayelom, Assefa, and Avi Ostfeld. 2022. "Network Subsystems for Robust Design Optimization of Water Distribution Systems" Water 14, no. 15: 2443. https://doi.org/10.3390/w14152443
APA StyleHayelom, A., & Ostfeld, A. (2022). Network Subsystems for Robust Design Optimization of Water Distribution Systems. Water, 14(15), 2443. https://doi.org/10.3390/w14152443






