IrrigTool—A New Tool for Determining the Irrigation Rate Based on Evapotranspiration Estimated by the Thornthwaite Equation
Abstract
:1. Introduction
2. Methodology
- (m3/ha)—the minimum water reserve in the soil, corresponding to the wilting point, at the depth H,
- (m3/ha)—the maximum water reserve in the soil, corresponding to the water field capacity, at the depth H,
- DAH (t/m3)—the soil bulk density corresponding to the depth H,
- (%)—the water field capacity corresponding to the depth H,
- (%)—the wilting coefficient corresponding to the depth H.
- (t/m3)—the soil bulk density corresponding to the depth h,
- (%)—the water field capacity corresponding to the depth h.
- (%)—the minimum moisture level, defined as the limit under which the soil humidity should not decrease for ensuring normal conditions for the plant growth. It is computed at the depth h by [34]:
- The water reserve in soil must be lower than () in the cold (vegetation) season. When it is higher, the quantity that exceeds the above limits is considered lost by infiltration and cannot be used by plants;
- In the cold period, the water reserve can decrease without limitation except for the crops subject to water provision.
- In the vegetation period, the water reserve cannot decrease under If the reserve decreases under this value, watering must be applied.
- (a)
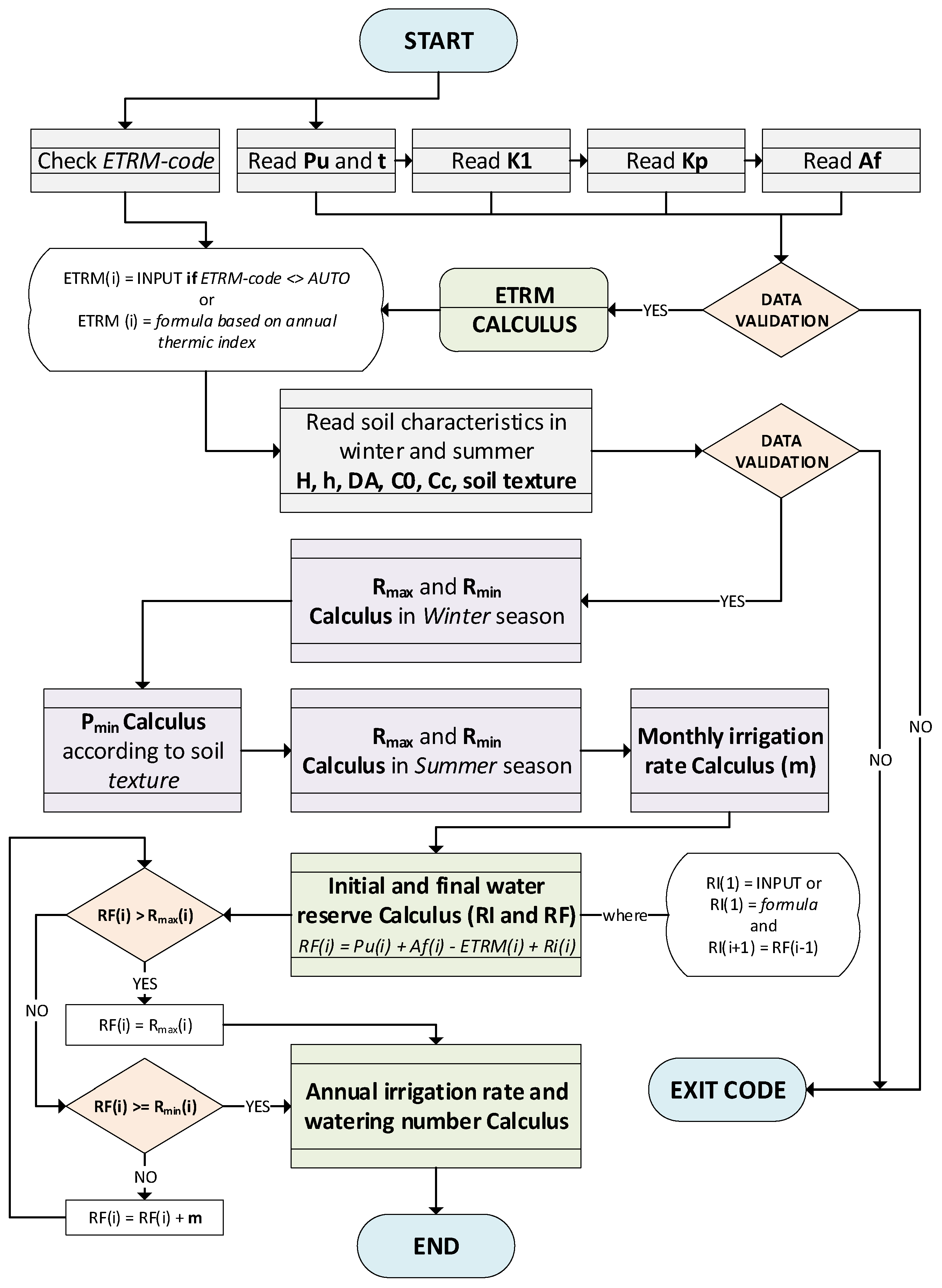
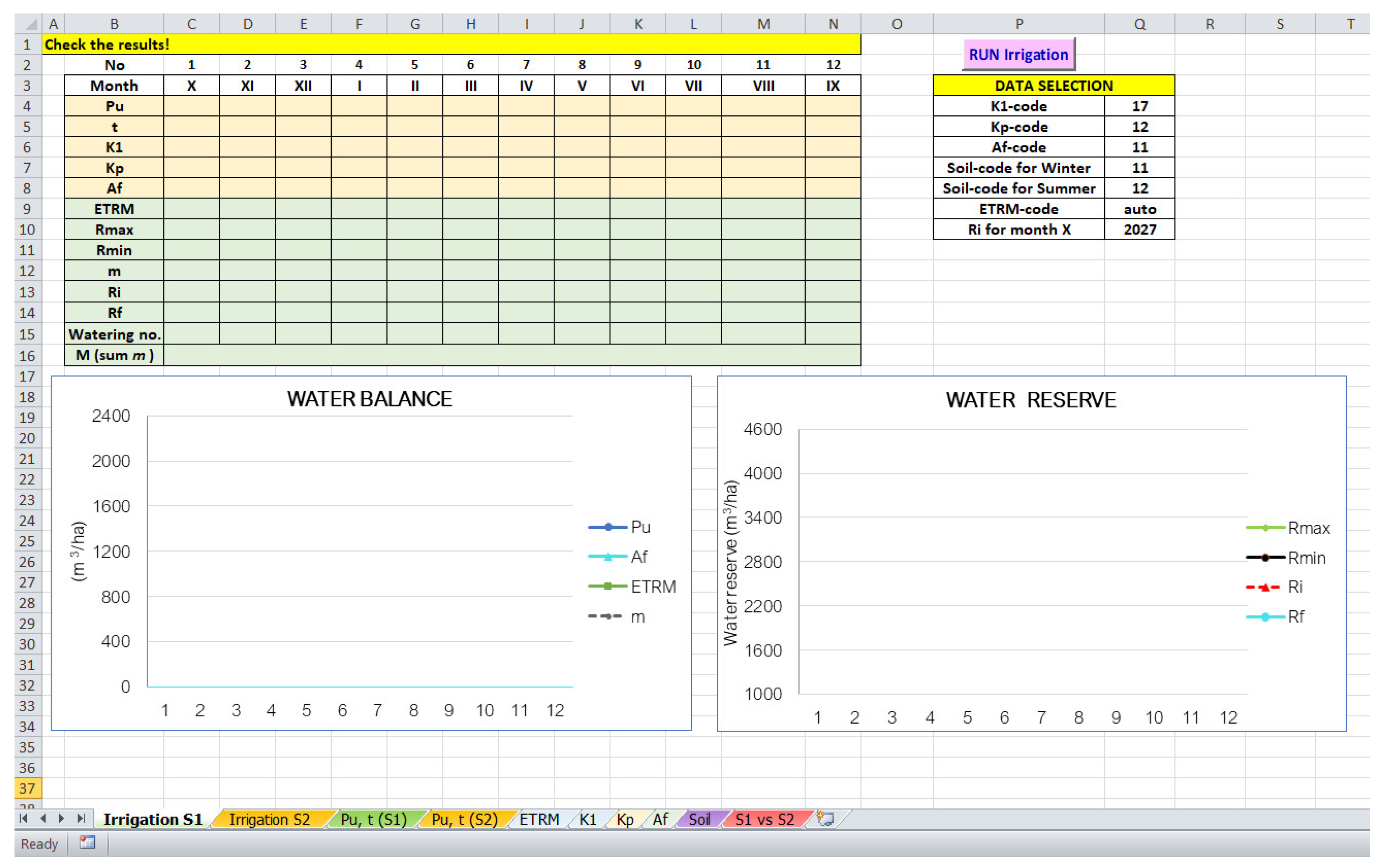
- Input data from the Excel files where they have been previously introduced. They are: monthly precipitation (Pu in the flowchart) and temperature series (t– in the flowchart), the series of the monthly coefficients K1 and Kp, and the series.The input data are validated by checking if the cells are filled in with numerical values. If not, the algorithm stops. Otherwise, it passes to the next step, as follows:
- (b)
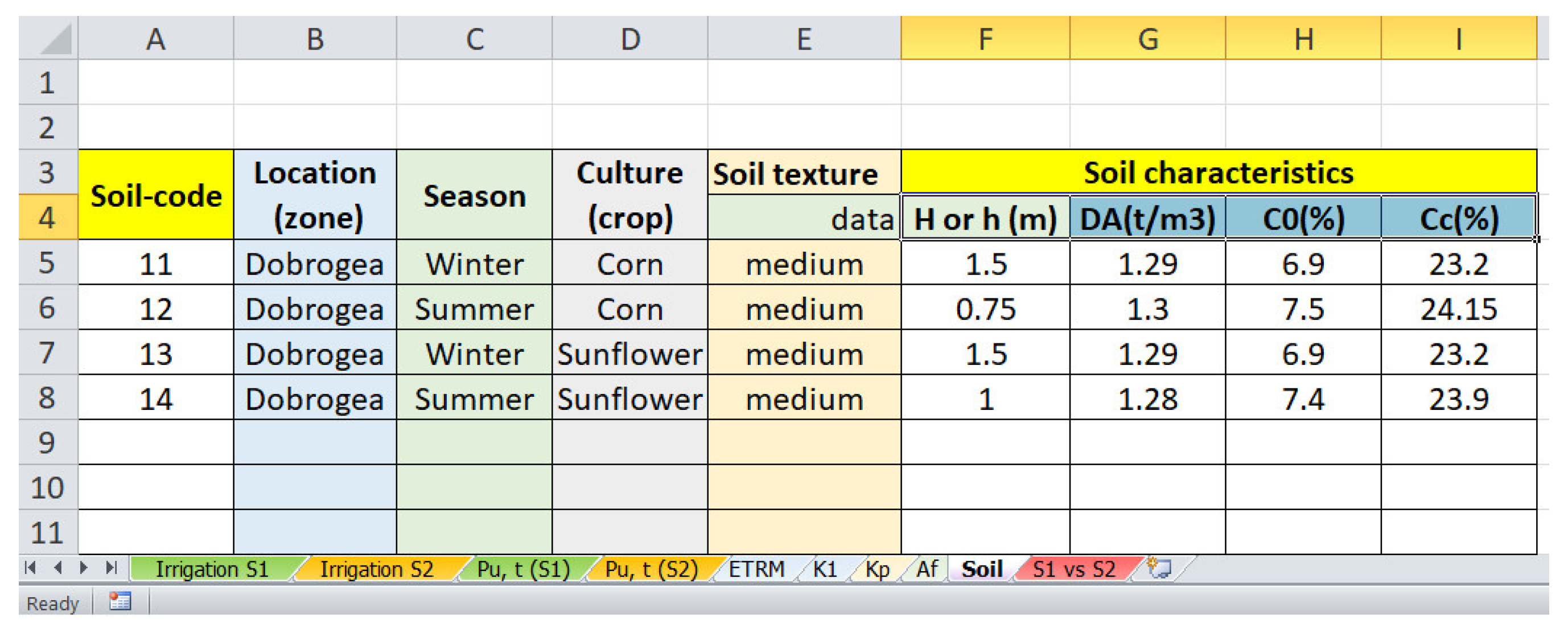
- Read the soil characteristics, namely H, h, DA, , and corresponding to h and H from the worksheets where they were previously introduced. If all the values are numerical, and none is absent, the algorithm passes to step (c). Otherwise, it stops.
- (c)
- Compute and for winter;
- (d)
- Compute ;
- (e)
- Compute and for summer;
- (f)
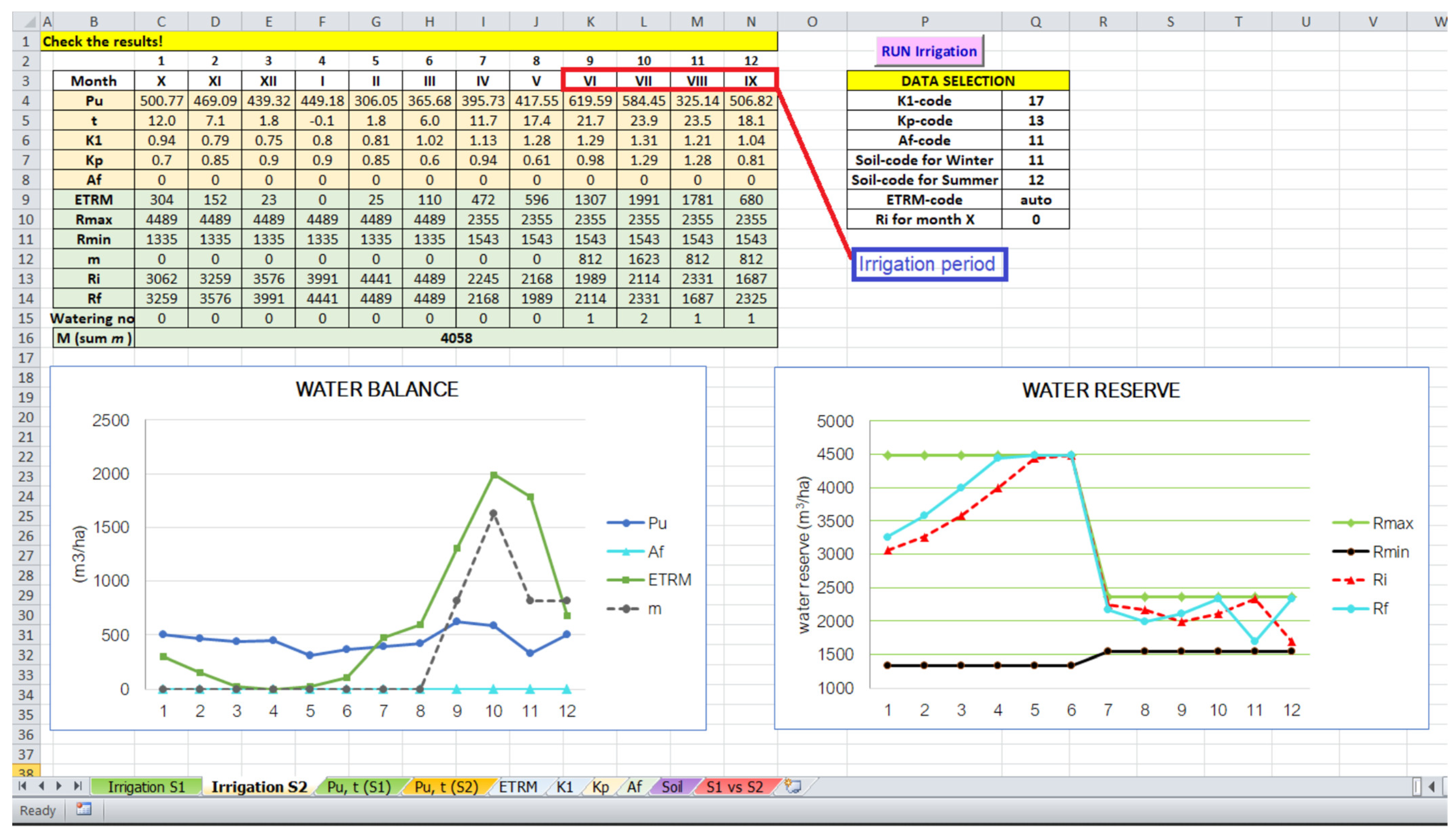
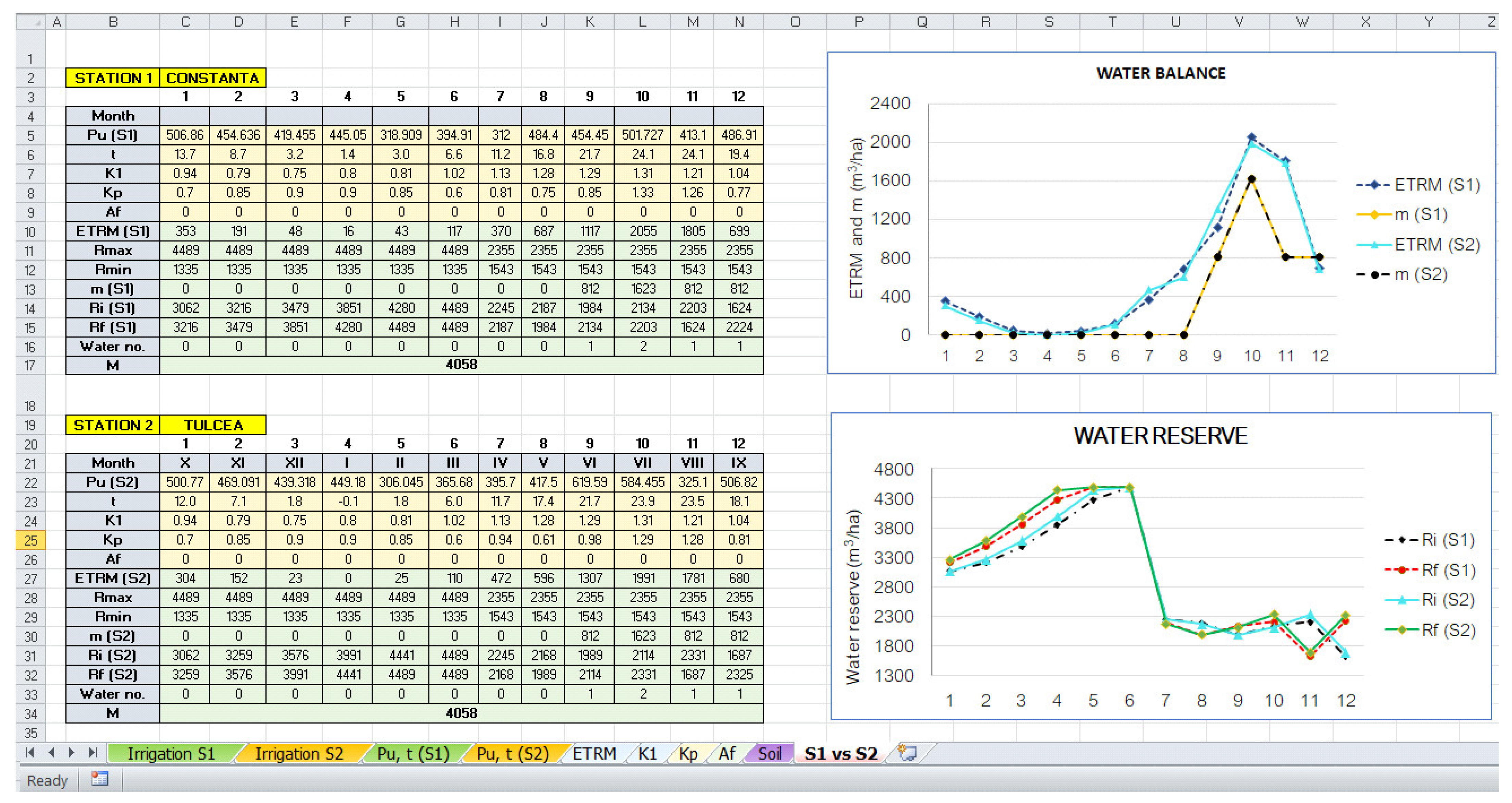
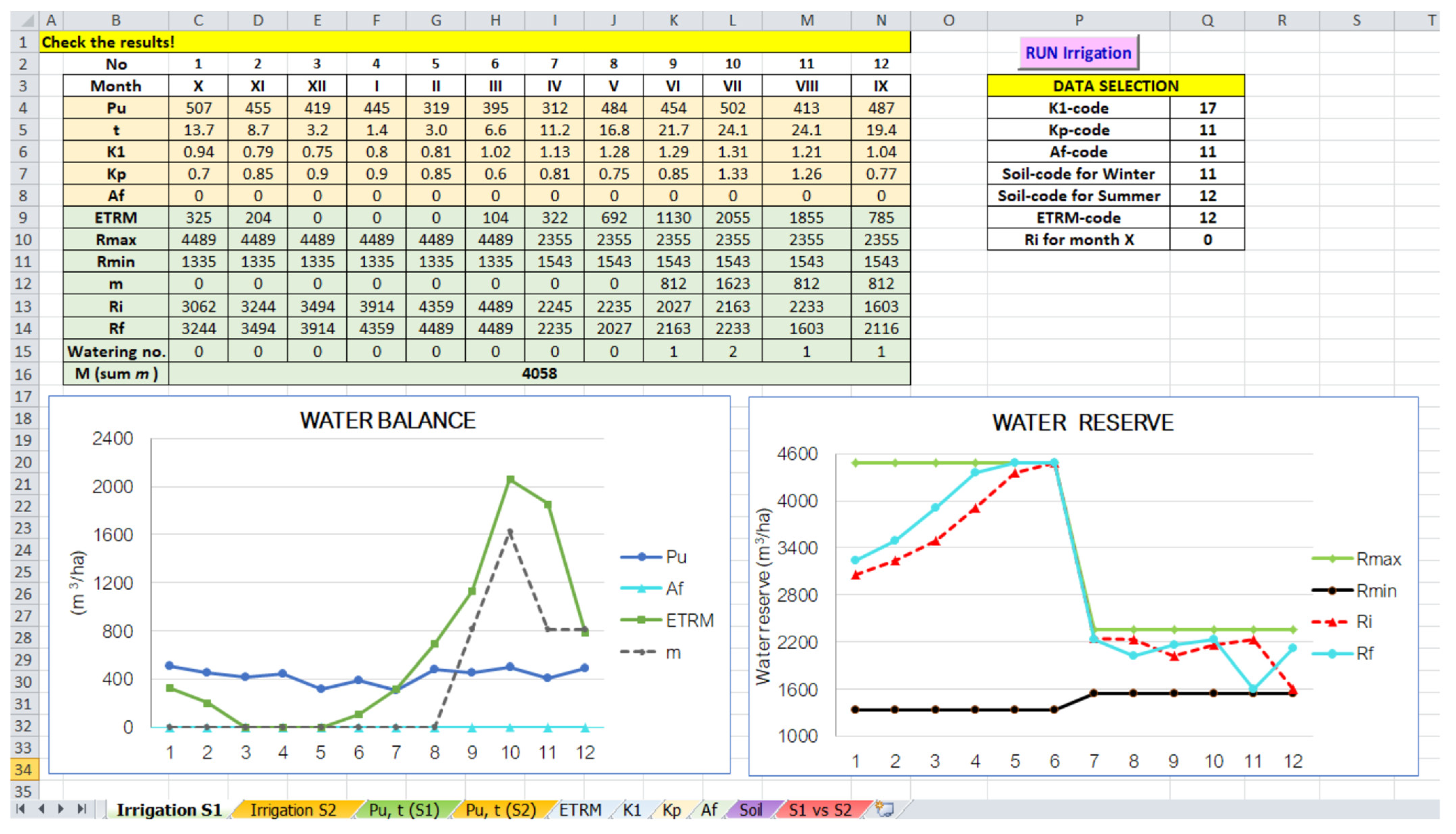
- Compute the monthly irrigation rate;
- (g)
- Compute the initial and final water reserve for each month;
- (h)
- Compute the water application rate and the annual irrigation rate;
- (i)
- Display the results and the graphical representation.
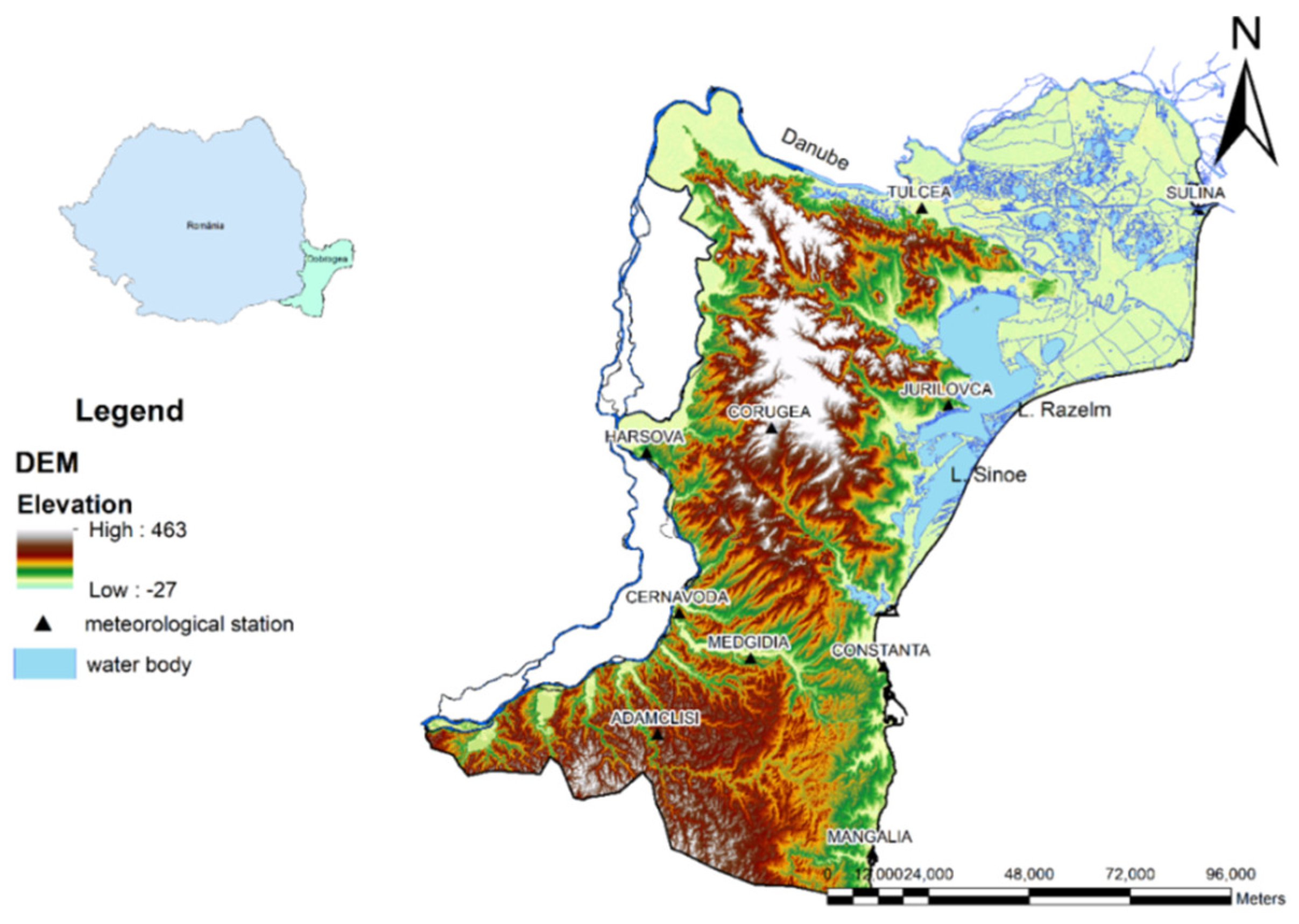
3. Data Series
4. Implementation
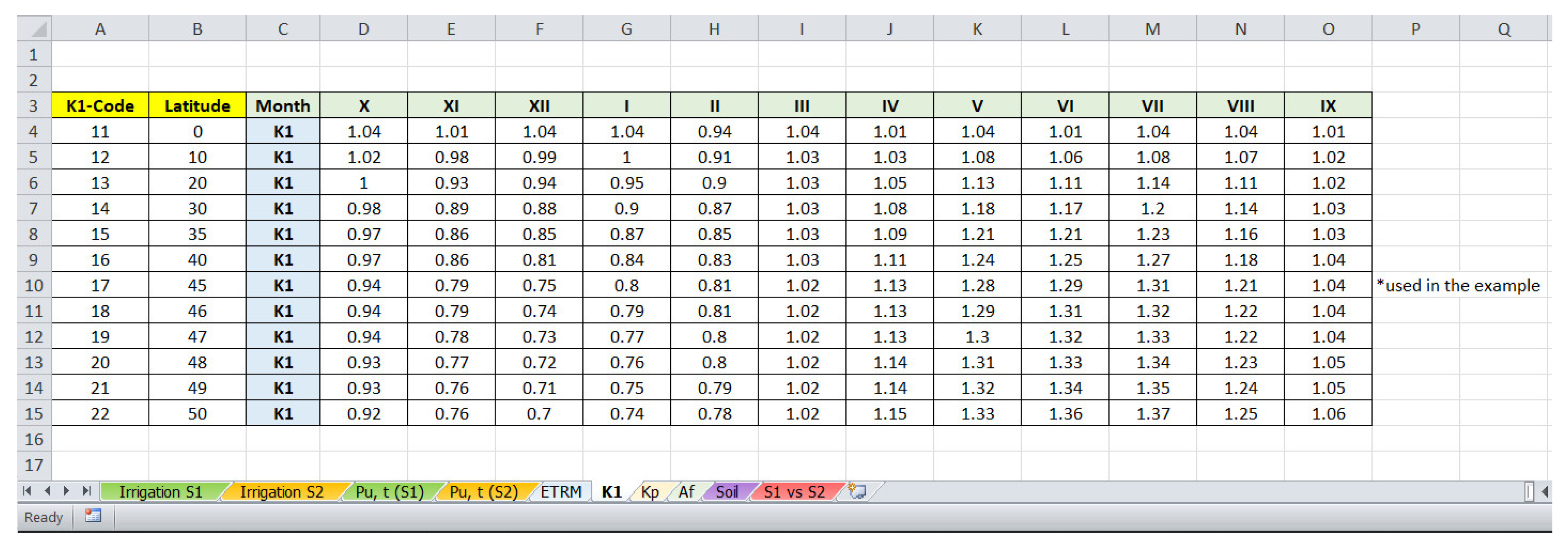
- − in Q4—a code selected from the first column of the worksheet “K1”;
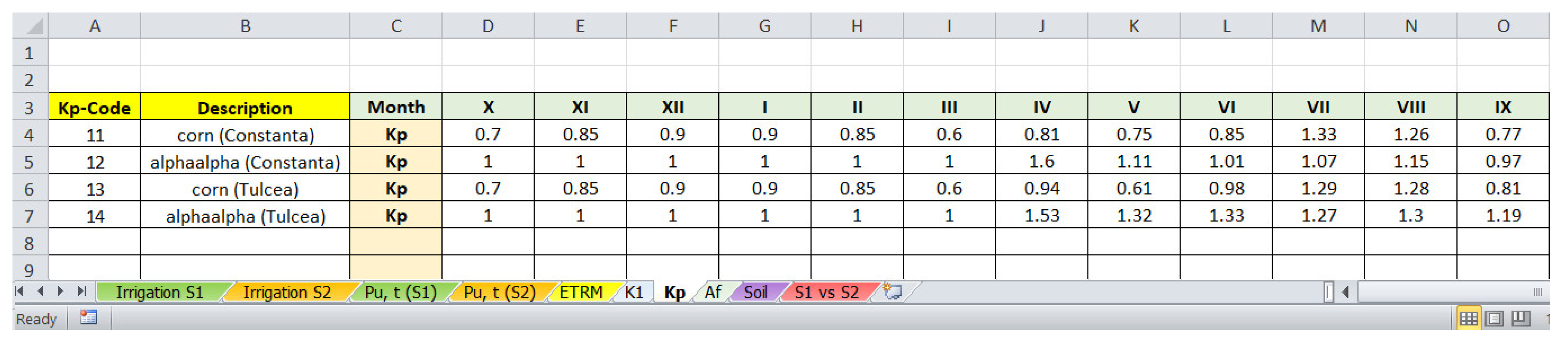
- − in Q5—a code selected from the first column of the worksheet “Kp”;
- − in Q6—a code selected from the first column of the worksheet “Af”;
- − in Q7—a code selected from the first column of the worksheet “Soil” corresponding to the winter season;
- − in Q8—a code selected from the first column of the worksheet “Soil” corresponding to the summer season;
- − in Q9—a code selected from the first column of the worksheet “ETRM” or “auto”;
- − in Q10—"0” or a value selected by the user.
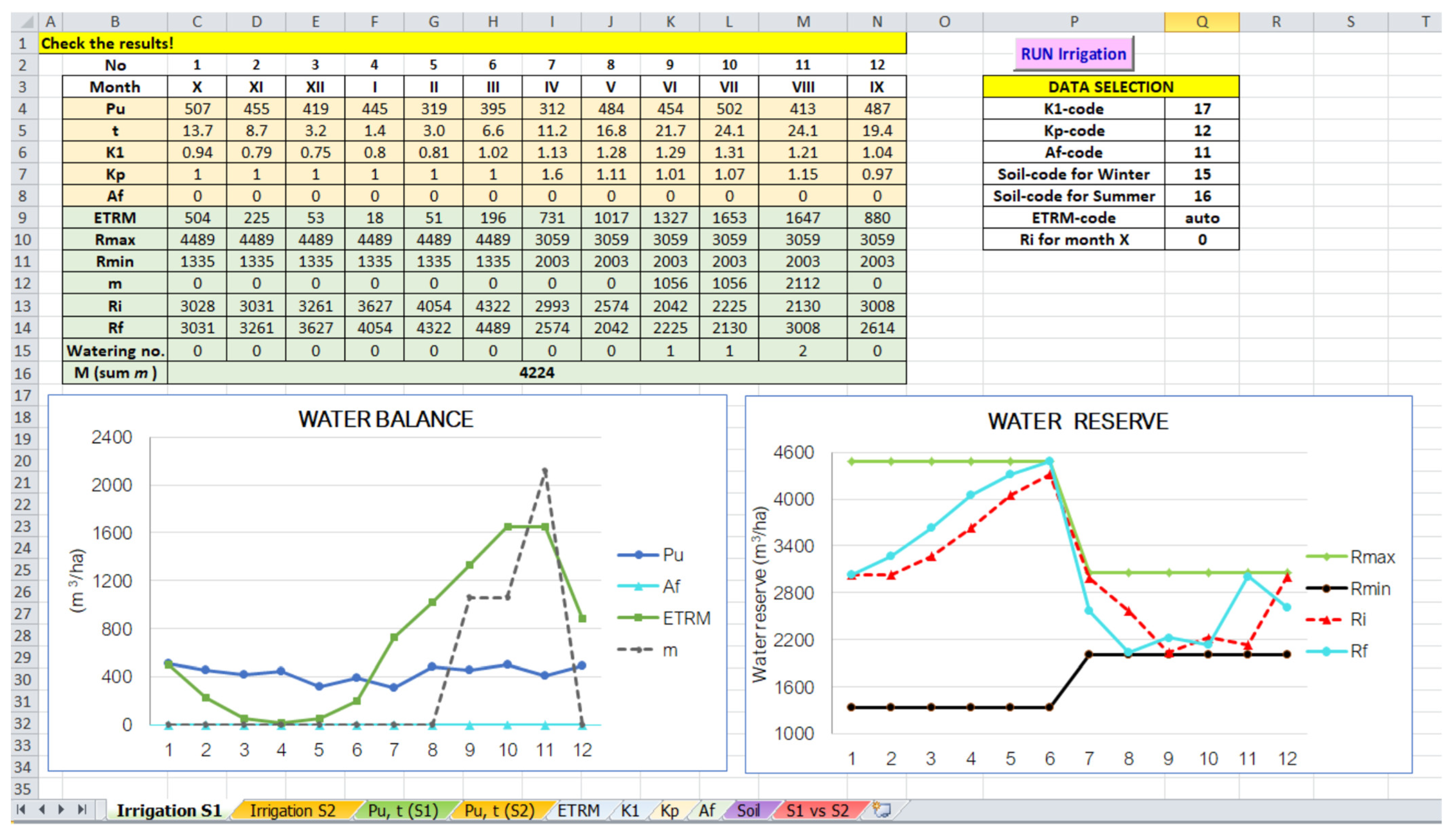
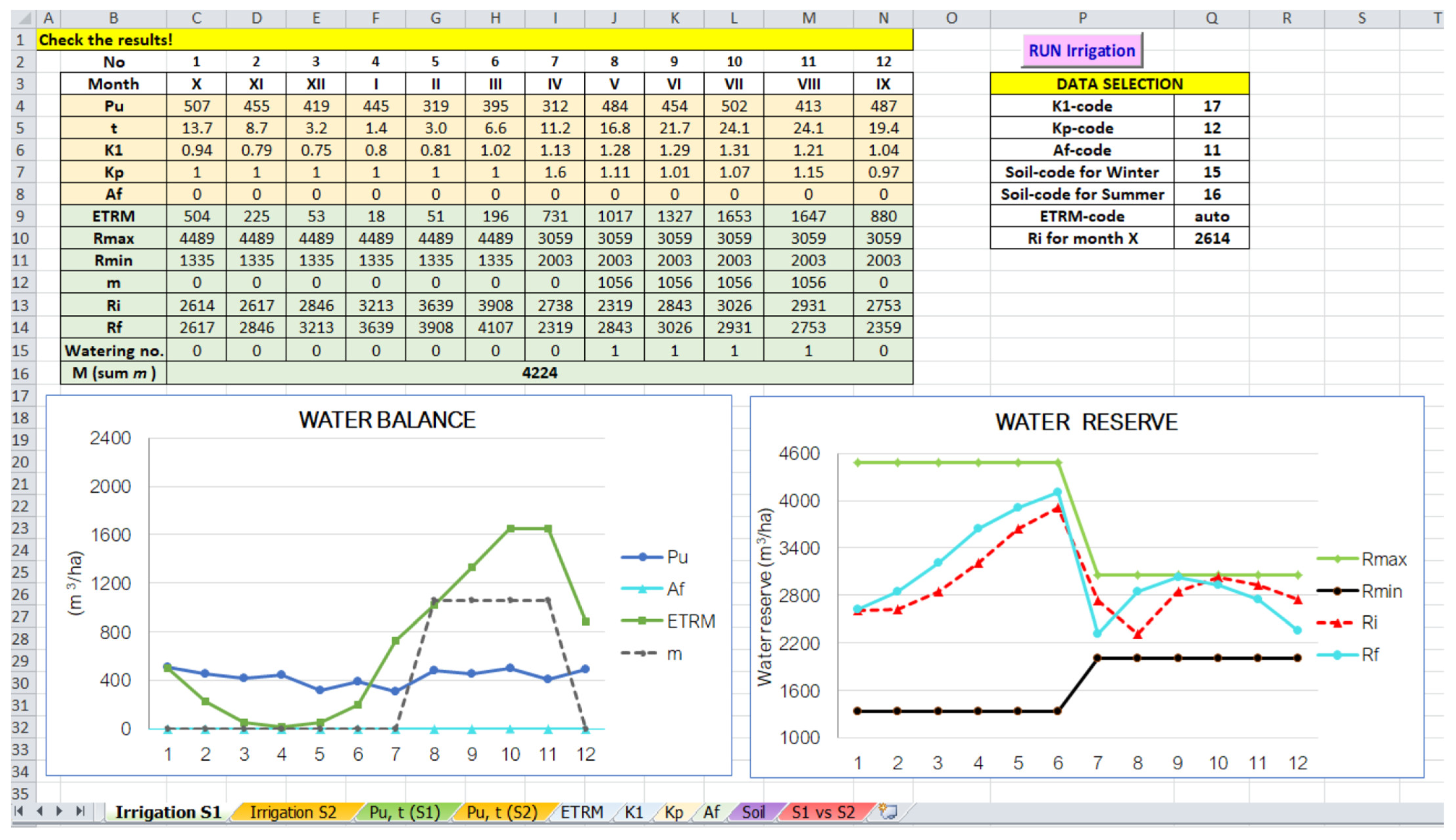
5. Results
6. Discussion
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bărbulescu, A.; Dumitriu, C.Ș. Assessing the water quality by statistical methods. Water 2021, 13, 1026. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Nazzal, Y.; Howari, F. Assessing the groundwater quality in the Liwa area, the United Arab Emirates. Water 2020, 12, 2816. [Google Scholar] [CrossRef]
- Gómez, V.M.R.; Gutiérrez, M.; Haro, B.N.; López, D.N.; Herrera, M.T.A. Groundwater quality impacted by land use/land cover change in a semiarid region of Mexico. Groundw. Sustain. Dev. 2017, 5, 160–167. [Google Scholar] [CrossRef]
- Towards a Water and Food Secure Future. Critical Perspectives for Policy-Makers, Food and Agriculture Organization of The United Nations Rome. Revised Reprint World Water Council Marseille. 2015. Available online: http://www.fao.org/3/i4560e/i4560e.pdf (accessed on 9 October 2021).
- United Nations World Water Assessment Programme. The United Nations World Water Development Report 2015: Water for a Sustainable World; UNESCO: Paris, French, 2015; Available online: http://www.unesco.org/new/en/natural-sciences/environment/water/wwap/wwdr/2015-water-for-a-sustainable-world/ (accessed on 9 October 2021).
- Hargreaves, G.H.; Riley, J.P.; Sikka, A. Influence of climate on Irrigation. Can. Water Resour. J. 1993, 18, 53–59. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Li, J.; Gao, L.; Tian, Y. Irrigation has more influence than fertilization on leaching water quality and the potential environmental risk in excessively fertilized vegetable soils. PLoS ONE 2018, 13, e0204570. [Google Scholar] [CrossRef] [PubMed]
- Haddeland, I.; Lettenmaier, D.P.; Skaugen, T. Effects of irrigation on the water and energy balances of the Colorado and Mekong river basins. J. Hydrol. 2006, 324, 210–223. [Google Scholar] [CrossRef]
- de Rosnay, P.; Polcher, J.; Laval, K.; Sabre, M. Integrated parameterization of irrigation in the land surface model ORCHIDEE: Validation over Indian Peninsula. Geophys. Res. Lett. 2003, 30, 1986. [Google Scholar] [CrossRef]
- Lobell, D.; Bala, G.; Mirin, A.; Phillips, T.; Maxwell, R.; Rotman, R. Regional Differences in the Influence of Irrigation on Climate. J. Clim. 2009, 22, 2248–2255. [Google Scholar] [CrossRef]
- Schaible, G.D.; Aillery, M.P. Water Conservation in Irrigated Agriculture: Trends and Challenges in the Face of Emerging Demands. Econ. Inform. Bull. 2012, 99, 67. Available online: https://www.ers.usda.gov/publications/pub-details/?pubid=44699 (accessed on 20 September 2021). [CrossRef] [Green Version]
- Huang, Q.; Xu, Y.; Kovacs, K.; West, G. Analysis of factors that influence the use of irrigation technologies and water management practices in Arkansas. J. Agric. Appl. Econ. 2017, 49, 159–185. [Google Scholar] [CrossRef] [Green Version]
- Henggeler, J. Software Programs Currently Available for Irrigation Scheduling. Available online: https://www.irrigation.org/IA/FileUploads/IA/Resources/TechnicalPapers/2002/SoftwareProgramsCurrentlyAvailableForIrrigationScheduling.pdf (accessed on 9 October 2021).
- Bos, M.G.; Kselik, R.A.L.; Allen, R.G.; Molden, D.J. Water Requirements for Irrigation and the Environment; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- CRIWAR 3.0. Available online: https://www.bos-water.nl/links-downloads (accessed on 10 July 2022).
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56, FAO—Food and Agriculture Organization of the United Nations Rome. 1998. Available online: http://www.fao.org/3/x0490e/x0490e00.htm (accessed on 9 October 2021).
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. FAO Irrigation and Drainage Paper no. 56, Evapotranspiration (Guidelines for Computing Crop Water Requirements). Available online: http://www.climasouth.eu/sites/default/files/FAO%2056.pdf (accessed on 10 May 2021).
- Raes, D. The ETo Calculator. Evapotranspiration from a Reference Surface. Available online: https://www.ipcinfo.org/fileadmin/user_upload/faowater/docs/ReferenceManualV32.pdf (accessed on 8 May 2021).
- Penman-Montieth, E.T. Worksheet with Solar Estimate and Equation Instructions. Available online: https://extension.umaine.edu/blueberries/factsheets/irrigation/penman-montieth-et-worksheet-with-solar-estimate/ (accessed on 8 May 2021).
- CROPWAT 8.0 for Windows. Available online: https://www.fao.org/land-water/databases-and-software/cropwat/en/ (accessed on 5 May 2021).
- Donker, N.H.W. WTRBLN: A computer program to calculate water balance. Comput. Geosci. 1987, 13, 95–122. [Google Scholar] [CrossRef]
- Sellinger, C.E. Computer Program for Estimating Evapotranspiration Using the Thornthwaite Method. In NOAA Technical Memorandum ERL GLERL-101; United States Department of Commerce: Washington, DC, USA, 1996. [Google Scholar]
- Armiraglio, S.; Cerabolini, B.; Gandellini, F.; Gandini, P.; Andreis, C. Calcolo informatizzato del bilancio idrico del suolo. Nat. Bresciana. Ann. Mus. Civ. Sci. Nat. Brescia 2003, 33, 209–216. [Google Scholar]
- McCabe, G.J.; Markstrom, S.L. A Monthly Water-Balance Model Driven by A Graphical User Interface; Open-File Report 2007-1088; U.S. Geological Survey: Reston, VA, USA, 2007; 6p. [CrossRef] [Green Version]
- Mammoliti, E.; Fronzi, D.; Mancini, A.; Valigi, D.; Tazioli, A. WaterbalANce, a WebApp for Thornthwaite–Mather water balance computation: Comparison of applications in two European watersheds. Hydrology 2021, 8, 34. [Google Scholar] [CrossRef]
- Droogers, P.; Immerzeel, W.W.; Lorite, I.J. Estimating actual irrigation application by remotely sensed evapotranspiration observations. Agric. Water Manag. 2010, 97, 1351–1359. [Google Scholar] [CrossRef]
- Olivera-Guerra, L.; Merlin, O.; Er-Raki, S. Irrigation retrieval from Landsat optical/thermal data integrated into a crop water balance model: A case study over winter wheat fields in a semi-arid region. Remote Sens. Environ. 2020, 239, 111627. [Google Scholar] [CrossRef] [Green Version]
- Brocca, L.; Tarpanelli, A.; Filippucci, P.; Dorigo, W.; Zaussinger, F.; Gruber, A.; Fernández-Prieto, D. How much water is used for irrigation? A new approach exploiting coarse resolution satellite soil moisture products. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 752–766. [Google Scholar] [CrossRef]
- Bretreger, D.; Yeo, I.Y.; Hancock, G. Quantifying irrigation water use with remote sensing: Soil water deficit modelling with uncertain soil parameters. Agric. Water Manag. 2022, 260, 107299. [Google Scholar] [CrossRef]
- Foster, T.; Mieno, T.; Brozović, N. Satellite-Based monitoring of irrigation water use: Assessing measurement errors and their implications for agricultural water management policy. Water Resour. Resear. 2020, 56, e2020WR028378. [Google Scholar] [CrossRef]
- CAWATERinfo. Irrigation and Water Application Rate. Available online: http://www.cawater-info.net/bk/4-2-1-1-3-3_e.htm (accessed on 7 June 2022).
- Roșu, L. Land Ameliorations; Ovidius University Press: Constanta, Romania, 1999. (In Romanian) [Google Scholar]
- Pleșa, I.; Florescu, G.; Mușat, I. Land Amelioration; Editura Didactică și Pedagogică: Bucharest, Romania, 1967. (In Romanian) [Google Scholar]
- Ștefan, V.; Bechet, S.; Tomiță, O.; Titz, L. Land Amelioration; Editura Didactică și Pedagogică: Bucharest, Romania, 1981. (In Romanian) [Google Scholar]
- Cismaru, C.; Gabor, V. Irrigation. Arrangements, Rehabilitations and Modernizations; Editura POLITEHNIUM: Iasi, Romania, 2004. (In Romanian) [Google Scholar]
- Cazacu, E.; Dorobantu, M.; Georgescu, I.; Sarbu, E. Irrigations Arrangements; Ceres: Bucharest, Romania, 1982. (In Romanian) [Google Scholar]
- Bărbulescu, A. Models for temperature evolution in Constanta area (Romania). Rom. J. Phys. 2016, 61, 676–686. [Google Scholar]
- Bărbulescu, A.; Deguenon, J. About the variations of precipitation and temperature evolution in the Romanian Black Sea Littoral. Rom. Rep. Phys. 2015, 67, 625–637. [Google Scholar]
- Bărbulescu, A.; Dumitriu, C.S.; Maftei, C. On the Probable Maximum Precipitation Method. Rom. J. Phys. 2022, 67, 801. [Google Scholar]
- Bărbulescu, A.; Maftei, C. Statistical approach of the behavior of Hamcearca River (Romania). Rom. Rep. Phys. 2021, 73, 703. [Google Scholar]
- Maftei, C.; Bărbulescu, A.; Rugină, S.; Nastac, C.D.; Dumitru, I.M. Analysis of the arbovirosis potential occurence in Dobrogea, Romania. Water 2021, 13, 374. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Maftei, C.; Dumitriu, C. The modeling of the climatic process that participates at the sizing of an irrigation system. Appl. Comput. Math. 2002, 2048, 11–20. [Google Scholar]
- Halford Tools. Available online: https://halfordhydrology.com/tools/ (accessed on 29 June 2022).
- GR2M Model. Available online: https://webgr.inrae.fr/en/models/monthly-model-gr2m/ (accessed on 29 June 2022).
- GR4J_FR. Available online: https://webgr.inrae.fr/modeles/journalier-gr4j-2/ (accessed on 29 June 2022).
- Niazkar, M. An Excel VBA-based educational module for bed roughness predictors. Comput. Appl. Eng. Educ. 2021, 29, 1051–1060. [Google Scholar] [CrossRef]
- Miller, S. Handbook for Agrohydrology; Natural Resources Institute: London, UK, 1994; Available online: http://www.nzdl.org/cgi-bin/library.cgi?e=d-00000-00---off-0hdl--00-0----0-10-0---0---0direct-10---4-------0-1l--11-en-50---20-about---00-0-1-00-0-0-11-1-0utfZz-8-00&cl=CL3.37&d=HASH3b4d99e5f9716ab628b9b2>=2 (accessed on 7 June 2022).
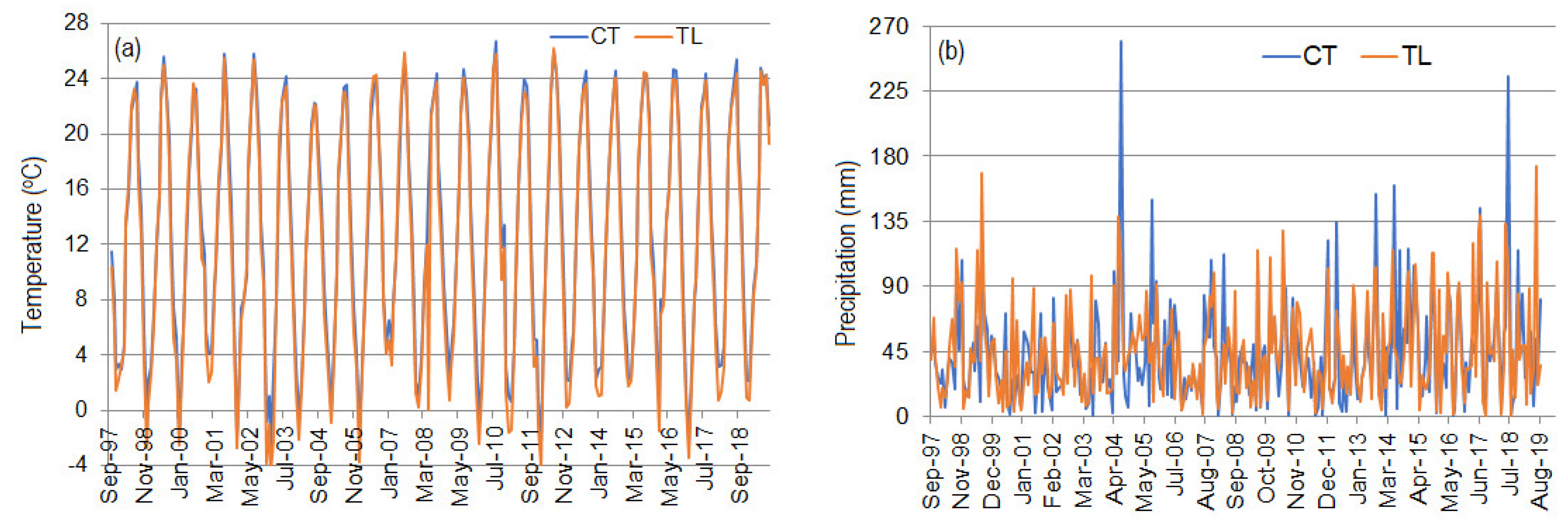




| Series | Max | Min | Mean | Median | Std. Dev. | Coef. of Variation | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|
| CT precipitation | 259.20 | 0.30 | 43.27 | 36.00 | 36.53 | 0.84 | 1.96 | 6.95 |
| TL precipitation | 173.00 | 0.00 | 44.83 | 37.35 | 33.91 | 0.76 | 1.06 | 0.85 |
| CT temperature | 26.70 | −0.20 | 12.83 | 12.60 | 8.17 | 0.64 | −0.03 | −1.29 |
| TL temperature | 26.20 | −4.50 | 12.08 | 11.65 | 8.60 | 0.71 | −0.06 | −1.28 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dumitriu, C.Ș.; Bărbulescu, A.; Maftei, C.E. IrrigTool—A New Tool for Determining the Irrigation Rate Based on Evapotranspiration Estimated by the Thornthwaite Equation. Water 2022, 14, 2399. https://doi.org/10.3390/w14152399
Dumitriu CȘ, Bărbulescu A, Maftei CE. IrrigTool—A New Tool for Determining the Irrigation Rate Based on Evapotranspiration Estimated by the Thornthwaite Equation. Water. 2022; 14(15):2399. https://doi.org/10.3390/w14152399
Chicago/Turabian StyleDumitriu, Cristian Ștefan, Alina Bărbulescu, and Carmen Elena Maftei. 2022. "IrrigTool—A New Tool for Determining the Irrigation Rate Based on Evapotranspiration Estimated by the Thornthwaite Equation" Water 14, no. 15: 2399. https://doi.org/10.3390/w14152399