Influence of Selected Environmental Factors on Diatom β Diversity (Bacillariophyta) and the Value of Diatom Indices and Sampling Issues
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Chemical and Physical Data
2.3. Diatom Data
2.4. Statistical Data
2.4.1. β Diversity of Diatoms
2.4.2. Seasonal Differences, Between-Lake Differences, and Effectiveness of Indices
2.5. Spatial Diversity
3. Results
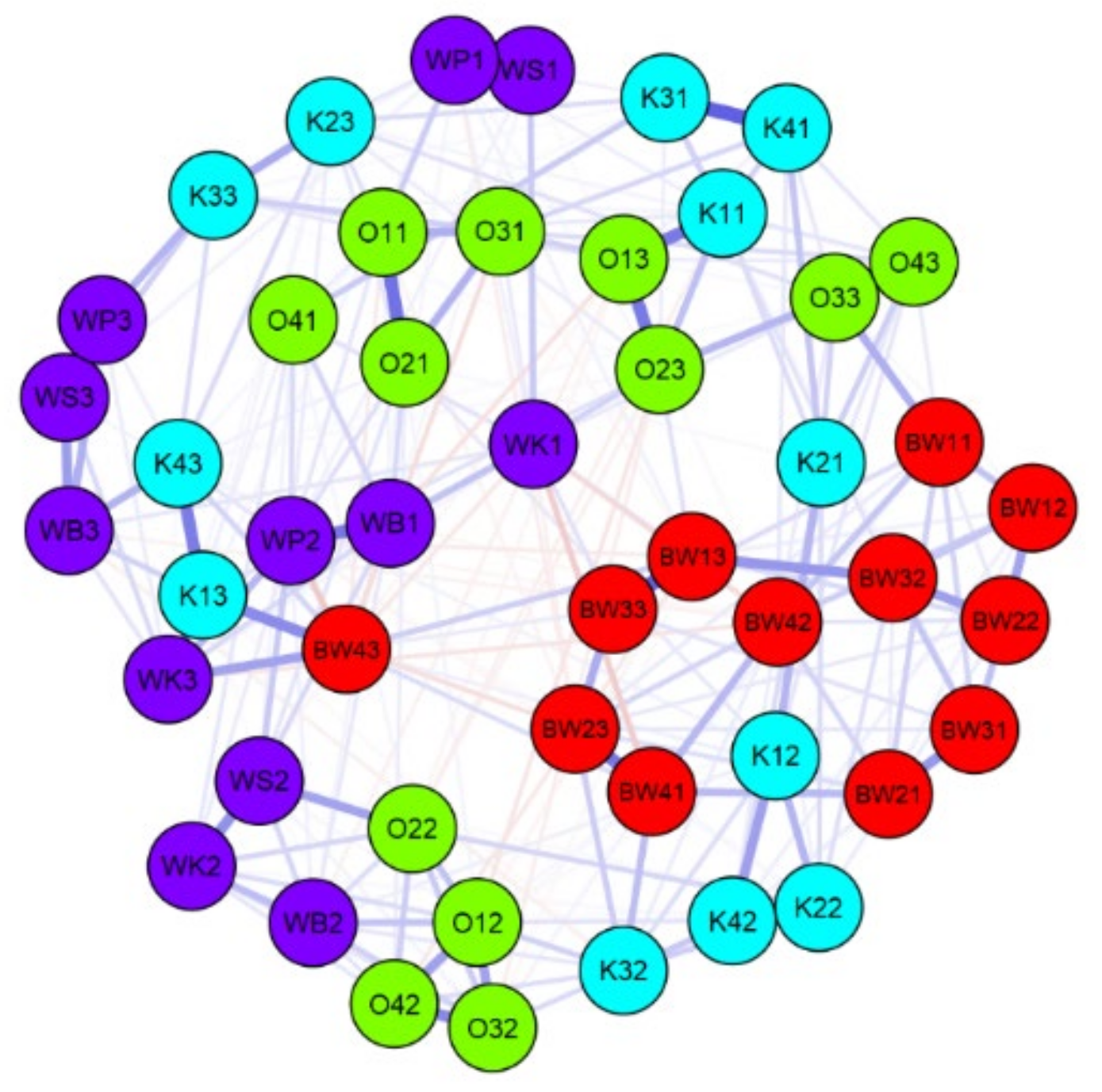
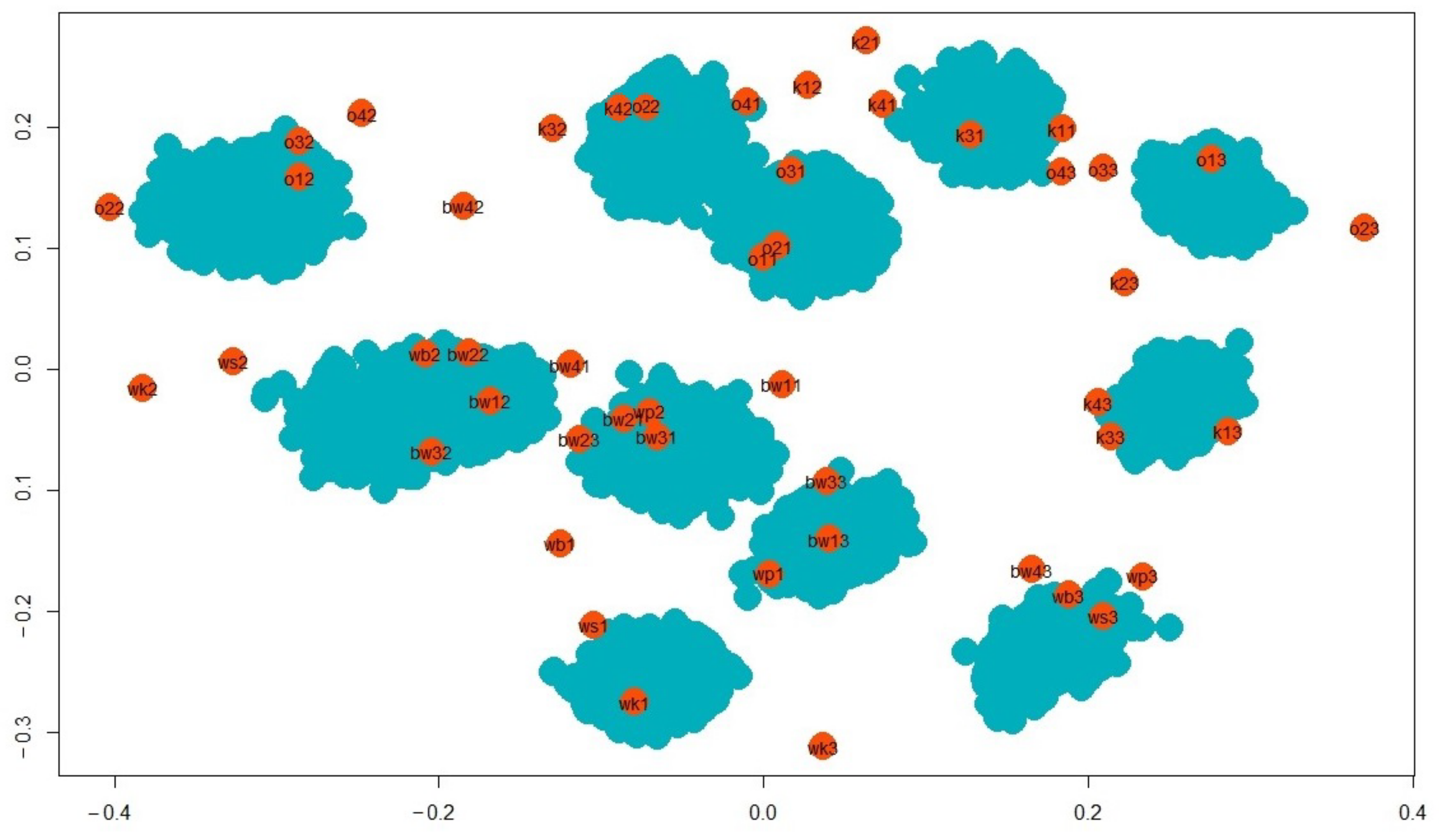
3.1. β Diversity
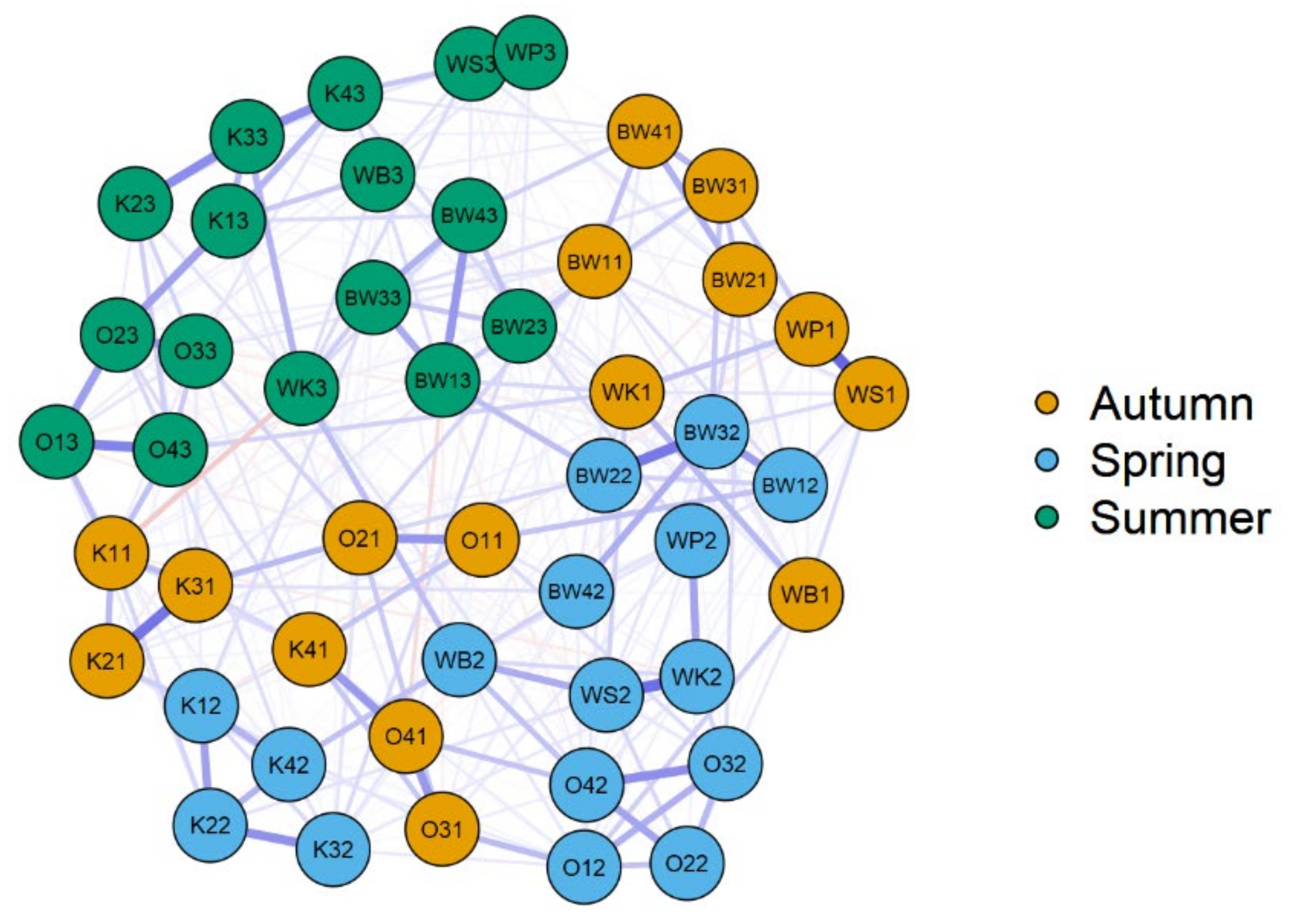
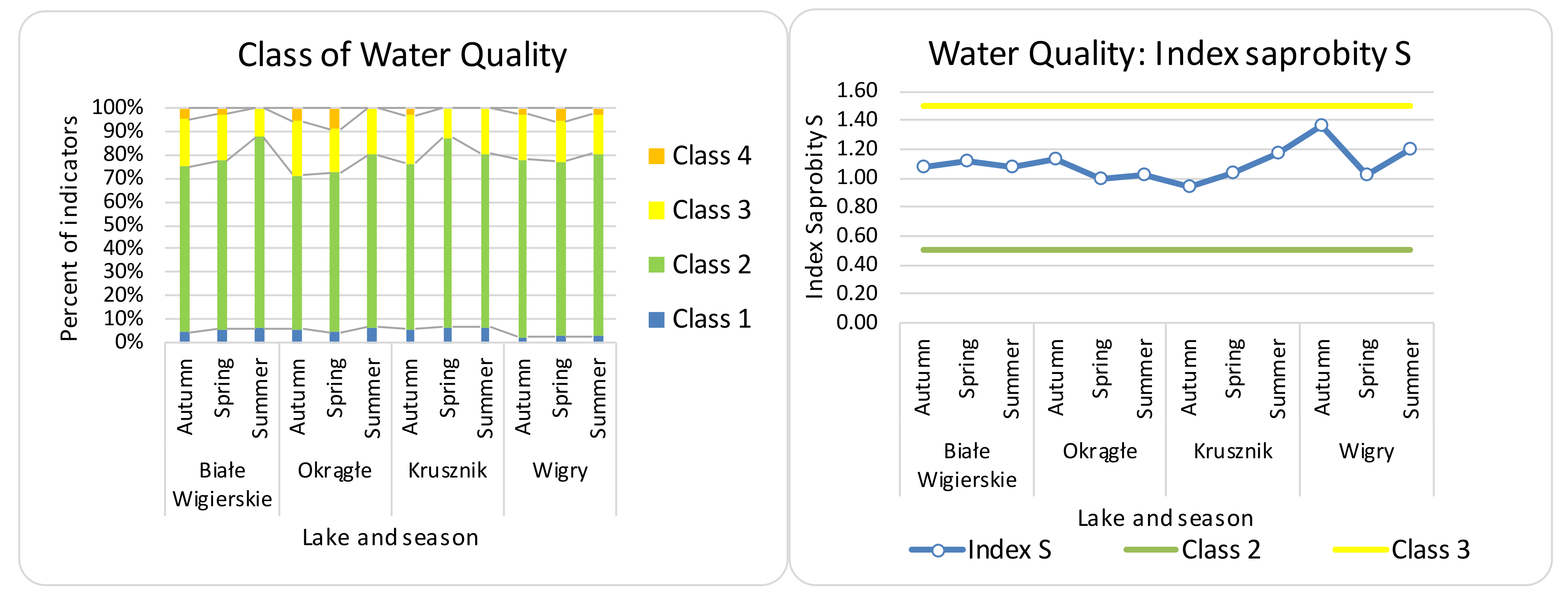
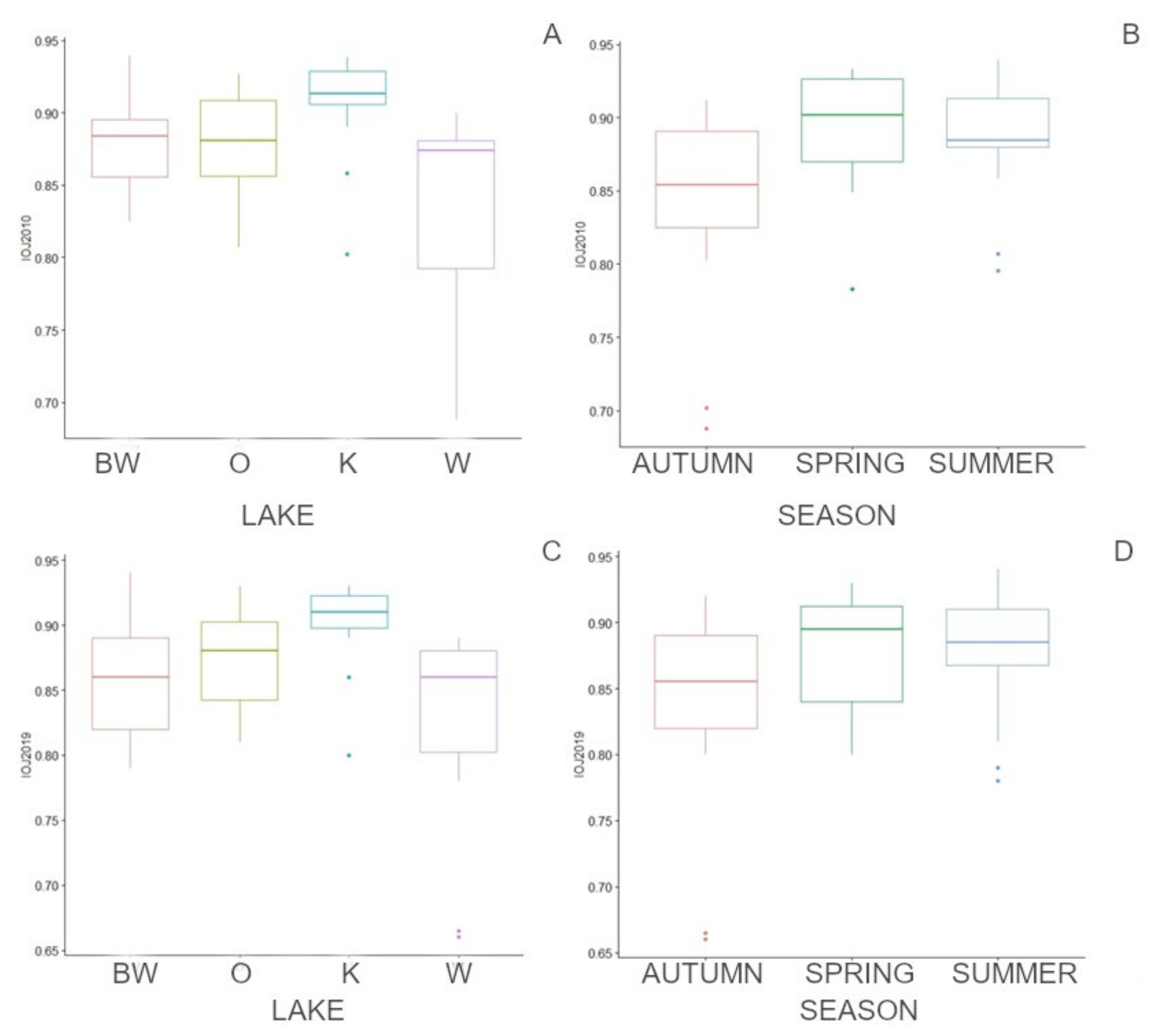
3.2. Seasonal Differences, Differences between Lakes, and Effectiveness of Indices
3.3. Spatial Diversity
4. Discussion
4.1. β Diversity
4.2. Spatial and Seasonal Differences
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, K.; Zhao, W.; Li, M.; Picazo, F.; Soininen, J.; Shen, J.; Zhu, L.; Cheng, X.; Wang, J. Taxonomic Dependency of Beta Diversity Components in Benthic Communities of Bacteria, Diatoms and Chironomids along a Water-Depth Gradient. Sci. Total Environ. 2020, 741, 140462. [Google Scholar] [CrossRef] [PubMed]
- Maloufi, S.; Catherine, A.; Mouillot, D.; Louvard, C.; Couté, A.; Bernard, C.; Troussellier, M. Environmental Heterogeneity among Lakes Promotes Hyper β-Diversity across Phytoplankton Communities. Freshw. Biol. 2016, 61, 633–645. [Google Scholar] [CrossRef]
- Szabó, B.; Lengyel, E.; Padisák, J.; Stenger-Kovács, C. Benthic Diatom Metacommunity across Small Freshwater Lakes: Driving Mechanisms, β-Diversity and Ecological Uniqueness. Hydrobiologia 2019, 828, 183–198. [Google Scholar] [CrossRef]
- Baselga, A.; Orme, C.D.L. Betapart: An R Package for the Study of Beta Diversity. Methods Ecol. Evol. 2012, 3, 808–812. [Google Scholar] [CrossRef]
- Baselga, A. Partitioning the Turnover and Nestedness Components of Beta Diversity: Partitioning Beta Diversity. Glob. Ecol. Biogeogr. 2010, 19, 134–143. [Google Scholar] [CrossRef]
- Legendre, P.; De Cáceres, M. Beta Diversity as the Variance of Community Data: Dissimilarity Coefficients and Partitioning. Ecol. Lett. 2013, 16, 951–963. [Google Scholar] [CrossRef]
- Specziár, A.; Árva, D.; Tóth, M.; Móra, A.; Schmera, D.; Várbíró, G.; Erős, T. Environmental and Spatial Drivers of Beta Diversity Components of Chironomid Metacommunities in Contrasting Freshwater Systems. Hydrobiologia 2018, 819, 123–143. [Google Scholar] [CrossRef] [Green Version]
- Legendre, P. Interpreting the Replacement and Richness Difference Components of Beta Diversity: Replacement and Richness Difference Components. Glob. Ecol. Biogeogr. 2014, 23, 1324–1334. [Google Scholar] [CrossRef]
- Nõges, P.; Poikane, S.; Cardoso, A.C.; van de Bund, W. Water Framework Directive the Way to Water Ecosystems Sustainability in Europe. LakeLine 2006, 21, 36–43. [Google Scholar]
- Kelly, M.; Bennion, H.; Burgess, A.; Ellis, J.; Juggins, S.; Guthrie, R.; Jamieson, J.; Adriaenssens, V.; Yallop, M. Uncertainty in Ecological Status Assessments of Lakes and Rivers Using Diatoms. Hydrobiologia 2009, 633, 5–15. [Google Scholar] [CrossRef]
- Dam, H.; Mertens, A.; Sinkeldam, J. A Coded Checklist and Ecological Indicator Values of Freshwater Diatoms from The Netherlands. Neth. J. Aquat. Ecol. 1994, 28, 117–133. [Google Scholar] [CrossRef]
- Hofmann, G.; Werum, M.; Lange-Bertalot, H.; Lange-Bertalot, H. Diatomeen im Süßwasser-Benthos von Mitteleuropa: Bestimmungsflora Kieselalgen für die Ökologische Praxis; über 700 der Häufigsten Arten und Ihre Ökologie; Gantner: Ruggell, Austria, 2011. [Google Scholar]
- Marra, R.C.; Algarte, V.M.; Ludwig, T.A.V.; Padial, A.A. Diatom Diversity at Multiple Scales in Urban Reservoirs in Southern Brazil Reveals the Likely Role of Trophic State. Limnologica 2018, 70, 49–57. [Google Scholar] [CrossRef]
- Cristóbal, G.; Blanco, S.; Bueno, G. (Eds.) Modern Trends in Diatom Identification: Fundamentals and Applications; Developments in Applied Phycology; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Birk, S.; Bonne, W.; Borja, A.; Brucet, S.; Courrat, A.; Poikane, S.; Solimini, A.; van de Bund, W.; Zampoukas, N.; Hering, D. Three Hundred Ways to Assess Europe’s Surface Waters: An Almost Complete Overview of Biological Methods to Implement the Water Framework Directive. Ecol. Indic. 2012, 18, 31–41. [Google Scholar] [CrossRef]
- Kelly, M.; Urbanic, G.; Acs, E.; Bennion, H.; Bertrin, V.; Burgess, A.; Denys, L.; Gottschalk, S.; Kahlert, M.; Karjalainen, S.M.; et al. Comparing Aspirations: Intercalibration of Ecological Status Concepts across European Lakes for Littoral Diatoms. Hydrobiologia 2014, 734, 125–141. [Google Scholar] [CrossRef] [Green Version]
- Poikane, S.; Kelly, M.; Cantonati, M. Benthic Algal Assessment of Ecological Status in European Lakes and Rivers: Challenges and Opportunities. Sci. Total Environ. 2016, 568, 603–613. [Google Scholar] [CrossRef]
- Schaumburg, J.; Schranz, C.; Foerster, J.; Gutowski, A.; Hofmann, G.; Meilinger, P.; Schneider, S.; Schmedtje, U. Ecological Classification of Macrophytes and Phytobenthos for Rivers in Germany According to the Water Framework Directive. Limnologica 2004, 34, 283–301. [Google Scholar] [CrossRef] [Green Version]
- Poikane, S.; Birk, S.; Böhmer, J.; Carvalho, L.; de Hoyos, C.; Gassner, H.; Hellsten, S.; Kelly, M.; Lyche Solheim, A.; Olin, M.; et al. A Hitchhiker’s Guide to European Lake Ecological Assessment and Intercalibration. Ecol. Indic. 2015, 52, 533–544. [Google Scholar] [CrossRef]
- Kelly, M.G.; Chiriac, G.; Soare-Minea, A.; Hamchevici, C.; Juggins, S. Use of Phytobenthos to Evaluate Ecological Status in Lowland Romanian Lakes. Limnologica 2019, 77, 125682. [Google Scholar] [CrossRef]
- Bielczyńska, A. Bioindication on the Basis of Benthic Diatoms: Advantages and Disadvantages of the Polish Phytobenthos Lake Assessment Method (IOJ—The Diatom Index for Lakes)/Bioindykacja Na Podstawie Okrzemek Bentosowych: Mocne i Słabe Strony Polskiej Metody Oceny Jezior Na Podstawie Fitobentosu (IOJ—Indeks Okrzemkowy Jezior). Ochr. Śr. Zasobów Nat. 2015, 26, 48–55. [Google Scholar] [CrossRef] [Green Version]
- Ciecierska, H.; Kolada, A. ESMI: A Macrophyte Index for Assessing the Ecological Status of Lakes. Environ. Monit. Assess. 2014, 186, 5501–5517. [Google Scholar] [CrossRef] [Green Version]
- Wiech, A.K.; Marciniewicz-Mykieta, M.; Toczko, B. Stan Środowiska w Polsce. Raport 2018; Główny Inspektorat Ochrony Środowiska: Warsaw, Poland, 2018.
- Picińska-Fałtynowicz, J.; Błachuta, J. Przewodnik Metodyczny. Zasady Poboru i Opracowania Prób Fitobentosu Okrzemkowego z Rzek i Jezior; GIOŚ: Wrocław, Poland, 2010.
- Zgrundo, A.; Peszek, Ł.; Poradowska, A. Podręcznik Do Monitoringu i Oceny Rzecznych Jednolitych Części Wód Powierzchniowych Na Podstawie Fitobentosu; OceanSense Maciej Fojcik: Gdańsk, Poland, 2018. (In Polish) [Google Scholar]
- King, L.; Clarke, G.; Bennion, H.; Kelly, M.; Yallop, M. Recommendations for Sampling Littoral Diatoms in Lakes for Ecological Status Assessments. J. Appl. Phycol. 2006, 18, 15–25. [Google Scholar] [CrossRef]
- Lodewijks, P.; Brouwers, J.; Van Hooste, H.; Meynaerts, E. Energie-En Klimaatscenario’s Voor de Sectoren Energie En Industrie; MIRA 2009 Wetenschappelijk Rapport; Vlaamse Milieumaatschappij: Mechelen, Belgium, 2009; Available online: https://www.academia.edu/19642138/Energie_en_Klimaatscenario_s_voor_de_sectoren_Energie_en_Industrie (accessed on 1 June 2022).
- Charles, D.F.; Kelly, M.G.; Stevenson, R.J.; Poikane, S.; Theroux, S.; Zgrundo, A.; Cantonati, M. Benthic Algae Assessments in the EU and the US: Striving for Consistency in the Face of Great Ecological Diversity. Ecol. Indic. 2021, 121, 107082. [Google Scholar] [CrossRef]
- Picińska-Fałtynowicz, J.; Soszka, H. Fitobentos. In Ocena Stanu Ekologicznego Wód Zlewni Rzeki Wel. Wytyczne Do Zintegrowanej Oceny Stanu Ekologicznego Rzek i Jezior na Potrzeby Planów Gospodarowania Wodami w Dorzeczu; Wydawnictwo IRŚ: Olsztyn, Poland, 2011. [Google Scholar]
- Gołdyn, R.; Messyasz, B. Ocena Stanu Ekologicznego Jeziora Durowskiego w Roku 2013; Wydział Biologii Uniwersytetu im. Adama Mickiewicza w Poznaniu: Poznań, Poland. 2013. Available online: https://www.wagrowiec.eu/assets/files/dzialy/ochrona_srodowiska/dokumenty-do-pobrania/ocena-stanu/2018-stan-ekologiczny-jeziora-durowskiego.pdf (accessed on 1 June 2022).
- Elias, C.L.; Vieira, N.; Feio, M.J.; Almeida, S.F.P. Can Season Interfere with Diatom Ecological Quality Assessment? Hydrobiologia 2012, 695, 223–232. [Google Scholar] [CrossRef]
- Hassan, G.S. Within versus Between-Lake Variability of Sedimentary Diatoms: The Role of Sampling Effort in Capturing Assemblage Composition in Environmentally Heterogeneous Shallow Lakes. J. Paleolimnol. 2018, 60, 525–541. [Google Scholar] [CrossRef]
- Riato, L.; Leira, M. Heterogeneity of Epiphytic Diatoms in Shallow Lakes: Implications for Lake Monitoring. Ecol. Indic. 2020, 111, 105988. [Google Scholar] [CrossRef]
- Rimet, F.; Bouchez, A.; Montuelle, B. Benthic Diatoms and Phytoplankton to Assess Nutrients in a Large Lake: Complementarity of Their Use in Lake Geneva (France-Switzerland). Ecol. Indic. 2015, 53, 231–239. [Google Scholar] [CrossRef]
- Andrzejczyk, T.; Brzeziecki, B. The Structure and Dynamics of Old-Growth Pinus sylvestris (L.) Stands in the Wigry National Park, North-Eastern Poland. Vegetatio 1995, 117, 81–94. [Google Scholar] [CrossRef]
- Drzymulska, D.; Zieliński, P. Phases and Interruptions in Postglacial Development of Humic Lake Margin (Lake Suchar Wielki, NE Poland). Limnol. Rev. 2014, 14, 13–20. [Google Scholar] [CrossRef] [Green Version]
- Górniak, A. Current Climatic Conditions of Lake Regions in Poland and Impacts on Their Functioning. In Polish River Basins and Lakes—Part I.; Korzeniewska, E., Harnisz, M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 86, pp. 1–25. [Google Scholar] [CrossRef]
- Nowicka, B.; Nadolna, A. Shorezone Functionality Index—Lake Charzykowskie Case Study. In Natural and Athropogenic Transformation of Lakes, Proceedings of the International Limnological Conference, Łagów Lubuski, Poland, 19–21 September 2012; Institute of Meteorology and Water Management: Poznań, Poland, 2012. [Google Scholar]
- Lange-Bertalot, H.; Hofmann, G.; Werum, M.; Cantonati, M.; Kelly, M. Freshwater Benthic Diatoms of Central Europe: Over 800 Common Species Used in Ecological Assessment; English edition with updated taxonomy and added species; Koeltz Botanical Books: Schmitten-Oberreifenberg, Germany, 2017. [Google Scholar]
- Wojtal, A.Z.; Ector, L.; Van de Vijver, B.; Morales, E.A.; Blanco, S.; Piatek, J.; Smieja, A. The Achnanthidium Minutissimum Complex (Bacillariophyceae) in Southern Poland. Algological Stud. 2011, 136–137, 211–238. [Google Scholar] [CrossRef]
- Lange-Bertalot, H.; Ulrich, S. Contributions to the Taxonomy of Needle-Shaped Fragilaria and Ulnaria Species. Lauterbornia 2014, 78, 1–73. [Google Scholar]
- Van de Vijver, B. Analysis of the Type Material of Navicula Brachysira Brébisson with the Description of Brachysira Sandrae, a New Raphid Diatom (Bacillariophyceae) from Iles Kerguelen (TAAF, Sub-Antarctica, Southern Indian Ocean). Phytotaxa 2014, 184, 139. [Google Scholar] [CrossRef]
- Delgado, C.; Novais, M.H.; Blanco, S.; de Almeida, S.F. Examination and Comparison of Fragilaria Candidagilae sp. nov. with Type Material of Fragilaria Recapitellata, F. Capucina, F. Perminuta, F. Intermedia and F. Neointermedia (Fragilariales, Bacillariophyceae). Phytotaxa 2015, 231, 1. [Google Scholar] [CrossRef]
- Legendre, P.; Borcard, D.; Peres-Neto, P.R. Analyzing Beta Diversity: Partitioning the Spatial Variation of Community Composition Data. Ecol. Monogr. 2005, 75, 435–450. [Google Scholar] [CrossRef]
- Lichstein, J. Multiple regression on distance matrices: A multivariate spatial analysis tool. Plant Ecol. 2006, 188, 117–131. [Google Scholar] [CrossRef]
- Biau, G.; Scornet, E. A Random Forest Guided Tour. TEST 2016, 25, 197–227. [Google Scholar] [CrossRef] [Green Version]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation Importance: A Corrected Feature Importance Measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Ramírez, J.; Ávila-Villanueva, M.; Fernández-Blázquez, M. Selecting the Most Important Self-Assessed Features for Predicting Conversion to Mild Cognitive Impairment with Random Forest and Permutation-Based Methods. Sci. Rep. 2020, 10, 20630. [Google Scholar] [CrossRef]
- Van den Wollenberg, A. Redundancy Analysis an Alternative for Canonical Correlation Analysis. Psychometrika 1977, 42, 207–219. [Google Scholar] [CrossRef]
- Vilmi, A.; Karjalainen, S.M.; Landeiro, V.L.; Heino, J. Freshwater Diatoms as Environmental Indicators: Evaluating the Effects of Eutrophication Using Species Morphology and Biological Indices. Environ. Monit. Assess. 2015, 187, 243. [Google Scholar] [CrossRef]
- Heggen, M.P.; Birks, H.H.; Heiri, O.; Grytnes, J.-A.; Birks, H.J.B. Are Fossil Assemblages in a Single Sediment Core from a Small Lake Representative of Total Deposition of Mite, Chironomid, and Plant Macrofossil Remains? J. Paleolimnol. 2012, 48, 669–691. [Google Scholar] [CrossRef]
- Kenkel, N.; Orloci, L. Applying Metric and Nonmetric Multidimensional Scaling to Ecological Studies: Some New Results. Ecology 1986, 67, 919–928. [Google Scholar] [CrossRef]
- Beals, E. Bray-Curtis Ordination: An Effective Strategy for Analysis of Multivariate Ecological Data. In Advances in Ecological Research; Academic Press: Cambridge, MA, USA, 1984; pp. 1–55. [Google Scholar] [CrossRef]
- Anderson, M. Permutational Multivariate Analysis of Variance (PERMANOVA); Balakrishnan, N., Colton, T., Everitt, B., Piegorsch, W., Ruggeri, F., Teugels, J.L., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2017; pp. 1–15. [Google Scholar] [CrossRef]
- Anderson, M. Distance-Based Tests for Homogeneity of Multivariate Dispersions. Biometrics 2005, 62, 245–253. [Google Scholar] [CrossRef] [PubMed]
- Love, J.; Selker, R.; Marsman, M.; Jamil, T.; Dropmann, D.; Verhagen, J.; Ly, A.; Gronau, Q.F.; Smíra, M.; Epskamp, S.; et al. JASP: Graphical Statistical Software for Common Statistical Designs. J. Stat. Soft. 2019, 88, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Krupa, E.; Barinova, S.; Romanova, S.; Aubakirova, M.; Ainabaeva, N. Planktonic Invertebrates in the Assessment of Long-Term Change in Water Quality of the Sorbulak Wastewater Disposal System (Kazakhstan). Water 2020, 12, 3409. [Google Scholar] [CrossRef]
- Dufrêne, M.; Legendre, P. Species assemblages and indicator species: The need for a flexible asymmetrical approach. Ecol. Monogr. 1997, 67, 345–366. [Google Scholar] [CrossRef]
- Zuur, A.; Ieno, E.; Smith, G. Principal coordinate analysis and non-metric multidimensional scaling. In Analysing Ecological Data; Statistics for Biology and Health; Springer Science: New York, NY, USA, 2007; pp. 259–264. [Google Scholar] [CrossRef]
- Kelly, M.G. Use of Similarity Measures for Quality Control of Benthic Diatom Samples. Water Res. 2001, 35, 2784–2788. [Google Scholar] [CrossRef]
- Soininen, J. A Quantitative Analysis of Species Sorting across Organisms and Ecosystems. Ecology 2014, 95, 3284–3292. [Google Scholar] [CrossRef]
- Epele, L.B.; Brand, C.; Miserendino, M.L. Ecological Drivers of Alpha and Beta Diversity of Freshwater Invertebrates in Arid and Semiarid Patagonia (Argentina). Sci. Total Environ. 2019, 678, 62–73. [Google Scholar] [CrossRef]
- Bennion, H.; Sayer, C.D.; Tibby, J.; Carrick, H.J. Diatoms as Indicators of Environmental Change in Shallow Lakes. In The Diatoms: Applications for the Environmental and Earth Sciences; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Prygiel, J.; Carpentier, P.; Almeida, S.; Coste, M.; Druart, J.-C.; Ector, L.; Guillard, D.; Honoré, M.-A.; Iserentant, R.; Ledeganck, P.; et al. Determination of the biological diatom index (IBD NF T 90–354): Results of an intercomparison exercise. J. Appl. Phycol. 2002, 14, 27–39. [Google Scholar] [CrossRef]
- Marzin, A.; Archaimbault, V.; Belliard, J.; Chauvin, C.; Delmas, F.; Pont, D. Ecological Assessment of Running Waters: Do Macrophytes, Macroinvertebrates, Diatoms and Fish Show Similar Responses to Human Pressures? Ecol. Indic. 2012, 23, 56–65. [Google Scholar] [CrossRef]
- Blanco, S.L.; Ector, L.; Bécares, E. Epiphytic Diatoms as Water Quality Indicators in Spanish Shallow Lakes. Vie Milieu 2004, 54, 71–80. [Google Scholar]
- Szczepocka, E.; Żelazna-Wieczorek, J.; Nowicka-Krawczyk, P. Critical Approach to Diatom-Based Bioassessment of the Regulated Sections of Urban Flowing Water Ecosystems. Ecol. Indic. 2019, 104, 259–267. [Google Scholar] [CrossRef]
- Cantonati, M.; Angeli, N.; Virtanen, L.; Wojtal, A.Z.; Gabrieli, J.; Falasco, E.; Lavoie, I.; Morin, S.; Marchetto, A.; Fortin, C.; et al. Achnanthidium Minutissimum (Bacillariophyta) Valve Deformities as Indicators of Metal Enrichment in Diverse Widely-Distributed Freshwater Habitats. Sci. Total Environ. 2014, 475, 201–215. [Google Scholar] [CrossRef] [PubMed]
- Kelly, M. The Semiotics of Slime: Visual Representation of Phytobenthos as an Aid to Understanding Ecological Status. Freshw. Sci. 2012, 5, 105–119. [Google Scholar] [CrossRef]
- Eliasz-Kowalska, M.; Wojtal, A.Z. Limnological Characteristics and Diatom Dominants in Lakes of Northeastern Poland. Diversity 2020, 12, 374. [Google Scholar] [CrossRef]
- Stenger-Kovács, C.; Hajnal, É.; Lengyel, E.; Buczkó, K.; Padisák, J. A Test of Traditional Diversity Measures and Taxonomic Distinctness Indices on Benthic Diatoms of Soda Pans in the Carpathian Basin. Ecol. Indic. 2016, 64, 1–8. [Google Scholar] [CrossRef]
- Besse-Lototskaya, A.; Verdonschot, P.F.M.; Coste, M.; Van de Vijver, B. Evaluation of European Diatom Trophic Indices. Ecol. Indic. 2011, 11, 456–467. [Google Scholar] [CrossRef]
- Poulíčková, A.; Letáková, M.; Hašler, P.; Cox, E.; Duchoslav, M. Species Complexes within Epiphytic Diatoms and Their Relevance for the Bioindication of Trophic Status. Sci. Total Environ. 2017, 599–600, 820–833. [Google Scholar] [CrossRef]
- Poikane, S.; Zohary, T.; Cantonati, M. Assessing the Ecological Effects of Hydromorphological Pressures on European Lakes. Inland Waters 2020, 10, 241–255. [Google Scholar] [CrossRef]
- Kelly, M. Data Rich, Information Poor? Phytobenthos Assessment and the Water Framework Directive. Eur. J. Phycol. 2013, 48, 437–450. [Google Scholar] [CrossRef]
- Krztoń, W.; Kosiba, J. Variations in Zooplankton Functional Groups Density in Freshwater Ecosystems Exposed to Cyanobacterial Blooms. Sci. Total Environ. 2020, 730, 139044. [Google Scholar] [CrossRef] [PubMed]
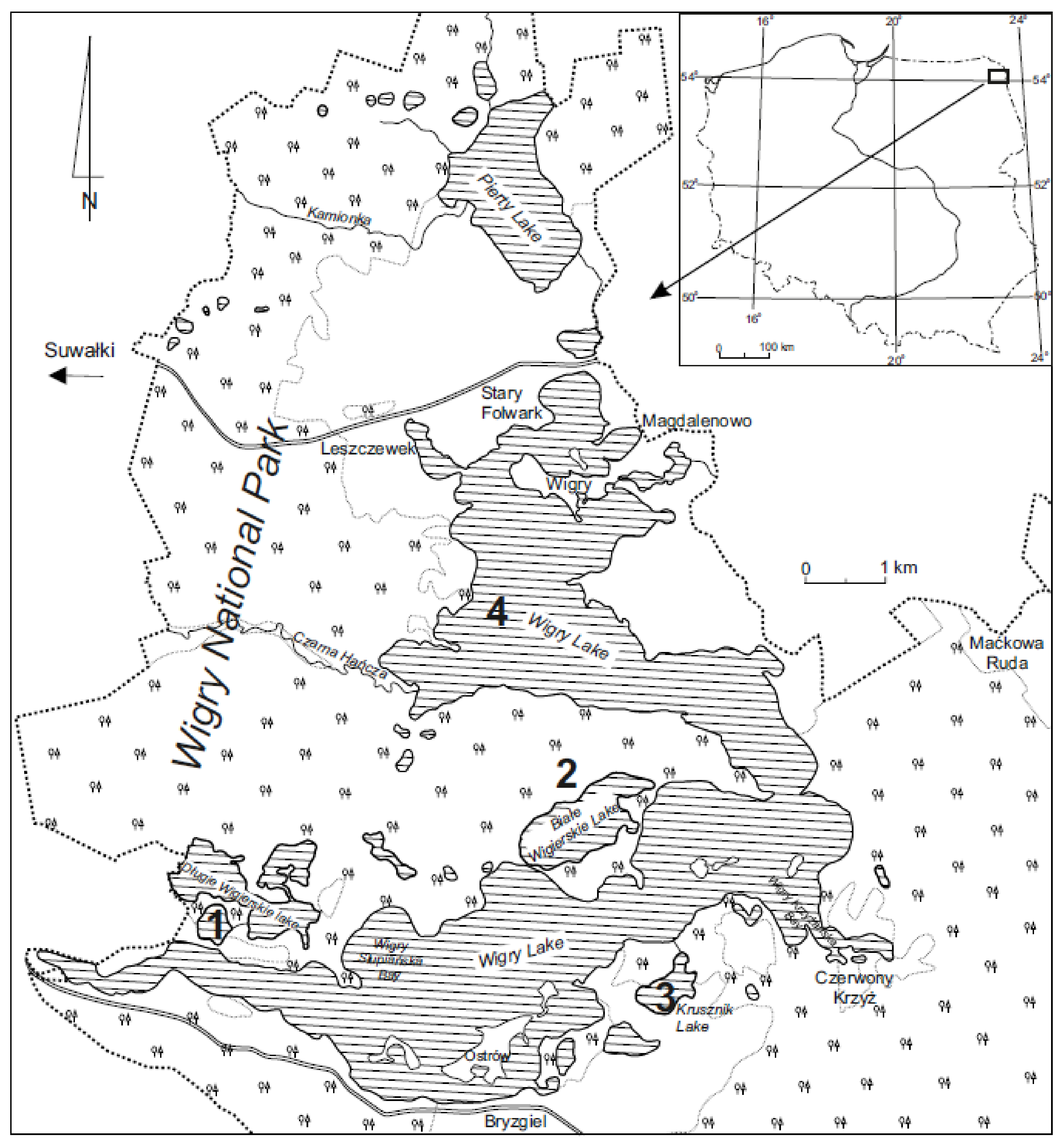
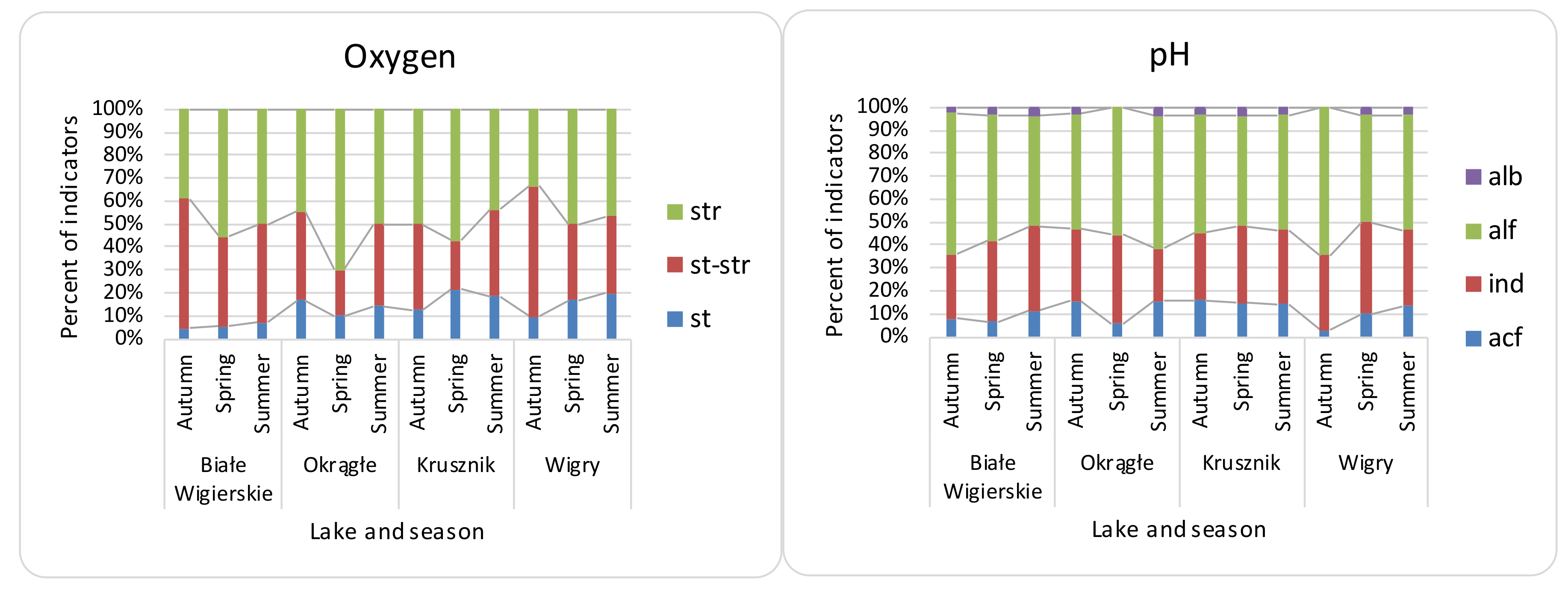
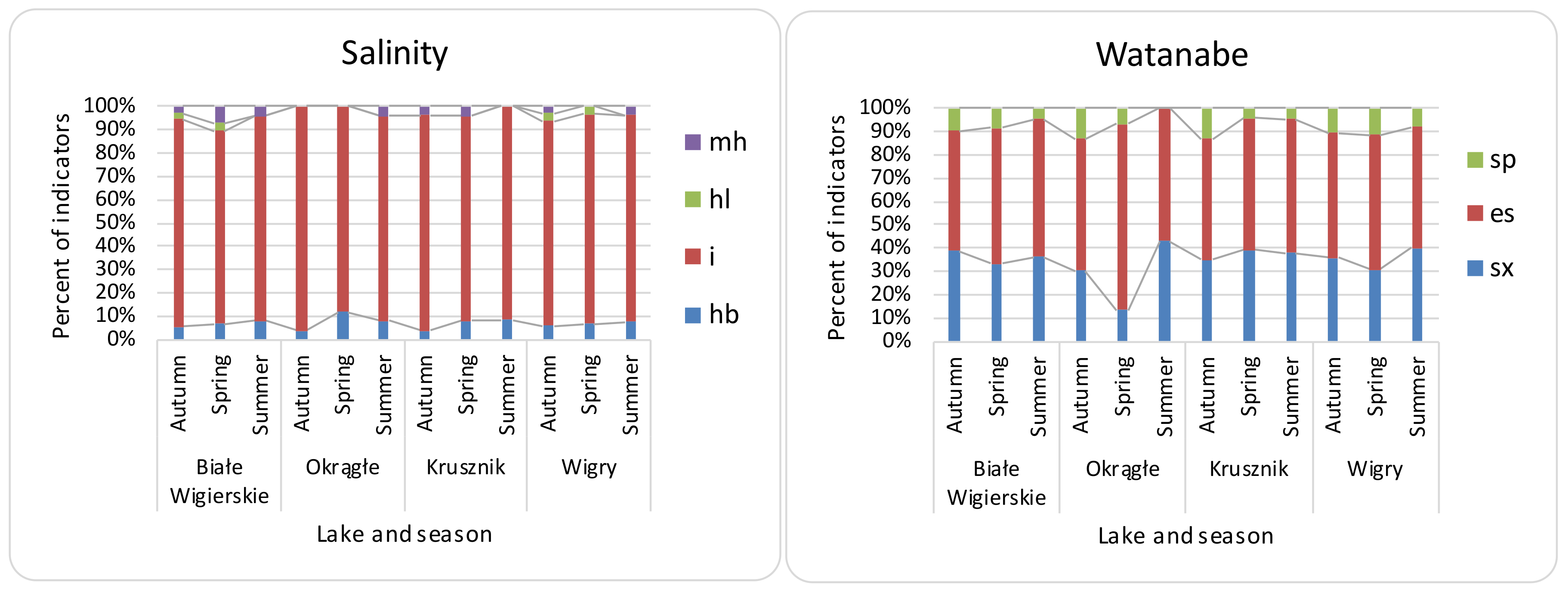
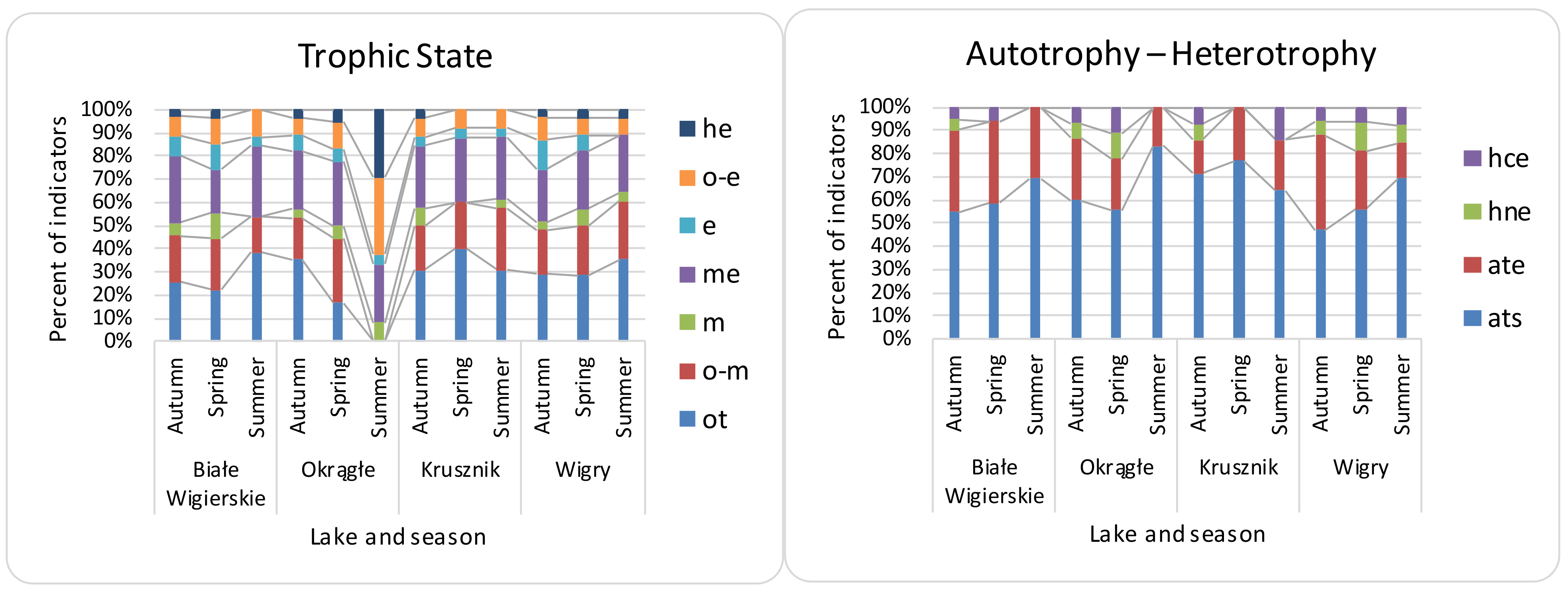
| Name of Lake | Lake Area (ha) | Max. Depth (m) | Coastline Length (m) | Direct Catchment (ha) | Catchment (ha) |
|---|---|---|---|---|---|
| 1. Okrągłe (O) | 13.7 | 13 | 1459 | 28.5 | 906.8 |
| 2. Białe Wigierskie (BW) | 99.9 | 34 | 5117 | 329.1 | 329.1 |
| 3. Krusznik (K) | 26.7 | 18 | 2643 | 70.7 | 70.7 |
| 4. Wigry (W) | 2163.3 | 73 | 63,920 | 5159.8 | 45,293.1 |
| Lakes | Cl− | CO32− | SO42− | NO3− | NH4+ | Mg2+ | PO43− | Ca2+ | pH | Conductivity |
|---|---|---|---|---|---|---|---|---|---|---|
| (mg/L) | (µS/cm) | |||||||||
| O | 4.10–9.96 | 103.52–144.61 | 12.21–28.56 | 0.03–0.22 | 0.036–0.23 | 9.17–16.17 | 0.000–0.003 | 34.85–73.46 | 7.31–8.26 | 231–361 |
| BW | 2.70–2.78 | 73.39–94.93 | 5.92–6.34 | 0.00–0.02 | 0.01–0.13 | 5.53–6.96 | 0.000–0.005 | 25.05–38.07 | 7.28–8.44 | 161–174 |
| K | 4.46–10.21 | 127.44–129.29 | 12.33–27.23 | 0.22–0.24 | 0.036–0.23 | 8.63–13.85 | 0.002–0.001 | 35.87–57.07 | 7.29–8.33 | 251–327 |
| WK | 16.31–17.06 | 129.32–147.83 | 21.68–23.47 | 0.01–0.09 | 0.012–0.12 | 13.09–16.07 | 0.000–0.005 | 42.05–67.50 | 7.55–8.25 | 349–374 |
| WS | 15.82–16.50 | 119.93–155.12 | 20.61–22.39 | 0.01–0.05 | 0.01–0.12 | 12.96–17.14 | 0.000–0.001 | 40.93–67.94 | 7.26–8.41 | 339–378 |
| WP | 16.18–17.02 | 130.66–141.17 | 20.56–22.31 | 0.01–0.03 | 0.20–1.26 | 13.16–16.67 | 0.001–0.001 | 39.77–61.53 | 7.65–8.26 | 334–370 |
| WB | 15.31–17.02 | 129.92–150.38 | 20.64–22.36 | 0.02–0.07 | 0.00–0.20 | 13.11–16.78 | 0.001–0.006 | 42.51–67.38 | 7.51–8.21 | 352–372 |
| Analysis | LCBD Total | LCBD Turnover | LCBD Nestedness | Beta Sørensen Total | Beta Sørensen Turnover | Beta Sørensen Nestedness | |
|---|---|---|---|---|---|---|---|
| Function | |||||||
| 1. Redundancy analysis | Model variance constrained | 0.3763 | 0.4172 | 0.2580 | 1.056 | 0.3421 | 0.716 |
| Model variance uncontrained | 4.6237 | 4.5828 | 4.742 | 3.944 | 4.6579 | 4.284 | |
| Model p | 0.011 * | 0.006 ** | 0.048 * | 0.001 ** | 0.017 * | 0.001 ** | |
| Axis p | 0.008 ** | 0.006 ** | 0.048 * | 0.002 ** | 0.012 * | 0.002 ** | |
| 2. Variation partitioning | Adj R2SO42− | 0.013 | 0.01842 | −0.02015 | 0.16979 | −0.02171 | 0.33897 |
| Adj R2NO3− | 0.00721 | −0.01534 | 0.09121 | 0.45749 | 0.13798 | 0.20454 | |
| Adj R2PO43− | 0.04678 | 0.03172 | 0.01942 | 0.00153 | −0.02019 | 0.00510 | |
| Adj R2NH4+ | −0.01761 | −0.01066 | −0.01324 | 0.04875 | 0.03053 | −0.01343 | |
| 3. Multiple regression on distance matrices | p SO42− | - | - | - | - | - | - |
| p NO3− | 0.001 ** | 0.001 ** | - | 0.004 ** | 0.020 * | - | |
| p Ca2+ | - | - | - | 0.001 ** | 0.001 ** | ||
| p Cl− | 0.001 ** | - | |||||
| p PO43− | 0.032 * | 0.018 * | - | - | - | - | |
| R2 | 0.1085 | 0.1124 | Not significant | 0.2041 | 0.05953 | 0.1297 |
| Analysis | LCBD Total | LCBD Turnover | LCBD Nestedness | Beta Sørensen Total | Beta Sørensen Turnover | Beta Sørensen Nestedness | |
|---|---|---|---|---|---|---|---|
| 1. Random forest—best parameters | Bootstrap | True | True | True | True | True | True |
| Max depth | 80 | 110 | 50 | 30 | 80 | 80 | |
| Max features | 3 | Sqrt | 3 | 2 | 2 | 2 | |
| Min samples leaf | 3 | 2 | 2 | 2 | 1 | 1 | |
| Min samples split | 5 | 2 | 2 | 4 | 4 | 4 | |
| N estimators | 600 | 400 | 200 | 100 | 200 | 200 | |
| OOB score | True | True | True | True | True | True | |
| 2. Random forest feature importance (rfpimp) | SO42− | 0.305 | 0.232 | 0.128 | 0.419 | 0.241 | 0.140 |
| NO3− | 0.266 | 0.201 | 0.122 | 0.229 | 0.236 | 0.293 | |
| Ca2+ | 0.130 | 0.146 | 0.562 | 0.403 | 0.176 | 0.400 | |
| Cl− | 0.210 | 0.278 | 0.121 | 0.079 | 0.212 | 0.150 | |
| NH4+ | 0.067 | 0.097 | 0.189 | 0.195 | 0.125 | 0.167 | |
| PO43− | 0.083 | 0.106 | 0.083 | 0.062 | 0.104 | 0.098 | |
| R2 | 0.83 | 0.85 | 0.89 | 0.88 | 0.82 | 0.81 | |
| 3. Random forest feature importance (eli5) | SO42− | 0.299 | 0.241 | 0.129 | 0.409 | 0.251 | 0.123 |
| NO3− | 0.236 | 0.193 | 0.135 | 0.245 | 0.263 | 0.284 | |
| Ca2+ | 0.132 | 0.159 | 0.536 | 0.351 | 0.169 | 0.371 | |
| Cl− | 0.210 | 0.320 | 0.147 | 0.0756 | 0.223 | 0.166 | |
| NH4+ | 0.071 | 0.104 | 0.191 | 0.160 | 0.143 | 0.167 | |
| PO43− | 0.098 | 0.148 | 0.096 | 0.055 | 0.100 | 0.91 | |
| OOB score | 0.52 | 0.42 | 0.55 | 0.44 | 0.31 | 0.28 | |
| 4. Linear model (single values) | p SO42− | 0.0020 ** | 0.000811 *** | - | 0.0311 * | - | 0.00000005 *** |
| p NO3− | 0.000549 *** | 0.002330 ** | 0.0204 * | 0.00000126 *** | 0.00541 ** | 0.00000126 *** | |
| p Ca2+ | 0.000284 *** | 0.000240 *** | - | - | - | 0.0000852 *** | |
| p Cl− | - | - | - | - | - | - | |
| p PO43− | - | - | - | - | - | - | |
| p NH4+ | 0.0399 * | 0.044987 * | - | - | - | 0.0123 * | |
| Adj R2 | 0.26 | 0.257 | 0.0921 | 0.4992 | 0.138 | 0.597 |
| Lakes | Taxon 1 | Indicator Value | p | Taxon 2 | Indicator Value | p | Taxon 3 | Indicator Value | p |
|---|---|---|---|---|---|---|---|---|---|
| Nitzschia palea | 0.31 | 0.025 | - | - | - | - | - | - |
| Gomphonema procerum | 0.52 | 0.001 | Encyonema ventricosum | 0.46 | 0.002 | Nitzschia lacuum | 0.39 | 0.001 |
| Brachysira neoexilis | 0.45 | 0.001 | Brachysira procera | 0.44 | 0.03 | Eunotia arcubus | 0.43 | 0.004 |
| Cymbella excisa | 0.65 | 0.001 | Fragilaria subconstricta | 0.51 | 0.002 | Cocconeis placentula | 0.41 | 0.006 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eliasz-Kowalska, M.; Wojtal, A.Z.; Barinova, S. Influence of Selected Environmental Factors on Diatom β Diversity (Bacillariophyta) and the Value of Diatom Indices and Sampling Issues. Water 2022, 14, 2315. https://doi.org/10.3390/w14152315
Eliasz-Kowalska M, Wojtal AZ, Barinova S. Influence of Selected Environmental Factors on Diatom β Diversity (Bacillariophyta) and the Value of Diatom Indices and Sampling Issues. Water. 2022; 14(15):2315. https://doi.org/10.3390/w14152315
Chicago/Turabian StyleEliasz-Kowalska, Monika, Agata Z. Wojtal, and Sophia Barinova. 2022. "Influence of Selected Environmental Factors on Diatom β Diversity (Bacillariophyta) and the Value of Diatom Indices and Sampling Issues" Water 14, no. 15: 2315. https://doi.org/10.3390/w14152315








