Research on Influence of Rotation Center Eccentricity on Radial Force of Single-Blade Centrifugal Pump
Abstract
:1. Introduction
2. Numerical Calculations
2.1. Calculate Model
2.2. Meshing
2.3. Turbulence Model and Boundary Conditions
3. Experimental Verification
3.1. External Characteristic Verification
3.2. Pressure Distribution
4. Results and Analysis of Numerical Calculation
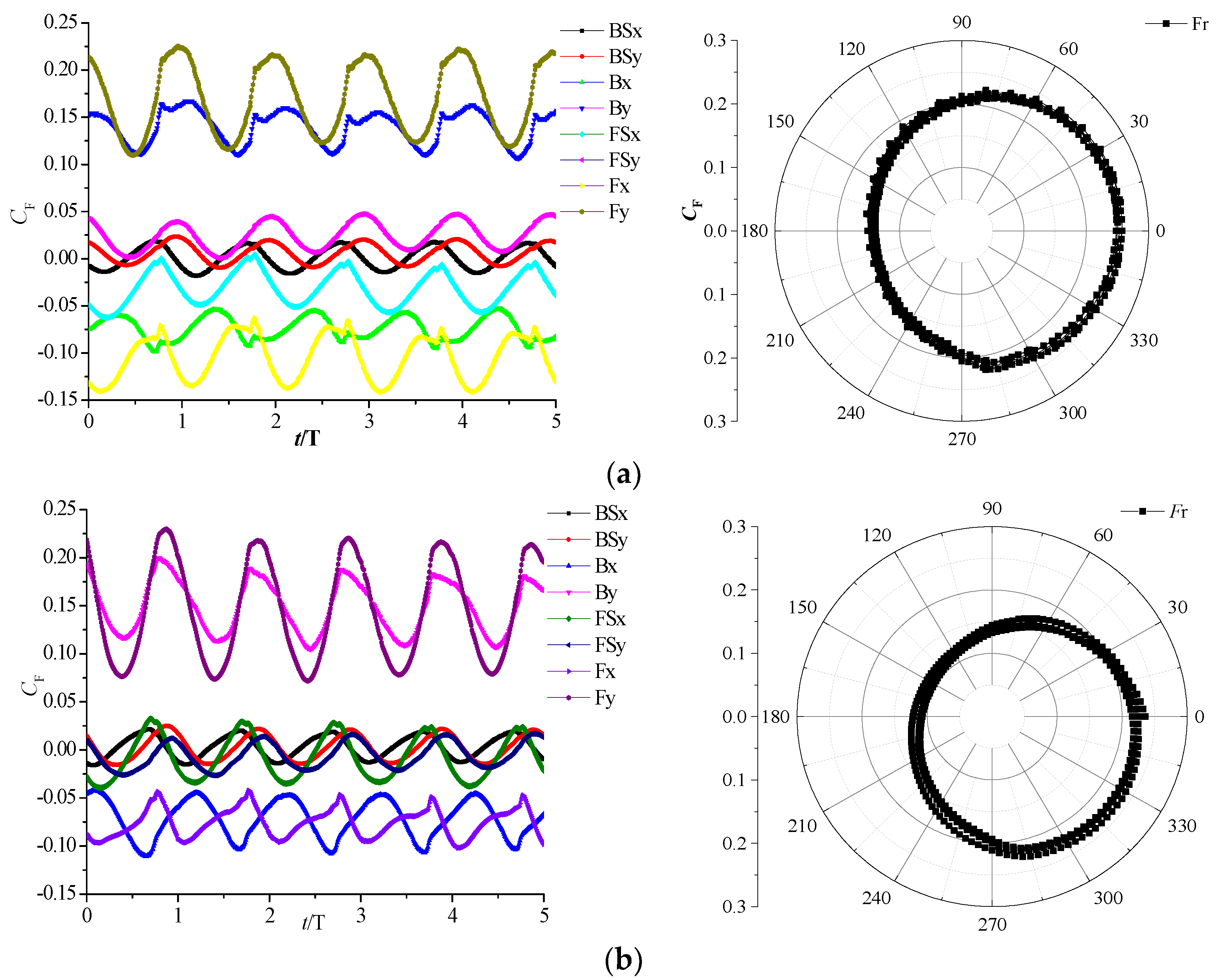
4.1. Influence of Impeller Eccentricity on Radial Force
4.2. Balance Radial Force through Impeller Eccentricity
5. Conclusions
- (1)
- Compared with the case without eccentricity, when the eccentricity coordinates of the impeller are (1,0) and (0,−1), the radial force on the impeller is reduced by 10.8% and 8.1%, respectively, which means the offset of the impeller center to the x-positive direction and y-negative direction can effectively reduce the radial force.
- (2)
- The hydraulically induced radial force of the impeller fluctuates periodically with the impeller rotation. The radial force varies with the impeller rotation, the curve being a distorted circle deviating from the center, and the radial force increases when the center of the impeller is close to the volute tongue.
- (3)
- The mean time of radial force on the impeller decreases after eccentricity (2,−2) under different conditions. It decreases by 17% under designed conditions 1.0 Qd, 12.5% under large flow conditions 1.4 Qd, and 6% under small flow conditions 0.6 Qd, which means the way is feasible.
Author Contributions
Funding
Conflicts of Interest
References
- Hirschberger, M.; Kuhlmann, J.; Benra, F.K. Designing high-power sewage water pumps. World Pumps 2009, 2009, 20–25. [Google Scholar] [CrossRef]
- Nishi, Y.; Fujiwara, R.; Fukutomi, J. Design method for single-blade centrifugal pump impeller. J. Fluid Sci. Technol. 2009, 4, 786–800. [Google Scholar] [CrossRef] [Green Version]
- Aoki, M. Instantaneous interblade pressure distributions and fluctuating radial thrust in a single-blade centrifugal pump. Bull. JSME 1984, 27, 2413–2420. [Google Scholar] [CrossRef]
- Nishi, Y.; Fukutomi, J. Effect of Blade Outlet Angle on Unsteady Hydrodynamic Force of Closed-Type Centrifugal Pump with Single Blade. Int. J. Rotating Mach. 2014, 2014, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Meng, D.; Jiang, T.; Deng, H.; Hou, G. Numerical Simulation Research on Radial Force of Centrifugal Pump with Guide Vanes. Shock. Vib. 2021, 2021, 6638123. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R. Influence of guide vanes on the flow fields and performance of axial pump under unsteady flow conditions: Numerical study. J. Mech. Eng. Sci. 2020, 14, 6570–6593. [Google Scholar] [CrossRef]
- Cui, B.; Li, J.; Zhang, C.; Zhang, Y. Analysis of Radial Force and Vibration Energy in a Centrifugal Pump. Math. Probl. Eng. 2020, 2020, 6080942. [Google Scholar] [CrossRef]
- Cui, B.; Li, X.; Rao, K.; Jia, X.; Nie, X. Analysis of unsteady radial forces of multistage centrifugal pump with double volute. Eng. Comput. 2018, 35, 1500–1511. [Google Scholar] [CrossRef]
- Jiang, W.; Li, G.; Liu, P.F.; Fu, L. Numerical investigation of influence of the clocking effect on the unsteady pressure fluctuations and radial forces in the centrifugal pump with vaned diffuser. Int. Commun. Heat Mass Transfer. 2016, 71, 164–171. [Google Scholar] [CrossRef]
- Cao, W.D.; Yao, L.J.; Liu, B.; Zhang, Y.N. The influence of impeller eccentricity on centrifugal pump. Adv. Mech. Eng. 2017, 9, 1687814017722496. [Google Scholar]
- Tan, L.W.; Yang, Y.F.; Shi, W.D.; Chen, C.; Xie, Z.S. Influence of Blade Wrap Angle on the Hydrodynamic Radial Force of Single Blade Centrifugal Pump. Appl. Sci. 2021, 11, 9052. [Google Scholar] [CrossRef]
- Chen, J.F.; Shi, W.D.; Zhang, D.S. Influence of blade inlet angle on the performance of a single blade centrifugal pump. Eng. Appl. Comput. Fluid Mech. 2021, 15, 462–475. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R. Analysis of the Effect of Various Impeller Blade Angles on Characteristic of the Axial Pump with Pressure Fluctuations Based on Time- and Frequency-Domain Investigations. Iran. J. Sci. Technol. Trans. Mech. Eng. 2021, 45, 441–459. [Google Scholar] [CrossRef]
- Tan, L.; Shi, W.; Zhang, D.; Wang, C.; Zhou, L.; Mahmoud, E. Numerical and experimental investigations on the hydrodynamic radial force of single-channel pumps. J. Mech. Sci. Technol. 2018, 32, 4571–4581. [Google Scholar] [CrossRef]
- Zhou, R.; Yang, J.; Liu, H.L.; Dong, L. Effect of Volute Geometry on Radial Force Characteristics of Centrifugal Pump during Startup. J. Appl. Fluid Mech. 2022, 15, 25–36. [Google Scholar]
- Yuan, Y.; Yuan, S.Q.; Tang, L.D. Numerical Investigation on the Mechanism of Double-Volute Balancing Radial Hydraulic Force on the Centrifugal Pump. Processes 2019, 7, 689. [Google Scholar] [CrossRef] [Green Version]
- Hao, Y.; Tan, L. Symmetrical and unsymmetrical tip clearances on cavitation performance and radial force of a mixed flow pump as turbine at pump mode. Renew. Energy 2018, 127, 368–376. [Google Scholar] [CrossRef]
- Jia, X.; Yuan, S.; Zhu, Z.; Cui, B. Numerical study on instantaneous radial force of a centrifugal pump for different working conditions. Eng. Comput. 2020, 37, 458–480. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R. Investigation of the influence of various numbers of impeller blades on internal flow field analysis and the pressure pulsation of an axial pump based on transient flow behaviour. Heat Transfer. 2020, 49, 2000–2024. [Google Scholar] [CrossRef]
- Xiaoqing, C.; Ri, Z.; Yongtao, H.; Dan-Qing, Y. Optimization Design of Deep—Well Centrifugal Pump based on CFX Orthogonal Test. Fluid Mach. 2015, 43, 22–25, (In Chinese with English abstract). [Google Scholar]
- Lang, T.; Shi, W.D.; Chen, K.Q.; Li, W.; Cheng, C. Research on the Flow Field and Abrasion Characteristics in Sewage Pump with Pre-mixing Device. Fluid Machinery 2015, 43, 29–33, (In Chinese with English abstract). [Google Scholar]
- ANSYS CFX Tutorials 14.5; ANSYS, Inc.: Canonsburg, PA, USA, 2012.
- Benenra, F.K.; Dohmen, H.J.; Schneider, O. Calculation of hydrodynamic forces and flow-induced vibrations of centrifugal sewage water pumps. Fluids Eng. Div. Summer Meet. 2003, 36975, 603–608. [Google Scholar]
- González, J.; Parrondo, J.; Santolaria, C.; Blanco, E. Steady and unsteady radial forces for a centrifugal pump with impeller to tongue gap variation. J. Fluids Eng. 2006, 128, 454–462. [Google Scholar] [CrossRef]
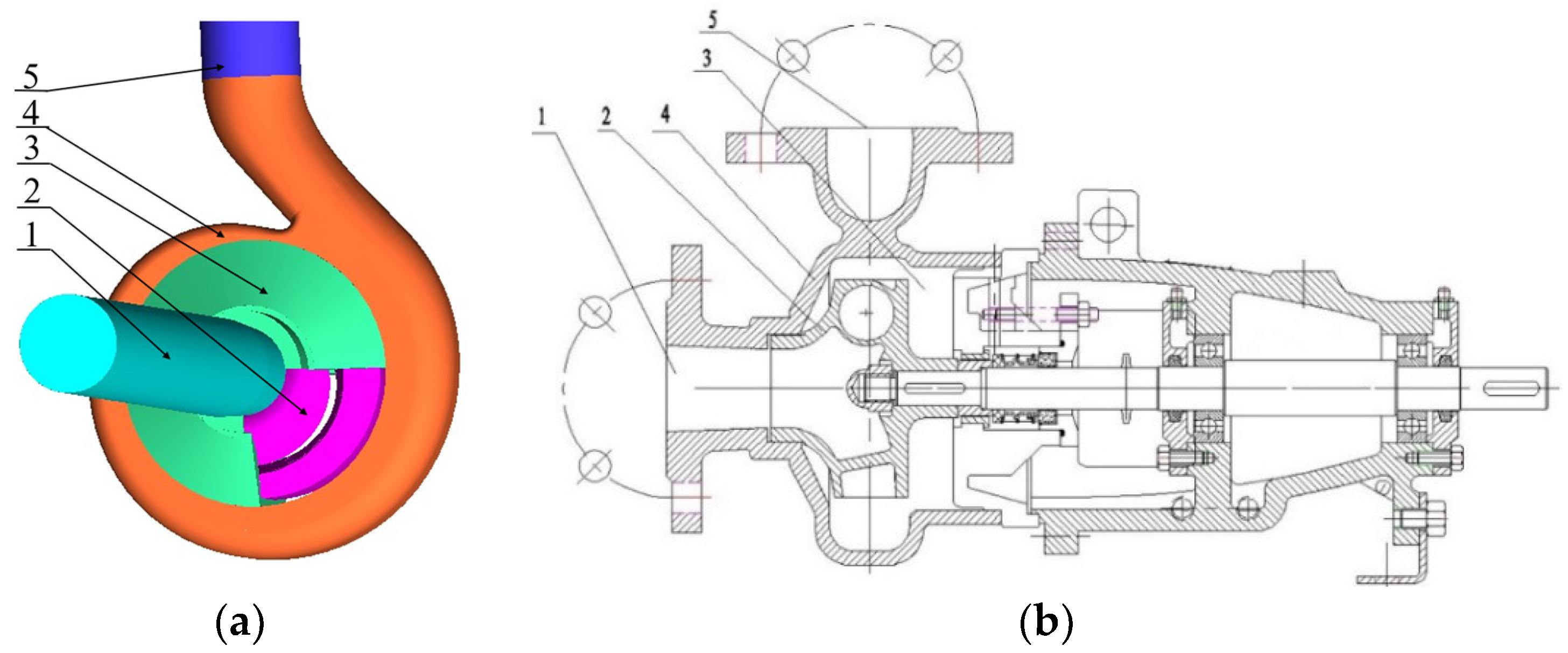













| Grid number | 618,866 | 1,162,332 | 1,457,264 | 2,727,422 | 2,899,675 |
| Head (m) | 12.38 | 12.35 | 12.18 | 12.20 | 12.19 |
| Model a | Model b | Model c | Model d | Model e | Non-Eccentricity | |
|---|---|---|---|---|---|---|
| Fx | −0.0799 | −0.0953 | −0.0920 | −0.0755 | −0.0823 | −0.1047 |
| Fy | 0.1779 | 0.1720 | 0.1573 | 0.1631 | 0.1728 | 0.1702 |
| Fr | 0.1963 | 0.1988 | 0.1846 | 0.1812 | 0.1929 | 0.2008 |
| 0.6 Qd | Non-Eccentricity 0.6 Qd | 1.0 Qd | Non-Eccentricity 1.0 Qd | 1.4 Qd | Non-Eccentricity 1.4 Qd | |
|---|---|---|---|---|---|---|
| Fx | −0.0801 | −0.1241 | −0.0759 | −0.1047 | −0.0738 | −0.0833 |
| Fy | 0.1784 | 0.1662 | 0.1452 | 0.1702 | 0.1505 | 0.1788 |
| Fr | 0.1961 | 0.2078 | 0.1664 | 0.2008 | 0.1747 | 0.1997 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Tan, L.; Shi, W.; Chen, C.; Francis, E.M. Research on Influence of Rotation Center Eccentricity on Radial Force of Single-Blade Centrifugal Pump. Water 2022, 14, 2252. https://doi.org/10.3390/w14142252
Wang C, Tan L, Shi W, Chen C, Francis EM. Research on Influence of Rotation Center Eccentricity on Radial Force of Single-Blade Centrifugal Pump. Water. 2022; 14(14):2252. https://doi.org/10.3390/w14142252
Chicago/Turabian StyleWang, Chuanlong, Linwei Tan, Weidong Shi, Cheng Chen, and Egbo Munachi Francis. 2022. "Research on Influence of Rotation Center Eccentricity on Radial Force of Single-Blade Centrifugal Pump" Water 14, no. 14: 2252. https://doi.org/10.3390/w14142252






